Assessment of plant diversity index in degraded desert grassland using UAV hyperspectral multimodal data and Encoder-CNN

Abstract

The biodiversity function of the desert steppe ecosystem faces many challenges under the pressure of climate change and human activities. Accurate and efficient assessment of plant diversity is critical for guiding desert steppe restoration efforts. However, desert steppe vegetation has sparse leaves and sparse distribution. It is difficult to accurately distinguish micro-vegetation types based on a single spectrum, vegetation index or texture feature, and the resolution of satellite remote sensing cannot meet the needs of high-precision diversity assessment. To this end, this study proposed a novel method for assessing plant diversity index in degraded desert grassland based on multimodal UAV hyperspectral data and Encoder-CNN. Through experiments on different modal feature combinations, spatial spectra, vegetation indices and texture features were targeted and fused. Channel Attention Fusion (CAF) was introduced into Encoder to achieve cross-layer “soft” residual fusion, the Encoder and CNN models were fused to construct a global-local co-expression structure, and finally the quantitative calculation of the plant diversity index at the pixel level was realized. The results show that the vegetation types determined by the fusion of multimodal data and deep learning are consistent with the existing species, dominant species and sub-dominant species of the actual community, and the calculated diversity index results are also consistent with the actual situation. The use of multimodal data combining spatial spectral features with index features, combined with the Encode-CNN model, can provide the most accurate information on community composition. The overall accuracy of sparse vegetation classification can reach 90.01%, and the average accuracy can reach 85.23%, which is better than single mode or traditional 3DCNN, VIT models. This study demonstrates the application potential of UAV hyperspectral multimodal technology and deep learning in the assessment of desert steppe plant diversity, providing important technical support for ecological protection and conservation.

Introduction

Desert steppe is widely regarded as the last barrier preventing the transition of grasslands into deserts. It not only provides detailed data that reveal the current state and changing trends of vegetation diversity in grassland ecosystems can be provided¹, but also the root causes and main driving forces of degradation can be timely identified². However, with escalating human exploitation and the compounded effects of adverse environmental factors, grasslands are facing a serious threat of degradation, which weakens their ability to support biodiversity, ecosystem services, and the well-being of human beings^3,4. As global demand for livestock products rises alongside growing concerns over ecological sustainability, the issue of grassland degradation has received considerable attention from scientific community⁵. A critical step toward the restoration and rehabilitation of ecosystems is the rigorous scientific assessment of grassland biodiversity⁶, which is essential in addressing the growing problem of grassland degradation.

In the assessment of grassland biodiversity, the structural composition and characteristics of vegetation communities serve as critical indicators of plant diversity^7,8,9. The precision of these indicators directly influences the scientific rigor and applicability of the assessment outcomes¹⁰. However, its short stature, sparse distribution, small and narrow leaves and staggered growth make it difficult to distinguish and present a major challenge to data collection and analysis. Traditional field survey methods are labor-intensive, costly, and inefficient for covering extensive grassland areas¹¹. Remote sensing, as a pivotal tool for vegetation mapping and environmental surveillance^12,13,14, has emerged as an essential method for monitoring grassland ecosystems^15,16. Viable plant community research encompasses vegetation disease phenotyping^17,18, classification mapping^19,20, crop monitoring^21,22,23, crop yield forecasting²⁴, and parameter reliability estimation^{25,26,27,28,29} etc. Although these methods have been widely applied with success in forested areas and urban environments, most of the existing methods are applicable to the classification of vegetation with large areas and easily distinguishable boundaries, and the classification of sparse vegetation for desert steppe with narrow foliage and short plants still needs to be explored to a large extent, and requires high-resolution low-altitude remote sensing to acquire the data, coupled with representative and abundant features to achieve high-precision classification.

Compared to satellite and airborne remote sensing, Unmanned Aerial Vehicles (UAVs) offer distinct advantages, including rapid deployment, low operational costs, high temporal resolution particularly excelling in spatiotemporal resolution and mobility. Consequently, they are swiftly emerging as a widely adopted technological tool^{30,31,32,33,34,35}. An increasing number of researchers are employing Unmanned Aerial Vehicle (UAV) remote sensing systems, combined with advanced technologies and methodologies, to conduct regional plant studies^{36,37,38,39,40}. UAVs are capable of capturing diverse forms of remote sensing data, with hyperspectral imagery being widely used due to its ability to record continuous narrow spectral bands, effectively characterize structural and textural features, and invert extensive spectral information^41,42,43,44. Vegetation in desert grasslands with leaf widths less than 2 cm and scattered and sparse vegetation distribution, and the resolution of satellite remote sensing is more than meters. UAV hyperspectral remote sensing has high resolution and can obtain surface vegetation spectral data with high spatial and spectral resolution, presenting new opportunities for extracting and analyzing sparse, small-scale vegetation information in desert steppe ecosystems.

With the widespread application of hyperspectral remote sensing technology in vegetation monitoring, deep learning (DL) has become a core means to improve classification accuracy and efficiency due to its significant advantages in complex feature extraction and pattern recognition^45,46,47,48. However, traditional methods that rely only on a single spectrum or index or texture feature^49,50,51, often fail to capture representative discriminant information. Therefore, many scholars have begun to integrate multiple index features (such as normalized vegetation index (NDVI), green normalized difference vegetation index (GNDVI), difference vegetation index (DVI), ratio vegetation index (RVI), soil-adjusted vegetation index (SAVI), enhanced vegetation index (EVI), etc^52,53,54., and texture features^55,56, to collaboratively mine multimodal data and provide richer and more interpretable feature expressions^57,58,59. For example, Han et al. developed a deep learning network named residual-in-residual dense block (RRDB) NDVI reconstruction net (RDNRnet) to obtain optimal land cover type⁶⁰. Qian et al. constructed a stacking ensemble model to perform wetland classification achieving the highest overall accuracy of 94.33%⁶¹. However, these methods still have difficulty in taking into account multimodal information, cross-layer multi-scale features, and deep interaction between global and local details in scenes with narrow leaves and sparse plants in desert steppes. To this end, this study proposes an Encoder-CNN framework of fusion algorithms: through three mechanisms: feature adaptation for specific application scenarios, Innovations in the feature extraction and fusion module, and Global-local feature co-expression, spatial spectrum, index and texture features are specifically fused to achieve more accurate recognition of sparse small-scale vegetation.

The specific objectives are as follows: (1) To explore the contribution of three types of modal data, namely spatial-spectral, index and texture features, in the classification of desert steppe vegetation, and quantitatively compare the classification accuracy of single-modal and multi-modal combinations to determine which feature combination is most suitable for characterizing sparse vegetation types; (2) To construct a model combining Encoder and CNN, comprehensively learn local and global features, and introduce the CAF module to enhance feature dependence. Compare the model with conventional 3DCNN and VIT to verify the effectiveness of global-local feature collaborative learning; (3) To combine modal data and classification results, calculate the pixel-level vegetation diversity index, analyze and judge the vegetation community structure, and evaluate the feasibility of the proposed method in plant diversity evaluation. This study aims to explore the value of UAV hyperspectral and multimodal data in assessing the plant diversity of sparse vegetation in desert grasslands.

Materials and methods

Data acquisition

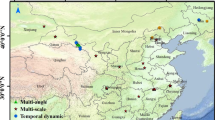
As depicted in Fig. 1a, the area studied is located in a natural pasture within Shengli Team, Ertok Banner, Erdos City, Inner Mongolia Autonomous Region. Situated in the western Ordos Plateau, the area represents a typical desert steppe (Fig. 1a). The region is approximately 1,300 m above sea level, characterized by ample sunshine, an average annual precipitation of 250 mm, and an average annual evaporation of 2,300 mm. In the natural pasture, a 45 m × 45 m test area was selected, with the vertices A, B, C, and D marked clockwise using red, green, blue, and yellow flags, respectively. 20 vegetation plots, each measuring 1 m × 1 m, were selected as illustrated in Fig. 1b.

Fig. 1

The map illustrates the location of the study region (a) and the distribution of vegetation plots (b). Experimental equipment including hyperspectral UAV, DJI UAV, anemometer, geographic spectrometer, vegetation plots, record books (c). Experimental output data including hyperspectral image, RGB image, vegetation photos, field-based records, spectral curve (d). 10 ground objects in the test area (e). Figure 1a generated by the authors using ArcMap version 10.8 (Esri, https://www.esri.com).

During the vegetation fruiting period, from July to September, 2023, field data collection occurred (Fig. 1c). First, the average reflectance values of the features in the test area were used as standard spectral data using a Lisen Optics iSpecField geo-spectrometer at 1.0 m above ground. Next, the vegetation condition of the 20 plots was recorded using a ground survey method to identify 10 different objects, include: 0) bare soil, (1) stone garlic, (2) Artemisia capillaris, (3) thistles, (4) Setaria viridis, (5) Caragana korshinskii, (6) dead Artemisia capillaris (referred to as dead grass), (7) Artemisia salina, (8) Corylus aurantium, and (9) colorful flags (hereafter labelled as T0-T9) (Fig. 1e). Vegetation data recorded included species, number, cover, height, canopy diameter/scrub diameter, and site photographs. Then, Hyperspectral image (hereafter labeled as H²) was collected using Optosky ATH9010W UAV equipped with a hyperspectral imager over the designated test area. The UAV operated at an altitude of 20 m, with a speed of 2 m/s, sideward overlap of 50%. The images exhibited a spatial resolution of 1.3 cm, spectral range from 392.59 nm to 1017.81 nm (480 distinct wavelengths). During the flight, there was less than 2% cloud cover, wind speeds of less than 5.4 m per second and temperatures of approximately 36° C. Finally, a DJI M300 drone photographed the study area from an altitude of 25 m at a speed of 10 m per second (Fig. 1 d).

Test setup

To ensure the quality of the data, we used a multi-stage quality assurance process during the field data collection and labelling process: A 1 × 1 m standard sample plot was established at each observation point and accurately subdivided into 10 × 10 sub-grids using white lines to improve the accuracy of spatial records. All species identifications were determined by two university teachers with an associate professor or above degree. After the sub-grid survey, each tagger is required to take high-resolution ground photographs from directly above the sample plot for auxiliary verification. If there is a disagreement between the two independent tagging results, the team will review them one by one at a central discussion meeting based on the actual photographs taken until a consensus is reached to ensure the consistency and scientific of the final tagging data.

The H² images were preprocessed by ENVI, including radiometric correction, cropping, stitching and geometric correction, and finally the 45 m×45 m H² images were obtained. Using the vegetation spectral curve collected by the geographic spectrometer as a reference standard, and cross-referencing with field images, regions of interest were labeled in ENVI on a pixel-by-pixel basis, yielding 25,600 pixel labels for each plot (Table S.1), with a total of 20 plots (hereafter referred to as P1-P20, Fig. S.1). During model training, the samples were partitioned into a training set and a validation set with a ratio of 3:7, ensuring minimal sample size while encompassing all categories. Each batch consisted of 32 samples, and the model was trained over a total of 100 epochs, utilizing a learning rate of 0.0005. Data was randomly shuffled at the start of each epoch.

The experiment was completed in the following environment:

GPU: NVIDIA GeForce RTX 4060 Ti, 32.0 GB

CPU: Intel i7-12700 K, 12 cores, 3.60 GHz

Memory: 32GB, D4 3200 MHz

Software environment: Python 3.9, PyTorch 2.1.2

Methods

The RF algorithm was used to rank the importance of wavelengths on a pixel-by-pixel basis and to analyze the relationship between wavelengths and vegetation physiology. Hyperspectral images were reconstructed by selecting the optimal wavelength combinations. The samples were then augmented by cropping, rotation and splicing, pixel mixing, denoising and noise reduction to ensure that each vegetation type was represented by at least 10,000 samples. The classification accuracy of single and combined features was then compared across the three dimensions of spatial-spectral, index and texture features to identify key features suitable for sparse vegetation analysis. Encoder from CAF transformer was used to extract high-level features, which were then fed into the CNN model to achieve highly accurate classification results. Finally, using the classification results and field survey data, the diversity of the vegetation community in the test area was calculated and analyzed using diversity parameter formulas, thus completing the assessment of the plant diversity of the desert steppe (Fig. 2).

Fig. 2

Framework for assessing plant diversity.

Hyperspectral image dimensionality reduction

RF was employed to rank the importance of all spectral bands, optimize wavelength combinations, and analyze the correlation between wavelengths and vegetation physiology. Feature importance evaluation is calculating the average contribution of each wavelength across all trees in the forest. In this study, the Gini index was selected as the evaluation metric for feature importance. For the 20 plots, each H² image contains 25,600 pixels. The importance of 480 wavelengths was calculated for the pixels within each plot, and the overall wavelength importance was derived by averaging the values across all plots. Subsequently, voting was conducted across all plots, and the voting results for the 20 plots were aggregated.

Sample augmentation

In this study, three main methods were used: cropping, mirroring, and rotation; mixed pixels; denoising and adding noise. Mixing pixels means randomly selecting three different image pixels of the same kind P_i, P_j, and P_k and using their linear combination to generate virtual samples with weighted noise.

$${P_{{\text{ijk}}}}={\alpha _i}{P_i}+{\alpha _j}{P_j}+{\alpha _k}{P_k}+{\lambda _n},{\text{ }}0<{\alpha _i},{\alpha _j},{\alpha _k}<1,{\text{ }}{\alpha _i}+{\alpha _j}+{\alpha _k}=1$$

(1)

Where λ_n is the Gaussian noise with mean 0 and variance 0.001.

Denoising were determined through the peak signal-to-noise ratio (PSNR) of the combination of six wavelet basis functions (Daubechies 4-wavelet, Daubechies 6-wavelet, Haar wavelet, Symlets 4-wavelet, Coiflets 1-wavelet, and Biorthogonal 1.3-wavelet) and three decomposition levels (2, 3, and 4). Gaussian noise with a mean of 0 and variances of 0.01 and 0.005 was introduced. With the sample sizes of other vegetation types exceeding tens of thousands, data expansion was primarily conducted on plots 1, 3, 6, 8, 10, and 20, focusing on types 3, 5, 7, 8, and 9 (Table S.2).

Feature selection

Three groups of features from multimodal data were selected: spatial-spectral features, index features, and texture features. All data were derived from the same spectral set of the same H² image. The specific information of features is provided in Table 1. Regarding red-edge vegetation indices, accounting for the periodic fluctuations in growth stages and phenological traits of various vegetation types, the red-edge chlorophyll index (CIre), red-edge normalized difference (NDRE), red-edge normalized difference vegetation index (RNDVI), and red-edge chlorophyll sensitivity index (MTCI) were selected. When integrated with 12 commonly utilized vegetation indices, a total of 16 red-edge vegetation index features were constructed. The texture features were calculated by gray level co-occurrence matrix (GLCM) on Environment for Visualizing Images (ENVI), extracting eight specific features. To ensure a consistent comparison of feature contributions under identical input conditions, the feature count for all three groups was standardized to 128.

Table 1 The specific information of features.

Encoder - CNN model

The proposed model consists of two primary components: a high-order feature extraction module based on an encoder architecture, and a pixel-level classification module leveraging CNNs. The input comprises three types of multi-source feature images with identical spatial resolution: spatial-spectral features, index features, and texture features. Taking the spatial-spectral features as an example, the model first employs the encoder in combination with CAF module to jointly model and extract 128-dimensional high-order feature representation for each pixel. This process reconstructs a high-order feature image to enhance its representational capacity. At this stage, the spectral dimension is transformed from raw reflectance values into high-order feature representations, while the spatial structure is preserved. The high-order feature image is then fed into a classification network integrating both 3D-CNN and 2D-CNN architectures. The 3D-CNN captures local spectral-spatial details, while the 2D-CNN further aggregates contextual spatial information, ultimately enabling precise pixel-level classification (Fig. 3).

Fig. 3

Encoder - CNN model.

The high-order feature extraction module is based on an enhanced Transformer Encoder architecture. It consists of a patch embedding layer, five Encoder blocks, CAF module and a feature transformation layer. The process begins by dividing the image into fixed-size patches and applying positional encoding. The embedding spectrum is formed by mapping the features to the input dimensions through linear layers. The Encoder is composed of five identical layers, each containing two sublayers: the first sublayer incorporates multi-head attention, a normalization layer, and residual connections, while the second sublayer comprises a feedforward fully connected network, a normalization layer, and residual connections. In this case, the multi-head attention mechanism was configured with 4 heads. Each layer uses residual connections and layer normalization to mitigate gradient vanishing and enhance training stability. The CAF is a fusion module centered on two-dimensional convolution. Specifically, it concatenates the outputs of two non-adjacent Encoder blocks along the feature dimension, and then applies a 1 × 2 convolution kernel to perform adaptive fusion. The resulting fused features are used as input to the subsequent encoder block, enabling the interaction and integration of information across different hierarchical levels. Finally, the feature transformation layer maps the Encoder output to the target spectral dimension, producing a high-order feature image with a feature dimension of 128 that preserves the original spatial structure.

Taking the input of Encoder4 as an example, the cross-layer fusion process in the CAF module can be described in the following five steps:

Step 1. Input preparation. Select the outputs ${z^{(l - 2)}}$ of Encoder1 and the outputs ${z^{(l)}}$ of Encoder3 as the fusion targets. Both outputs have a tensor shape of B×P×D, where B denotes the batch size, P represents the number of patches plus one (in this model, a learnable classification token (CLS) is prepended to the input patch sequence, resulting in a sequence length of P + 1), and D indicates the feature dimension;

Step 2. Dimension expansion. Add an extra dimension to both inputs ${z^{(l - 2)}} \in {{\mathbb{R}}^{B \times P \times D}}$and${z^{(l)}} \in {{\mathbb{R}}^{B \times P \times D}}$ by performing an ‘unsqueeze’ operation, changing their shape to B×P×D×1. This prepares the tensors for subsequent concatenation and convolution operations;

Step 3. Feature concatenation. Concatenate the two inputs ${z^{(l)}}$and ${z^{(l - 2)}}$ along the feature dimension (D) to create a fused tensor $x \in {{\mathbb{R}}^{B \times P \times D \times 2}}$ containing the combined feature:

$$x=C{\text{on}}cat\left[ {{z^{(l - 2)}},{z^{(l)}}} \right]$$

(2)

Step 4. Convolution-based fusion. Pass the tensor x into the corresponding 2D convolution module within ‘self.skipcat’. This convolution uses a kernel size of 1 × 2, a stride of (1, 1), and no padding. The operation slides over the last two dimensions, performing a linear weighted fusion of the two concatenated cross-layer features. The convolution kernel weights are trainable parameters. They adaptively adjust to integrate information from the skip connection through learning:

$${{{\hat {z}}}^{(l)}} \leftarrow \omega \left( {\begin{array}{*{20}{c}} {{{\text{z}}^{(l - 2)}}} \\ {{{\text{z}}^{(l)}}} \end{array}} \right)={\omega _1} \times {{\text{z}}^{(l - 2)}}+{\omega _2} \times {{\text{z}}^{(l)}}$$

(3)

Where $\:\omega\:$ represents the network parameter for adaptive learning, $\:{\omega\:}_{1}$ is the weight of ${z^{(l - 2)}}$, $\:{\omega\:}_{2}$ is the weight of ${z^{(l)}}$.

Step 5. Dimension restoration. Finally, apply a ‘squeeze’ operation to ${\widehat {z}^{(l)}}$ remove the redundant dimension and restore the tensor shape to ××. This completes the cross-layer feature fusion process.

The pixel-level classification module based on CNNs mainly consists of 3D convolutional layers and 2D convolutional layers. The 3D-CNN performs local window modelling on the multidimensional feature image via 3D convolution, capturing the correlation between spatial continuity and spectral features. The 2D-CNN further improves the representation of spatial structures to support precise pixel-wise classification. This module combines the strengths of 3D and 2D convolutional structures. By preserving the coupled representation of spatial and feature information, it enhances the model’s ability to distinguish between different land cover classes. As shown in Eq. (4), each element of 3D convolutional kernel is multiplied by the corresponding element of the input data block and subsequently summed. After the bias term is added, the output is generated via the activation function.

$${Y_{xyz}}=f\left( {\sum\nolimits_{{i=0}}^{{m - 1}} {\sum\nolimits_{{j=0}}^{{m - 1}} {\sum\nolimits_{{k=0}}^{{m - 1}} {X\left( {x+i,y+j,z+k} \right) \times {K_{ijk}}+{b_{ij}}} } } } \right)$$

(4)

Here, Y_xyz represents the output value at position (x, y, z), X_xyz denotes the input value at position (x, y, z), K_ijk corresponds to the weight of the convolution kernel at position (i, j, k), m refers to the size of the convolution kernel, b_ij represents the bias term for adjusting the output offset, and f is the activation function.

Assessment of vegetation diversity

Plant diversity was analyzed from three dimensions: species composition, quantitative characteristics, and composite traits. Based on taxonomic data, community members were identified, and fundamental ecological metrics such as abundance, density, cover, frequency, importance value, and dominance were calculated. In addition, widely accepted biodiversity indices such as the Shannon-Wiener index, Simpson index, and evenness were incorporated to enhance the comprehensiveness and scientific rigor of the diversity assessment. A vegetation community classification table was subsequently constructed to systematically characterize community structure and species diversity patterns, providing a sound basis for ecosystem status evaluation and functional analysis.

The formulas of data characteristics, abundance (A), density(Di), coverage(C), and frequency(F), used for these calculations are presented as follows:

$$A=n$$

(5)

$${D_i}=\frac{n}{{{A_S}}}$$

(6)

$$C=\frac{{{A_C}}}{{{A_t}}} \times 100\%$$

(7)

$$F=\frac{{{P_S}}}{{{P_t}}} \times 100\%$$

(8)

Where: n = Total number of individuals of a species; A_s​ = Sampled area or volume; A_t​ = Total area sampled; A_C​ = Area covered by the species; P_s​ = Number of plots where the species is present; P_t​ = Total number of plots sampled.

The relative density (RD), relative coverage (RC), and relative frequency (RF) are presented as follows:

$$RD=\frac{{{D_i}}}{{{D_t}}} \times 100\%$$

(9)

$$RC=\frac{{{C_i}}}{{{C_t}}} \times 100\%$$

(10)

$$RF=\frac{{{F_i}}}{{{F_t}}} \times 100\%$$

(11)

Where: D_i​ = Density of the individual species; D_t​ = Total density of all species in the sampled area; C_i​ = Coverage of the individual species; C_t​ = Total coverage of all species in the sampled area; F_i​ = Frequency of the individual species; F_t​ = Total frequency of all species in the sampled area.

The Shannon-Wiener index (H), Simpson index (D), and evenness (E) calculation formula are as follows:

$$H= - \sum\limits_{{I=1}}^{S} {\left( {{p_i}\ln {p_i}} \right)}$$

(12)

$$D=1 - \left( {\frac{{\sum {n\left( {n - 1} \right)} }}{{N\left( {N - 1} \right)}}} \right)$$

(13)

$$E=\frac{H}{{{H_{\hbox{max} }}}}=\frac{H}{{\ln S}}$$

(14)

Where: S = Number of species in the community; P_i​ = Proportion of ith species to all species; N = Total number of individuals of all species in the population.

Results and discussion

Hyperspectral image dimensionality reduction

H² images are rich in spectral information and redundant, so we use Random Forest (RF) algorithm to reduce dimensionality and determine the final 128 wavelengths by comparing them to the standard spectra acquired by the geo-spectrometer.

Fig. 4

(a) Spectral curves of different ground objects. (b) Voting results produced by the algorithm, where the wavelength importance is greater than 5 votes.

Notes: The feature groups and corresponding wavelengths from Fig. 4(b) are presented in the Table S.3.

The band with yellow background in Fig. 4(a) demonstrates the extraction of 128 significant wavelengths using RF on H² images of 20 plots. Vegetation-dominated images with characteristic wavelengths concentrated at 430–480 nm, 580 nm, 630–690 nm and 760 nm. For example, T6 dead vegetation-dominated images with characteristic wavelengths concentrated at 690 nm and 720 nm, and the T8 Cynanchum otophyllum-dominated image with characteristic wavelengths concentrated at 480 nm and 650 nm. Images dominated by bare soil (e.g. T14 with 70% bare soil) have characteristic wavelengths concentrated at 610 nm and 760 nm.

Table 2 Classification results for different numbers of wavelengths.

In our experiments, we evaluated the effect of different numbers of wavelengths on the results-20, 32, 64, 128, 160, 256 and 480 (Table 2). Classification accuracy progressively improved as the number of features increased, peaking at 90.01% with 128 wavelengths. However, only marginal improvements in accuracy were observed with further increases to 160, 256, and 480 wavelengths, yielding gains of 0.56% (90.57%), 1% (91.01%), and 1.3% (91.31%), respectively. Therefore, 128 wavelengths were selected for the results of the wavelength importance voting for all plots, which match those expressed by the vegetation types and can effectively represent the overall spectral features.

Influence of single and combined features on classification results

To assess the contribution of multimodal data to sparse vegetation classification, this study developed both single and combined feature sets for classification accuracy validation, as presented in Table 3. The results revealed that the combination of spatial-spectral features and index features achieved the highest classification accuracy, reaching 90.01%. In contrast, three feature combinations performed moderately well, affected by redundant and irrelevant features, resulting in a slight decrease in classification accuracy, and too many features can lead to model over-fitting, where the model remembers training data containing noise rather than capturing valid information. Although texture features are able to capture the subtle differences between vegetation and background, the limited information available makes the feature representation weak and the accuracy low because it uses only 16 wavelengths of information. Index features can sensitively capture vegetation changes and effectively reflect vegetation growth and health, and their importance can also be seen in the classification results, so index information is still an important complement to spectral information.

Table 3 Classification results based on feature groups.

Comparative results of different models

This study employed six models for performance comparison. These include the traditional Transformer model (referred to as VIT), the enhanced Transformer model with CAF (referred to as CAF) and a CNN-based model, as well as two advanced models: ResNet-18 and U-Net, along with the proposed Encoder-CNN model. VIT performs global dependency modelling by dividing the input features into patches and applying multiple layers of self-attention. CAF builds on VIT by introducing cross-layer feature interaction to improve multi-scale information representation. The CNN model adopts a hybrid structure combining 3D and 2D convolutions to strengthen local feature learning. ResNet-18 employs residual connections for deep convolutional feature extraction, while U-Net uses an encoder–decoder structure with downsampling to achieve multi-scale feature aggregation. The architecture details and parameter configurations of all models are summarized in Table S.4.

1. Model performance assessment.

The performance metrics employed for evaluation include overall accuracy (OA), average accuracy (AA), kappa coefficient, and confusion matrix, as detailed in Table 4; Fig. 5.

Table 4 Algorithm performance metrics comparison.

Among the six models, Encoder-CNN achieved the best performance, with overall accuracy reaching 90.01% and average accuracy of 85.23%, followed closely by the standard CNN. These results confirm that convolution-based methods are highly effective for hyperspectral classification. This is likely due to their ability to capture local spatial-spectral structures, which are crucial for distinguishing complex vegetation types. By contrast, Transformer-based models performed poorly. The VIT baseline yielded the lowest accuracy, indicating that global attention alone is insufficient for modelling fine-grained spatial variability in scenarios with limited samples. Although the CAF-enhanced Transformer offered moderate improvements via cross-layer fusion, it still lagged behind CNN-based approaches. This suggests that attention mechanisms require deeper integration with local encoding strategies. While ResNet-18 achieved competitive accuracy, its deeper structure resulted in longer training times. U-Net demonstrated lower accuracy and the highest computational cost, which is likely due to redundant upsampling and inefficient feature reuse. In terms of computational efficiency and model complexity, Encoder–CNN achieved a balance between performance and training cost.

Fig. 5

Confusion matrices for various models. (a) VIT Model. (b) CAF Model. (c) CNN Model. (d) ResNet-18. (e) U-Net. (f) Encoder-CNN Model.

Analysis of the confusion matrix revealed that vegetation classes in general were frequently misclassified as bare soil, reflecting the strong influence of background interference. Among these, T2 and T6 exhibited particularly high confusion, which can be attributed to their spectral similarity and the fact that they are variants of the same vegetation type. In contrast, the high misclassification rate observed in T4 is likely due to the limited number of original samples. Although data augmentation was employed, synthetic data may not fully capture the spectral variability of real-world conditions, thereby reducing classification accuracy for underrepresented classes.

2. Vegetation mapping of desert steppe.

The pixel-level desert vegetation map of 20 plots is shown here, due to the large amount of data in the research field (Fig. 6).

Fig. 6

Vegetation mapping of desert steppe. (a) VIT Model. (b) CAF Model. (c) CNN Model. (d) ResNet-18. (e) U-Net. (f) Encoder-CNN Model.

Although the overall classification was effective, the distinction between vegetation and bare soil was unclear in some areas, leading to misclassifications, particularly along the edges of vegetation patches. The VIT found it difficult to capture small or fragmented vegetation patches. For example, the yellow vegetation in P1 and the cyan vegetation in P20 were largely missed, suggesting that it is not very adaptable to fine-scale spatial patterns. The CAF showed modest improvement by incorporating cross-layer spatial information, resulting in better structural continuity, though detailed features remained insufficiently captured. The CNN model performed consistently across vegetation types, but continued to underperform in boundary delineation, particularly in transition zones. ResNet-18 introduced noticeable noise within otherwise homogeneous regions, such as scattered misclassifications in the cyan vegetation of P2 and P19, indicating reduced spatial consistency. U-Net exhibited the weakest performance, with pronounced boundary blurring and misclassification of sparse vegetation. In contrast, the proposed Encoder–CNN model produced the most accurate and spatially coherent classification maps. Despite minor misclassifications along certain edges due to background interference, it significantly outperformed all other models and proved highly effective for mapping sparse vegetation in desert steppe environments.

3. Misclassification analysis of T2 and T6.

In the classification results, we noticed that there was a notable misclassification between the T2 and T6. This phenomenon can be attributed to the fact that T2 and T6 actually represent different physiological states of the same species, corresponding to healthy and partially withered vegetation individuals, respectively. Although this distinction is important in ecological terms, the spectral differences between these states in hyperspectral imagery are relatively subtle, making them difficult to distinguish through spectral signatures alone.

Fig. 7

(a) 128 wavelengths of T2 and T6. (b) 128 key features of T2 and T6.

Figure 7a presents the spectral reflectance curves composed of 128 bands for the two target types. It can be seen from the figure that, the surface reflectance f two types exhibit a high degree of overlap. To further investigate this similarity, we extracted the 128 key features identified by the Encoder for each type and plotted the mean spectral curves (Fig. 7b). The results reveal substantial overlap in the key spectral features: only six features exhibited opposite trends between the two types, while ten displayed similar trends with notable magnitude differences. The remaining features showed minimal variation, which increases the difficulty of subsequent 3DCNN model discrimination. In addition, since the vegetation patches sampled in the field often have mixed physiological states, that is, healthy branches and withered branches may exist in the same bush at the same time, this spatial interlacing is averaged by the camera during the image acquisition stage, further introducing systematic bias. To address this issue, future studies will consider the integration of thermal infrared remote sensing data to enable pre-classification separation of vegetation health status, thereby reducing misclassification.

Pixel-level classification results for sparse vegetation

Figure 8 shows the vegetation classification results for the 20 samples, from which it can be seen that most of the features can be correctly distinguished, but the spectrally similar vegetation is misclassified. The bare ground background interfered with the reflectivity of the image, causing the vegetation in the image to be misclassified.

Fig. 8

(a) shows the vegetation pixel labels for 20 plots, (b) shows the pixel-level classification results for 20 plots.

Table 5 Classification report.

The classification report (Table 5) shows an accuracy of 90.01%, an average prediction accuracy of 85.50%, an average recall of 85.23%, and an F1 score of 85.29%. The spatial resolution and spectral resolution of remote sensing data interact with each other, and the original H² image has a spectral dimension of 480, which has a low spatial resolution, and information such as radiance and video data can be considered to be added later. For desert grassland, the training samples of small vegetation are insufficient, especially in the case of uneven distribution of vegetation species, the training effect is not good. For instance, Setaria viridis had a width of approximately 0.1 cm and a length ranging from 0.1 cm to 3 cm, resulting in a classification accuracy of only 75.98% and a recall rate of 67.56%.

Uncertainty analysis of the model

To assess the robustness of the model under conditions of uncertainty, we employed a Monte Carlo simulation approach. By introducing controlled perturbations to the original input data, we generated multiple realizations of possible model outputs and evaluated the resulting classification error. Specifically, we randomly selected 5 plots, constructed a normal distribution model based on their original spectral data, and used the mean and standard deviation of the pixels as parameters to generate 25,600 simulated pixels for each plot. The simulation process was repeated five times to enhance statistical reliability. All simulated data were subsequently fed into the pre-trained Encoder-3DCNN, and classification outputs under varying perturbation scenarios were recorded.

Fig. 9

Classification outputs of all simulated data.

As illustrated in Fig. 9, the simulated samples exhibited marked differences in classification probability distributions under perturbed conditions. Among the five samples, P1 has the best simulation classification results, with an average accuracy of approximately 83%. This superior performance is likely attributable to the predominance of dominant vegetation types within P1, which were well-represented in the training dataset and thus facilitated more effective feature learning by the model. In contrast, P3 has the worst simulation results, and its classification accuracy is only 65.79% on average in the five simulations. Further analysis found that P3 contains some vegetation types (such as colorful flags) with very few samples in the training set, which makes the model unable to fully learn its feature expression, resulting in poor simulation results. The remaining three samples achieved relatively stable accuracies around 72%, though misclassification still occurred to some extent, indicating that there is still room for improvement in the model’s response to some boundary samples or mixed patches.

Overall, the simulation results demonstrate that the model exhibits robust classification stability for dominant vegetation types. However, in cases where training data are limited or species exhibit ambiguous spectral characteristics, classification deviations may still occur. Future model improvements should therefore prioritize enhancing the model’s discriminative capacity for rare or underrepresented classes.

Analysis of plant diversity in sparse vegetation

Based on the classification results, the species present in each plot were identified, the pixel count for each species was calculated, and plotted the species-pixel number curve for the same vegetation type across different plots (Fig. 10).

Fig. 10

Species-pixel number curves of the same vegetation type in different plots.

The pixel count for T0, T1, T2, and T6 was relatively high, ranging from 2,000 to 18,000, whereas the pixel counts in T3, T4, T5, T7, T8, and T9 were comparatively lower, ranging from 0 to 1,500. T0 exhibits a high pixel count in each plot, suggesting sparse vegetation and extensive bare soil. The pixel count for T2 and T6 is relatively high, suggesting that Artemisia ordosica dominates the community. The pixel count for T1 ranged from 500 to 5,000, suggesting that Sphenostylis stenocarpa occupies the dominant ecological niche. As can be seen in the localized zoomed-in image, The number of T4 pixels in most of the plots is in the range of 200 to 1300, and Q18 had 2,913 pixels, suggesting that Setaria viridis is subordinate to the dominant species. Nevertheless, it still plays a key role in shaping the community’s structure and influencing environmental regulation. The pixel count for other categories was small and mainly coexisted with the dominant species. Artemisia ordosica, as an indicator species of degradation, accounted for a significant proportion in each plot, indirectly reflecting the intensification of grassland desertification.

Fig. 11

Diversity indicators: abundance, density, coverage, frequency, and relative density, relative coverage, relative frequency.

Figure 11 showed the diversity indicators of ground objects. As illustrated in Fig. 11b, bare soil coverage was the highest at 58.5%, signifying an abundance of exposed soil with sparse vegetation. Figure 11a and c show that, T2 had the highest count, with substantial coverage and frequency, indicating it as the dominant vegetation type. T6 was also present in significant numbers, further affirming the ecological significance of Artemisia ordosica, with some individuals having perished due to climatic conditions. Additionally, T1 exhibited a high count, with 6.1% coverage and a frequency of 0.7, suggesting that Sphenostylis stenocarpa occupies a prominent ecological niche, consisting of medium-sized plants. T4, despite being relatively abundant, had low coverage and a frequency of 0.6, indicating that Setaria officinalis is a small, sparsely distributed species, yet it still exerts some influence on the community. Other vegetation types exhibited low numbers, minimal frequency, and weak adaptability.

Figure 11(d) showed that, T2 had the highest proportion in the community, signifying that Artemisia ordosica is the dominant community-forming species. It efficiently utilizes available resources, stabilizes soil structure, and provides crucial habitats for animals. T6 exhibited high relative frequency but low relative density and cover, suggesting that the growth of Artemisia ordosica is sparse, with frequent die-offs, potentially due to environmental stressors. T1 displayed high relative frequency, with medium relative density and cover, indicating that Sphenostylis stenocarpa is an ecologically significant species, exhibiting both ubiquity and ecological adaptability. Nevertheless, its growth conditions and resource utilization may be restricted, and is classified as dominant species. T4 exhibited high relative density and frequency but low relative cover, suggesting that Setaria officinalis is short yet abundant, with moderate ecological significance, potentially facing competition, and is classified as a sub-dominant species. The remaining species (T3, T5, T7, and T8) were few in number, in a vulnerable state, and are likely to function as companion species.

The diversity indicators of the vegetation communities were compiled, resulting in the vegetation community classification table for 20 plots, as presented in Table S.5. Artemisia ordosica is the predominant plant species in the experimental area. Although some of them have died due to climatic and environmental factors, their diversity index is high and they dominate the competition, thus being classified as a community-forming species. Sphenostylis stenocarpa exhibits rapid growth and fulfills important ecological roles as a nitrogen-fixing species. With high abundance and coverage, it has established itself as a dominant species within the community. Setaria viridis is a small yet abundant species, playing a crucial role in enhancing soil structure and mitigating soil erosion, thus classified as a sub-dominant species.

Fig. 12

Diversity indicators of plot: Shannon-Wiener index, Simpson index, and evenness.

We calculated the Shannon–Wiener index, Simpson index, and species evenness for 20 plots to assess biodiversity and community structure (Fig. 12). The results showed that the Shannon-Wiener index ranged from 0.799 to 1.199, with the majority of plots concentrated between 0.90 and 1.10, indicating that the community has a certain species richness, which is at a moderate level overall. The Simpson index values fell between 0.466 and 0.667, suggesting the presence of dominant or co-dominant species in some plots, which may reduce overall community stability. Species evenness ranged from 0.56 to 0.86, reflecting heterogeneous distribution patterns among plots. Specifically, P2 and P4 exhibited relatively high evenness (~ 0.85), indicating more uniform species abundance, whereas P1 and P10 showed lower evenness (~ 0.57), pointing to a more uneven distribution of species.

Specifically, P2 exhibited the highest Shannon–Wiener index (1.199) and species evenness (0.865), along with a relatively high Simpson index (0.667), indicating that this plot had rich species diversity, even distribution, and a more desirable community structure. In contrast, P15 recorded lower values for both the Shannon index (0.799) and Simpson index (0.497), indicating that the number of species in its community was lower or the distribution among species was uneven, which might be disturbed to a certain extent or the degree of species dominance was higher.

Overall, a positive correlation was observed between the Shannon–Wiener and Simpson indices, indicated that plots with a higher number of species tended to be characterized by a lower distribution of dominance as well. Additionally, the strong alignment between the Shannon index and species evenness (E) indicating that the high diversity values mainly came from rich and evenly distributed communities.

Challenge of cross-regional generalization

The test site of this study is located in Ordos, Inner Mongolia, covering an area of approximately 45 m × 45 m. The dominant species include Artemisia ordosica and Stipa breviflora, with vegetation cover typically below 20%. The soil type is primarily light chestnut calcareous sandy loam, and the climate is semi-arid, with an annual rainfall of around 400 mm^62,63. However, pronounced ecological heterogeneity across different regions is exhibited by desert steppe ecosystems. For example, the typical desert steppe in Xinjiang is dominated by medium-tall grass species such as Stipa klemenzii, Agropyron michnoi, and Cleistogenes squarrosa, and has a higher vegetation cover of 30–50%. The region’s soils are mostly sandy loam or saline-alkali, and it is strongly affected by wind erosion and desertification processes^64,65. By contrast, the desert steppe of the Qinghai Plateau is characterized by sparse vegetation, frequent permafrost in the soil, a fragile ecosystem and harsh climatic conditions, as well as highly seasonal precipitation^66,67. These substantial differences in vegetation composition, soil properties, and disturbance regimes result in distinct spatial-spectral feature distributions across regions. This affects the model’s decision boundaries and generalization performance. Consequently, the high level of accuracy observed at the current test site cannot be extrapolated directly to other desert steppe regions. Furthermore, the dataset’s limited spatial coverage increases the risk of overfitting.

Ecological significance of the study

The restoration of degraded grassland often involves decisions on species selection, restoration prioritization, and restoration methods. Through accurate plant diversity assessment, we can identify the species composition and ecological characteristics of different areas and provide targeted restoration strategies for managers. For example, in more severely degraded areas, we can analyze the growth, coverage, and health of different plant species based on H² data, and use DL models to assess which areas have strong restoration potentials and prioritize them for restoration.

In addition, with long-term ecological monitoring, we can control the dynamic changes of vegetation restoration in a timely manner, so as to adjust the management strategy. For example, data from different seasons or years can help identify key factors in the restoration process (e.g., water, soil, climate, etc.) and optimize restoration strategies based on this information, including artificial rainfall during dry spells, the application of soil amendments to improve nutrient retention, and the selection of stress-tolerant native species suited to projected climatic conditions. Such interventions ensure that restoration strategies remain adaptive and ecologically aligned over time.

In conclusion, the integration of H² data and DL for assessing plant diversity in desert grasslands not only improves the accuracy of plant diversity assessment, but also provides strong technical support for restoration planning in degraded areas.

Conclusion

In this study, we demonstrated a new plant diversity index assessment method, using UAV hyperspectral multimodal data and Encoder-CNN, we efficiently and quantitatively identified regional feature species and quantities, and accurately assessed the degraded desert grassland plant diversity. It was found that among all combinations of multimodal data, the community composition obtained by fusing spatial spectral features and index features was the most accurate, suggesting that the index information can be used as an effective supplement when spectral information is insufficient. In addition, the Encoder-CNN model combines global features with local features to improve the accuracy of sparse vegetation classification. Our study not only explores the potential of multimodal data and deep learning in the analysis of sparse vegetation communities, but also provides a technical support for quantitative evaluate the plant diversity of degraded desert grassland.

Future and prospect

In this study, we developed a classification model for desert steppe vegetation by integrating spectral–spatial information, vegetation indices, and texture features. The model demonstrated promising performance in a representative test area. However, several limitations remain, and future research may expand and refine the framework in the following directions:

First, the current experimental area was selected from the Shengli Team of Ordos City, Inner Mongolia, and although the area is representative in terms of climate, vegetation and ecological disturbances, its spatial coverage is limited. To address this limitation, a feasible multi-site validation plan will be implemented in future work. This plan will cover typical desert steppe regions in Inner Mongolia, Xinjiang and Qinghai. These regions were chosen because of their distinctive differences in vegetation composition, soil types, disturbance intensities and climatic conditions. Multi-source remote sensing data and ground truth measurements will be collected across these sites to create a comprehensive, cross-regional training and testing dataset. This approach will allow the model’s adaptability and generalization across heterogeneous ecological contexts to be evaluated thoroughly. Furthermore, sensitivity analysis will be employed as a key method to evaluate the robustness of the model by examining its performance under different levels of vegetation cover, disturbance and environmental conditions. While the current dataset lacks sufficient ecological gradients for such analyses, future research involving expanded multi-regional and multi-condition data will leverage sensitivity analysis to quantitatively characterize and enhance model generalization and optimization.

Second, for the special climate-induced situation that some branches of the same species are withered and some are healthy, we propose the integration of thermal infrared remote sensing data. With the help of the thermal infrared band information that has significant differences, a pre-classification step will be introduced to separate vegetation health states, thereby substantially improving the model’s discriminatory power.

In addition, we plan to establish a long-term ecological monitoring program to systematically collect vegetation data across multiple spatial and temporal scales in desert steppe ecosystems. This effort will enable the capture of dynamic vegetation responses to environmental drivers such as climate variability, land use change, and restoration interventions. The resulting time-series datasets will serve as a foundation for temporal model validation, trend analysis, and the development of more adaptive and resilient classification frameworks.

Finally, the current model remains susceptible to background soil effects, especially in desert grassland, where large areas of soil are exposed, and the camera usually collects based on the average value of the area, so it may also introduce systematic errors. Future efforts will consider the incorporation of soil-adjusted vegetation indices, as well as advanced correction techniques using neural networks, to mitigate these confounding influences and enhance model reliability in real-world applications.