Introduction

As a critical component of freshwater ecosystems, predicting river water quality parameters is essential for supporting the sustainable development of the water quality environment. DO concentration is one of the key indicators for water quality assessment, and it is closely influenced by factors such as water temperature, air pressure, air temperature, etc. When DO concentration is too low, it negatively impacts the survival of aquatic organisms and disrupts the ecological balance. Conversely, excessively high DO concentration can lead to eutrophication, odor, acidification, and an increase in harmful substances, thus affecting the water quality. Therefore, accurately predicting DO concentration is essential for assessing water quality and enabling timely and effective water quality management1.

In recent years, with the development of artificial intelligence technology, data-driven modeling has been widely used in water quality prediction. Currently, water quality prediction research methods include the following three main categories: traditional prediction methods, machine learning prediction methods, and combined prediction methods. Traditional statistical methods include autoregressive (AR), autoregressive integral moving average (ARIMA)2, Markov model3, rely on time-series approximation for prediction. While these methods have been widely used, they tend to have limited learning capabilities and often fail to capture the nonlinear relationships present in the data, resulting in poor generalization4. In response to this issue, an increasing number of scholars have employed neural network models such as machine learning to study water quality prediction for addressing complex nonlinear problems. Currently, many scholars have utilized machine learning techniques such as Back Propagation5, Extreme Learning Machine6, and Support Vector Machines7 to conduct research on water quality prediction, and have achieved a large number of experimental research results. Xu8 et al. used multiple machine learning models based on wavelet transform to predict the daily DO concentration of a certain river. The results indicated that the WT-ANN and WT-MLR models performed best under the combined model, confirming that preprocessing methods such as denoising can effectively enhance the accuracy of DO prediction. However, traditional machine learning has some shortcomings. For instance, the BP neural network is prone to overfitting and getting trapped in local optima. When training the SVM model, as the sample size increases, the training time and memory usage show a sharp growth trend. Additionally, the determination of the penalty parameter and kernel function parameter in the SVM model has a significant impact on the model’s accuracy. The ELM model has a single-layer feedforward structure and possesses advantages such as fast training speed, avoidance of local optima, and low computational complexity. However, the static feedforward structure of ELM is not suitable for modeling nonlinear time series data, and its prediction results often exhibit considerable instability. Deep learning has been widely embraced in both academia and industry in recent years. With the generation of massive data by devices, an increasing number of researchers are adopting deep learning models for prediction studies. Models such as Long Short-Term Memory Networks, Bidirectional Long Short-Term Memory Networks and Temporal Convolutional Networks have been widely used at present9,10,11. These approaches enhance the ability to capture intricate relationships between various features in water quality data, offering better performance in feature extraction. Fu et al.10 proposed a new method for predicting dissolved oxygen using TCN. The TCN network model extracts time series features and deep data features by introducing dilated causal convolution, thus demonstrating excellent prediction performance. Alfwzan et al.11 used the BiLSTM model to predict the variables that affect groundwater quality and compared the effectiveness of the proposed model with that of LSTM, RNN and GRU. The proposed model achieved an accuracy and precision of 98%.

However, during the development of research in recent years, a large number of scholars began to use a combination of prediction models to replace a single model for prediction, the combination of models using different neural network models to extract key features of the data, so that the key features can be extracted more effectively, which greatly improves the predictive ability of the model. Wang et al.12 proposed a combined ARIMA-SSA-LSTM approach, which improves the predictive accuracy by effectively extracting data features and optimizing the neural network’s hyperparameters. Zuo et al.13 proposed a WSWOA algorithm to optimize an combined VMD-TCN-ARIMA model, further enhancing both prediction accuracy and efficiency. These methods are characterized by optimizing the hyperparameters of the neural network5,14,15.

Actually, the selection of hyperparameters is very important. To address the challenge of optimizing neural network hyperparameters, researchers have turned to swarm intelligence algorithms, which are widely used in areas such as power load forecasting16, stock price prediction17, and atmospheric environment modeling18,19, Wind power prediction20. Che et al.21 proposed a multivariate approach that combines a genetic algorithm based feature selection framework (GAFSF) and a bidirectional gated recurrent unit (DBiGRU) to establish a model. And utilize the adversarial learning sparrow search algorithm (OLSSA) to optimize the hyperparameters of DBiGRU. When testing four seasonal datasets, four minimum average absolute percentage errors were obtained. Among these algorithms, the sparrow search algorithm is a newer swarm intelligence optimization algorithm that has attracted much attention due to its simplicity, local search capability, and effectiveness compared to other methods such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Whale Optimization Algorithm (WOA)22. Despite its advantages, SSA still faces some challenges such as dependence on initial population diversity, unstable convergence rate and susceptibility to local optimization.

This study primarily focuses on analyzing the characteristics of long-term DO time series. The TCN often fails to capture the dynamic fluctuations present in DO data, resulting in suboptimal prediction performance. To overcome this limitation, the BiLSTM network is integrated into the TCN framework, forming a TCN-BiLSTM prediction module. This module effectively captures both forward and backward temporal dependencies, improving the model’s ability to track the dynamic trends in the data and enhancing its prediction accuracy. The purpose of parameter optimization is to enhance the performance of the model so that it performs better on specific tasks. Specifically, we improve the Sparrow Search Algorithm to optimize the hyperparameters of the TCN-BiLSTM module. Solved the instability of the results caused by the random setting of parameters. Finally, a series of comprehensive experiments demonstrate the applicability and superiority of the proposed SMI-TCN-BiLSTM hybrid model for dissolved oxygen prediction. The contributions of this study can be summarized as follows:

  1. 1.

    We proposed a hybrid prediction model of dissolved oxygen SMI-TCN-BiLSTM. Aiming at the fact that TCN cannot effectively capture the dynamic trend of the fluctuating data in the prediction process, which reduces the prediction performance, and the dissolved oxygen has the feature of large diurnal temperature difference, we introduced BiLSTM to build the TCN-BiLSTM combined prediction model, and BiLSTM captures the forward and backward rule features of the time series data, which is helpful for obtaining the dynamic trend of the data and improves the prediction performance of the model, and applied the ISSA optimization algorithm to solve the hyperparameter selection problem in the TCN-BiLSTM prediction module. Performance, and apply ISSA optimization algorithm to solve the hyperparameter selection problem in TCN-BiLSTM prediction module.

  2. 2.

    We propose the ISSA optimization algorithm. To address the issue of the SSA getting trapped in local optima, we investigate three key strategies: initializing the population using tent chaotic mapping, employing a butterfly optimization strategy, and introducing an adaptive T-distribution mutation technique to enhance its ability to find the optimal hyperparameters. These strategies overcome the traditional SSA’s tendency to converge prematurely, enhance its ability to find optimal solutions, and improve the algorithm’s convergence speed.

  3. 3.

    We conduct experiments using a real river water quality dataset, comparing our model with nine other mainstream models to demonstrate the better predictive performance of the proposed approach.

The main content of this article is arranged as follows: Section "Materials and methods" introduces the source of the dataset and the research methods used in this article; Section "Experimental evaluation" conducts experimental evaluations, including the experimental results on real datasets, and compares the model proposed in this paper with other widely used models. Section 4 summarizes and looks forward to the contributions of this article.

Materials and methods

In this section we are organized as follows, Section "Description of the study area and data sources" gives a brief description of the study area as well as on the dataset; Section "Savitzky-Golay filter" introduces the SG filter; Section "Maximum information coefficient-based feature selection" outlines the MIC related content; Section "TCN and BiLSTM" we respectively introduced the TCN and BiLSTM models; Section "Improved sparrow search algorithm" elaborates on the introduction of the three strategies to improve the original sparrow algorithm; and Section "SMI-TCN-BiLSTM dissolved oxygen prediction model" describes the entire prediction process framework structure of the model.

Description of the study area and data sources

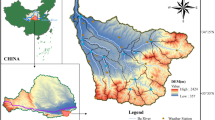
The experimental data were collected from real-time monitoring real data of a river in Ying Jiang District, Anqing City, Anhui Province. The specific geographic location of the study area is shown in Fig. 1. The river has an approximate depth of 50 m and is equipped with various types of sensors, providing a solid foundation for water quality monitoring. As an important tributary of the Yangtze River, it is crucial to monitor changes in its water quality.

Fig. 1
figure 1

Geographic location map of the study area. Note: Produced using Arcgis software, version number 10.8, address https://www.esri.com/en-us/arcgis/products/arcgis-desktop/resources.

Full size image

The data are collected by water quality sensors and a small meteorological station. The monitoring indicators include both water quality and meteorological data Specifically, 11 indicators were recorded, comprising water quality parameters such as water temperature, dissolved oxygen, and pH, as well as meteorological parameters, including temperature, humidity, atmospheric pressure, wind direction, wind speed, rainfall, PM2.5, PM10. These indicators are collected every 30 min by the sensors and stored on a server, allowing for real-time access through a terminal. A detailed descriptive of the raw water quality data is shown in Table 1. The standardized variance is an important measure of the degree of dispersion of the data, indicating the extent to which the data points deviate relative to the mean. In forecasting, a smaller standard variance indicates that the forecast is more stable and less susceptible to extreme values.

Table 1 Description of water quality indicators.
Full size table

Savitzky-Golay filter

In order to reduce the impact of noise on the model prediction effect in the original water quality dataset, this paper utilizes the Savitzky-Golay to denoise the original water quality dataset. The SG filter, proposed by Savitzky and Golay in 1964, widely used for smoothing and denoising data stream. It is a time-domain filtering method based on local polynomial least-squares fitting. One of the key advantages of the SG filter is its ability to denoise while preserving the shape and width of the signal23,24,25.

Maximum information coefficient-based feature selection

MIC can effectively capture the degree of correlation between variables and has been widely used in various fields. With sufficient data samples, MIC can detect both linear and nonlinear relationships between variables26,27, thus responding to the degree of correlation between water quality indicators and meteorological indicators. The monitoring of IoT devices obtains a variety of characteristic parameters involving water bodies and meteorology. However, an excess of parameters can negatively impact model training speed and prediction performance. Features that are weakly correlated or irrelevant to the prediction of dissolved oxygen can reduce the model’s accuracy28. Therefore, it is necessary to further select the most relevant features for prediction. At present, commonly used correlation coefficient analyses include Pearson correlation coefficient analysis, Spearman correlation coefficient analysis, etc. However, some of the correlation analysis methods mentioned above have some issues in terms of applicability, computational complexity, robustness, and other characteristics. The idea of MIC is to discretize the relationship between two variables in a two-dimensional space. Dividing a certain number of intervals in the x and y directions in two-dimensional space and examining the scatter points falling into each square solves the problem of difficult joint probability calculation in mutual information.

TCN and BiLSTM

TCN uses convolutional operations to capture temporal dependencies within sequences and has been applied in many continuous tasks. Zhao et al.29 demonstrated that TCN outperforms variant networks, such as RNN, in analyzing longer sequence inputs. This feature facilitates parallel computation, model simplification and prevents gradient explosion. The TCN model mainly consists of causal convolution, extended convolution, and residual connectivity. The structure of the neural network of TCN is shown in Fig. 2 From a modeling perspective, however, the TCN model alone is not sensitive enough to the time-series nature of water quality data. Although TCN effectively capture local features, they struggle to adapt to sudden events, trend changes, or sharp fluctuations in the time series, leading to reduced prediction effectiveness. This is particularly problematic in complex water quality data, where fluctuations are common.

Fig. 2
figure 2

Structure of TCN neural network.

Full size image

LSTM network can process only forward information to make predictions, while BiLSTM30 network, based on LSTM network, adopts a bidirectional design that allows them to integrate both forward and backward information. This bidirectional approach enhances prediction accuracy by incorporating the temporal dependencies in both directions of the time series. The structure of the BiLSTM network is shown in Fig. 3. BiLSTM is highly sensitive to time-series data, enabling it to better adapt to the dynamic changes, and capture the dependencies within water quality data more effectively.

Fig. 3
figure 3

BiLSTM structure.

Full size image

Improved sparrow search algorithm

Sparrow Search Algorithm (SSA) was proposed by Jiankai Xue et al. in 2020. It has been found that the quality of the initial population affects the overall performance of the SSA. In this paper, an improved SSA (ISSA) based algorithm is proposed to address the shortcomings of SSA.

The standard SSA uses a random initialization population, but its distribution is often uneven, which may lead to insufficient early diversity in the population, thereby affecting the global search ability. Tent mapping is a chaotic mapping method with good traversal, uniformity, and initial sensitivity, which can effectively enhance the distribution uniformity and diversity of the initial population. By introducing Tent chaotic mapping to initialize individual positions, it helps to cover a wider search space and improve the algorithm’s ability to jump out of local extremum points. The update strategy of discoverers in SSA has a certain global search ability, but it is still prone to getting stuck in local optima in complex multimodal functions. The Butterfly Optimization Algorithm (BOA) has strong exploratory ability. Introducing this strategy into the discoverer update mechanism can improve the convergence direction control ability of SSA in high-dimensional space, further enhancing the algorithm’s global search performance and ability to escape local optima. The individual updates of SSA are relatively fixed and lack local perturbation ability, which affects the search accuracy in the later stage. The T-distribution has a heavy tailed characteristic and is more suitable for generating long-range disturbances to escape local optima compared to the normal distribution. By adaptively adjusting the degree of freedom parameters, the mutation gradually shifts from “heavy perturbation” to “micro perturbation”, achieving a natural transition from global coarse search to local fine search, thereby improving the optimization accuracy and stability of the algorithm.

Chaotic mapping is known for its randomness and traversal, which can well overcome the issue of uneven population distribution. It is commonly used to generate chaotic sequences that improve the initialization process of population optimization algorithm. In this paper, we use tent chaotic mapping, which has a broader coverage and more uniform distribution, making it ideal for initializing the population. The mathematical expression for tent chaotic mapping is shown in Eq. (1):

$$x_{i + 1} = \left\{ {\begin{array}{*{20}l} {2x_{i} } & {0 \le x \le 1/2} \\ {2(1 - x_{i} )} & {{\text{1/2 < x}} \le 1} \\ \end{array} } \right.$$
(1)

The expression of the Tent mapping through the Benuli-displacement transformation is shown in Eq. (2):

$$x_{i + 1} = (2x_{i} )\bmod 1$$
(2)

However, in tent chaotic sequences there are characteristics such as small period, instability, etc., to avoid the above characteristics, some researchers have introduced random variables on the tent mapping expression and improved the expression as shown in Eq. (3):

$$x_{{i + 1}} = \left\{ {\begin{array}{*{20}l} {2x_{i} + rand(0,1) \cdot \frac{1}{N}} & {{\text{0}} \le x \le 1/2} \\ {2(1 - x_{i} ) + rand(0,1) \cdot \frac{1}{N}} & {{\text{1/2 < }}x \le {\text{1}}} \\ \end{array} } \right.$$
(3)

The transformed expression is then obtained by Bernoulli as shown in Eq. (4):

$$x_{i + 1} = (2x_{i} )\bmod 1 + rand(0,1) \cdot \frac{1}{N} \,$$
(4)

In this paper, the initial position of the sparrow population in the feasible domain is obtained by introducing the improvement is tent chaotic perturbation to avoid it falling into local optimality, and the initial position of the sparrow population in the feasible domain is obtained by Eq. (5).

$$x_{id} = lb_{id} + \left( {ub_{id} - lb_{id} } \right) \times X_{id}$$
(5)

where, ubid and lbid are the upper and lower bounds representing the feasible solution interval, respectively, xid is the mapped individual, and Xid is the variable generated by Eq. (4).

The SSA algorithm’s position update formula for the discoverer tends to converge prematurely toward the zero point in the early stages of iteration, which can trap the algorithm in local optima. To mitigate this, we introduce the global search phase from the BOA to improve the position update strategy. The modified position update formula is shown in Eq. (6):

$$X_{{i,j}}^{{t + 1}} = \left\{ {\begin{array}{*{20}l} {X_{{i,j}}^{t} + \left( {r^{2} * X_{{best}}^{t} - X_{{i,j}}^{t} } \right) * f_{i} ,} & {R_{2} < ST} \\ {X_{{i,j}}^{t} + Q \cdot L,} & {R_{2} \ge ST} \\ \end{array} } \right.$$
(6)

where r is a random number between 0 and 1,\({X}_{best}^{t}\) is the current iteration of the global optimal solution. ƒi is the optimal fitness value.

The formula for updating the position of the joiner is shown in Eq. (7):

$$X_{i,j}^{t + 1} = \left\{ \begin{gathered} Q \cdot \exp \left( {\frac{{X_{worst}^{t} - X_{i,j}^{t} }}{{i^{2} }}} \right),i > n/2 \hfill \\ X_{p}^{t + 1} + \left| {X_{i,j}^{t} - X_{p}^{t + 1} } \right| \cdot A^{ + } \cdot L,\;otherwise \hfill \\ \end{gathered} \right.$$
(7)

where i denotes the number of joiners; n denotes the total number of sparrows; Xp is the best position currently occupied by the discoverer; \({X}_{worst}^{t}\) indicates the current global worst position; A denotes a 1 × d matrix in which each element is randomly assigned a value of 1 or -1, and \({A}^{+}={A}^{T}{(A{A}^{T})}^{-1}\).

The formula for updating the position of a sparrow that realizes the danger is shown in Eq. (8):

$$X_{i,j}^{t + 1} = \left\{ \begin{gathered} X_{best}^{t} + \beta \left| {X_{i,j}^{t} - X_{best}^{t} } \right|,f_{i} > f_{g} \hfill \\ X_{i,j}^{t} + K\left( {\frac{{X_{i,j}^{t} - X_{worst}^{t} }}{{(f_{i} - f_{w} ) + \varepsilon }}} \right),f_{i} = f_{g} \hfill \\ \end{gathered} \right.$$
(8)

where \(x_{best}^{t}\) is the current global optimal position;βas a step control parameter, it is a random number that obeys a normal distribution with mean 0 and variance 1; \(K \in [ - 1,1]\) is a random number indicating the direction of the sparrow’s movement and also the step control parameter; ƒ is the fitness value of the current sparrow individual; \(f_{g}\) and \(f_{w}\) are the current global maximum and minimum fitness values, respectively; \(\varepsilon\) is the smaller constant so that the denominator does not appear to be zero.

To further address the issue of the population becoming concentrated around local optima, reducing diversity and impeding the algorithm’s ability to escape local solutions, we introduce an adaptive T-distribution variation strategy to update the sparrow positions. The advantage of T-distribution lies in its integration of the characteristics of both the Cauchy and Gaussian distributions, improving the algorithm’s ability and robustness to escape local optima. The formula for this update is shown in Eq. (9):

$$x_{i}^{t} = x_{i} + x_{i} \cdot t(iter)$$
(9)

where \(x_{i}^{t}\) is the position of the variant sparrow, \(x_{i}\) is the position of sparrow i, \(iter\) is the current iteration number, and \(t(iter)\) is the T-distribution with the degrees of freedom parameterized by the number of iterations.

SMI-TCN-BiLSTM dissolved oxygen prediction model

Water quality data are inherently complex and nonlinear, with unstable time series data that present challenges for accuracy prediction using a single method is limited. To improve accuracy of water quality prediction, this paper utilizes the SG filter to denoise the original time series data and the MIC to select the indicator factors with high correlation with dissolved oxygen. Since the performance of neural network models is highly sensitive to their parameters, this study conducts hyper-parameter optimization through ISSA to fine-tune the combined TCN-BiLSTM prediction module. The optimal parameter set obtained is then used for DO prediction. The overall experimental workflow mainly divided into the following steps in Fig. 4.

Fig. 4
figure 4

Overall prediction flowchart.

Full size image

The TCN-BiLSTM-based model proposed in this paper consists of one input layer, five TCN modules, one BiLSTM layer, two fully connected layers, and The TCN consists of a five-layer structure, the first layer consists of causal dilation convolution, the size of convolution kernel is 7, the dilation factor is 1, and the number of filters is 32. The dilation factors of the second, third, fourth, and fifth layers of the network are 2, 4, 8, and 16, respectively, and the rest of the parameters are the same as that of the first layer of the network. To compensate for the time series insensitivity of TCN to dissolved oxygen information, the effective features extracted by TCN are transmitted to the BiLSTM layer, which is used to extract the long-term dependence from the forward and backward directions, respectively, through bidirectional LSTM. Then the fully connected layers are followed and finally the predicted dissolved oxygen concentration values are output through the output layer.

Step1: Data denoising. During the data collection process at water quality monitoring stations, issues such as sensor malfunctions, network failures, and communication errors often lead to missing or anomalous data. These irregularities can result in significant deviations between predicted and actual water quality values. To enhance prediction accuracy, it is essential to preprocess the raw water quality data by cleaning and denoising it. In this paper, the SG filter is used to denoise the original data. Additionally, to mitigate the impact of outlier values on model predictions, data normalization is performed. Specifically, Min–Max normalization31 is applied to scale the data to a range of 0 to 1, ensuring that the variables are suitable for input into the model.

Step2: Feature selection. After data denoising, feature selection will be performed for all parameter indicators. Using the method of MIC, the correlation coefficient between each index affecting DO change and DO will be calculated. The key index with significant influence will be selected as the input of the model to determine the input index system of the DO prediction model.

Step3: Model construction. Based on the data denoising and feature selection, the TCN-BiLSTM module is optimized using ISSA to fine-tune the hyperparameters. This results in the development of the SMI-TCN-BiLSTM prediction model, which incorporates the optimal parameter values identified through the optimization process.

Step4: Evaluation and analysis. We use real data from real-time monitoring of a river in Ying Jiang District, Anqing City, Anhui Province, to validate and evaluate the performance of the proposed SMI-TCN-BiLSTM model. Meanwhile, nine current mainstream models are selected for comparative analysis to assess the superiority and applicability of the DO prediction model proposed in this paper.

Experimental evaluation

Denoising process

For the phenomenon of missing data in the water quality data, we excluded data points with a missing duration of three hours. For the remaining missing values, we use linear interpolation method to fill. After preliminary processing, a total of 4000 data points, spanning from August 15, 2023 to November 9, 2023, were retained.

Water quality data are inevitably collected with noisy data and data drift due to its complex monitoring environment. In this paper, a Savitzky-Golay filter is used to denoise the dataset, reducing noise interference and minimizing the impact of local outliers on the overall data trends. In SG filter, window size (W) and highest order term (R) play crucial roles in determining the filter’s effectiveness.  Figures 5 and 6 illustrate the DO time series after filtering with SG filters, using different W and R.

Fig. 5
figure 5

DO time series filtered by SG filters with different W.

Full size image
Fig. 6
figure 6

DO time series filtered by SG filters with different R.

Full size image

As can be seen in Fig. 6, as R increases, the data smoothing becomes less effective, while too low an R also changes the trend of the data. Similarly, Fig. 5 reveals that at sample point 210, the filter with W = 5 produces the most consistent result with the original data trend, while larger values of W distort the data’s trend. From Fig. 6, it is also evident that at sample point 210, the trend most closely aligns with the original data when R = 4, and any R smaller than 4 disrupts the data’s trend. Based on this, W = 5 and R = 4 were selected in this study to smooth the original dataset.

As shown in Fig. 7, a randomly selected graph of DO changes over the course of a day was plotted. Dissolved oxygen is compared with the original data set before and after using the SG filter. It is clear that the denoised data show a clear smoothing trend, with a significant reduction in noise and local perturbations.

Fig. 7
figure 7

DO comparison chart before and after using the SG filter.

Full size image

Feature selection

A heat map of the MIC correlation analysis is shown in Fig. 8 From the figure, it can be seen that the correlation with predicted dissolved oxygen (DO) is from high to low, followed by water temperature (WT), pH, air pressure (AP), and air temperature (AT). The correlation coefficients were 0.66, 0.47, 0.44 and 0.41, respectively. Among them, water temperature (WT) and pH had the highest correlation with DO, followed by air pressure (AP) and air temperature (AT). Therefore, the variables with little correlation with DO were removed, and the final features used for model training were reduced to four features: water temperature (WT), pH, air pressure (AP), and air temperature (AT).

Fig. 8
figure 8

MIC correlation analysis.

Full size image

Model evaluation criteria

In this paper, we choose five indicators as criteria for water quality prediction, which are mean square error (MSE), root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and coefficient of determination (R2). The formulas are shown in Eqs. (10–14).

$$MSE = \frac{1}{n}\sum\limits_{i = 1}^{n} {(y_{i} - \tilde{y}_{i} )^{2} }$$
(10)
$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {(f_{i} - y_{i} )^{2} } }$$
(11)
$$MAE = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {y_{i} - \tilde{y}_{i} } \right|}$$
(12)
$$MAPE = \frac{1}{n}\sum\limits_{i = 1}^{N} {\left| {\frac{{y_{i} - \tilde{y}_{i} }}{{y_{i} }} \times 100\% } \right|}$$
(13)
$$R^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {(y_{i} - \tilde{y}_{i} )^{2} } }}{{\sum\nolimits_{i = 1}^{n} {(y_{i} - \overline{y} )^{2} } }}$$
(14)

Results and discussion

Experimental setup

The experiments in this paper were conducted under Windows operating system, configured to handle Intel Core i5-12490F 3GHz CPU, 16GB RAM and NVIDIA GeForce RTX 3060 Ti. The experimental environment was Pycharm2021.3, which was completed based on the Tensorflow framework. In order to determine the appropriate time step, this paper investigates the effect of different time steps in the sliding window on the DO prediction model and tests it on the river monitoring dataset in Anqing City, Anhui Province. Figure 9 shows the RMSE and MAE values corresponding to different window steps.

Fig. 9
figure 9

RMSE and MAE values corresponding to different window orders.

Full size image

As shown in Fig. 9, the RMSE and MAE of the prediction model reach the lowest value when the window size T = 5. When T increases from 5 to 9, the RMSE tends to increase. Therefore, in the experiments of this paper, we choose T = 5.

Since the setting of model parameters will have a certain impact on the overall prediction, in order to ensure the consistency of the experimental results, this paper sets the same model parameters on the same dataset. The specific situation is shown in Table 2.

Table 2 Parameter settings of the dataset on TCN-BiLSTM.
Full size table

Comparison experiment

To evaluate the performance of the proposed model, we compare it with several mainstream water quality prediction models. This includes single models BP, SVR, LSTM, BiLSTM, and current mainstream models such as CNN-LSTM32, TCN-LSTM33, and CNN-GRU-Attention14. The various performance metrics of each model are shown in Table 3.

Table 3 Comparison of SMI-TCN-BILSTM with other neural network models.
Full size table

From Table 3, it is evident that all the models can realize the prediction of dissolved oxygen, but with different effects. The SMI-TCN-BiLSTM model proposed in this paper, achieved the following evaluation metrics: RMSE = 0.0132, MAE = 0.1147, MAPE = 0.0851, R2 = 0.96%, and R = 98.43%. In comparison, the single models BP, SVR, and BiLSTM exhibited higher RMSE values of 0.317, 0.182, and 0.1571, representing increases of 63.8%, 36.9%, and 27% relative to the SMI-TCN-BiLSTM model. For the combined models, TCN-LSTM has an RMSE of 0.2081, CNN-LSTM has an RMSE of 0.1711, CNN-GRU-Attention has an RMSE value of 0.1738, TCN-BiLSTM has an RMSE value of 0.1566. SSA-TCN-BiLSTM provided an RMSE of 0.1501, indicating increases of 44.88%, 32.96%, 34%, 26.76%, 23.58%, respectively, compared to the proposed SMI-TCN-BiLSTM model. These results confirm that the SMI-TCN-BiLSTM model performs best on the pre-processed dataset. To provide a more intuitive understanding of the prediction performance, Fig. 10 visualizes the prediction results of the different models. Specifically, the first 400 samples from 20% of the test set are shown, with the results divided into four images, each containing 100 predicted values.

Fig. 10
figure 10figure 10

Fitting of SMI-TCN-BILSTM with different model predictions.

Full size image

As shown in Fig. 10, while all models are capable of predicting dissolved oxygen concentrations, the actual prediction results differ considerably. Traditional neural network models, such as BP and SVR, show significant discrepancies. These models are essentially static and fail to account for the time-dependent relationships inherent in time series data, leading to poor prediction accuracy. In contrast, the hybrid models generally outperform the single models. The SMI-TCN-BiLSTM curve is closest to the true curve, followed by SSA-TCN-BiLSTM, while TCN-BiLSTM performs relatively worse. The ISSA optimizes the model parameters in TCN-BiLSTM, resulting in improved hyperparameter combinations and superior prediction performance for dissolved oxygen. The SMI-TCN-BiLSTM method proposed in this paper proves to be an effective method for enhancing prediction accuracy through various optimization techniques. It provides valuable insights for future research in the field of water quality prediction.

Alation experiment

The four optimal hyperparameters of the neural network model were determined by ISSA: the size of the convolution kernel in the TCN was 4, the number of neurons in the BiLSTM was 32, and the optimum number of training iterations was 100, learning rate was set to 0.01. In order to verify the effectiveness of different optimization operations, ablation experiments were conducted, and the dissolved oxygen prediction results are presented in Table 4.

Table 4 Dissolved oxygen prediction effect under different optimization operations.
Full size table

As shown in Table 4, the SMI-TCN-BiLSTM model proposed in this study yields the best results on the dataset. Although all models are capable of predicting dissolved oxygen, their performance varies significantly. By applying SG filtering to the original dataset, the indicators of the SG- TCN- BiLSTM model are significantly improved. Compared with TCN- BiLSTM, the MSE, RMSE, MAE, and R2 metrics are improved by 37.64%, 21.02%, 33.48%, and 6.15%, respectively. These improvements suggest that SG filtering effectively reduces noise in the original data, making the data smoother and, in turn, enhancing the model’s predictive accuracy. Based on the SG filtering operation, we used the MIC optimization operation to screen the relevant influencing factors, from screening out the factors that have a greater impact on the dissolved oxygen as the input to the model. The experimental results demonstrate that the MSE, RMSE, MAE, R2 indexes of the SG-MIC-TCN-BiLSTM model compared to the SG- TCN-BiLSTM were improved by 77.25%, 47.31%, 44.38%, and 7.47%, which indicates that the MIC feature screening can reduce the information interference of the indicator data with low DO correlation and effectively improve the accuracy of the prediction model. The MSE, RMSE, MAE, MAPE and R2 of SG-MIC-SSA-TCN-BiLSTM model reached 0.0225, 0.1501,0.1082, 1.23% and 97.31% respectively. Based on the improved sparrow search algorithm we seek optimization to get a set of optimal hyperparameters, and the MSE, RMSE, MAE, MAPE, and R2 of the SMI-TCN-BiLSTM model reached 0.0132, 0.1147, 0.0851, 0.96%, and 98.43%, respectively. The performance of the improved prediction model is better than the previous optimization algorithm. The above data well illustrate that the SMI-TCN-BiLSTM model proposed in this paper has good predictability for DO. To verify the effectiveness of the different optimization operations, we employed visualization operations to compare the prediction errors of different models. The results are shown in Fig. 11, where we visualized the first 400 predicted samples from 20% of the test set. To enhance clarity, the 400 predicted values were displayed across four images, each containing 100 predictions.

Fig. 11
figure 11

Error profiles under different optimization operations.

Full size image

As shown in Fig. 11, we visualize the results for the first 400 prediction samples in the test set. We can visualize that the black dashed line is the zero reference line, and the closer it is to the line indicates that the model predicts better performance with less error. Compared with several other models, the error of the SMI-TCN-BiLSTM proposed in this paper is the smallest and closest to the zero reference line. It proves the effectiveness of SG filtering and MIC correlation analysis operations, which can improve the prediction accuracy well. However, the SMI-TCN-BiLSTM is not effective in predicting dissolved oxygen at certain time periods, such as the 175th sample points in Fig. 11b, the 275th sample points in Fig. 11c, and the 325th sample points in Fig. 11d. These time points correspond to transition periods between 7:00 a.m. and 12:00 p.m., during which significant temperature fluctuations occur, leading to frequent changes in dissolved oxygen levels. Additionally, the presence of numerous organisms in the river, particularly algae, contributes to fluctuations in dissolved oxygen during this period, which further complicates accurate predictions.

Improved sparrow search algorithm

To evaluate the performance and optimization of the ISSA algorithm proposed in this paper, six commonly used test functions F1-F6 are used for testing. Among them, F1-F3 are single-peak functions, which can better test the convergence speed and accuracy of the algorithm. Functions F4-F6 are multi-peak functions, which can better test the convergence speed and accuracy of the function as well as the ability to jump out of the local optimum. The specific information of dimensions, value ranges, and best fitness values are shown in Table 5.

Table 5 Test function basic information.
Full size table

To further verify the feasibility and superiority of the ISSA algorithm, this paper compares this algorithm with other commonly used intelligent optimization algorithms, including SSA, PSO, WOA, BOA. The same parameters are maintained for ISSA and SSA, with the population size set to 30, and the maximum number of iterations set to 1000. The parameter settings of each optimization algorithm are shown in Table 6.

Table 6 Other parameter settings of each optimization algorithm.
Full size table

To eliminate the errors caused by randomness, 30 independent experiments were conducted for each of the six test benchmark functions. Table 7 presents the mean, standard, and optimal fitness values of PSO, BOA, WOA, SSA, and the proposed ISSA algorithms after 30 independent runs on the standard test functions.

Table 7 Optimization results of different intelligent algorithms in test function.
Full size table

From Table 7, we can see that both the improved sparrow search algorithm and the sparrow counting algorithm based on the ISSA find the best fitness value on the single-peak multi-peak test function. And in terms of mean and standard deviation, the improved sparrow search algorithm is significantly due to other categories of algorithms. In order to present the superiority of the improved sparrow search algorithm more intuitively, we also plotted the iterative convergence curves of the benchmark test functions to further visualize the convergence of each algorithm and the optimization results of the algorithms. Figure 12 illustrates these convergence curves, with each curve representing the performance of a different algorithm. The horizontal axis denotes the number of iterations, while the vertical axis represents the fitness value.

Fig. 12
figure 12

Convergence curves of the 6 test functions.

Full size image

It can be intuitively found from Fig. 12 that the improved sparrow search algorithm has a faster convergence speed and better convergence results on the single-peak test function compared to the other four swarm intelligence optimization algorithms. For the multi-peak test functions (F4 and F5), the ISSA also outperforms the other algorithms in terms of convergence speed, achieving better fitness values.

Conclusion

Water quality monitoring data exhibit strong nonlinear characteristics, and traditional machine learning models often struggle to effectively capture the complex relationships between features, leading to poor prediction performance. To address this issue, we propose a combined prediction model of dissolved oxygen based on SMI-TCN-BILSTM. First, the SG filter is applied to denoise the water quality data, and the MIC system is used to identify and extract the key factors influencing dissolved oxygen fluctuations, which are then fed into the prediction model. This process reduces the impact of noisy data and redundant information on the prediction of dissolved oxygen. Secondly, the traditional Temporal Convolutional Network often fails to capture the dynamic fluctuations present in DO data, resulting in suboptimal prediction performance. To overcome this limitation, a Bi-directional Long Short-Term Memory network is integrated into the TCN framework, forming a TCN-BiLSTM prediction module. This module effectively captures both forward and backward temporal dependencies, improving the model’s ability to track the dynamic trends in the data and enhancing its prediction accuracy. ISSA is then employed to optimize the hyperparameters of the neural network model, ensuring stable and reliable predictions by preventing the influence of random parameter choices. Based on the real-world experiments, the SMI-TCN-BILSTM prediction model is compared with the current mainstream prediction model. Experimental results show that the SMI-TCN-BILSTM model exhibits high prediction accuracy and provides valuable theoretical insights for water quality forecasting.

In future work, we will also explore the model under long-term prediction. In addition, only one monitoring site’s water quality data is used in this paper. Future research will incorporate data from multiple sites within the study area. This will allow us to account for spatial and temporal correlations among monitoring locations, which may further improve the prediction accuracy.