Dual graph attention network for robust fault diagnosis in photovoltaic inverters

Abstract

This paper presents a novel deep learning framework based on a Dual Graph Attention Network (DualGAT) to enhance the accuracy and robustness of fault diagnosis in photovoltaic (PV) inverters operating under diverse environmental and operational conditions. Given the critical role of PV inverters in ensuring stable energy conversion, early and reliable detection of open-circuit faults is essential to prevent performance degradation and equipment failure. To address this, a detailed simulation model of a grid-connected PV inverter was developed in MATLAB/Simulink, incorporating variations in irradiance and temperature to generate realistic fault scenarios. Discrete Wavelet Transform (DWT) was employed to extract energy-based fault signatures from the inverter’s current signals, forming a rich dataset for model training. The proposed DualGAT architecture combines spatial and temporal attention mechanisms through two complementary modules—DisGAT and TempGAT—enabling the model to learn both structural dependencies and time-evolving patterns of inverter faults. Experimental results show that the model achieves a test accuracy of 97.35%, significantly outperforming traditional machine learning and recent deep learning approaches. Furthermore, the model demonstrates strong resilience under noisy conditions, maintaining high diagnostic performance even with signal distortion. These findings underscore the effectiveness of the DualGAT framework in capturing complex spatio-temporal fault characteristics, offering a promising solution for intelligent condition monitoring in PV-based power systems.

Introduction

Photovoltaic (PV) inverters play a vital role in converting the direct current (DC) output of a PV panel into alternating current (AC) for use in the grid or storage in battery systems¹. However, inverters are susceptible to various faults, particularly open-circuit faults, which can severely compromise their performance and reliability. Common causes of such faults include aging of components, electrical overstress, physical damage, corrosion, and poor manufacturing quality^2,3. These faults disrupt the core functionality of the system, leading to reduced energy production, increased maintenance costs, diminished revenue for PV system owners, and, in extreme cases, safety risks such as electrical fires⁴. If left unaddressed, these faults can propagate to other components, undermining the integrity and sustainability of the entire system. Timely diagnosis of PV inverter issues is, therefore, critical for ensuring a reliable energy supply, as it enables swift restoration of normal operation and mitigates potential adverse effects⁵.

Fault diagnosis encompasses identifying and assessing inverter switch failures, helping to minimize voltage sags and improve the durability, reliability, and adaptability of grid-connected PV systems⁶. In general, inverter faults can be classified into two categories: short-circuit and open-circuit faults⁷. Short-circuit faults occur when the electrical circuit in the inverter switch completes without a load, resulting in excessive current flow. Most modern industrial machinery is equipped with mechanisms to protect against short circuits. Conversely, open-circuit faults arise when the electrical circuit in the inverter switch is broken, leading to a complete loss of current flow due to disconnected conductors or overloaded equipment. Open-circuit faults, in particular, demand more attention, as they can cause one or more switches to malfunction, leading to a complete system shutdown or significantly reduced functionality⁸. These challenges highlight the need for fault diagnosis algorithms with improved exclusionary capabilities.

Despite considerable research on inverter fault diagnosis, many existing methods are unsuitable for solar applications⁹. In grid-connected states, the utility grid regulates the system’s voltage, while in islanded conditions, auxiliary power sources assume control. Consequently, many diagnostic techniques rely on analyzing voltage characteristics. For instance, inverters’ output voltage was evaluated under continuously varying loads¹⁰, and a similar method was used to diagnose faults in full-bridge converters¹¹. In cases of open-circuit faults, voltage impulses tend to attenuate only slightly, or the output signal may be severely impacted. Thus, voltage-based diagnostic methods alone are insufficient for PV inverter fault detection¹².

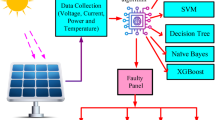
Moreover, Photovoltaic (PV)-based inverters are exposed to highly variable environmental conditions, such as fluctuating irradiance and temperature, which directly affect the inverter’s input characteristics. These input variations have a substantial impact on the inverter’s dynamic behavior, altering current and voltage profiles in ways that are not observed in traditional grid-tied or standalone inverters with stable power sources. For instance, an increase in temperature decreases the open-circuit voltage of PV panels, which in turn reduces the output power. Similarly, variations in sunlight irradiance influence the current generation, further modifying the inverter’s operational profile. These non-linear and stochastic input conditions can mask or distort the signatures of internal faults, making conventional fault diagnosis techniques less effective. Therefore, inverter faults in PV systems demand specialized detection strategies that account for these input-induced variations. The dataset used in this study captures a wide range of such environmental influences to reflect realistic PV operating scenarios. The proposed fault diagnosis model is developed with this context in mind, enabling it to learn and generalize fault characteristics under PV-specific operating conditions. This PV-contextualized approach enhances the model’s applicability and reliability for real-world solar inverter systems. Similarly, decreased sunlight irradiance results in a substantial reduction in current and, consequently, output power. Fault diagnosis methods that overlook such variations, as seen in the surveyed papers by Pillai et al.¹³, Alam et al.¹⁴, and Zhao et al.¹⁵, indicates the inadequacy for comprehensive PV inverter fault detection. In this work, a framework of inverter fault diagnosis is proposed that consists of three main components: (1) a comprehensive fault data generation process using a controlled testbed environment, (2) our novel Dual-GAT architecture featuring integrated spatial and temporal attention mechanisms, and (3) extensive experimental validation and analysis. Each component is designed to address specific challenges in PV inverter fault diagnosis while ensuring robust and generalizable performance across varying operational conditions. Figure 1 presents the overall framework of our proposed PV inverter fault diagnosis system.

The remainder of this paper is organized as follows: Related works discuss existing research on PV inverter fault detection. Motivation and contributions outline the challenges addressed in this study and the key contributions. The PV inverter testbed configuration and fault data generation section details the experimental setup and dataset creation process. The proposed Dual Graph Attention Network architecture is then introduced, followed by an analysis of experimental results. Ablation studies evaluate the impact of architectural choices, and the paper concludes with a summary of findings and potential future work.

Fig. 1

Overview of the proposed PV inverter fault diagnosis framework utilizing Dual Graph Attention Networks (Dual-GAT).

Related works

Model-based and signal-based techniques

Significant advancements have been made in diagnosing PV inverter faults through model-based and signal-based techniques, each offering distinct advantages and limitations. Model-based approaches hinge on the creation of mathematical representations that capture the expected behavior of an inverter under normal operating conditions¹⁶. Techniques such as sliding mode observers, extended Kalman filters, adaptive observers, and linear residual generation have been employed to detect anomalies by monitoring deviations from these models^17,18. While these methods provide insightful diagnostics, their performance is closely tied to the accuracy of the underlying models. In complex PV systems—where nonlinearities, environmental variabilities, and dynamic operating conditions prevail—maintaining such models with high fidelity becomes increasingly difficult. Moreover, model-based approaches often require extensive domain-specific knowledge and precise system specifications, limiting their adaptability to diverse inverter architectures or evolving operational scenarios¹⁹.

In contrast, signal-based techniques leverage the direct analysis of electrical signals, such as voltage and current, to extract fault-relevant features. Methods like empirical mode decomposition, fast Fourier transform (FFT), short-time Fourier transform (STFT), and wavelet transform are widely used to analyze signal components, spectral content, and time-frequency characteristics^20,21. These techniques are adept at detecting transient and periodic faults by identifying distortions in the signal’s frequency or time-domain profiles²². However, signal-based approaches are not without their challenges. In real-world applications, signal data is often contaminated by noise from environmental factors, grid interactions, or operational disturbances, complicating the detection process²³. Moreover, as inverter systems become more complex, the efficacy of signal-based techniques diminishes, with difficulties arising in distinguishing between overlapping fault signatures²⁴.

Statistical methods

Statistical-based approaches have shown significant results in fault detection for PV inverters and micro-grids, such as optimizer-based approaches²⁵, feature extraction approaches²⁶, and transfer learning-based approaches²⁷. Manohar et al.²⁸ introduced a discrete wavelet transform (DWT)-based feature extraction technique combined with a K-Nearest Neighbor (K-NN) classifier. The K-NN method relies on a distance-based similarity metric. DWT was used to extract features from three-phase voltage and current signals during shunt faults, and the standard deviation of the approximate coefficients served as input features for the K-NN classifier. For more robust pre-processing steps, an wolf optimization approach has been feature in²⁹ to figure out unknown parameters of the one-diode model of PV. The final diagnosis has been conducted via kernel modified random forest. This end-to-end pipelines improves the fault diagnosis performance on several metrics but does not cover accurate representation learning. Similar to this architecture, Independent Component Analysis has been utilized in³⁰ to reduce the dimension of initial feature input. This work also utilizes random forest for accurate classification result. In order to handle imbalance data, in³¹, several statistical-based strategies has been deployed for inverter fault diagnosis. Among all methods, ANN has best result in terms of performance due to its robust feature extraction capabilities. Similar to this work, Al et al.³² proposed an ensemble machine learning approach that integrated several statistical-based solutions to improve fault diagnosis performance further. The ensemble method, combining the strengths of multiple algorithms, achieved better fault detection accuracy and robustness, demonstrating that hybrid approaches can outperform single-method solutions.

Data-driven strategies

Recent advancements in computational resources have also pushed the boundaries of fault diagnosis accuracy^33,34. Due to having high performance, gradient-based models have demonstrated the ability to learn complex patterns in inverter signals^35,36. Yan et al.³⁷ proposed a fault diagnosis method for voltage source inverters (VSI) in motor drives using a pyramid-structured deep neural network. This approach extracts ten key features from the three-phase current signals of a permanent-magnet synchronous motor drive to detect single and double open-circuit faults with high diagnostic accuracy. Aljafari et al.³⁸ developed a real-time fault detection system for grid-connected photovoltaic (GCPV) systems using a one-dimensional convolutional neural network (1D-CNN) integrated with IoT technology. By utilizing real-time data from a 15kWp GCPV system, the model classifies various faults such as open-circuit and partial shading issues. Sun et al.³⁹ introduced a hybrid convolutional neural network (HCNN) combining 1D and 2D CNNs for diagnosing faults in three-phase inverters. The model leverages frequency spectrum preprocessing from current signals to extract spatial features, which are fused and classified using a softmax classifier. Kang et al.⁴⁰ proposed an CNN-LSTM model for fault diagnosis in wave energy converter gearboxes. The combination of CNNs for feature extraction and LSTMs for time-series analysis enhanced the model’s ability to detect faults amidst environmental noise. While gradient-based techqniques show high diagnostic accuracy, most approaches rely on extensive preprocessing and may not generalize well across different operating conditions and systems. Sun et al.³⁹ proposed a hybrid CNN (HCNN) combining 1D and 2D architectures to extract deeper fault features. 1D CNN can cover limited receptive areas and 2D CNN often disrupt spatial dependencies. HCNN aims to improve diagnosis accuracy and robustness across variable operating conditions for three-phase inverters by using a multiscale approach. This strategy highly increases the performance but does not consider the time-series nature of the input data. Considering the time-series behaviour in PV fault analysis, an LSTM based CNN architecture has been introduced in⁴⁰ for efficient time-series analysis and robust representation learning.

While spatio-temporal architectures such as CNN-LSTM and HCNN have made notable progress in modeling fault dynamics in inverter systems, our DualGAT framework introduces structural innovations that overcome inherent limitations in these traditional models through both theoretical and performance-based advancements. CNN modules extract spatial features across the signal domain (e.g., voltage/current waveform images or time slices), while LSTM models capture long-range temporal dependencies in sequential data. However, these models treat spatial and temporal features as disjoint modalities, often lacking explicit interaction mechanisms between them during learning. HCNNs utilize multi-scale convolutions (e.g., 1D+2D CNN) to jointly capture frequency and localized spatial patterns. While this hybridization improves robustness, it struggles with structured relational reasoning and lacks the ability to model system topology or inter-component dependencies, which are crucial in photovoltaic inverter fault propagation. In contrast, DualGAT explicitly encodes system-aware graph structures. The DisGAT module captures component-level topological dependencies, where nodes represent inverter subsystems and edges represent functional/physical interactions. This structured modeling is beyond the scope of CNN kernels, which are spatially local and weight-shared without respect to component identity. The TempGAT module constructs a temporal graph, where edges are not merely based on sequence proximity (as in LSTM), but on learned inter-time dependencies reflecting real inverter operational dynamics (e.g., recurring fault symptoms across non-contiguous time frames). Furthermore, DualGAT introduces a mutual cross-attention mechanism, unlike any seen in CNN-LSTM or HCNN models. This bi-directional attention mechanism allows spatial and temporal embeddings to modulate each other, resulting in a fused representation that better captures spatio-temporal interdependencies crucial for distinguishing between similar fault signatures. Table 1 summarizes the key characteristics, advantages, limitations, and notable works across different fault diagnosis approaches, highlighting the evolution from traditional model-based methods to modern deep learning techniques.

Recent studies have expanded fault diagnosis beyond inverter components to include array-level anomalies, particularly line-to-line (L-L) and line-to-ground (L-G) faults that pose significant fire hazards. Murtaza et al.⁴¹ proposed a single sensor-based fault detection mechanism featuring an additional DC-bus and capacitor-diode pair for each string, enabling millisecond detection at the string level while automatically isolating faulty strings through a passive RC network. This approach offers the advantage of low-cost implementation with minimal active-power field circuits. In a complementary study, Murtaza et al.⁴² developed a circuit analysis-based fault finding algorithm for PV arrays that identifies specific faulty strings and classifies fault types without requiring training data. Their comprehensive DC circuit analysis established five critical fault indicators that provide accurate diagnosis across various fault scenarios. These works highlight the importance of considering both inverter-level and array-level fault detection strategies in developing comprehensive PV system diagnostic frameworks.

Table 1 Comparative analysis of PV inverter fault diagnosis approaches.

Motivation and contributions

While PV inverter fault diagnosis has advanced through both traditional diagnostic techniques and data-driven methods, significant challenges persist in achieving robust and generalizable fault detection. Current approaches, which heavily rely on handcrafted feature extraction (e.g., statistical moments, time-domain parameters), demonstrate limited effectiveness when confronted with diverse operational conditions and varying environmental factors such as fluctuating irradiance and temperature. These methods primarily focus on isolated component analysis and local fault signatures, often examining individual components (e.g., single IGBT switches or capacitors) without considering the broader system-level interactions that are crucial for accurate diagnosis. The fundamental challenges in PV inverter fault diagnosis stem from three key aspects. First, PV inverter systems involve intricate interactions between power semiconductors, capacitors, and inductors, which traditional methods struggle to capture effectively¹³. Second, conventional approaches face degraded performance with increasing system complexity, resulting in higher computational demands and reduced diagnostic accuracy⁴³. Finally, existing methods show limited robustness to varying environmental conditions, struggling to adapt to dynamic system behaviors and changing operational states⁴⁴. To address these challenges, the authors propose Dual Graph Attention Networks (DualGAT), with the following key contributions such as Dual-Structure Neural Architecture, where the framework combines DisGAT for spatial fault dependencies and TempGAT for temporal pattern recognition, enabling comprehensive fault analysis across both dimensions. Moreover, the authors implement a differential regularizer and mutual cross-attention mechanism, promoting diverse feature learning and complementary feature extraction between spatial and temporal domains. The architecture employs adaptive attention weights to prioritize critical components and fault relationships.

These advancements collectively contribute to a robust and accurate fault diagnosis framework for PV inverter systems, addressing the limitations of traditional methods and enhancing reliability under diverse operating conditions.

PV inverter testbed configuration and fault data generation

Testbed grid-connected PV inverter

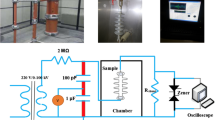
In this study, the authors investigate a comprehensive inverter-based photovoltaic (PV) generation system, illustrated in Fig. 2. The system consists of a PV source connected to a 2-level, 3-phase inverter on the grid side, with a DC-DC boost converter positioned on the source side; which was built in a MATLAB/Simulink environment. The boost converter and inverter are designed to operate within the same power range. The inverter’s input includes a DC link capacitor, and its output is connected to the grid at a common reference point. A low-impedance filter is implemented to mitigate current harmonics generated by the inverter. The inverter comprises six insulated-gate bipolar transistor (IGBT) switches, each paired with an antiparallel diode. These switches facilitate the DC-AC conversion through sinusoidal pulse width modulation (SPWM) signals. Additionally, an auxiliary battery system is integrated on the source side, connected via a dual active bridge.

Fig. 2

Inclusive design of grid-connected PV inverter system.

The inverter under investigation utilizes three-phase bridge arms, where each arm consists of two power switches $(S_{i}; i = 1, 2, 3...)$. The current conversion from DC to AC is performed by actuating these switches with sinusoidal pulse width modulation signals. When an open-circuit fault occurs, a significant shift is observed in the three-phase current signals ($I_a$, $I_b$, and $I_c$) on the grid side. If a fault affects any of the upper bridge switches (S1, S3, S5), the positive half-cycle magnitude of the corresponding phase current is truncated. Conversely, when an open-circuit fault occurs in one of the lower bridge switches (S2, S4, S6), the negative half-cycle magnitude of the respective phase current is affected. In the case of double-switch open-circuit faults, both the positive and negative half-cycles of the current signals experience simultaneous degradation.

Two types of open-circuit faults are considered: single IGBT open-circuit faults and double IGBT open-circuit faults, as it is uncommon for three or more switches to become faulty simultaneously. The single switch open-circuit faults occur in six fault conditions: S1, S2, S3, S4, S5, and S6, where the fault is labeled based on the affected IGBT switch (e.g., S1 Open-circuit fault, S2 Open-circuit fault, etc.). For faults in the upper and lower IGBT switches within the same bridge, there are three fault conditions: $S1 - S2$, $S3 - S4$, and $S5 - S6$. Additionally, there are six fault conditions for two IGBT switches of the same half-bridge, including $S1 - S3$, $S3 - S5$, $S1 - S5$, $S2 - S4$, $S4 - S6$, and $S2 - S6$. Similarly, six fault conditions arise when faults occur in two IGBT switches of different half-bridges, such as $S1 - S4$, $S1 - S6$, $S2 - S3$, $S3 - S6$, $S2 - S5$, and $S4 - S5$. The converter remains in a healthy condition (NF) when all power switches are operational. This results in five categories of converter fault conditions, leading to a total of 22 modes of operation (including 1 healthy mode) that are examined in this study. Table 2 represent the necessary parameters involved in the envisaged system.

In this study, data acquisition was performed using virtual sensing components available in the Simulink environment. A current measurement block was employed at the inverter output to extract the output current signal under various fault and normal scenarios. Additionally, the PV source block was configured to simulate dynamic environmental conditions such as irradiance and temperature variations, which indirectly affect inverter performance. These variations were reflected in the PV output voltage and current, captured virtually within the simulation. While no physical sensors were used, in a practical setup, current and voltage sensors would be essential for capturing inverter output, and irradiance and temperature sensors would be required for accurate PV input monitoring.

Table 2 PV inverter system specifications for simulation.

Decomposition of fault information

In the realm of inverter fault diagnosis, the precise identification of open-circuit faults in switching devices necessitates a meticulous analysis of the three-phase output currents measured at the load-side. The complexity of this task is exacerbated by the high volume of synthesized data instances present in the acquired current pulses. To address this challenge, the authors employ the Discrete Wavelet Transform (DWT) technique, which facilitates the decomposition of the current signals into specific wavelet packets. This approach offers the advantage of signal processing without the burden of handling excessive data volumes, enabling the decomposition of wavelengths into their constituent elements.

The DWT methodology utilizes a series of digital filters with varying cutoff harmonics to identify non-stationary signal transients at multiple scales. Transient signals with specific data instances are propagated through a cascade of low-pass and high-pass filters. To maintain computational efficiency, our analysis focuses on lower-order wavelengths, with waveforms sampled at 20 Hz for 200 instances. The mathematical formulation of the DWT process can be expressed as the integration of a stimulus S(t) amplified within the dilation and translation of a fundamental wavelet function $\psi$:

$$\begin{aligned} W(a, b) = \int _{R} S(t) a^{-\frac{1}{2}} \psi \left( \frac{t-b}{a}\right) \textrm{d}t; \quad a,b \in R \end{aligned}$$

(1)

where a and b represent the wavelet parameter scaling and positional properties, respectively. The parameter a controls the compression or dilation of the wavelet, while b governs the translation of the wavelet function along the time axis.

Based on prior investigations in electrical system signal analysis, the Daubechies (db) wavelet family has demonstrated superior performance compared to alternatives such as Morlet and Biorthogonal wavelets. For analysis, the authors employ the Daubechies wavelet of 4th order (db4). The Daubechies mother wavelet function is defined as:

$$\begin{aligned} X(t) = \sum _{l=2-N}^{1}(-1)^{n} q_{l-n} a(2t-n) \end{aligned}$$

(2)

where $q_n$ ($n=0,1,2,3,...,N-1$) represents a series of wavelet filtering parameters, and N is an even number.

In the DWT operation, a time-domain signal DWT(t) is decomposed into approximations (A) using a sequence of high-pass filters through the father wavelet W(t). Concurrently, the mother wavelet X(t) transforms the signal into interpretable variables via a series of low-pass filters. The mathematical representations of these processes are:

$$\begin{aligned} W_{\alpha \gamma }(t)= & 2^{-\frac{\alpha }{2}} W\left( 2^{-i} t-a\right) \end{aligned}$$

(3)

$$\begin{aligned} X_{pq}(t)= & 2^{-\frac{\alpha }{2}} X\left( 2^{-i} t-a\right) \end{aligned}$$

(4)

Here, $\alpha$ and $\gamma$ are integers, with the subscript “a” denoting the time unit for the functions being transformed, and “$2^a$” specifying the scaling of these functions.

To comprehensively understand the wavelet transform’s performance, the authors consider the M-level decomposition stage:

$$\begin{aligned} \text {DWT}(t) = \sum _{\gamma =0}^{2^{M-\alpha -1}} A_{\alpha \gamma } W_{\alpha \gamma }(t) + \sum _{\alpha } \sum _{\gamma =0}^{2^{M-\alpha -1}} D_{\alpha \gamma } X_{\alpha \gamma }(t) \end{aligned}$$

(5)

In this process, the outputs of the low-frequency and high-frequency filtering are downsampled by a factor of 2, yielding approximation coefficients A and detail coefficients D at the ith level of decomposition. This procedure is iterated until the A and D coefficients at level 5 are established.

Energy information extraction

In attempt to retrieve meaningful attributes, the wavelet packages are eventually confined to an energy computation. The wavelet data’s signal energy is crucial for identifying fault transients. The wavelet knowledge can be used to describe the expression for a signal’s total energy, which is displayed as:

$$\begin{aligned} E_{I_{x}}=\sum _{i=1}^{P}\left| d_{i}\right| ^{2} \end{aligned}$$

(6)

In this case, P stands for quantity of data points for each piece of wavelet data for scale $\{i = 1,2,3.......l\}$, and so on. The wavelet data illustrates how a signal’s energy alters in response to disruptions.

Energy information provides integrated metrics for quantitative determination and conveys the unpredictability of signal condition pattern and the attributes of signal complexities in an aggregate manner. It is a distinctive quantitative numerical value that is obtained from the pattern of the decomposed current and serves as the instantaneous signature of a particular circumstance. These signatures are specific to the originating circumstance and the inverter switches that caused those originating events. This implies that utilizing this alternating information of the event, the switch or switches causing the fault effects can be determined. In essence, the signature of the fault occurring on a certain single switch or double switches, will be different form the signature of normal condition. Also, variation in the source side of the inverter will cause the energy signal values of output current waveform to change in a manner that is different for every instance of changing source parameters. In the investigated system, the authors varied the photovoltaic source parameters: irradiance (E) and temperature (T), in order to depict the changes in energy information of grid-side current. As shown in Table 3, energy information is seen to be changed within the change of source parameters for four categories of faulty condition and one normal condition.

Table 3 Changes in energy information ($E_{I_{x}}$) per unit (p. u.) of current signals for different conditions with varied source parameters: (a) for no fault condition (NF), (b) for single switch and upper lower switch fault condition, and (c) for double switch fault condition.

Generation of diagnostic features and dataset

The three-phase current signals ($I_a$, $I_b$, and $I_c$) are measured as the irradiance and temperature of the PV array vary to evaluate the performance of the proposed method. The irradiance (E) is adjusted in increments of $1, \text {W/m}^2$, ranging from $250, \text {W/m}^2$ to $750, \text {W/m}^2$, while the temperature (T) is varied from $25^{\circ }C$ to $35^{\circ }C$ in $1^{\circ }C$ intervals. Each current signal contains 5,511 sample sets, with three current signals corresponding to the three phases for each fault type. In total, the dataset comprises 121,242 samples across 22 classes, including the normal operating condition. 80% and 20% of the data from the dataset has been taken for training and testing purpose respectively.

Data preprocessing pipeline

The data preprocessing pipeline encompassed signal sampling, wavelet decomposition, feature extraction, and normalization to enhance model efficacy in fault diagnosis for grid-connected PV inverter systems. Fault half power-frequency cycle waveforms were extracted, yielding 200 data points per sample at a 20 kHz sampling rate for a 50 Hz system, balancing computational efficiency with fault signature preservation. Discrete Wavelet Transform (DWT) using a 4th order Daubechies wavelet (db4) decomposed three-phase waveforms into approximation and detail coefficients via cascaded low-pass and high-pass filtering. Feature extraction was performed by computing Wavelet Detail Level Coefficient Energy (WDLCE), transforming transient signals into distinctive quantitative signatures. Min-max normalization scaled features to the [0,1] range, mitigating numerical disparities and enhancing model convergence. To ensure robustness, an 80/20 data split was used for training and testing, with k-fold cross-validation (k=5) applied to the training set, iteratively validating model performance across different partitions to minimize overfitting. Final model evaluation on the untouched test set confirmed the model’s ability to reliably identify fault signatures across diverse operational conditions.

Dual graph attention network architecture

The proposed DualGAT architecture builds upon the foundational work in graph attention networks while introducing novel components for robust fault diagnosis. This study begin by formally defining the fault detection task for three-phase photovoltaic inverters. The input data sequence consists of operational inputs $(a_i, b_i, c_i)$ for $i = 1, \dots , N$, where $y_i$ represents the corresponding operating conditions, and N denotes the total number of inputs. Our objective is to assign a fault diagnosis label $y_i \in Y$ to each observation $a_i$, where Y encompasses the set of possible fault types. The system is designed to identify 22 distinct fault types, including DC-link voltage anomalies, phase overcurrents, grid frequency deviations, voltage imbalances, ground faults, short circuits, thermal issues, and power tracking failures. The proposed fault detection framework comprises three primary components: the representation learning module, the DualGAT component layer, and the fault classifier. Figure 3 illustrates the complete architecture of our proposed system.

Fig. 3

The proposed neural architecture of Dual Graph Attention Network. The core part of this network paradigm is the feature extraction process. The DualGAT component is responsible for learning intuitive relation among multiple feature inputs.

DualGAT component layer

The DualGAT layer integrates fault architecture with system-aware context within a PV inverter system. This component is responsible for exploiting the inter-relational feature dependencies among all input features. The system consists of three essential modules: the interaction module, FeatureGAT mechanism, and TempGAT module. This methodology begin by defining the computational procedure for each module in the initial layer before extending this to multiple additional layers.

FeatureGAT component layer

The FeatureGAT module enables the distribution of fault information through a structured fault dependency graph, facilitating the integration of system structural data. The authors initially describe how to build the fault dependency graph, subsequently detailing the inference mechanisms employed by the FeatureGAT module. A fault dependency graph is defined as $G_{Feature} = (V_{Feature}, E_{Feature})$, where $V_{Feature}$ represents a set of nodes corresponding to key fault categories and $E_{Feature}$ denotes the adjacency matrix describing the dependencies between these fault types. In the context of three-phase photovoltaic inverter fault detection, each fault type is represented as a node. The authors incorporate multiple fault dependency types relevant to system dynamics, including overvoltage, undercurrent, and temperature faults, collectively referred to as $\mathscr {R}_{Feature}$.

The construction of this graph involves using historical fault data and predefined system relationships to model dependencies between fault types. Each node $v_{i}^{Feature}$ corresponds to a specific fault type $f_i$ and is initialized with a feature representation $P_i$. The edge $E_{Feature}[i][j]$ is assigned a dependency type $r_{i,j}^{Feature} \in \mathscr {R}_{Feature}$ if a connection between faults $f_i$ and $f_j$ is observed in historical or simulated fault data. Once the fault dependency graph is constructed, the FeatureGAT mechanism propagates and aggregates fault structural information across the nodes in the graph. Built upon the Graph Attention Network framework, it incorporates type coding to differentiate between fault dependencies. Specifically, for a given fault node $v_{i}^{Feature}$, the FeatureGAT aggregates information from neighboring fault nodes as follows:

$$\begin{aligned} \begin{aligned} \alpha _{ij}&= \textit{softmax}(\texttt {LeakyReLU}(x^{T} [W P_i \parallel W P_j \parallel e_{i,j}^{Feature}])) \\ P_{i}^{Feature}&= \sum _{j \in \textrm{N}_{i}^{Feature}} \alpha {ij} W P_j \end{aligned} \end{aligned}$$

(7)

where, $\alpha _{ij}$ represents as a function of node edge weight $v_{i}^{Feature}$ close to it $v_{j}^{Feature}$, while W and x are trainable parameters. The term $e_{i,j}^{Feature} \in \mathbb {R}^{|\mathscr {R}_{Feature}|}$ represents the one-hot encoding of the dependency type between nodes $v_{i}^{Feature}$ and $v_{j}^{Feature}$. The operator $\parallel$ denotes concatenation, $\mathscr {N}_{i}^{Feature}$ represents the set of fault nodes adjacent to it$v_{i}^{Feature}$, and $P_{i}^{Feature} \in \mathbb {R}^{z_h}$ denotes the node’s updated hidden representation after the FeatureGAT update, where $z_h$ is the obscured representation dimension. The updated obscured representations of all nodes are known as $P_{Feature} \in \mathbb {R}^{N \times z_h}$. In summary, the FeatureGAT in the initial layer is calculated as:

$$\begin{aligned} P_\textit{Feature} = \texttt {FeatureGAT}(P_\textit{u}, E_\textit{Feature}) \end{aligned}$$

(8)

TempGAT module

The TempGAT component propagates fault information on a temporal dependency graph to integrate time-based contextual details specific to the inverter’s fault types. The authors first define the process of growth of this temporal dependency graph, followed by the inference process of TempGAT on the developed graph. The temporal graph is defined as:

$$\begin{aligned} G_{\textit{Temp}} = (V_{\textit{Temp}}, E_{\textit{Temp}}) \end{aligned}$$

(9)

where $V_{\textit{Temp}}[i]$ or $v_i^{\textit{Temp}}$ represents the i-th temporal observation, with its representation initialized using the corresponding representation of features $P_i$. $E_{\textit{Temp}}$ is the matrix of adjacency that establishes the temporal dependencies connecting nodes (observations) according to fault characteristics and their progression over time.

For any $u_i$ and $u_j$, $E_{\textit{Temp}}[i][j]$ or $e_{i,j}^{\textit{Temp}}$ exists if they satisfy a temporal dependency type $r_{\textit{Temp}} \in R_{\textit{Temp}}$. After constructing the temporal dependency graph, TempGAT propagates and aggregates temporal contextual details across the graph nodes. The computation for the first neural stage can be expressed as:

$$\begin{aligned} P_{\textit{Temp}} = \textit{TempGAT}(P_{u}, E_{\textit{Temp}}) \end{aligned}$$

(10)

Communication module

To extract discrete information from the temporal and complex feature space, the authors implement a differential regularization technique that promotes divergence between the updated FeatureGAT and TempGAT module representations. The regularization strategy is formulated as:

$$\begin{aligned} \ell _{\textit{reg}} = \frac{1}{\Vert P_{\textit{Feature}} - P_{\textit{Temp}}\Vert _F} \end{aligned}$$

(11)

where, the subscript F implies the Frobenius norm. For the integration of the FeatureGAT and TempGAT modules to enable the exchange of relevant information between them, a mutual cross-attention mechanism has been used as a bridge. The computation process is described below:

$$\begin{aligned} \begin{aligned}&{\bf Q}_1 = \textit{softmax}(P_{\text {Feature}}W_1(P_{\text {Temp}})^T) \\&{\bf Q}_2 = \textit{softmax}(P_{\textit{Temp}}W_2(P_{\textit{Feature}})^T) \\&P_{\textit{Feature}}', P_{\textit{Temp}}' = Q_1P_{\textit{Temp}}, Q_2P_{\textit{Feature}} \end{aligned} \end{aligned}$$

(12)

where $W_1, W_2$ are adjustable weights and $Q_1, Q_2 \in \mathbb {R}^{N \times N}$ are temporary weights projecting from $P_{\text {Temp}}$ to $P_{\text {Feature}}$ and $P_{\text {Feature}}$ to $P_{\text {Temp}}$, respectively. Here, $P_{\text {Feature}}' \in \mathbb {R}^{N \times z_h}$ represents a projection from $P_{\text {Temp}}$ to $P_{\text {Feature}}$, and $P_{\text {Temp}}' \in \mathbb {R}^{N \times z_h}$ follows an similar principle.

Complete pipeline

The authors generalise the calculating method of the initial layer to continuously modify and communicate the structure of discourse information and system-aware contextual details over numerous levels afterwards. The full processes are described as below:

$$\begin{aligned} \begin{aligned} P_{\textit{Feature}}^{[l]}&= \textit{FeatureGAT}(D^{[l]}, E_{\textit{Feature}}) \\ P_{\textit{Temp}}^{[l]}&= \textit{TempGAT}(S^{[l]}, E_{\textit{Temp}}) \\ P_{\text {Feature}}'^{[l]}, P_{\textit{Temp}}'^{[l]}&= \textit{Inter}(P_{\textit{Feature}}^{[l]}, P_{\textit{Temp}}^{[l]}) \\ D^{[l+1]}, S^{[l+1]}&= P_{\textit{Feature}}'^{[l]}, P_{\textit{Temp}}'^{[l]} \end{aligned} \end{aligned}$$

(13)

where $D^{[0]} = S^{[0]} = P_u$ and $l \in [0, L-1]$.

Fault prediction

By integrating the results of the L-layer DualGATs, the study derives the most comprehensive expression $u_i$. The concluding representations is established using a Multi-Layer Perceptron.

$$\begin{aligned} \begin{aligned}&l_i = \text {ReLU}(W_h [h^{{Feature'}}_i \parallel h^{{Temp'}}_i] + b_h) \\&p_i = \text {softmax}(W_l l_i + b_l) \\&\hat{y} = \mathop {\textrm{arg}\,\textrm{max}}\limits _{k \in Y} p_i[k] \end{aligned} \end{aligned}$$

(14)

where, $\hat{y}_i$ is the predicted fault label for the inverter instance $u_i$. $h^{\text {Feature}'}_i, h^{{Temp}'}_i \in \mathbb {R}^{z_h}$ denote the i-th representation in $H^{\text {Feature}'}_{[L]}$ and $H^{{Temp'}}_{[L]}$, respectively. $W_h \in \mathbb {R}^{z_h \times 2z_h}, W_l \in \mathbb {R}^{d_e \times z_h}, b_h \in \mathbb {R}^{z_h}$, and $b_l \in \mathbb {R}^{d_e}$ are the adjustable variables of the MLP, and $d_e$ indicates the number of defect labels in the set of data.

Objective function

The objective is to reduce this proposed objective function:

$$\begin{aligned} \mathscr {L}_{\textit{total}} = \mathscr {L}_{\textit{CE}} + \lambda \mathscr {L}_{\textit{reg}} \end{aligned}$$

(15)

In Eq. (15), $\lambda$ represents the regularization coefficient.The notation $\mathscr {L}_{\textit{CE}}$ indicates the traditional cross-entropy loss, given as:

$$\begin{aligned} \mathscr {L}_{\textit{CE}} = -\sum _{\gamma =1}^{B}\sum _{i=1}^{N^{(\gamma )}} \log p_{\gamma ,i}[y_{\gamma ,i}] \end{aligned}$$

(16)

where, B indicates the total count of datapoints, $N^{(\gamma )}$ indicates the number of classes in the $\gamma$th dataset, and $y_{\gamma ,i}$ specifies the ground truth label calculated using a one-hot conversion. The goal of our training is to reduce the overall objective function $\mathscr {L}_{\textit{total}}$, which integrates the fault diagnosis component $\mathscr {L}_{\textit{CE}}$ with a regularisation. term $\mathscr {L}_{\textit{reg}}$, weighted by the coefficient $\lambda$.

Experimental results analysis

This section explicates about the structure of our dataset, the experimental parameters, environment, and settings. This study has also described both quantitative and qualitative results.

Experimental settings for diagnosis

The experiments were conducted using the PyTorch framework⁴⁵ (python version 3.11.0) on a machine attached with an Intel Core i7 processor, an NVIDIA 2090 GPU, and 16GB of RAM. The Adam optimizer was employed with hyperparameters set to $\beta _1 = 0.9$ and $\beta _2 = 0.999$, and a learning rate of 0.0001 was used for training the neural network. Xavier initialization was applied for kernel initialization. ReLU activation function has been adopted in the complete network. No normalization and regularization techniques are used while the training process. The neural architecture comprised five hidden layers to ensure adequate model capacity for the task at hand.

Result and discussion

The performance comparison between data-driven and statistical-based methods, as shown in Table 4, highlights the superiority of data-driven approaches for fault diagnosis in photovoltaic (PV) inverters. Among the neural-network-based methods, the propose DualGAT model achieves the highest results across all metrics, with a test accuracy of 97.35%, F1-Score of 0.941, Precision of 0.951, and Recall of 0.930, demonstrating its robust ability to capture both spatial and temporal fault patterns. Other temporal models, such as GAT and RNN, also exhibit strong performance, with accuracies of 95.18% and 94.12%, respectively, surpassing traditional methods like RF and SVM which achieve accuracies of 87.11% and 85.37%. Despite the statistical-based methods showing reasonable performance, they generally underperform compared to the more advanced deep learning techniques, with DT and BC being the most competitive in this category, achieving F1-Scores of 0.825 and 0.834, respectively. Overall, the results clearly indicate that data-driven approaches, particularly DualGAT, provide a significant advantage in accurately diagnosing faults under varying operational conditions. The training and testing accuracy and loss are depicted in Fig. 4. The figure justifies our results during the training process. to further substantiate the proposed DualGAT model’s advantages, the authors extended our comparative analysis by benchmarking it against several cutting-edge deep learning architectures that have recently demonstrated strong performance in fault diagnosis tasks. These include transformer-based models, temporal convolutional networks (TCNs), GRU with attention mechanisms, ResNet-1D, and InceptionTime, each representing a distinct class of temporal or multi-scale architectures capable of handling complex patterns in inverter signal data. Despite their architectural sophistication, these models generally fall short in explicitly modeling the physical and relational structure of PV systems. For instance, transformer and TCN architectures are highly effective in capturing temporal dependencies but lack inductive biases to represent spatial correlations among inverter components. GRU-attention and ResNet-1D show competitive precision and recall values but struggle to separate time-variant fault characteristics from system-level dependencies.

Table 4 Performance comparison of data-driven and statistical methods on various metrics. The best result for each metric within each category is highlighted in bold.

Fig. 4

The left-side figure presents the training and testing accuracy and the right-side figure shows the training and testing loss against 100 epochs using our proposed DualGAT model.

Fig. 5

This confusion matrix shows the classification accuracy of the DualGAT model in diagnosing 22 fault conditions for a three-phase inverter system. High diagonal values indicate accurate fault detection across most categories, with some minor misclassifications among similar fault types.

In Fig. 5, confusion matrix for the three-phase inverter fault diagnosis with 22 classes. Each cell represents the classification accuracy as a percentage for each class, with the diagonal showing the high accuracy rates for correct classifications. There are some key insights that can be drawn from the confusion matrix for the three-phase inverter fault diagnosis. Misclassifications are more common in certain off-diagonal cells, particularly among faults with similar fault mechanisms. For instance, faults involving pairs of IGBTs within the same bridge (e.g., $S 1-S 2, S 3-S 4, S 5-S 6$ ) show slight overlap, suggesting the need for additional feature extraction or model tuning to improve distinction among these conditions. In addition, fault pairs involving switches from different half-bridges (e.g., $S 1-S 4, S 2-S 5$ ) show some misclassification, which could be due to the similar impact these faults have on the inverter’s output signal patterns. This observation can guide future work in refining model sensitivity to these specific fault types. Nevertheless, Robustness in Single Switch Fault Detection: Single IGBT open-circuit faults (e.g., S1, S2, etc.) generally show very high classification accuracy, indicating that the model effectively captures the unique signatures of individual open-circuit faults. The healthy mode (NF) has a very low misclassification rate, which is crucial for avoiding false positives in fault diagnosis. This capability adds reliability to the model, ensuring that normal operation is accurately identified without unnecessary alerts.

Ablations

Performance under noisy situation

When modelling an inclusive system, specific considerations are initiated in every quantitative arrangement, such as precise calculations of the processes and measurements of the physical properties. These presumptions might not be entirely correct in every situation. There can be cases where the measurements are associated with uncertainties and errors⁶⁰. These uncertainties can be white noises that are included with the signal. Additionally, most of the systems behave linearly despite not being completely linear. Disruptions could result from a difference between the system’s actual behaviour and its assessed behaviour, as a result of noises. PV inverter systems are subject to a variety of environmental factors in addition to performing their function, therefore, noise is an important factor to take into account. The three-phase signals obtained from inverters are frequently muddled with interference signals such as degradation of parasitic resistance of inductors, electromagnetic noise in high power IGBTs, and the noise generated by the integrated apparatus⁶¹. The presence of noise distorts basic sinusoidal properties of the obtained waveform, which eventually disrupts the classification results of the learning algorithm. The averaged total of all the noises resembles a Gaussian distribution if the noise origin is thought of as an individual one. In order to verify the robustness of the suggested framework, white Gaussian noise was used in this research to corrupt the raw data. To depict the effect of noise, two redundant classes superimposed with noise at 7 dB of Signal-to-Noise Ration (SNR) were injected for normal condition and S1-S4 fault condition as exemplar. The Fig. 6 shows the waveform for both the classes without noise and with noise (after 0.15s).

Fig. 6

Noise injection of inverter conditions occurring at 0.15s (SNR of 7dB), where the current amplitude is in per-unit (p.u.): the normal condition and the S1-S4 fault condition.

The investigation show, the corresponding learning algorithm is capable of distinguishing between observable defects and disruptions brought on by white noise, while maximizing the effectiveness of the identification of actual failures. To evaluate its robustness, the entire dataset was injected with noise at a 7 SNR level and subsequently trained and tested using our model. The results obtained were satisfactory. The training and testing accuracy and loss - for the noise injected dataset—are depicted in Fig. 7.

Fig. 7

The left-side figure presents the training and testing accuracy (noise-injected) and the right-side figure shows the training and testing loss (noise-injected) against 100 epochs using our proposed DUALGAT model.

A confusion matrix is show for the classification performance after adding white Gaussian noise to the dataset in Fig. 8, which resulted in an overall accuracy drop to 93%. This matrix reflects a slight increase in misclassifications, as shown by more off-diagonal values compared to the previous, cleaner data version. This visualization provides insights into how noise affects the model’s ability to accurately differentiate between certain fault types, especially those with similar characteristics. The key insights based on the updated confusion matrix after adding white Gaussian noise to the dataset are - The overall accuracy decreased from 97 to 93%, indicating that the added noise has increased the model’s misclassification rate. This change suggests that the DualGAT network may be somewhat sensitive to noise, affecting its ability to consistently differentiate fault classes. There is also a noticeable rise in misclassification among similar fault types, especially those in the same bridge (e.g., $S 1-S 2, S 3-S 4, S 5-$ S6 ) and across half-bridges (e.g., $S 1-S 4, S 2-S 5$ ). The noise likely masks subtle differences between these conditions, causing the model to confuse them more frequently. This insight suggests the need for noise-robust feature extraction techniques. Double IGBT faults, especially those involving two switches in the same half-bridge (e.g., $S 1-S 3, S 3-S 5$, etc.), also show slightly more misclassification with noise. This result highlights the model’s need for enhanced fault discrimination for more complex fault types under noisy conditions. Although some misclassifications into fault categories are observed, the healthy mode (NF) still shows relatively low misclassification.

Fig. 8

This confusion matrix illustrates the performance of the DualGAT model in diagnosing 22 fault conditions for a three-phase inverter system with added white Gaussian noise, resulting in a reduced accuracies. The introduction of noise has led to increased misclassifications, particularly among similar fault types and double IGBT faults.

GAT component analysis

To evaluate the effectiveness of each component within our proposed DualGAT architecture for fault diagnosis in photovoltaic (PV) inverters, the authors conducted an ablative analysis. The results are presented in Table 5, showing the performance impact on F1-score, test accuracy, precision, and recall when key components of the model are removed.

Table 5 Ablative analysis of each component in the proposed neural architecture.

Effect of FeatureGAT

When the FeatureGAT component is removed, responsible for capturing fault dependencies, the model’s F1-score drops to 0.812 from the baseline score of 0.924 (with all components included). This decrease highlights the importance of FeatureGAT in accurately detecting fault relationships within the local components of the inverter system. The precision also decreases slightly to 0.823, indicating reduced confidence in the predicted fault labels. The recall drops to 0.801, which demonstrates a lower ability to capture all true faults.

Effect of TempGAT

Removing the TempGAT component, which integrates temporal context, results in a further reduction in performance. The F1-score decreases to 0.781, and test accuracy falls to 87.62%, demonstrating the critical role of temporal information in improving the model’s ability to capture evolving fault conditions over time. Both precision (0.794) and recall (0.769) are affected, indicating that temporal dependencies are essential for identifying recurring and time-dependent faults.

Effect of regularizer

Without the differential regularizer, the model’s F1-score remains relatively high at 0.835. However, both precision (0.846) and recall (0.819) show minor declines, implying that the regularizer contributes to balancing these metrics by encouraging the model to learn more diverse features. While the drop in performance is not drastic, the regularizer plays a role in refining the feature learning from both the FeatureGAT and TempGAT components, leading to more generalizable fault detection.

Effect of cross-attention

The removal of the mutual cross-attention mechanism results in a notable reduction in both F1-score and precision. This suggests that cross-attention, which allows the model to integrate complementary information between FeatureGAT and TempGAT, significantly enhances fault diagnosis. The recall remains relatively stable at 0.874, demonstrating that cross-attention is particularly effective in improving the accuracy of fault detection rather than increasing the number of identified faults.

All components active

When all components of the DualGAT architecture are active, the authors observe the highest performance across all metrics. The F1-score reaches 0.924, and test accuracy rises to 97.35%, showcasing the effectiveness of combining both spatial and temporal fault characteristics. The precision and recall demonstrate the model’s robust ability to accurately identify and generalize across different fault types within the PV inverter system.

Conclusion and future directions

This paper proposed a novel Dual Graph Attention Network (DualGAT) framework for fault diagnosis in photovoltaic (PV) inverter systems, integrating both spatial and temporal attention mechanisms to effectively capture fault characteristics under varying environmental and operational conditions. The key contributions include the design of a robust simulation-based PV inverter testbed, the generation of a diagnostic dataset using wavelet-based energy feature extraction, and the development of the DualGAT architecture incorporating differential regularization and cross-attention modules.

The model achieved a high diagnostic accuracy of 97.35

However, the current work is limited to simulation-based validation and is subject to computational complexity concerns in real-time deployment. To address these gaps, we recommend the following directions for future work:

• Dataset Generalization: Validate the model using real-world datasets and publicly available PV benchmarks to enhance applicability and generalizability.

• Advanced Feature Engineering: Investigate other signal decomposition techniques such as EMD or VMD, as well as deep learning-based feature extraction methods to further improve discriminative performance.

• Model and Architecture Optimization: Explore hyperparameter tuning, lightweight design variants, and integration with alternative architectures like TCNs or Transformers.

• Real-time Deployment: Adapt the model for deployment in edge or embedded systems through compression and optimization for low-latency inference.

• Fault Prognosis: Extend the framework to not only detect faults but also predict their progression over time for proactive maintenance planning.

By addressing these aspects, this research aims to contribute toward the development of intelligent, scalable, and deployment-ready fault management systems for future PV infrastructure.