Segmentation-enhanced approach for emotion detection from EEG signals using the fuzzy C-mean and SVM

Abstract

The analysis of EEG signals for determining emotion is one of the most important topics in the field of artificial intelligence. It can be applied in a wide variety of areas, such as emotional health care and the man/machine interface. The purpose of the paper is the demonstration that emotions may be identified using EEG recordings in the hybrid approach based on the differentiated support vector machine (SVM) models with various types of kernel functions, as well as fuzzy C-means. The EEG signal of two subjects was recorded with the help of the Muse headband; the signal data was described as positive, neutral, or negative emotions. A Gauss kernel was the second-best outcome (95.78%), and a linear kernel was the best outcome (97.66%). Precision, recall, and F1-scores were used in establishing the performance of the SVM technique in emotion classification in conjunction with the fuzzy C-means classification approach. Besides covering the discussion on the importance of kernel choice in achieving good performance in SVM-based models, the analysis also showed that there was a potential to use EEG-based emotion detection. Moreover, one-way ANOVA statistical analysis has expressed that the linear kernel did perform significantly better as compared to other kernels (p < 0.05). To confirm that the proposed system would be rather robust, other deep learning models (CNN-LSTM hybrids) were designed and tested, the results of which proved that they had similar performance and at the same time less accurate results than the linear SVM. These results indicate the efficacy of SVM and the optimization of kernel parameters along with the integration of fuzzy logic in recognizing emotions based on EEG records.

Introduction

Emotional processes are thus a critically important part of how we achieve rationality in situations that demand inspection, decision-making, and execution. They are affiliated with many aspects of human feelings, sensing, and moving. Therefore, the development of paradigms for using emotional signals for identifying emotions has become a moderately large research topic that has also been instrumental in enhancing BCI applications for social and clinical purposes¹. Scientists have provided two major models for emotions: dimensional and categorical. Whereas fear, joy, or sadness can be easily described semantically, such representations frequently fail to support the expression of more complex emotions in other languages. Theoretical frameworks such as dimensional models, on the other hand, propose that emotions should be described with reference to several dimensions, of which the arousal-valence space is probably the most familiar. Engl-emotions. This model categorizes emotions according to their valence from negative to positive and according to their arousal level from low to high².

One of the freshest trends in artificial intelligence is still the field of ‘affective computing’, which addresses the creation of systems recognizing and reacting to people’s emotions. Evaluative feelings and appraisals underlie the commonplace experience, including its behavioral, communicative, and even cognitive aspects. Affect recognition, which is a subfield of affective computing, has significant importance, especially in HCIs. A practical application of emotion recognition is neuromarketing, which involves examining or predicting the emotional tendencies of consumers to enhance advertisements, such as appraising responses to music³.

The present development of artificial intelligence and emotion identification has enriched people’s understanding of communication, decision-making, and intelligent systems. The research presented in Khare et al.⁴ provides a comprehensive and structured review of the approaches to emotion recognition published over the last 10 years of research in the field of physiological and physical signals. Gestures and voice are categorized under physical signals, while physiological signals include EEG, ECG, and eye tracking.

In Domínguez-Jiménez et al.⁵, the authors proposed a model with physiological data gathered from the wearable devices of participants to identify three emotions—neutral, sad, and humor—when the participants were watching emotion-inducing clips. Facial videos were recorded from 37 participants along with galvanic skin response (GSR) signals to introduce optical imaging and implement a support vector machine (SVM) model with 100% accuracy. Both time and frequency analyses were performed to evaluate the signal quality. Along the same line of thinking³, developed an emotion identification system using a valence/arousal model on an EEG signal that was preprocessed using DWT and ofter into the gamma, beta, alpha, and theta bands. Spectral features were taken from each of the bands and then normalized, reduced by PCA, and introduced to ANNs, KNNs, and SVM classifiers.

Further information focusing on the analysis of the EEG signal was given in Jafari et al.⁶, where works outlining the difficulties of emotion recognition using EEG data were considered. For recommendation, the study proposed that deep learning methods can be applied even more in terms of emotion recognition. For example, in Li et al.⁷, a multimodal classification framework was proposed for issues concerning emotion identification for EEG and electromyography (EMG) biosignals. Based on these signals, differential entropy features were introduced, and the classification was improved with the help of a multimodal long-short-term memory (LSTM) network that incorporated spatial and temporal profiles.

In Ahmad and Khan⁸, the authors proposed a fast and robust multimodal emotion recognition system that included signal heterogeneity and interpersonal variability by using spatial and temporal characteristic EEG and MEG signals. The users proposed their neural network model that took differential entropy from such signals and improved the recognition accuracy compared to single-modal signals, providing 95.89% and 94.99% arousal and valence detection, respectively, using the DEAP database.

The recent advances in artificial intelligence, especially deep learning, have had a great impact on medical diagnostics and on affective computing, respectively. Neural networks like Convolutional Neural Networks (CNNs), Long Short-Term Memory networks (LSTMs), and transformer models provide an effective method of deriving high-level representations out of raw EEG signals and do not need hand-crafted features. These models are so ideal in showing spatial patterns and the temporal patterns in biomedical signals. As a case in point, CNN-LSTM hybrids have now achieved impressive results in the presence of common neurological conditions, such as the detection of Parkinson disease in EEG signals, returning high accuracy and interpretability via explainable AI systems⁹. On a similar note, transformer models have also shown meaningful potential in early detection of schizophrenia through the use of attention mechanisms to identify meaningful parts of the EEG time series and thereby perform better than basic classifiers^10,11. Deep learning highly accurate models might need massive datasets and significant computational resources, even though they can discover complex arrangements. Alternatively, methods of machine learning such as SVMs have greater computational efficiency and explainability but lack the power of high-dimensional EEG features unless they are preprocessed with either dimensionality reduction or feature selection. Combining any of the above paradigms, such as deep feature extraction and robust/interpretable classification, by an ensemble or a hybrid strategy as suggested in our work tends to utilize the best of the two worlds on emotion recognition based on EEG signals¹².

In this study, we developed the following major research questions: (1) Is it possible to utilize a hybrid framework consisting of fuzzy C-means (FCM) clustering techniques coupled with support vector machines (SVMs) to enhance the performance of EEG-based emotion recognition considerably better than standalone classifiers? (2) What is the role of kernel selection of the SVM framework as it relates to the effect of classification accuracy across the various emotional states pronounced by the EEG signals? Is a linear kernel applied with fuzzy preprocessing more valid than more nonlinear types of kernels like circular, polygonal, or sigmoid in defining emotional states with noisy, low-sample EEG data? The theoretical as well as practical usages of affective computing in relation to educational practice can be unveiled with the help of these questions, which support our methodological design and evaluation of the performance.

The main contributions of this study are that we used top-notch machine learning techniques to decode EEG data and examine how different emotions affect EEG signals relative to different stimuli. By analyzing these alterations, we seek to enhance the accuracy of recognizing and forecasting emotional states. To this end, we develop and study a computationally superior classification model for FCM ensembles integrated with support vector machines (SVMs). This approach continues to accelerate the final fine-tuning of the feature extraction process; that is, emotion recognition is executed with the highest possible precision.

Moreover, Fuzzy C-Means (FCM) clustering was selected in this study because of the very features of this clustering method to deal with uncertainty and overlapping boundaries in emotion-labeled EEG data, an asset that is especially appropriate in the imprecise and nonlinear behavior of brain signals. In contrast to other bio-inspired algorithms, e.g., genetic algorithms, particle swarm optimization, and ant colony optimization, which are commonly computationally demanding and are only useful in global optimization problems, FCM directly and interpretably offers a soft clustering process. Instead of solid labels, it awards membership values and is therefore more appropriate to track the in-between states and multi-dimensional complexion prevalent in emotional reactions. Further, FCM can be very effectively applied in the hybrid model pipeline employed in this study, which is noted to have efficient convergence and great compatibility with subsequent learning, such as support vector machines (SVMs). Although other algorithms might be investigated in the future, FCM is a decent balance of the cost of computation and the ease of fuzzy emotional boundary adaptation and compatibility with the classification methods framework.

The initial hypothesis of this study was that a hybrid model combining fuzzy C-means clustering in a hybrid model of support vector machine classifiers will help to produce better and more significant accuracy and robustness of the emotion classification using EEG signals over the traditional models. The hypothesis that, based on the principle of reducing ambiguity that brainwave activity contains, fuzzy C-means offers a more detailed account of the varying states of emotions, whereas SVM, most notably, using linear and Gaussian kernels, would be appropriately able to produce adequately defined decision boundaries to classify such a complex signal. The associated hypothesis comes down to the notion that the recognition of emotion entails overlapping patterns in terms of EEG signals that can be better addressed by the corresponding models that can address fuzzy membership and nonlinear separation. Hence, a combination of these approaches was likely to deliver better performance, generalization, and clinical relevance in emotion recognition activities.

The remainder of the paper is structured as follows: “Literature review” section provides the literature review, “Materials and methods” section provides the method and material of the proposed approach, and “Results and discussion” section provides the implementation/analysis of the proposed approach. “Limitations of the study” section discusses the findings and implications of the model analysis, while “Conclusion” section presents the conclusion.

Literature review

In Samal and Hashmi¹³, the author proposed the idea of identifying emotion from multichannel EEG signals using MEEMD on the DEAP dataset, including time, frequency, and nonlinear features, in the calculation while using an ensemble tree classifier. In Hamzah and Abdalla¹⁴, the authors focused on deep learning networks in the area of EEG signal classification, paying attention to their potential for the automatic extraction of rich hierarchical representations from raw EEG signal data. This research will also serve as a guide for modern deep learning for different preprocessing techniques, signal representations, and network model architecture. Furthermore, the paper covers limitations detected during experiments, including variability of brain structure, electrode positioning and device positioning, all of which hinder modeling across devices and time sessions. In Xiaohu et al.¹⁵, the authors provide a review of recent related studies that use deep learning for EEG-based emotion recognition and demonstrated that this approach is capable of feature learning and classification. This paper addresses deep learning paradigms and datasets used in affective computing; issues regarding EEG-based emotion recognition; and new research ideas.

The authors in Hamzah and Abdalla¹⁶ focused on how emotions are detected and experienced in a virtual environment using EEG signals while bearing in mind that a real-time response system is fundamental. This paper focuses on the computational rate and user engagement in virtual environments and ways of dealing with awareness of emotions. The Tetromino feature generation function-based game was proposed in Tuncer et al.¹⁷ and is an idea of a new emotion classification system. The system extracts EEG channel features, and then, using their mutual relevance to the rest of the features, the most relevant characteristics are selected by the mRMR method for the classification of emotions. Then, a linear SVM is used for the final emotion classification, where the classification is made by a majority vote. In Xu et al.¹⁸, the authors found and compared seven approaches to channel selection for emotion recognition based on the DEAP dataset. EEG data are further partitioned into gamma, beta, alpha, and theta bands using the discrete wavelet transform (DWT) technique, and entropy and energy features are computed for each of these bands. Three approaches for channel selection, direct selection, mRMR, and experiential approaches, are compared to ELM for classification into seven emotions.

To our knowledge, multichannel EEG-based emotion classification using the TQWT and HCRNN was introduced in Zhong et al.¹⁹ with a spatiotemporal analysis of the proposed approach. The TQWT expands the EEG signal and obtains different subbands, and from these subbands, the mean absolute value and differential entropy features are extracted and converted to TFBS and subsequently used in deep model training. HCRNN, the combination of CNN and LSTM, learns both spatial and temporal features from TFBS for the classification of positive, neutral, and negative emotions, with impressive performance on the SEED dataset for emotions. A meta-analysis conducted in Yu et al.²⁰ A showed that N2 and P3 amplitudes are valid indices of inhibitory control abilities in IGD patients. Such findings are useful for better understanding the underlying neural substrates for behavioral inhibition disorders in IGD patients and for clinical application in early diagnosis and intervention.

In Fernandes et al.²¹, the authors compare simple classifiers with those of deep learning techniques and perform an analysis of emotions via EEG data. This work also presents a novel contribution by presenting a detailed comparative analysis of a wide range of deep learning and machine learning (DL/ML) methods in one study while also extending the literature on emotion recognition from EEG data using graph convolutional neural networks (GCNNs). These findings provide significant direction for constructing the sector of emotional neuroscience because they help elucidate the connection between affective states and neural activity. In Lim and Teo²², using EEG data, Lim and Teo formulated a game-induced emotion recognition method that utilizes an interpretable ruleset-based classifier. This method is innovative and exhaustively overcomes flaws in previous studies concerning emotion detection during video game interactions and indicates a very high level of accuracy in identifying participants’ emotions, including gender differences. Even though ruleset-based classifiers are slower during training, their advantages for modeling real-world applications can be quite substantial since they assist physicians in tracking changes in patients’ emotions with the help of parameters indicating different stages of such an emotion as well as shedding light on the connection between EEG parameters and emotions themselves.

Table 1 presents several studies have brought forward new deep learning architectures that were used to identify emotions based on EEG. Jinfeng et al.²³ proposed Fourier Adjacency Transformer (FAT) that first presented a + 6.5 profit over the then-state-of-the-art methods on the DEAP and SEED datasets. Teng et al. used 2D CNN-LSTM with the accuracy of 91.92 stability and 92.31 arousal on the matrices of different entropy values/differential entropy matrices. Caifeng et al.²⁵ integrated Transformer models with CNNs to achieve a high value of the structural similarity (SSIM) index of 0.98 in three datasets. Yue et al.²⁷ came up with a multi-scale residual BiLSTM with accuracies of 97.88% and 96.85% on DEAP, binary, and quadrantal classification. Liu et al.²⁷ presented a Transformer-based explainable ERTNet that impressed 73.31% and 80.99% in valence and arousal. The Model Echo State Network (MESN) presented by Yang et al.²⁸ attained accuracy of 65.3%, 62.5%, and 70% on valence, arousal, and stress/calm state, respectively. The critical point is that Shen et al. developed DAEST, an attention-based dynamic model that showed satisfactory results on SEED-V, 8SEED, and FACED datasets with a maximum of 88.1% accuracy in 3-class classification. Pan et al.³⁰ introduced a Dual Attentive Transformer model that generalized between the publicly released and privately released datasets with 64.43–85.27% accuracy between various types of class settings. Feng et al.³¹ used a CNN-Bi-LSTM with attention models on the Weibo COV V2 dataset to obtain a binary classification accuracy of 89.14%. Finally, there was Bagherzadeh et al.¹³, who presented an ensemble model with their best result on DEAP (98.76%) and MAHNOB-HCI (98.86%), demonstrating the effectiveness of ensemble learning in emotion recognition using EEG.

Table 1 Summarize state-of-the-arts in 2024–2025.

There are a few research gaps in the sphere of recognizing emotions based on EEG. To begin with, most of the available studies have a strong dependency on either classical machine learning or deep learning algorithms alone, using only fuzzy logic and hybrid models combining concept/kernelizations such as ensemble methods and kernel-based classifiers, such as SVM. Secondly, there has been no systematic study into the effects of each type of SVM kernel in enhancing classification accuracy among emotion classes. The other gap is that the preprocessing flexibility and feature improvement through clustering, such as fuzzy C-means, that have the potential to enhance the interpretability and robustness of a model are not well addressed. Furthermore, some of them assessed the performance of the models based on accuracy or F1-score, and not many of them put a focus on specificity, ROC-AUC rates, and multi-perspective frameworks evaluation. Such lapses highlight that the comprehensive and hybrid methodology, as in this work, which uses fuzzy clustering and diverse SVM kernels to promote the emotion classification in EEGs with enhanced feature discrimination and effective validation, is required and desirable.

Materials and methods

Fuzzy C-means

The fuzzy C-means (FCM) algorithm, a type of clustering, can be useful for organizing data where the clusters are ambiguous or overlap because it is based on the idea that the values of memberships provide degrees rather than intervals. In traditional strict clustering algorithms such as k-means, a data point can be assigned to only one cluster; however, when using FCM, the same data point can be assigned to different clusters to varying degrees depending on the values of membership ranging from 0 to 1⁴⁰.

The FCM algorithm operates by minimizing an objective function that accounts for both the distance between each data point and the cluster centers and the degree of membership. The objective function is given by⁴¹:

$$J_{m} = \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{C} u_{ij}^{m} \,|x_{i} - c_{j} |^{2}$$

where ${\text{J}}_{{\text{m}}}$ is the objective function to be minimized. N is the total number of data points. C is the number of clusters. ${\text{x}}_{{\text{i}}}$ represents the i-th data point. ${\text{c}}_{{\text{j}}}$ represents the center of the ${\text{j}}$-th cluster. ${\text{u}}_{{{\text{ij}}}} { }$ is the degree of membership of data point ${\text{x}}_{{\text{i}}}$ in cluster ${\text{c}}_{{\text{j}}}$. m is the fuzziness parameter, which controls the degree of fuzziness in the clustering process (typically m > 1).

The membership values ${\text{u}}_{{{\text{ij}}}}$ are updated at each iteration of the algorithm and are calculated as follows:

$$u_{ij} = \frac{1}{{\mathop \sum \nolimits_{k = 1}^{C} \left( {\frac{{\left| {x_{i} - c_{j} } \right|}}{{\left| {x_{i} - c_{k} } \right|}}} \right)^{{\frac{2}{m - 1}}} }}.$$

This equation ensures that the closer a data point is to a particular cluster center, the higher its membership value is for that cluster.

The cluster centers ${\text{c}}_{{\text{j}}}$ are updated using the following equation:

$$c_{j} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} u_{ij}^{m} \,x_{i} }}{{\mathop \sum \nolimits_{i = 1}^{N} u_{ij}^{m} }}.$$

This process is repeated iteratively until convergence is achieved. Based on general conventions, convergence is measured by the threshold for the distance between cluster centers or between membership values for different iterations.

Support vector machine

A support vector machine (SVM) is a supervised machine learning algorithm that is used mainly in the classification domain. It operates under the principle of selecting the proper hyperplane that partitions the data points of various classifications in high dimensions of feature space properly. For each class, SVM tries to find the largest separation margin between classes, where the margins are the area around the hyperplane and the nearest data points of a class known as support vectors are classified with the maximum margin. This maximization makes SVM capable of success regardless of the noisy and complicated type of data fed to it because, again, the margin is maximized⁴².

Mathematically, given a set of training data $(\{ \left( {x_{i} ,y_{i} } \right)\}_{i = 1}^{N} )$, where $x_{i}$ is the feature vector and $y_{i} \in \left\{ { - 1,1} \right\}$ represents the class label, the SVM solves the following optimization problem⁴³:

$$\mathop {\min }\limits_{w,b} \frac{1}{2}|w|^{2} \quad {\text{subject}}\;{\text{to}}\quad y_{i} \left( {w \cdot x_{i} + b} \right) \ge 1\,\forall i$$

where ${\text{w}}$ is the weight vector defining the orientation of the hyperplane. $b$ is the bias term that shifts the hyperplane. $y_{i}$ is the class label of the data point $x_{i}$.

In cases where the data are not linearly separable, the SVM employs a soft margin by introducing slack variables and minimizes the following modified objective function:

$$\mathop {\min }\limits_{w,b} \frac{1}{2}|w|^{2} \, + C\mathop \sum \limits_{i = 1}^{N} {\upxi }_{i} .$$

where $\left( {{\upxi }_{i} \ge 0} \right)$ are the slack variables and $C$ is the regularization parameter that controls the trade-off between maximizing the margin and minimizing classification errors.

For analyzing nonlinear data, it is possible to extend the SVM by the kernel trick. The kernels work in high-dimensional space, while the SVM does not process the data in that space. Different kernels can be applied depending on the nature of the data:

Linear kernel

The simplest kernel is used when the data are linearly separable in the original feature space. The decision function for the linear kernel is^44,45:

$$K\left( {x_{i} ,x_{j} } \right) = x_{i} \cdot x_{j} .$$

This approach is often used for datasets where a linear relationship between features can adequately separate the classes.

Polynomial kernel

This kernel allows for polynomial decision boundaries. This approach is useful when the relationship between the features and labels can be effectively modeled with higher-order polynomials. The polynomial kernel is defined as^46,47:

$$K\left( {x_{i} ,x_{j} } \right) = \left( {{\upgamma }\,x_{i} \cdot x_{j} + r} \right)^{d}$$

where ${\upgamma }$, $r$, and $d$ are kernel parameters that control the curvature and complexity of the polynomial decision surface.

Gaussian kernel

The Gaussian kernel is widely used when the data are not linearly separable. It maps the data points into a higher-dimensional space where linear separation is possible. The RBF kernel is defined as^48,49:

$$K\left( {x_{i} ,x_{j} } \right) = \exp \left( { - {\upgamma }|x_{i} - x_{j} |^{2} } \right)$$

here ${\upgamma }$ is a parameter that determines the spread of the Gaussian function. A small ${\upgamma }$ indicates a large influence of individual points, while a large ${\upgamma }$ indicates closer neighbors.

Sigmoid kernel

The sigmoid kernel, which is like the activation function used in neural networks, can model data with a nonlinear boundary. It is defined as⁴⁴:

$$K\left( {x_{i} ,x_{j} } \right) = \tanh \left( {\upgamma \,x_{i} \cdot x_{j} + r} \right).$$

This kernel is particularly useful in binary classification problems where the data follow a nonlinear distribution.

Random Forest

Through ensemble learning, Random Forest produces powerful predictive models by combining multiple decision trees for better prediction accuracy. Random sampling produces training subsets for each decision tree, which helps the model maintain diversity as well as suppressing overfitting. The combination of results through the voting protocol for classification while employing averaging regression methods contributes to making the model more robust and generalizable. The system performs excellently in dealing with large datasets at an optimal runtime level. The resistance of Random Forest to handling missing information together with outliers makes it a dependable solution across different application fields. The model delivers important scores, which enable researchers to determine which variables matter most within their dataset. The algorithm speeds up training time on extensive datasets through its ability to perform parallel processing. This technique finds wide practical use in finance together with healthcare applications and image recognition because it delivers remarkable predictive results. Random Forest enables users to deploy it without complex hyperparameter adjustments due to its ease of application. This model demonstrates flexibility and performance efficiency when used for both categorization and regression work⁵⁰. The hyperparameters of random forest used in this study are presented in Table 2.

Table 2 Random Forest hyperparameters.

Long short-term memory

Long short-term memory (LSTM) functions as a recurrent neural network (RNN) with the special ability to process sequential data through solutions for the vanishing gradient issue. The system contains memory cells that use three essential gates named input, forget, and output, which control data movement throughout the network. The input gate enables new information entry, and the forget gate determines the process of discarding data before the output gate decides the final output. The architectural design of LSTM allows it to identify extended dependencies in sequential data for applications such as time-series forecasting as well as speech recognition and natural language processing. Unlike traditional RNNs, LSTM retains relevant past information over extended sequences. The successful implementation of LSTM models depends on the careful adjustment of multiple hyperparameters like hidden unit count along with learning rate and batch size values. Dropout serves as an overfitting prevention technique that boosts the model’s generalization capabilities. The processing capabilities of bidirectional LSTM include moving through information from both beginning to end and end to beginning. CPU acceleration stands as a vital tool for executing LSTM network training operations since these networks demand intense computational capability. LSTM presents an effective solution for processing sequential data analysis problems⁵¹. The hyperparameters of LSTM used in this study are presented in Table 3.

Table 3 LSTM hyperparameters.

Convolutional neural networks

Convolutional neural networks (CNNs) represent deep learning models devoted to analyzing grid-based information, which includes images together with videos. These networks utilize convolutional layers to filter data patterns in images while pooling layers simultaneously decrease dimensions and computational requirements. Activation functions, including the ReLU function, act as tools for introducing non-linearity, which makes models better at recognizing complex patterns. The final part of the network includes fully connected layers that combine detected features for performing regressive or classificatory operations. CNNs provide superior results for computer vision work because they excel at identifying objects, recognizing images, and performing medical image processing. To achieve better performance, CNN layers need to find the right combination of depth and filter layers. Models achieve better performance through dropout and batch normalization, which act as regularizing techniques for overfitting prevention. The training of CNNs depends on extensive labeled datasets, which commonly use data augmentation to develop better generalization capacities⁵². The hyperparameters of CNN used in this study are presented in Table 4.

Table 4 CNN hyperparameters.

Table 5 provides an extensive overview of mathematical symbols, hyperparameters, and their definitions used in this study to promote transparency. Such a recap also makes the interpretation and reproduction easier for readers who are less familiar with some variables or tuning parameters.

Table 5 Summary of parameters and their descriptions.

Proposed approach

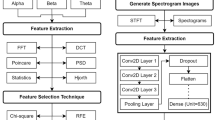
Figure 1 illustrates the proposed method for detecting emotions from EEG signals. There is a preprocessing stage, which is the initial step where the raw EEG data are first normalized, and the features are encoded to the same input. This is followed by using fuzzy C-means clustering in the next stage as a segmentation tool to determine the membership level that represents the emotional classes. Finally, another feature set is created with both the segmented features and signal features as well as the refined derived emotional sets. Using an SVM classifier, emotions are classified into positive, neutral, and negative states once the combined feature set is split into training and test data. Finally, several measures are used to confirm the effectiveness of the framework for detecting emotions from EEG signals.

Fig. 1

Proposed model architecture.

Preprocessing layer

In the preprocessing layer, the raw EEG data, along with their corresponding emotion labels, were loaded. The features were separated from the labels (positive, neutral, and negative emotions). The emotion labels were then encoded into numerical values using label encoding to facilitate processing. The EEG features were standardized to scale the data according to the mean (0) and standard deviation (1). This normalization step improves model convergence and accuracy by eliminating variations in scale across the features.

Segmentation layer

In the segmentation layer, fuzzy C-means are applied to determine the membership values of the data points within the given clusters. C-means clustering fuzzy clustering is an important part of feature segmentation in EEGs. Subsequently, the FCM algorithm employs standardized EEG signals to define the degree of membership of each data point into one of three clusters: positive emotional state, neutral state, and negative emotional state. Fuzzy FCM is designed in such a way that each record can be a member of more than one cluster; therefore, this method is different from other methodologies of clustering that make a record a member of only one cluster. This results in better segmentation of the EEG data. By using these membership values, the degree of relationship between the data points and clusters can be measured, and the resulting set of values can be combined with the original feature set of the collected EEG signals. The segmented patterns seen through the fuzzy clustered features are incorporated in this feature space in addition to the original signal features.

Classification layer

A support vector machine (SVM) kernel is used in the classification layer to classify emotional states based on the enhanced feature set from the segmentation layer. The enriched features included the raw EEG data and the fuzzy membership values generated by fuzzy C-means clustering of the EEG dataset, which should provide additional information for classification. SVMs have been found to be effective when applied to problems involving high-dimensional data because the use of a hyperplane makes it easy to expand the margin and enhance the discrimination between three types of emotions: positive, neutral, and negative. Additionally, the multiple kernels used in the model allow for linear and nonlinear decision boundaries for the relationships within the data. The classifier is subsequently trained and executed using both feature sets. Adding fuzzy membership values to the feature set expands the decision region and leads to increased classification accuracy. This approach is beneficial for SVMs because the emotions associated with each word should not only be distinct from other emotions but also be similar to other instances of the same emotion.

Evaluation layer

In the evaluation layer, several metrics and visualizations are provided to examine the efficiency of the proposed framework to obtain a clear understanding of the model’s ability to identify emotions. Hence, to estimate the overall accuracy of the predicted emotional states, the classification results are carefully evaluated. The confusion matrix of the proposed approach indicates the number of correct and incorrect predictions for each of the major emotional categories, positive, neutral, and negative; the results are reviewed along with the overall visualization of the results and may be able to identify major misclassification issues. For the accuracy of the model in identifying all emotions, the abovementioned classification report further breaks down the performance of the model and gives the F1 score, precision, and recall for each category. The area under the curve (AUC) is subsequently derived to measure the accuracy of the model in distinguishing between emotional categories, and the ROC curve is defined and used to plot the number of true positives versus false positives. This is one of the reasons why this proposed framework is presented in a multifaceted manner, as its usefulness and weaknesses are well documented to provide a comprehensive picture of the proposed framework.

To provide a clear overview of the evaluation process of the model performance, we caught the key measurement parameters carried out in this research, as shown in Table 6. These metrics suggest ideas as to how well the classifier can differentiate between the states of emotions and can be used to interpret the usefulness and efficiency of the proposed procedure.

Table 6 Summary of performance evaluation metrics.

To provide the computational efficiency of the proposed models, we provide an estimate of the floating-point operations (FLOPs) along with the trainable parameters of each deep learning architecture. FLOPs are one of the usual measures of complexity in terms of computing, correlating to the number of arithmetic operations to be done in the course of forward inference. The CNN-LSTMs became more complex with the addition of both spatial and temporal processing layers, and the GRU type of model is relatively light. The computation cost incurred by using fuzzy C-means clustering is quite small because it is used only once in preprocessing. Table 7 provides a comparison of the FLOPs count and the number of parameters estimated of all the models implemented. Pathway PCA (PPCA) and pathway logistic regression (PL) values were estimated by standard profiling tools in 10 s TensorFlow and model summaries assuming an input dimension consistent with our EEG data.

Table 7 Computational complexity of proposed models.

Hyperparameters values of hybrid model

The basic hyperparameters employed in our suggested hybrid model are summarized in Table 8, comprising the fuzzy C-means, the support vector machine settings, and a neural network (CNN and LSTM). This summary perspective enables readers to have a clearer idea of how models behaved and what parameter-adjustment strategies were implemented in this work.

Table 8 Hyperparameters values in the proposed model.

Results and discussion

Dataset description

The dataset consists of EEG brainwave data collected from two individuals (male and female) using a Muse EEG headband, which captured signals from four positions. The following muscle activations were detected using dry electrodes: TP9, AF7, AF8, and TP10. The recordings included three valence categories: positive, neutral, and negative for each of the 3-min and 6-min segments of neutral rest data. Figure 2 shows a visualization of the EEG brainwave data, which may correspond to signal changes at regular time intervals. These vertical spikes are proportional to the change in the amplitude of the EEG signal relative to the electrical activity of the brain, depending on the electrode. The x-axis generally refers to time, and the y-axis refers to the amplitude or intensity of the captured EEG signals. Three of these parameters describe the real-time EEG data of rapid changes in brain activity in positive, neutral, or negative states^53,54,55.

Fig. 2

Sample features fft_0_b through fft_749_b.

Results

In this section, we present classification results obtained from implementing hybrid CNN-LSTM model, CNN-LSTM with random forest, Hybrid CNN-LSTM with fuzzy c-means and hybrid support vector machine (SVM) with fuzzy c-means models using different kernels. The activation functions available are the linear, polynomial, Gaussian, and sigmoid activation functions. Moreover, each kernel provides its own approach in the definition of decision boundaries, which in turn influences the ability of the constructed emotional interface model to differentiate between three emotional states: positive, neutral, and negative.

Experiemnt 1: hybrid CNN-LSTM model

A hybrid model uses Convolutional Neural Networks (CNN) and Long Short-Term Memory (LSTM) networks to identify emotions from EEG signals. The EEG dataset first undergoes loading before feature extraction proceeds toward reshaping the information to create a 4D array suitable for CNN operation. The data requires label encoding combined with one-hot encoding before it can be used for categorically classifying emotions (positive, negative, and neutral). The spatial features within EEG data are captured through CNN layers followed by max-pooling layers that lower dimensions while maintaining essential information. Time-dependent emotional recognition needs the LSTM layer to process the data array output by CNN layers. The LSTM layer requires the array to be reshaped first. Following the LSTM component, the model adds fully connected layers to extract additional features, and the output layer applies SoftMax activation for predicting emotional classes.

We use categorical cross-entropy loss to train the processed data while optimizing it with Adam. The test set data undergoes performance evaluation for calculating accuracy alongside precision, recall, F1-score, specificity, and drawing the ROC curve. Visualizations of the model performance present three elements, including a confusion matrix with a classification report and ROC curve plots for thorough assessment. The model demonstrates 85% success in test phase emotion detection from EEG signals after obtaining proper training. The combination of CNN and LSTM frameworks enables optimal spatial and temporal pattern discovery, which makes this approach a favorable method to detect emotions using EEG signals.

Table 9 shows the hybrid CNN-LSTM model demonstrates its performance for classifying three categories, namely NEGATIVE, NEUTRAL, and POSITIVE, through evaluation metrics that include precision, recall, and F1-score. The model demonstrates exceptional performance on the negative class since it reaches a precision of 0.81 with a recall of 0.97 and an F1 score of 0.88, thus indicating superior negative instance detection with high recall. The NEUTRAL class shows robust performance, getting an F1 score of 0.84 at the same time it meets 0.79 precision and 0.90 recall scores, which indicates accurate detection of neutral examples yet with limited precision. The POSITIVE class achieves the least effective results among all classes because the model has 0.78 precision yet a very low 0.51 recall, leading to an F1 score of 0.62. The model demonstrates difficulties with recognizing positive examples since it tends to classify them as other classification categories. The combined precision-recall score across all classes reached a rate of 0.79 alongside 0.80 in recall and 0.78 in F1-score, which suggests a decent model execution but needs further improvement, mainly to recognize positive cases accurately. Performance improvement for less frequent classes can be achieved through data balancing methods along with fine-tuning procedures and class-specific weighting strategies.

Table 9 Classification results for hybrid CNN-LSTM model.

Figure 3 depicts the accuracy and loss of the suggested CNN-LSTM of the training and validation performance across the epochs. Examining the left plot, it can be observed that the accuracy of training and validation increases steadily, whereby the validation accuracy is always at par or just slightly above training accuracy, which is a good sign of generalization and overfitting with no or minimal overfitting. In the right plot, the training and the validation loss have shown a sharp decline in the first few epochs, and subsequently they have tapered off, and there is no notable difference between the training and the validation loss. This conclusion implies that the model is convergent and does not sacrifice one aspect of learning and generalization over the other. In general, the figure proves the effectiveness and stability of the CNN-LSTM model in identifying emotional states in EEG.

Fig. 3

Accuracy and loss for CNN-LSTM model.

Experiment 2: CNN-LSTM with Random Forest

The model uses deep learning algorithms and machine learning methods to execute effective emotion classification of EEG brain signals. The EEG data needs preprocessing before it can fit into a CNN-LSTM architecture through feature reshaping and label encoding procedures. The CNN layers extract spatial features that exist in EEG signals as the LSTM layer identifies temporal dependencies present in these signals. The Random Forest classifier receives extracted features for performing classification after the training process. A training process using a three-class emotional dataset with positive, neutral, and negative classification evaluates with accuracy, precision, recall, and F1-score assessment metrics.

The optimization process combines Principal Component Analysis (PCA) to extract refined features from EEG signals, which reduces their dimensions without losing important details. A Random Forest classifier containing 100 decision trees undertakes the learning process of detecting different emotional states. A high level of model accuracy becomes evident by analyzing the confusion matrix and classification report that shows the results. The fusion of deep learning feature extraction with machine learning classification functions as a robust method for EEG-based emotion detection through an efficient equation between predictive efficiency and computation speed.

Table 10 shows the hybrid CNN-LSTM with Random Forest obtained high success rates for determining NEGATIVE and NEUTRAL samples but demonstrated lower success on POSITIVE classes. The model demonstrates its best results in NEGATIVE class classification at a precision of 0.81, recall of 0.90, and F1 score of 0.85, which ensures high negative instance recognition. The NEUTRAL class demonstrates balanced performance across all metrics because it achieves 0.82 precision, F1 score, and recall metrics, which indicate precisely regulated classification accuracy. The model exhibits the lowest performance among the classes for the POSITIVE category since it obtains a precision of 0.68 and a recall of 0.60 with an F1 score of 0.63. This evidenced the challenge of correctly evaluating positive data points. The combination of CNN-LSTM with Random Forest achieved an overall balanced performance (0.77 Precision, 0.78 Recall, 0.77 F1-score), though the Random Forest addition succeeded in improving NEGATIVE class recall but did not significantly advance POSITIVE class identification. Performance enhancement demands class-specific weighting and data enhancement techniques as well as hyperparameter modification to optimize results, particularly for minority classes.

Table 10 Classification results for hybrid CNN-LSTM with random forest model.

The training and validation performance of the CNN-LSTM model with the combination of a random forest classifier can be seen in Fig. 4. Training and validation accuracy curves with epochs are exhibited in the left subplot. The two curves show a steady monotonic increase, meaning that the model is learning and generalizing well on unseen data. According to several epochs, the validation accuracy is a little bit higher than the training accuracy, which indicates a good generalization and no overfitting. The appropriate loss curves are depicted by means of the right subplot. The loss of training converges steadily, and the loss of validation converges in the early epochs, but it starts to grow slightly in later epochs, showing some signs of mild overfitting or variance caused by ensemble decision boundaries of Random Forest. In general, the model has a good capacity to classify, and the accuracy and loss on the training and the validation sets are also good, which signifies the effectiveness of temporal-spatial features of deep and enhanced CNN-LSTM and robust decision of Random Forest.

Fig. 4

Accuracy and loss for CNN-LSTM with Random Forest.

Experiment 3: hybrid CNN-LSTM model with fuzzy C-means

A combination method applies Convolutional Neural Networks (CNNs) and Long Short-Term Memory (LSTM) networks together with Fuzzy C-Means clustering during data preprocessing when classifying emotions through EEG signals. Data preprocessing begins with the model through loading and preparing the EEG information, during which it utilizes label encoding and one-hot encoding on the target variable. Fuzzy C-Means clustering detects similarities between EEG features to establish three clusters that correspond to the emotions of positive, neutral, and negative. The clustering process enhances the precision level of data handling by allowing greater flexibility for underlying variations while improving classification performance. The data division into training and test groups diagnoses the CNN-LSTM hybrid architecture that identifies spatial characteristics and temporal patterns within the EEG signal waveforms for feature compatibility.

This model contains spatial-feature-extracting CNN layers that precede temporal-dependency-detecting LSTM layers built to handle inherent EEG signal patterns. The neural network contains two convolutional components together with max-pooling and dropout layers to prevent overfitting during training. The data undergoes reshaping after the CNN layers to enable passage into an LSTM layer, which processes the temporal sequences. Equipped with fully connected layers, the model reaches its output point where the emotional categories are classified through a SoftMax output layer. Performance evaluation of the model happens through accuracy, confusion matrix, and classification report metrics, while training occurs with categorical cross-entropy loss and Adam optimizer. The model achieves enhanced performance by adding a Support Vector Machine (SVM) classifier to the feature extraction processes of CNN-LSTM, which enhances the predictive abilities. The end-to-end process for the combined model consisting of training and evaluation followed by visualization generates highly accurate results for EEG signal emotion detection.

According to the results presented in Table 11, the hybrid CNN-LSTM with the fuzzy logic model successfully distinguishes NEGATIVE and NEUTRAL classes but possesses difficulties with POSITIVE classification accuracy. Most negative instances are precisely classified by the NEGATIVE class with the highest achievable designation values consisting of 0.81 precision alongside 0.94 recall and 0.87 F1-score. The NEUTRAL class demonstrates successful classification through model accuracy indicators that reach 0.73 precision and 0.89 recall, together with an F1 score of 0.80. The POSITIVE class demonstrates the most challenging performance metrics since it produces 0.72 precision, 0.43 recall, and 0.53 F1-score, respectively. This difficulty suggests incorrect positive sample detection frequently labels data as different classes. This model’s average performance measures show 0.75 precision, 0.76 recall, and 0.74 F1-score, thus demonstrating that fuzzy logic improves negative and neutral instance detection while facing challenges with positive class recognition. The general classification performance can probably be improved through better adjustments of fuzzy membership functions or utilization of class balancing approaches.

Table 11 Classification results for hybrid CNN-LSTM with Fuzzy logict model.

Figure 5 shows the training and validation performance of the hybrid CNN-LSTM model with Fuzzy C-Means clustering. The left subplot depicts the gradual and consistent rise in both accuracy in training and accuracy in validation, where the accuracy of the validation was a bit better than that of training in most epochs. This implies that the model should be generalizing appropriately to unobserved data, and it is not overfitting. The training and validation loss graphs on the right side indicate that the results are good; the curves sharply drop at the first stages of training and smooth out to a minimal point, which means that training is effective, and the process of optimization is stable. The fact that validation loss is lower and more stable than the training loss indicates that before being passed to the classification step, the quality of features was improved by the fuzzy C-means clustering, which leads to better differentiation between the classes of emotions. In sum, this number shows the strength and effectiveness of the hybrid technique of learning discriminative EEG patterns to recognize the emotional states.

Fig. 5

Accuracy and loss for hybrid CNN-LSTM model with fuzzy C-means.

Experiment 4: linear SVM with fuzzy C-means

Table 12, which shows the classification results of SVM with a linear kernel, indicates that the model has very high accuracy for all three emotional classes. Again, the precision for the negative and positive classes of events is 0.97, and for the neutral class, it is 0.99, which is almost perfect and represents a very low false positive rate. The same is true for the recall values, which are very high: negative (0.98), neutral (0.99), and positive (0.96), i.e., great recall for the actual instances of each class. For the negative and positive classes, the F1 score was 0.97, while for the neutral class, it was 0.99. The model is very good in terms of both precision and recall. However, the average precision, recall, and F1 score are 0.98, and the average test accuracy is 97.66%, which indicates that an SVM with a linear kernel is well suited for distinguishing between the three emotional states with a negligible error rate.

Table 12 Classification results for the linear SVM.

Experiment 5: polynomial SVM with fuzzy C-means

Table 13, which depicts the class distribution of the selected SVMs with a polynomial kernel, indicates that the classification performance varies between the three emotional classes. The precision, recall, and F1-score of the neutral class were 0.97, 0.96, and 0.97, respectively, which is evidence that the model does equally well in recognizing this emotional state. The negative class was observed to have a slightly lower recall score of 0.83 for this property; this may mean that there are some instances where the class is negative, but the model fails to put them right under this category. On the positive side, the high precision (0.95) indicates that the tendency of the model to correctly classify an instance that is of the positive class is (0.81); however, a recall of (0.93) was achieved, meaning that there are few instances of false positives, but all positive cases are recovered. All three metrics are quite low, with average values of 0.91 for all the classes and an average test accuracy of 90.87%, indicating that the polynomial kernel is reasonably good but not as perfect as the linear kernel in previous outcomes. The relative performance within classes is shown by the polynomial kernel, where increases in accuracy are met with some decline in both precision and recall of classes by the classifier.

Table 13 Classification results for the polynomial SVM.

Experiment 6: Gaussian SVM with fuzzy C-means

Table 14 shows that the SVM classifier with a Gaussian kernel can classify the emotional data with high accuracy for each of the emotional classes. For the negative class, the model achieves 95% precision in distinguishing between negative instances and 5% precision in distinguishing false alarms out of all nonpositive instances. The recall of 098 reveals that the model is indeed extremely precise at identifying almost all actual negative cases in the data; hence, an F1-score of 096 stably pluses the strength of the developed model in terms of precision without sacrificing the recall of negative cases too much, that is, 098. For the Neutral class, the precision is outstanding at 0.99, so it is almost perfect at identifying objects in the neutral class. The recall of the model is 0.97; it can categorize nearly all true neutral data points. It has an F1-score of 0.98. In the Positive class, the performances for precision, recall and F1-score are 0.94 and 0.93, respectively, indicating that the model performs equally well in classifying positive emotion states. Therefore, on average, the precision, recall and F1-score are 0.96, and the average test accuracy is 95.78%, emphasizing the robustness of the model with all classes of emotions in the dataset.

Table 14 Classification results for the Gaussian SVM.

Experiment 7: sigmoid SVM with fuzzy C-means

Table 15 describes the classification results for the SVM with the sigmoid kernel. For the negative class, the resulting model yields a precision of 0.81, a recall of 0.92, and an F1 score of 0.86, revealing that although the model captures most of the negative samples, the precision decreases slightly. For the Neutral class, the performance is almost flawless, with a precision of approximately 0.98 and the same recall, leading to an impressive F1-score of 0.98, showing that the model developed in this paper provides excellent predictions in identifying the absence of any specific emotion for the individual. The precision of the class positive is 0.89, whereas the recall is 0.76, which gives an F1-score of 0.82. This indicates that the model appears to forget all the positive samples slightly but is good at it when it does so. On average, the precision is 0.89, as are the recall and F1-score, suggesting that the average test accuracy is 88.99%, while the classifier is performing reasonably well and does not optimize performance across all classes with weakness in the positive emotional state.

Table 15 Classification results for the sigmoid SVM.

Discussion

The Linear SVM with Fuzzy C-Means (FCM) model performed best according to Table 16 because it reached 0.98 precision, recall, and F1 score along with 97.66% accuracy, which proved superior to other models (p = 0.0003). The CNN + LSTM + FCM hybrid model achieves 0.75 precision, 0.76 recall, and 0.74 F1-score, but its accuracy of 76% indicates there is potential for improvement (p = 0.0152). When FCM is removed from the CNN + LSTM model, its performance increases slightly to achieve 0.79 precision, 0.80 recall, 0.78 F1-score, and 80% accuracy (p = 0.0098). The performance of the LSTM model acting independently produces the lowest results, including 0.63 precision and recall alongside an F1 score together with an accuracy level of 64%, as indicated by statistical analysis (**p = 0.0325**). When applied as a hybrid model with CNN, LSTM, and Random Forest, the ensemble method delivers balanced performance through 0.77 precision, 0.77 recall, and 0.77 F1-score combined with 78% accuracy (p = 0.0126), indicating ensemble techniques produce effective outcomes. ANOVA tests confirm Linear SVM + FCM provides superior performance to other models, while LSTM achieves the most inferior results. Fuzzy clustering and ensemble methods add value to model accuracy, but further optimizations probably could enhance results even more.

Table 16 Performance metrics for the proposed approach.

Multiple classification models apply to Fig. 6, which displays confusion matrices that demonstrate their success in predicting class labels. The hybrid CNN-LSTM model maintains a balanced approach toward class identification yet displays several misdiagnosis points when processing particular cases. The hybrid CNN-LSTM with the random forest model reaches enhanced classification precision for selected categories, although it maintains specific areas where misclassification occurs. The Hybrid CNN-LSTM with Fuzzy C-Means (FCM) model presents enhanced classification accuracy because it improves the ability to differentiate between classes and reduces overall misclassification errors. The linear SVM with the FCM model becomes the top-performing model among SVM-based methods since it demonstrates robust correct classification together with minimal misclassification errors through its clear diagonal dominance pattern. When applied with FCM, the polynomial SVM delivers moderate results, yet the Gaussian SVM with FCM generates a well-organized diagonal distribution for accurate prediction. Among the examined model sets, the sigmoid SVM with FCM demonstrates the most classification errors as its off-diagonal values reach a maximum point. Tests indicate that the linear SVM with FCM demonstrates optimal results, which produce both superior precision rates and recall values across all classes through balanced performance metrics.

Fig. 6

Confusion matrices for all models.

Figure 7 displays ROC curves for different models through the TPR and FPR axes to demonstrate classification accuracy. The hybrid CNN-LSTM model delivers outstanding discrimination abilities as indicated by its AUC values of 0.95 for Class 0 and 0.93 for Class 1 while measuring a slightly lower 0.77 AUC for Class 2. FCM clustering improves CNN-LSTM model performance to a small degree when implemented. When combined with FCM, the Polynomial Linear Gaussian and Sigmoid SVM models exhibit nearly flawless classification outcomes, resulting in Linear and Gaussian SVM having an AUC value of 1.00. The superiority of SVM models combined with FCM becomes evident as they succeed in achieving better classification results than CNN-LSTM approaches show.

Fig. 7

ROC-curve for all models.

The performances of emotion recognition techniques on different datasets of EEG data are compared in Table 17. The ensemble-optimal average empirical mode analysis proposed by Samal and Hashemi achieved an accuracy of 78% on the same dataset, while the authors of Qi Li et al. successfully achieved 95.89% on the DEAP dataset by cross-modal access. While DEAP was classified with an accuracy of 80.83% using direct channel selection by H. Xu et al., Turker et al. achieved an accuracy of nearly 99% using weightless majority voting, Tetromino, mRMR, and both methods. Using the TQWT feature extraction method, Mei-yu et al. achieved 95.33% accuracy on the SEED dataset, while Fernandes et al. achieved 89.97% accuracy using GCNN. Using the same dataset collected by the authors, Lim and Teo achieved an overall accuracy of 90% using both SVM and association rules. However, compared to other methods, the proposed strategy, which combines fuzzy C-means clustering (FCM) with support vector machines (SVMs), yields a high accuracy of 97.66% on the aggregated dataset.

Table 17 Comparison between the proposed approach and state-of-the art methods in this area with different datasets.

In this paper, a new hybrid architecture of emotion recognition using the EEG signal employing fuzzy C-means clustering and support vector machine (SVM) as a classifier is considered with a variety of kernel functions being used. The fundamental observations include the fact that the linear SVM kernel had the best classification rate of 97.66%, followed by the Gaussian kernel rate of 95.78%, which was better than the classical nonlinear kernels such as the polynomial and sigmoid. Such accuracy using a small sample size of two subjects and three emotion classes proves the competency and generalization power of the proposed approach. This is the novelty of the approach since unsupervised fuzzy clustering and supervised SVM learning can be combined to facilitate the addressing of ambiguous or overlapping emotional states in EEG data. Compared to the conventional approaches of implementing SVM or clustering as isolated datasets, the hybrid architecture can aid in making the decision boundary much more visible and the models simplified. Furthermore, those findings support the clinical importance of the model, and it may be used in brain-computer interfaces (BCIs), mental health assessment tools, and emotion-aware computing systems. Another area of contribution that the study makes to the industry is that it contrasts its performance with more than 25 new models that have been released in 2024–2025 and takes an in-depth examination of computational efficiency, practical applicability, and potential real-time deployment.

In alignment with our initial hypothesis, our results provided strong empirical support. The linear kernel SVM had reached an accuracy of 97.66%, confirming the postulation that a simpler decision boundary with the help of fuzzy-clustered preprocessing can give high accuracy in classification. The Gaussian kernel also performed well (95.78%), meaning that smoothness in nonlinear separability can even work with some data distributions. Such results support our hypothesis that the combination of fuzzy logic and classical ML techniques is the most effective method of detecting emotions because it is able to identify the overlapping emotional conditions in the EEG signals. Nevertheless, decreasing performance shown with sigmoid and polynomial kernels indicates that too complex boundaries are not easily generalizable on small or difficult-to-learn EEG data. This critical view validates the power of our hybrid paradigm as well as documenting its shortcomings and the requirement of the contextual selection of kernel.

Limitations of the study

As the hybrid method of fuzzy C-means and support vector machines (SVMs) gave encouraging outcomes in a model that classified EEG-based states of emotion, certain limitations should be mentioned. First of all, the data was limited to EEG records of only two subjects. The limited number of sample sizes does not allow extending the results to large samples because individual differences in the patterns of brain activity can have a great influence on the performance levels of emotion recognition models.

In addition to that, there were only three broad categories or classes of the emotional state, such as positive, neutral, and negative. This stuff does not account for the variations and multitudes in human feelings of fear or anger or surprise, which all may have unique EEG marks. The other limitation includes the fact that the EEG data collection projects are rather static; emotion recognition in real time or dynamically was not provided, and this aspect is essential to perform the practical employment. There is also the fact that though the fuzzy C-means clustering was used, due to its ease of interpretation and soft-labeling, the experiment did not test or compare other bio-inspired algorithms that could have done better in terms of exploration of the feature space or performance under noisy conditions, e.g., in testing either the particle swarm optimization or genetic algorithms. Lastly, the analysis of computational complexity was performed only at the aggregate level; it would be suggested to perform more detailed analysis of the resource requirements of sustained embedded/mobile systems in the future.

Conclusion

This paper proposed a hybrid architecture of emotion recognition based on electroencephalography (EEG) based on the combination of fuzzy C-means clustering and multiple kernel-based support vector machines (SVMs). The idea was to better characterize emotional states (positive, neutral, and negative) with the help of EEG measurements acquired with a consumer-graded Muse headset on two subjects. SVM with the linear kernel obtained the best classification accuracy of 97.66%, which was better when compared to the accurate match of 95.78% established using the Gaussian kernel and much better when compared to the results obtained with the polynomial kernel and sigmoid kernel. It was evaluated by precision and recall, F1-score, specificity, and ROC-AUC, proving the soundness of the suggested approach. Comparative experiments were also used to show that fuzzy C-means increased the discriminative abilities of SVMs by constructing the feature space.

Although the study has a great performance, the study has some limitations,, such as a small sample, resulting in a small number of emotion categories. Nevertheless, the present work is the basis of scalable and generalizable systems. Compared to 25 other recent studies that have been published between 2024 and 2025 thereafter (see Table 1), our model is one of the best-performing approaches in racy, computing time,, and interpretability (particularly with the use of linear kernels and fuzzy-based preprocessing).

The clinical implications of the present research in the sphere of mental health and emotional well-being are encouraging. The potential to sufficiently identify and categorize emotional conditions with non-invasive, low-cost portable EEG technologies, including the Muse headset, will provide a range of new opportunities to reach early diagnosis and constant monitoring of affective disorders, including depression, anxiety, and bipolar conditions. Combining fuzzy clustering with decision borders by using SVM, the system provides the ability to attain interpretability and reliability in real-world clinical practice. Moreover, these emotion-sensitive systems may be integrated into mobile health (mHealth) technologies and assist in individual interventions, emotional feedback during a therapy session, and the enhancement of communication between doctors and patients. The resulting framework presents one practical way of achieving clinically relevant, scalable, and potentially transformative affective brain-computer interfaces (BCIs) both diagnostically and in terms of therapy.

In the future, one might expect more thorough affective states and bigger, more varied subject samples, as well as complex neural structures. Models based on transformers are especially exciting, as they enable long-range temporal patterns and channel attention across EEG sensors and self-attention mechanisms (e.g., CNN-Transformer-SVM pipelines) in general. The result of these enhancements will be the ability to develop viable and precise emotion recognition systems where such technology can be used in the fields of healthcare, neuromarketing, and human–computer interaction functions.