Introduction

With the rapid expansion of the global economy, the surge in energy consumption has not only intensified energy shortage but also posed serious challenges to energy security, particularly in developing countries1. According to the International Energy Agency (IEA), global energy demand is projected to increase by 25% by 2040, with developing nations accounting for over 70% of this growth. This trend exacerbates energy security concerns and hinders global efforts to mitigate climate change. In response, many developing countries—including China—are actively pursuing renewable energy development as a long-term strategy to ensure energy security and meet climate targets2. As the world’s largest energy consumer, China still depends on coal for approximately 70% of its energy supply3. This coal-intensive energy structure not only undermines energy security but also contributes to severe environmental degradation and climate change. Against this backdrop, reducing EI—defined as the amount of energy consumed per unit of economic output—has emerged as a critical strategy for enhancing energy security, addressing environmental challenges, and promoting sustainable development4,5. EI is not only a key indicator of energy efficiency but also serves as a comprehensive metric for evaluating the sustainability of socio-economic development6. Lowering EI enables the decoupling of economic growth from energy consumption and carbon emissions, which is particularly vital for achieving long-term sustainable development in developing economies7.

In the era of the knowledge economy, TP is widely recognized as a key factor influencing EI. Theoretically, TP affects EI through several channels. First, it enhances energy efficiency by improving production processes, optimizing equipment performance, and promoting the adoption of energy-saving technologies, thereby directly reducing energy consumption per unit of output8,9. Second, TP facilitates industrial upgrading by promoting the transition from energy-intensive industries to low-energy, high-value-added sectors, further contributing to a decline in overall EI10. However, TP does not always lead to a reduction in EI. Due to the inherent bias in technological progress, its effect on EI may not be significantly negative. In fact, TP-driven economic growth can trigger a “rebound effect,” where gains in energy efficiency reduce production costs and stimulate higher energy consumption, thereby offsetting the intended energy savings. Yang and Zhu (2017) challenged the widely held view that technological innovation inherently improves energy efficiency. They argued that the impact of technological innovation on energy use remains uncertain, largely due to the biased nature of TP11.

Moreover, the spatial spillover effects of TP cannot be overlooked. Innovation in one region inevitably facilitates the flow and diffusion of technological factors across neighboring areas. TP may generate both positive and negative externalities in surrounding regions through mechanisms such as technology diffusion, industrial relocation, and regional cooperation. For instance, local TP may promote industrial upgrading, leading to the relocation of energy-intensive industries to adjacent regions and thereby creating an uneven spatial distribution of EI. These complex spatial dynamics underscore the multidimensional and evolving nature of the relationship between TP and EI. When TP influences local EI, its impact often extends to neighboring areas through mechanisms such as “demonstration effects” and “warning effects”.

In summary, although existing studies have examined the relationship between TP and EI, several important gaps remain. First, most research relies on traditional linear econometric models, which often overlook the spatial diffusion characteristics of technology. The assumption of spatial homogeneity in these models may lead to biased or incomplete conclusions. Second, the majority of studies focus solely on the direct impact of TP on EI, without considering the underlying mechanisms through which TP may influence EI from a spatial perspective. Third, the heterogeneous effects of different types of technological progress are frequently neglected, limiting the depth and accuracy of current findings.

Building on this foundation, this study adopts a productivity improvement perspective to examine how technological progress (TP) affects energy intensity (EI). Using provincial panel data from China spanning 2006 to 2020, this study employ a SDM to examine both the direct and spillover effects of TP on EI. China is selected as the study context not only because it is the world’s largest energy consumer, but also due to its pronounced regional disparities in economic development and technological capacity—factors that provide an ideal setting for exploring spatial spillovers and technological heterogeneity. Furthermore, the study delves into the underlying mechanisms and heterogeneity of TP’s effects. This paper makes three key contributions: (1) Adopting a productivity improvement perspective, this study offers a comprehensive empirical assessment of both the direct and spatial spillover effects of TP on EI, demonstrating that TP significantly reduces local EI and exerts positive spillover effects that lower EI in adjacent provinces—an area largely neglected in prior research. Notably, spillover effects account for 43–53% of TP’s total impact on EI. (2) It explores the mediating pathways through which TP influences EI, identifying energy consumption structure as a significant channel, while also uncovering a masking effect through industrial structure adjustments. (3) It provides new evidence on the heterogeneity of TP’s impact, revealing that its effect on EI has become more pronounced in the post-2013 period. The mechanisms vary spatially: local reductions in EI are mainly driven by efficiency improvements, whereas spillover effects are more closely linked to technological change.

Literature review and research hypotheses

Technological progress and energy intensity

A large number of studies recognize that TP is the most influential factor affecting EI8,12,13. Although the conclusions of existing studies are not entirely consistent, most scholars believe that improvements in technological levels will effectively contribute to the decline of EI. For example, Huang et al. (2022) summarized that TP is significant in reducing EI, and technological absorptive capacity plays a crucial role in this process14. Fan and Zheng (2019) confirmed the positive contribution of TP in reducing EI based on an econometric model utilizing the Kalman filter15. Lin and Tan (2017) used a study of six energy-intensive industries in China to demonstrate that TP can effectively reduce EI16. Solangi et al. (2024) expanded the research perspective on TP from the technology itself to its underlying driving mechanisms, and revealed the multi-dimensional implementation pathways of TP in practice17. Imran et al.(2024) demonstrated that the application of green innovation technologies signifies a broader transition towards cleaner and more sustainable energy alternatives18. These studies provide an important theoretical perspective for understanding the complex relationship between TP and EI. Certainly, some scholars have voiced differing opinions. For instance, based on the rebound effect, TP can lead to an expansion in the scale of economic growth, which in turn may require higher energy input, thereby increasing EI19. Ma et al. (2008) revealed that the increase in the use of technology resulted in increased EI20. The presence of rebound effect makes the impact of TP on EI uncertain10.

That is, the impact of TP on EI depends on the magnitude of energy-saving effects and rebound effects, which are closely tied to the actual level of energy-saving technologies. Çabaş et al. (2024) pointed out that the share of green technologies among all technologies has shown an overall increasing trend21 providing some support for our preliminary inclination toward the view that “TP can suppress the growth of EI”. Additionally, it is necessary to consider the actual level of technological advancement in China. In China, technological progress has demonstrated rapid development in recent years. Significant achievements have been made in areas such as new energy technology research and development, as well as improvements in advanced production processes. Numerous enterprises have mastered core technologies through independent research and development, substantially enhancing energy efficiency. For example, in the steel industry, new smelting technologies have significantly reduced energy consumption per unit of product22; in the power sector, efficient power generation technologies and smart grid technologies have improved energy conversion and transmission efficiency. These signs indicate that, in the context of China, technological innovation (whether through independent research and development, technology introduction, or imitation innovation) and technological efficiency can largely promote improvements in production efficiency. Therefore, this paper tentatively posits that, in China, TP can suppress the growth of EI.

In addition, the subjects of economic activities do not exist independently, and some spatial dependency is bound to exist among the subjects. Therefore, as one region has an innovative technology or when its technological efficiency improves, it will not only have an impact on the EI of that region, but may also affect the neighboring regions, i.e., show a spillover effect23,24. From this process, inter-regional socio-economic activities can lead to the transfer of technology, management practices, etc., from one region to other regions, and also, the region is subject to passive influences from neighboring regions. Therefore, there may be spatial spillover effects of TP on EI. Besides, considering the current level of TP, this paper tends to believe that the energy-saving effect of TP is more prominent. Hypotheses 1 and hypotheses 2 are proposed.

Hypotheses 1: TP can inhibit the growth of EI.

Hypotheses 2: TP has a significant negative spillover effect on EI.

Technological progress, energy consumption structure and energy intensity

TP inevitably influences the energy consumption structure, and it can even be argued that fundamental changes in this structure must rely on TP, which acts as a “catalyst” for its optimization25,26. TP enhances energy conversion efficiency, reduces dependence on fossil fuels and coal, and accelerates the adoption of renewable energy technologies27. In recent years, the view that optimizing the energy consumption structure can significantly reduce EI has gained widespread recognition28,29. Scholars believe that by increasing the share of renewable energy and reducing reliance on inefficient fossil fuels, energy efficiency can be improved, thereby reducing EI. However, earlier studies suggested that the contribution of energy consumption structure to EI was negligible30,31. These studies were often based on older data and economic contexts, where the demand for energy conservation was less urgent, and the impetus for structural adjustment through technological innovation was limited. As a result, the impact of energy consumption structure on EI was considered insignificant. However, as energy resources become increasingly scarce, the concept of sustainable development takes deeper root, and the application of renewable energy technologies and changes in resource endowments are being continuously realized32. The adjustment of energy consumption structure, especially by increasing the proportion of renewable energy, has become an important way to improve energy efficiency. Recent researches have also provided support in this regard. For instance, the study by Shi and Yu (2024) demonstrates that renewable energy has contributed to the reduction of energy consumption, a contribution that is related to factors such as market size and geographical availability33. Jiao et al. (2024) attribute the decline in energy intensity to technological advancements and changes in the energy structure, particularly the share of renewable energy34. Utilizing a dynamic panel threshold regression model, Yu et al. (2022) have validated the threshold effect of renewable energy on national energy intensity, as well as the heterogeneity between developed and developing countries, revealing that the higher the level of renewable energy development, the more pronounced its effect on reducing energy intensity35. These studies provide robust empirical support for the pivotal role of adjusting the energy consumption structure in enhancing energy efficiency.

Therefore, we contend that under the impetus of TP, optimizing the energy consumption structure can make a significant contribution to reducing EI. The process by which TP reduces EI through the improvement of energy consumption structure can be understood as an enhancement in energy efficiency. While innovations in production technologies and improvements in manufacturing processes, such as the adoption of intelligent control systems and energy-saving equipment, play a role, the broader significance of TP lies in its ability to drive systemic changes9. This includes advancing smart grid technologies, improving energy storage solutions, and promoting the widespread use of renewable energy. These developments collectively optimize energy consumption patterns and improve overall energy efficiency.

Therefore, hypothesis 3 can be proposed.

Hypotheses 3: The energy consumption structure plays a mediating role between TP and EI.

Technological progress, industrial structure and energy intensity

A large amount of research supports that TP can promote the optimization and upgrading of industrial structure. For example, Wang and Li (2022) pointed out that TP has reduced the marginal production quota of resources and increased the resource utilization of the secondary and tertiary industries, which has a positive effect on promoting the optimization and upgrading of industrial structure36. Shao et al. (2021) stated that TP can give rise to the emergence of new industries and formats, affecting the composition and layout of industrial structures37. Other scholars have also stated that TP is the key to industrial structural transformation38,39,40. TP breaks through existing technological levels41 improves production efficiency, and gives birth to new industries and markets. As a result, both production and consumption structures are reshaped, driving industrial structure towards a more advanced and efficient direction. The transformation of industrial structure has had a profound impact on energy demand and EI. Li et al. (2017) explained that the industrial structure effect is the main effect that suppresses energy demand. The adjustment of industrial structure leads to a reduction in the production and supply of electricity, natural gas, and water, that is, a decrease in energy consumption sources42. Some studies have confirmed that an increase in the proportion of the secondary industry (e.g., heavy industry, manufacturing, and construction) will lead to an increase in EI, and a shift towards the tertiary industry (e.g., services, commerce, and high-tech industries) can promote energy conservation43,44,45. The upgrading and optimization of the industrial structure, characterized by a transition from energy-intensive sectors (e.g., heavy manufacturing) to less energy-intensive sectors (e.g., high-tech industries), can reduce the inefficient use of energy resources. This transformation, from low energy efficiency to high energy efficiency, can significantly improve energy efficiency and reduce energy intensity46,47. Undoubtedly, it has become a consensus in the academic community that promoting TP and upgrading industrial structure is an effective way to reduce EI48,49,50.

In summary, TP has significantly reduced EI and supported sustainable economic development by promoting the optimization and transformation of industrial structure, as well as promoting the application of efficient and renewable energy technologies. Therefore, Hypothesis 4 can be proposed:

Hypotheses 4: The industrial structure plays a mediating role between TP and EI.

Summary of representative literature

Given the extensive body of literature on the relationship between technological progress and energy intensity, we present a condensed summary of selected representative studies in Table 1. Rather than aiming for exhaustiveness, this overview highlights different research perspectives and empirical findings that serve as a background and contrast to this study.

Table 1 Summary of key literature.
Full size table

Table 1 summarizes a carefully selected set of studies examining the relationship between technological progress (TP) and energy intensity (EI). Most existing literature supports the view that technological progress can reduce energy intensity, although some studies note the presence of rebound effects associated with energy savings from technological advances. These studies vary in terms of methodologies, data scopes, and analytical depth. Notably, many previous studies have overlooked the spatial interdependencies across regions, while energy consumption and technological progress do not occur in isolation, especially in the context of geographic and economic diversity. Addressing this gap, this study is the first to introduce the Spatial Durbin Model (SDM) into the research framework to systematically reveal the spatial spillover effects of technological progress on energy intensity, thereby enriching both theoretical and empirical analyses in this field.

Moreover, this paper innovatively constructs a transmission mechanism in which technological progress affects energy intensity through the transformation of energy consumption structure and the upgrading of industrial structure, clarifying the key roles of these two mediating pathways in the impact of technological progress. Although existing literature has confirmed the influence of technological progress on energy and industrial structures, few studies have deeply explored the mediating effects of these factors in the relationship between technological progress and energy intensity. By combining spatial econometric methods with mediation analysis, this study not only fills a theoretical gap but also provides more targeted empirical evidence for policy-making, thus enhancing the unique contribution and practical significance of the research.

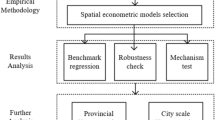
Based on the above analysis and the introduction section, we present the mechanism diagram of our study in Fig. 1.

Fig. 1
figure 1

Schematic diagram of the conduction mechanism.

Full size image

Research design

Variable selection

Explained variable: energy intensity (EI)

EI reflects the efficiency with which a region utilizes energy resources in its production processes. This indicator is widely used in the literature and serves as a key metric for assessing the impact of technological progress on energy consumption51,52. EI is measured by the amount of energy consumed per unit of output5,43,44. The EI calculation method is as follows:

$$\:{EI}_{i,j}=\frac{{Energy}_{i,j}}{{GDP}_{i,j}}$$
(1)

Where \(\:{Energy}_{i,j}\) is total energy consumption of region i in year t. Specifically, energy sources such as coal, coke, petroleum, crude oil, gasoline, kerosene, diesel, fuel oil, liquefied petroleum gas (LPG), and natural gas are converted into standard coal equivalents for statistical purposes. The total energy amount is then calculated and expressed in units of 10,000 tons of standard coal equivalent (10,000 tce). \(\:{GDP}_{i,j}\) is the real regional gross domestic product in region i in year t.

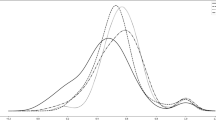
Figure 2 shows that China’s energy intensity is generally on the rise. From the perspective of spatial characteristics, it shows a pattern of “western > central > eastern”. And with the passage of time, the energy intensity gap between the three regions is getting larger and larger.

Fig. 2
figure 2

Temporal characteristics of energy intensity.

Full size image

Data sources: China Energy Statistical Yearbook and China Statistical Yearbook.

Explanatory variable: technological progress (TP)

To better capture the multifaceted nature of technological progress (TP) and its influence on energy intensity, this study adopts two distinct indicators, referred to as TP1 and TP2. TP1 It covers a comprehensive reflection of technological change and technological efficiency, reflecting both the progress of innovation driving production frontiers and the improvement of existing technology application effects. TP2 reflects the ability to promote technological accumulation through the mobilization of financial resources.

TP1: total factor productivity (TFP)

Refer to existing research53,54 TP not only includes the expansion of the production frontier driven by technological innovation but also encompasses improvements in the efficiency of applying existing technologies. In other words, TP is understood as a comprehensive manifestation of both technical change and technical efficiency change. This understanding raises higher requirements for the choice of indicators used to measure technological progress. While some studies measure technological progress through R&D input and output metrics, such approaches often fail to capture the intrinsic significance of TP, particularly its impacts on production efficiency and output quality55,56 which cannot effectively reflect the essential significance of technological progress57. TFP is well suited to measure TP53,58. Unlike indicators such as R&D investment and the number of patents, TFP captures the portion of output growth in production activities that cannot be explained by input factors, thereby revealing the true driving role of technological progress in economic growth. In essence, TFP reflects the overall effect brought about by TP. A considerable body of academic research employs TFP as a proxy for TP. For instance, Cheng et al. (2018), Li & Lin (2016) and Zhang et al.(2020) utilized TFP to measure TP in their analyses of the relationship between TP and carbon intensity, further decomposing TFP into technical change and technical efficiency change57,58,59. Xu & Liu (2024) adopted green total factor productivity(GTFP) as an indicator of technological progress in their study on its influence on fiscal resilience60. Hulten (2000) proposed that TFP can reveal the impact of technological innovation on the marginal productivity of production, an effect that is often difficult to fully capture through the quantification of individual inputs such as capital or labor61. Thus, using TFP as the core indicator for measuring technological progress provides a more accurate economic perspective.

In this study, the Global Malmquist Index method is employed to measure TFP. This method also decomposes TFP into technological change (TC) and technical efficiency change (TEC), each reflecting a different type of technological progress. TC captures the innovation component of TP, measuring shifts in the production frontier resulting from technological innovation. EC reflects the effectiveness of implementing existing technologies, indicating the ability to catch up with the current production frontier53,62. Therefore, EC is also considered an important manifestation of technological progress.

Referring to the methodology employed by Cheng et al. (2018)57 this study measures TFP by selecting capital stock and labor as input variables, and GDP as the output variable. Capital stock is calculated using the perpetual inventory method63,64 based on data of total fixed asset formation to estimate the fixed capital stock. Labor input is measured by the total employed population in the region. GDP is deflated with 2005 as the base year to eliminate the impact of inflation. After determining the input and output variables, Maxdea8 software is used to measure total factor productivity through the SBM model and the global Malmquist index method65,66. The SBM and global-Malmquist index model is as follows:

$$\:{\rho\:}^{*}=min\rho\:=\frac{1-\frac{1}{m}{\sum\:}_{i=1}^{m}\frac{{s}_{i}^{-}}{{x}_{ik}}}{1+\frac{1}{q}{\sum\:}_{r=1}^{q}\frac{{s}_{r}^{+}}{{y}_{rk}}}$$
(2)
$$\:st.\left\{\begin{array}{c}X\lambda\:+{s}^{-}={x}_{k}\\\:Y\lambda\:-{s}^{+}={y}_{k}\\\:\lambda\:,{s}^{-},{s}^{+}\ge\:0\end{array}\right.$$
$$\:{GMI}^{t,t+1}\left({x}^{t+1},{y}^{t+1};{x}^{t},{y}^{t}\right)=\frac{1+{D}_{G}^{T}({x}^{t},{y}^{t})}{1+{D}_{G}^{T}({x}^{t+1},{y}^{t+1})}$$
(3)

Where x and y are input and output, respectively. \(\:{s}^{-}\) and \(\:{s}^{+}\) are input slack value and output slack value, respectively. λ is the weight vector. m and q are the number of input and output indicators, respectively. \(\:{\rho\:}^{*}\) is the efficiency value, which indicates effective when \(\:{\rho\:}^{*}\) ≥ 1, and \(\:{\rho\:}^{*}\)<1 indicates an inefficient state. The GMI value greater than 1 indicates an increase in TFP. Conversely, a decrease in TFP.

TP2: local government science and technology expenditure ratio

As an alternative measure, this study also utilizes the ratio of local government science and technology expenditure to total general public budget expenditure to reflect regional policy orientation toward technological development. This indicator emphasizes the governmental and institutional dimension of TP, capturing the intensity of fiscal support aimed at fostering scientific and technological progress. A higher ratio indicates a stronger commitment to promoting innovation, industrial upgrading, and potentially cleaner production processes, all of which contribute to lowering energy intensity.

TP2 thus provides a complementary perspective, focusing on the input-side policy efforts that may indirectly influence energy performance outcomes. It is particularly useful in capturing interregional variations in the prioritization of TP through fiscal instruments.

Trends and spatial characteristics of TP

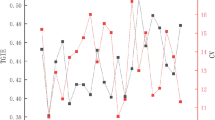
To further illustrate the dynamics of technological progress over time and across regions, this study presents the evolution of TP based on the TFP indicator (TP1), which allows for decomposition into technological change (TC) and technical efficiency change (TEC). This decomposition provides additional insights into the underlying drivers of TP and their potential effects on energy intensity. Therefore, Fig. 3 in this paper is drawn based on TP1.

Fig. 3a shows the trend of TP and its decomposition into technological change and technical efficiency change. Overall, there has been technological advancement from 2006 to 2021, with an increasing level of progress. Decomposition indicates that TP is a combination of technological change and technical efficiency change, with technological change having a stronger driving force. This is because new technologies are more easily imitated and learned compared to improvements in efficiency. Figure 3b displays the progress of technology in the eastern, central, and western regions. The level of TP is increasing in each region. Interestingly, the rates of change in TP across the eastern, central, and western regions are converging, reflecting a strengthening of the technology diffusion mechanism nationwide.

Fig. 3
figure 3

(a) The degree of TP and its decomposition (technological change (TC) and technical efficiency change (EC)); (b) The degree of TP in the eastern, central, and western regions Data sources: The data were calculated using DEA-Max8 software.

Full size image

Control variables

Drawing on relevant research4,30,67,68,69 this paper selects level of regional economic development, energy consumption structure, industrial structure, energy prices and government intervention as the control variable.

Data explanation and statistics

To ensure the validity of the study, provinces with missing data were excluded, resulting in the selection of 30 provinces (municipalities and autonomous regions) in China. The TFP data was calculated over the period from 2005 to 2021, with the derived TFP results and empirical analysis focusing on the years 2006 to 2021. The calculation data for energy intensity and energy consumption structure are sourced from “China Energy Statistical Yearbook”. The data for other control variables are sourced from “China Statistical Yearbook”.

Table 2 presents the descriptive statistics of variables. In order to ensure data stability, logarithmic processing was applied to all indicators in the subsequent work.

Table 2 Statistical characteristics.
Full size table

Model method

All operations of spatial metrology are based on Stata16 software.

Spatial correlation testing model

This paper uses the global Moran’s index and local Moran’s scatterplot to measure the spatial correlation of EI. Moran’s I reflects the correlation between observations and the spatially lagged term, i.e., the correlation of a variable in one region with the same variable in a neighboring region70. Global Moran’s I index is used to assess whether there is spatial autocorrelation across regions, helping identify whether a variable’s values are randomly distributed or exhibit spatial clustering71. The calculation of the Global Moran’s I index (Eq. 4) allows us to assess whether spatial dependence exists across the study area, while the Local Moran’s I (Eq. 5) identifies spatial clusters or outliers at the individual region level72.

Global Moran’s I index calculation model:

$$\:{\text{M}\text{o}\text{r}\text{a}\text{n}}^{{\prime\:}}\text{s}\:\text{I}=\frac{n\sum\:_{i=1}^{n}\sum\:_{j=1}^{n}{w}_{ij}({X}_{i}-\stackrel{-}{X})({X}_{j}-\stackrel{-}{X})}{\sum\:_{i=1}^{n}{({X}_{i}-\stackrel{-}{X})}^{2}\sum\:_{i=1}^{n}\sum\:_{j=1}^{n}{w}_{ij}}$$
(4)

Localized Moran’ s I exponential computational modeling:

$$\:{{\text{M}\text{o}\text{r}\text{a}\text{n}}^{{\prime\:}}\text{s}\:\text{I}}_{i}=\left({X}_{i}-\stackrel{-}{X}\right)\sum\:_{i=1}^{n}{w}_{ij}\left({X}_{j}-\stackrel{-}{X}\right)$$
(5)

Where \(\:{X}_{i}\) and \(\:{X}_{j}\) are the lnEI values in region i and region j. \(\:\stackrel{-}{X}\) means average value of regional lnEI. \(\:{w}_{ij}\) is spatial weight matrix.

A positive Moran’s I implies that the observed variables are spatially correlated and exhibit a spatial agglomeration state. The opposite means that the observed variables have heterogeneity in space and are in a spatially dispersed condition.

Spatial Durbin model

When examining the impact of technological progress on energy intensity, there exists significant spatial correlation and spillover effects among regions. Technological progress in one region not only affects its own energy use efficiency but may also influence the energy intensity of neighboring regions through economic linkages, industrial transfer, and technology diffusion. Therefore, traditional panel data models fail to capture such interregional interactions effectively, which may lead to model misspecification and biased estimation results. This necessitates the adoption of spatial econometric models in our analysis. Spatial econometric models include the Spatial Lag Model (SAR), the Spatial Error Model (SEM), and the Spatial Durbin Model (SDM), which accounts for spatial correlations. In comparison, SDM is particularly suitable for examining both direct and indirect effects in spatial data73,74 as it can more accurately capture the interdependencies within spatial datasets. Recent studies have also corroborated the effectiveness of the SDM in capturing interregional spillover effects75.

Additionally, we applied a series of tests to determine the most suitable model for this study (Table 3). The results of the Lagrange Multiplier (LM) tests indicate that the test statistics for both the spatial error term and the spatial lag term are significant at the 1% level, suggesting that spatial error variables and spatial lag variables need to be incorporated when constructing the panel regression model. The Hausman test results show that the test statistic is significant at the 1% level, indicating that the spatial panel model should be specified as a fixed effects model. The Likelihood Ratio (LR) test and Wald test statistics are significant at the 1% level, demonstrating that the SDM model cannot be simplified to either the SAR or SEM model. Therefore, the comprehensive test results suggest that the SDM model with fixed effects should be adopted.

Table 3 Diagnostic tests of Spatial measurement models.
Full size table

Model as shown in Eq. (6):

$$\begin{aligned} \ln EI_{{it}} & = \alpha + \beta \mathop \sum \limits_{j} w_{{ij}} \ln EI_{{jt}} + ~\rho \ln TP_{{it}} \\ & + ~\sigma \mathop \sum \limits_{j} w_{{ij}} \ln TP_{{jt}} + \varphi Con_{{it}} \\ & + \omega \mathop \sum \limits_{j} w_{{ij}} Con_{{jt}} + ~u_{i} + v_{i} + \varepsilon _{{it}} \\ \end{aligned}$$
(6)

Where subscripts i, j, t represent region i, region j, and year t, respectively. EI represents energy intensity. TP represents technological progress. Con is control variables. \(\:{w}_{ij}\) is an element of the spatial weight matrix. \(\:{u}_{i}\) and \(\:{v}_{i}\) denote regional-fixed and time-fixed effect, respectively. \(\:{\epsilon\:}_{it}\) means a randomly perturbed error term.

Spatial weight matrix

To capture the spatial interaction mechanisms more comprehensively, this paper adopts two types of spatial weight matrices. The spatial adjacency matrix captures pure geographical proximity and assumes that spillover effects mainly occur between adjacent regions. This matrix is widely used in spatial econometric studies and serves as a benchmark model for measuring regional spillover effects. However, relying solely on geographical proximity may not fully reflect the true intensity of spatial interactions, especially in a vast and economically diverse country like China. Economic linkages such as trade, technology transfer, and industrial integration often occur between non-adjacent regions. To take these practical situations into account, we additionally construct a geographical-economic nested spatial weight matrix. This matrix enables us to capture the spatial dependence arising from geographical proximity and economic similarity, thus presenting the inter-regional connections more realistically and comprehensively.

By using these two matrices, we can more reliably test whether the impact of technological progress on energy intensity varies under different spatial dependence assumptions. The spatial adjacency matrix and the geographical-economic nested spatial weight matrix are shown in Eqs. (7) and (8) respectively:

$$\:{W}_{1ij}=\left\{\begin{array}{c}1,\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:\:i\:is\:adjacent\:to\:j\:\\\:\:0,\:\:\:if\:i\:is\:not\:adjacent\:to\:j\:or\:i=j\end{array}\right.$$
(7)
$$\:{W}_{2ij}=\left\{\begin{array}{c}\varnothing\:\frac{1}{{d}_{ij}}+\left(1-{\varnothing}\right)\frac{1}{\left|\stackrel{-}{{GDP}_{i}}-\stackrel{-}{{GDP}_{j}}\right|},\:\:\:\:\:\:\:\:\:\:\:if\:i\ne\:j\\\:0,\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:i=j\end{array}\right.$$
(8)

In the equation, \(\:{d}_{ij}\) means the nearest highway mileage in provinces i and j. \(\:\stackrel{-}{{GDP}_{i}}\) and \(\:\stackrel{-}{{GDP}_{j}}\) represents the annual per capita GDP of province i and province j, respectively. \(\:\varnothing\:\) means the weight, which value is taken as 0.576.

Results

Spatial correlation of energy intensity

Table 4 Global Moran Index.
Full size table

Table 4 displays the global Moran’s I of EI and its average values from 2006 to 2021. The results of W1 matrix and W2 matrix are both positively significant. There is a positive correlation in EI among various provinces in China, exhibiting spatial agglomeration characteristics. Furthermore, we explored the local spatial correlation of EI through Moran scatter plots.

Fig. 4 shows the local spatial correlation of EI with a Moran scatter plot, the first three subplots and the last three subplots are derived based on the \(\:{w}_{1ij}\) matrix and \(\:{w}_{2ij}\) matrix, respectively. The horizontal and vertical axes represent the EI and its spatial lag value, respectively. Scattered points are mostly distributed at quadrants I and III, and less at quadrants II and IV, which means that EI has obvious spatial agglomeration characteristics and a certain degree of stability.

Fig. 4
figure 4

Moran scatter plot (Figure data source: Stata 16 generated after analysis and processing).

Full size image

Regression results of spatial econometric models

SDM estimation results

Table 5 presents the test results under the two spatial weight matrices. For local effects, both TP1 and TP2 show that TP leads to a significant reduction in EI. Specifically, a 1% increase in TP1 leads to a 0.448% reduction in EI under W1 and 0.369% under W2, while TP2 results in a 0.043% reduction in EI under W1 and 0.032% under W2, all statistically significant. These negative values indicate that TP can significantly reduce local EI. The absolute value of the TP coefficient under W1 is larger than that under W2. This is because the geographic proximity of W1 more directly facilitates the localized application of technology, whereas W2 focuses more on interregional economic linkages. Although economic linkages can also promote the diffusion and application of technology, their influence is relatively indirect.

Turning to the spatial spillover effects, increases in both TP1 and TP2 also contribute to reducing EI in neighboring regions. A 1% increase in TP1 leads to a 0.242% and 0.407% reduction in EI under W1 and W2, both statistically significant, while TP2 leads to a 0.046% and 0.029% reduction in EI under W1 and W2. Overall, the results consistently support the hypotheses that technological progress—measured by either TP1 or TP2—has a significant and negative impact on both local and neighboring regions’ energy intensity. This robustness across different technological progress indicators strengthens the reliability of our findings.

Both Hypothesis 1 and Hypothesis 2 are supported.

Table 5 Regression results of Spatial econometric models.
Full size table

Marginal effect analysis

Table 6 presents the results of the marginal effect analysis based on TP1. The coefficients of direct influence are significantly negative, which indicates that TP has an appreciable inhibitory effect on EI. The indirect impact is also significantly negative. This indicates that TP and EI possess significant spillover effects. Due to the combined effects of direct and indirect impacts, the overall impact is significantly negative. Notably, the spillover effects account for 43% of the total impact of TP on EI under W1, and 53% under W2, emphasizing the substantial contribution of spatial effects in the relationship between TP and EI. only the marginal effect results based on TP1 are presented. The corresponding results of TP2 are consistent and do not substantially change the overall conclusions.

Table 6 Decomposition results of Spatial spillover effects.
Full size table

Robustness testing and endogeneity test

Robustness testing

To further test the reliability of this study, the following two methods are employed for robustness checks in the subsequent analysis. (1) Artificial intelligence experiments. The LASSO regression method from machine learning is utilized to screen the variables involved in the study, extracting variables corresponding to non-zero coefficients, and reconstructing the research model for re-estimation. (2) Analysis after outlier treatment. The data is winsorized at the 1% and 99% percentiles to mitigate the impact of outliers. (3) Changing the measurement of the independent variable. TFP is measured using Stochastic Frontier Analysis (SFA) to re-estimate the model. (4) Use of a dynamic SDM. This method incorporates both the time-lagged term and the spatial-time-lagged term of the dependent variable, allowing for a more comprehensive capture of dynamic dependencies in both time and space, thereby effectively alleviating endogeneity issues. Methods (1), (2), and (4) are specifically conducted based on TP1.

The robustness tests are given in Table 7, indicating that the results in this study are highly robust.

Table 7 Robustness tests.
Full size table

Endogeneity test

To mitigate potential endogeneity concerns, this study adopts 2SLS approach combined with SDM. Specifically, the lagged proportion of the population with higher education (L.HEP) is employed as an instrumental variable. On the one hand, higher education enhances human capital and innovation capacity, thereby promoting technological progress. Using its one-period lag allows us to capture the persistent effect of educational investment on technological development while avoiding contemporaneous feedback from energy policies on education resource allocation. On the other hand, higher education primarily influences energy intensity indirectly through technological progress.

The results of the endogeneity test are presented in Table 8. In the first length regression, the coefficient of the instrumental variable is 2.893 and is significant at the 1% level, indicating that the instrumental variable has a strong explanatory power for technological progress. The CD Wald F - statistic is greater than the critical value at the 15% level of Stock - Yogo. The P - value of the Kleibergen - Paap rk LM statistic is 0.0000, suggesting that the test for “under - identification of instrumental variables” is passed. Evidently, the instrumental variable constructed in this paper is reasonable and valid in a statistical sense. In the second length regression, the coefficient of lnTP1 is − 0.244 and is significant at the 5% level. This indicates that after accounting for endogeneity, the effect of technological progress in reducing energy intensity still holds.

Overall, the introduction of instrumental variables has effectively mitigated the potential endogeneity of the technological progress variable, enhancing the robustness and explanatory power of the empirical results.

Table 8 Endogeneity test.
Full size table

The intermediary effect test of energy consumption structure and industrial structure

It is clear from the above analysis that TP can inhibit EI. In addition, further discussion is needed on the possible pathways through which TP affects EI. According to the analysis in Chap. 2, this paper conducts mediation effect tests using energy consumption structure and industrial structure as mediating variables. The results of the mediation effect experiment are shown in Table 9 (model experiment based on W1 matrix. Energy consumption structure and industrial structure are excluded from the control variables).

The regression coefficient of lnTP1 in column (1) is −0.903 (at the 1% significance test level), indicating that a 1% increase in TP leads to a 0.903% reduction in EI. Due to the fact that the energy consumption structure measurement method used in this article is the share of coal in total energy consumption, the magnitude of the energy consumption structure value is inversely proportional to the energy consumption structure optimization status, i.e., the smaller the energy consumption structure value, the more optimized the energy consumption structure. Therefore, this regression result indicates that TP has significantly improved energy consumption structure. Regression coefficients of lnTP1 and lnECS in column (2) are significantly negative and significantly positive, respectively. This indicates that the energy consumption structure plays a mediating role, that is, there exists a transmission mechanism whereby TP facilitates the reduction of EI by promoting energy consumption structure. Hypothesis 3 gets certified. In terms of spatial effect, both the W*lnTP1 and W*lnECS coefficients are negatively significant, which reveals that energy consumption structure has a positive spillover effect on EI.

The lnIS coefficient in column (3) is significantly negative, indicating that TP inhibits industrial structure upgrading, which is inconsistent with our hypothesis 4. There is academic research showing that the effect of TP on industrial structure presents an inverted “U” shape77. Therefore, the result that TP inhibits industrial structure up-grading of this study may be in the latter half of the inverted “U” shape. The coefficients of IS and TP in column (4) are significantly negative, meaning that there is a masking effect of industrial structure. In terms of spatial effects, the insignificance of coefficients indicates the absence of mediating effects.

Table 9 Mediation effect test.
Full size table

Heterogeneity analysis

Heterogeneity analysis of technological progress categories

According to the measurement and analysis of TP mentioned above, TP can be decomposed into technological change and technical efficiency change. It is undeniable that there is heterogeneity in the effect of TP on EI in different forms of TP12,78.

The outcomes of the test for heterogeneity in technology dimensions are presented in Table 10 (based on the model test results using the W1 matrix), where the SDM model results show a significant negative coefficient of technical efficiency change, while that of technological change has no statistical significance. It follows that the direct effect of TP on EI is mainly transmitted through technical efficiency change. As for indirect effects, the coefficient of w*lnTEC is significantly positive, while the coefficient of w*lnTC is significantly negative. Technological change has a significant negative spillover effect on EI, that is, a 1% increase in technological change results in a 0.134% decrease in EI, while technical efficiency change has a significant positive spillover effect on EI, with a 1% increase in technical efficiency change leading to a 0.183% increase in EI. Combined with analysis above, the extent of negative spillovers from technological change is greater than the extent of positive spillovers from technical efficiency change.

Table 10 Heterogeneity analysis of technology types.
Full size table

Heterogeneity analysis of different time periods

The heterogeneous analysis results of TP’s impact on EI across different periods are presented in Table 11. During the period of 2006–2013, the effects of TP on EI, including both local direct effects and spatial spillover effects, were not significant, indicating that TP did not have a notable impact on energy intensity during this phase. However, in the 2014–2021 period, TP significantly reduced EI, with a 1% increase in TP leading to a 0.178% reduction in EI. Additionally, TP exhibited significant spatial spillover effects, with a 1% increase in TP leading to a 0.264% reduction in EI in surrounding regions. This finding aligns with the dual nature of TP’s impact on energy intensity discussed in our research hypothesis analysis, which is closely related to the development stages of technology.

Table 11 Heterogeneity analysis of different time periods.
Full size table

Discussion

This section is based on TP1, as the heterogeneity analysis employs the decomposition indicators of TFP, which corresponds to the TP1 measurement. Therefore, to maintain consistency and interpretability, only the results derived from TP1 are discussed.

Spatial econometric analysis shows that TP has a significant suppressive effect on EI, along with notable spillover effects. Further marginal effect analysis indicates that both the direct effect of TP on local EI and the indirect effect on neighboring regions are significantly negative. The energy-saving impact of TP is not limited to the local region but also generates broader influence through interregional technology diffusion. This finding not only confirms existing studies on the direct effect of TP in reducing EI79,80 but more importantly, unveils the spatial spillover pathways of TP and its external energy-saving effects. It extends the current research frontier on the relationship between TP and energy efficiency, demonstrating notable originality and theoretical significance. These insights also offer valuable policy implications for promoting regional collaborative energy conservation and optimizing resource allocation. Local technological progress can influence energy intensity through multiple channels, thereby reducing EI. First, TP enables more efficient energy extraction, refining, and utilization, resulting in higher output value under the same energy consumption. Second, TP can affect energy intensity by promoting the development of new energy sources and improving the structure of energy consumption and supply. Third, TP enhances regional innovation capacity, reducing energy use under constant output levels. Given the frequent information exchange and the existence of imitation and learning among regions, the spatial spillover effects of technology are particularly evident. Technological advancements often diffuse from central to surrounding areas, thus affecting the EI of neighboring regions, which constitutes the indirect effect. This finding also suggests that, at the national level in China, the energy-saving effect induced by TP significantly outweighs the rebound effect, providing solid support for achieving the “dual carbon” goals.

The mediation effect analysis shows that the energy consumption structure has a significant mediating effect between TP and EI, both in the local and spatial spillover categories. In this study, the energy consumption structure is calculated based on the proportion of coal consumption in total energy consumption. TP can enhance the efficiency of renewable energy utilization and reduce coal consumption intensity, thereby optimizing the energy consumption structure. Due to the low efficiency of coal usage, replacing coal with other types of energy can improve energy efficiency and achieve the goal of reducing EI. However, it is noteworthy that in earlier studies, the impact of the energy consumption structure on energy intensity was not given sufficient attention30,31. This was mainly because energy conservation and emission reduction had not yet become a research priority, and the public’s awareness of the need to adjust the energy consumption structure was relatively low. With the increasing scarcity of energy resources, mounting environmental pressures, and the deepening awareness of sustainable development, adjustments in the energy consumption structure have gradually become an important factor influencing changes in energy intensity. The continuous advancement of technological innovation has also profoundly transformed energy production and consumption patterns, providing greater possibilities for optimizing the energy structure. Against this backdrop, the energy consumption structure has gradually emerged as a crucial transmission pathway through which technological progress affects energy intensity. This study further confirms and extends existing findings33,34,35 by emphasizing the intrinsic mechanism through which technological progress reduces energy intensity via optimizing the energy structure—particularly by lowering the share of coal and increasing the proportion of renewable energy. Moreover, the study finds that the impact of technological progress on the energy structure is significantly constrained by regional resource endowments25. Therefore, as China’s “coal reduction” strategy advances, the role of technological progress in optimizing the energy structure will become increasingly prominent. This indicates that our study not only aligns with current energy transition trends but also offers a forward-looking perspective on the mechanisms through which technological progress influences energy intensity.

In contrast, the industrial structure exhibits a masking effect, which is an intriguing finding of this study. In the initial stages, TP can promote the development of the tertiary sector, thereby achieving industrial upgrading. However, in the later stages, the development of the secondary and tertiary industries tends to stabilize. At this point, if TP does not reach the corresponding level, it may actually limit further industrial upgrading45. Therefore, it is reasonable to conclude that TP can have an inhibitory effect on industrial structure. However, in the context of socio-economic development, the constraints of industrial structure are very unfavorable for the reduction of EI. Thus, industrial structure plays a masking role in the impact of TP on EI. In terms of space, the industrial structure has not played a mediating role. This is related to the characteristics of industrial structure. The formation and evolution of industrial structure are of-ten constrained by various local specific factors, such as local resource endowment, policy environment, market demand, and historical development foundation. In the spatial domain, there are significant differences in the factors that affect industrial structure among different regions, and the development of industrial structure in each region lacks sufficient synergy, making it difficult to transmit and play an inter-mediary role in space.

Finally, on the analysis of technological heterogeneity, we found that the direct effect of local TP on EI is mainly transmitted via technical efficiency change, while spillover effect has different results. Technological change has significant negative spillover effects on EI, while technical efficiency change exhibit significant positive spatial effects. There are the following possible explanations for this. Innovative technologies are easily imitated and learned, largely based on neighboring geographical distances. Therefore, technological change exhibits negative spillover effect on EI. Technical efficiency change refers to the effect achieved on the original technology, which depends on the level of technical management and is difficult to imitate. The siphon effect of TP caused by efficiency improvement promotes local industrial structure upgrading. Industrial adjustment has forced some of the more sub-industrial grade firms to relocate to surrounding areas, thus increasing the EI of surrounding areas. In addition, TP did not have a significant effect on EI during the period of 2006–2013, while it showed a significant inhibitory effect during the period of 2014–2021. In the early stages, clean energy and energy-saving technologies were not yet mature, their adoption was limited, and policy support and market mechanisms were insufficient, resulting in an insignificant reduction in energy intensity due to TP. In contrast, during the later stages, as technologies matured and were applied on a larger scale, coupled with strengthened policy support (e.g., subsidies, carbon trading mechanisms) and enhanced regional collaboration and knowledge sharing, the role of TP in improving energy efficiency became more pronounced, and its spatial spillover effects contributed to the enhancement of energy efficiency in surrounding regions. This mirrors findings by Lin and Huang (2023). Their study focused on digital technology. It found digital technologies reduced energy intensity only after reaching a certain development stage81.

Conclusions, policy recommendations and research limitations

Conclusions and policy recommendations

The whole paper is centered on EI. Methodologically, the spatial econometric modeling approach is adopted for the empirical evidence examining the effect of TP on EI, which bridges the ignorance of geospatial spillover effects of EI in other researches. Specifically, this paper presents three aspects. Firstly, it introduces the spatial distribution state as well as spatial autocorrelation of EI in China. Secondly, it adopts spatial measurement model to explore the effect of TP on EI. Lastly, it analyzes the heterogeneous effect of TP on EI in terms of the type of TP. Following main conclusions were drawn: (1) The analysis using Moran’s I index reveals that China’s EI exhibits significant positive spatial autocorrelation, indicating a spatially clustered distribution pattern. This suggests that EI is not randomly distributed across space but demonstrates clear regional interdependencies. Regions with high EI tend to be adjacent to other high-energy-intensity areas, while low-energy-intensity regions also show similar clustering characteristics. (2) TP has a significant inhibitory effect on China’s EI and demonstrates a negative spatial spillover effect. This implies that TP not only reduces EI in the local region but also enhances energy efficiency in neighboring areas through technology diffusion and knowledge spillovers. This conclusion underscores the critical role of TP in promoting the coordinated improvement of regional energy efficiency. (3) The energy consumption structure plays a significant mediating role between TP and EI, which is evident in both local effects and spatial spillover effects. This indicates that TP significantly reduces EI by optimizing the energy consumption structure, such as increasing the share of clean energy. However, the industrial structure only exhibits a masking effect locally and does not show a mediating role in spatial spillover effects. The adjustment of the industrial structure relies more on local policies and economic conditions, making its influence difficult to transmit to other regions through spatial spillovers. (4) The effect of TP on EI is heterogeneous. The inhibitory effect on localized areas is mainly played by efficiency improvement, and the inhibitory effect of spatial spillover is mainly caused by technology improvement. In addition, TP did not have a significant effect on EI during the period of 2006–2013, while it showed a significant inhibitory effect during the period of 2014–2021.

With the findings of this paper, we put forward three suggestions to provide some reference for reducing EI.

Strengthen regional collaborative governance to unleash spatial spillover effects

Given the significant spatial clustering of energy intensity and the cross-regional spillover effects of TP, it is recommended that governments incorporate the concept of spatial collaborative governance into energy policy formulation and promote the establishment of integrated regional coordination mechanisms. Based on economically interconnected regional units such as urban agglomerations and economic zones, a coordinated mechanism for improving energy efficiency should be established to achieve the cross-regional allocation and sharing of information, technologies, and policy resources. A regional green technology collaboration platform can be established to break down geographical barriers and facilitate the free flow of key energy-saving and carbon-reducing technologies across regions—particularly directing low-carbon technologies to high energy-consuming areas, enabling a better match between “technology supply areas” and “energy efficiency improvement areas”. Meanwhile, it is crucial to strengthen regional energy intensity monitoring and early warning systems. This can be achieved by developing dynamic monitoring platforms based on big data and remote sensing technologies, thereby enhancing transparency and evaluability of energy use efficiency. On the policy side, the development of inter-provincial carbon trading markets should be encouraged to optimize the allocation of energy efficiency resources through market mechanisms. In addition, fiscal incentive mechanisms based on energy performance should be established to support regions that achieve coordinated energy reduction targets through transfer payments.

Increase investment in R&D and absorptive capacity to enhance the energy efficiency potential of TP

Given that TP significantly reduces EI and exhibits spatial spillover effects, it is essential to enhance both R&D and the capacity to absorb and apply advanced technologies, thereby maximizing its role in energy efficiency improvement. On one hand, investment in green and low-carbon technologies should be continuously increased, with a focus on key areas such as energy-saving equipment, green manufacturing, and renewable energy substitution. This will promote self-reliance in core technologies and reduce dependency on high-energy-consumption development paths. On the other hand, the effectiveness of TP also depends on local capacities to absorb and transform technologies. Therefore, it is particularly important to enhance the technological absorptive and re-innovation capacity in central and western regions, as well as in traditional energy-intensive industries. It is suggested to establish special public funds to support the development of regional technology incubators and demonstration zones for energy technologies, and to deepen the integration of industry, academia, research, and application to build a complete chain for green technology diffusion and adoption. Moreover, tax incentives and green finance tools such as preferential loans can be employed to encourage especially small and medium-sized enterprises to accelerate the upgrading of equipment and technologies, effectively translating TP into tangible energy efficiency gains.

Advance energy structure transformation and reinforce market-based mechanisms

The study finds that the energy consumption structure plays a significant mediating role in the relationship between TP and EI. To fully leverage the energy efficiency potential of technological advancement, efforts must be made to simultaneously promote the optimization of the energy structure and increase the share of clean energy in end-use consumption. Under the framework of the “dual carbon” goals, it is recommended that the country further improve the policy system for clean energy development and increase the penetration of renewable energy in both supply and consumption. Specifically, financial subsidies and green pricing mechanisms can be used to lower the cost of renewable energy adoption and enhance the willingness of enterprises and households to adopt clean energy. Meanwhile, it is important to accelerate the development of a flexible and efficient power system to improve the grid integration capacity of new energy sources and eliminate institutional bottlenecks that prevent available technologies from being effectively utilized. Enterprises across various sectors should be encouraged to comprehensively promote clean energy substitution in their production processes, such as adopting models like “renewable energy + production” or “green electricity + industrial parks”, which promote deep integration of green energy with daily operations. Local governments should also promote green energy infrastructure based on local conditions, such as developing integrated systems of generation, grid, load, and storage, to improve energy efficiency and system resilience. In this way, the optimization of the energy structure can become a key lever through which TP reduces EI.

Research limitations

This study uses TFP as the primary indicator of TP, drawing on its widespread application and practical feasibility in existing literature. However, we acknowledge that the concept of TP may be understood in both broad and narrow senses, and using TFP as a measure of TP may lead to some conceptual ambiguity. The measurement based on TFP may still involve a degree of conceptual generalization. Future research could consider employing more detailed or multidimensional indicators to more accurately align with the theoretical connotation of TP.

Regarding endogeneity, this study adopts the classical two-stage least squares (2SLS) instrumental variable regression approach to ensure robustness of the estimation results. However, this method does not fully account for spatial dependence and spatial spillover effects, which may lead to insufficient capturing of spatial correlations and thus affect the explanatory power of the results. Therefore, the endogeneity test results have certain limitations. Future research should explore more advanced econometric methods that can simultaneously address spatial effects and endogeneity, thereby improving the accuracy and comprehensiveness of causal inference.