Introduction

The power supplies used in communication circuits, Personal Computers (PC), onboard chargers, etc. employ a Diode Bridge Rectifier (DBR) with an electrolytic capacitor, which is inevitable in converting AC voltage into a constant DC voltage. This power supply introduces high harmonic content into the utility due to uncontrolled discharging and charging. The harmonic content introduced is much above the limits suggested by the IEEE and IEC standards. The efficiency and voltage regulation of the power supplies at the load end can be improved if the power factor is improved and the harmonic content is reduced at the Point of Common Coupling (PCC). Many single- and two-stage active Power Factor Correction (PFC) converters are employed in PCs for better performance and PQ improvement. However, single-stage converters are not much preferred due to their complexity in control, low frequency ripples, large capacitance, poor dynamic performance, and high stress across the components1,2,3. In two-stage converters, the first stage takes care of PFC for a significant variation in supply voltage. The second stage achieves voltage regulation of multiple isolated voltages. Two-stage converters with isolated multiple DC output voltages are preferred in PC power supplies to overcome the drawbacks of single-stage converters. The two-stage converters have better voltage regulation on the output side, reduced harmonic content on the utility side, fast dynamic response, and avoid the usage of large capacitance.

Different front-end converters are designed and employed for PFC and voltage regulation. For PFC, boost converters are the most preferred but unsuitable for PC power supply applications as they require a wide input range. Thus, the buck-boost configuration is suitable for PCs as it can handle the considerable load and input range variation. The ripples on the output voltage of the PC power supply should be as low as possible as many PCBs involving several ICs are inside the PC. Singe-stage power converters supply power for better voltage regulation and PQ improvement. However, the voltage regulation is sluggish for varying load conditions in PC, and the stress across the switches is high for single-stage converters. The two-stage converters with better efficiency overcome the drawbacks of single-stage converters4.

To improve the power supply’s efficiency, several bridgeless PFC topologies have been proposed by researchers. The bridgeless topology has fewer components in the conduction path, which makes the current magnitude low. This results in low current stress on the components and switches of the circuit, thus reducing the conduction losses and improving efficiency. In turn, it increases the overall performance of the converter. The bridgeless topologies are preferred for PFC despite their increased cost due to their enhanced efficiency, more extensive output range, improved PQ, and fewer conduction losses4,5,6,7,8,9,10. SEPIC and cuk converters can step down/up voltage and remove the additional stages with high-quality input side current and no dead angle. The cuk converters have advantages such as reduced %THD, increased power density, and efficiency. However, the drawbacks of the converter are challenges in the design of components, DCM operation, and increased current stress. Thus, the SEPIC is preferred over the cuk. The highlights of the SEPIC are the UPF operation, improved voltage conversion ratio, mitigation of harmonics, and more reliable over-cuk converter. Thus, the SEPIC is preferred for low-voltage battery charging stations and computer power supplies. The switching frequency has to be increased to attain improved power density and reduce the passive component size. But this, in turn, increases the switching losses. Zero current and zero voltage soft switching techniques are preferred for bridgeless converters to minimize the switching losses. The combination of buck and flyback converters can operate in a soft-switching condition with no dead angle for input current.However, it increases the number of elements and makes the structure complex11,12,13.

The challenge of the controller designed for AC/DC converters of power supply applications is to achieve accuracy and maintain the desired output voltage. Conventional control employs either voltage or current modes of control. Generally, it would be a single loop with feedback as voltage in voltage mode, incorporating the PI, Type I, and II compensators. The design of the voltage mode is simple, but the converter’s performance during load disturbance is inferior. The performance can be improved by introducing an inductor current control on the inner loop. Due to two nested loop configurations, the response time of the outer voltage loop could be affected. The design of the PI controller also requires a precise mathematical model of the system14. The ANN control overcomes the above drawbacks as it has the nature of parallel computation and quickly learns complex functions by adapting to the system’s dynamics, which makes it more attractive. Various ANN structures are implemented to control power electronics. ADALINE & Feedforward Multilayer Neural Network (FFMNN) is the most preferred ANN structure. ANFIS is preferred for better dynamic response in the DC-DC converters. Machine learning technique-based controllers have been the trend in recent years for the control of power electronic circuits15,16,17. The advantage is that nonlinear control of a wide range is possible with a simple structure at low cost. The online deep reinforcement learning method can effectively handle the constant power load of unknown time-varying conditions for better transient response. It has been inferred from the literature survey that many researchers have not worked so far on implementing ANN in the power quality improvement of computer power supplies with bridgeless PFC converters18,19,20.

A bridgeless SEPIC PFC converter is proposed in this paper to overcome the drawbacks mentioned, especially for computer applications. Four isolated output voltages required by different PC parts are obtained using a half-bridge converter connected to the output of the PFC converter. The SEPIC converter in DCM provides good PFC at all load conditions. The DCM operation is preferred as it requires one voltage sensor for control. The exclusion of DBR at the input side increases the efficiency for a wide output voltage variation with decreased conduction loss. Including a half-bridge converter at the output improves core utilization for the variable DC outputs and provides better regulation and isolation. The proposed ANN-controlled SEPIC configuration is tested for supply voltage and load variations. The performance of the power supply is analyzed based on input PQ indices such as PF at the supply side, the percentage Total Harmonic Distortion (THD) of the supply current, Displacement Power Factor (DPF), Distortion Factor (DF)and output voltage ripple for all the four terminals, at rated load and half load conditions. The performance of the proposed system with ANN and the conventional controller is analyzed based on the settling time and overshooting and undershooting of the output voltage. The simulation results of the proposed configuration are compared with those of the Canonical Switching Cell (CSC) converter configuration, which implements ANN and a conventional controller to identify a suitable bridgeless converter for the PC power supply. The ANN and conventional controller for the proposed SEPIC configuration are developed using an FPGA processor in the hardware setup. The hardware and simulation results demonstrate the proposed control’s effectiveness. The highlights of the paper are:

  • Design of bridgeless SEPIC converter-based MOSMPS with ANN-based control approach.

  • Implementation of ANN in MATLAB/Simulink environment for converter control.

  • Implementation of ANN controller in FPGA.

  • Validation of the proposed MOSMPS through hardware implementation under various source and load situations.

  • The simulation and experimental results of the proposed MOSPMS comply with IEEE 519 standards and IEC 61000-3-2 guidelines.

The rest of the paper is organized as follows: The subsequent section details the system configuration of MOSMPS with PFC converters. Section “Control of the MOSMPS systems” demonstrates the ANN control and its implementation. Simulation results are presented, and the performance comparison of MOSMPS with SEPIC and CSC PFC converters is interpreted in Sect. “Simulation results and discussion”. The experimental verification is focused on Sect. “Hardware implementation”, and the paper concludes with the scope of future work in Sect. “Conclusion”.

Two-Stage Converter-Based MOSMPS employing bridgeless PFC converters

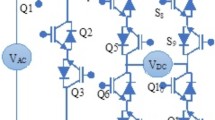
The system layout of a MOSMPS with a two-stage converter employs a bridgeless PFC converter as depicted in Fig. 1. When the single-phase AC supply is applied to the PFC converter, an inductor and a capacitor filter out high-frequency switching ripples. Two independent bridgeless converters are employed in the converter configuration to operate during the negative and positive half cycles. For inherent PFC, the inductors of the bridgeless converters are designed to operate under DCM. The neural network controller-1 regulates the PFC converter’s output voltage, and the controlled voltage across the capacitor is fed as input to the half-bridge Voltage Source Inverter (VSI).

Fig. 1
figure 1

MOSMPS system configuration using bridgeless PFC converters.

Full size image

The capacitor at the bridgeless converter’s output functions as a filter for the bridgeless converter’s intermediate DC voltage. The high-frequency transformer (HFT) is involved in an isolated half-bridge converter that supports the isolation of various multiple DC outputs and voltage scaling. The four multiple output voltages V01, V02, V03, and V04 of the MOSMPS are derived from the secondary windings of HFT. By controlling the converter’s duty ratio, the neural network controller-2 regulates the output voltages in the secondary windings of HFT. The two stages of the MOSMPS are controlled independently for voltage regulation and input PQ improvement.

MOSMPS employing bridgeless SEPIC PFC converter

Operation and design of bridgeless SEPIC PFC converter

Figure 2 represents the MOSMPS with a bridgeless SEPIC converter for PFC and an isolated half-bridge converter for multiple outputs. In this configuration, the isolated half-bridge converter is operated under CCM, while the bridgeless SEPIC converter is operated under DCM to have inherent PFC. The configuration includes two power semiconductor switches, S1 and S2, that are triggered alternately at every half cycle. Three operation modes can be realized for each switching cycle for the converter’s DCM operation21.

Fig. 2
figure 2

MOSMPS circuit configuration with bridgeless SEPIC PFC converter.

Full size image

Mode I:

The current path is Vin - Lr - L11 - S1 - D11 - Vin when switch S1 is turned on. During this time, the AC supply energizes the inductor L11. The inductor current linearly increases and attains its peak value. The capacitor C11 discharges and charges the inductor L12. The capacitor discharges through the path C11 - S1 - L12 - C11. The corresponding equations of mode I are given using KVL and KCL. Ceq is the equivalent capacitance of a series combination of C1 & C2.

$$\:{v}_{in}-\:{L}_{11}\frac{{di}_{in}}{dt}=0$$
(1)
$$\:{C}_{11}{dv}_{{c}_{11}}+{i}_{in}=0$$
(2)
$$\:{L}_{12}\frac{{{di}_{{L}_{12}}}_{\:}}{dt}-{v}_{{c}_{11}}=0$$
(3)
$$\:{C}_{eq}\frac{{{dv}_{{c}_{eq}}}_{\:}}{dt}+\:\frac{{v}_{{c}_{eq}}}{R}=0$$
(4)

Mode II:

When S1 is switched off, the inductor’s maximum current level drops to zero, and the diode D12 starts to conduct. The output capacitors C1 and C2 acquire energy stored in the inductors L11 and L12. The equations corresponding to mode II are given using KVL and KCL.

$$\:{v}_{in}={L}_{11}\:\frac{{di}_{in}}{dt}+{v}_{{c}_{11}}+{v}_{{c}_{eq}}$$
(5)
$$\:{L}_{12}\frac{{di}_{{L}_{12}}}{dt}+{v}_{{c}_{eq}}=0$$
(6)
$$\:{C}_{11}\frac{{dv}_{{c}_{11}}}{dt}-{i}_{in}=0$$
(7)
$$\:{C}_{eq}\frac{{dv}_{{c}_{eq}}}{dt}-{i}_{in}-\:{i}_{{L}_{12}}+\frac{{v}_{{c}_{eq}}}{{R}_{L}}=0$$
(8)

Mode III:

In this mode, no circuit component is in the state of conduction, and the inductor’s current is at zero. This mode assures the converter’s DCM operation. The other converter goes through the same process sequence in the negative half cycle. The average value of the source voltage is calculated as 198 V using Eq. (9) for Vin = 220 V and the duty cycle (D) of the switches S1 and S2 can be calculated using Eq. (10)

$$\:{\text{V}}_{\text{d}}=\:\frac{2\sqrt{2}{\text{V}}_{\text{i}\text{n}\:\:}}{{\uppi\:}}$$
(9)
$$\:\text{D}=\frac{{\text{V}}_{\text{c}}}{{\text{V}}_{\text{d}}+{\text{V}}_{\text{c}}}=\:0.6$$
(10)

where Vc= 300 V, the PFC converter’s output voltage. The regulated DC output voltage (Vc) of the PFC converter stays constant at 300 V despite variations in the supply voltage (Vin= 170 to 270 V). Hence, the duty ratios are calculated considering these variations in supply voltage. The duty ratio for minimum voltage (170 V), maximum voltage (270 V) and rated voltage (220 V) are Dmin = 0.66, Dmax= 0.552 and Drated = 0.6, respectively. Efficient control of the converter is possible when the value of D is chosen less than the Drated. Equation (11) is used to compute the value of the inductor L11 while accounting for a 40% ripple content in the input current.

$$\:{\text{L}}_{11}=\:\frac{\text{D}{{T}_{s}\text{V}}_{\text{d}}}{{\varDelta\:i}_{Li}}=9.2\:\text{m}\text{H}$$
(11)

where, Ts = switching time = 50 µs; \(\:{\varDelta\:i}_{Li}=\) 40% of Iin = 40% of 0.8116 A = 0.324 A.

$$\:{\text{K}<K}_{\text{c}}<\frac{1}{{2\left(\frac{{\text{V}}_{\text{c}}}{\sqrt{2}{\text{V}}_{\text{m}}}+\text{n}\:\right)}^{2}}<\frac{1}{{2(\frac{300}{311}+1)}^{2}}<0.129$$
(12)

where n = 1, for the SEPIC converter (non-isolated) and Kc = critical conduction parameter. For DCM operation of the converter, K is considered less than 2/3rd of Kc. The K is selected as 0.086. The Leq is calculated as shown below:

$$\:{\text{L}}_{\text{e}\text{q}}=\:\frac{\text{R}\text{K}}{2{\text{f}}_{\text{s}}}=\frac{{\text{L}}_{11}{\text{L}}_{12}}{{\text{L}}_{11}+{\text{L}}_{12}}\:=1.10\:\text{m}\text{H}$$
(13)

From the values of L11 and Leq, the value of inductor L12 can be calculated using Eq. (14) as

$$\:{\text{L}}_{12}=\frac{{\text{L}}_{11}{\text{L}}_{\text{e}\text{q}}}{{\text{L}}_{11}-{\text{L}}_{\text{e}\text{q}}}=1.25\:\text{m}\text{H}$$
(14)

For DCM, the value of L12 is selected as 1 mH. The oscillation of the input current can be minimized if the resonant frequency (fr) of (C11, L11 and L12) is more significant than line frequency fl. The condition fr< fs should be satisfied during every switching period to maintain the converter’s constant DC link voltage. Based on the above conditions, the value of fr is 2000 Hz. Thus, the value of C11 can be calculated using Eq. (15) as

$$\:{\text{C}}_{11}=\:\frac{1}{\left({{\upomega\:}}_{\text{r}}^{2}\right)\left({\text{L}}_{11}+\:{\text{L}}_{12}\right)}=0.62\:{\upmu\:}\text{F}$$
(15)

Operation and design of half-bridge converter

The half-bridge VSI is designed and built using the switches Sp, Sn, the capacitors C1, C2, and multiple outputs HFT. The four output windings of the HFT are center-tapped to reduce the losses. The inductors L01 - L04 and capacitors C01 - C04 of HFT help filter the current and voltage ripples. The secondary winding with the largest voltage rating is sensed and used by the NN controller- 2 to regulate the output voltage. The remaining output voltages are controlled by regulating the isolated converter’s duty cycle operating in CCM. Each half-bridge VSI switching cycle has four distinct operation stages, and stages II and IV follow the same sequence21,22.

Stage I:

When the switch Sp is turned on, the HFT’s primary winding is energized and the current flow path is completed through capacitance C2. The inductors (Lo1 - Lo4) store energy when the diodes D01, D03, D05 and D07 are forward-biased. As a result, the inductor currents increase linearly until they reach their peak value. The filter capacitances Co1 - Co4 discharge through the loads.

Stage II:

The switches Sp and Sn are turned off in this stage. Hence, the diodes (Do1 - Do8) help to freewheel the energy held in the inductors (Lo1 - Lo4). The inductor currents and the voltage across the HFT must both be zero for the freewheeling action to stop.

Stage III:

The switch Sn is turned on to energize the HFT’s primary winding through capacitance C1. The diodes Do2, Do4, Do6 and Do8 are forward-biased and the associated inductors (Lo1 - Lo4) store energy. During this stage, the currents in the inductor rise linearly and attain the peak value. The Sn is switched off when the inductor currents reach the steady state.

Stage IV:

The circuit operates in the same way as Stage II.

The capacitor in the half-bridge VSI is selected to eliminate the ripple of 100 Hz frequency reflected from the AC supply side. The C1 and C2 are chosen to be 0.310 mF, considering ω = 314 rad/sec, \(\:{{\Delta\:}\text{V}}_{\text{c}}=6\:\text{V}\left(2\text{\%}\right)\) and\(\:\:{\text{I}}_{0}=0.58\:\text{A}\). These converters are designed for PC power supply applications and can withstand power failure for some time. The capacitor value calculated for a withstand time of 10 ms is 0.18 mF. As two capacitors are connected in series in the input of half-bridge VSI, each capacitor equals 0.36 mF. In HFT, the inductors L01- L04 are designed to be 0.12 mH, 0.023 mH, 1.3 mH, and 1.25 mH, respectively. The switching frequency is 60 kHz with a 2% inductor current ripple and a duty ratio of 0.4. The turns ratio n1- n4 of the HFT are 0.1, 0.042, 0.042, and 0.1, respectively.

MOSMPS employing bridgeless canonical switching cell converter

The MOSMPS is also simulated with a bridgeless CSC converter for PFC and an isolated half-bridge converter for multiple outputs as shown in Fig. 3. The PFC bridgeless converter has two back-to-back connected CSC converters. The operation of the two CSC converters remains the same in both half cycles, and the design parameters are presented in Table 1. The inductor current is preferred to be in DCM for all the modes of operation22. The simulation results of MOSMPS with bridgeless SEPIC and CSC converters are compared to identify the suitable configuration for the computer power supply.

Fig. 3
figure 3

MOSMPS circuit topology with bridgeless CSC converter.

Full size image
Table 1 Design parameters of the converters.
Full size table

Control of the MOSMPS systems

The choice of control strategy of the MOSMPS determines the improvement of PQ at the source side and regulation of the output DC voltage during steady state and transient conditions. The primary requirements of the controller are (i) good dynamic response, (ii) less computation time and (iii) high accuracy in sensing the signals and calculation.

Control of bridgeless PFC converter

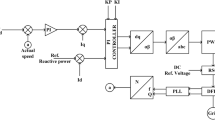
An NN-based control scheme is adopted for power quality improvement in the bridgeless topologies. High-frequency power semiconductor switches S1 and S2 of the converters are triggered periodically during the respective half cycles of the supply. The capacitor voltage (Vc) at the PFC converter’s output is sensed, and the error Ve is calculated by comparing it to the reference voltage Vcref. The signal \(\:{\text{V}}_{\text{e}}\), which is fed to the NN controller (NN-1), is determined as \(\:{\text{V}}_{\text{c}\text{r}\text{e}\text{f}}\left(\text{n}\right)-\:{\text{V}}_{\text{c}}\left(\text{n}\right)\), where n represents the nth sampling instant. The triggering pulses for S1 and S2 are generated by comparing NN-1 (Vcc) output and a high-frequency saw tooth signal (St1) as depicted in Fig. 4. The conditions for generating the triggering pulses are

$$\begin{aligned} \:\text{F}\text{o}\text{r}\:{\text{v}}_{\text{i}\text{n}}<0;\:\left\{\begin{array}{c}\text{if}\:{\text{S}}_{\text{t}1}<{\text{V}}_{\text{c}\text{c}},\:\:\text{then}\:{\text{S}}_{2}=\text{on}\\\:\text{if}\:{\text{S}}_{\text{t}1}\ge\:\:{\text{V}}_{\text{c}\text{c}},\:\:\text{then}\:{\text{S}}_{2}=\text{off}\end{array}\right\} \\ \:\text{F}\text{o}\text{r}\:{\text{v}}_{\text{i}\text{n}\:}>0;\:\left\{\begin{array}{c}\text{if}\:{\text{S}}_{\text{t}1}<{\text{V}}_{\text{c}\text{c}},\:\:\text{then}\:{\text{S}}_{1}=\text{on}\\\:\text{if}\:{\text{S}}_{\text{t}1}\ge\:\:{\text{V}}_{\text{c}\text{c}},\:\:\text{then}\:{\text{S}}_{1}=\text{off}\end{array}\right\}\end{aligned}$$
(16)
Fig. 4
figure 4

Control scheme of bridgeless converter-based MOSMPS.

Full size image

Control of Half-Bridge converter

Implementing an NN-based control scheme regulates the output voltage of the half-bridge converter. The highest output voltage (V01 = + 12 V) is sensed and compared with reference V01ref to generate the error signal of Ve1. The input to the NN controller-2 is the error signal, and a carrier saw tooth waveform (St1) is compared with the controller output to generate pulses. Thus, the output voltage of the half-bridge converter is maintained constant. The regulation of the remaining output voltages is taken care of by the converter’s duty cycle since secondary windings of the other outputs are connected to the common core of the HFT. If voltage variations occur on the other windings, the duty ratio is changed accordingly by the proposed closed-loop control to regulate the output voltage irrespective of the variations of the load. The other winding’s response will be sluggish in comparison with the sensed winding.

State space modeling of SEPIC converter

Creating a model of the system is necessary to analyze the behavior of a SEPIC converter and design appropriate controllers. One widely used approach is the state space averaging method, which involves averaging all system variables within a switching period to derive an equivalent model in matrix form23. This matrix can then be used to obtain the converter’s steady-state model, transfer functions, and dynamic model. Equations (17) and (18) can be given to express the general state space equations for the SEPIC converter operation in Mode I.

$$\:\dot{x\left(t\right)}\:=\:{J}_{1}x\left(t\right)+{M}_{1}u\left(t\right)$$
(17)
$$\:\text{y}\left(\text{t}\right)\:={v}_{1}x\left(t\right)$$
(18)

Equations (19) and (20) can now be given to express the state matrix of the SEPIC converter in Mode I Operation.

$$\:\left[\begin{array}{c}\frac{{di}_{in}}{dt}\\\:\frac{{di}_{{L}_{12}}}{dt}\\\:\frac{{dv}_{{c}_{11}}}{dt}\\\:\frac{{dv}_{{c}_{eq}}}{dt}\end{array}\right]=\left[\begin{array}{cccc}0&\:0&\:0&\:0\\\:0&\:0&\:\frac{1}{{L}_{12}}&\:0\\\:0&\:\frac{-1}{{C}_{11}}&\:0&\:0\\\:0&\:0&\:0&\:\frac{1}{{R}_{{c}_{eq}}}\end{array}\right]\left[\begin{array}{c}{i}_{in}\\\:{i}_{{L}_{12}}\\\:{v}_{{c}_{11}}\\\:{v}_{{c}_{eq}}\end{array}\right]+\left[\begin{array}{c}\frac{1}{{L}_{11}}\\\:0\\\:0\\\:0\end{array}\right]{v}_{in}$$
(19)
$$\:\text{y}\left(\text{t}\right)\:=\left[\begin{array}{ccc}0&\:0&\:\begin{array}{cc}0&\:1\end{array}\end{array}\right]\left[\begin{array}{c}{i}_{in}\\\:{i}_{{L}_{12}}\\\:{v}_{{c}_{11}}\\\:{v}_{{c}_{eq}}\end{array}\right]$$
(20)

Similarly, Eqs. (21) and (22) can be given to express the general state space equations for the SEPIC converter operation in Mode II.

$$\:\text{x}\left(\text{t}\right)\:={J}_{2}x\left(t\right)+{M}_{2}u\left(t\right)$$
(21)
$$\:{\text{y}\left(\text{t}\right)\:=\:v}_{2}x\left(t\right)$$
(22)

Equations (23) and (24) can now be expressed to show the state matrix of the SEPIC converter in Mode II operation.

$$\:\left[\begin{array}{c}\frac{{di}_{in}}{dt}\\\:\frac{{di}_{{L}_{12}}}{dt}\\\:\frac{{dv}_{{c}_{11}}}{dt}\\\:\frac{{dv}_{{c}_{eq}}}{dt}\end{array}\right]=\left[\begin{array}{cccc}0&\:0&\:\frac{-1}{{L}_{11}}&\:\frac{-1}{{L}_{11}}\\\:0&\:0&\:0&\:\frac{-1}{{L}_{12}}\\\:\frac{1}{{C}_{11}}&\:0&\:0&\:0\\\:\frac{1}{{C}_{eq}}&\:\frac{1}{{C}_{eq}}&\:0&\:\frac{-1}{{RC}_{eq}}\end{array}\right]\left[\begin{array}{c}{i}_{in}\\\:{i}_{{L}_{12}}\\\:{v}_{{c}_{11}}\\\:{v}_{{c}_{eq}}\end{array}\right]+\left[\begin{array}{c}\frac{1}{{L}_{11}}\\\:0\\\:0\\\:0\end{array}\right]{v}_{in}$$
(23)
$$\:\text{y}\left(\text{t}\right)\:=\left[\begin{array}{ccc}0&\:0&\:\begin{array}{cc}0&\:1\end{array}\end{array}\right]\left[\begin{array}{c}{i}_{in}\\\:{i}_{{L}_{12}}\\\:{v}_{{c}_{11}}\\\:{v}_{{c}_{eq}}\end{array}\right]$$
(24)

The state matrix for the SEPIC converter averaged over a switching cycle can be found in Eqs. (25) and (26).

$$\:\left[\begin{array}{c}\frac{{di}_{in}}{dt}\\\:\frac{{di}_{{L}_{12}}}{dt}\\\:\frac{{dv}_{{c}_{11}}}{dt}\\\:\frac{{dv}_{{c}_{eq}}}{dt}\end{array}\right]=\left[\begin{array}{cccc}0&\:0&\:\frac{D-1}{{L}_{11}}&\:\frac{D-1}{{L}_{11}}\\\:0&\:0&\:\frac{D}{{L}_{12}}&\:\frac{D-1}{{L}_{12}}\\\:\frac{1-D}{{C}_{11}}&\:\frac{-D}{{C}_{11}}&\:0&\:0\\\:\frac{1-D}{{C}_{eq}}&\:\frac{1-D}{{C}_{eq}}&\:0&\:\frac{-1}{{R}_{{C}_{eq}}}\end{array}\right]\left[\begin{array}{c}{i}_{in}\\\:{i}_{{L}_{12}}\\\:{v}_{{c}_{11}}\\\:{v}_{{c}_{eq}}\end{array}\right]+\left[\begin{array}{c}\frac{1}{{L}_{11}}\\\:0\\\:0\\\:0\end{array}\right]{v}_{in}$$
(25)
$$\:\text{y}\left(\text{t}\right)\:=\left[\begin{array}{ccc}0&\:0&\:\begin{array}{cc}0&\:1\end{array}\end{array}\right]\left[\begin{array}{c}{i}_{in}\\\:{i}_{{L}_{12}}\\\:{v}_{{c}_{11}}\\\:{v}_{{c}_{eq}}\end{array}\right]$$
(26)

Where J = System matrix; M = input matrix; V = output matrix; D = SEPIC converter duty cycle.

Design of PI controller

Substituting the parameter values given in Table 1 into Eqs. (25) and (26), the fourth-order transfer function is derived and given below

$$\:\text{G}1\left(s\right)\:=\:\frac{{2.415e}^{05}{s}^{2}-{8.953e}^{-06}s+{1.87e}^{14}}{{s}^{4}+{555.6s}^{3}+{4.934e}^{08}{s}^{2}+{2.736e}^{11}s+{1.247e}^{14}}$$
(27)

The PI controller tuning is performed using the Ziegler-Nichols (Z-N) method. The Z-N formula for the PI controller is Kp = 0.45\(\:{k}_{cr}\) and Ki=\(\:\:\frac{\:\:{0.54k}_{cr}}{{T}_{cr}}\). Where \(\:{k}_{cr}\)= ultimate gain (the value at which oscillation occurs),\(\:\:{T}_{cr}\)= ultimate period (the time period of oscillations). Applying the Z-N formula, the Kp and Ki values are calculated as 0.5 and 18. The closed-loop transfer function is computed as follows

$$\:\:\text{G}2\left(s\right)\:=\frac{120.8{s}^{3}+{4.347e}^{07}{s}^{2}+{9.35e}^{10}s+3.366\:{e}^{16}}{{s}^{5}+555.6\:{s}^{4}+{4.934{e}^{08}s}^{3}+{2.736e}^{11}{s}^{2}+{1.247e}^{14}s}$$
(28)

From the Bode plot shown in Fig. 5, it can be inferred that the open-loop system has a negative phase margin of −4.34°, implying that the system is unstable. Whereas for the closed-loop system, the phase and gain margin are 45.8⁰ and 6.27 dB. This proves that the closed-loop system of the SEPIC converter is stable.

Fig. 5
figure 5

Bode diagram for the closed-loop system.

Full size image

After successfully tuning the PI controller using the derived system model, the same model is utilized to design a feedforward multilayer neural network (FFMNN)-based controller. From the closed-loop PI controller system, the input-output dataset is generated. This dataset serves as the training input to the neural network to learn the control behavior exhibited by the tuned PI controller. The model-informed FFMNN training process replicates and further enhances control performance, particularly in robustness and adaptability to varying operating conditions.

Feedforward multilayer neural network

Input, hidden and output are the three layers that constitute the FeedForward Multilayer Neural Network (FFMNN). Modifiable weights interconnect these layers and are mentioned as the link between the layers in the pictorial representation. Each layer is made up of neurons or nodes. The neurons in the input layer process their input through pure linear function. The neurons in the hidden layer process through nonlinear function. In regression & estimation applications, the output neurons process through linear function. The other neurons in the input and hidden layer are bias neurons that produce output as 1 and connect to the next layer neurons through adjustable weights. The information in the FFMNN propagates through the input, hidden and output layers in one direction, i.e., forward. The structure of FFMNN is shown in Fig. 6 below.

Fig. 6
figure 6

Structure of FFMNN.

Full size image

Based on the input pattern vector, the input neurons are assigned. The output layer size is based on the output to be estimated. The complexity of the problem decides the hidden layer neurons24,25.

The I and J augmented with a unity bias can be expressed as

$$\:{I=\left[{I}_{1\:}{I}_{2}\dots\:\dots\:\:{I}_{J}\:1\right]}^{W}$$
(29)

Where I = input layer with the input vector and J = dimensional input pattern vector.

The input neurons are connected to the corresponding mth hidden neuron through weight U and it can be expressed in the format (Um) as:

$$\:{U}_{m}^{W}=\left[{U}_{m1}\:{U}_{m2}\dots\:.\:{U}_{mJ}\:\:{U}_{m}^{0}\right]$$
(30)

The scalar net activation designated as netm is produced by each hidden unit (m) by the following Eq. 

$$\:{net}_{m}={U}_{m}^{W}I=\:\sum\:_{i=1}^{J}{U}_{mi}{I}_{i}+\:{U}_{m}^{0}\:$$
(31)

Where J = features of the input vector and i = input neuron.

The nonlinear output (Km) of (netm) of each hidden neuron can be expressed as:

$$\:{K}_{m}=f\left({net}_{m}\right)$$
(32)

Where f represents the tan-sigmoid function and is given by

$$\:f\left({net}_{m}\right)=tanh\left({net}_{m}\right)\approx\:\frac{2}{1+\:{e}^{-2{net}_{m}}}-1$$
(33)

Similarly, the net activation function (netn) of each output neuron is expressed as

$$\:{net}_{n}=\:{V}_{n}^{W}K=\:\left[\begin{array}{c}{V}_{n1}\\\:{V}_{n2}\\\:\begin{array}{c}\vdots\\\:\begin{array}{c}{V}_{nh}\\\:{V}_{n}^{0}\end{array}\end{array}\end{array}\right]\:\left[\begin{array}{ccc}{K}_{1}&\:{K}_{2}&\:\begin{array}{cc}\dots\:&\:\begin{array}{cc}{K}_{h}&\:1\end{array}\end{array}\end{array}\right]=\:\sum\:_{m=1}^{h}{V}_{nm}{K}_{m}+\:{V}_{n}^{0}$$
(34)

Where

\(\:{V}_{nm}\) = weight connecting the nth output neuron and the mth hidden neuron.

\(\:{V}_{n}^{0}\) = bias value of the output neuron (n).

h = hidden neuron number.

As pure linear operator is preferred at the output side, the estimated output Zn will be equal to \(\:{net}_{n}.\)

$$\:{Z}_{n}=\:{net}_{n}=\:\sum\:_{m=1}^{h}{V}_{nm}f\left(\sum\:_{i=1}^{J}{U}_{mi}{I}_{i}+\:{U}_{m}^{0}\right)+\:{V}_{n}^{0}$$
(35)

The FFMNN main objective is to match the estimated output with the target by adjusting the weight. The backpropagation algorithm is adopted for training the weights. Let Δn be the training error of a sample that can be expressed as

$$\:{Y}_{n}=\frac{1}{2}\:{\left({\varDelta\:}_{n}\right)}^{2}=\:\frac{1}{2}\:{\left(target-estimated\:output\right)}^{2}$$
(36)

Where \(\:{Y}_{n}\) = nth output node criterion function. The output layer GD can be expressed as

$$\:\nabla\:Y\left({V}_{nm}\right)=\:-{\varDelta\:}_{n}.\frac{\partial\:{Z}_{n}}{\partial\:{V}_{nm}}=\:-{\varDelta\:}_{n}{K}_{m}$$
(37)
$$\:\nabla\:Y\left({V}_{n}^{0}\right)=\:-{\varDelta\:}_{n}.\frac{\partial\:{Z}_{n}}{\partial\:{V}_{n}^{0}}=\:-{\varDelta\:}_{n}$$
(38)

The updation of input-hidden layer weight is performed by calculating the gradient via the chain rule.

$$\begin{aligned} \:\nabla\:Y\left({U}_{mi}\right) & =\:-{\varDelta\:}_{n}.\frac{\partial\:{Z}_{n}}{\partial\:{U}_{mi}}=-{\varDelta\:}_{n}.\frac{\partial\:{Z}_{n}}{\partial\:{net}_{m}}.\frac{\partial\:{net}_{m}}{\partial\:{U}_{mi}}\\ & =\:-{\varDelta\:}_{n}{V}_{nm}{f}^{{\prime\:}}\left({net}_{m}\right).{I}_{i}\end{aligned}$$
(39)

Similarly

$$\:\nabla\:Y\left({U}_{m}^{0}\right)=\:-{\varDelta\:}_{n}.\frac{\partial\:{Z}_{n}}{\partial\:{U}_{m}^{0}}=\:=\:-{\varDelta\:}_{n}{.V}_{nm}{f}^{{\prime\:}}\left({net}_{m}\right)$$
(40)

Where

$$\:{f}^{{\prime\:}}\left({net}_{m}\right)=\frac{{4e}^{-{2net}_{m}}}{{\left(1+{e}^{-{2net}_{m}}\right)}^{2}}=1-{\left[f{net}_{m}\right)}^{2}$$
(41)

From Eqs. (37) & (38) it is clear that the error from the output is feedback to the hidden layer for the updation of neurons. This process clearly explains the backpropagation technique. The following equation summarizes the updated rule for input-hidden synapses & hidden output.

$$\:{V}_{nm\:\:=\:\:}^{k}{V}_{nm\:\:}^{k-1}.{\eta\:}_{v}.\nabla\:{Y}^{k}\left({V}_{nm}\right)={V}_{nm\:\:}^{k-1}+{\eta\:}_{v}.\:{\varDelta\:}_{n}.\:{K}_{m}$$
(42)
$$\:{\left({V}_{n}^{0}\right)}^{k}=\:{\left({V}_{n}^{0}\right)}^{k-1}-{\eta\:}_{v}.\nabla\:{Y}^{k}\left({V}_{n}^{0}\right)={\left({V}_{n}^{0}\right)}^{k-1}+{\eta\:}_{v}.\:{\varDelta\:}_{n}$$
(43)
$$\:{U}_{mi\:=}^{k}\:{U}_{mi}^{k-1}+{\eta\:}_{W}.\:{\varDelta\:}_{n}.{U}_{m}\:.\:{f}^{{\prime\:}}\left({net}_{m}\right).{I}_{i}$$
(44)
$$\:{\left({U}_{m}^{0}\right)}^{k}=\:{\left({U}_{m}^{0}\right)}^{k-1}+{\eta\:}_{W}.\:{\varDelta\:}_{n}.\:{V}_{nm}.\:{f}^{{\prime\:}}\left({net}_{m}\right)$$
(45)

Where.

\(\:{\eta\:}_{v}\) = learning rate for the hidden-output.

\(\:{\eta\:}_{w}\) = learning rate for input hidden weight update rules.

Basic GD is incorporated to derive these update rules.

Implementation of feedforward MNN-Based control in MATLAB/SIMULINK

The load is not constant in real-time applications and varies with time. The controller selected must be capable of monitoring and tracking the changes accurately. Thus, the FFMNN controller has to be adequately trained to avoid errors during the load variation. For the FFMNN to perform better, it has to be trained for various load conditions and types. Thus, the FFMNN is trained for 25%, 50%,75%, and 100% load conditions. The FFMNN is developed in MATLAB by implementing the NN toolbox after obtaining the training and target data using the following procedure24,25,26,27,28.

a) Compose the matrices for network targets (W) and inputs (I). The I & W matrices can be formulated as.

$$\:{I}_{J\:\times\:\:M\:}=\:\left[\begin{array}{ccc}{I}_{11}&\:{I}_{12}&\:\cdots\:\\\:{I}_{21}&\:{I}_{22}&\:\cdots\:\\\:\begin{array}{c}\vdots\\\:{I}_{J1}\end{array}&\:\begin{array}{c}\vdots\\\:{I}_{J2}\end{array}&\:\begin{array}{c}\dots\:\\\:\dots\:\end{array}\end{array}\:\:\:\:\begin{array}{c}{I}_{1M}\\\:{I}_{2M}\\\:\begin{array}{c}\vdots\\\:{I}_{JM}\end{array}\end{array}\right]$$
(46)
$$\:{W}_{O\:\times\:\:M\:}=\:\left[\begin{array}{ccc}{W}_{11}&\:{W}_{12}&\:\cdots\:\\\:{W}_{21}&\:{W}_{22}&\:\cdots\:\\\:\begin{array}{c}\vdots\\\:{W}_{O1}\end{array}&\:\begin{array}{c}\vdots\\\:{W}_{O2}\end{array}&\:\begin{array}{c}\dots\:\\\:\dots\:\end{array}\end{array}\:\:\:\:\begin{array}{c}{W}_{1M}\\\:{W}_{2M}\\\:\begin{array}{c}\vdots\\\:{W}_{OM}\end{array}\end{array}\right]$$
(47)

where O = target variables, J = number of features and M = number of training cases.

b)”newff” is the function in the NN toolbox that constructs the feedforward NN. The command mentioned below is utilized to form an FFMNN.

$$\text{net} = \text{newff (I, W, H, AFs, TA, UR, P)}$$
(48)

where, H = Hidden layer (D – dimensional), AF = Activation functions, TA = training algorithm, UR = weight update, P = Performance function. The H is a column or row matrix where the number of hidden layers is represented by the length (D). dth element value represents the neuron numbers for the respective dth hidden layer. The H matrix with D hidden layers can be formulated as.

$$\:{H}_{1\:\times\:\:D}=\:\left[{h}_{1\:}{h}_{2\:}\cdots\:\:{h}_{d\:}\dots\:\:{h}_{D\:}\right]$$
(49)

For example, if H has three hidden layers with 5, 10, and 15 neurons in the 1 st, 2nd, and 3rd layers, respectively, it can be represented as H =5,10,14. Based on the training error and performance, the number of neurons of hidden layers is chosen heuristically. Since the load varies non-linearly, tansigmoid is chosen as AF for hidden neurons, and pure linear AF is selected for output neurons. In MATLAB, the AFs are written in the cell format as below:

$$\:AFs=\:\left\{``tansig,"\:``purelin"\right\}$$
(50)

Tan-sigmoid and pure linear functions are expressed in MATLAB by the keywords tansig and purelin. Multiple training algorithm features are available in MATLAB. The scaled conjugate gradient algorithm (SCG) is more suitable for SMPS applications. The SCG is the most accurate and fastest BP training algorithm. Similarly, gradient descent with momentum (GDM) is preferred in the UR function. In MATLAB, SGTA & GDM UR syntax is “trainscg” and “learngdm” respectively. The mean squared error (MSE) is chosen as the performance function (P). The syntax of P is “mse.“The NN “newff” command of the SMPS can be written as.

\(\:net=newff(\:J,W,\:15,\:\left\{``\text{tansig}," ``\: \text{purelin"}\right\}\,\:``\text{trainscg,}"\) \(\:``\text{learngdm},\:" ``\text{mse}").\) The FFMNN is trained by the code “train” from the NN toolbox. The following code can train the command developed in Eq. (48) for FFMNN. \(\:net\:=\:train\:\left(net,\:I,\:W\right).\)

c)The training data (I) is utilized to evaluate the performance of the trained FFMNN networks. The input I is fed to the trained network to anticipate the output by implementing the following code in the MATLAB.

Z = sim (net, I).

d)The mean absolute error criterion is preferred for comparing the target (W) and the anticipated output (Z). The training performance can be evaluated using the following code.

\(\:MAE=\frac{1}{K}\:\sum\:_{n=1}^{K}\left|Z\left(n\right)-W\left(n\right)\right|\:\) Where K = training cases number.

e)The trained network’s Simulink model can be created using the command below.

\(\:gensim\left(net\right)\)

The proposed simulation file is then loaded with the trained Simulink model to obtain the simulation results.

Simulation results and discussion

To identify a suitable SMPS system for computer power supply application, computer-aided simulation is performed in MATLAB/SIMULINK environment with neural network controllers for Input PFC and output voltage regulation. The MOSMPS performance is analyzed with bridgeless SEPIC and CSC converter configurations modeled as per the specifications in Table 2 for various conditions specified in Table 3. The performance of the MOSMPS with different converter configurations is analyzed at varying conditions, based on PQ indices such as % THD of source current, DF, PF, DPF and output voltage ripple for all the four terminals, at rated load and half load conditions. Based on the system’s settling time, overshoot, and undershoot of the output voltage at terminal 1, the system’s performance with NN and conventional controllers is compared.

Table 2 Specifications of the MOSMPS.
Full size table
Table 3 Details of various simulation conditions.
Full size table

Performance comparison of bridgeless SEPIC and CSC Converter-Based MOSMPS under Steady-State conditions

Performance characteristics of MOSMPS involving SEPIC and CSC converters with NN control are depicted in Figs. 7 and 8, respectively. The traces illustrate the regulation of four output voltages, mains voltage and source current (Iin) at Vin= 220 V. The potency of the NN controller in regulating the output voltages Vo1 to Vo4 is evident from the traces of output voltages. The efficacy of the NN controller in maintaining the PF nearly unity is justified by the sinusoidal and in-phase source voltage and current waveforms.

Fig. 7
figure 7

Traces of output voltages, Vin, Iin and harmonic spectrum of Iin of SEPIC converter-based MOSMPS with rated supply voltage.

Full size image
Fig. 8
figure 8

Traces of output voltages, Vin and Iin of CSC converter-based MOSMPS with rated supply voltage.

Full size image

Performance comparison of MOSMPS under increased supply voltage condition

Figures 9 and 10 illustrate the traces of four output voltages, mains voltage, and Iin at Vin= 250 V of MOSMPS with bridgeless SEPIC and CSC converters, respectively. The traces infer that the NN controller effectively regulates the output voltages Vo1 to Vo4 and the sinusoidal Iin, which is in phase with the voltage claims unity power factor.

Fig. 9
figure 9

Traces of output voltages, Vin, Iin, and harmonic spectrum of Iin of SEPIC converter-based MOSMPS with increased supply voltage.

Full size image
Fig. 10
figure 10

Traces of output voltages, Vin and Iin of CSC converter-based MOSMPS with increased supply voltage.

Full size image

Performance comparison of MOSMPS under decreased supply voltage condition

Figures 11 and 12 demonstrate the traces of four output voltages, mains voltage, and Iin at Vin= 170 V of MOSMPS with SEPIC and CSC converters, respectively. At steady state condition of the simulation with decreased Vin, the %THD of Iin of bridgeless SEPIC converter-based MOSMPS is retained at 2.50%, whereas in a CSC converter-based MOSMPS it is maintained at 3.98%, which is well below the PQ standard limits. The traces in Figs. 11 and 12 infer that the NN controller effectively regulates the output voltages Vo1 to Vo4 and the sinusoidal Iin, which is in phase with Vin claims unity PF.

Fig. 11
figure 11

Traces of output voltages, Vin, Iin, and harmonic spectrum of Iin of SEPIC converter-based MOSMPS with decreased supply voltage.

Full size image
Fig. 12
figure 12

Traces of output voltages, Vin and Iin of CSC converter-based MOSMPS with decreased supply voltage.

Full size image

Performance comparison of MOSMPS under varying load

The traces of four output voltages, mains voltage, and Iin at Vin = 220 V and variation in load at terminal Vo2, are illustrated in Fig. 13 for MOSMPS with SEPIC converter. In Fig. 14, the traces of four output voltages, mains voltage, and Iin at Vin = 220 V are represented for the MOSMPS with CSC converter. The NN controller efficiently regulates output voltages Vo1 to Vo4 even under a load change from half load to full load at 0.5 s at terminal 2. The traces of output current at 0.5 s illustrate the load change at terminal 2. The source voltage is in phase with the sinusoidal Iin drawn from the utility and the PF is maintained closer to unity even under load variation. The performance of the MOSMPS is superior with SEPIC converter when compared to CSC converter while analysing the PF and THD of Iin specified in Tables 4 and 5.

Fig. 13
figure 13

Traces of Output voltages, Supply voltage and currents and output currents of SEPIC converter-based MOSMPS with rated supply voltage and load variation at Vo2.

Full size image
Fig. 14
figure 14

Traces of output voltages, Vin and Iin of CSC converter-based MOSMPS with rated supply voltage and load variation at Vo2.

Full size image
Table 4 Parameter values of bridgeless converter configurations of MOSMPS at full load condition.
Full size table
Table 5 Parameter values of bridgeless converter configurations of MOSMPS at half load at V02.
Full size table
Table 6 Performance comparison of converter configurations of MOSMPS at full load.
Full size table

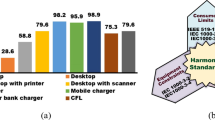
The performance of MOSMPS with bridgeless SEPIC and CSC converter configurations is analyzed under various source conditions. Tables 4 and 5 present the performance parameters of the MOSMPS. Based on the simulation results presented in Tables 4 and 5, it is evident that NN-based MOSMPS with the bridgeless SEPIC converter has a superior performance in terms of PQ indices such as % THD of Iin, DF, DPF and PF at the source side and output voltage ripple for all four terminals at full and half load conditions. Table 6 highlights the superior performance of SEPIC converter-based MOSMPS in terms of overshoot, settling time, and undershoot at full load conditions. Figure 15 illustrates the % THD and PF of Iin drawn by MOSMPS with the proposed and conventional controller. The % THD of Iin is lower in both converter topologies that employ the NN controller than in the conventional controller. Figure 16 compares the % overshoot, settling time, and % undershoot of Vo1. The performance of the NN-controlled bridgeless SEPIC converter-based MOSMPS is superior compared to the bridgeless CSC converter-based MOSMPS under varying conditions.

Fig. 15
figure 15

Comparison of %THD and PF of Iin at full load condition under varying supply voltage.

Full size image
Fig. 16
figure 16

Comparison of settling time, overshoot and undershoot at full load condition.

Full size image

Hardware implementation

Figure 17 depicts the experimental setup for the proposed SEPIC converter-based MOSMPS. The proposed NN-based control algorithm uses an Xilinx Spartan-6 XC6SLX25 FPGA in an FT256 package. The proposed NN can be implemented in hardware by incorporating every layer and all the network’s neurons. Let J1, J2 …. Jm represent the neuron numbers of the corresponding layer, and Jsum = J1 + J2 …. + Jm gives the sum of the neurons required for the proposed network. The resource requirement for implementing NN in FPGA is represented in slices. It can be calculated by Mtotal = M x Jsum where M represents the resource required to implement a neuron. Slice in the FPGA incorporates (i) two flip-flops, (ii) two look-up tables and (iii) related control logic, mux, and carry. The hardware’s implementation cost and resource requirement increase in line with the number of layers. The neurons in each layer and the NN layers of the network are processed in parallel and sequentially. The minimum hardware requirement can be realized in FPGA by sequentially processing layers in a multilayer network29. The NN layer multiplexing concept is preferred for the minimum hardware implementation, regardless of size.

Fig. 17
figure 17

Hardware setup of SEPIC PFC-based MOSMPS with ANN control.

Full size image

The layer multiplexing in NN architecture is depicted in Fig. 18. Each neuron in the most significant layer with the maximum number of inputs is considered for implementing layer multiplexing. The start signal in the control block initiates the network operation. The control block provides the biases, weights and perfect set of inputs for every neuron in the layer.

Fig. 18
figure 18

Schematic for hardware implementation of NN with layer multiplexing.

Full size image

The output of the neurons processed in parallel is fed as input to the next layer through the layer control block. Once the process is completed for the entire network, the end of the computation signal is passed to latch the output of NN. The Xilinx ISE tool is implemented to develop the VHDL program to control the MOSMPS. The code synthesization is carried out in the Xilinx ISE platform. The FPGA controller configures the program bit file in the hardware setup, and thus, the triggering pulse is generated for the MOSMPS. The switching frequency is 20 kHz to reduce the component size and have better control. IC TLP250 isolates the power and control circuit. The voltage at the output side is sensed using HCPL 7840. A Hysteresis controller is incorporated to generate firing pulses. The Digital signal oscilloscope & and Yokogawa WT 1800 power quality analyzer are connected to the hardware set up to record the test results. The simulation results of the two MOSMPS converters indicate that the bridgeless SEPIC converter’s performance is superior. Thus, hardware is fabricated for the ANN-controlled bridgeless SEPIC converter-based MOSMPS. The ANN-based proposed SEPIC configuration simulation results are validated through the fabricated hardware. The hardware and simulation results are compared and validated in terms of output voltage regulation and power quality.

Performance of ANN-Controlled SEPIC Configuration-Based MOSMPS

Performance under rated supply voltage condition with rated load

The effectiveness of NN-controlled MOSMPS with SEPIC configuration at full load condition with a supply voltage of Vin = 220 V is depicted in Figs. 19 and 20. The waveforms of source current and source voltage indicate that the AC primary current drawn by the proposed MOSMPS is pure sinusoidal for the rated load and input voltage of 220 V. The source voltage and current are in phase; thus, the PF of the input side is maintained nearly unity, i.e., 0.9998. The %THD of source current Iin is 2.818%, which complies with the limits of International PQ standards. Figure 20 exhibits the well-regulated output voltage waveforms at rated conditions.

Fig. 19
figure 19

Traces of Vin, Iin and harmonic spectrum of Iin of the SEPIC converter-based MOSMPS at full load.

Full size image
Fig. 20
figure 20

Traces of Vin and Iin and output voltages of the SEPIC converter-based MOSMPS at full load.

Full size image

Performance under supply voltage variation with rated load

When the proposed MOSMPS is fed from the utility mains, it performs efficiently even under supply voltage variations. The source voltage varies from 170 V to 250 V to test the performance of the MOSMPS under source variations. The PF and %THD of the Iin for the varying voltages of 250 V and 170 V are shown in Figs. 21 and 22. The THD of the source currents for 170 V is 2.522%, and for 250 V is 2.833%. It can be inferred from Figs. 21 and 22 that for both the increase and decrease of source voltages, the % THD of the Iin is within the limit suggested by International PQ standards. During over-voltage and under-voltage conditions of the supply, PF is maintained closer to unity. Figures 23 and 24 represent the regulated output voltages of the MOSMOS at Vin equal to 250 V and 170 V, respectively. Hence, the performance of the MOSMPS is appreciable under varying supply voltage conditions.

Fig. 21
figure 21

Traces of Vin, Iin and harmonic spectrum of Iin of the SEPIC converter-based MOSMPS at increased supply voltage.

Full size image
Fig. 22
figure 22

Traces of Vin, Iin and harmonic spectrum of Iin of the SEPIC converter-based MOSMPS at decreased supply voltage.

Full size image
Fig. 23
figure 23

Traces of Vin and Iin and output voltages of the SEPIC converter-based MOSMPS at increased supply voltage.

Full size image
Fig. 24
figure 24

Traces of Vin, Iin and output voltages of the SEPIC converter-based MOSMPS at decreased supply voltage.

Full size image

Performance with load variation and rated source voltage condition

To highlight the dynamic response of the SEPIC converter-based MOSMPS, the load at terminal Vo2 is varied. The change in load is inferred from Fig. 25, with the output current decreasing from 16 A to 8 A. This, in turn, causes a decrease in supply current as depicted in Fig. 25, and the supply current is sinusoidal even under load reduction. The PF and THD values under light load conditions are 0.99 and 2.834%, as mentioned in Fig. 26. Figure 27 shows the increase in load at terminal Vo2 with an increase in load current from 8 A to 16 A, and the supply current is sinusoidal even under load increment.

Fig. 25
figure 25

Waveforms of the SEPIC converter-based MOSMPS during load reduction - Vin & Iin, Output voltages and currents(V01, V02, I01, I02) with load reduction at + 5 V terminal.

Full size image
Fig. 26
figure 26

Details of input power, PF and % THD of Iin at half load of the proposed MOSMPS.

Full size image
Fig. 27
figure 27

Waveforms of the SEPIC converter-based MOSMPS during load increment at + 5 V terminal- Vin & Iin, Output voltages and currents(V01, V02, I01,I02).

Full size image

Performance of SEPIC configuration with conventional controller

Performance under rated supply voltage condition with rated load

The performance of the SEPIC converter-based MOSMPS with the conventional controller at full load condition with a supply voltage of Vin = 220 V is depicted in Fig. 28. It implies that the MOSMPS draws distorted current from the AC mains. The supply side PF is 0.8018. From the results, it is evident that the THD of the supply current Iin is 8.034%. The performance of the SEPIC converter-based MOSMPS with the NN controller is superior when compared to that with the conventional controller in terms of PF and THD of supply current. Figure 29 depicts the output waveforms of the MOSMPS with the conventional controller at rated load condition.

Fig. 28
figure 28

Traces of Vin, Iin and harmonic spectrum of Iin of the SEPIC converter-based MOSMPS with the conventional controller at full load.

Full size image
Fig. 29
figure 29

Traces of output voltages of the SEPIC converter-based MOSMPS with the conventional controller at full load.

Full size image

Performance under supply voltage variation with rated load

To demonstrate the performance of the MOSMPS with conventional controller under varying source voltage conditions, the supply voltage is varied from 170 V to 250 V. When the supply voltage is reduced to 170 V, the PF and THD of the supply current are shown in Fig. 30 and the THD of the supply current is 7.733%. When the supply voltage is increased to 250 V, the PF and THD of the supply current are represented in Fig. 31 and the THD is 7.222%. The performance of the SEPIC converter-based MOSMPS with the NN controller under varying supply voltage conditions is superior when compared to that with the conventional controller in terms of PF and THD of supply current.

Fig. 30
figure 30

Traces of Vin, Iin, and harmonic spectrum of Iin of the SEPIC converter-based MOSMPS with conventional controller at decreased supply voltage.

Full size image
Fig. 31
figure 31

Traces of Vin, Iin and harmonic spectrum of Iin of the SEPIC converter-based MOSMPS with the conventional controller at increased supply voltage.

Full size image

Performance with load variation and rated source voltage condition

To analyse the dynamic response of the MOSMPS with the conventional controller, the load at Vo2 is varied. The change in load causes a decrease in the output current from 16 A to 8 A. There is a corresponding reduction in the supply current, which is slightly distorted. The PF and THD are maintained at 0.8889 and 7.726%, as shown in Fig. 32 under light load conditions. Figures 33 and 34 depict the supply voltage and current waveforms at load increment and decrement, respectively. The supply current waveform is distorted in all cases. The performance of the SEPIC converter-based MOSMPS with the NN controller under varying load conditions is superior when compared to that with the conventional controller in terms of PF and THD of supply current.

Fig. 32
figure 32

Vin, Iin with input power, PF and % THD of Iin at light load condition.

Full size image
Fig. 33
figure 33

Traces of Input voltage and current of SEPIC converter based MOSMPS with conventional controller during load increment.

Full size image
Fig. 34
figure 34

Vin & Iin of SEPIC converter based MOSMPS with conventional controller during load decrement.

Full size image

Tables 7 and 8 compare the experimental and simulation outcomes of the proposed NN-based SEPIC converter MOSMPS. Figures 35 and 36 infer that the experimental results obtained with ANN and conventional controllers align with the simulation results. It is also evident from Figs. 35 and 36 that the performance of the MOSMPS is better with the ANN controller than the conventional one. The NN-controlled SEPIC converter-based MOSMPS performs better regarding input PF and % THD.

Fig. 35
figure 35

Comparison of input PF and %THD for hardware and simulation results.

Full size image
Fig. 36
figure 36

Comparison of PF and %THD of Iin under varying source conditions.

Full size image
Table 7 Comparison of simulation and hardware results of MOSMPS at rated supply voltage.
Full size table
Table 8 Comparison of simulation and hardware results.
Full size table

Conclusion

Using a bridgeless SEPIC PFC converter, an FFMNN-controlled MOSMPS is designed and simulated for computer power supply applications. To validate its performance, the MOSMPS is evaluated regarding input PQ and output voltage regulation under various source and load circumstances with ANN and conventional controllers. The PFC bridgeless converter configurations with NN control draw sinusoidal current from the supply, thereby improving the input PF. The %THD of the Iin is mitigated well below the limits suggested by PQ standards. The tightly regulated output voltages highlight the efficacy of the proposed ANN control for load and source variation. The performance of MOSMPS with bridgeless SEPIC PFC front-end converter is superior and employed for developing the prototype model. The NN control in the hardware is implemented through an FPGA processor. The prototype model’s performance measures align with the simulation’s outcomes, proving the ANN controller’s effectiveness. The proposed converter topology can be implemented for EV charging as future work.