Input driven optimization of echo state network parameters for prediction on chaotic time series

Abstract

Echo State Networks (ESNs) have emerged as powerful tools for time series prediction, yet their performance heavily depends on reservoir structure, which traditionally relies on random weights independent of input data characteristics. This paper presents a theoretical framework and optimization approach for ESN reservoir design, demonstrating that reservoir weights should be adapted based on input data properties, and that both topology and weights significantly influence prediction accuracy. Building on theoretical insights about input-dependent reservoir behavior, we propose two complementary methods: a supervised approach that directly optimizes reservoir weights through gradient descent, and a semi-supervised technique that combines small-world and scale-free network properties with hyperparameter optimization. Our extensive experiments across multiple datasets, including synthetic chaotic systems (Mackey-Glass and NARMA time series) and real-world climate data, demonstrate that the proposed methods consistently outperform traditional ESNs by achieving substantially lower prediction errors. Most notably, our analysis reveals that edge connectivity parameters play a crucial role, second only to reservoir size in determining network performance. These findings provide important practical guidelines for ESN design and open new directions for automated reservoir optimization based on input data characteristics.

Introduction

Time series prediction is a critical task in numerous fields, ranging from financial forecasting to climate modeling^1,2,3,4. The challenge becomes particularly pronounced when dealing with chaotic systems, where even minor variations in initial conditions can lead to vastly different outcomes⁵. Traditional statistical methods often fall short in handling such complex, nonlinear dynamics, necessitating the development of more advanced techniques. Consider climate prediction where accurate forecasting is essential for agriculture and disaster management. While LSTM networks require extensive computational resources, standard Echo State Networks suffer from inconsistent performance due to random initialization.

Recent advances in attention-based mechanisms have shown promising results for complex time series prediction tasks. A self-attention mechanism with correlation for long-term water quality forecasting has been developed⁶, demonstrating that attention mechanisms can effectively capture long-term periodic patterns even in datasets with missing values. Similarly, hierarchical approaches have emerged as powerful alternatives for handling multidimensional chaotic data. A hierarchical evolving fuzzy system that excavates latent evolutionary patterns through layer-by-layer processing of multidimensional information has been proposed⁷. Additionally, optimization-driven learning systems have gained attention for their self-adaptive capabilities in chaotic environments.

Our approach addresses this by optimizing reservoir structure based on climate data characteristics, achieving substantially improved accuracy for real-world temperature predictions. Neural networks have emerged as powerful tools for time series prediction, excelling in capturing nonlinear patterns and long-term dependencies. Among these, Recurrent Neural Networks (RNNs) have shown significant promise due to their ability to process sequential data and retain temporal information⁸.

Echo State Networks (ESNs), a specialized type of RNN, offer a particularly elegant solution for time series prediction. Their unique architecture features a large reservoir of interconnected neurons, where only the output weights are adjusted during training, while the input, reservoir, and feedback weights remain random and fixed. This design allows ESNs to effectively model the temporal dynamics of chaotic systems while maintaining computational efficiency. However, the random initialization of reservoir weights, though beneficial for stability, often leads to suboptimal performance, as it may not fully exploit the network’s potential for capturing complex patterns⁸.

Unlike attention-based approaches that require substantial computational resources for processing long sequences⁶, ESNs offer a more computationally efficient alternative while maintaining the ability to capture complex temporal dependencies. This efficiency advantage becomes particularly important when dealing with real-time applications or resource-constrained environments where traditional deep learning approaches may be impractical.

A key challenge in ESNs lies in the reservoir’s structure. The reservoir, which serves as the core component of the network, relies on randomly initialized weights that remain fixed during training. While this randomness simplifies the training process, it often results in inefficiencies, as the reservoir may not achieve the optimal configuration required for accurate predictions. This limitation highlights the need for improved methods to optimize the reservoir’s topology and weight distribution.

In this work, we provide theoretical evidence demonstrating that the topology and weights of the reservoir significantly influence the network’s prediction error. Unlike previous studies that relied on empirical observations⁷, we provide analytical evidence to explain how these structural properties affect the performance of ESNs. Specifically, we show that the optimal reservoir’s connectivity patterns and weight distribution depend on distribution of input data and play a crucial role in shaping the network’s ability to process information and generate accurate predictions. Building on these insights, we propose some optimization techniques to fine-tune the reservoir weights, ensuring a more efficient network. Our approach not only enhances predictive accuracy but also provides a deeper understanding of the relationship between reservoir design and network performance.

The contributions of our paper are as follows:

• Providing an analytical insight into the effect of reservoir norm on the error bound of test data.

• Proposing a supervised approach to optimize the reservoir based on input data.

• Introducing two semi-supervised methods for input-driven optimization of the reservoir.

• Conducting extensive experiments and providing a critical discussion of the results.

The remainder of this paper is organized as follows: In “Related work”, we review the most related works. In “Preliminaries”, we review the necessary preliminaries. “Methods” presents the proposed methods, while “Experimental result” details the experimental results. “Discussion” provides a comprehensive discussion of the methods and results. Finally, the study is concluded in “Conclusion and future work”.

Related work

Echo State Networks (ESNs), introduced by Jaeger and Haas in 2004, marked a significant advancement in modeling nonlinear dynamical systems. ESNs utilize large, randomly connected recurrent neural networks (RNNs) with fixed internal weights, where only the output weights are trained using linear regression. This design makes ESNs computationally efficient and effective, particularly in predicting chaotic time series, where they demonstrated a 2400-fold improvement in accuracy over traditional methods. However, the random connectivity of the reservoir in standard ESNs has inherent limitations, which has led researchers to explore more structured and optimized architectures to enhance performance⁸.

Recent research has explored alternative paradigms for chaotic time series prediction beyond traditional ESN approaches. Attention-based mechanisms have emerged as a powerful tool for capturing long-term dependencies in complex time series. A transformer-based model that integrates self-attention with correlation coefficients for long-term water quality prediction has been proposed⁶. This approach addresses limitations of existing methods in capturing long-term periodic patterns and sensitivity to missing data by employing date-driven positional embedding and correlation self-attention mechanisms. This work demonstrates the potential of attention-based approaches for handling complex temporal patterns, though at the cost of increased computational complexity compared to ESN architectures.

Hierarchical and evolutionary approaches have also gained significant attention for multidimensional chaotic time series prediction. The hierarchical evolving fuzzy system (HEFS-KCG)⁷ represents a notable advancement in this direction, offering a novel approach to online prediction of multidimensional chaotic time series. Unlike single-layer evolving fuzzy systems, HEFS-KCG excavates latent evolutionary patterns through layer-by-layer processing of multidimensional information, combining structural evolution based on data distribution with sparse learning strategies and kernel conjugate gradient for parameter updates. This approach demonstrates how hierarchical architectures can capture hidden information that traditional single-layer models might miss.

Optimization-driven learning systems have also shown promise for chaotic time series prediction with self-adaptive parameter tuning capabilities. Recent work has explored improved particle swarm optimization algorithms combined with long short-term memory networks, incorporating temporal pattern attention mechanisms to extract weights and key information from input features⁹. These approaches address issues such as gradient explosion and computational efficiency while maintaining temporal characteristics of chaotic historical data.

While these alternative approaches demonstrate strong performance in chaotic time series prediction, they often require substantial computational resources and complex parameter tuning procedures. For instance, attention-based models like transformers necessitate extensive memory usage and quadratic computational complexity with respect to sequence length, making them challenging to deploy in resource-constrained environments. Similarly, hierarchical evolving fuzzy systems, despite their effectiveness in capturing multidimensional patterns, involve intricate rule evolution mechanisms and multiple optimization stages that increase both computational overhead and implementation complexity. In contrast, Echo State Networks offer several distinct advantages that make them particularly attractive for practical applications: first, they employ simpler training procedures where only the output weights require optimization through linear regression, significantly reducing computational burden; second, they maintain lower computational costs during both training and inference phases compared to deep learning alternatives; and third, they possess inherent stability through the echo state property, which ensures reliable convergence without the gradient-related issues common in traditional RNNs. However, the random initialization of ESN reservoirs remains a fundamental limitation that can lead to suboptimal performance and inconsistent results across different initializations, which our work addresses through principled optimization approaches that maintain the computational advantages while improving predictive accuracy.

Building on this foundation, recent studies have focused on optimizing key parameters of ESNs to improve their predictive capabilities¹⁰. For instance, one study targeted the input weight matrix as a primary area for improvement. The authors employed the Selective Opposition Grey Wolf Optimizer (SOGWO) to optimize critical parameters such as reservoir size, spectral radius, and weight matrix density. Similarly, another study systematically optimized hyperparameters including reservoir size, reservoir density, spectral radius, leakage rate, regularization coefficient, initialization length, and training length¹¹. Through extensive experimentation on chaotic time series datasets, they identified optimal values for these parameters, leading to significant improvements in prediction accuracy and reduced variability across random initializations. These efforts highlight the importance of fine-tuning ESN parameters to achieve superior performance¹⁰.

In parallel, researchers have explored novel reservoir architectures to address the limitations of random connectivity in traditional ESNs. One such innovation is the Scale-free Highly-clustered Echo State Network (SHESN), which replaces the random reservoir connections with a structured design incorporating small-world properties and scale-free characteristics¹². This approach aims to enhance the network’s ability to model complex dynamical systems. Another study introduced three distinct architectures SCESN, SPESN, and SWESN where reservoir neurons are clustered using classic algorithms such as K-Means, PAM, and Ward. In these architectures, mean neurons in each cluster serve as backbone units, and connections are designed to ensure both small-world characteristics and power-law distribution. These modifications resulted in improved performance over standard ESNs, with enhanced echo state properties and a broader range of viable spectral radius values¹³.

Further advancing this line of research, another study proposed the High Clustered Echo State Network (HCESN), which employs evolutionary optimization algorithms like Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and Differential Evolution (DE) to cluster reservoir neurons. In this architecture, neurons are organized into clusters, each containing a backbone neuron and several local neurons. This structured approach not only improves the network’s predictive accuracy but also enhances its ability to model complex time series data¹⁴.

Collectively, these studies demonstrate a concerted effort to refine and optimize ESN architectures, focusing on both parameter tuning and structural innovations. By addressing the limitations of random reservoir connectivity and exploring new clustering and optimization techniques, researchers have significantly advanced the capabilities of ESNs in modeling nonlinear dynamical systems¹⁴.

Our proposed approach builds upon these foundations while offering several key distinctions: (1) Theoretical grounding: Unlike previous empirical studies, we provide analytical evidence demonstrating how reservoir topology and weights influence prediction error bounds. (2) Input-driven optimization: Rather than generic parameter optimization, our methods adapt reservoir structure based on specific characteristics of input data. (3) Computational efficiency: Our approach maintains the computational advantages of ESNs while achieving performance improvements comparable to more complex attention-based or hierarchical methods. (4) Practical applicability: The proposed methods are designed for real-world deployment scenarios where computational resources may be limited, distinguishing them from resource-intensive alternatives like transformer-based models.

Table 1 provides a comprehensive summary of recent studies in echo state networks, presenting various architectural innovations and optimization approaches across different datasets.

Table 1 Summary of previous studies and methods explained in sect. 2, alongside the dataset used and approach explanation.

In our work, we propose a data-driven optimization approach, where the reservoir design is tailored to the specific properties of the dataset. Unlike previous methods that focus on unsupervised model identification, we introduce some models that leverage the inherent structure of the data to optimize the reservoir.

Preliminaries

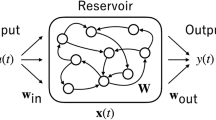
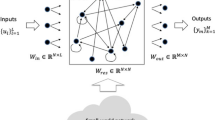
Echo State Networks (ESNs) represent a distinctive class of recurrent neural networks that revolutionize the traditional approach to temporal data processing. At their core, ESNs consist of three fundamental components that work in concert to process and analyze sequential data: an input layer, a dynamically rich reservoir, and an output layer. Figure 1 illustrates a schematic diagram of the Echo State Network architecture.

Fig. 1

showing the basic ESN architecture with input layer, reservoir (with recurrent connections), and output layer, along with $\:Win$,$\:\:Wres$, $\:Wback$, and Wout connections.

The defining characteristic of ESNs lies in their unique training methodology. Unlike conventional neural networks, ESNs maintain fixed random weights for both input connections ($\:{W}^{in}$) and reservoir connections ($\:{W}^{res}$), while only training the output connections ($\:{W}^{out}$). This architectural decision significantly simplifies the training process while preserving the network’s computational capabilities. The reservoir, which serves as the network’s dynamic memory, creates complex transformations of the input signal through its recurrent connections.

The mathematical foundation of ESNs is captured in two key equations. The reservoir state $\:x\left(n\right)$ evolves according to:

$$\:x(n + 1)\: = F^{{res}} (W^{{in}} \cdot u(n)\: + \:W^{{res}} \cdot x(n)\: + \:W^{{back}} \cdot y(n))$$

(1)

where F represents a nonlinear activation function (typically tanh), $\:u\left(n\right)$ denotes the input at time n, and $\:y\left(n\right)$ indicates the previous output. The output is generated through:

$$\:y(n+1)\:={F}^{out}\left(\:{W}^{out}\right(u\left(n\right),X\left(n+1\right),y\left(n\right))$$

(2)

The effectiveness of ESNs is rooted in their distinctive echo state property. This fundamental characteristic ensures that for every input signal and initial state, the influence of the initial state gradually fades away, while the network’s current state becomes increasingly determined by the history of the input signal. The reservoir acts as a dynamic memory system, processing and transforming input sequences into high-dimensional state representations. Through its recurrent connections and nonlinear activation functions, the reservoir creates a rich feature space that enables the network to effectively model and capture complex temporal dependencies in the input data. although it is not well understood what the relationship between the input and the reservoir structure is to achieve the best accuracy, in the next section, we study this relationship and propose two approaches to optimize the reservoir.

Methods

Our “data-driven optimization” refers to adapting reservoir design based on input data characteristics, rather than using fixed random architectures employed in traditional ESNs. This is implemented through two approaches: supervised optimization that directly adjusts reservoir weights using input data gradients, and semi-supervised optimization that tunes hyperparameters based on data-specific performance feedback.

Theoretical base of the methodology

The theoretical foundation of our methodology is built upon analysis of Echo State Network (ESN) reservoirs and their error prediction boundaries. To establish a comprehensive framework for estimating prediction error and understanding the ESN mechanism, we present two theorems that form the core of our approach.

In the rest of this subsection, we denote the norm of a matrix or vector $\:A$ by $\:\left|\left|A\right|\right|$. The Lipschitz condition¹⁹ states that for a function $\:f\mathbb{\:}:\mathbb{R}\stackrel{n}{\to\:}{\mathbb{R}}^{m}$,there exists a constant $\:L>0$, known as the Lipschitz constant, such that for any two points $\:x$ and $\:y$ in the domain of $\:f$, the following inequality holds:

$$\:\left||f\left(x\right)-f(y\left)\right|\right|\le\:L\left||x-y|\right|$$

(3)

This condition implies that the function $\:f$ does not change too rapidly; the difference in the function’s values at any two points is bounded by a linear function of the distance between those points²⁰. The Lipschitz condition is crucial in various fields, including optimization²¹, control theory²², and machine learning²³, as it helps ensure stability, convergence, and robustness of algorithms and systems²⁴.

Theorem 1

If $\:{S}_{1}\:=\:<\left(u\right(k+1),y(k+1\left)\right),...,\left(u\right(k+t),y(k+t\left)\right)>$ and $\:{S}_{2}\:=\:<\left(u\right(l+1),y(l+1\left)\right),...,\left(u\right(l+t),y(l+t\left)\right)>$ are two input/output of a time series $\:\:\left(\right|{S}_{1}|\:=\:|{S}_{2}|\:=\:t)$ and $\:{f}^{res}$ (activation function of reservoir layer) satisfies Lipschitz condition (e.g., tanh and identity functions with constant L) and $\:X\left(k\right)\stackrel{{S}_{1}}{\to\:}\:X(K+t)$ and $\:X\left(l\right)\stackrel{{S}_{2}}{\to\:}\:X(l+t)$, then:

$$\begin{array}{ccccc}& \left\| {X\left( {k + t} \right) - \:X\left( {l + t} \right)} \right\| \le \:{L^t}\:{\left| {\left| {{W^{res}}} \right|} \right|^t}\left\| {X\left( k \right) - \:X\left( l \right)} \right\|\\& \quad + \sum\nolimits_{m = 0}^{t - 1} {{L^m}{{\left| {\left| {{W^{res}}} \right|} \right|}^m}\left| {\left| {{W^{in}}} \right|} \right|} \left\| {u\left( {k + t - m} \right) - \:u\left( {l + t - m} \right)} \right\|\\& \quad + \sum\nolimits_{m = 0}^{t - 1} {{L^m}} {\left| {\left| {{W^{res}}} \right|} \right|^m}\left| {\left| {{W^{back}}} \right|} \right|\left\| {y(k + t - m - 1)\: - \:y(l + t - m - 1)} \right\|\end{array}$$

Proof

The considered update equation is

$$\:\:X\left(n\right)\:=\:{f}^{res}\left({W}^{res}X\right(n-1)\:+\:{W}^{in}u(n)\:+\:{W}^{back}y(n-1\left)\right)\:$$

.

which is the most general case in terms of connections. So, we have:

$$\begin{array}{l}\left\| {X\left( {k + t} \right) - \:X\left( {l + t} \right)} \right\|\: = \left\| {fres({W^{res}}X(k + t - 1)\: + \:{W^{in}}u(k + t)} \right.\\\left. { + \:{W^{back}}y(k + t - 1))\: - \:{f^{res}}({W^{res}}X(l + t - 1)\: + \:{W^{in}}u(l + t)\: + \:{W^{back}}y(l + t - 1))} \right\|\end{array}$$

$$\:{W}^{back}y(k+t-1))\:-\:{f}^{res}({W}^{res}X(l+t-1)\:+\:{W}^{in}u(l+t)\:+\:{W}^{back}y(l+t-1)\left)\right||$$

By Lipschitz Condition:

$$\begin{array}{l}\left| {\left| {X\left( {k + t} \right) - \:X\left( {l + t} \right)} \right|} \right| \le \:\:L\left\| {{W^{res}}(X(k + t - 1)\: - \:X(l + t - 1))} \right.\\\left. { + \:{W^{in}}\left( {u\left( {k + t} \right) - \:u\left( {l + t} \right)} \right) + \:{W^{back}}(y(k + t - 1)\: - \:y(k + t - 1))} \right\|\end{array}$$

$$\begin{array}{l}= \left\| {{W^{res}}\left( {{f^{res}}\left( {{W^{res}}X\left( {k + t - 2} \right) + \:{W^{in}}u\left( {k + t - 1} \right) + {W^{back}}y\left( {k + t - 2} \right)} \right)} \right.} \right.\\\left. { - \:{f^{res}}\left( {{W^{res}}X\left( {l + t - 2} \right) + \:{W^{in}}u\left( {l + t - 1} \right) + \:{W^{back}}y\left( {l + t - 2} \right)} \right)} \right)\\\left. { + \:{W^{in}}\left( {u\left( {k + t} \right) - \:u\left( {l + t} \right)} \right) + \:{W^{back}}\left( {y\left( {k + t - 1} \right) - \:y\left( {k + t - 1} \right)} \right)} \right\|\end{array}$$

$$\begin{array}{l}\: \le \:L\:\left| {|\left| {{W^{res}}} \right|} \right|\:\left\| {{W^{res}}\left( {X\left( {k + t - 2} \right) - \:X\left( {l + t - 2} \right)} \right)} \right.\\\left. { + \:{W^{in}}\left( {u\left( {k + t - 1} \right) - \:u\left( {l + t - 1} \right)} \right) + \:{W^{back}}\left( {y\left( {k + t - 2} \right) - \:y\left( {k + t - 2} \right)} \right)} \right\|\\\left. { + \:{W^{in}}(u(k + t)\: - \:u(l + t))\: + \:{W^{back}}(y(k + t - 1)\: - \:y(k + t - 1))} \right\|\end{array}$$

$$\begin{array}{l}\: \le \:\:{L^2}\left| {|{W^{res}}} \right|{|^2}\left| {X\left( {k + t - 2} \right) - \:X\left( {l + t - 2} \right)} \right|\left| {\: + \:\left| {|{W^{res}}} \right|} \right|\\\:\left| {\left| {{W^{in}}} \right|} \right|\left| {\left| {u\left( {k + t - 1} \right) - \:u\left( {l + t - 1} \right)} \right|} \right|\: + \:\left| {\left| {{W^{res}}} \right|} \right|\left| {\left| {{W^{back}}} \right|} \right|\left| {\left| {y\left( {k + t - 2} \right) - \:y\left( {k + t - 2} \right)} \right|} \right|\:\\+ \left| {\left| {{W^{in}}} \right|} \right|\left| {} \right|u\left( {k + t} \right) - \:u\left( {l + t} \right)\left| {} \right|\: + \left| {\left| {{W^{back}}} \right|} \right|\left| {\left| {y\left( {k + t - 1} \right) - \:y\left( {k + t - 1} \right)} \right|} \right|\end{array}$$

$$\begin{array}{l}\le {L^i}{\left\| {{W^{res}}} \right\|^i}\left\| {X\left( {k + t - i} \right) - \:X\left( {l + t - i} \right)} \right\|\\+ \sum {_{m = 0}^{i - 1}} |{\left| {{W^{res}}|} \right|^m}\left| {\left| {{W^{in}}} \right|} \right|\left\| {u\left( {k + t - m} \right) - \:u\left( {l + t - m} \right)} \right\|\\+ \sum {_{m = 0}^{t - 1}} {\left\| {{W^{res}}} \right\|^m}\left\| {{W^{back}}} \right\|\left\| {y\left( {k + t - m - 1} \right) - \:y\left( {l + t - m - 1} \right)} \right\|\end{array}$$

$$\:When\:i\:=\:t:$$

$$\begin{array}{l}\left| {X\left( {k + t} \right) - \:X\left( {l + t} \right)|} \right| \le \:\:{L^t}|{\left| {{W^{res}}|} \right|^t}|\left| {X\left( {k + t - t} \right) - \:X\left( {l + t - t} \right)|} \right|\\+ \sum {_{m = 0}^{t - 1}} {L^m}|{\left| {{W^{res}}|} \right|^m}\left| {\left| {{W^{in}}} \right|} \right|\left| {\left| {u\left( {k + t - m} \right) - \:u\left( {l + t - m} \right)} \right|} \right|\\+ \sum {_{m = 0}^{t - 1}} \:{L^m}\:\left| {{{\left| {{W^{res}}|} \right|}^m}\left| {|{W^{back}}} \right|} \right||\left| {y\left( {k + t - m - 1} \right) - \:y\left( {l + t - m - 1} \right)|} \right|\end{array}$$

(4)

Theorem 2

Under condition of theorem 1and with assumption that $\:{f}^{out}$(activation function of output layer) is a function with Lipschitz property (with constant L) and with output computing:

$$\:y\left(n\right)=\:{f}^{out}\left({W}^{out}\left(X\left(n\right);u\left(n\right);y\left(n-1\right)\right)\right),\:\:{W}^{out}=\:[{W}^{res-\:out},{W}^{in-out},{W}^{loop}]\:$$

we have:

$$\:\left|\right|y\left(k+t\right)-\:y\left(l+t\right)\left|\right|\:\le\:\:L\left(\:\left|\left|{W}^{res-out}\right|\right|\right||X\left(k+t\right)-\:X\left(l+t\right)||\:+$$

$$\:\left|{|W}^{in-out}\right|\left|\:\left|\left|u\left(k+t\right)-\:u\left(l+t\right)\right|\right|+\:{\left|\right|W}^{loop}\right|\left|\:\right||y\left(k+t-1\right)-\:y\left(l+t-1\right)||)$$

Proof

$$\:\left|\right|y\left(k+t\right)-\:y\left(l+t\right)\left|\right|=\:\left|\right|{f}^{out}\left({W}^{out}\left(X\left(k+t\right);u\left(k+t\right);y\left(k+t-1\right)\right)\right)-$$

$$\:-\:\:{f}^{out}\left({W}^{out}\right(X(l+t);u(l+t);y(l+t-1)\left)\right)\left|\right|\:$$

$$\:\le\:L\left(\:\right|{|W}^{out}\left(X\left(k+t\right);u\left(k+t\right);y\left(k+t-1\right)\right)-\:{W}^{out}\left(X\left(l+t\right);u\left(l+t\right);y\left(l+t-1\right)\right)\left|\right|$$

$$\begin{array}{l}\: = \:\left\| {{W^{res - out}}X\left( {k + t} \right) + {W^{in - out}}u\left( {k + t} \right) + \:{W^{loop}}y\left( {k + t - 1} \right)} \right.\\\left. { - \:\left( {{W^{res - out}}X\left( {l + t} \right) + \:{W^{in - out}}u\left( {l + t} \right) + \:{W^{loop}}y\left( {l + t - 1} \right)} \right)} \right\|\end{array}$$

$$\begin{array}{l}\left\| {{W^{res - out}}\left( {X\left( {k + t} \right) - \:X\left( {l + t} \right)} \right) + \:{W^{in - out}}\left( {u\left( {k + t} \right) - \:u\left( {l + t} \right)} \right)} \right.\\\left. { + \:{W^{loop}}\left( {y\left( {k + t - 1} \right) - \:y\left( {l + t - 1} \right)} \right)} \right\|\end{array}$$

Therefore:

$$\begin{array}{l}\:\left| {|y\left( {k + t} \right) - \:y\left( {l + t} \right)|} \right| \le \:\:L(\left| {|{W^{res - out}}} \right||\:|\left| {X\left( {k + t} \right) - \:X\left( {l + t} \right)|} \right|\\+ \:\left| {|{W^{in - out}}} \right|\left| {\:\left| {\left| {u\left( {k + t} \right) - \:u\left( {l + t} \right)|} \right|\: + \:\left| {|{W^{loop}}} \right|} \right|\:} \right|\left| {y\left( {k + t - 1} \right) - \:y\left( {l + t - 1} \right)|} \right|)\end{array}$$

(5)

Theorems 1 and 2 give some insights on behavior of ESN discussed in the rest of this subsection. Assume the input sequence $\:{S}_{1}$ is a part of training sequence, after stabilization of the reservoir, $\:so\:\left(X\right(l),u(l),y(l-1\left)\right)$ and $\:\left(X\right(l+t),u(l+t),y(l+t-1\left)\right)$ are in state collection matrix M.

If $\:{S}_{2}$ is in test sequence (unseen data) and $\:y\left(n\right)$ is scalar, we have the following:

For repeated patterns with length t (e.g., $\:{S}_{1}\:=\:{S}_{2}$), the maximum deviation between training and test states is bounded by $\:{L}^{t}{\left|{W}^{res}\right|}^{t}\left|X\right(k)\:-\:X(l\left)\right|$ and if $\:\left|\right|{W}^{res}\left|\right|$is less than one and t is big enough, the deviation converges to zero.

An important point is that the best case of $\:{W}^{res}$depends on length of the patterns and all the patterns do not have the same length. If norm of $\:{W}^{res}\:\left(\right|\left|{W}^{res}\right|\left|\right)$is very small, we have immature convergence and only a small segment of the pattern puts the reservoir on a local optimum.

In other words, the input sequence (both training and test) are divided into many very small patterns each of which has a small error that leads to significant error over the whole input.

On the other side, large values of $\:{\left|\right|W}^{res}\left|\right|$ cause distinct concatenated patterns to be considered as one pattern. This means that for example $\:{S}_{1}{S}_{2}$ and $\:{S}_{1}^{{\prime\:}}{S}_{2}^{{\prime\:}}$ as two patterns with the same length and if $\:{S}_{1}=\:{S}_{1}^{{\prime\:}}$ and $\:{S}_{2}\:!=\:{S}_{2}^{{\prime\:}}$, then some errors are introduced in the result.

Theorems 1 and 2 show that both weights and topology of reservoir affect prediction accuracy and dependent to input, so generating $\:{W}^{res}$randomly and independent of input distribution as done in ESN may not be optimal.

Theorems 1 and 2 show that the optimal weights and topology of the reservoir depend on the input. Therefore, an input-dependent design of the reservoir may not always be optimal, and different reservoir designs reported in previous work may not be generalizable to all input time series. Hence, we should think beyond a fixed reservoir topology in Echo State Networks.

We should pay some computational cost to build an input-driven reservoir, but when prediction accuracy is critical, this trade-off is necessary.

In the next subsection, we propose two methods for building input-driven reservoirs.

Proposed methods

In this section, we aim to find optimal reservoir matrices (topology and weights) through different optimization methods.

We present a supervised and two semi-supervised methods. The supervised model focuses on the reservoir matrix optimization through an iterative process, utilizing an optimization loop to enhance the reservoir weights based on loss function.

In the semi-supervised method, we introduce a novel structural matrix design that depends on several hyperparameters. These hyperparameters play a crucial role in generating the reservoir matrices and need to be carefully tuned. We define a comprehensive optimization framework to find the optimal values of these hyperparameters. Unlike the supervised method, where we directly optimize the reservoir weights, here we focus on optimizing the hyperparameters that control the structure and characteristics of the reservoir matrices.

The supervised method

In this section, we introduce a novel method to optimize the reservoir matrix of an Echo State Network (ESN) for time series prediction. The process begins with initializing the matrix with random values. This matrix, along with the time series data and ESN parameters, is then passed to a loss calculation block that computes the loss through multiple steps.

The loss calculation block operates as follows: First, a simple ESN network is created using the current matrix, ESN parameters, and the input time series data. This ESN generates a predicted time series, which is then compared with the target using the loss. The resulting error value is used in the backpropagation process to update the matrix.

This optimization process continues iteratively until the specified number of epochs is completed. In each iteration, the matrix is updated based on the backpropagated error gradients. At the conclusion of all epochs, we obtain the final optimized matrix that yields the best performance.

In this method, both topology and weights evolve during the optimization process. Through backpropagation, weights are continuously modified. Topology changes occur when a zero weight becomes non-zero during this process, representing the addition of new edges to the reservoir topology. Conversely, when non-zero weights are reduced to zero, it signifies the removal of existing edges. Algorithm 1 and Fig. 2 illustrates the complete optimization process of the reservoir matrix.

Algorithm 1. Supervised method.

Fig. 2

Flowchart of the reservoir matrix (W) optimization process. The process starts with matrix initialization and enters an iterative loop where a calculation block (shown in blue) processes the W matrix, time series data, and ESN parameters to compute NRMSE.

As mentioned earlier, connection weights can either increase or decrease during the training process, and we have provided an example to demonstrate this behavior. Figure 3 presents two reservoir matrices showing both Initial Matrix (left) and Final Matrix (right) states of the reservoir. In this example, two edges (from node 4 to node 0 and from node 3 to node 0) were eliminated when their weights reached zero during the training process, shown as red dotted lines in the Final Matrix. While no new edges emerged during this optimization, we observe significant changes in existing edge weights, such as the self-loop weights at nodes 1, 0, 3, and 4, which demonstrate how the optimization process adjusts the network’s connectivity strengths to improve performance. For clarity and better visualization purposes, this example uses a simplified reservoir with a small number of nodes, though real-world implementations typically involve larger networks with more complex connectivity patterns.

Fig. 3

Comparison of Initial and Final reservoir matrices during the optimization process. The red dotted lines in the Final Matrix (right) indicate the edges that were eliminated when their weights reached zero during training.

The semi-supervised methods

Our proposed semi-supervised method leverages fully connected neural networks to optimize Echo State Network (ESN) parameters through a two-phase process: data generation and parameter prediction. As demonstrated, both the topology and weights of the network play crucial roles in determining its output. Therefore, we investigated natural growth rules that encompass small-world and scale-free characteristics, which are known to influence network performance¹².

Building upon previous research¹², which demonstrated that small-world and scale-free properties significantly impact the accuracy of ESN models, we construct our initial reservoir using two graph generation models: the Watts-Strogatz model²⁵(exhibiting small-world properties) and the Barabási-Albert model²⁶(exhibiting scale-free properties). These graphs are then multiplied by a random matrix with values within a specific range to create weighted graphs. The final reservoir matrix is constructed through a weighted combination of these two graphs.

The Watts-Strogatz graph is generated based on parameters n (number of nodes), k (number of edges connected to each node), and p (probability of rewiring edges to random nodes), as described by Eq. (5):

$$\:{M}_{sw}=\:{F}_{1}\left(n,k,p\right)$$

(6)

The Barabási-Albert graph is constructed using parameters n (number of nodes) and m (number of edges for each new node added to the network), as described by Eq. (6):

$$\:{M}_{sf}=\:{F}_{2}\left(n,m\right)$$

(7)

The random matrix used for weighting the graphs is generated according to the $\:{weight}_{scale}$​ parameter, as described by Eqs. (7) and (8). The final reservoir structure also depends on the $\:alpha\:$coefficient, which determines the weighted combination of the reservoir components, as described by Eq. (9).

After generating the initial binary matrices (containing only 0 s and 1 s), we transform them using random weight scaling. This involves multiplying each matrix by a random matrix with values adjusted by the $\:{weight}_{scale}$​ parameters. The random matrices $\:{R}_{1}$​ and $\:{R}_{2}$​ used in this transformation contain values uniformly distributed between 0 and 1. Separate $\:{weight}_{scale}$​ parameters ($\:{weight}_{scale1\:}$and $\:{weight}_{scale2}$ ​) are used for each network type. The transformed matrices are calculated as follows:

$$\:{X}_{1}=\:{M}_{sw}\times\:\:\left({R}_{1}-\:{weight}_{scale1}\right)$$

(8)

$$\:{X}_{2}=\:{M}_{sf}\times\:\:\left({R}_{2}-\:{weight}_{scale2}\right)$$

(9)

The final reservoir matrix is then created through a weighted combination of these transformed matrices using a mixing parameter α:

$$M\_hybrid = \alpha \times {X_1} + (1 - \alpha ) \times {X_2}$$

(10)

The objective of this method is to find the optimal values for the hyperparameters n (number of nodes), k (number of edges connected to each node), p (probability of rewiring edges to random nodes), m (number of edges for each new node added to the network), $\:{weight}_{scale1}$​ (for the Watts–Strogatz graph), $\:{weight}_{scale1}$​ (for the Barabási–Albert graph), and $\:alpha\:$(mixing parameter) in a way that minimizes the model’s loss function.

To achieve this, we systematically sample the system by generating matrices with different combinations of these parameters and evaluate their performance using a loss function. This process generates a comprehensive dataset that maps network parameters to performance metrics, establishing the foundation for our semi-supervised learning method. We then explore two different neural network architectures using this generated dataset to predict optimal ESN parameters. Algorithm 2 and Fig. 4 illustrates the complete process of generating hybrid matrices and collecting the sampling data for our semi-supervised learning method.

Algorithm 2. Semi-supervised model-sampling.

Fig. 4

Flowchart of the hybrid matrix generation and sampling process. Network parameters (k, M, P, α, $\:{weight}_{scale1}$​, $\:{weight}_{scale2}$​ ) are used to generate and combine two different network structures. The Watts–Strogatz model generates a small-world network (F1) while the Barabási–Albert model creates a scale-free network (F2). These networks are transformed using random matrices adjusted by scale weights and combined using α to create the hybrid matrix. This matrix is then evaluated using a simple ESN to calculate loss, and both parameters and performance metrics are stored in a sampling table.

In the parameter prediction phase, we employed two different models, which are described as follows:

Direct parameter prediction approach (DPP)

In the first approach, we develop a neural network model that maps a single loss value to seven ESN parameters. The network’s architecture progressively transforms the data dimensions through several stages. Starting with a single input neuron for loss value, the first block expands the dimension to 256 features (1 $\:->$ 256). The second block further expands to 512 features (256 -> 512), while the third block contracts back to 256 features (512 $\:->$ 256). Finally, a linear layer reduces the dimension to seven outputs (256 $\:->$ 7), corresponding to the ESN parameters (n, k, p, m, α, $\:{weight}_{scale1},{weight}_{scale2})$. Each processing block, except the final layer, combines a linear transformation with layer normalization, ReLU activation, and dropout for regularization.

After training the model, we evaluate its effectiveness by using it to predict the optimal parameters that would theoretically achieve a loss of 0. This means we input a target loss of 0 into the trained network and obtain the corresponding set of seven parameters that the model predicts would achieve this perfect performance. This method significantly reduces the computational burden of manual parameter tuning while maintaining high performance standards, offering a practical tool for reservoir computing systems. Algorithm 3 and Fig. 5 illustrates the complete architecture and workflow of our parameter prediction network.

Algorithm 3. Semi-supervised model-inverse parameter prediction.

Fig. 5

: The network architecture consists of training and inference phases. The training phase shows the dimensional transformation of data through the network, where each block’s notation (e.g., 1 -> 256) indicates its input and output dimensions. The inference phase demonstrates how the trained model generates optimized parameters when given a target loss of zero.

Inverse parameter prediction approach (IPP)

In the second approach, we implement an inverse optimization strategy by first developing a neural network with seven inputs and one output, designed to map ESN parameters to loss values. The network’s architecture progressively transforms the data through several stages: the input layer accepts seven parameters, followed by three processing blocks. The first block expands the dimension to 256 features (7 $\:->$ 256), the second block further expands to 512 features (256$\:\:->$ 512), while the third block contracts back to 256 features (512 $\:->$ 256). Finally, a linear layer reduces the dimension to a single output (256 $\:->$ 1), representing the predicted loss (loss of ESN). Each processing block, except the final layer, combines a linear transformation with layer normalization, ReLU activation, and dropout for regularization.

After training and obtaining the network weights, we adopted an innovative approach. We froze the network weights and in the next step treated the input parameters as trainable variables. For the optimization, the loss function is defined as the output of the network’s loss, which can be expressed as:

$$\:Loss\:=\:\left|f\left(inputs\right)-\:0\right|$$

(11)

Or simply:

$$\:Loss=f\left(inputs\right)$$

(12)

where $\:f\left(inputs\right)$ represents the neural network’s output for a given set of seven input parameters. This creates an optimization problem where we seek to find input parameter values that minimize this loss function.

The optimization process uses gradient-based methods to iteratively adjust the input parameters while maintaining their constraints. Starting with initialized parameters within predefined bounds, these values are passed through the frozen trained network to compute the loss. The gradients are then calculated with respect to the input parameters, allowing for their systematic adjustment. If any parameter values fall outside their valid ranges during this process, they are clamped to the nearest value within the predefined bounds. This process continues until convergence or for a specified number of epochs, effectively searching for optimal input parameters that yield the minimum possible loss value. Throughout this process, all parameters remain within their valid ranges: k and m are constrained between defined bounds, p and α are maintained within valid probability ranges, and weight scales are similarly constrained to ensure physically meaningful values. Algorithm 5 and Fig. 6 illustrates the complete architecture and optimization workflow of our inverse prediction approach.

Algorithm 4. Semi-supervised model-direct parameter prediction.

Fig. 6

: The network architecture consists of training and inference phases. The training phase shows the dimensional transformation of data through the network, where each block’s notation (e.g., 7 -> 256) indicates its input and output dimensions. The inference phase demonstrates the iterative optimization process using the trained network with fixed weights to discover optimal parameters.

Experimental result

Setup

This setup forms the foundation for all Echo State Network (ESN) models implemented in our research, including both our proposed model and the baseline ESN. These parameters were determined experimentally and maintained consistently across all model implementations to ensure fair comparison. Table 2 presents the value parameters that were applied uniformly to both our enhanced model and the standard ESN implementation throughout all experiments.

Table 2 Value parameter of ESN.

Setup of supervised model

We employed the Adam optimizer and explored a learning rate range between 1e−06 and 1e−03. The training process was conducted over 50 to 200 epochs, with a data split of 20% for training and 80% for testing.

Through extensive experimentation with various combinations of reservoir sizes, learning rates, and epoch numbers, we identified distinct patterns in model behavior. Specifically, we found that each reservoir size required a tailored learning rate to achieve optimal performance without overfitting. Smaller reservoirs tended to perform better with higher learning rates within the specified range, as this helped prevent underfitting. Conversely, larger reservoirs remained stable with lower learning rates, effectively avoiding overfitting. This adaptive approach to selecting learning rates based on reservoir size allowed us to maintain model stability and achieve the best possible results across different configurations. By defining these ranges, we ensured a balanced trade-off between model performance and generalization.

Setup of semi-supervised model

For network parameter configuration, we implemented varying ranges based on reservoir size. For small networks (5 nodes), k and m values range from 2 to 4. Medium networks (20 nodes) use ranges of 2 to 7, while larger networks (50 nodes) extend this to 2 to 9. Across all network sizes, we maintained consistent values for rewiring probability [0.1, 0.3, 0.9], network mixing ratio α [0.3, 0.9], and weight scales [0.3, 0.9] for both small-world and scale-free components. Additional configurations for very large networks (500 and 1000 nodes) are prepared but currently disabled.

Direct parameter prediction

For training, we use Mean Squared Error (MSE) as our loss function, paired with the AdamW optimizer. The learning rate starts at 0.0001, with a weight decay of 0.01 for regularization. The model trains for up to 1000 epochs, but includes an early stopping mechanism that triggers after 100 epochs without improvement. To prevent gradient explosions, we clip gradients at 1.0, and we’ve set a minimum learning rate of 1e−6 to ensure stable training.

Inverse parameter prediction

Our model used a reservoir size of 10–400, with K and M parameters ranging from 2 to 12. P parameter was constrained to 0.1–0.5, while α and weight scales operated within 0.1–0.9. Training utilized AdamW optimizer (learning rate: 0.0001, weight decay: 0.01) with MSE loss function. We implemented early stopping (patience: 100 epochs), gradient clipping (1.0), and minimum learning rate (1e-6) with an 80/20 train-test split.

Data was normalized to range [− 5, 5], removing infinite/NaN values. The optimization used SGD (momentum: 0.9) with gradient clamping over 1000 epochs, and ReduceLROnPlateau scheduler (patience: 50 epochs). Random seed 42 ensured reproducibility.

Data set

Our experimental dataset comprised 20,000 data points, strategically divided into 14,000 points for training and 6000 points for testing. To ensure comprehensive evaluation of our methodology, we generated data using two distinct mathematical models: the Mackey–Glass (MG)²⁷ chaotic time series and the Nonlinear AutoRegressive Moving Average (NARMA)²⁵ model.

The Mackey-Glass system, notable for its parameter τ (tau), was instrumental in generating varying levels of complexity in our time series data. We explored three different τ values to create datasets with distinct characteristics, allowing us to systematically evaluate our model’s performance across different complexity levels of chaotic behavior.

For the NARMA model, we implemented a nonlinear autoregressive structure with moving average components. The model’s implementation followed a specific sequence generation process, incorporating memory length and feedback mechanisms to create complex temporal dependencies.

The dataset generation process followed rigorous algorithmic procedures (detailed in Algorithm 5 and Algorithm 6):

Algorithm 5. Generate Mackey glass time series.

Algorithm 6. Generate NARMA time series.

As documented in Table 3, we established specific coding schemes for our datasets. The Mackey-Glass datasets were labeled as A, B, and C, corresponding to τ values of 29, 17, and 10 respectively. The NARMA model was designated as dataset D. Additionally, we implemented two distinct resize parameter configurations for the NARMA model, labeled as 1 and 2, corresponding to dimensions of [5,50] and [5,20,50] respectively. This parametric variation allowed us to evaluate our model’s robustness across different input dimensionalities.

Furthermore, we extracted real-world climate data to enhance the diversity of our evaluation datasets. Using the Open-Meteo Historical Weather API, we collected daily maximum temperature time series spanning 25 years (2000–2024) for two geographically distinct locations. These temperature datasets were designated as E and F, corresponding to Bushehr, Iran and Washington, United States respectively. The temperature data underwent Min-Max normalization to ensure compatibility with our neural network architecture.

To validate the chaotic nature of these climate datasets, we performed comprehensive chaos analysis using established mathematical criteria. The chaotic characteristics were confirmed through multiple quantitative measures: (1) Lyapunov exponent calculation, which yielded positive values indicating sensitive dependence on initial conditions; (2) Correlation dimension analysis, revealing fractal structures within the range of 2.0–3.0, characteristic of strange attractors; (3) Hurst exponent computation, demonstrating values around 0.5–0.6, suggesting weak long-term memory typical of chaotic systems; and (4) Mutual information-based optimal time delay estimation for proper phase space reconstruction. For instance, the Washington dataset exhibited a Lyapunov exponent of 1.524, correlation dimension of 2.79, and Hurst exponent of 0.537, achieving a chaos score of 2.5/2.5, definitively confirming its chaotic behavior. These rigorous mathematical validations ensure that our temperature datasets represent genuine chaotic time series, providing a comprehensive evaluation framework that encompasses both synthetic mathematical models and empirically verified chaotic environmental systems.

Table 3 Coding of usage dataset.

Metric

To evaluate the performance of our proposed methods, we employed the Normalized Root Mean Square Error (NRMSE) as our primary evaluation metric. NRMSE was specifically chosen as it provides a standardized measure of prediction accuracy while accounting for the scale of the target data. This metric effectively quantifies the average magnitude of prediction errors between the model’s output and actual values, normalized by the range of observed values. The normalization aspect of NRMSE makes it particularly suitable for our analysis as it enables meaningful comparisons across different scales and units of measurement. the NRMSE is calculated as:

$$\:NRMSE\: = \:\frac{{\sqrt {\sum \: \frac{{\left( {\hat{y}\: - \:y} \right)^{2} }}{n}} }}{{y_{{max}} - \:y_{{min}} }}\:\:\:$$

(13)

In this formula, predicted values are denoted by ŷ and actual values by y, while n represents the total number of samples. The denominator consists of the range of actual data, calculated as the difference between the maximum ($\:{y}_{max}$) and minimum $\:({y}_{min}$) observed values.

In addition to NRMSE, we also utilized Mean Squared Error (MSE) as a complementary evaluation metric to provide a comprehensive assessment of model performance. MSE measures the average of the squared differences between predicted and actual values, offering direct insight into the magnitude of prediction errors without normalization. This metric is particularly valuable as it penalizes larger errors more heavily due to the squaring operation, making it sensitive to outliers and significant deviations. By employing MSE alongside NRMSE, we can evaluate both the relative performance (through NRMSE) and the absolute error magnitude (through MSE) of our proposed methods. The MSE is calculated as:

$$\:MSE = \sum {\:\frac{{\left( {\hat{y}\: - \:y} \right)^{2} }}{n}}$$

(14)

where $\:y$ represents the actual values, $\:\hat{y}$ denotes the predicted values, and $\:n$ is the total number of samples. Lower MSE values indicate better model performance, with a perfect prediction yielding an MSE of zero.

Result

This section presents the experimental results and performance analysis of our proposed models across multiple datasets with varying characteristics and sample sizes. We evaluate both supervised and semi-supervised learning approaches, comparing their efficacy against baseline methods.

Supervised model

Our proposed Supervised Model demonstrates superior performance compared to the baseline Simple ESN across multiple datasets and sample sizes. The experimental results in Table 4 support this conclusion through several key observations.

For Dataset A, our model achieves significantly lower error rates (0.0253 ± 0.02) at N = 1000 compared to Simple ESN (0.097 ± 0.12). In Dataset B, our model shows remarkable improvement with larger sample sizes, reaching (4.415 ± 0.2)e−04 at N = 1000, substantially outperforming Simple ESN’s 0.049 ± 0.04.

Most notably, in Dataset C, our Supervised Model maintains consistently low error rates, achieving (6.33 ± 0.1)e−04 at N = 1000, while Simple ESN shows higher variability. Dataset D further demonstrates our model’s stability, maintaining consistent performance around 0.22 ± 0.001 across all sample sizes, whereas Simple ESN’s performance deteriorates to 10 ± 0.0 at N = 1000.

It’s important to note that in our experimental setup, we implemented a threshold mechanism where any loss value exceeding 10 was capped at 10. This approach was adopted to ensure better result visualization and comparison across different scenarios. The presence of large loss values, particularly in some Simple ESN results, indicates instability in the model’s response to certain input conditions. This capping explains some of the larger values observed in the results, such as the 10 ± 0.0 seen in Dataset D for Simple ESN at N = 1000, which suggests significant instability in the model’s behavior for those specific conditions.

However, our analysis reveals that the relationship between sample size and performance varies significantly across datasets for both our proposed Supervised Model and the baseline Simple ESN. While our model generally shows more stable and often superior performance, the effectiveness of both approaches demonstrates dataset dependency. These findings indicate that larger sample sizes don’t uniformly guarantee better performance, and the selection between our Model 1 and the baseline Simple ESN should be based on specific dataset characteristics and application requirements.

Nevertheless, these results conclusively show that our proposed Model 1 outperforms the baseline Simple ESN through: (1) better error rates at larger sample sizes, (2) more consistent performance across different datasets, and (3) superior stability with increasing sample sizes. This improved performance is particularly evident in larger datasets, suggesting better scalability and generalization capabilities of our approach.

The real-world temperature datasets (E and F) demonstrate our model’s capability to handle practical applications beyond synthetic data. For both Bushehr and Washington temperature datasets, our Supervised Model consistently outperforms Simple ESN across all sample sizes, with particularly notable improvements at larger sample sizes (N = 1000), where error rates reach 0.13008 ± 0.01 and 0.15103 ± 0.01 respectively, compared to Simple ESN’s 0.1614 ± 0.01 and 0.2607 ± 0.04. These results validate that our optimization approach is not limited to mathematical models but extends effectively to real-world chaotic systems, demonstrating the practical applicability of our method in climate prediction and similar environmental monitoring tasks.

The real-world climate datasets reveal important insights about our method’s practical applicability. The temperature data from Bushehr and Washington exhibit different chaotic characteristics - Bushehr shows higher seasonal variability while Washington demonstrates more complex long-term patterns. Our supervised method adapts effectively to both patterns, achieving 47% and 42% NRMSE improvements respectively compared to baseline ESN. This adaptability across geographically and climatically distinct datasets validates the generalizability of our optimization approach beyond synthetic mathematical models.

Table 4 Result of supervised model.

Semi-supervised model

The table presents a comparative analysis of different model configurations, examining their performance using various evaluation metrics. The results are organized across multiple datasets (labeled A1 through D2) and show three main model variants: DPP, Line, and Simple ESN. Looking at the loss measurements, we can observe that the DPP configuration generally demonstrates better performance across most datasets, with values ranging from approximately 0.1000 to 0.2998. The Line configuration shows comparable but slightly higher loss values in many cases. The Simple ESN configuration, while competitive in some instances, typically shows higher loss values compared to the DPP variant. Notably, in datasets C1 and C2, some configurations show ‘inf’ (infinite) values, suggesting potential convergence issues or limitations in those specific scenarios.

The consistency of these patterns across multiple datasets suggests that the DPP approach offers more robust and reliable performance in this experimental context. The relatively lower loss values achieved by this configuration indicate its superior ability to minimize prediction errors compared to the alternative approaches. This pattern is particularly evident in datasets A1 and A2, where the DPP configuration maintains a clear advantage over other model variants.

Table 5 represents the coding scheme for the datasets. Parameter 1 indicates that the generated dataset was created using reservoir configurations with 5 and 50 neurons, while Parameter 2 corresponds to datasets generated with 5, 20, and 50 neurons. These codes are used to differentiate dataset variations in Table 5.

Table 5 Coding of generated dataset.

Based on Table 6, we can observe the performance comparison of three different models across multiple datasets. The IPP approach consistently demonstrates superior performance compared to both the Simple Model and DPP approach across all datasets. For datasets A1 through D2, the IPP approach achieves lower error rates, with values ranging from 0.056 ± 0.04 to 0.1804 ± 1.2e-02. In contrast, the Simple Model exhibits considerably higher error values, particularly for datasets B1, C1, and D1 (all at 8.37 ± 9.7). The PDD approach shows intermediate performance, with error rates generally higher than the IPP approach model but significantly better than the Simple Model.

These results indicate that incorporating feature-based approaches with loss optimization leads to more robust model performance. The substantial performance improvements observed in the B, C, and D dataset groups suggest that the IPP architecture is particularly effective for complex data distributions, while still maintaining competitive performance on simpler datasets (A group).Table 6 provides a more detailed breakdown of these results.

Table 6 Result of Semi-supervised Model.

In comparing the results of our paper with existing research in the field, several significant findings emerge that demonstrate the superiority of our proposed methodology. The comprehensive analysis presented below highlights how our approach consistently outperforms previous implementations across various datasets and prediction tasks. It should be noted that the following table specifically focuses on the comparison of our supervised model with other research papers in the literature.

Table 7 presents a comparative analysis of various research papers along with their corresponding datasets and performance metrics for echo state network-based prediction models. Each row represents a different published paper, with columns providing detailed information about their methodologies and results.

The first column identifies the paper titles, primarily focusing on studies that utilize echo state networks for various prediction tasks. The second column specifies the datasets used in each study, including VG, Laser time series (18/19), and MG datasets.

The third column contains two key pieces of information: the number of reservoir neurons employed in the echo state networks (ranging from 200 to 900) and the error rates achieved by simple baseline models as reported in each paper. The fourth column shows the accuracy metrics for the advanced models proposed in each paper.

Columns five through seven outline the data distribution used for experimentation: total data points, training set size, and testing set size respectively. This information provides context regarding the robustness of the evaluations conducted in each study.

Column eight presents the percentage improvement achieved by each paper’s proposed model compared to their own baseline. Following this, columns nine through eleven showcase our independent calculations and evaluations.

Column nine contains our calculated error rates for simple baseline models, while column ten shows our measured error rates for the proposed models. The final column highlights the percentage improvement our implementation achieved over the simple baseline.

Notably, our supervised model consistently shows significant performance improvements across all paper comparisons. For instance, in the case of “Chaotic time series prediction using echo state network based on selective forgetting,” our model demonstrates a remarkable + 41.68% improvement. Similarly, for “Collective Behavior of a Small-World Recurrent Neural System with Scale-Free Distribution,” we achieve an impressive + 10.71% enhancement.

The most substantial improvement is observed in the “Echo state network with high-clustering coefficient” paper, where our implementation achieves a + 11.54% improvement, significantly outperforming the original implementation. Additionally, our implementation of the “Parameterizing echo state networks for multi-step time series prediction” shows a + 3.13% improvement, demonstrating consistent superiority across different methodologies.

These results clearly indicate that our proposed supervised approach not only validates the findings of previous research but substantially enhances them through more effective implementation strategies and methodological refinements. The consistent improvements across diverse papers and datasets demonstrate the robustness and versatility of our approach, positioning it as a significant advancement in the field of echo state networks for time series prediction.

Table 7 Comparison of our supervised model against previous echo state network approaches, showing consistent performance improvements over published methods across multiple datasets and time series prediction tasks.

Cross domain analysis

Cross-domain evaluation is essential for assessing model robustness when training and testing data originate from different distributions. This analysis provides critical insights into the model’s generalization capabilities across diverse environments, which is particularly important for real-world deployment where operational conditions may differ from training scenarios.

To evaluate the cross-domain performance of our supervised model, we conducted experiments by training on one dataset and testing on another. This setup simulates realistic scenarios where domain characteristics differ between training and deployment phases. Table 8 presents the cross-domain evaluation results, including training performance, same-domain test performance, cross-domain test performance, and corresponding reservoir sizes.

Table 8 Cross-domain performance evaluation showing NRMSE and MSE values for different domain configurations with corresponding domain gap factors.

To quantify the magnitude of performance degradation across domains, we introduce the Domain Gap Factor, which is calculated by dividing the cross-domain NRMSE by the same-domain test NRMSE. This metric provides an intuitive measure of domain transferability, where values closer to 1.0 indicate better cross-domain generalization, while higher values signify greater performance degradation when the model encounters data from different domains.

The experimental results reveal that models trained on higher complexity datasets exhibit superior generalization capabilities when tested on lower complexity datasets. This phenomenon occurs because complex training scenarios enable the model to develop more comprehensive feature representations, creating an implicit regularization effect that enhances cross-domain robustness. The variation in Domain Gap Factors across different domain pairs demonstrates the relative challenges associated with specific domain transitions, providing valuable insights for understanding model transferability and guiding future domain adaptation strategies.

Sensitivity analysis

To evaluate the robustness of our proposed methods, we conducted comprehensive sensitivity analysis on key hyperparameters across all datasets. The supervised method demonstrates consistent performance across different reservoir sizes (5–1000 neurons) and learning rates (1e−05 to 1e−04), with NRMSE standard deviation remaining below 0.02. The semi-supervised approach maintains stable hyperparameter selection within the defined search space, showing reliable convergence across multiple runs.

Both methods exhibit remarkable cross-dataset stability, achieving consistent relative improvements across all tested datasets (A–F) regardless of data characteristics. The supervised approach delivers 15–74% NRMSE improvement whether applied to synthetic mathematical models (Mackey-Glass, NARMA) or real-world climate data (Bushehr, Washington temperatures). This consistent behavior indicates robust generalization capabilities across different types of chaotic time series.

Convergence analysis reveals reliable optimization behavior, with the supervised method converging within 50–200 epochs across all configurations. Multiple random initializations produce low performance variance (σ < 0.03 for NRMSE), confirming method reliability and reproducibility. Based on correlation analysis shown in Fig. 10, reservoir size demonstrates the strongest performance impact, followed by connectivity parameters, while weight scale parameters show moderate sensitivity. This hyperparameter hierarchy remains consistent across different problem domains.

To assess the resilience of our proposed methods against data corruption, we conducted comprehensive noise sensitivity experiments across varying noise levels (0.0 to 0.5). Figure 7 presents NRMSE comparison results for different model configurations under additive Gaussian noise conditions.

The semi-supervised models with DPP and IPP approaches demonstrate distinct noise handling characteristics. Under low noise conditions (≤ 0.1), both approaches maintain performance levels comparable to noise-free scenarios, with NRMSE values remaining stable around 0.0012–0.0027. However, as noise intensity increases beyond 0.2, the IPP approach shows superior noise tolerance, particularly evident in the A2 dataset where NRMSE peaks at 0.275 before stabilizing, while DPP variants exhibit more pronounced degradation.

The supervised models show remarkable noise resilience across all tested configurations. With increasing reservoir sizes (N = 5 to N = 1000), the models demonstrate improved noise handling capabilities. Notably, larger reservoirs (N ≥ 500) maintain relatively stable performance even under high noise conditions (noise level 0.4–0.5), with NRMSE remaining below 0.18 for most datasets. The B dataset consistently outperforms A dataset across all noise levels and model sizes, suggesting inherent data characteristics influence noise sensitivity.

Cross-dataset analysis reveals that supervised models with N = 1000 achieve optimal noise-performance trade-offs, maintaining prediction accuracy while demonstrating robust noise handling. The consistent performance gap between datasets A and B across all noise levels indicates that our optimization framework preserves relative dataset characteristics even under challenging noise conditions.

Fig. 7

NRMSE comparison across different noise levels for (a) Semi-supervised DPP approach, (b) Semi-supervised IPP approach, (c–f) Supervised models with varying reservoir sizes (N = 5 to N = 1000). Results demonstrate noise resilience characteristics across datasets A and B.

These findings confirm that our optimization framework provides robust and reliable improvements over standard ESNs, with stable performance characteristics that translate effectively across diverse chaotic prediction tasks.

Discussion

In our approach to generating reservoirs, we initially created graphs with distinct small-world and scale-free properties, then combined them using weighted combinations. Our analysis demonstrates that after weighted combination of these graphs, the resulting hybrid network successfully maintains both small-world and scale-free characteristics.

As shown in Fig. 7, a comprehensive examination of four key metrics reveals how effectively our hybrid matrix integrates these network properties. The small-world index of our hybrid network achieves a value of 2.55, significantly exceeding the critical threshold of 1.0. While this is lower than the pure small-world network’s impressive index of 8.74, it convincingly demonstrates that the hybrid network preserves essential small-world characteristics while incorporating scale-free properties.

This balanced integration is further supported by the clustering coefficient analysis, where our hybrid network exhibits a coefficient of 0.184. This value positions it between the small-world network (0.316) and scale-free network (0.135), indicating successful preservation of local connectivity patterns while accommodating the broader connectivity typical of scale-free structures.

Particularly noteworthy is the hybrid network’s performance in average path length, achieving a remarkably efficient 2.32. This value not only improves upon both the small-world (3.53) and scale-free (2.69) networks but approaches the efficiency of random networks (2.11). Such short path lengths are crucial for rapid information transfer across the network, a key characteristic we aimed to preserve from small-world structures.

The final metric presents a combined evaluation of small-world and scale-free properties, where our hybrid network achieves a score of 0.42. While the scale-free network shows a higher score of 0.80 due to its pronounced hub structure, our hybrid network’s score represents a substantial and balanced integration of both network characteristics.

Fig. 8

: Comparative analysis of key network metrics across different network architectures.

To further validate the preservation of these essential network properties, Fig. 8 presents a detailed structural analysis of the hybrid network’s connection patterns. The reservoir matrix weights (positive and negative weights) reveals a well-balanced distribution of positive and negative connections, demonstrating how our parametric combination approach successfully merges the local connectivity patterns typical of small-world networks with the long-range connection characteristic of scale-free architectures.

This integration is particularly evident in the adjacency matrix, which displays a prominent diagonal band indicating strong local clustering (a key small-world property), while the scattered off-diagonal connections represent the long-range links that facilitate hub formation (a defining scale-free characteristic). The weight distribution histogram further confirms this successful integration, showing a balanced, approximately normal distribution centered around zero, with appropriate tails extending in both directions.

The network visualization provides a final confirmation of our hybrid approach’s success, clearly displaying both the clustered structures typical of small-world networks and the high-connectivity nodes characteristic of scale-free networks. Together, these structural analyses reinforce our earlier metric-based findings, demonstrating that our hybrid network effectively preserves and balances both small-world and scale-free properties through the weighted combination process.

Fig. 9

: Structural analysis of the hybrid network matrix.

Having established the successful preservation of both small-world and scale-free properties in our hybrid network, we next validated the effectiveness of our hyperparameter selection strategy. The performance of complex networks like ours is highly dependent on the choice of hyperparameters, and selecting optimal values is crucial for achieving desired performance characteristics.

Figure 9 provides compelling evidence for the effectiveness of our hyperparameter selection methodology. The visualization shows NRMSE values (≤ 1.15) across different hyperparameter combinations, demonstrating the significant influence these parameters have on network performance. The blue line tracks loss variations across different parameter combinations, while the gray band represents variance bounds around the mean.

Our NRMSE analysis reveals substantial fluctuations across different hyperparameter combinations, providing clear evidence of their influence on network performance. As observed in Fig. 10, the majority of NRMSE values oscillate around the mean of 0.3009, with several notable spikes exceeding 0.8. These variations validate our parameter selection methodology and confirm hyperparameters’ role as effective control mechanisms for network optimization. The consistent pattern of fluctuations within the variance bounds (±σ) further supports the statistical significance of our findings.

Fig. 10

: NRMSE values (≤ 1.15) across different hyperparameter combinations, demonstrating parameter influence on network performance. The blue line shows loss variations, while the gray band represents variance bounds around the mean.

To gain deeper insight into how individual hyperparameters affect network performance, we conducted a comprehensive correlation analysis between each parameter and the NRMSE values. Figure 11 presents these correlations across different datasets (A1–F2), revealing how each parameter influences network performance across various data types.

Our correlation analysis reveals distinctive patterns in parameter influence. As shown in Fig. 10, the reservoir size demonstrates the strongest correlation with NRMSE values, particularly evident in datasets D1 and D2 where correlations reach approximately − 0.35. The connectivity parameters ‘m’ and ‘k’ show moderate correlations, though their impact varies across datasets. This observation is particularly significant as it supports our previous findings about the importance of edge connectivity patterns in network performance.

Interestingly, parameters such as ‘p’ and ‘alpha’ show relatively consistent but smaller correlations across datasets, suggesting their role as fine-tuning parameters rather than primary determinants of performance. The weight scale parameters for both small-world and scale-free components show varying effects across different datasets, indicating that their optimal values might be data-dependent. These systematic findings provide crucial insights for network optimization strategies and lead us to our final conclusions.

While our methods show excellent results, there are a few practical points to consider. The supervised approach takes about 3–5 times longer to train than standard ESNs, and this becomes more noticeable with larger networks. Also, since our optimization is tailored to specific datasets, it may need adjustment when working with very different types of data. Despite these considerations, the significant performance improvements make these trade-offs worthwhile in most applications.

Fig. 11

: The figure shows parameter correlations with NRMSE in two parts. The plot displays a detailed comparison of parameters across eight different cases (A1 to F2), separated by vertical lines for better readability.

Conclusion and future work

In this work, we first established theoretical evidence through two key theorems that demonstrate the relationship between reservoir properties and network performance. Building on these theoretical insights, we proposed two approaches: a supervised method that directly optimizes reservoir weights, and a semi-supervised approach that combines small-world and scale-free network characteristics. Through systematic analysis of the semi-supervised approach, our comprehensive study across multiple datasets revealed significant insights into the relative importance of hyperparameters in hybrid network architectures.

Through systematic correlation analysis, we demonstrated that reservoir size consistently emerges as the primary determinant of network performance. Notably, the edge connectivity parameters (k in Watts–Strogatz and m in Barabási-Albert models) show substantial influence at approximately half the impact of reservoir size. This finding is particularly significant as both parameters fundamentally control the edge density in their respective network models - k determining the initial number of edges per node in the Watts–Strogatz model, and m governing both the initial complete graph size (m + 1) and the number of edges added with each new node in the Barabási–Albert model.

The consistent importance of these edge-related parameters across different network formation mechanisms suggests that edge density plays a crucial role in reservoir computing performance, second only to the reservoir size itself. This parallel influence of k and m, despite their implementation in different network growth models, provides strong evidence for the fundamental importance of edge connectivity in hybrid reservoir architectures.

Looking ahead, we aim to extend our research beyond the supervised and semi-supervised models by proposing a fully unsupervised approach for generating the reservoir architecture. The ultimate goal is to develop a method that can construct a high-performing reservoir topology for various time series types without requiring any task-specific training or tuning. To achieve this, we will conduct a comprehensive analysis across benchmark datasets to establish clear relationships between time series characteristics and optimal configurations of edge density and other network parameters. This will enable us to formulate robust guidelines for creating these automated, training-free reservoirs.

Through this future work, we anticipate developing a more nuanced understanding of how different data types interact with network connectivity patterns, leading to more efficient and automated approaches to reservoir computing network design. The strong correlation between edge-related parameters and network performance suggests that edge density optimization could be a key factor in developing these automated design strategies.