Introduction

Woody vegetation, characterized by well-developed woody tissues and perennial growth, constitutes a primary component of natural terrestrial carbon sequestration. Through photosynthesis, the dense branches and leaves of woody plants convert substantial amounts of carbon dioxide into organic compounds, storing carbon within the plant biomass1. This process not only contributes to maintaining the ecological balance of the Earth but also plays a crucial role in global climate regulation2,3,4. Forests are biotic communities predominantly composed of woody plants. Accurately quantifying the spatial distribution of woody vegetation biomass is crucial for developing scientifically sound regional vegetation management policies and promoting the sustainable development of carbon sequestration in vegetation5,6.

Traditional field survey methods have limitations, including delays, restricted spatial scale, and high labor costs7. Remote sensing technology, with its advantages of extensive coverage and high spatiotemporal resolution, provides new perspectives for obtaining vegetation biomass8,9.The estimation of biomass and forest structural parameters through remote sensing is primarily achieved using passive optical imagery and active remote sensing, such as light detection and ranging (lidar). In recent years, freely available optical imagery has gained unique advantages in estimating forest AGB due to its spatial continuity, and high temporal and spatial resolution, covering large spatial areas3,10. Optical remote sensing images establish empirical relationships to estimate vegetation biomass between vegetation indices and plot-based biomass11,12. However, the ability of optical images to penetrate the forest canopy is limited. When the tree canopy closes or the biomass exceeds a certain range, optical signals are no longer sensitive to AGB variations, resulting in the signal saturation problem13. Feldpausch et al.14 found that tree height is a crucial factor in biomass estimation. Ignoring height information can lead to an underestimation of carbon stocks in tropical regions. Future research should incorporate tree height information to reduce errors in biomass estimates. Airborne LiDAR, utilizing laser pulse ranging principles, can accurately acquire elevation and structural information of ground vegetation15. Moreover, it is not affected by signal saturation16,17,18. However, its limitations include a relatively small coverage and high flight costs, which pose challenges for acquiring extensive data19. Spaceborne LiDAR, with its extensive coverage and high spatial resolution, has the potential for large-scale biomass estimation20. Nevertheless, the discrete footprint distribution prevent continuous spatial coverage. Therefore, current research increasingly focuses on integrating multiple data sources to generate large-scale and high-spatial-resolution maps of forest AGB distribution21.

In recent years, numerous scholars have conducted research on biomass estimation in Australia. Keith et al.22 noted that analysis of biomass data from 136 global primary forest sites revealed that the average carbon density in Australia’s temperate moist eucalypt forests is higher than that of northern and tropical forests. This is attributed to Australia’s unique climate (characterized by relatively high precipitation and lower temperatures) and minimal human disturbance. Taking the forests of Victoria, Australia, as an example, Grierson et al.23 developed age-based regression equations for forest biomass accumulation across different forest types, based on field survey data, to estimate the average aboveground carbon density of the primary forests in Victoria. Liu et al.24 compared tree parameters derived from airborne laser scanning with field-measured AGB data. They subsequently proposed a localized DBH (diameter at breast height) regression model, which ultimately led to the development of a biomass estimation model based on airborne LiDAR-derived tree parameters. Nguyen et al.25 developed a Random Forest (RF)-based k-nearest neighbors (kNN) model using Landsat time series data and a single plot output, generating annual forest AGB maps for Victoria from 1988 to 2017.

Although some significant progress has been made in remote sensing biomass estimation studies in Australia, challenges persist. For instance, while airborne LiDAR has demonstrated good performance in vegetation biomass estimation, the high cost of data acquisition limits its widespread application at large scales26,27. This highlights the need for effective model integration across multiple data sources to improve the accuracy of biomass predictions over large areas.

With the development of computer technology, data-driven machine learning algorithms have increasingly been applied in the field of remote sensing, and have become an effective tool for large-scale biomass estimation28,29. However, different models exhibit varying applicability across regions30,31, making it particularly important to explore a robust method for large-scale biomass estimation. Stacking model is an efficient ensemble learning method that combines the predictions of multiple base learners of different types as inputs and then a meta-learner is trained to make the final prediction32. Unlike traditional ensemble algorithms such as Bagging and Boosting, the Stacking model can further improve predictive accuracy by integrating information from different learners33. Its primary advantage lies in reducing both the bias and variance of individual models, thereby effectively leveraging the strengths of each learner. In addition, Stacking can flexibly handle various types of input data and complex nonlinear relationships, making it highly promising for tasks such as forest AGB estimation34. Although Stacking is more complex in terms of model construction and training, it achieves greater predictive power than individual models through sophisticated combination strategies. This advantage is particularly evident in applications involving large-scale datasets and diverse data sources, where Stacking has demonstrated significant advantages.

The main objectives of this study are: (1) to perform feature selection using RFE and compare model performance; (2) to generate spatial maps of aboveground biomass; and (3) to analyze associated uncertainties. Using Australia as the study area and field-measured biomass data as a reference, we extracted predictor variables from the vegetation canopy height map developed by Scarth et al. (2019)35, and integrated them with Landsat imagery and topographic data as inputs to the biomass estimation models. For model evaluation, the Stacking regression model was compared with several individual machine learning algorithms. Finally, regional AGB maps of woody vegetation were generated using the three models with the highest predictive performance.

Study area and data

Biomass plot data

Fig. 1
figure 1

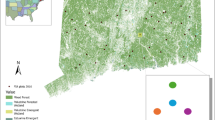
Spatial distribution of biomass plots in the study area. Biomass data were obtained from the publicly available TERN database. The colored points represent the spatial distribution and value range (0.05–350, after filtering) of woody vegetation biomass. The majority of the biomass plots are concentrated in northern Australia, the eastern coastal region, and the southwest. Non-woody samples, shown in gray, are primarily distributed in the central part of the study area.

Full size image

We utilized the biomass library released by the Australian Tern (https://portal.tern.org.au) as the reference data for aboveground Biomass36. The primary purpose of establishing this biomass plot database was to calibrate and validate satellite-derived products in support of national-scale aboveground biomass mapping. The plot database integrates tree inventory data from a wide range of sources, including federal, state, and local government agencies, academic institutions, private enterprises, and other relevant organizations across Australia. It includes comprehensive tree and shrub census data collected nationwide. The generalized allometric equations used in the database are based on the universal allometric model developed by Paul et al.37, which is tailored to Australian plant functional types and accounts for aboveground, belowground, and total biomass, including both live and dead components. These equations are further adjusted using decay correction factors proposed by Lucas et al38. The biomass density at the plot level is derived by aggregating the biomass of individual trees within each plot. Following the methodology described by Liao et al.39, we excluded plots with an area smaller than 0.03 hectares and those with an absolute error exceeding 75 Mg/ha or a relative error exceeding 25%. Outliers were removed using the 2-sigma rule40,41. The final dataset after screening contained 3,054 sample plots from 2007 to 2011 (Fig. 1). However, the absence of non-woody plots in the dataset led to an overestimation of vegetation biomass39. Therefore, we randomly added 1550 non-woody sample plots at a nearly 1:2 ratio to enhance the AGB database. The non-woody sample plots were selected based on a combination of land use data and vegetation cover data. The vegetation cover information was derived from the canopy height product35, which includes a vegetation cover layer. The land cover data were obtained from the European Space Agency (ESA). Land use data were used to identify non-woody areas, while the vegetation cover data were used to select regions with no tree cover. This approach ensured that the selected non-woody plots corresponded to vegetation types such as grasslands, bare land, urban areas, and water bodies. Specifically, random points were generated in ArcGIS, and the “Extract Multi Values to Points” tool was applied to obtain attribute values (i.e., land cover type and vegetation cover). Points were then selected where the vegetation cover was zero and the land cover type was neither shrubland nor forest.

Landsat data

Since the launch of Landsat-1 in 1972, the Landsat program has provided long-term, high-quality global coverage data. Due to its appropriate spatial and temporal resolution, reliable data quality, and open-access policy, Landsat data have been widely used by governments and the remote sensing scientific community42,43.

When sunlight reaches vegetation leaves, chlorophyll within the leaves strongly absorbs visible light to facilitate photosynthesis, while the leaf cellular structure reflects near-infrared radiation44,45. The visible spectrum reflects the “greenness” of vegetation, whereas the near-infrared and shortwave infrared bands are highly responsive to vegetation water content and dry matter content46. A relatively simple vegetation index is the Ratio Vegetation Index (RVI)47, which is calculated by dividing the reflectance in the near-infrared band by that in the red band. A higher ratio typically indicates healthy vegetation, while lower values are indicative of soil or water. The Normalized Difference Vegetation Index (NDVI) assesses vegetation status by computing the difference and sum ratio between near-infrared and visible light48. NDVI values range from \(-1\) to 1. Values close to 1 indicate dense vegetation, values near 0 suggest tundra or bare ground, and negative values often correspond to clouds or snow. The Green Normalized Difference Vegetation Index (GNDVI) is a modified form of NDVI that substitutes the red band with the green band, making it more sensitive to chlorophyll content and less prone to saturation, thus better suited for dense canopies49,50.The Soil Adjusted Vegetation Index (SAVI) introduces a soil adjustment factor (L) to the NDVI formula to mitigate the influence of soil brightness, effectively reducing background interference while retaining vegetation signals51. This makes it more applicable in areas with sparse vegetation where soil is visible through the canopy. The Visible Atmospherically Resistant Index (VARI) is designed to minimize atmospheric effects on vegetation indices and better account for illumination variability52. Similarly, the Atmospherically Resistant Vegetation Index (ARVI) is less sensitive to aerosols, making it suitable for regions with high aerosol content such as areas affected by smoke or precipitation53. The Leaf Area Index (LAI)54, defined as the total leaf area per unit ground surface area, reflects both leaf density and canopy structure. The Enhanced Vegetation Index (EVI)55 was developed to address NDVI saturation in regions with high LAI, while simultaneously minimizing soil background and atmospheric interference to improve vegetation monitoring. The Difference Vegetation Index (DVI)56, calculated as the difference between near-infrared and red reflectance, can be used to evaluate vegetation presence and density. In remote sensing imagery, texture features capture spatial heterogeneity and patterns of land surface cover57,58,59. Even when different land cover types exhibit similar spectral characteristics, their spatial arrangements can be distinguished through texture, making it a valuable non-spectral complement with strong discriminatory capabilities. A variety of remote sensing features are considered to address diverse conditions, facilitating more accurate estimation of vegetation biomass.

We acquired Landsat data (USGS Landsat 5 Level 2, Collection 2, Tier 1) through the Google Earth Engine (GEE) platform. The data underwent atmospheric correction, and cloud masking was performed using the “SR_CLOUD_QA” band during subsequent processing. The imagery was collected between September 2008 and May 31, 2009 (growing season). To represent peak vegetation conditions, we selected the scene with the highest NDVI value to generate a composite image for the peak of the growing season. Extracted features included reflectance from the visible spectrum (blue, green, red), near-infrared (NIR), and shortwave infrared (SWIR) bands. In addition, we calculated multiple vegetation indices commonly used for biomass estimation, and extracted texture features using the Gray-Level Co-occurrence Matrix (GLCM) method (Table 1).

Table 1 Remote sensing feature extraction from Landsat imagery during the vegetation growing season, including various vegetation indices, spectral bands from visible to shortwave infrared, and texture features derived using the gray-level co-occurrence matrix (GLCM) method. These features are critical for biomass estimation and vegetation analysis.
Full size table

Vegetation height parameter acquisition

We obtained vegetation height and structure products35 from the Australia TERN website (https://portal.tern.org.au/metadata/TERN/de1c2fef-b129-485e-9042-8b22ee616e66). This data product is derived from a combination of ICESat GLAS, ALOS PALSAR, and Landsat data products, including features such as vegetation height, age class, and coverage. The data product is from the year 2009 and has a spatial resolution of 30 meters. We selected four canopy height images from this dataset, which included four canopy height features: the 25th, 50th, 75th, and 95th.

Land cover classification data and DEM

Fig. 2
figure 2

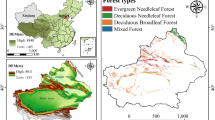
(a) Elevation map of Australia at a spatial resolution of 300 m, showing topographic variation across the continent. (b) The Australian land cover map reclassified into six vegetation types: broadleaf forest, coniferous forest, mixed forest (trees and shrubs), shrubland, other (non-forest and non-shrubland areas), and urban areas.

Full size image

The land cover classification data was obtained from the European Space Agency (ESA) website http://maps.elie.ucl.ac.be/CCI/viewer/index.php with a resolution of 300 m. The 2009 Australian land cover comprised 22 categories, and we reclassified it into six types based on their vegetation characteristics (Fig. 2a): 1. Broadleaved forest, 2. Needleaved forest, 3. Tree and shrub mix, 4. Shrubland, 5. Other (non-forested and non-shrubland, including cropland, grassland, herbaceous vegetation, water bodies, and bare soil.), and 6. Urban areas.

Topographic factors can influence ecological processes such as sunlight exposure, airflow, and vegetation growth, thereby impacting vegetation biomass. Particularly in the tall mountains of eastern Australia, which block warm and humid airflows from the Pacific Ocean, the vegetation growth on either side of the mountains varies. Therefore, slope and aspect are crucial factors influencing vegetation growth. Digital Elevation Model (DEM) data were obtained from the Shuttle Radar Topography Mission (SRTM) released by NASA and the National Imagery and Mapping Agency (NIMA). The spatial resolution of DEM is 30m. We calculated the elevation, slope, and aspect based on the DEM data (Fig. 2b).

Temperature and precipitation data

Fig. 3
figure 3

Spatial distribution of soil temperature, air temperature at 2 m above ground, and total annual precipitation across the study area. Soil temperature and air temperature are derived from the ERA5-Land hourly dataset, while precipitation is obtained from the CHIRPS daily dataset.

Full size image

Australia spans a vast area with significant regional variations in precipitation and temperature—both of which play critical roles in vegetation growth. Favorable temperature and precipitation conditions can promote healthy vegetation development, whereas extreme heat may lead to drought and wildfires, resulting in substantial biomass loss60. Our study area covers a wide range of climatic zones, including tropical rainforest, humid subtropical, tropical savanna, subtropical steppe, temperate oceanic, Mediterranean, and arid desert climates. These climate zones differ in seasonal patterns of temperature and rainfall, both of which are closely linked to vegetation dynamics61,62. Moreover, the impact of soil temperature on vegetation growth varies across different elevations and climatic regions63,64.

To account for these environmental influences, daily mean air temperature, soil temperature, and precipitation were incorporated as predictors into the biomass estimation model. Climate data were acquired from the GEE platform, including temperature and soil temperature from the ERA5-Land hourly dataset (ERA5-Land Hourly - ECMWF Climate Reanalysis), and precipitation from the CHIRPS daily dataset (Climate Hazards Center InfraRed Precipitation With Station Data (Version 2.0 Final)) (Fig. 3).

Comparison with other biomass maps

The result of this study were compared with two existing biomass maps, including the comprehensive pan-tropical biomass map published by Avitabile et al.65 and the global aboveground and belowground biomass carbon density map provided by NASA ORNL DAAC for 2010. The second biomass map was generated by Spawn et al.66, and we obtained it through the GEE (https://developers.google.com/earth-engine/datasets/catalog/NASA_ORNL_biomass_carbon_density_v1). The “Avitabile” map integrates existing aboveground biomass data from “Saatchi” and “Baccini” using weighted linear averaging and bias removal techniques to create a pan-tropical vegetation biomass map. The spatial resolution is 1 km, suitable for the early 2000s. The “Spawn” atlas integrated biomass remote sensing images based on land cover types (including woody, agricultural, grassland, etc.) in 2010, with a spatial resolution of 300 m.

Research methods

Fig. 4
figure 4

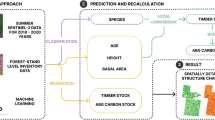
Workflow for biomass estimation. The framework consists of three main components: (1) extraction of remote sensing feature variables and spatial matching with field plots; (2) model selection, including a comparison between individual machine learning models and stacked models; and (3) spatial mapping of biomass distribution combined with comparison against other biomass products.

Full size image

The overall methodological framework of this study is illustrated in Fig. 4. We collected Landsat, SRTM, and canopy height data to extract a variety of remote sensing features related to biomass. Biomass plot data were obtained, and the corresponding remote sensing features at each plot location were extracted. These plots and their associated feature parameters were used to train the models, including several individual machine learning models and an Stacking model. First, a total of 37 feature variables were used to compare the predictive performance of the Stacking regression model with that of other models. Subsequently, RFE was applied to all remote sensing parameters to identify the optimal subset of features, which were then used for further model training. Finally, the optimal model was selected based on accuracy evaluation to generate a spatial distribution map of biomass, which was compared with existing biomass products.

Methods for biomass estimation

In this study, we compared the Stacking regression model with several other models, including seven individual machine learning algorithms (Fig. 5). The Stacking regression model, along with two relatively high-performing machine learning models, was employed to estimate biomass in the study area.

Stacking regression is a powerful ensemble learning method32,67. The main process is as follows: First, multiple base regression models are trained, and the predictions of these base models are used as new features to form a new training set for the meta-model68,69. The meta-model (typically a simple linear regression, ridge regression, etc.) is used to learn how to optimally combine the predictions from different base models70. The goal of the meta-model is to learn how to weight the predictions from the base models by minimizing the error. The Stacking regression model is highly flexible and allows for the selection of different base models and meta-models according to the task requirements. The base learning models include seven machine learning models, while the meta-model employs Multiple Linear Regression (MLR).

Fig. 5
figure 5

Flowchart of the stacking regression framework. The framework integrates seven base learners (RF, GBR, SVR, KNN, AdaBoost, XGBoost, and DT), whose predictions are used as inputs to a meta-model to generate the final biomass estimates. Predictions from individual models are also provided for comparison.

Full size image

Base models

The base models we selected included RF, GBR, Support Vector Regression (SVR), Decision Tree Regression (DT), KNN, Adaptive Boosting (AdaBoost), and XGBoost (Extreme Gradient Boosting).

DT and RF are both based on decision trees as base learning models71,72. They recursively split the data into smaller parts, selecting a feature and setting a threshold at each split, until a stopping condition is met. Random Forest, however, consists of multiple decision trees, each making independent predictions, with the final prediction being the average of all tree predictions. Compared to DT, Random Forest is more robust.

GBR, AdaBoost, and XGBoost are commonly used boosting algorithms. GBR is an ensemble learning method based on gradient descent, which incrementally adds the predictions of decision trees to the current model through an additive model73,74. Each new weak learner (usually a decision tree) fits the residuals (prediction errors) of the previous model to reduce the overall loss of the model. AdaBoost optimizes the model by adjusting the weights of the samples. Unlike GBR, AdaBoost updates the model output through weighted averaging. XGBoost is an optimized version of GBR, which introduces a regularization term to control the model’s complexity and prevent overfitting75.

KNN predicts by calculating the distance between the input feature point and other sample points in the training set, and then making predictions based on the K nearest neighbors76. The output of KNN is the average (or weighted average) of the target variable values of the K neighbors.

The core idea of SVR is to tolerate small errors (within the \(\varepsilon\) range) as much as possible during the regression process, and only penalize larger errors, thereby resulting in a more robust regression model77.

We selected the optimal hyperparameter combinations for multiple models through repeated comparative experiments(Table 2).

Table 2 Optimized hyperparameter settings of various regression models, including Random Forest (RF), K-Nearest Neighbors (KNN), AdaBoost, Gradient Boosting Regression (GBR), Support Vector Regression (SVR), Decision Tree (DT), and Extreme Gradient Boosting(XGBoost), aimed at enhancing model performance.
Full size table

Meta-model

The core function of the meta-model is to integrate the predictions from various base learners78. It learns how to adjust the weights based on the outputs of the base learners, thereby improving the accuracy of the final prediction. Unlike simple averaging methods (such as Bagging), Stacking performs more refined integration through the meta-model, capturing the strengths of different base learners. Typically, the meta-model is a simple regression model, such as MLR, Ridge Regression, or other types of regression models. The study employed MLR to determine the optimal combination weights, aiming to effectively integrate the predictions from base models in order to minimize the overall prediction error.

Feature selection of the image spectrum

Due to the large number of image feature variables, multicollinearity may exist, or the model may suffer from overfitting. RFE is a commonly used feature selection method79. It calculates the “importance” or “contribution” of each feature based on coefficients, weights, or other model evaluation metrics. Features are ranked according to their importance in the model, and the least important features (i.e., those with the smallest importance) are removed. The model is then retrained, and the most useful features for model prediction are ultimately selected. The RFE method helps reduce the number of features and enhances the model’s interpretability80.

Accuracy assessment and validation

Model performance is assessed using K-fold cross-validation. The data is divided into K equal subsets, with each subset used in turn as the validation set, while the remaining subsets are used for training. For each fold, the evaluation result is calculated, and the average of the K evaluations is used as the final performance assessment of the model81. The accuracy of the results is assessed using the coefficient of determination (\(R^2\) ), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE) to evaluate model performance, as described by the following formulas:

$$\begin{aligned} & R^2=1-\frac{\sum _{i=1}^n\left( y_i-{\hat{y}}_i\right) ^2}{\sum _{i=1}^n\left( y_i-{\bar{y}}\right) ^2} \end{aligned}$$
(1)
$$\begin{aligned} & RMSE=\sqrt{\frac{\sum _{i=1}^n\left( y_i-{\hat{y}}_i\right) ^2}{n}} \end{aligned}$$
(2)
$$\begin{aligned} & M A E=\frac{1}{n} \sum _{i=1}^n\left| \left( {\hat{y}}_i-y_i\right) \right| \end{aligned}$$
(3)

where \({\hat{y}}_i\) represents the prediction value of AGB, \(y_i\) is the true value of AGB, and n is the number of samples.

Uncertainty analysis

To evaluate the uncertainty of model predictions, we incorporated Monte Carlo simulation into the Stacking Regressor framework. The Monte Carlo method, through repeated random perturbations and resampling, characterizes the variability of model outputs under changes in inputs and parameters, thereby reflecting the confidence intervals of the predictions. In biomass estimation, the presence of nonlinear relationships and complex interdependencies among variables makes it difficult for a single prediction to quantify such uncertainty. Monte Carlo simulation provides an effective approach to address this issue. By performing statistical analyses (e.g., standard deviation, extreme values, and quantiles) on the results of multiple simulations, we were able to systematically characterize the distribution of prediction uncertainty.

Results

Performance of biomass estimation models

To select the optimal biomass estimation model for regions with large-scale spatial heterogeneity, this study employed a Stacking ensemble framework that integrates the advantages of multiple base models through a dual-level optimization mechanism at both the feature and decision levels (Table 3). The results indicate that, in typical ecological study areas of Australia, the Stacking model (\(R^2\) = 0.73) significantly outperforms all individual machine learning models, demonstrating the theoretical suitability of ensemble learning—specifically the Stacking approach—for heterogeneous landscapes. Specifically, DT model exhibited the poorest performance (\(R^2\) = 0.45, RMSE = 71.66 Mg/ha) due to limitations in capturing feature interactions, highlighting the constraints of single models in fragmented habitats. Compared with the relatively optimal single model, RF model (\(R^2\) = 0.72), Stacking reduced RMSE by 0.96 Mg/ha (a 1.86% decrease), and by 21.03 Mg/ha (a 29.4% decrease) relative to the worst-performing DT model.

These findings confirm that Stacking, through a bias–variance trade-off mechanism, effectively mitigates the fitting risks of individual machine learning models across diverse ecological regions, offering a novel theoretical pathway for developing robust regional carbon estimation paradigms.

Table 3 Performance metrics of various regression models for biomass estimation, including \({R}^2\), RMSE, and MAE. The Stacking model achieves the highest accuracy, demonstrating its superior effectiveness in enhancing predictive performance compared with individual machine learning models (best results are highlighted in bold, and the second-best results are italics).
Full size table

Model feature selection

To address the modeling uncertainty arising from redundancy in high-dimensional ecological features, this study proposes a“feature selection-ensemble learning” collaborative optimization framework.Initially, 37 image feature parameters were selected with the aim of improving AGB estimation accuracy through the integration of diverse feature types. However, an excessive number of features can lead to multicollinearity, increased computational complexity, and a higher risk of model overfitting. To evaluate the relationships and significance levels among variables, Pearson correlation analysis (correlation coefficient r range: [-1, 1]) was conducted (Fig. 6). The results revealed strong correlations between various spectral vegetation indices and image bands. Therefore, feature selection proved essential to reduce the number of model parameters. Ultimately, the RFE method was applied, resulting in the selection of 15 features, including four canopy height metrics (25th, 50th, 75th, and 95th), one vegetation index (GNDVI), four spectral bands (B1, B4, B5, and B7), one texture feature (gray_savg), two topographic variables (elevation and slope), and three climatic factors (precipitation, soil temperature, and temperature). Based on the correlation analysis (Fig. 6) and feature selection results: 1. Canopy height remains the most critical predictor of biomass, highlighting that the three-dimensional canopy structure is a fundamental parameter for AGB estimation. 2. The synergistic mechanism of multi-source features and the combination of key parameters validate the cross-scale coupling theory of “terrain-climate-spectral” factors. Specifically, terrain (elevation and slope) governs the large-scale spatial patterns of biomass, climate factors (precipitation/temperature) explain phenology-driven mechanisms, and near-infrared bands (B5/B7) quantify canopy biochemical components. Additionally, GNDVI was identified as an important variable in this study, consistent with previous research, indicating its excellent performance in biomass estimation, particularly in medium- to high-density forests.

Fig. 6
figure 6

Pearson correlation coefficients between AGB and feature variables with significance levels (p-values) (When the correlation coefficient \(|r|> 0.5\), \(*\),\(**\),\(***\) is white; otherwise, it is black; When the significance level is \(0.01 \leqslant p<0.05\), denoted as \(*\), significant; when \(0.001 \leqslant \textrm{p}<0.01\), denoted as \(**\), more significant; when \(\textrm{p}<0.001\), denoted as \(***\), highly significant.).

Full size image

After inputting the optimized feature set into the Stacking ensemble framework (Table 4), our model still achieved the best performance: \(R^2\) = 0.74, RMSE = 49.79 Mg/ha, and MAE = 30.56 Mg/ha. The key findings are as follows: 1. Validation of the ecological response advantage of tree-based models: RF and GBR maintained the strongest performance among individual models after feature optimization (RMSE = 51.00 and 52.18 Mg/ha, respectively), confirming their inherent robustness in mapping heterogeneous environmental parameters. 2. The DT model still performed the worst (\(R^2\) = 0.47, RMSE = 70.38 Mg/ha), owing to its limitations in modeling high-dimensional feature interactions and complex nonlinear relationships, thereby highlighting the inherent deficiencies of a single-tree model in complex ecosystems. 3.Superiority of the Stacking model: Compared with the best single model (RF), the Stacking model further reduced RMSE by 1.21 Mg/ha (a 2.4% decrease), demonstrating an enhanced capacity for regional biomass estimation beyond that of individual models. This collaborative framework successfully establishes a dual-path optimization paradigm of “feature compression–model fusion”, providing a novel perspective for biomass estimation.

In addition, independent validations were conducted using data from different years to evaluate the robustness of our model. The results demonstrated that the model maintained consistently high and stable performance across all tested years. Specifically, we divided the data by year, selecting five individual years from 2007 to 2011. For each iteration, data from four years were used for model training, while data from the remaining year were used for validation to assess model accuracy. Among all five years, our model consistently achieved the highest predictive accuracy, followed by the RF and GBR models (Table 5). The \(R^2\) values of the RF model were only 0.01 lower than ours during 2008–2011. However, in 2007, the \(R^2\) of the RF model decreased by 0.03, and the RMSE increased by 1.86 Mg/ha. For the GBR model, its \(R^2\) was 0.01–0.02 lower than ours during 2007–2009. In 2010 and 2011, the \(R^2\) values were 0.05 and 0.04 lower, respectively, with corresponding increases in RMSE of 4.56 Mg/ha and 3.87 Mg/ha.

Table 4 Results of biomass estimation using various regression models after RFE-based feature selection. The Stacking model achieved the highest performance with an \({R}^2\) of 0.74, while RF and GBR also performed well. The metrics include \({R}^2\), RMSE, and MAE for each model (best results are highlighted in bold, and the second-best results are italics).
Full size table
Table 5 Annual comparison of biomass estimation performance across various regression models from 2007 to 2011. The results show that some models demonstrate high stability and accuracy, with the Stacking model consistently exhibiting superior predictive capability over the others (best results are highlighted in bold, and the second-best results are italics).
Full size table

Spatial distribution and uncertainty analysis of biomass

We selected three models (Stacking model, GBR, RF) with relatively high predictive performance to estimate aboveground biomass, aiming to reveal their estimation potential at a large regional scale. The results included scatter plots of model predictions (Fig. 7), spatial distribution maps of AGB (Fig. 8) , and AGB uncertainty and relative uncertainty maps (Fig. 9).

Fig. 7
figure 7

Comparison of biomass estimation accuracy under the framework of ensemble learning. The Stacking model is compared with individual machine learning algorithms (GBR and RF). Scatter density plots of observed versus predicted values are shown for GBR, RF, and the Stacking model. The Stacking model achieves the best performance (\({R}^2\) = 0.74), with predictions closer to the 1:1 line and smaller errors. GBR and RF exhibit slightly lower accuracy, but overall trends are consistent. The color gradient represents predicted biomass values, illustrating the distribution characteristics of each model across different AGB ranges.

Full size image
Fig. 8
figure 8

Maps of aboveground biomass in Australia predicted by three models: (a) stacking model, (b) GBR, and (c) RF. All models consistently show higher AGB in the eastern and southwestern regions and lower AGB in the central and western regions, reflecting spatial patterns influenced by precipitation and topography.

Full size image

As shown in Fig. 8, we observed that the three models exhibited similar trends in spatial distribution. The eastern and southwestern regions of the study area have higher biomass, while the central and western regions exhibit lower biomass. The uneven distribution of precipitation is the primary cause of this spatial heterogeneity. The Great Dividing Range in Australia stretches for thousands of kilometers along the eastern coast, playing a significant role in uplifting precipitation and forming a relatively moist local climate at higher altitudes, which contributes to the lush forests in eastern Australia (AGB ranging from 100 to 300 Mg/ha). The mountain range also blocks the warm, moist air from the Pacific, resulting in a significant reduction in precipitation on the western side of the mountains, leading to a marked decline in biomass (AGB ranging from 40 to 100 Mg/ha). Secondly, the hilly areas in the southwestern region also exhibit relatively high AGB levels (ranging from 40 to 300 Mg/ha), which can be attributed to the influence of the South Indian Ocean monsoon and local maritime climate that together create favorable conditions for vegetation growth. In contrast, the central region of Australia is dominated by vast basins and desert landscapes with poor soil water retention, coupled with extremely low annual precipitation and high evaporation, resulting in very low biomass (AGB ranging from 0 to 30 Mg/ha). The Stacking model predicted a biomass range from 0 to 307.14 Mg/ha, while the GBR and RF models predicted biomass ranges of 0 to 306.7 Mg/ha and 0 to 279.03 Mg/ha, respectively.

The uncertainty metrics of the Stacking model are presented in Fig. 9. Figure 9 (1) shows the prediction standard deviation, where larger values indicate greater variability of pixel-level predictions, i.e., higher uncertainty, whereas smaller values suggest more stable predictions. Overall, the uncertainty values are primarily concentrated within 0–20 Mg/ha, accounting for as much as 99.95%, which indicates that the predictions are generally stable and associated with high confidence. Figure 9 (2) and (3) display the lower (minimum) and upper (maximum) bounds of the predictions, respectively. Figure 9 (4) and (5) present the 25th and 75th percentile, which describe the interquartile range of the prediction distribution. Together, these statistics provide a more comprehensive understanding of the uncertainty range in regional biomass estimation. Figure 9 (6) illustrates the distribution of relative uncertainty, showing that most areas exhibit extremely low relative uncertainty, further confirming the robustness of the model predictions.

Fig. 9
figure 9

Uncertainty metrics of the Stacking model shown across six visualizations. (1) The predicted standard deviation indicates variability, with values mainly concentrated between 0–20 Mg/ha, reflecting relatively high confidence. (2) The minimum predicted boundary and (3) the maximum predicted boundary provide key insights into the prediction range. (4) and (5) show the 25th and 75th percentiles, respectively, illustrating the interquartile range of predictions. (6) Depicts the distribution of relative uncertainty, indicating that most areas exhibit low uncertainty, which reinforces the robustness of the model for regional biomass estimation.

Full size image

Comparison with other AGB maps

We compared our three predicted AGB maps with other existing biomass products (Fig. 10). We calculated the mean and standard deviation of the spatial differences between our model predictions and the existing products were calculated (Table 6). Compared with our results, the “Avitabile” map shows higher AGB values, while the “Spawn” product shows relatively lower values. The mean spatial differences between our three AGB maps and the “Avitabile” product range from –18.59 to –17.82 Mg/ha, while those with the “Spawn” product range from 14.99 to 15.48 Mg/ha. The standard deviation of the spatial differences between our maps and the two existing products ranges from 21.90 to 26.17 Mg/ha.

Fig. 10
figure 10

Comparative validation of Australian biomass estimation based on multi-source remote sensing fusion and different modeling approaches. The spatial consistency of AGB products from the Stacking model, RF, and GBR is compared with existing global products. The first column shows the comparison with the “Avitabile” dataset, while the second column shows the comparison with the “Spawn” dataset. The main panels depict the spatial distribution of differences, and the insets present histograms of difference frequencies.

Full size image

We conducted spatial correlation analyses between each of our three biomass distribution maps and two existing biomass products (as shown in Table 7). The results indicate that our products exhibit high overall spatial correlations with the other two datasets, demonstrating consistency in the spatial variation patterns of biomass.

Table 6 Mean error and standard deviation of biomass estimates from three different models compared with existing remote sensing products (“Avitabile” and “Spawn”). The table highlights the mean differences in biomass values, indicating the relative performance of each model with respect to the reference products.
Full size table
Table 7 Correlation coefficients (r) and significance levels (p-values) between biomass products estimated by the Stacking, GBR, and RF models and two global biomass products (“Avitabile” and “Spawn”). The high correlations indicate strong consistency in the spatial distribution patterns of biomass across different datasets.
Full size table

Discussion

Influence of feature variable selection on aboveground biomass estimation

Feature variable selection plays a critical role in the modeling of aboveground biomass estimation. In this study, a total of 37 image features were initially considered, including spectral reflectance, vegetation indices, topographic factors, texture information, and climatic variables. These features collectively provided comprehensive information across spectral, biophysical, and structural dimensions, while also incorporating key environmental conditions that influence vegetation growth. However, an excessive number of variables can introduce multicollinearity, increase model complexity, and elevate the risk of overfitting. To address this, the RFE method was employed to select 15 optimal variables from the initial 37. This feature reduction enhanced model robustness and generalizability.

Among the selected variables, canopy height percentiles (25th, 50th, 75th, and 95th) exhibited strong correlations with AGB and emerged as critical predictors—findings consistent with previous studies that emphasize the close relationship between tree height and carbon storage capacity82,83. Notably, the inclusion of GNDVI highlighted the utility of spectral indices in monitoring medium- to high-density vegetation. Compared to traditional NDVI, GNDVI offers improved resistance to saturation, particularly in closed-canopy forests84,85. The selection of topographic factors, specifically elevation and slope, supports the role of the Great Dividing Range in modulating hydrothermal gradients across eastern Australia. In addition, the inclusion of climate variables (precipitation, soil temperature, and air temperature) reflects the significant influence of environmental heterogeneity on vegetation growth at the continental scale. It is worth noting that climatic variables are typically excluded in studies conducted over small or localized regions, but they are especially relevant and informative in large-scale biomass mapping efforts. Furthermore, the study found that texture features also contributed meaningfully to the model, indicating that spatial heterogeneity can effectively complement spectral information. Texture metrics such as those derived from the GLCM are capable of capturing spatial arrangements of surface features—such as patch size, vegetation density variation, and edge transitions—that are not easily detected by spectral data alone86. Following feature selection, the model’s RMSE was reduced by 0.84 Mg/ha, validating the effectiveness of parameter simplification in mitigating overfitting. However, this also underscores the need for future development of advanced techniques to detect and model feature interactions, which may further enhance predictive accuracy and model interpretability.

Robustness analysis of the method

Our biomass estimation model exhibits strong robustness across multiple dimensions. First, we incorporated diverse data sources during model construction, including Landsat imagery, SRTM-derived topographic data, climate information, and canopy height data provided by TERN. This multi-source data fusion strategy effectively addressed the limitations of single-source datasets in terms of spatial coverage and information diversity, thereby enhancing the model’s adaptability to complex environmental conditions87,88.

Second, we employed a Stacking regression model based on ensemble learning, integrating multiple heterogeneous base learners. Compared to single machine learning models, the Stacking approach leverages the strengths of individual learners to reduce both variance, thus improving overall prediction accuracy and robustness89,90. Our experimental results demonstrates that the Stacking model consistently outperformed individual models across different forest types (Table 8). Specifically, the \(R^2\) values were improved by 0.01 to 0.28 in shrublands and 0.02 to 0.35 in broadleaf forests. This indicates that the Stacking method can effectively adapt to varying biomass distribution patterns and possesses strong generalization capability. Moreover, we conducted independent validation using datasets from different years. The Stacking model maintains consistently high and stable prediction performance over time, further confirming its temporal robustness.

Table 8 Comparison of accuracy metrics for various biomass estimation models in shrubland and broadleaf forest. The Stacking model consistently demonstrates superior performance in terms of \({R}^2\), RMSE, and MAE, highlighting its effectiveness in biomass estimation compared with individual models (best results are highlighted in bold, and the second-best results are italics).
Full size table

In addition, feature selection further contributes to model robustness. By applying the RFE method, we reduce the original 37 features to 15 optimal variables. This not only enhances the model’s predictive accuracy but also reduced its complexity, which improves interpretability and operational stability. Even after feature reduction, the Stacking model achieves an \(R^2\) of 0.74, underscoring the importance of feature engineering in improving model robustness.

In summary, this study systematically enhanced the robustness of biomass estimation through multi-source data integration, ensemble learning, and optimized feature selection. The proposed Stacking model demonstrates strong and stable predictive performance across different forest types and time periods, providing a reliable technical foundation for biomass mapping at broader spatial and temporal scales. This is particularly valuable for supporting ecological carbon sink monitoring and management. Nevertheless, future research should explore the integration of ecological process mechanisms into data-driven models to further improve the accuracy and interpretability of biomass estimation91.

Analysis of spatial distribution differences and uncertainty

This study not only produces a high-resolution spatial distribution map of aboveground biomass, but also systematically analyzed both the absolute and relative uncertainties of model predictions. Furthermore, the results are compared with two AGB products—“Avitabile” and “Spawn”—through difference and correlation analyses.

The findings indicate that our predicted AGB product shows higher biomass values in the eastern tropical rainforest region and the southwestern forested zone, while substantially lower values are observed in the central arid areas. This pattern of spatial heterogeneity is consistent with previous studies and observed climatic conditions, thereby enhancing the credibility of the model. Comparisons with the “Avitabile” and “Spawn” datasets further confirm the advantages of our model in structurally complex regions. The mean difference between our product and the Spawn dataset was approximately 15 Mg/ha, whereas the difference with the “Avitabile” dataset was around -18 Mg/ha. Despite these systematic biases, a high spatial correlation (Pearson’s r > 0.80) is observed between the products, indicating strong consistency in spatial trends92.

Our results indicate that combining ensemble learning with Monte Carlo simulation provides an effective approach for characterizing uncertainty in biomass estimation. The study shows that, although uncertainty is relatively high in a few regions (e.g., humid areas in the eastern part), the standard deviation and relative uncertainty for the vast majority of pixels remain low (Fig. 9 (1) and (6)), indicating strong stability and reliability of the model for large-scale predictions. The spatial distributions of the minimum and maximum values (Fig. 9 (2) and (3)) as well as the 25th and 75th percentiles (Fig. 9 (4) and (5)) further reveal the prediction range across different regions. Relative uncertainty is slightly higher in arid and data-sparse regions, while it is lower in humid forest areas, which can be attributed to the distribution of training samples across ecological zones and terrain complexity.

Compared with traditional point-estimate methods, Monte Carlo simulation not only provides mean predictions but also reveals prediction intervals and probability distributions, offering more informative references for subsequent forest resource management and carbon stock assessment. However, the Monte Carlo approach has certain limitations. First, it is computationally intensive, particularly when applied to large-scale, high-resolution raster data, as a large number of iterations are required to obtain stable distribution estimates. Second, Monte Carlo simulation assumes that input error distributions are known and independent, whereas in practice, correlations among different remote sensing features may exist, potentially leading to under- or overestimation of uncertainty. Finally, for boundary regions or data-sparse areas (e.g., the white regions in Fig. 9 (2)), simulation results may be constrained by insufficient training samples, affecting the reliability of local predictions. Therefore, incorporating additional auxiliary data or adopting spatially correlated modeling in these regions may further improve the robustness of predictions and the accuracy of uncertainty characterization.

Limitations

This study presents several challenging technical limitations in vegetation biomass modeling in Australia. First, due to current technological constraints and monitoring costs, the sample plot data primarily cover woody vegetation, making it difficult to obtain large-scale ground truth data for non-woody vegetation such as grasslands and croplands. At the same time, we added 1,550 zero-biomass plots for field validation, which may introduce systematic bias (e.g., sparse vegetation or young trees being misclassified as zero). This data gap may affect the model’s generalization capability in complex ecosystems. Second, although machine learning models perform well in data-driven modeling, the physical mechanisms underlying vegetation biomass formation (e.g., carbon cycle dynamics and species interactions) have not been fully integrated into the model framework. Mechanistic modeling requires the integration of knowledge from multiple disciplines, such as ecology and remote sensing, posing a significant challenge. While this study provides a feasible pathway for large-scale biomass estimation, improving model accuracy still requires overcoming key technical bottlenecks, including multi-source data fusion in heterogeneous environments and the integration of mechanistic and data-driven modeling. Addressing these challenges necessitates continuous methodological innovation and cross-disciplinary collaboration.

Conclusion

Based on field plot data from Australia, this study integrates Landsat imagery, vegetation canopy height data, and auxiliary variables such as meteorological and topographic information. After applying RFE for feature selection, three high-performing models are used to develop aboveground biomass estimation models for the Australian continent. The main conclusions are as follows:

1.Our results demonstrates that for large-scale regions with high spatial heterogeneity, in addition to conventional vegetation indices and spectral bands, topographic and climatic variables also play a critical role in biomass estimation.

2. In this study, the Stacking regression model outperformed all individual models in estimating AGB. It consistently achieved the best performance across different forest types and data splitting scenarios, demonstrating strong robustness. The Stacking model yielded an \(R^2\) of 0.74 and an RMSE of 49.79 Mg/ha. Compared with previous studies, this work highlights the advantage of combining multi-source remote sensing data with ensemble learning approaches.

3. We selected the top three performing models—Stacking models, GBR, and RF—to generate regional AGB maps. The results revealed significant spatial heterogeneity in biomass distribution across Australia, with higher AGB values mainly concentrated in the eastern coastal and southwestern regions. In addition, AGB uncertainty analysis indicated that the model maintained strong predictive stability in high-biomass areas.

However, the lack of long-term tree height data remains a limiting factor for accurately estimating AGB over extended time periods. This study provides a valuable reference for applying multi-source remote sensing data and ensemble modeling to AGB estimation in data-scarce or monitoring-limited environments.