Introduction

In the context of the rapid advancements being made in energy storage technologies, high-capacity and high-rate Li-ion battery energy storage systems (BESS) are being increasingly deployed in grid-scale applications. This development imposes stricter demands on system safety and efficiency. Thermal management systems (TMS) are of critical importance in ensuring safe, efficient, and reliable operation of BESS. Firstly, it is important to note that temperature has a significant impact on the performance of Li-ion batteries. Low temperatures can severely degrade the capacity and efficiency of the battery, while elevated temperatures can accelerate internal chemical reactions, leading to electrolyte decomposition, electrode structural degradation, and accelerated capacity and lifetime fade1. Secondly, temperature directly correlates with battery safety risks: lithium dendrite growth at low temperatures may puncture separators, causing internal short circuits, whereas extreme heat can trigger thermal runaway reactions, resulting in catastrophic failures such as explosions2.

A plethora of thermal management strategies have been employed for Li-ion batteries, including air cooling, liquid cooling, phase change cooling, and heat pipe cooling3,4. Phase change and heat pipe cooling have been shown to exhibit superior thermal regulation; however, their complex structures, high costs, and technological immaturity currently limit their use to laboratory-scale research5,6. Conversely, air cooling, which is distinguished by its structural simplicity and cost-effectiveness, has become a prevalent method in energy storage systems7. However, its low heat transfer coefficient restricts its applicability to low-rate systems (e.g., 0.3P–0.5P, where P denotes the rated power of the battery, with 0.3P–0.5P representing 30–50% of the rated power of the battery operation range). In contrast, liquid cooling offers higher efficiency and cost-effectiveness, emerging as a preferred solution for large-capacity, high-energy-density, and high-rate BESS8. A typical liquid-cooled TMS consists of chillers, piping networks, cold plates, and coolant (50% water + 50% ethylene glycol). The key factors influencing thermal performance include the geometry of the cold plate channels, the flow rate of the coolant, and the temperature of the coolant.

A substantial body of research has been dedicated to the enhancement of the thermal performance of liquid cooling systems. Xiao et al.9 proposed a bidirectional equal-length channel cold plate, wherein the channel width, spacing, and coolant flow velocity were optimized to enhance heat dissipation efficiency. In a similar vein, Wang et al.10 have devised liquid-cooled structures with both vertical and horizontal cold plate orientations. Through finite element simulations, they analyzed the impacts of coolant velocity, temperature, channel quantity, and inlet orientation under constant-flow conditions, proposing a variable flow rate strategy to balance cooling efficiency and energy consumption. In a further study, Luo et al.11 developed a serpentine-channel cold plate that combines series-connected reverse-flow and parallel-branch configurations. Numerical simulations revealed the effects of channel geometry, system layout, and inlet velocity on battery module thermal behavior. Kang et al.12 evaluated a range of cold plate designs (horizontal-parallel, S-shaped, stepped, and vertical-parallel), identifying optimal channel structures by assessing inlet diameter, wall thickness, and coolant temperature. However, these studies predominantly employed small-capacity cells and compact modules, with certain configurations facing practical implementation challenges.

The present study investigates thermal management of industrially relevant high-capacity, high-rate liquid-cooled battery modules. Through orthogonal experimental design, we systematically explore the effects of serpentine-channel geometry (depth: 3–6 mm, width: 26–32 mm) and coolant parameters (inlet flow rate: 1.413 L/min–2.826 L/min, inlet temperature range: 16–26 °C) on thermal performance.

* “All si mulations were conducted using Dassault Systems SolidWorks (Version 2022 SP5) for 3D modeling and STAR-CCM+ (Version 2306) for computational fluid dynamics analysis.” *.

Liquid-cooled battery module thermal structure and orthogonal experimental design

Thermal structure of liquid-cooled battery module

As demonstrated in Fig. 1, the Liquid-cooled battery module integrates a 1P52S configuration (52 cells in series) with individual cells having a rated capacity of 314 Ah and an aluminium alloy cold plate. The module provides 52.25 kW (1P) and an energy capacity of 52.25 kWh. The cold plate, which is positioned in direct contact with the cell bases, incorporates serpentine flow channels. These channels are connected via a piping network to a chiller unit, forming a closed-loop cooling system. During operation, the coolant, driven by the chiller, enters the cold plate inlet, traverses the serpentine channels beneath the cells, absorbs heat through convective exchange, and exits through the outlet to return to the chiller for recirculation.

Fig. 1
figure 1

Liquid-cooled battery module and its thermal management structure.

Full size image

The cross-sectional configuration of the serpentine-channel cold plate is illustrated in Fig. 2, where channel width (L) is 26 mm, channel depth (D) is 3 mm, plate thickness (T) is 8 mm, and channel spacing (S) is 17 mm. The cold plate, with dimensions of 1024 mm (length) × 724 mm (width), consists of a base plate and a cover plate. The flow channels on the base plate are fabricated via an aluminium extrusion process, while the cover plate is hermetically bonded to the base plate through welding. During thermal operation, the coolant circulates within the enclosed channels, transferring heat to the cover plate via forced convection. Consequently, the cooled cover plate facilitates the conductive thermal exchange process, thereby enabling the effective regulation of the cell temperature.

Fig. 2
figure 2

Cross-sectional view of serpentine liquid-cooled plate channel width (L), channel depth (D), plate thickness (T), channel spacing (S).

Full size image

Orthogonal experimental design

The temperature characteristics of the liquid-cooled battery module are primarily influenced by four factors: cold plate channel depth, channel width, coolant inlet velocity, and coolant inlet temperature. It is acknowledged that the coolant inlet temperature exerts a significantly greater influence than other parameters; therefore, this study first establishes the optimized cold plate structural parameters (channel dimensions) and coolant flow velocity under a fixed inlet temperature (22 °C) through orthogonal experimental methodology. The experimental matrix, as outlined in Table 1, encompasses four factors with the following levels:

Factor 1: Channel depth (3 mm, 4 mm, 5 mm, 6 mm)

Factor 2: Channel width (26 mm, 28 mm, 30 mm, 32 mm)

Factor 3: Coolant inlet flow rate (1.413 L/min, 1.884 L/min, 2.355 L/min, 2.826 L/min)

Factor 4: Coolant inlet temperature (fixed at 22 °C)

Subsequently, the influence of coolant inlet temperature (16 °C, 18 °C, 20 °C, 22 °C, 24 °C, 26 °C) on thermal performance is investigated, to balance chiller energy consumption and cooling efficacy, based on the optimized channel geometry and flow velocity.

Table 1 Orthogonal experimental matrix (inlet temperature: 22 °C).
Full size table

Thermal simulation methodology

Governing equations

A three-dimensional model of the liquid-cooled battery module is established using Siemens STAR-CCM + simulation software to perform numerical simulations of the temperature field. The governing equations employed in the simulations (the continuity equation, momentum equation, and energy equation) are formulated as follows.

$$\:\frac{{\partial\:}_{\mu\:}}{{\partial\:}_{x}}+\frac{{\partial\:}_{\nu\:}}{{\partial\:}_{y}}+\frac{{\partial\:}_{\omega\:}}{{\partial\:}_{z}}=0$$
(1)
$$\:\left\{\begin{array}{c}\rho\:(\frac{\partial\:u}{\partial\:\tau\:}+u\frac{\partial\:u}{\partial\:x}+\nu\:\frac{\partial\:u}{\partial\:y}+w\frac{\partial\:u}{\partial\:z})={f}_{x}-\frac{\partial\:P}{\partial\:x}+\mu\:(\frac{{\partial\:}^{2}u}{\partial\:{x}^{2}}+\frac{{\partial\:}^{2}u}{\partial\:{y}^{2}}+\frac{{\partial\:}^{2}u}{\partial\:{z}^{2}})\\\:\rho\:(\frac{\partial\:v}{\partial\:\tau\:}+u\frac{\partial\:v}{\partial\:x}+\nu\:\frac{\partial\:v}{\partial\:y}+w\frac{\partial\:v}{\partial\:z})={f}_{y}-\frac{\partial\:P}{\partial\:y}+\mu\:(\frac{{\partial\:}^{2}v}{\partial\:{x}^{2}}+\frac{{\partial\:}^{2}v}{\partial\:{y}^{2}}+\frac{{\partial\:}^{2}v}{\partial\:{z}^{2}})\\\:\rho\:(\frac{\partial\:w}{\partial\:\tau\:}+u\frac{\partial\:w}{\partial\:x}+\nu\:\frac{\partial\:w}{\partial\:y}+w\frac{\partial\:w}{\partial\:z})={f}_{z}-\frac{\partial\:P}{\partial\:z}+\mu\:(\frac{{\partial\:}^{2}w}{\partial\:{x}^{2}}+\frac{{\partial\:}^{2}w}{\partial\:{y}^{2}}+\frac{{\partial\:}^{2}w}{\partial\:{z}^{2}})\end{array}\right.$$
(2)
$$\:\rho\:C(\frac{{\partial\:}_{T}}{{\partial\:}_{t}}+\mu\:\frac{{\partial\:}_{T}}{{\partial\:}_{x}}+\nu\:\frac{{\partial\:}_{T}}{{\partial\:}_{y}}+\omega\:\frac{{\partial\:}_{T}}{{\partial\:}_{z}})=\lambda\:\left(\frac{{\partial\:}_{T}^{2}}{{\partial\:}_{{x}^{2}}}+\frac{{\partial\:}_{T}^{2}}{{\partial\:}_{{y}^{2}}}+\frac{{\partial\:}_{T}^{2}}{{\partial\:}_{{z}^{2}}}\right)+\dot{\phi\:}$$
(3)

In the equations, u, v, and w represent the coolant velocity components in the x-, y-, and -z directions, respectively (L/min); ρ denotes the fluid density (kg/m³); f signifies the volumetric force (N); and µ indicates the dynamic viscosity coefficient of the coolant (Pa·s); C corresponds to the specific heat capacity (J/(kg·K)); λ represents the thermal conductivity (W/(m·K)); and \(\:\dot{\phi\:}\) denotes the volumetric heat source term (W).

Geometric modeling and mesh generation

The geometric model of the liquid-cooled battery module was developed in Siemens STAR-CCM+. The battery cells are modelled as rectangular prisms (174 mm × 204 mm × 72 mm). Simplifications are applied to minor geometric features such as fillets and chamfers in both cells and cold plate channels. A polyhedral mesh scheme is adopted, with distinct strategies for solid and fluid domains:

Solid regions (battery cells and cold plate): Surface wrapping and polyhedral mesh generators are employed to ensure geometric fidelity.

Fluid regions (coolant channels): Surface wrapping, polyhedral meshing, and prism layer generators are utilized, with boundary layer refinement applied near channel walls to resolve viscous flow gradients.

Key modeling assumptions are as follows:

Temperature-independent material properties: The thermal conductivity, specific heat capacity, and density of the battery cells, the cold plate, and the coolant (50:50 (v/v) water-ethylene glycol aqueous solution) are assumed to be constant and independent of temperature.

Negligible contact thermal resistance: Thermal resistance at the interfaces between adjacent battery cells and between the battery cells and the cold plate is assumed to be negligible. This implies that perfect thermal contact is assumed at these interfaces. It is noted that thermal grease is applied at the actual interfaces in practice.

Coolant model: The coolant is modeled as an incompressible Newtonian fluid.

The final meshed configuration of the liquid-cooled battery module is illustrated in Fig. 3, with an average skewness below 0.45 and orthogonality exceeding 0.85, ensuring numerical stability and convergence. During meshing, the maximum y⁺ value is 15.5, the maximum skewness is 0.75, the average skewness is less than 0.3, the average aspect ratio of the grid is 7.1, and only 1.5% of the grid cells exceeded an aspect ratio of 30.

Fig. 3
figure 3

Mesh generation of liquid-cooled battery module.

Full size image

Mesh independence verification was conducted by means of a comparison of simulated Tmax and the minimum temperature (Tmin) of the battery module under five mesh densities, as summarized in Table 2. The results obtained from this process indicate that when the total mesh count exceeds 1,551,330, Tmax and Tmin stabilise (variation < 0.2%), thus confirming numerical convergence and independence from further mesh refinement. For this configuration, the minimum mesh size in the cell regions was set to 5 mm, while the cold plate and coolant fluid domains were discretized with a minimum element size of 2 mm. This mesh sizing strategy was adopted for all subsequent simulations of variant cold plate geometries to ensure computational accuracy and efficiency.

Table 2 Mesh independence verification of the liquid-cooled battery module simulation model.
Full size table

Thermophysical properties and boundary conditions

In the simulation model, battery cells were assumed to generate uniform volumetric heat. The heat generation rate q is calculated using electrochemical-thermal coupling model of Bernardi13,14, expressed as:

$$\:q=\frac{I}{V}\left[\left({U}_{0}-U\right)-T\frac{{dU}_{0}}{{d}_{T}}\right]$$
(4)

where I is the discharge current (A); V denotes the cell volume (m³); U0 represents the open-circuit voltage (V); U is the terminal voltage (V); T signifies the temperature (K); and\(\:\:\frac{{dU}_{0}}{{d}_{T}}\) corresponds to the temperature coefficient of the open-circuit voltage (V/K).

Thermophysical properties of the battery cell (Model: PF 173–314 A; Manufacturer: Cornex New Energy Co., Ltd.), aluminum alloy cold plate, and the coolant composition is specified as 50:50 (v/v) water-ethylene glycol aqueous solution are summarized in Table 3, including density (ρ), specific heat capacity (Cp), thermal conductivity (λ), and viscosity (µ).

Table 3 Simulation parameters of battery module.
Full size table

It is assumed that the thermophysical parameters do not change with temperature. The simulation initial conditions are configured as follows:

Ambient temperature: 25 °C

Initial module temperature: 25 °C

Coolant inlet: Velocity inlet boundary condition

Coolant outlet: Pressure outlet boundary condition (gauge pressure: 0 Pa).

Battery thermal model validation

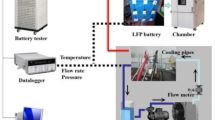
To validate the thermal simulation model, experimental temperature measurements of a single battery cell under identical operating conditions were compared with simulation results. The test cell (Model: PF 173–314 A; Manufacturer: Cornex New Energy Co., Ltd.) has a rated capacity of 314 Ah and nominal voltage of 3.2 V. As illustrated in Fig. 4, the experimental setup consists of:

Battery cycler (Dahua Pinnacle Tech., PEBC 05-300; Voltage: 0–5 V, Current: ± 300 A).

Thermal chamber (Giant Force, ECT-150-40-CP-AR; Range: −20 to + 80 °C).

Data acquisition system (CTS monitor software):

The cell was maintained at 25 ± 2 °C within the thermal chamber and charged at constant power (1004.8 W, 1 P). Simulation parameters mirrored experimental conditions, with temperature monitoring points at the geometric center of the cell’s largest surface area. Voltage and temperature data were recorded by the cycler and processed via CTS monitor.

Experimental procedure:

Rest: Stabilize the cell at 25 ± 2 °C for 2 h

Discharge: 1P discharge to cutoff voltage (2.5 V)

Rest: 2 h idle

Charge: 1P charge to cutoff voltage (3.65 V)

As shown in Fig. 5, simulated temperature profiles exhibit strong agreement with experimental data (maximum deviation: 0.6 °C), confirming model fidelity for subsequent liquid-cooled module simulations.

Fig. 4
figure 4

Schematic of the single-cell experimental setup with annotated components.

Full size image
Fig. 5
figure 5

Temperature testing and simulation results comparison of the battery cell.

Full size image

Results and analysis

Temperature field simulation results of liquid-cooled battery module

As demonstrated in Fig. 6, the temperature field simulation results of the battery module with a Liquid-cooling plate channel depth of 3 mm are illustrated. When the coolant inlet temperature is set at 22 °C, Simulation 4 (channel width: 32 mm, inlet flow velocity: 2.826 L/min) demonstrated the Tmax (42.0 °C) and temperature difference (ΔT) (19.3 °C) within the battery module. In contrast, Simulation 1 (channel width: 26 mm, inlet flow velocity: 1.413 L/min) exhibit the highest Tmax (45.0 °C) and ΔT (22.0 °C). The low-temperature zone is observed in proximity to the coolant inlet, while the high-temperature zone is located at the coolant outlet. This distribution arises because the coolant temperature is lowest at the inlet, gradually increasing as it flows through the channel and exchanges heat with the battery cells. Consequently, the thermal gradient (∇T) between the coolant and battery module diminishes along the flow direction, resulting in reduced cooling capacity and higher battery temperatures near the outlet.

Fig. 6
figure 6

Temperature field simulation results of the battery module under flow channel depths of 3 mm.

Full size image

As demonstrated in Fig. 7, the simulation results for a Liquid-cooling plate channel depth of 4 mm with an identical inlet temperature (22 °C) are presented. Simulation 7 (channel width: 30 mm, inlet flow velocity: 2.826 L/min) achieved the lowest Tmax (42.4 °C) and ΔT (19.5 °C), whereas Simulation 6 (channel width: 28 mm, inlet flow velocity: 1.413 L/min) displayed the highest values (45.3 °C and 22.1 °C, respectively). The findings of this study demonstrate that an increase in the depth of the channel results in elevated Tmax and ΔT in the battery module. This phenomenon is attributed to the augmented channel cross-sectional area under constant inlet flow velocity conditions, which concomitantly diminishes coolant flow velocity and consequently undermines the system capacity for heat dissipation.

Fig. 7
figure 7

Temperature field simulation results of the battery module under flow channel depths of 4 mm.

Full size image

As illustrated in Fig. 8, the temperature field simulation results of the battery module with a Liquid-cooling plate channel depth of 5 mm and a coolant inlet temperature of 22 °C are presented. Simulation 10 (channel width: 28 mm, inlet flow velocity: 2.826 L/min) yielded the lowest Tmax (43.2 °C) and ΔT (20.2 °C), while Simulation 11 (channel width: 30 mm, inlet flow velocity: 1.413 L/min) exhibited the highest values (46.6 °C and 23.3 °C, respectively).

Fig. 8
figure 8

Temperature field simulation results of the battery module under flow channel depths of 5 mm.

Full size image

As illustrated in Fig. 9, the simulation results for a channel depth of 6 mm are presented under conditions of identical inlet temperature (22 °C). Simulation 13 (channel width: 26 mm, inlet flow velocity: 2.826 L/min) achieved the minimum Tmax (44.0 °C) and ΔT (20.9 °C), whereas Simulation 16 (channel width: 32 mm, inlet flow velocity: 1.413 L/min) show the maximum values Tmax (47.2 °C) and ΔT (23.7 °C). These results further corroborate the inverse relationship between cooling performance and channel depth under fixed inlet flow velocity conditions, as increased cross-sectional area reduces coolant velocity and heat dissipation efficiency.

Fig. 9
figure 9

Temperature field simulation results of the battery module under flow channel depths of 6 mm.

Full size image

Comparative analysis of battery module temperature fields under different influencing factors

The orthogonal experimental results based on the Tmax of the liquid-cooled battery module are summarized in Table 4.

Table 4 Statistical results of orthogonal experiments based on maximum temperature (inlet temperature: 22 °C).
Full size table

The results of the orthogonal experiment, based on the Tmax of the liquid-cooled battery module, are summarized in Table 4. In this analysis, the mean value Aij for any column is calculated as the sum of experimental results corresponding to the bracketed index i (i = 1, 2, 3, 4) divided by the number of occurrences of i (in this orthogonal design, i occurs 4 times per column), where j denotes the column number (j = 1, 2, 3). The optimal parameter configuration is determined by identifying the lowest mean Tmax, as lower values indicate superior heat dissipation performance.

The range Pj for any column is defined as the difference between the maximum and minimum mean values within that column:

$$\:{P}_{j}=max\left\{{A}_{1j},{A}_{2j},{A}_{3j},{A}_{4j}\right\}-min\left\{{A}_{1j},{A}_{2j},{A}_{3j},{A}_{4j}\right\}$$
(5)

The range Pj quantifies the amplitude of variation in experimental indicators across factor levels, where a larger Pj indicates a stronger influence of factor-level changes on the target metric.

As demonstrated in Table 4, the minimum mean Tmax of the liquid-cooled battery module is observed for A11 (43.325 °C), A22 (44.175 °C), and A43 (42.900 °C). Consequently, the optimal cooling parameters were determined as follows: channel depth = 3 mm, channel width = 28 mm, and coolant inlet velocity = 2.826 L/min. The calculated ranges Pj further revealed the hierarchical significance of the influencing factors: coolant inlet velocity > channel depth > channel width.

Table 5 offers a concise overview of the outcomes of the orthogonal experiment, which were based on the ΔT observed in the liquid-cooled battery module. This table provides additional insights into the uniformity of temperature across the module and the effects of variations in geometric parameters and fluid flow conditions.

Table 5 Statistical results of orthogonal experiments based on temperature difference (inlet temperature: 22 °C).
Full size table

As demonstrated in Table 5, the minimum mean ΔT for the liquid-cooled battery module are observed at A11 (20.475 °C), A22 (21.100 °C), and A43 (19.975 °C), which is consistent with the distribution of mean Tmax.

The calculated ranges Pj further confirmed that the hierarchical significance of factors influencing ΔT aligned with the hierarchy for Tmax: coolant inlet velocity > channel depth > channel width.

The orthogonal experimental analysis identified the optimal thermal management parameters for the serpentine-channel liquid-cooled plate as follows:

Channel depth: 3 mm

Channel width: 28 mm

Coolant inlet velocity: 2.826 L/min.

It is noteworthy that a reduction in channel depth below 3 mm results in a substantial increase in flow resistance, consequently elevating the power requirement of the chiller unit. Furthermore, exceeding the inlet velocity of 2.826 L/min necessitates higher chiller power, rendering further velocity increases impractical for energy-efficient operation.

Impact of coolant Inlet temperature on battery module temperature field

As illustrated in Fig. 10, the simulated temperature fields of the battery module are shown under varying coolant inlet temperatures (16–26 °C) for the optimized serpentine-channel liquid-cooled plate configuration (channel depth: 3 mm, width: 28 mm, inlet velocity: 2.826 L/min). The results demonstrate a linear reduction in the module’s Tmax by 2 °C for every 2 °C decrease in coolant inlet temperature. This phenomenon is attributed to enhanced heat dissipation, driven by the increased ∇T between the battery module and the cooled plate at lower inlet temperatures.

However, the ∇T within the module increased progressively with decreasing inlet temperature. Specifically, the lower regions of the battery module, adjacent to the cooling plate, exhibited more pronounced temperature reductions compared to the upper regions, where thermal resistance impeded efficient heat transfer. This observed spatial thermal heterogeneity aligns with the findings of prior studies on thermal management in energy storage systems.

In order to strike a balance between thermal regulation and energy efficiency, it is recommended that adaptive control of coolant inlet temperature be based on ambient conditions. This strategy has been shown to minimize chiller power consumption while maintaining operational safety and temperature uniformity.

Fig. 10
figure 10

Temperature fields of the battery module corresponding to different coolant inlet temperatures.

Full size image

Conclusions

This study systematically investigates the impacts of serpentine-channel geometric parameters (depth/width) and coolant operational conditions (inlet velocity and temperature) on the thermal performance of a Liquid-cooled battery module During 1P charge-discharge cycles. The study’s key findings are summarized as follows.

Quantitative demonstration of parameter hierarchy (velocity > depth > width). Identification of optimal 3 mm/28 mm/2.826 L/min configuration achieving 41.9 °C Tmax with 19.2 °C ∇T. Tmax and ∇T of the battery module has a linear dependence on coolant inlet temperature is established. The core reasons can be analyzed from the following aspects:

1. Channel depth and boundary layer effect.

Although the shallow channel depth of 3 mm reduces the heat transfer area, it significantly decreases the boundary layer thickness, enhancing near-wall fluid perturbation.

2. Synergistic effect of high flow velocity and turbulence intensity.

The inlet flow rate 2.826 L/min elevates the Reynolds number beyond 4000 (calculated based on hydraulic diameter), triggering a fully developed turbulent state. Coupled with the periodic elbow structure of the serpentine channel, this generates vortices; however, the pressure drop increase is partially offset due to the smaller channel cross-sectional area.

3. Flow distribution advantage.

The width of 28 mm balances flow uniformity and flow resistance within the serpentine channel.

Fundamental mechanism: The configuration of shallow channel depth (3 mm) + high inlet flow velocity (2.826 L/min) sacrifices a portion of the heat transfer area to achieve stronger turbulent perturbation and boundary layer disruption, while the 28 mm width optimizes flow uniformity in the serpentine structure. This combination is particularly suitable for the transient cooling demands of high-heat-density battery modules.

Current limitations primarily stem from:

Absence of multi-module coupling effects in simulations. Deviations between modeling assumptions (e.g., constant material properties) and physical realities.

Future investigations should:

Incorporate temperature-dependent thermophysical property curves to enhance simulation fidelity, and implement hybrid structures (e.g., 45° oblique ribs) for ∇T reduction below 15 °C. Develop phase-change-material integration strategies compatible with > 3 C fast-charging. Conduct thermo-hydraulic-mechanical multi-objective optimization.