Introduction

Motivation

The increasing complexity of modern life and the depletion of fossil fuel reserves have driven a substantial rise in global energy demand, leading to more frequent power losses and voltage fluctuations in electrical distribution networks. This growing demand underscores the need to integrate distributed generation (DG) units, especially those based on renewable energy sources, into radial distribution systems (RDS)1. Unlike traditional power networks, where electricity flows in a single direction from the grid to consumers, DG units introduce bidirectional power flows, presenting both challenges and opportunities. DGs can offer numerous benefits when integrated effectively, including reduced power losses, improved voltage stability, enhanced reliability, energy savings, and delayed infrastructure upgrades. However, realizing these advantages depends on precisely optimizing DG placement and sizing. Inadequate planning can increase losses, destabilize voltage profiles, and raise operational costs, making strategic DG deployment essential for improving network efficiency and performance.

DG units are decentralized power sources connected to radial distribution systems and can be broadly categorized into four types. The first type comprises technologies such as photovoltaic cells and fuel cells, which generate only active power (P). The second category includes devices like capacitors and synchronous compensators, which produce only reactive power (Q). The third type features DG units such as synchronous machines and voltage source converters (VSCs) that can supply both active and reactive power (P & Q). Finally, the fourth type consists of induction generators, commonly used in wind farms, which provide active power (P) but require reactive power (Q) for operation2.

Incorporating capacitor banks (CBs) into distribution systems enables reactive power generation, improving voltage at load buses and reducing power losses, which in turn lessens the demand for reactive power from the main grid3. Fixed-switched capacitor banks can also stabilize voltage fluctuations caused by certain DGs types4. The combined use of DGs and CBs is expected to reduce distribution losses further, enhance voltage profiles, and boost overall system performance. Effective optimization tools are crucial for determining the optimal placement and sizing of DGs and CBs to address voltage deviation issues and maximize these benefits.

Advancements in optimization techniques have made it possible to harness the full potential of distributed generators. Metaheuristic algorithms, in particular, have gained popularity due to their ability to tackle complex optimization problems more effectively than conventional methods. Extensive research has focused on minimizing system losses by optimizing the capacity and location of DG units, with various methods and strategies being developed to improve the performance of electrical networks.

Related work

For instance, the research in5 introduces a hybrid method combining artificial ecosystem optimization with an incremental conductance-based maximum power point tracking (MPPT) technique to enhance efficiency in tracking the maximum power point (MPP) in photovoltaic systems. Simulations conducted under varying environmental conditions demonstrate that this approach stabilizes DC voltage while complying with IEEE standards for total harmonic distortion (THD). Similarly, Jordehi6 proposes an improved Particle Swarm Optimization (PSO) method using time-varying acceleration coefficients (TVACPSO) to optimize parameter estimation in photovoltaic cells and modules. By dynamically adjusting these coefficients, the method prevents premature convergence and balances exploration and exploitation. The TVACPSO technique outperforms conventional PSO and other optimization approaches in parameter estimation tasks.

Another study, Rezaee Jordehi7, focuses on photovoltaic systems with high power output, where precise parameter estimation is critical. Though PSO is widely used, it often suffers from premature convergence, reducing efficiency. To address this, the study presents an Enhanced Leader PSO (ELPSO), which surpasses standard PSO and other optimization techniques. In8, a Quadratic Binary Particle Swarm Optimization (QBPSO) method is proposed for optimizing the scheduling of shiftable appliances in smart homes. Tested in a smart home environment with 10 appliances and 264 decision variables, this method significantly reduces electricity costs while maintaining user comfort, outperforming other binary PSO variants.

A further study, Sambhi et al.9, evaluates a hybrid power plant combining solar PV and diesel generators for a campus, analyzing various battery storage configurations and assessing both performance and economic factors to identify the most efficient solution. This research emphasizes the hybrid system’s cost-effectiveness and environmental benefits across different scenarios. In10, recent work introduces a model for the joint allocation of capacitor banks and distributed generation (DG), accounting for uncertainties in DG units. Similarly, Das et al.11 presents a method for sustainable operation of distribution networks aimed at reducing energy losses, improving voltage profiles, and decreasing grid dependency.

In12, a hybrid optimization technique combines Weight Improved Particle Swarm Optimization with the Gravitational Search Algorithm to optimize the placement of distributed generators and capacitors, maximizing cost-efficiency. The study in13 introduces an improved Grey Wolf Optimizer for allocating distributed generators, capacitor banks, and voltage regulators to minimize power losses and enhance voltage stability. Meanwhile, Milovanović et al.14 presents a hybrid metaheuristic algorithm for optimal placement and sizing of distributed generation units and shunt capacitors.

In15, a hybrid optimization strategy combining the Enhanced Grey Wolf Optimizer with Particle Swarm Optimization (AREP-EGWO-PSO) is proposed for optimizing the sizing and placement of distributed generation units and capacitor banks, leveraging renewable energy resources. Saonerkar and Bagde16 introduce a genetic algorithm for optimal placement and sizing of combined distributed generation units and capacitor banks. Jannat and Savic17 propose a method that incorporates renewable energy uncertainties into the placement and sizing of DGs. Sayyid Mohssen Sajjadi et al.18 employ a memetic algorithm using the voltage stability index to optimize the size and location of distributed generators and capacitors, achieving technical, economic, and environmental goals. Moradi et al.19,20 propose using a combination of genetic algorithms and particle swarm optimization (GA/PSO), as well as imperialist competitive algorithms and genetic algorithms (ICA/GA), to address multi-objective optimization problems considering both technical and economic factors. Similarly, S. Gopiya Naik et al.21 utilize an analytical method based on the loss sensitivity factor for optimal placement and sizing of distributed generation units and capacitors to minimize losses.

In22,23, the Firefly Algorithm and Backtracking Search Algorithm are highlighted as nature-inspired evolutionary techniques. In24, a comparison is made between these algorithms and others, such as genetic algorithms, particle swarm optimization (GA/PSO), imperialist competitive algorithms, and genetic algorithms (ICA/GA), as well as analytical methods from25, for optimizing the placement of distributed generators and fixed capacitor banks, reducing power losses and improving voltage profiles. In26, Mohamed et al. apply the Loss Sensitivity Factor (LSF) method to determine optimal locations for distributed generators and capacitor banks, using the Bacterial Foraging Optimization Algorithm (BFOA) for sizing. Saonerkar et al.27 propose a genetic algorithm for the optimal placement of distributed generators and capacitor banks in distribution networks. In28, the Intersect Mutation Differential Evolution Algorithm is introduced to allocate distributed generators and circuit breakers simultaneously while ensuring current flow limits are not exceeded. Partha et al.29 propose an evolutionary approach based on decomposition verification for allocating distributed generators and capacitor banks, focusing on reducing power loss and enhancing system reliability.

Recent developments in power system optimization highlight the inadequacy of traditional single-objective and multi-objective optimal power flow (OPF) solutions to meet the complex demands of modern electricity networks. The many-objective optimal power flow (MaOPF) methods have gained attention as a critical research area. One notable study proposed the many-objective marine predators algorithm (MaMPA) to effectively address MaOPF problems, showing superior performance in minimizing operational costs and optimizing objectives such as emissions and voltage stability in IEEE 30- and 118-bus systems30.

Another study introduced the Two-Archive Harris Hawk Optimization (TwoArchHHO) algorithm for many-objective optimal power flow (MaOOPF) problems, enhancing searchability and performance through two-archive concepts, resulting in improved solutions across various IEEE standard systems31.

The role of battery energy storage systems (BESS) in optimizing energy utilization in distribution networks has also been emphasized. A study using the crayfish optimization algorithm (COA) for optimal sizing and placement of multiple BESSs demonstrated significant improvements in voltage regulation and power loss mitigation compared to single BESS installations32.

Additionally, the Energy Valley Optimizer (EVO) algorithm has been proposed for optimizing distributed generation (DG) allocation, focusing on photovoltaic (PV) and wind turbine (WT) technologies. Evaluated using the IEEE 33-bus test system, the EVO algorithm effectively minimizes power and energy losses compared to other recent optimization techniques33.

Finally, Dixit et al.34 presents a Gbest-guided Artificial Bee Colony algorithm for optimizing the placement of distributed generation units and capacitor banks in networks with variable loads. Adel et al.35 propose a water cycle algorithm to optimize the allocation of DGs and capacitor banks for techno-economic and environmental improvements. Similarly, Sambaiah et al.36 employs the Salp Swarm Algorithm, inspired by the collective movement of salps, to optimize the placement of distributed generators and capacitors with a focus on technical, economic, and environmental objectives. Lastly, Pal et al.37 introduces a modified search algorithm integrated with several soft computing techniques for optimizing the placement and sizing of distributed generators in distribution networks, with comparisons to recent studies.

A summary of different methods for optimal allocation of distributed generators (DGs) and capacitor banks (CBs) in distribution systems is provided in Table 1.

Table 1 Overview of different techniques for optimal placement of distributed generators (DGs) and capacitor banks (CBs) in distribution networks (“✓” signifies that the method is being considered, while “✗” signifies it is not).
Full size table

Contribution

This study introduces the Efficient Metaheuristic BitTorrent (EM-BT) algorithm, designed to minimize daily energy losses and voltage fluctuations while accounting for varying load profiles over a 24-h period. The algorithm has been tested on multiple distribution networks, including the IEEE 33, 69, and ZB-ALG-Hassi Sida 157-bus systems, optimizing the placement of photovoltaic renewable energy sources (PVRES) and capacitor banks (CBs) for improved overall performance.

A key innovation in this research is the consideration of temperature effects on PVRES efficiency, which is often overlooked in similar studies. This comprehensive approach integrates both temperature and solar irradiance, providing a more robust solution for distribution network optimization. Temperature variations can significantly impact photovoltaic efficiency, material conductivity, and network reliability, making it essential to address these factors.

Comparative tests against methods such as Particle Swarm Optimization (PSO), Grey Wolf Optimizer (GWO), and Whale Optimization Algorithm (WOA) demonstrate that EM-BT outperforms these techniques in reducing energy losses and voltage fluctuations. While increasing the deployment of PVRES and CBs further reduces losses, this improvement comes with higher economic costs. The subsequent sections detail the mathematical formulation of the EM-BT algorithm (Section “Model mathematics of EM-BT”), modeling for PVRES allocation (Section “Optimal placement and size of capacitor banks (CB) and photovoltaic renewable energy sources (PVRES) for supportive services in distribution networks”), and a thorough analysis of simulation results under varying load conditions (Section “Simulation and results”). The study concludes in Section “Conclusion”.

Model mathematics of EM-BT

In 2022, the Efficient Metaheuristic BitTorrent (EM-BT) algorithm was introduced as a new optimization method, inspired by the BitTorrent protocol, widely used for peer-to-peer file sharing. This protocol enables users to exchange file segments directly, alleviating the burden on central servers. The EM-BT algorithm leverages this concept by encouraging interaction and information sharing among candidate solutions, ultimately improving overall performance45. What distinguishes EM-BT is its capacity to provide innovative solutions across diverse domains, even in fields where many other metaheuristic techniques have been applied. This underscores the algorithm’s versatility and efficiency in addressing problems that traditional optimization methods may not solve as effectively.

Similar to other metaheuristic techniques, the EM-BT approach begins by generating a random population of candidate solutions.

$$x = B_{Low} + \left( {B_{Up} - B_{Low} } \right) \times rand$$
(1)

where \(B_{Low}\) and \(B_{Up}\) represent the maximum and minimum boundaries of the search space, and \(rand\) signifies a random number uniformly distributed within the range [0, 1].

The matrix containing all candidate solutions can be expressed as follows:

$$X = \left[ {\begin{array}{*{20}l} {\begin{array}{*{20}c} {x_{1,1} } & {\quad x_{1,2} } \\ {x_{2,1} } & {\quad x_{2,2} } \\ \end{array} } \hfill & {\begin{array}{*{20}c} {\quad \cdots } & {\quad x_{1,D} } \\ {\quad \cdots } & {\quad x_{2,D} } \\ \end{array} } \hfill \\ {\begin{array}{*{20}c} \vdots & {\quad \vdots } \\ {x_{N,1} } & {\quad x_{N,2} } \\ \end{array} } \hfill & {\begin{array}{*{20}c} {\quad \ddots } & {\quad \vdots } \\ {\quad \cdots } & {\quad x_{N,D} } \\ \end{array} } \hfill \\ \end{array} } \right]$$
(2)

\(N\) and \(D\) indicate the population size and the problem’s dimension respectively.

This population is then evaluated using a fitness function, to measure the abilities of each solution, comparing them at each iteration, and selecting the best one.

$$F = \left\lceil {\begin{array}{*{20}l} {f\left( {x_{1} } \right)} \hfill & {\quad f\left( {x_{2} } \right)} \hfill & {\quad \ldots } \hfill & {\quad f\left( {x_{i} } \right)} \hfill & {\quad \ldots } \hfill & {\quad f\left( {x_{N} } \right)} \hfill \\ \end{array} } \right\rceil$$
(3)

\(F\) is a vector that stores the fitness values acquired from the considered fitness function, denoted as \(f\).

In the BitTorrent protocol, users are regrouped into three levels: seed, peers, and new peers. Users within the same level download certain file pieces from those in the higher level while exchanging the remaining pieces among themselves.

Using the same concept of the BitTorrent protocol, and based on the fitness values, the EM-BT algorithm divides the population into three groups: seed, peers, and new-peers. The seed represents the best solution discovered thus far, while the peers consist of the first, second, third, and fourth best solutions. The remaining individuals in the population form the new peers group.

The candidate solutions are updated at each iteration as follows:

  1. (a)

    The seed \(x_{s}\), representing the optimal global solution, is updated in each iteration utilizing the following equation

    $$x_{s}^{iter + 1} = \mathop {argmin}\limits_{i = 1:N} \left( {f\left( {x_{i} } \right)} \right)$$
    (4)
  2. (b)

    The peers, which denote the solutions in the second level, download file pieces by communicating with the seed \(x_{s}\) and among themselves (peer-to-peer communication). Thus, the peer solutions are updated in two phases using the following equations:

    • Communication with the seed

      $$\left\{ {\begin{array}{*{20}l} {x_{{i,j}}^{{iter + 1}} = x_{{s,j}}^{{iter}} - \alpha \times r \times \left( {x_{{s,j}}^{{iter}} - x_{{i,j}}^{{iter}} } \right)} \hfill & {\quad if~rand \le 0.5} \hfill \\ {x_{{i,j}}^{{iter + 1}} = x_{{i,j}}^{{iter}} } \hfill & {\quad Otherwise} \hfill \\ \end{array} } \right.$$
      (5)

      Each peer solution \(x_{i,j}^{iter + 1}\) is updated using (5).

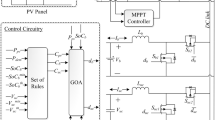
      The EM-BT flowchart is illustrated in Fig. 1.

      Where, the subscripts \(i\) and \(j\) denote the solution and dimension indices, respectively. \(i = 1, 2, 3, 4\) and \(j = 1,2, \ldots ,D\).

      \(r\) and \(rand\) are two random numbers taken uniformly from \(\left[ {0,1} \right]\).

      The parameter \(\alpha\) decreases from 2 to 0, enabling the algorithm to transition from exploration to exploitation.

      This progression is controlled using the following equation:

      $$\alpha = 2 - \frac{iter}{{MaxIter}} \times 2$$
      (6)

      To introduce a random aspect into the EM-BT approach, the candidate solution are updated, if a random number, \(rand\), was less than or equal to 0.5; otherwise, it remained unchanged.

    • Communication peer-to-peer

      $$\left\{ {\begin{array}{*{20}l} {x_{{i,j}}^{{iter + 1}} = x_{{k,j}}^{{iter}} - \alpha \times r \times \left( {x_{{k,j}}^{{iter}} - x_{{i,j}}^{{iter}} } \right)} \hfill & {\quad if~rand \le 0.5} \hfill \\ {x_{{i,j}}^{{iter + 1}} = x_{{i,j}}^{{iter}} } \hfill & {\quad Otherwise} \hfill \\ \end{array} } \right.$$
      (7)

    For each peer solution \(x_{i,j}^{iter}\), another peer \(x_{k,j}^{iter}\) is selected, then it is updated using (4).

    $$k = 1, 2, 3, 4, with k \ne i$$
  3. (c)

    New-peers communicate with the peers and with other New peers to share information, they update their positions, in two phases, using the following equations:

    • Communication with the peers

      $$\left\{ {\begin{array}{*{20}l} {x_{i,j}^{iter + 1} = x_{l,j}^{iter} - \alpha \times r \times \left( {x_{l,j}^{iter} - x_{i,j}^{iter} } \right)} \hfill & {if\;rand \le 0.5} \hfill \\ {x_{i,j}^{iter + 1} = x_{i,j}^{iter} } \hfill & {Otherwise} \hfill \\ \end{array} } \right.$$
      (8)

      For each new peer \(x_{i,j}^{iter}\), a peer solution \(x_{l,j}^{iter}\) is selected, where \(i = 5,6,7, \ldots ,N\), and \(l\) assumes values within the range1,2,3,4

    • Communication with other new peers

      $$\left\{ {\begin{array}{*{20}l} {x_{i,j}^{iter + 1} = x_{n,j}^{iter} - \alpha \times r \times \left( {x_{n,j}^{iter} - x_{i,j}^{iter} } \right)} \hfill & {if rand \le 0.5} \hfill \\ {x_{i,j}^{iter + 1} = x_{i,j}^{iter} } \hfill & {Otherwise} \hfill \\ \end{array} } \right.$$
      (9)

    For each new peer solution \(x_{i,j}^{iter}\), another new peer \(x_{n,j}^{iter}\) It is selected from its neighbours and then updated using (9), where. \(n = 5,6,7, \ldots ,N, with n \ne i\).

    In the EM-BT algorithm, new solutions replace older ones if their fitness values show improvement. This updating process continues through multiple iterations until a specified stopping condition is met. Each optimization algorithm operates with unique parameters that impact its overall performance. For example, EM-BT incorporates a parameter ‘a’ that controls the electromagnetism force and is tied to temperature. In Particle Swarm Optimization (PSO), parameters such as cognitive and social coefficients and inertia weight guide the algorithm’s behaviour. Similarly, the Grey Wolf Optimizer (GWO) relies on parameters that define the positions of alpha, beta, and delta search agents, while the Whale Optimization Algorithm (WOA) uses parameters that balance exploration and exploitation rates.

Fig. 1
figure 1

Flowchart of EM-BT.

Full size image

The flowchart of the whole implementation process

  • Step 1: Input data preparation

    • Collection of solar irradiance, temperature, and load profiles.

  • Step 2: Initialization

    • Start the EM-BT algorithm and generate candidate solutions for PVRES and CBs.

  • Step 3: Iterative optimization process

    • Evaluate candidate solutions.

    • Group solutions into Seed, Peers, and New Peers.

    • Update solutions through BitTorrent-inspired interactions.

  • Step 4: Final placement and sizing

    • Identify the optimal locations and sizes for PVRES and CBs.

  • Step 5 : Performance evaluation

    • Assess energy losses and voltage profiles.

    • Compare the EM-BT algorithm’s performance with other methods, such as PSO, GWO, and WOA.

Optimal placement and size of capacitor banks (CB) and photovoltaic renewable energy sources (PVRES) for supportive services in distribution networks

Modeling techniques for photovoltaic renewable energy sources

Power output from PVRES modules is highly influenced by local weather conditions, especially solar radiation and ambient temperature46. The geographical location largely determines these conditions. Consequently, assessing solar radiation levels in a particular region is essential for optimizing the efficiency of PVRES panels. Typically, historical data is used to estimate hourly solar radiation and daily temperature fluctuations. This information is then divided into various phases, each defined by specific solar radiation and temperature thresholds47,48.

A practical model is employed to enhance the power output of photovoltaic modules49, focusing on maximizing efficiency under varying environmental conditions. This model takes into account factors such as solar irradiance, temperature, and module characteristics to ensure optimal performance of the PV system:

$$P_{Pv - max} = FF \cdot \left( {I_{sc} \cdot \frac{G}{{G_{ref} }}} \right) \cdot \left( {V_{oc} \cdot \frac{{ln\left( {P_{1} \cdot G} \right)}}{{ln\left( {P_{1} \cdot G_{ref} } \right)}} \cdot \frac{{T_{jref} }}{{T_{j} }}} \right)$$
(10)

The highest power output that a photovoltaic (PV) system can achieve is represented by PPv-max, while Isc refers to the short-circuit current produced by the system. Solar irradiance, or sunlight intensity, at any specific moment, is denoted by Gref, which is the standard reference value for irradiance. The voltage of the PV system when open-circuited is expressed as Voc. Additionally, Tjref indicates the reference junction temperature of the PV system, and Tj represents the junction temperature at a particular time.

The following formula is used to calculate the constant coefficient P1​.

$$P_{1} = \frac{{I_{sc} }}{G}$$
(11)

The filling factor (FF) can be expressed as:

$$FF = \frac{{P_{pvmax} }}{{V_{oc} \cdot I_{sc} }} = \frac{{V_{mpp} I_{mpp} }}{{V_{oc} I_{sc} }}$$
(12)

The voltage at the Maximum Power Point (MPP) of the photovoltaic system is represented by Vmpp, while Impp denotes the current at the MPP of the system.

Optimal allocation and size of capacitor banks (CB) and photovoltaic renewable energy sources (PVRES) for auxiliary services: constraints and objectives

In the allocation of Photovoltaic Renewable Energy Sources (PVRES) and capacitor banks (CBs) for auxiliary services in distribution systems, the primary objective is to minimize daily energy losses. This objective is mathematically expressed as:

$$E_{loss} = \sum_{h = 1}^{24} \left( {\sum_{br = 1}^{{N_{br} }} \quad I_{br} \left( h \right) ^{2} \cdot R_{br} } \right)$$
(13)

Eloss represents the total energy loss per day.

In this context, the number of distribution branches is indicated as Nbr, while the current flowing through each branch is represented by Ibr, and Rbr denotes the resistance of each branch. The aim of minimizing these parameters is encapsulated in a single-objective model, Fobj, as outlined in Eq. (14).

$$F_{obj} { = }\frac{{E_{loss} \;after\,DG }}{{E_{loss\;before\;DG} }}$$
(14)

Ensuring that the real and reactive power injections from the Photovoltaic Renewable Energy Systems (PVRES) and Capacitor Banks (CB) remain within their predefined operational limits is crucial. These limits are specified as \({PPVRES}_{k\_max}\) for real power injection from PVRES and Qcb j_max for reactive power injection from the CB. Adherence to these constraints at all times is essential for maintaining system stability, reliability, and optimal performance, thereby preventing risks of overloading or imbalances within the network.

$$0 < PPVRES_{K} < PPVRES_{k\_max} \quad k = 1,. \ldots ,nPV$$
(15)
$$0 < Q_{{cb_{j} }} < Q_{{cb_{j\_max} }} \quad j = 1, \ldots .,ncb$$
(16)

PPVRES denotes the real power supplied to the grid by photovoltaic renewable energy sources (PVRES), whereas QCB indicates the reactive power contributed by capacitor banks (CB)50. Additionally, it is essential to maintain the voltage at each distribution node and the current in all distribution branches within designated safe limits at all times. These precautions are vital for ensuring the power distribution network’s overall stability, efficiency, and safety51.

$$V_{m\_min} < V_{m} < V_{m\_max} \quad m = 1,. \ldots ,nB$$
(17)
$$I_{br} < I_{{br_{i\_max} }} \quad i = 1,. \ldots ,nbr$$
(18)

In this context, m​ expressed the voltage at bus m, with \(V_{m\_min}\) and \(V_{m\_max}\) denoting the respective minimum and maximum voltage limits for that particular bus. These limits are typically set within a 10% tolerance range to ensure the stability of the entire network. Furthermore, \(I_{{br_{i\_max} }}\) defines the maximum allowable thermal capacity of the branch, which is a crucial constraint for preventing overheating or overloading of network components. These operational constraints must be consistently satisfied across all hours, nodes, and branches to maintain reliable and secure power distribution.

Additionally, the photovoltaic (PVs) penetration threshold is regulated using the coefficient \(K_{P}\)52. It ensures that the total installed capacity of PV systems, \(\left( {\sum\limits_{{k \in nPV}} {P_{{PV_{k} }} } } \right)\), equals 50% of the system’s total active power demand, \(P_{{D_{m} }}\). This constraint helps balance renewable energy integration with system stability.

$$\mathop \sum \limits_{k \in nPV} P_{{PV_{k} }} = K_{P} \cdot \mathop \sum \limits_{m \in nB} P_{{D_{m} }}$$
(19)

The inequality constraints associated with the control variables, as described in Eqs. (15) and (16), are automatically managed by the EM-BT mechanism. However, the inequality constraints in Eqs. (17) and (19) require special attention.

Model of distribution networks

Generally, the resistance of an AC line is determined by:

$$R = r_{0} \cdot l$$
(20)

r0 represents the linear resistance in [Ω/km], and l denotes the line length in meters. In this study, we adjust the resistance values for all network buses (33, 69, and 157) to reflect real conditions by incorporating 24 daily temperature values, as follows:

$$R_{ti} = R\left[ {1 + \alpha 25\left( {t_{i} {-}25} \right)} \right]$$
(21)

The value of Rti ​ indicates the resistance at the i-th hour, with i ranging from 1 to 24 throughout the day. The resistance R corresponds to the material’s resistance at a standard reference temperature, typically 25 °C, measured in ohms [Ω]. The parameter α25​ represents the temperature coefficient of resistance at this reference temperature, while t denotes the temperature (in Celsius) at which the resistance, adjusted for temperature, is calculated.

Simulation and results

The EM-BT algorithm has been utilized to reduce energy losses by accounting for fluctuations in PVRES output, capacitor bank output, and daily load variations. This approach has been applied to three different distribution Networks: IEEE 33, IEEE 69, and ALG-AB-Hassi Sida, which comprises 157 buses. For the IEEE 33 system, three and six PVRES units were allocated alongside nine capacitor banks. In contrast, due to the larger size of the IEEE 69 and ZB-ALG-Hassi Sida systems, more PVRES units were deployed. The IEEE 69 system received five and ten PVRES units along with eighteen capacitor banks, whereas the ZB-ALG-Hassi Sida system was allocated ten and twenty PVRES units and twenty-five capacitor banks. Each system was assessed with various profiles for capacitor banks, PVRES, and load over a 24-h timeframe. The input data (detailed in Table 2) and the results for each testing system are elaborated upon in the following sections.

Table 2 Evaluation of daily energy loss across various distribution systems with peak and minimum bus voltage levels.
Full size table

Three scenarios were evaluated for all networks (IEEE 33, IEEE 69, and ZB-ALG-Hassi Sida 157), as described below:

  • Scenario 1 A load flow analysis was performed for each hour of loading, accounting for temperature effects across all networks.

  • Scenario 2 The proposed EM-BT algorithm was compared to Particle Swarm Optimization (PSO), Grey Wolf Optimization (GWO), and the Whale Optimization Algorithm (WOA) for the placement of PVRES and capacitor banks. The objective was to minimize the function defined in Eq. (14).

  • Scenario 3 A similar comparison was conducted, focusing exclusively on PVRES placement. This scenario used twice as many PVRES units as Scenario 2 while keeping the number of capacitor banks unchanged, to further reduce the objective function.

In both scenarios involving optimization, the EM-BT algorithm was executed for 100 iterations using 30 search agents. For Scenario 1, voltage adjustments were applied to ensure that node voltages remained within 10% of the nominal value. In all scenarios, each algorithm was tested over 10 iterations to standardize the number of function evaluations.

The EM-BT algorithm’s performance was tested on three networks: IEEE 33, IEEE 69, and ZB-ALG-Hassi Sida 157. The IEEE 33 network consists of 32 branches and 33 nodes, IEEE 69 has 68 branches and 69 nodes, and the ZB-ALG-Hassi Sida system includes 156 branches and 157 nodes. Detailed information about the branches and nodes in these networks is available in the literature53,54. Diagrams of these systems, each operating at a nominal voltage of 12.66 kV, are shown in Fig. 2.

Fig. 2
figure 2

Schematic representation of the three networks.

Full size image

The LGEB laboratory located at Mohamed Khider University in Biskra, Algeria, offers extensive statistical insights into the variations of photovoltaic renewable energy sources (PVRES) influenced by solar irradiance and temperature across the IEEE 33, IEEE 69, and ZB-ALG-Hassi Sida 157 networks.

Figure 3a to c display the daily average power generation fluctuations of PVRES across the 33, 69, and 157 bus networks, effectively illustrating the impact of solar irradiance variations throughout the day. These figures highlight the influence of sunlight intensity on PVRES output, with power generation peaking during midday and diminishing in the early morning and late afternoon. Meanwhile, Fig. 4 presents the average PVRES output variations over a 24-h timeframe, incorporating the combined effects of both solar irradiance and temperature fluctuations. This figure emphasizes the compounded impact of environmental factors on PVRES efficiency, with temperature increases reducing output during peak irradiance hours. Furthermore, Fig. 5 provides a comprehensive overview of load variations across all three networks, showcasing the demand fluctuations that occur alongside generation variations. Together, these figures underscore the dynamic interaction between power generation and demand, as well as the importance of adaptive strategies for optimizing PVRES placement and operation in response to these environmental and load-related variations.

Fig. 3
figure 3

Yearly daily average PVRES variations due to irradiance for the three networks.

Full size image
Fig. 4
figure 4

Yearly daily average PVRES fluctuations considering irradiance and temperature effects across the three networks.

Full size image
Fig. 5
figure 5

Yearly daily average variations for the three distribution Networks.

Full size image

The influence of temperature on photovoltaic modules, as shown in Figs. 3 and 4, demonstrates a noticeable reduction in power output from PVRES. For the IEEE 33 system, the output drops from 2100 kW at 50% efficiency to 1,155 kW at 27.5% efficiency. In the IEEE 69 system, the output decreases from 1925 kW at 50% efficiency to 1,058 kW at 26% efficiency. For the ZB-ALG-Hassi Sida 157 system, power output falls from 13,650 kW at 50% efficiency to 7,507.5 kW at 27.5% efficiency.

Figure 5a–c shows that peak load demand typically occurs around 12:00 p.m. and lasts for 4 h for both the IEEE 33 and IEEE 69 systems, fully meeting 100% of the demand. Conversely, Fig. 5c indicates that the peak demand for the ZB-ALG-Hassi Sida 157 system occurs around 6:00 p.m., extending for 3 h, during which the system also fulfils 100% of the load.

Scenario 1

In this case, load flow estimates are performed hourly, taking into account the effects of temperature on demand. Figure 6a–c show the voltage profiles for the IEEE 33, IEEE 69, and ZB-ALG-Hassi Sida 157 networks across all distribution nodes, highlighting distinct characteristics for each loading hour. Notably, these voltage profiles remain below the baseline lower bound. During peak consumption at hour 14, the ZB-ALG-Hassi Sida 157 network experiences a minimum voltage of 0.87 pu, while the IEEE 33 and IEEE 69 networks reach a minimum of 0.89 pu. Additionally, Table 3 provides a detailed overview of daily energy loss, underscoring the impact of temperature on network performance.

Fig. 6
figure 6

Hourly voltage profiles over a 24-hour period for each of the three networks in the initial scenario.

Full size image
Table 3 Daily energy loss for all distribution networks considering the impact of temperature.
Full size table

The results in Fig. 6 and Table 3 reveal that the energy losses for the ZB-ALG-Hassi Sida 157, IEEE 69, and IEEE 33 distribution networks are 19,367 kWh, 4,085.7 kWh, and 3,813 kWh, respectively. These observed losses exceed the base case estimates of 17,995 kWh for the ZB-ALG-Hassi Sida 157 network, 3797 kWh for the IEEE 69 network, and 3567.7 kWh for the IEEE 33 network. Consequently, this translates to an increase in energy losses of 7.62% for the ZB-ALG-Hassi Sida 157 network, 7.60% for the IEEE 69 network, and 6.88% for the IEEE 33 network. The higher energy losses reflect the effects of factors such as temperature, load variations, and network structure on power efficiency, particularly under less-than-ideal conditions. These findings underscore the necessity for optimizing network configurations, the placement of PVRES and capacitor banks, and the selection of loss-reducing measures to mitigate inefficiencies and improve overall performance in each network scenario.

Senario 2

In this case, the EM-BT approach is compared to the PSO, GWO, and WOA methods, aiming to minimize the objective function defined in Eq. 14. Various allocations of PVRES and capacitor banks (CBs) were considered during the evaluation process. Table 4 summarizes the energy losses, voltage variations, and reduction rates for the IEEE 33, IEEE 69, and ZB-ALG-Hassi Sida 157 networks. The results indicate that the EM-BT method significantly reduces energy losses: from 3,831.3 kWh/day to 1,951.5 kWh/day for the IEEE 33 network, from 4,085.7 kWh/day to 1,764.7 kWh/day for the IEEE 69 network, and from 19,367 kWh/day to 8,141.4 kWh/day for the ZB-ALG-Hassi Sida 157 network. Additionally, voltage magnitudes improve across all buses, with notable enhancement at the weakest bus.

Table 4 Optimal sizing and placement of capacitor banks and PVRES: energy losses, minimum bus voltage (pu), and reduction rates for scenario 2 across various distribution networks.
Full size table

Figure 7a–c illustrate the convergence behaviors of the optimization techniques (EM-BT, PSO, GWO, and WOA) for the IEEE 33, IEEE 69, and ZB-ALG-Hassi Sida 157 networks. The EM-BT approach demonstrates excellent convergence properties, consistently achieving optimal PVRES and CB configurations more efficiently. For the IEEE 33 network, as depicted in Fig. 7a, EM-BT converges faster and more reliably than the other methods. Similarly, Fig. 7b shows that EM-BT performs exceptionally well in terms of speed and stability for the IEEE 69 network. For the ZB-ALG-Hassi Sida 157 network, Fig. 7c highlights the superior convergence of EM-BT, achieving minimal energy losses. Overall, Fig. 7 confirms that the EM-BT approach excels in delivering rapid and consistent convergence across all networks.

Fig. 7
figure 7

Convergence evaluation of EM-BT, PSO, GWO, and WOA for all distribution networks in the second scenario.

Full size image

Scenario 3

In this analysis, we evaluate the performance of the EM-BT algorithm in comparison with three alternative optimization techniques: Particle Swarm Optimization (PSO), Grey Wolf Optimizer (GWO), and Whale Optimization Algorithm (WOA). Various configurations were tested, incorporating six, ten, and twenty allocations of Photovoltaic Renewable Energy Sources (PVRES) along with multiple capacitor banks. The primary objective was to minimize the function defined in Eq. 14.

Table 5 summarizes the results, highlighting reductions in voltage deviations, energy losses, and energy loss percentages for the IEEE 33, IEEE 69, and ZB-ALG-Hassi Sida 157 networks. For the IEEE 33 network, the EM-BT algorithm reduces energy losses by 57.60%, lowering them from 3,831.3 kWh/day to 1,624.4 kWh/day, while also improving the voltage at the weakest bus from 0.89 pu to 0.93 pu. Similarly, in the IEEE 69 network, EM-BT achieves a 65.44% reduction in energy losses, decreasing them from 4,085.7 kWh/day to 1,412 kWh/day, and raising the voltage at the weakest bus from 0.89 pu to 0.92 pu. In the ZB-ALG-Hassi Sida 157 network, EM-BT results in a 63.17% reduction in energy losses.

Table 5 Optimal sizing and placement of capacitor banks and PVRES: energy losses, minimum bus voltage (pu), and reduction rates for scenario 3 across various distribution networks.
Full size table

Figure 8a–c illustrate the convergence behaviours of EM-BT, PSO, GWO, and WOA across the three networks, with Fig. 8b specifically showing an enhanced voltage profile under Scenario 3. The EM-BT algorithm demonstrates superior convergence properties across all networks, affirming its effectiveness in optimally sizing and placing capacitor banks and PVRES to minimize energy losses, as also seen in Scenario 2 (Fig. 7).

Fig. 8
figure 8

Examination of the convergence of EM-BT, PSO, GWO, and WOA techniques across all distribution systems in the third scenario.

Full size image

Figure 9a–c illustrate the voltage characteristics for the IEEE 33, IEEE 69, and ZB-ALG-Hassi Sida 157 networks, each exhibiting distinct operational features. In particular, Fig. 9b demonstrates marked voltage stability improvements in the IEEE 69 network achieved through the EM-BT algorithm. Unlike in the baseline scenario, all voltage levels in this network remain above the minimum acceptable threshold, even under increased load conditions. During peak demand, both the IEEE 69 and ZB-ALG-Hassi Sida 157 networks experience a minimum voltage drop to 0.92 per unit (pu), while the IEEE 33 network maintains a slightly higher minimum voltage of 0.93 pu. These results underscore the effectiveness of the EM-BT approach in optimizing the placement and sizing of PVRES and capacitor banks, which not only mitigates voltage drops but also preserves voltage stability across all nodes. Consequently, this optimization significantly enhances power supply reliability, particularly during high consumption periods, ensuring robust operational resilience in diverse network environments.

Fig. 9
figure 9

Voltage profile variations over a 24-hour cycle for the third scenario across all three networks.

Full size image

Figure 10a–c illustrate the percentage reduction in energy losses achieved across the second and third optimization scenarios for the IEEE 33, IEEE 69, and ZB-ALG-Hassi Sida 157 systems. The results demonstrate a clear trend: as the number of PVRES units integrated into the network increases, the reduction in energy losses becomes more pronounced. This correlation suggests that a higher density of distributed generation from PVRES enhances the network’s capacity to meet local demand directly, thereby reducing the need for energy transmission over longer distances and minimizing associated losses. Additionally, the strategic placement and sizing of PVRES units, as guided by the EM-BT algorithm, ensure that these reductions are maximized by mitigating power flow imbalances and optimizing voltage profiles. This outcome underscores the potential for distributed PVRES deployment to significantly improve energy efficiency and reduce operational costs in electrical distribution systems.

Fig. 10
figure 10

Percentage decrease in energy loss for the second and third scenarios across all distribution systems.

Full size image

Conclusion

This study introduces the EM-BT optimization method, designed for the strategic placement and sizing of Photovoltaic Renewable Energy Sources (PVRES) and Capacitor Banks (CB) within distribution systems. The main goal of EM-BT is to minimize energy losses while considering various load scenarios over a 24-h period, along with temperature fluctuations. Our results indicate that EM-BT significantly outperforms traditional optimization methods, such as the Grey Wolf Optimizer (GWO), Particle Swarm Optimization (PSO), and Whale Optimization Algorithm (WOA), particularly in reducing energy losses while adhering to operational constraints.

The strength of EM-BT lies in its innovative integration of PVRES and CB, effectively managing the interplay between solar irradiance and temperature changes. Additionally, EM-BT exhibits faster convergence and provides high-quality solutions more efficiently than competing methods, making it well-suited for real-world energy management applications.

The practical implications of EM-BT are valuable for utility companies and renewable energy stakeholders, as it enhances the reliability and efficiency of distributed energy systems. Future research should focus on scaling EM-BT for more complex distribution networks, improving data accuracy, and incorporating additional environmental factors. Economic analysis will also be crucial to evaluate the cost-effectiveness and environmental advantages of PVRES-CB configurations, contributing to global renewable energy objectives.