Wind energy assessment and hybrid micro-grid optimization for selected regions of Saudi Arabia

Abstract

This study investigates the optimization of wind energy integration in hybrid micro grids (MGs) to address the rising demand for renewable energy, particularly in regions with limited wind potential. A comprehensive assessment of wind energy potential was conducted, and optimal sizing of standalone MGs incorporating photovoltaic (PV) systems, wind turbines (WT), and battery storage (BS) systems was performed for six regions in the Kingdom Saudi Arabia. Wind resource analysis utilizing the Weibull distribution function shows that all regions exhibited Class 1 wind energy characteristics, with average annual wind power densities ranging from 36.74 W/m² to 149.56 W/m², thereby rendering them suitable for small-scale hybrid applications. A multi-strategy serial cuckoo search algorithm was employed to evaluate three distinct configurations, and the results indicated that the integration of PV, WT, and BS yielded the most cost-effective solution for the majority of regions, achieving a levelized cost of energy of 0.148$/kWh and a loss of power supply probability below 0.05%. Notably, alternative configurations demonstrated superior reliability in locations such as Al-Baha, Taif, and Tabuk. The rseults of this study provide valuable insights into the design of scalable, sustainable, and cost-efficient hybrid MGs tailored to regions with low wind potential, thereby contributing to enhanced energy access and economic development in remote locations.

Introduction

Hybrid systems integrating solar and wind energy have become essential for off-grid electrification, driven by advancements in renewable energy (RE) technologies. The reliance on fossil fuels has severe environmental impacts due to greenhouse gas (GHG) emissions¹. Rapid industrialization and population growth have heightened energy demand, depleting finite fossil fuel resources and making renewable energy sources (RESs) increasingly attractive as sustainable alternatives². A country’s industrial growth depends on balancing energy production and consumption, with RESs playing a vital role due to the decline in non-renewable resources³.

In 2011, Saudi Arabia established the King Abdullah City for Atomic and RE (K. A. CARE) to develop a strategic energy supply plan, targeting 16 GWp of photovoltaic (PV) panel capacity by 2032⁴. Saudi Arabia, spanning about 2.2 million km², includes many remote villages not connected to the power grid and reliant on diesel generators (DG). DGs, however, incur high maintenance and operational costs. Solar and wind generators, combined with DGs or energy storage systems (ESS), offer cost-effective and sustainable alternatives⁵. AlQadah et al.⁶. used the Weibull Distribution Function (WDF) to assess wind energy potential in Medina, demonstrating its feasibility with the Aventa AV-7 Wind Turbine (WT). Similarly, Alanazi et al.⁷evaluated Weibull parameter estimation methods to assess wind energy in Saudi Arabia’s Qassim region, finding the Moment Method most accurate for small off-grid projects. Eltamaly and Farh⁸developed software to select optimal WTs by maximizing capacity factor and minimizing energy costs, applying it to five Saudi locations. The program estimated Weibull parameters and identified the best cost estimation methods for the region’s economic conditions. Globally, renewable resources, being naturally replenished and environmentally friendly, are replacing conventional energy sources⁹. A separate study focused on stand-alone hybrid renewable energy (HRE) systems aimed at improving reliability and reducing total annual costs (TAC). Wind farm planning relies on accurate wind potential estimates, with the Weibull function commonly used to model wind data and evaluate energy capacity¹⁰. By estimating wind potential effectively, reliable wind farm planning can be achieved, contributing to sustainable energy solutions in six Saudi Arabian regions. Estimating wind capacity requires understanding wind characteristics comprehensively^11,12,13.

Researchers worldwide have modeled wind speeds using mathematical formulas and statistical distributions like the Weibull function, a two-parameter model widely adopted for fitting wind data¹⁴. From 2006 to 2008, Islam et al.¹⁵. estimated wind energy potential in Malaysia’s Kudat and Labuan regions using the Weibull model. In 2008, Kudat recorded wind energy of 590.40 kWh/m²/year, with peak wind speeds of 6.02 m/s, while Labuan’s peak was 2.44 m/s in 2007. Analyzing ten years of wind data from ten Malaysian stations, Sopian et al.¹⁶ found Mersing had the highest wind energy density of 85.61 W/m² at 10 m. In Saudi Arabia, Baseer et al.¹⁷. analysed five years of wind data from seven locations, finding the Maximum Likelihood Method most effective for Weibull parameter estimation. Deb et al.⁶⁹ conducted a comprehensive review on local energy systems, focusing on modeling, tools, and pilot projects. Udo et al.⁷⁰ explored the optimization of wind energy systems using machine learning to enhance predictive maintenance and efficiency.

Integrating RE resources into microgrids (MGs) requires optimal design to balance regulation and energy efficiency. Techniques and algorithms have been employed to optimize micro-source (MS) sizes for cost and reliability goals, such as reducing Loss of Power Supply Probability (LPSP)¹⁸. To address energy and emission constraints¹⁹, implemented Evolution Strategy, while Wang et al.²⁰. proposed a Cooperative Operation and Optimal Design method for Islanded MGs, achieving low Net Present Costs (NPC). Nelson et al.²¹. developed an economic assessment method for sizing hybrid wind, PV, and fuel cell MGs, and Kimball et al.²². proposed a technique to configure PV and battery sizes to meet availability targets²³. proposed modified simulated annealing and harmony search algorithms to optimally size off-grid hybrid systems integrating wind, solar, hydrogen, and battery storage for a remote area in Iran. The study found wind/solar systems with battery storage (BS) to be more cost-effective and reliable than those using hydrogen storage (HS).

²⁴developed six grid-independent HRES combining solar, wind, reverse osmosis desalination (ROD), and battery or HS, optimized using an improved bees algorithm. The study concluded that systems with BS are more cost-effective than those using HS, with solar/battery/ROD configurations being the most economical²⁵. presented a novel harmony search-based algorithm for optimizing solar/wind hybrid systems with HS, aiming to minimize total cost while ensuring system reliability. The improved harmony search with a weighting factor (IHS-W) outperformed other algorithms, achieving cost savings of up to 30%at varying reliability indices (1%, 2%, and 3%), demonstrating its effectiveness in cost reduction, convergence speed, and robustness²⁶. designed and optimized four stand-alone hybrid desalination plants powered by PV, WT, DGs, and energy storage, focusing on cost, environmental impact, and reliability. Using a hybrid meta-heuristic optimization method, the study demonstrated that a solar/battery/DG system achieves the most cost-effective and environmentally friendly solution for potable water and electricity supply in remote areas²⁷. optimized a stand-alone PV/BS using an improved harmony search algorithm to minimize the total life cycle cost (TLCC) while ensuring system reliability based on the loss of load probability (LOLP). The study revealed that increasing the reliability index reduces the number of panels and batteries significantly, while decreasing the reliability index leads to higher TLCC and system component costs²⁸. optimized a HRESs with PV, wind, batteries, and desalination using six algorithms, identifying particle swarm optimization (PSO) and Multi objective PSO (MOPSO) as the best for single and multi-objective optimization, respectively. Sensitivity analysis showed solar panel prices significantly affect the system’s TAC²⁹. designed an optimized off-grid hybrid system combining WTs, PV panels, a biogas generator, and ESS to minimize costs, CO₂ emissions, and improve reliability for a rural area in Iran. Results showed the hybrid system achieved a cost of $0.201/kWh and reduced annual CO₂ emissions by 97% compared to a diesel-based system.

However, most studies relied on region-specific weather data, limiting broader applicability.

Existing research on RESs and hybrid MGs often neglects areas with low wind energy potential (Class 1 regions, power densities below 200 W/m²). Most studies focus either on cost or reliability, seldom addressing both through multi-objective optimization in low-potential regions. While the Weibull distribution remains a standard for wind energy evaluation, advanced optimization techniques tailored to low-potential areas are lacking. Additionally, the role of ESS in improving system reliability under such conditions is underexplored, leaving gaps in achieving cost-effective and dependable RE solutions for tropical, remote, or off-grid locations.

This study makes several key contributions to RE optimization, focusing on regions with low wind energy potential. It employs a multi-strategy serial cuckoo search (MSSCS) algorithm to optimize hybrid MG designs with WTs, PV, and BS. The study targets six Class 1 wind regions in Saudi Arabia—Abha, Al-Baha, Arar, Qassim, Tabuk, and Taif—traditionally considered unsuitable for large-scale wind energy. By using the Weibull distribution function for wind energy evaluation, the research highlights opportunities for integrating small-scale wind energy into hybrid systems.

A major contribution of this research is its dual focus on cost-effectiveness and reliability in hybrid MG designs, often overlooked in prior studies. By analyzing three MG configurations (integrating PV, WTs, and BS), the study identifies optimal solutions for each region, minimizing LPSP and Levelized Cost of Energy (LCOE). The results demonstrate that small-scale wind energy, combined with solar power and batteries, can offer viable solutions in low-potential areas.

This study provides a robust optimization framework adaptable to regions with similar climatic challenges, advancing global RE development. By addressing the challenges of RES planning in underutilized regions, it offers sustainable, dependable, and cost-effective energy solutions for off-grid and remote locations.

The remainder of this paper is structured as follows: Sect. 2 details wind energy evaluation techniques, emphasizing the Weibull distribution function for estimating wind energy potential in Saudi Arabia. Section 3 describes the methodology for hybrid MG optimization, including the MSSCS algorithm and system configuration. Section 4 presents simulation results, comparing three MG configurations in terms of cost, and reliability. Section 5 discusses incorporating small-scale wind energy into hybrid systems based on regional wind energy potential. Section 6 concludes with key findings, limitations, and future research directions.

Wind energy assessment

This section evaluates wind energy to determine the potential capacity of the location. The wind energy evaluation was performed using the WDF for its straightforwardness and precision^30,31.

Weibull distribution

The Weibull function is an empirical model used to characterize wind velocity at a specific location. It is widely utilized, along with the Rayleigh distribution, to model wind speed distributions over a defined area and time period. Among these, the Weibull distribution provides the best fit for wind data, making it the focus of this study^32,33. The cumulative distribution function (CDF) and probability density function (PDF) of the Weibull distribution, expressed in terms of wind velocity v, are as follows⁴:

$$\:f\left(v\right)=\frac{k}{c}\cdot\:({\frac{v}{c})}^{a}\cdot\:B$$

(1)

$$\:F\left(v\right)=1-\text{B}$$

(2)

$$\:a=k-1$$

(3)

$$\:\text{B}=\text{e}\text{x}\text{p}[-{\left(\frac{v}{c}\right)}^{k}]$$

(4)

where $\:f\left(v\right)\:$represents the pdf for observing wind velocity ($\:v$), $\:c$ is the scale parameter of the Weibull distribution (m/s), $\:k$ denotes the dimensionless shape parameter of the Weibull distribution and $\:F\left(v\right)$ stands for the CDF of observing $\:v$. Several methods exist for determining k and c.

Weibull k and c parameters

In this study, the maximum likelihood technique is employed to determine the k and c parameters of the Weibull distribution. The mathematical expressions for this method are well-documented in the literature³⁴. Although both graphical and approximated methods are commonly discussed, this work adopts the approximated method exclusively due to its higher accuracy in predicting wind power and wind speed³⁵.

$$\:K={(\frac{\sum\:_{i=1}^{n}{v}_{i}^{k}\cdot\:ln{v}_{i}}{\sum\:_{i=1}^{n}{v}_{i}^{k}}-\frac{1}{n}\cdot\:\sum\:_{i=1}^{n}ln{v}_{i})}^{-1}$$

(5)

$$\:c={(\frac{1}{n}\cdot\:\sum\:_{i=1}^{n}{v}_{i}^{k})}^{\raisebox{1ex}{$1$}\!\left/\:\!\raisebox{-1ex}{$k$}\right.}$$

(6)

Graphical method

As stated in³, by applying the natural logarithm twice to both sides of Eq. (2), the equation can be linearized, yielding:

$$\:\text{ln}(\text{l}\text{n}[F\left(v\right)-1\left]\right)=kln\left(v\right)-kln\left(c\right)$$

(7)

A plot of $\:\text{ln}\left\{-\text{ln}\left[1-F\left(v\right)\right]\right\}$ against ln(v) produces a straight line, with a slope of k and a y-intercept of $\:-kln\left(c\right)$. The values of c and k can be determined using the least squares method, as illustrated in Eq. (8)¹.

$$\:y=mx+b$$

(8)

Where,

$$\:y=\text{l}\text{n}(\text{l}\text{n}[F\left(v\right)-1\left]\right)$$

(9)

$\:x=\text{l}\text{n}\left(v\right)$. The values of $\:c$ and $\:k$ can be determined using Eqs. (10) and (11):

$$\:c={e}^{\left(\frac{b}{-k}\right)}$$

(10)

Approximated technique

The parameters k and cof the Weibull distribution are given in³⁶ as:

$$\:k={\left(\frac{\partial\:}{{v}_{m}}\right)}^{-1.086}$$

(11)

$$\:c=\frac{{v}_{m}}{\lceil(\frac{1}{k}+1)}$$

(12)

Here, $\:\partial\:$ represents the standard deviation, $\:{v}_{m}$ denotes the mean wind speed (m/s), and $\lceil(x)$ is the gamma function of $\:x$. These parameters are described in³:

$$\:\lceil\left(x\right)={\int\:}_{0}^{x}{t}^{x-1}\cdot\:{e}^{-t}dt$$

(13)

$$\:{v}_{m}=\frac{1}{n}\cdot\:\sum\:_{i=1}^{n}{v}_{i}$$

(14)

$$\:{\partial\:}^{2}=\frac{1}{n-1}\sum\:_{i=1}^{n}{({v}_{i}-{v}_{m})}^{2}\:$$

(15)

From Eq. (11), c and k are related according to³.

$\:{v}_{m}=c\cdot\:\:\lceil(\frac{1}{k}+1)$ (16)

Error analysis

To evaluate the suitability of the Weibull function as a model for the observed wind data, goodness-of-fit tests were performed. These tests include the Root Mean Square Error (RMSE) and the Coefficient of Determination (R²), which are briefly summarized below. The RMSE measures the difference between the values predicted by the fitted model and the actual observed values, as expressed in³:

$$\:RMSE=\sqrt{(\frac{1}{n}\cdot\:\sum\:_{i=1}^{n}{({y}_{i}-{x}_{i})}^{2})}$$

(15)

The R² test assesses the percentage of variance in the dependent variable that can be explained by the independent variable. The calculation for the R² error metric is presented below as follows³.

$$\:{R}^{2}=\frac{\sum\:_{i=1}^{n}{({y}_{i}-{z}_{i})}^{2}-\sum\:_{i=1}^{n}{({y}_{i}-{x}_{i})}^{2}}{\sum\:_{i=1}^{n}{({y}_{i}-{z}_{i})}^{2}}$$

(16)

Where n denote the data points number, $\:{y}_{i}$ represents the predicted data value of $\:{x}_{i}$ and $\:{z}_{i}$ is average wind speed. The R² value varies from 0 to 1; a low R² signifies a weak prediction, whereas a high R² indicates a stronger prediction, which is the reverse for RMSE. A value close to 0 indicates a better fitness value while a high value indicates poor fitness.

Wind power generation system

To accurately estimate wind energy potential, the site data is modeled using a continuous distribution function. The Weibull distribution is utilized for this purpose and is subsequently integrated with the WT power curve³⁷. The actual wind energy is calculated by integrating the data across the turbine’s power curve. The primary power output of the WT is determined by its characteristic curve, expressed as³⁷:

$$\:{P}_{w}=\:\left\{\begin{array}{c}0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:v<{v}_{in}\ge\:{v}_{co}\\\:P\cdot\:{P}_{r}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{v}_{in}\le\:v\le\:{v}_{r}\\\:{P}_{r\:}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:v\le\:v\le\:{v}_{co}\end{array}\right.\:$$

(17)

Here, P represents the mathematical function that defines the Wt’s performance curve. In this case, a cubic polynomial is utilized to model the characteristic curve of the selected WT. The resulting performance curve for the turbine is described by Eq. (18) as follows^37,38,39:

$$\:P=\frac{3.031}{1000}\cdot\:{x}^{3}+\frac{7.521}{100}\cdot\:{x}^{2}-\frac{4.528}{10}\cdot\:x+\frac{8.347}{10}$$

(18)

and $\:{P}_{r}$is the rated power given as in^33,34:

$$\:{P}_{r}=\frac{1}{2}\cdot\:{P}_{a}\cdot\:A\cdot\:{v}_{r}^{3}$$

(19)

Here, A represents the intercepted area of the turbine rotor, $\:{v}_{r}$ is the rated wind speed, and $\:{v}_{in}$ and $\:{v}_{co}$ are the cut-in and cut-out wind speeds of the selected turbine. The wind energy is calculated by multiplying $\:{P}_{a}$​ with the modified wind speed probability distribution function $\:f\left(v\right)$ using the equations provided below:

$$\:{E}_{TA}=T\underset{{v}_{r}}{\overset{{v}_{co}}{\int\:}}{P}_{w}\left(v\right)f\left(v\right)dv=T{P}_{r}\left\{\underset{{v}_{in}}{\overset{{v}_{r}}{\int\:}}P\cdot\:f\left(v\right)dv+{\int\:}_{{v}_{r}}^{{v}_{co}}f\left(v\right)dv\right.$$

(20)

And

$$\:{E}_{w}=T\cdot\:{P}_{r}\underset{{v}_{in}}{\overset{{v}_{r}}{\int\:}}P\cdot\:\frac{k}{c}\cdot\:{\left(\frac{v}{c}\right)}^{k-1}\cdot\:\text{exp}\left(-{\left(\frac{v}{c}\right)}^{k}\right)dv+T{P}_{r}\underset{{v}_{r}}{\overset{{v}_{co}}{\int\:}}\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}\text{e}\text{x}\text{p}(-({\frac{v}{c})}^{k})dv\:$$

(21)

Where, $\:{E}_{w}$ is the wind energy obtained using the WDF.

Wind data employed for the analysis

Wind data spanning 11 years (2012–2022) were collected for the regions of Abha, Al-Baha, Arar, Qassim, Tabuk, and Taif in Saudi Arabia from meteorological stations operated by the Saudi Arabia Meteorological Agency. The measurements were taken at a height of 10 m, with the geographical coordinates provided in Table 1. The data, recorded hourly, facilitated the calculation of monthly wind speeds and related parameters, as shown in Fig. 1.

Table 1 Geographical coordinates of the chosen Saudi locations.

Table 1 provides the geographical coordinates (latitude and longitude) and station height (10 m) for six selected cities in Saudi Arabia. The cities include Abha, Al-Baha, Arar, Qassim, Tabuk, and Taif. The latitudes range from 18.13°N (Abha) to 30.58°N (Arar), while the longitudes range from 36.34°E (Tabuk) to 43.48°E (Qassim). All stations are situated at a height of 10 m above sea level. This data is essential for analyzing regional characteristics related to climate, weather patterns, and RE potential across the locations.

Fig. 1

Wind speed details of the 6 selected region.

Figure 1 illustrates the wind speed distribution across six regions in Saudi Arabia: Abha, Al-Baha, Arar, Qassim, Tabuk, and Taif. It highlights regional variations in wind speed, which are crucial for evaluating wind energy potential and determining the feasibility of integrating WTs into HRES. This spatial context underscores the need for location-specific designs to optimize energy generation.

Table 2 Monthly fluctuations in wind characteristics for Abha.

Table 3 Monthly fluctuations in wind characteristics for Al Baha.

Table 4 Monthly fluctuations in wind characteristics for Arar.

Table 5 Monthly fluctuations in wind characteristics for Qassim.

Table 6 Monthly fluctuations in wind characteristics for Tabuk.

Table 7 Monthly fluctuations in wind characteristics for Taif.

Table 8 Average annual wind speed characteristics for the six chosen locations.

The table provides an overview of the wind characteristics at six locations in Saudi Arabia, including the average wind speed, average power density, and the classification of the energy potential. The average wind speed varies across the locations, with Qassim experiencing the highest at 5.9991 m/s, followed by Tabuk at 5.6082 m/s and Arar at 5.4564 m/s. The lowest wind speed is observed in Abha at 3.7573 m/s. Power density, which reflects the amount of energy available per square meter, follows a similar pattern, with Qassim again showing the highest value at 149.5598 W/m², followed by Tabuk (122.1869 W/m²) and Arar (112.53 W/m²). All sites fall within Class 1 wind energy, indicating relatively low wind potential. While this class is not ideal for large-scale WT installations, these locations could support smaller, stand-alone systems, such as for local energy needs, battery charging, or hybrid energy setups that integrate wind, solar, and other energy sources.

Table 9 Wind power classification^38,40,41.

Optimal sizing of hybrid micro-grid (MG) system

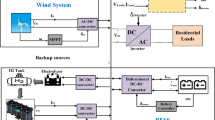
Optimal sizing of the HRES was carried out in this section to determine the best configuration for the site, considering both cost and reliability. The proposed system model integrates two RESs, namely PV and WTs. The system architecture is depicted in Fig. 2.

Due to the intermittent and variable nature of RESs, their power output often exhibits irregular and unpredictable patterns. To mitigate these fluctuations, the system incorporates an ESS comprising batteries organized in a bank. The energy produced by the RESs can result in three possible scenarios, as outlined below.

• The RESs generate enough energy to satisfy the energy demand, fulfilling the required energy needs. In this scenario, there is no surplus energy available for storage.

• The RESs generate more energy than what consumers require. The surplus energy produced by the RESs is stored in the battery bank.

• The production from the RESs was inadequate to satisfy consumer demand. As a result, the energy needs of consumers cannot be fully met by the RESs alone due to this shortfall. The ESS is utilized to supplement the output of the RESs to fulfil the energy requirements.

Modelling and system formulation

This section outlines the modeling of the key components of the MG, including PV, WTs, total power generation, consumer energy requirements, energy storage, and system reliability. The proposed system configuration is shown in Fig. 2.

PV system modelling

The production of PV power is influenced by solar irradiation (I) and temperature (T), as represented in Eq. (1)⁴¹ as:

$$\:{PV}_{p}\left(t\right)={Pr}_{pv}\times\:\left(\frac{I}{{I}_{ref}}\right)\times\:[1+{T}_{cof}({T}_{c}-{T}_{ref}\left)\right]$$

(22)

In this context, $\:{PV}_{p}\left(t\right)\:$represents the total power output from PV systems operating at their rated power, $\:{Pr}_{pv}.$ The solar irradiation I is normalized to$\:\:\:{I}_{ref}$​, which corresponds to the standard irradiation level of 1 kW/m². The temperature coefficient for PV systems, $\:{T}_{c}$, is set to 3.7 × 10⁻³ °/C, for both monocrystalline and polycrystalline silicon. $\:{T}_{ref}$ denotes the reference temperature for PV cells under standard conditions, typically set at 25 °C. $\:{T}_{c}$ is determined as follows:

$$\:{T}_{c}={T}_{amb}+({T}_{noct}-20)/800$$

(23)

Where $\:{T}_{amb}$ and $\:{T}_{noct}$ denotes the ambient temperature and the operating cell temperature, respectively. $\:{T}_{noct}$ is specified by PV manufacturer standards. For multiple PVs, denoted by $\:{N}_{pv}$, the total generated power $\:{PV}_{p}\left(t\right)$is represented in EQ (22) as in³⁴.

$$\:{PV}_{pow}\left(t\right)={N}_{pv}\times\:{PV}_{p}$$

(24)

Fig. 2

Proposed Micro-Grid.

Figure 2 depicts the proposed MG, integrating PV, WTs, and BS. This hybrid system is designed to ensure reliable and cost-effective energy supply for remote regions by optimizing resource utilization and storage.

Wind turbine system modelling

The power generated by WTs is primarily influenced by wind speed. To enhance efficiency, WTs are typically installed at significant heights on towers. The power output of a single WT can be calculated using Eq. (17), while the total power generated by multiple WTs is determined by Eq. (25).

$$\:{WT}_{Pow}\left(t\right)={N}_{wt}\times\:Pw$$

(25)

Table 10 Previous studies on Hybrid renewable power systems with their strength and weaknesses.

Battery bank modelling

The storage system acts as an ESS to stabilize fluctuations in RES production, storing surplus power when the RES output exceeds user demand. The calculation for storing charge in the battery bank follows the approach outlined in⁴⁰ and is presented below:

$$\:{B}_{store}\left(t\right)={B}_{store}\left(t-1\right)\cdot\:\left(1-\tau\:\right)+[{P}_{T}\left(t\right)-\frac{{P}_{load}}{{\eta}_{inv}}]\cdot\:{\eta}_{b}$$

$\forall\:{P}_{T}\left(t\right)>{P}_{T}\left(t\right)$ (26)

The energy stored in the ESS is represented as $\:{B}_{store}\left(t\right)$ and $\:{B}_{store}\left(t-1\right)$ at time 𝑡 and 𝑡−1, respectively. Similarly, $\:\tau\:$ denotes the self-discharge condition, and $\eta_{b}$ represents the efficiency of the storage bank.

When the power output $\:{P}_{T}\left(t\right)$ falls below $\:{P}_{load}$, the ESS is activated to compensate for the energy deficit and meet the consumers’ load demands. At this point, the battery bank enters discharge mode. Assuming 100% discharging efficiency and neglecting temperature effects, the current status of the ESS is modeled as follows⁵⁷.

$$\:{B}_{store}\left(t\right)={B}_{store}\left(t-1\right)\cdot\:\left(1-t\right)-[\frac{{P}_{T}\left(t\right)}{{\eta}_{inv}}-{P}_{T}\left(t\right)]/{\eta}_{b}$$

$\forall\:{P}_{T}\left(t\right)<{P}_{load}\left(t\right)$ (27)

Battery bank formulation

The number of batteries, denoted as $\:{N}_{b}$, is a crucial decision variable in hybrid RESs comprising PV, WT, and batteries, as it determines the total count required in the battery bank. The value of $\:{N}_{b}$ can be determined by considering both the energy demand and the energy output from the RESs. If the energy produced by the RESs exceeds the consumers’ energy requirements at time (t), the excess power is stored in the battery bank, as indicated by Eq. (41). If the energy generation from RESs falls below the energy demand, then Eq. (47) is used for energy storage.

Total power production from PVs and WTs

The total power produced by WTs and PVs is modelled below:

$$\:{P}_{T}\left(t\right)={PV}_{pow}\cdot\:{\eta}_{inv}+{WT}_{pow}$$

(28)

where $\eta_{inv}$ represents the inverter’s efficiency.

Resource allocation

This section covers the input resources that formed the MG analysis:

Estimated load data

Given the abundance of RES in Saudi Arabia, the government should explore these options as alternative energy solutions for the region. The projected energy demand is for approximately 127 households, serving a total population of 536 in the designated areas. The average household size is four individuals, many of whom have limited or no access to electricity. The primary occupations of the residents include agriculture, small businesses, and poultry and cattle farming. In these households, electricity is mainly used for energy-efficient lighting, fans, and charging mobile phones. Figure 3illustrates the hourly load demand, as referenced in⁶¹. The total power consumption is estimated to be 7,620 kWh per day, with an annual peak load projected at 754 kW. Accurately estimating the total electrical demand is essential for effective system design.

Fig. 3

24 h Load demand profile.

Figure 3 shows the 24-hour load demand profile, illustrating daily variations in electricity consumption, which helps in optimizing the MG’s capacity and configuration.

Solar and wind energy resources

Data on solar radiation intensity over a horizontal surface, average temperature, and wind speeds for the year 2022, which were used for optimal sizing, were obtained from NASA. Figures 3, 4 and 5 present the detailed potential of temperature, wind speed, and solar irradiance for the six selected sites. Figure 6 illustrates solar irradiance levels across the six selected locations, with maximum values recorded in 2022, providing critical input for optimal sizing of renewable energy systems.

Fig. 4

Wind speed data.

Figure 4 shows the wind speed data, indicating peak values of 10.8 m/s, 13.8 m/s, 12.1 m/s, 10.2 m/s, 13.7 m/s, and 13.7 m/s for Abha, Al-Baha, Arar, Qassim, Tabuk, and Taif, respectively, suggesting reasonable wind speeds for the year 2022.

Fig. 5

Temperature variation across all cities.

The temperature values obtained for these sites indicated maximum values of 41.2, 44, 45, 45, 45, and 41 °C for the year 2022 in Abha, Al-Baha, Arar, Qassim, Tabuk, and Taif, respectively.

Fig. 6

Solar Irradiance across the 6 locations.

The solar irradiance values obtained for these sites indicated maximum values of 1080, 1060, 1010, 1015, 1020, and 1080 W/m² for the year 2022 for Abha, Al-Baha, Arar, Qassim, Tabuk, and Taif, respectively.

System’s reliability

In an off-grid system, maintaining reliability is a crucial factor that must be addressed. To ensure a dependable HRES, this paper incorporates the concept of LPSP. The LPSP value ranges from 0 to 1, where 0 signifies the system’s consistent ability to meet consumers’ load demands. Conversely, an LPSP value of 1 indicates that the system is unreliable and cannot fulfil the energy requirements. Equation (29) outlines the LPSP over the course of a year, as explained in⁵⁰.

$$\:LPSP=\frac{\sum\:_{t=1}^{8760}LOPS\left(t\right)}{\sum\:_{t=1}^{8760}{P}_{load}\left(t\right)}$$

(29)

$$\:LOPS\left(t\right)={P}_{load}-{P}_{T}\left(t\right)$$

(30)

In this context, LOPS(t) refers to the loss of power supply, which happens when the energy generated by the HRES falls short of the demand at time t. The definition of LOPS is provided by Eq. (14), as explained in⁶².

System cost analysis

The economic analysis plays a critical role in optimizing integrated HRES. When designing RES, it is essential to prioritize efficiency and cost-effectiveness. Various techniques have been employed to calculate system costs. In this study, the LCOE is applied. It is determined by dividing the total cost of the system by the total energy generated by the system⁶³.

$$\:LCOE=\frac{Total\:System\:Cost\:\left({C}_{A\_total}\right)}{Total\:generated\:energy\:\left({E}_{Total}\right)}$$

(31)

System constraints

The charging level of the ESS at any given time, denoted as $\:{B}_{store}\left(t\right)$, is governed by the system’s maximum and minimum storage capacity limits. These constraints are outlined in detail below³.

$$\:{B}_{store}^{min}\left(t\right)<{B}_{store}\left(t\right)<{B}_{store}^{max}\left(t\right)$$

(31)

Here, $\:{B}_{store}^{max}\left(t\right)$ and $\:{B}_{store}^{min}\left(t\right)$ represent the battery bank’s maximum and minimum energy storage levels, respectively. The peak storage level, $\:{B}_{store}^{max}$, is equivalent to the nominal capacity of the battery bank, $\:{B}_{store}$. Conversely, the minimum storage level, $\:{B}_{store}^{min}$, can be determined using the formula given below, as shown in³.

$$\:{B}_{store}^{min}\left(t\right)=(1-{D}_{d})\times\:{B}_{store}$$

(32)

where $\:{D}_{d}$ represents depth of discharge. Constraints on the minimum and maximum numbers of PVs, WTs, and batteries are taken into account as shown as follows:

$$\:0\le\:{N}_{Pv}\le\:{N}_{pv\left(max\right)}$$

$$\:0\le\:{N}_{wt}\le\:{N}_{wt\left(max\right)}$$

$$\:0\le\:{N}_{bat}\le\:{N}_{bat\left(max\right)}$$

Proposed methodology

This section presents the MSSCS algorithm, which aims to address the issue of optimal unit sizing in this research. The Cuckoo Search (CS) algorithm, developed by Yang and Deb, is modeled after the brood parasitism behaviors observed in specific cuckoo species⁶². It integrates inclined random walk, greedy selection, and Lévy flight to explore the global optimum. The long leaps enabled by Lévy flight allow for a broader search solution area. The CS has proven effective, outperforming PSO and Genetic Algorithms (GA) due to its straightforward approach and few control parameters⁶².

However, CS’s reliance on one search strategy may lead to a lack of diversity in the search space when addressing complex optimization problems, potentially causing the algorithm to easily converge to local minima. The MSSCS has proven effective in global optimization problems due to its hybridization of exploration and exploitation mechanisms. The development of cuckoo offspring is significantly influenced by both the process and the environment in which they live⁶⁴. To improve the performance of the proposed algorithm, three new learning strategies inspired by specific cuckoo behaviors have been integrated: single-dimension, saltation, and Gaussian walk learning (GWL)⁶⁴.

To address the growing complexity of choosing suitable strategies for the multi-strategy algorithm, a multi-strategy serial framework has been introduced, drawing on the three sequential behaviors observed in a cuckoo’s development. This framework includes a serial strategy pool (SSP) comprising the three learning strategies⁵⁹. If the prerequisites for utilizing the SSP are met, it will be selected for solution updates; otherwise, a Lévy flight with strong global search performance will be employed. During the initial stages of the algorithm’s search phase, the Single-Dimension Learning (SDL) strategy will be selected from the SSP. This selection aims to prevent premature convergence and identify a promising solution, establishing a strong basis for optimization in the later stages of the algorithm⁶⁵.

MSSCS details

The sequential behaviours proposed aim to enhance the efficiency of individual learning strategies and streamline the multi-strategy algorithm⁶¹.

• (a) Saltation Learning (SL).

The choice of a host nest is critical for the survival of the cuckoo, with female cuckoos using high branches to monitor host birds and lay eggs undetected. In the algorithm, the initial search utilizes the SL strategy, which prioritizes global search over local search to hasten convergence and prevent premature convergence⁶⁶. This strategy involves updating only one dimension around a random dimension of the optimal individual in each generation, ensuring good convergence performance and reducing premature convergence. The SL approach is detailed in⁵⁵.

$$\:{X}_{i,j}^{t+1}=a\left({X}_{a1,n}^{t}-{X}_{w,n}^{t}\right)+{X}_{B,m}^{t}$$

(33)

The worst and best solutions from the t^th generation are represented by $\:{X}_{w}^{t}$ and $\:{X}_{B}^{t}$ respectively. Here, n, j, and m are randomly chosen integers from the range [1, D], where D represents the problem’s dimension. The population scale is denoted by [1, N], and is an integer randomly chosen from N.

• (b) Gaussian walk learning (GWL).

After the cuckoo successfully lays its eggs, the hatchling quickly ejects the host’s eggs from the nest. This behavior enhances the nestling cuckoo’s access to the host bird’s food, increasing its chances of survival⁶¹. To balance exploitation and exploration during the algorithm’s intermediate search phase, the GWL strategy is introduced, inspired by the eviction behavior of nestling cuckoos. Unlike the SDL strategy, which modifies only one dimension of the solution in each generation, GWL updates the entire solution and can be explained as follows⁶⁶.

$$\:{X}_{i}^{t+1}=\left({a}_{1}\cdot\:{X}_{B}^{t}-{a}_{2}\cdot\:{X}_{i}^{t}\right)+Gaussian({X}_{B}^{t},SD)$$

(34)

$$\:SD=c\cdot\:\text{e}\text{x}\text{p}(-t/{t}_{M})({X}_{i}^{t}-{X}_{w}^{t})$$

(35)

The current iteration count is represented as t, and the peak iteration count is represented as $\:{t}_{M}$. Two random numbers, $\:{a}_{1}$ and $\:{a}_{2}$ ($\:{a}_{1},{a}_{2,}\in\left[\text{0,1}\right]$), are selected from a uniform distribution with ɛ ranging between 0 and 1. It follows a Gaussian distribution with SD representing the standard deviation and $\:{X}_{B}^{t},SD$ as the expectation, as detailed in Eq. (35) above. The value of c always falls within the range of 0 to 1. The term $\:c\times\:\text{exp}\left(-\frac{t}{{t}_{M}}\right)$ is intended to regulate the step size of GWL, while the term ($\:{X}_{i}^{t}-{X}_{w}^{t}$) is employed to adjust the search direction of GWL.

• (c) Single Dimension Learning (SDL).

Once the nestling eviction phase is complete, a young cuckoo loudly calls for attention from its host parents. As the host bird approaches, the young cuckoo intensifies both the volume and duration of its calls, thereby increasing its chances of being fed and, consequently, its survival⁶⁴. The SDL strategy was integrated into the algorithm’s later search phase to accelerate convergence and guide the solution closer to the optimal outcome. This approach was inspired by the begging behavior of young cuckoos⁶⁷. In SDL, a single dimension is randomly altered for each individual in every generation, with the update information originating from that same dimension. This behavior, which focuses on a single dimension, reduces inter-dimensional correlation and enhances the algorithm’s ability to conduct local searches, thus improving the convergence rate towards the end of the search. SDL is described in⁵⁹.

$$\:{X}_{i,j}^{t+1}=a\left({X}_{a1,j}^{t}-{X}_{w,j}^{t}\right)+{X}_{B,m}^{t}$$

(36)

Here, a is an integer randomly selected from the range [1, N], where N indicates the population size, and jis randomly picked from the set⁵⁸. The random number a is uniformly distributed within the range of [−1, 1], allowing the algorithm to perform bidirectional searches and improve its local search abilities.

• (d) Multi-strategy serial structure.

A multi-strategy serial framework is proposed, inspired by the three sequential behaviors observed during the cuckoo’s growth process. This framework aims to streamline the algorithm and enhance the effectiveness of each learning method. Within this structure, a switching parameter (SP) is introduced, allowing users to decide whether to utilize an approach from the SSP. Each strategy is defined in⁵⁹.

$$\:{SSP}_{i}\left\{\begin{array}{c}SL={X}_{i}^{t+1}=a\left({X}_{a1}^{t}-{X}_{w,n}^{t}\right)+{X}_{B,m}^{t}\:if\:t\in\:[1\cdot\:PA*MaxIt]\\\:GWL={X}_{i}^{t+1}=\left({a}_{1\cdot\:{X}_{B}^{t}}-{a}_{2\cdot\:{X}_{i}^{t}}\right)+Gaussian\left({X}_{B}^{t},SD\right),\:ift\in\:\left[PA*MaxIt\right]\\\:SDL={X}_{i,j}^{t+1}=a\left({X}_{a1,j}^{t}-{X}_{W,j}^{t}\right)+{X}_{B,m}^{t}\:otherwise\end{array}\right.\:$$

(37)

The strategy in the SSP is denoted by I∈^1,2,3 where t and MaxIt represent the current and maximum number of iterations, respectively, and PA denotes the probability. The SP is used to count the number of unimproved solutions. If SP exceeds the threshold T, the algorithm adjusts the solution using a strategy from the SSP. Otherwise, the algorithm applies Lévy flight, known for its robust global search capabilities, to continuously update the solution for L iterations.

• (e) Parameter Dynamic turning (PDT).

The count of unimproved solutions must be equal to or greater than T, which represents the minimum threshold for employing the SSP. The PDT governs the use of SSP and Lévy flights, influencing the algorithm’s balance between exploration and exploitation. Additionally, T is related to the population size N, as detailed in⁶⁸.

$$\:{T}_{i}=\frac{N}{2.5}$$

(38)

The parameter PA, which compute the proportion of each learning approach in the SSP, is modified according to⁶⁸.

$$\:{PA=PA}_{m}+\frac{{{PA}_{M}-PA}_{m}}{D}$$

(39)

Where $\:{PA}_{M}\:$ and $\:{PA}_{m}\:$represent the maximum and minimum values of PA, respectively, and D signifies the dimension of the problem.

Results

This section introduces and examines the wind energy assessment results, as well as the optimal sizing for the six selected locations.

Wind energy assessment

This section presents the annual and monthly wind speed features for the six regions considered.

Annual mean wind speed

Tables 2, 3, 4, 5, 6, 7 and 8 present the monthly wind characteristics for Abha, Al-Baha, Arar, Qassim, Tabuk, and Taif at a height of 10 m. The data shows that Abha has the lowest average annual wind speed in August at 2.97 m/s, while Qassim records the highest wind speed in February at 7.23 m/s. In March, Qassim experiences the lowest monthly wind speed that yields maximum energy at 6.5664 m/s, with the most frequent wind speed at 6.8 m/s. Abha’s maximum and minimum wind speeds occur in October at 4.74 m/s and August at 2.97 m/s, respectively, corresponding to the highest and lowest energy. Tabuk’s wind speeds range from 4.38 m/s in September to 6.7 m/s in February and March, with corresponding maximum and minimum energy. In Taif, the wind speed reaches a minimum of 4.00 m/s in October and peaks at 6.69 m/s in March. Overall, Qassim exhibits the most favorable wind speeds based on the data.

The annual Weibull parameters, k and c, derived from the data using Eqs. (5) and (6), are shown in Tables 2, 3, 4, 5, 6 and 7. The scale parameter c ranges from 3.4008 m/s in August in Al-Baha to 6.7205 m/s in February in Qassim, while the shape parameter k spans from 8.8071 in August in Arar to 40.8131 in July in Tabuk, indicating significant variation in wind speeds across the region. Table 8 summarizes the average annual wind speed characteristics, showing that the mean yearly wind speed ranges from 3.7573 m/s in Abha to 5.9991 m/s in Qassim. The annual average power density ranges from 36.7432 to 149.5598 W/m², all below 200 W/m², classifying these areas within Class 1 wind energy resources (see Table 9). While this level of wind resource is not ideal for large-scale WT applications, it may be suitable for smaller, stand-alone energy systems, such as battery charging, mechanical applications like water pumping, and hybrid systems incorporating wind, solar, batteries, and DGs. Furthermore, Tables 2, 3, 4, 5, 6, 7 and 8 present statistical error metrics used to evaluate the data fit. RMSE values, ranging from 0.00071129 to 0.01295, are nearly zero, indicating a strong fit. Additionally, $\:{R}^{2}$ values range from 0.9499 to 1.02610, with values close to 1 confirming the accuracy of the fit. Table 10 provides an overview of previous studies on hybrid renewable power systems, highlighting their objectives, energy sources, constraints, software tools used, and the strengths and weaknesses of each approach. This comparison underscores the gaps our study aims to address by proposing a more robust optimization methodology.

Weibull frequency distributions

Figures 7, 8, 9, 10, 11 and 12 present the yearly Weibull probability density and cumulative distribution functions based on the time series data for the entire study period, representing the Weibull distribution for each of the six locations. The probability density and cumulative plots show relatively consistent curve patterns across the study duration for each site. In general, wind speeds in Abha and Al-Baha rarely exceed 5.8 m/s in most months, while those in Arar, Tabuk, and Taif stay below 6.8 m/s. Only Qassim occasionally experiences wind speeds above 7 m/s, with a maximum of 7.2 m/s. As a result, all locations are classified as Class 1 wind resources. The Weibull probability density function for Al-Baha is shown in Fig. 8, highlighting the distribution pattern and the predominance of wind speeds below 6 m/s across most months. As depicted in Fig. 9, the Weibull distribution for Arar demonstrates peak wind speeds generally below 6.8 m/s, confirming its classification as a low-wind energy resource region​. Figure 10 presents the Weibull distribution for Qassim, with occasional peak wind speeds reaching 7.2 m/s, indicating its higher wind energy potential compared to other locations in this study​. The Weibull distribution for Tabuk is shown in Fig. 11, illustrating a consistent pattern of wind speeds generally below 6.8 m/s, characteristic of its moderate wind energy profile​. Figure 12 shows the Weibull probability density function for Taif, where wind speeds exhibit slight variations, mostly remaining under 6.5 m/s, aligning with the region’s classification as a low-wind energy resource.

Fig. 7

Weibull probability density function for Abha.

Figure 7 shows a peak at 3 m/s, with a significant portion of the curve between 2 m/s and 4 m/s, it suggests that wind power generation in Abha is limited because the wind is mostly low. In such a case, WTs would only produce small amounts of energy, so a hybrid system with solar power would be more effective to meet energy demands.

Fig. 8

Weibull probability density function for Al-Baha.

Figure 8 shows a peak at 4 m/s, with a significant distribution around this value, it indicates that Al-Baha has moderate wind energy potential. The WTs will generate power most efficiently at this wind speed, but the overall wind energy output will be lower than in regions with higher peak wind speeds. A HRES integrating wind with solar and storage technologies could optimize energy production in this region.

Fig. 9

Weibull probability density function for Arar.

Figure 9 shows a peak at around 5 m/s, with a reasonably wide distribution, it suggests that Arar has moderate to good wind energy potential. The WTs will likely operate efficiently around 5 m/s, but the variation in wind speeds might require additional systems to ensure consistent energy supply, especially if there are periods with low wind speeds.

Fig. 10

Weilbull probability density function for Qassim.

Figure 10 shows a peak at 4 m/s with a relatively narrow curve, it suggests that Qassim has moderate and fairly consistent wind energy potential. The WTs would operate efficiently around the peak wind speed, providing steady energy generation. However, if the distribution is wider or the peak is lower, it might indicate the need for additional RE (like solar) or energy storage to ensure a reliable power supply.

Fig. 11

Weibull probability density function for Tabuk.

Figure 11 shows a peak at 5 m/s with a relatively narrow distribution, it indicates that Tabuk has a moderate, consistent wind energy potential. The WTs would generate the most energy at around 5 m/s. However, if the distribution is wide, fluctuations in wind speed might require the addition of solar energy or storage systems to ensure stable power generation.

Fig. 12

Weibull probability density function for Taif.

Figure 12 shows a peak at around 4 m/s with a relatively narrow distribution, it suggests that Taif has moderate wind energy potential, with consistent winds near the peak wind speed. The WTs would operate effectively in this range, but the energy generation potential might be limited compared to regions with higher wind speeds.

Optimal sizing of the proposed micro-grid

This section presents the results for the proposed MG models across the six selected locations. The study aimed to minimize both the LCOE and LPSP to identify the optimal configuration. For each site, the configurations considered include a PV & Battery system, a Wind & Battery system, and a combined PV, Wind & Battery system. These setups were selected to ensure a consistent RESs, capable of meeting the load demand while maintaining the charge of the battery bank.

Simulation results for Abha

The cost summary of the three configurations for Abha is presented in Table 11, while Fig. 13 shows the objective plots against iterations.

Table 11 Cost Summary for Abha.

The table above displays the quantities of individual components for each configuration after 100 iterations. It can be observed that the optimal sizing for the Abha region is Configuration 1, which integrates PV, a WT, and ESS. This configuration achieves the lowest values for the NPC, LCOE, and LPSP. Specifically, Configuration 1 has the most cost-effective and reliable setup, making it the best choice for the Abha region compared to the other configurations.

Fig. 13

LCOE iteration curve for Abha.

Figure 13 shows that Configuration 1 converges to the lowest LCOE after several iterations, it suggests that the hybrid microgrid design for Abha, integrating wind, solar, and storage, is the most cost-efficient. This configuration not only balances cost and performance but also represents the best economic option for providing reliable energy in the region.

Fig. 14

LPSP for Abha.

Figure 14 shows that Configuration 1 has the lowest LPSP, it implies that, for Abha, this configuration ensures the most reliable energy supply. This is crucial for off-grid or remote locations where consistent power is essential, and it strengthens the conclusion that Configuration 1 is the optimal choice due to its superior performance in NPC, LCOE, and LPSP.

Simulation results for Al Baha

The cost summary of the three configurations for Al-Baha is presented in Table 12, while Fig. 14 shows the objective plots against iterations.

Table 12 Cost summary for Al_Baha.

Table 12 presents the quantities of individual components for the three configurations after 100 iterations. From the table, it is evident that Configuration 1 is the optimal choice for the Al Baha site in terms of cost, as it integrates PV, WT, and BS systems and achieves the lowest NPC and LCOE values. Although Configuration 2 provides the best LPSP, with the lowest LPSP value among the three configurations, the higher costs associated with this configuration make Configuration 1 the more cost-effective and balanced option.

Fig. 15

LCOE iteration curve for Al-Baha.

Figure 15 shows Configuration 1 consistently achieving the lowest LCOE over iterations, it indicates that, for Al-Baha, this configuration offers the best economic solution for energy generation. This makes Configuration 1 the optimal choice in terms of cost-effectiveness, providing a reliable and affordable power supply for the region.

Fig. 16

LPSP for Al-baha.

Figure 16 shows Configuration 2 with the lowest LPSP but Configuration 1 very close behind, it suggests that Configuration 1 provides a nearly equally reliable system while offering better cost-effectiveness. Therefore, Configuration 1 remains the optimal choice, as its slight disadvantage in LPSP is outweighed by its superior financial performance, making it the best overall option for Al-Baha.

Simulation results for Arar

The cost summary for the three configurations in Arar is shown in Table 13, while Fig. 15 displays the objective plots across iterations.

Table 13 Cost summary for Arar.

Table 13 presents the quantities of individual components for three configurations after 100 iterations. From the table, it is observed that Configuration 1 is the most cost-effective option for the given site. This configuration, which integrates PV, WT, and BS systems, results in the lowest NPC and LCOE values, with an LPSP of 0.0491%. Although Configuration 2 and Configuration 3 result in higher NPC and LCOE values, Configuration 3 offers the lowest LPSP at 0.0729%, indicating a better performance in terms of reliability. However, considering the cost effectiveness, Configuration 1 remains the preferred choice.

Fig. 17

LCOE iteration curve for Arar.

Figure 17 shows Configuration 1 with the lowest LCOE across iterations, it indicates that Configuration 1 is the most cost-efficient solution for Arar, providing the best value for energy production. This configuration is optimal because it balances low costs with reliable performance, making it the preferred choice.

Fig. 18

LPSP for Arar.

Figure 18 shows Configuration 1 with the lowest LPSP, it indicates that Configuration 1 ensures the most reliable energy supply for Arar. This makes it the optimal configuration, as it combines low costs (NPC and LCOE) with the highest reliability, providing a robust and cost-efficient energy solution for the region.

Simulation results for Qassim

The cost summary for the three configurations in Qassim region is shown in Table 14, while Fig. 15 displays the objective plots across iterations.

Table 14 Cost summary for Qassim.

The table above presents the quantities of the individual components for each configuration after 100 iterations. From the table, it can be observed that the optimal sizing for the Qassim region is Configuration 1, which incorporates PV, WT, and BS systems. This configuration has the lowest values for NPC, LCOE, and LPSP, making it the most cost-efficient and reliable solution among the three configurations.

Fig. 19

LCOE iteration curve for Qassim.

Figure 19 shows that Configuration 1 consistently achieves the lowest LCOE across iterations, it suggests that this configuration is the most cost-effective solution for Qassim. By minimizing costs while maintaining adequate system performance, Configuration 1 is the optimal choice for providing affordable energy to the region.

Fig. 20

LPSP for Qassim.

Figure 20 shows that Configuration 1 has the lowest LPSP, it suggests that Configuration 1 provides the most reliable energy supply for Qassim. With the lowest costs in NPC and LCOE, and the highest reliability in terms of LPSP, Configuration 1 is the optimal solution for the region, ensuring both affordable and dependable energy production.

Simulation results for Tabuk

The cost summary for the three configurations in Tabuk region is shown in Table 15, while Fig. 15 displays the objective plots against iterations.

Table 15 Cost summary for Tabuk.

The table above shows the quantities of the individual components for the different configurations after 100 iterations for the Tabuk region. It can be observed that Configuration 1, which combines PV, WT, and BS systems, provides the optimal sizing in terms of cost, with the lowest NPC and LCOE values. While Configuration 2 offers the best LPSP value, the lowest among all three configurations, Configuration 1 still stands out as the most cost-effective solution, making it the optimal choice for the region.

Fig. 21

LCOE iteration curve Tabuk.

Figure 21 shows that Configuration 1 consistently achieves the lowest LCOE across iterations, it suggests that this configuration provides the best economic value for Tabuk, offering the lowest energy costs while maintaining reliable performance. This makes Configuration 1 the optimal choice for energy generation in the region.

Fig. 22

LPSP for Tabuk.

Figure 22 shows that Configuration 1 has an LPSP close to Configuration 2 but has better cost metrics (NPC and LCOE), it suggests that Configuration 1 is the optimal choice for Tabuk. Even though Configuration 2 is slightly more reliable in terms of LPSP, Configuration 1 provides a more favorable balance of cost and reliability, making it the preferred option.

Simulation results for Taif

The cost summary for the three configurations in Taif region is shown in Table 16, while Fig. 15 displays the objective plots against iterations.

Table 16 Cost summary for Taif.

The above table shows the quantities of the individual components for the different configurations after 100 iterations for the Taif site. It can be observed that Configuration 1 has the lowest NPC and LCOE values, making it the most cost-effective solution. However, Configuration 2 performs better in terms of LPSP, offering the lowest value among the three configurations. While Configuration 1 is optimal from a cost perspective, Configuration 2 is better suited for meeting the load demands. Therefore, Configuration 1 is recommended based on cost considerations, while Configuration 2 would be preferred for ensuring reliability in meeting the energy needs.

Fig. 23

LCOE iteration curve Taif.

Figure 23 shows Configuration 1 with the lowest LCOE after several iterations, it indicates that Configuration 1 is the optimal solution for Taif, offering the best value in terms of cost while maintaining reliable energy production.

Fig. 24

LPSP for Tabuk.

Figure 24 shows that Configuration 1 has an LPSP value that is very close to Configuration 2, but Configuration 1 offers the best cost values in NPC and LCOE, it suggests that Configuration 1 remains the optimal choice. It provides a very reliable system at a lower cost, making it the preferred option for Taif.

Conclusions and recommendations for future research

This study evaluates the wind energy potential and hybrid MG design in six Class 1 wind regions of Saudi Arabia—Abha, Al-Baha, Arar, Qassim, Tabuk, and Taif—using the Weibull distribution function and a MSSCS algorithm. Although these regions have low wind power densities below 200 W/m², the study demonstrates that hybrid systems combining small-scale WT, PV systems, and BS can offer effective solutions, especially for off-grid locations.

The optimization results show that Configuration 1, consisting of PV, WTs, and BS, achieved the lowest LCOE, with the lowest value of $0.148/kWh in Qassim. Additionally, Configuration 1 exhibited high reliability, with LPSP values below 0.05% in many regions. However, in areas like Al-Baha, Taif, and Tabuk, Configuration 2 demonstrated better reliability, achieving the lowest LPSP despite a slightly higher cost.

This study contributes to the field by focusing on Class 1 wind regions, which are underexplored in the literature. It combines small-scale WTs, solar PV, and BS in an optimized hybrid system, tailored for off-grid applications. This approach is novel compared to earlier studies, which have focused primarily on solar or wind alone. Moreover, the application of the MSSCS algorithm for optimizing hybrid systems is a key innovation, providing a more robust solution than traditional optimization methods.

The study also introduces a comprehensive framework for evaluating the LCOE, NPC, and LPSP, offering a holistic view of system feasibility. The findings highlight the importance of balancing cost, energy production, and reliability when designing hybrid systems in low-wind areas.

The insights from this research provide valuable guidance for implementing RES in low wind potential regions. Future work could explore the integration of advanced energy storage technologies, such as hydrogen fuel cells, and the use of artificial intelligence (AI) and machine learning for dynamic grid management. Expanding the research to regions with varying climates and RE profiles would enhance the optimization framework. Additionally, long-term feasibility studies, including economic incentives and policy frameworks, would further support the practical deployment of hybrid MGs.

Finally, investigating demand-side management strategies and decentralized energy markets could offer innovative approaches to optimize energy distribution and reduce system costs.