TOPSIS prefabricated building construction evaluation based on interval-valued Pythagorean fuzzy numbers based on prospect theory

Abstract

Prefabricated buildings have a series of advantages such as high efficiency, energy savings, and environmental protection, and are being strongly promoted by the Chinese government. However, due to the late start of prefabricated buildings in China, the installation process of prefabricated components is relatively complex, leading to difficulties in quality and safety control. A novel evaluation methodology integrating the technique for order preference by similarity to ideal solution (TOPSIS) with prospect theory and interval-valued Pythagorean fuzzy numbers (IVPFNs) is proposed. Fully considering the subjective value perceptions of decision-makers when faced with losses and gains, a risk evaluation model is established based on different types of decision-makers. This model is then compared with the weight correction coefficient model from a balanced perspective to prevent bias caused by over-reliance on decision-makers’ subjective preferences. This study establishes an assessment index system for assembly construction risk, considering personnel, materials, machinery, management, and technology factors. By merging prospect theory with the TOPSIS method, the application of Pythagorean fuzzy numbers is refined, enhancing the group decision-making process for evaluating risks in prefabricated construction projects. On the other hand, the prospect theory approach can focus on the actual psychological state of managers during decision-making, addressing the research gap concerning the impact of managers’ psychological states on the evaluation process. The study identifies critical risk factors and suggests specific risk management strategies to improve the risk mitigation capabilities of construction entities, offering a structured approach to enhancing the efficiency and safety of prefabricated construction projects.

Introduction

PC is an efficient construction method that allows for the manufacturing of prefabricated components in a controlled environment and their rapid assembly on-site¹. In recent years, with the emergence of labor shortages and the increasing demand for low-carbon emissions, energy savings, and environmental protection, prefabricated buildings have gradually become a focal point due to their energy-saving and emission-reduction benefits² and labor-intensive characteristics³. Table 1 compares prefabricated buildings with traditional construction methods. As shown in the table above, prefabricated buildings have significant advantages over conventional buildings in various aspects. With continuous technological advancements and the gradual reduction in costs, prefabricated buildings are expected to play an increasingly important role in the future of the construction industry.

Currently, industrialized construction has become an ideal approach to promoting high-quality development in the construction industry, with prefabricated buildings exemplifying sustainable development⁴. To support prefabricated buildings, the Chinese government has mandated that by 2025, prefabricated buildings should account for more than 50% of new constructions⁵. However, the development of prefabricated buildings in China started relatively late, and the construction process is more complex compared to conventional buildings, making it difficult to popularize⁶. Additionally, the management system is not yet fully developed⁷. The market share of prefabricated buildings in China remains relatively low, at only around 5%⁸. Therefore, scientifically and rationally assessing the construction risks of prefabricated buildings is of great significance for improving risk management in this sector.

Table 1 Comparison of prefabricated buildings and traditional buildings.

Despite the recognized benefits of prefabricated construction in enhancing efficiency and sustainability, the evaluation of its adoption and implementation faces significant challenges. Current evaluation methods, such as the grey assessment model⁹, combined weighted TOPSIS¹⁰, structural equation modeling¹¹, and AHP¹², show considerable limitations. The body of research, both within China and internationally, has focused predominantly on aspects such as structural design¹³, cost estimation¹⁴, and supply chain management¹⁵. However, there is a notable gap in the literature regarding the risks associated with the construction phase of prefabricated buildings, particularly those arising from uncertainties in component manufacturing, transportation, and assembly, which demand a high level of technical expertise among construction personnel¹⁶. Furthermore, the limited adoption of prefabricated construction within the domestic market suggests the presence of potential unforeseen risks in initiating prefabricated projects.

Xie et al.¹⁷ used a case-based reasoning method to study the issue of delays in prefabricated building construction. Shen et al.¹⁸ used the binomial coefficient method and entropy weight method to develop a material component model to assess the construction risks of prefabricated buildings. Zhao¹⁹ reviewed global construction risk management using literature co-citation and bibliometric coupling techniques, concluding that advanced risk analysis technologies and ICT-driven CRM are gaining increasing attention. Wuni et al.²⁰ conducted a risk assessment of on-site assembly risk factors for modular integrated construction projects, identifying top-ranked risks such as on-site module installation discrepancies and errors. Liu²¹ proposed a construction safety evaluation method for prefabricated buildings based on a cloud model, providing a new perspective for the objective evaluation of prefabricated engineering safety. Xu²² evaluated the safety factors of prefabricated building construction using ISM and ANP, highlighting their significance in reducing safety risks in prefabricated building construction.

The aforementioned methods establish models to evaluate prefabricated buildings from various perspectives, but they also have corresponding limitations: (1) There may be information loss when translating expert opinions. Although linguistic terms such as fuzzy numbers and intuitionistic fuzzy numbers can describe expert attitudes simply and quickly, they fail to accurately and delicately capture these attitudes during the translation process. (2) These methods cannot fully and accurately simulate the decision-making environment of managers. While many factors are considered in these methods, managers must take into account human psychological states when making decisions, which is crucial for enhancing the practical applicability of the models.

To address the research gaps identified in the existing literature, this paper proposes a TOPSIS model based on IVPFNs using an improved prospect theory for evaluating prefabricated building construction. This study differs from previous Pythagorean fuzzy models in the following ways: (1) Utilization of interval-valued Pythagorean fuzzy numbers. While current research focuses on the application of Pythagorean fuzzy numbers, this paper employs interval-valued Pythagorean fuzzy numbers to construct the risk evaluation model. Compared to Pythagorean fuzzy numbers, interval-valued Pythagorean fuzzy numbers can retain expert attitudes to a much greater extent during the translation process, providing a more accurate and nuanced description of expert opinions. (2) Introduction of prospect theory. Traditional risk evaluation methods effectively address the randomness, uncertainty, and interdependence of risks but often overlook the influence of managerial attitude shifts on evaluation outcomes during the decision-making process. Therefore, this model incorporates prospect theory, thoroughly considering managers’ psychological states during risk evaluation, thereby more comprehensively and accurately simulating the actual decision-making environment.

The scope of this study is limited to risk management during the construction phase of prefabricated buildings. The second section introduces the methods used in this paper. The third section presents the risk evaluation framework for prefabricated building construction. In the fourth section, the model is applied to a real case, and the impact of different decision-maker attitudes on the results is discussed. A comparison with other methods demonstrates the accuracy of the proposed model. The fifth section summarizes the overall research content of this paper. Finally, relevant suggestions are provided for future directions and prospects.

Preliminaries

Prospect theory

Kahneman and Tversky²³ were the first to conduct an in-depth study of decision-makers’ behavior from a dynamic perspective, discovering that decision-makers change their psychological state under the influence of surrounding environmental factors. The formula is as follows:

$$\phi \left( x \right) = \left\{ {\begin{array}{*{20}l}{\Delta x^{\alpha } ,\Delta x \ge 0}\\{ - \theta \left( { - \Delta x} \right)^{\beta } ,\Delta x < 0} \\ \end{array} } \right.$$

(1)

where, parameter $\:\alpha\:>0$ and $\:\beta\:<1$ represents the sensitivity of decision makers to gains and losses respectively; parameter $\:{\uptheta\:}>1$ indicates that decision makers are more sensitive to losses than to benefits. A large number of experiments and calculations prove that the coefficient of the above formula is usually $\:\alpha\:=\beta\:=0.88$ and $\:\theta\:=2.25$. In the following, the above definition is extended to the Pythagorean fuzzy environment, and the Pythagorean fuzzy foreground value function is proposed. Introducing IVPFNs into the framework of prospect theory, a Pythagorean fuzzy prospect value function was proposed.

Definition 1 ²⁴

Suppose the Pythagorean fuzzy number P₁ and P₂, if P₂ is taken as the decision-making reference point, then the prospect value function of P₁ is:

$$\phi \left( {P_{1} } \right) = \left\{ {\begin{array}{*{20}c} {d\left( {P_{1} P_{2} } \right)^{\alpha } ,P_{1} \ge P} \\ {~ - \theta \left( {d\left( {P_{1} ,P_{2} } \right)} \right)^{\beta } ,P_{1} < P_{2} } \\ \end{array} } \right.$$

(2)

Prospect theory considering decision-makers’ subjective preferences

Due to the varying psychological characteristics of decision-makers, they can generally be categorized into three types: optimistic, pessimistic, and neutral. By studying the decision-making problems of these three types of decision-makers, it is observed that after accounting for risk preferences, all three groups can make corresponding behavioral adjustments based on their psychological expectations.

Definition 2

For distance measures, there exist two types of measurement attributes: cost-type and benefit-type. When a smaller distance measure between two entities is preferable, it is referred to as a cost-type distance measure; conversely, when a larger distance measure is preferable, it is referred to as a benefit-type distance measure.

Assumption 1

For optimistic decision-makers, when the distance measure is cost-type, their psychological expectation is the minimum distance between fuzzy numbers. In this case, the decision reference point is$\:{D}^{L}={min}_{j}d\left({P}_{1}{P}_{2}\right),j=\text{1,2},\cdots\:,n$. Conversely, when the distance measure is benefit-type, their psychological expectation is the maximum distance between fuzzy numbers, and the decision reference point becomes$\:{D}^{L}={max}_{j}d\left({P}_{1}{P}_{2}\right),j=\text{1,2},\cdots\:,n$.

Assumption 2

For pessimistic decision-makers, when the distance measure is cost-type, their psychological expectation is the maximum distance between fuzzy numbers. In this case, the decision reference point is$\:{D}^{B}={max}_{j}d\left({P}_{1}{P}_{2}\right),\:\:j=\text{1,2},\:\cdots\:,n$. Conversely, when the distance measure is benefit-type, their psychological expectation is the minimum distance between fuzzy numbers, and the decision reference point becomes$\:{D}^{B}={min}_{j}d\left({P}_{1}{P}_{2}\right),j=\text{1,2},\cdots\:,n$.

Assumption 3

For neutral decision-makers, regardless of whether the distance measure is cost-type or benefit-type, their psychological expectation is the distance between fuzzy numbers: $\:{D}^{Z}=d\left({P}_{1}{P}_{2}\right),j=1,\:2,\cdots\:,\:n$.

Building upon the aforementioned assumptions, this paper constructs a model using neutral decision-makers as an example. The basic idea is to use the neutral-type $\:{D}^{Z}$ as the reference point and calculate the prospect value function for each alternative. Specifically, when $\:{\Delta\:}{d}_{j\:}<0$, the decision-maker perceives a loss, and the prospect value is given by $\:{V}_{j}=-\theta\:{\left(-{\Delta\:}{d}_{j}\right)}^{\beta\:}$; when $\:{\Delta\:}{d}_{j\:}\ge\:0$, the decision-maker perceives a gain, and the prospect value function is $\:{V}_{j}={\left({\Delta\:}{d}_{j}\right)}^{\alpha\:}$. Since $\:{V}_{j}$ can be both positive and negative, and the distance measure can be either cost-type or benefit-type, in order to ensure that all prospect values are positive and that larger values are preferable, the prospect values are transformed as follows:

$$\:\begin{array}{c}{V}_{j}^{\prime }=max\left\{{V}_{1},{V}_{2},\cdots\:,{V}_{n}\right\}-min\left\{{V}_{1},{V}_{2},\cdots\:,{V}_{n}\right\}+{V}_{j}\end{array}$$

(3)

$$V_{j}^{{\prime \prime }} = max\left\{ {V_{1} ,V_{2} , \cdots ,V_{n} } \right\} - min\left\{ {V_{1} ,V_{2} , \cdots ,V_{n} } \right\} - V_{j}$$

(4)

Among these, Eq. (3) represents the transformation of the prospect value calculated for the benefit-type distance measure, while Eq. (4) represents the transformation for the cost-type distance measure. After transformation, both $\:{V}_{j}^{\prime }$and $\:{V}_{j}^{\prime \prime}$ are positive, and larger values indicate better outcomes. For simplicity, the subsequent text will continue to use $\:{V}_{j}$ to represent both $\:{V}_{j}^{\prime }\text{a}\text{n}\text{d}{V}_{j}^{\prime \prime}$.

After transforming the prospect values calculated under different scenarios, normalization is then applied to obtain the weights associated with the distance measures.

$$\:\begin{array}{c}{\varrho\:}_{j}=\frac{{V}_{j}}{\sum\:_{j=1}^{n}{V}_{j}}\end{array}$$

(5)

Subjective weight adjustment coefficient based on an equilibrium perspective

To prevent bias caused by determining weights solely based on the decision-maker’s subjective preferences, a weight adjustment coefficient from a balanced perspective is introduced. The basic idea is to use the average value of all distance measures as the equilibrium benchmark. For all distance measures, this equilibrium benchmark represents an acceptable distance measure. The smaller the deviation of other distance measures from the equilibrium benchmark, the higher the consensus of that distance measure relative to others, and thus, it is assigned a more significant weight. Conversely, the greater the deviation, the smaller the weight assigned. Therefore, the degree of deviation of a distance measure from the equilibrium benchmark is given by:

$$\:\begin{array}{c}{DV}_{j}=\frac{\left|{d}_{j}-\stackrel{-}{{d}_{j}}\right|}{\stackrel{-}{{d}_{j}}}\end{array}$$

(6)

where, $\:\stackrel{-}{{d}_{j}}=\frac{1}{n}\sum\:_{j=1}^{n}{d}_{j}$. Based on this, the weight adjustment coefficient from a balanced perspective is:

$$\:\begin{array}{c}{\xi\:}_{j}=\frac{E-{DV}_{j}}{\sum\:_{j=1}^{n}\left(E-{DV}_{j}\right)}\end{array}$$

(7)

where, $\:E={max}_{j}{DV}_{j}+{min}_{j}{DV}_{j}$

The weight adjustment coefficients obtained from Eqs. (6) and (7) are applied to the weights derived from Eq. (5) to ensure the rationality of the results. Therefore, the adjusted weights are:

$$\:\begin{array}{c}{\varrho\:}_{j}^{\text{*}}=\frac{{\xi\:}_{j}{\varrho\:}_{j}}{\sum\:_{j=1}^{n}{\xi\:}_{j}{\varrho\:}_{j}}\end{array}$$

(8)

where, $\:{\varrho\:}_{j}$ represents the weights obtained from both the benefit-type distance measure and the cost-type distance measure.

IVPFNs

The applicable range for intuitionistic fuzzy sets is $\:\mu\:+\nu\:\le\:1$. However, in practical decision-making scenarios, situations of $\:\mu\:+\nu\:>1$ arise, posing challenges for managers and experts. In this context, the introduction of the Pythagorean fuzzy set to the global academic community, characterized by the sum of the squares of membership and non-membership degrees being less than 1, was first made in references^25,26. Compared to intuitionistic fuzzy sets, managers are not bound by understanding the associated constraints and usage rules; they can freely assign scores, reducing the constraints of valuation. Consequently, the Pythagorean fuzzy set has become the preferred method for describing fuzzy problems. This translation is structured to ensure clarity, precision, and appropriate utilization of professional terminology.

Definition 3 ²⁷

Interval-valued hesitation for IVPFNs sets $\:\stackrel{\sim}{P}$:

$$\:\begin{array}{c}{\stackrel{\sim}{\pi\:}}_{\stackrel{\sim}{p}}=\left[{\mu\:}_{\stackrel{\sim}{P}}^{L}\left(x\right),{\mu\:}_{\stackrel{\sim}{P}}^{U}\left(x\right)\right],\left[{\nu\:}_{\stackrel{\sim}{P}}^{L}\left(x\right),{\nu\:}_{\stackrel{\sim}{P}}^{U}\left(x\right)\right]\\\:=\left[\sqrt{1-{\left({\mu\:}_{\stackrel{\sim}{P}}^{U}\left(x\right)\right)}^{2}-{\left({\nu\:}_{\stackrel{\sim}{P}}^{U}\left(x\right)\right)}^{2}},\sqrt{1-{\left({\mu\:}_{\stackrel{\sim}{P}}^{L}\left(x\right)\right)}^{2}-{\left({\nu\:}_{\stackrel{\sim}{P}}^{L}\left(x\right)\right)}^{2}}\right]\end{array}$$

(9)

If $\:{\mu\:}_{\stackrel{\sim}{P}}^{L}\left(x\right)={\mu\:}_{\stackrel{\sim}{P}}^{U}\left(x\right)$ and$\:{\nu\:}_{\stackrel{\sim}{P}}^{L}\left(x\right)={\nu\:}_{\stackrel{\sim}{P}}^{U}\left(x\right)$, the IVPFNs set degenerates into a Pythagorean fuzzy set. Thus, IVPFNs sets are a generalization of Pythagorean fuzzy sets, and Pythagorean fuzzy sets are a special case of IVPFNs sets.

For the convenience of subsequent writing, $\:\left[{\mu\:}_{\stackrel{\sim}{P}}^{L}\left(x\right),{\mu\:}_{\stackrel{\sim}{P}}^{U}\left(x\right)\right],\left[{\nu\:}_{\stackrel{\sim}{P}}^{L}\left(x\right),{\nu\:}_{\stackrel{\sim}{P}}^{U}\left(x\right)\right]$ is called the IVPFNs number, which is abbreviated as$\:\stackrel{\sim}{\alpha\:}=\left(\left[a,b\right],\left[c,d\right]\right)$, among which $\:\left[a,b\right]\subseteq\:\left[\left[\text{0,1}\right]\right]\:$, $\:\left[c,d\right]\subseteq\:\left[\left[\text{0,1}\right]\right]\:$and $\:{b}^{2}+{d}^{2}\le\:1$.

Definition 4 ²⁸

Let $\:{\alpha\:}_{1}=\left(\left[{a}_{1}{,b}_{1}\right]\left[{c}_{1},{d}_{1}\right]\right)$ and $\:{\alpha\:}_{2}=\left(\left[{a}_{2}{,b}_{2}\right]\left[{c}_{2},{d}_{2}\right]\right)$ be two IVPFNs numbers, and the natural quasi-order relationship of IVPFNs numbers is defined as $\:\stackrel{\sim}{{\alpha\:}_{1}}>\stackrel{\sim}{{\alpha\:}_{2}}$ if and only if $\:{a}_{1}{\ge\:a}_{2}{b}_{1}{\ge\:b}_{2}{c}_{1}\le\:{c}_{2}$ and$\:{\:d}_{1}\le\:{d}_{2}$.

Definition 5 ²⁹

Let$\:\stackrel{\sim}{\alpha\:}=\left(\left[a,b\right]\left[c,d\right]\right)$ be an IVPFNs number, then the scoring function of $\:\stackrel{\sim}{\alpha\:}$ is defined as follows:

$$\:\begin{array}{c}S\:\left(\stackrel{\sim}{\alpha\:}\right)=\frac{1}{2}\left({a}^{2}+{b}^{2}-{c}^{2}-{d}^{2}\right)\end{array}$$

(10)

Obviously, a larger value of $\:S\:\left(\stackrel{\sim}{\alpha\:}\right)\in\:\left[\text{0,1}\right]$. $\:S\:\left(\stackrel{\sim}{\alpha\:}\right)$indicates a larger value of $\:\stackrel{\sim}{\alpha\:}$.

Definition 6

Let $\:\stackrel{\sim}{{\upalpha\:}}\in\:\text{I}\text{V}\text{P}\text{F}\text{N}\text{s}$, then the new precise function definition of $\:\stackrel{\sim}{{\upalpha\:}}$ considering the degree of hesitation is as follows:

$$\:\begin{array}{c}M\left(\stackrel{\sim}{\alpha\:}\right)=\frac{1}{2}\left[\left({a}^{2}+{b}^{2}\sqrt{1-{a}^{2}{-c}^{2}}\right)+\left({b}^{2}+{a}^{2}\sqrt{1-{b}^{2}-{d}^{2}}\right)\right]\end{array}$$

(11)

Based on the above functions, an order relationship between two IVPFNs numbers is proposed.

This paper uses Hamming distance based on Hausdorff measure, standardized Hamming distance formula, which is defined as follows³⁰:

$$\:\begin{array}{c}d\left(A,B\right)=\frac{1}{2}\sum\:_{i=1}^{N}\left\{\begin{array}{c}max\left\{\left|{{(\mu\:}_{A}^{L}\left({x}_{i}\right))}^{2}-{{(\mu\:}_{B}^{L}\left({x}_{i}\right))}^{2}\right|,\left|{{(\nu\:}_{A}^{L}\left({x}_{i}\right))}^{2}-{{(\nu\:}_{B}^{L}\left({x}_{i}\right))}^{2}\right|\right\}\\\:max\left\{\left|{{(\mu\:}_{A}^{U}\left({x}_{i}\right))}^{2}-{{(\mu\:}_{B}^{U}\left({x}_{i}\right))}^{2}\right|,\left|{{(\nu\:}_{A}^{U}\left({x}_{i}\right))}^{2}-{{(\nu\:}_{B}^{U}\left({x}_{i}\right))}^{2}\right|\right\}\end{array}\right.\end{array}$$

(12)

TOPSIS method

The method proposed by Hwang and Yoon³¹ in the 1980s was the first to compare the evaluation object with the idealized target. Many scholars sorted multiple decision-making options by constructing ‘positive ideal solutions’ and ‘negative ideal solutions’^32,33. On the basis of the original method, this paper makes a slight modification to it, drawing on the method of gray relational degree and TOPSIS, and organically combines prospect theory and TOPSIS to evaluate the risks that Chinese enterprises will encounter more accurately and effectively. According to the TOPSIS proximity formula:

Step 1: First, the data needs to be preprocessed to construct a normalized matrix.

Step 2: From the normalized matrix, determine the positive and negative ideal solutions in the decision-making problem according to the formula.

$$\:\begin{array}{c}{r}^{+}={\left({r}_{j}^{1+},{r}_{j}^{2+},\cdots\:,{r}_{j}^{l+}\right)}^{T}\end{array}$$

(13)

$$\:\begin{array}{c}{r}^{-}={\left({r}_{j}^{1-},{r}_{j}^{2-},\cdots\:,{r}_{j}^{l-}\right)}^{T}\end{array}$$

(14)

Step 3: According to the Step, calculate the distances $\:{r}^{+}$and $\:{r}^{-}$ between each indicator and the positive and negative ideal points.

Step 4: According to the formula, calculate the pasting progress of each scheme and the positive ideal solution.

$$\:\begin{array}{c}\theta\:=\frac{{r}_{i}^{-}}{{r}_{i}^{-}+{r}_{i}^{+}}\end{array}$$

(15)

Step 5: Sort the plans according to the posting progress. When the numerator is $\:{r}^{-}$, the greater the posting progress value, the better the plan; when $\:{r}^{+}$ is the numerator, the smaller the value, the better.

Step 6: Bring formula (2) into (15) to obtain the following formula:

$$\:{\varphi\:}^{-}\left({P}_{i}\right)=\sum\:_{i=1}^{n}-{w}_{j}\theta\:{\left(d\left({A}_{ij},{A}_{j}^{-}\right)\right)}^{\beta\:}\:;\:\begin{array}{c}{\varphi\:}^{+}\left({P}_{i}\right)=\sum\:_{j=1}^{n}{w}_{j}{\left(d\left({A}_{ij},{A}_{j}^{+}\right)\right)}^{\alpha\:}\end{array}$$

(16)

The benefit-loss ratio for each alternative can be calculated using the following formula:

$$\:\begin{array}{c}{S}_{i}=\frac{{\varphi\:}_{i}^{+}}{{\varphi\:}_{i}^{-}}\left(i=\text{1,2},3\cdots\:,n\right)\end{array}$$

(17)

According to the formula, the larger the value of $\:{S}_{i}$, the more favorable the alternative.

Risk assessment framework for prefabricated building construction

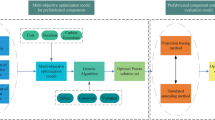
In this section, a risk assessment framework for prefabricated building construction will be established, and the most suitable evaluation method for selecting prefabricated building construction schemes will be chosen, as shown in (Fig. 1).

Fig. 1

Prefabricated building construction risk evaluation framework.

Establishment of risk identification and evaluation index system for prefabricated building construction

The process of establishing the risk evaluation index system in this paper is as follows:

Step 1: Select literature indexed by SCI and EI, and extract risk factors related to the theme of this study.

Step 2: Develop a questionnaire based on the risk factors summarized in the previous step and distribute it to technical professionals in enterprises and relevant research experts.

Step 3: Eliminate risk factors deemed unsuitable by experts and add necessary risk factors as suggested.

Step 4: Establish a risk evaluation index system based on the resulting risk factors. The specific sources of the risk assessment indicators are detailed in (Table 2). Figure 2 illustrates the risk evaluation index system for prefabricated construction projects.

Table 2 Lists the language terminology decision matrices provided by various experts.

Fig. 2

Risk assessment indicator system for prefabricated construction projects.

Steps for determining the weight of comprehensive indicators using IVPFNs AHP entropy method

The combination of AHP and entropy value method can complement each other. At the same time, this paper introduces the IVPFNs into AHP-entropy value method to determine the index weight. The determination of index weight is more accurate and delicate. The calculation steps are as follows^34,35.

Step1: Set up the IVPFNs set $\tilde{P} = \left\{ {x,\left[ {u_{{\tilde{P}}}^{L} \left( x \right),u_{{\tilde{P}}}^{U} \left( x \right)} \right],\left[ {v_{{\tilde{P}}}^{L} \left( x \right),v_{{\tilde{P}}}^{U} \left( x \right)} \right]\left| {x \in X} \right.} \right\}$. Initially, based on the relational terminology of the IVPFNs Analytic Hierarchy Process assignment chart, we solicit assessments on risk factors from pertinent experts to construct a pairwise comparison matrix, denoted as $\:R={\left({r}_{ik}\right)}_{m\times\:n}$.

Step 2: Find the upper and lower values of the affiliation and non-affiliation functions to compute the difference matrix $\:D={\left({d}_{jk}\right)}_{l\times\:l}$matrix elements $\:{d}_{jk}=\left[{d}_{jkL}{,d}_{jkU}\right]$:

$$\:{d}_{jkL}={\mu\:}_{jkL}^{2}-{\nu\:}_{jkU}^{2}$$

$$\:\begin{array}{c}{d}_{jkU}={\mu\:}_{jkU}^{2}-{\nu\:}_{jkL}^{2}\end{array}$$

(18)

In the formula: $\:{d}_{jkL}$ is the lower bound value of matrix element $\:{d}_{jk}$, and$\:\:{d}_{jkU}$ is the upper bound value of matrix element $\:{d}_{jk}$.

Step 3: Find the interval multiplication matrix $\:S={\left({s}_{jk}\right)}_{l\times\:l}$matrix elements $\:{s}_{jk}=\left[{s}_{jkL}{,s}_{jkU}\right]$:

$$\:{s}_{jkL}=\sqrt{100{0}^{djkL}}\:\begin{array}{c}{s}_{jkU}=\sqrt{100{0}^{djkU}}\end{array}$$

(19)

Step 4: Calculate the determined value $\:\tau\:={\left({\tau\:}_{jk}\right)}_{l\times\:l}$ matrix elements $\:{\tau\:}_{jk}$ as shown in the formula:

$$\:\begin{array}{c}\:\:\:{\tau\:}_{jk}=1-\left({\mu\:}_{jkU}^{2}-{\mu\:}_{jkL}^{2}\right)\left({\nu\:}_{jkU}^{2}-{\nu\:}_{jkL}^{2}\right)\end{array}$$

(20)

Step 5: Multiply the obtained determinant with the matrix $\:={\left({s}_{jk}\right)}_{l\times\:l}$, to obtain the weight matrix before normalization $\:T={\left({t}_{jk}\right)}_{l\times\:l}$:

$$t_{{jk}} = \left( {\frac{{s_{{jkL}} + s_{{jkU}} }}{2}} \right)\tau _{{jk}} ,\left( {j,k = 1,2, \cdots ,m} \right)$$

(21)

Step 6: Calculate the weight of each indicator:

$$\:\begin{array}{c}{w}_{j}=\frac{{\sum\:}_{k=1}^{l}{t}_{jk}}{{\sum\:}_{i=1}^{l}{\sum\:}_{k=1}^{l}{t}_{jk}},\left(j,k=\text{1,2},\cdots\:,m\right)\end{array}$$

(22)

Step7: Get the upper and lower bound values according to Eq. (19), and calculate the upper and lower bound information entropy according to the following equation

$$\:{E}_{j}^{-}=-{\left({ln}m\right)}^{-1}{\sum\:}_{i=1}^{m}{p}_{ij}^{-}{ln}{p}_{ij}^{-},\left(j=\text{1,2},\cdots\:,n\right)$$

$$\:\begin{array}{c}{p}_{ij}=\frac{{a}_{ij}^{-}}{{\sum\:}_{i=1}^{m}{a}_{ij}^{-}},\left(i=\text{1,2},\cdots\:,n\right)\end{array}$$

(23)

$$\:{E}_{j}^{+}=-{\left({ln}m\right)}^{-1}{\sum\:}_{i=1}^{m}{p}_{ij}^{+}{ln}{p}_{ij}^{+},\left(j=\text{1,2},\cdots\:,n\right)$$

$$\:{p}_{ij}=\frac{{a}_{ij}^{+}}{{\sum\:}_{i=1}^{m}{a}_{ij}^{+}},\left(i=\text{1,2},\cdots\:,n\right)$$

Step 8: Calculate the value of the IVPFNs indicator for each program interval

$$\:{E}_{j}\left(j=1,\:2,\:\cdots\:,n\right)$$

$$\:\begin{array}{c}{E}_{j}=\frac{1}{2}\left({E}_{j}^{-}+{E}_{j}^{+}\right)\end{array}$$

(24)

Step 9: Calculate the degree of impact of each indicator on the program $\:{d}_{j}\left(\text{1,2},\cdots\:,n\right)$

$$\:\begin{array}{c}{d}_{j}=1-{E}_{j}\end{array}$$

(25)

Step 10: Calculate the weight of each indicator $\:{d}_{j}\left(\text{1,2},\cdots\:,n\right)$

$$\:\begin{array}{c}{C}_{j}=\frac{{d}_{j}}{{\sum\:}_{j=1}^{n}{d}_{j}}\left(j=\text{1,2},\cdots\:,n\right)\end{array}$$

(26)

Step 11: Calculate AHP-Entropy method indicator weights

$$\:\begin{array}{c}{w}_{i}=\frac{{w}_{j}{\times\:C}_{j}}{{\sum\:}_{j=1}^{n}{w}_{j}{\times\:C}_{j}}\end{array}$$

(27)

Steps for calculating expert weights

Proximity and expert weight

In the problem of group decision-making, it is very important and necessary to determine the weight of each expert. As for the criterion, it is assumed that the positive and negative ideal distance of the scheme under the expert is $\:{r}^{+}={\left({r}_{j}^{1+},{r}_{j}^{2+},\cdots\:,{r}_{j}^{l+}\right)}^{T}$, and the negative ideal distance is $\:{r}^{-}={\left({r}_{j}^{1-},{r}_{j}^{2-},\cdots\:,{r}_{j}^{l-}\right)}^{T}$, among which $\:{r}_{j}^{k+},{r}_{j}^{k-}$ is the positive and negative ideal distance under the expert of $\:{E}_{k}(k\in\:l)$, as shown in the formula:

$$\:{r}_{j}^{k+}=\left(\left|{\mu\:}_{j}^{L+},{\mu\:}_{j}^{U+}\right|,\left|{\nu\:}_{j}^{L+},{\nu\:}_{j}^{U+}\right|\right),{r}_{j}^{k-}=\left(\left|{\mu\:}_{j}^{L-},{\mu\:}_{j}^{U-}\right|,\left|{\nu\:}_{j}^{L-},{\nu\:}_{j}^{U-}\right|\right)$$

In$\:{\:u}_{j}^{L+}=\underset{i\in\:m}{max}\left\{{u}_{ij}^{L}\right\},{u}_{j}^{U+}=\underset{i\in\:m}{max}\left\{{u}_{ij}^{U}\right\},{v}_{j}^{L+}=\underset{i\in\:m}{min}\left\{{v}_{ij}^{L}\right\},{v}_{j}^{U+}=\underset{i\in\:m}{min}\left\{{v}_{ij}^{U}\right\}$

$$\:\begin{array}{c}{u}_{j}^{L-}=\underset{i\in\:m}{min}\left\{{u}_{ij}^{L}\right\},{u}_{j}^{U-}=\underset{i\in\:m}{min}\left\{{u}_{ij}^{U}\right\},{v}_{j}^{L-}=\underset{i\in\:m}{max}\left\{{v}_{ij}^{L}\right\},{v}_{j}^{U-}=\underset{i\in\:m}{max}\left\{{v}_{ij}^{U}\right\}\end{array}$$

(28)

According to expert $\:{E}_{k}\left(k\in\:L\right)$, the smaller the value of $\:d\left({A}_{ij}^{k},{r}_{j}^{{k}^{+}}\right)$, the better the scheme $\:{A}_{i}$. At the same time, the larger the value of $\:d\left({A}_{ij}^{k},{r}_{j}^{{k}^{-}}\right)$, the better the scheme $\:{A}_{i}$. Therefore, the relative closeness of expert $\:{E}_{k}$ to option $\:{A}_{i}$ and criterion $\:{C}_{i}$ is:

$$R_{{ij}}^{k} = \frac{{d\left( {A_{{ij}}^{k} ,r_{j}^{{k^{ - } }} } \right)}}{{d\left( {A_{{ij}}^{k} ,r_{j}^{{k^{ + } }} } \right) + d\left( {A_{{ij}}^{k} ,r_{j}^{{k^{ - } }} } \right)}}$$

(29)

Obviously, $\:0\le\:{R}_{ij}^{k}\le\:1$ specifically, when $\:d\left({A}_{ij}^{k},{r}_{j}^{{k}^{+}}\right)=0$ is $\:{R}_{ij}^{k}=0$.When $\:d\left({A}_{ij}^{k},{r}_{j}^{k-}\right)$=0, $\:{R}_{ij}^{k}=1$. Further, if the value of $\:{R}_{ij}^{k}$ is larger, expert $\:{E}_{k}$ believes that scheme $\:{A}_{i}$ is better under criterion $\:{C}_{j}$.

For scheme $\:{A}_{i}$, the greater the sum of the relative closeness of experts$\:{\:E}_{k}$ to $\:{A}_{i}$ under the criterion, the greater the weight of expert$\:\:{C}_{j}$ under $\:{E}_{k}$. Therefore, the weight $\:{C}_{j}$ of $\:{E}_{k}$ experts $\:{w}_{j}^{k}$ under the criterion can be defined, which can be abbreviated as formula:

$$\:\begin{array}{c}{w}_{j}^{k}=\frac{{c}_{j}^{k}}{{\sum\:}_{k=1}^{l}{c}_{j}^{k}}\end{array}$$

(30)

$$\:\begin{array}{c}{c}_{j}^{k}={\sum\:}_{i=1}^{m}{R}_{ij}^{k}={\sum\:}_{i=1}^{m}\frac{d\left({A}_{ij}^{k},{r}_{j}^{{k}^{-}}\right)}{d\left({A}_{ij}^{k},{r}_{j}^{{k}^{+}}\right)+d\left({A}_{ij}^{k},{r}_{j}^{{k}^{-}}\right)}\end{array}$$

(31)

It can be obtained that the expert weight vector under criterion $\:{C}_{j}(j\in\:N)$ is $\:{{w}_{g}=\left({w}_{g}^{1},{w}_{g}^{2},\cdots\:,{w}_{g}^{l}\right)}^{T}\left(g\in\:N\right)$.

By using the method of closeness to calculate the weight of experts, it effectively changes the problem that experts can only be empowered as fixed values. The proportion of each expert to different criteria can not only be closer to the actual decision-making situation, but also effectively combine the information of experts. Integration will lay a good foundation for the determination of subsequent risk assessment.

Expert information integration

In group decision making, the selection of integration operators is very important. Choosing an operator suitable for this scheme can not only describe the information of experts more accurately, but also describe the subsequent evaluation process more accurately. At present, experts and scholars at home and abroad have relatively single research results on the integration operator of IVPFNs numbers. This article reads relevant literature, and finally selects the IVPFNs weighted average operator to gather expert information. This method uses the degree of closeness to calculate the weight of experts under different risk indicators, effectively solving the problem of assigning fixed weights to experts.

Definition 7

Let $\:\stackrel{\sim}{{\alpha\:}_{i}\:}\in\:IVPFNs$, the expert weight vector is $\:{{w}_{\text{g}}=\left({w}_{\text{g}}^{1},{w}_{\text{g}}^{2},\cdots\:,{w}_{\text{g}}^{\text{l}}\right)}^{\text{T}}\left(g\in\:\text{N}\right)$, which is the weight of $\:\stackrel{\sim}{{\alpha\:}_{i}\:}$, and if $\:{w}_{\text{g}}\ge\:0$$\:{\sum\:}_{i=1}^{n}{w}_{i=1}$ is satisfied, the interval-valued Pythagorean fuzzy weighted average operator (IVPFWA) is defined Shown:

$$\begin{gathered} IVPFWA\left( {\tilde{\alpha }_{i} , \cdots ,\tilde{\alpha }_{n} } \right) = w_{1} \tilde{\alpha }_{1} \oplus w_{2} \tilde{\alpha }_{2} \cdots \oplus w_{n} \tilde{\alpha }_{n} = ~~ \hfill \\ \left( {\left[ {\sqrt {1 - \prod _{{j = 1}}^{n} \left( {1 - \left( {a_{i} } \right)^{2} } \right)^{{w_{j} }} } ,\sqrt {1 - \prod _{{j = 1}}^{n} \left( {1 - \left( {b_{j} } \right)^{2} } \right)^{{w_{j} }} } } \right],\left[ {\prod _{{j = 1}}^{n} \left( {c_{j} } \right)^{{w_{j} }} ,\prod _{{j = 1}}^{n} \left( {d_{j} } \right)^{{w_{j} }} } \right]} \right) \hfill \\ \end{gathered}$$

(32)

Steps of TOPSIS method for interval-valued pythagorean fuzziness in improved prospect theory

The IVPFNs TOPSIS method based on prospect theory is proposed below. Specific steps are as follows:

Assume that $\:\text{l}$ experts need to rank n programs according to m criteria. Note that the scheme set is$\:\:A=\left\{{A}_{1},{A}_{2},\cdots\:{A}_{m}\right\}$, the criterion set is $\:C=\left\{{C}_{1},{C}_{2},\cdots\:{C}_{n}\right\}$, the expert set is $\:E=\left\{\text{1,2},\cdots\:,Q\right\}$, and the criterion weight vector is $\:\omega\:={\left\{{\omega\:}_{1},{\omega\:}_{2},\cdots\:,{\omega\:}_{n}\right\}}^{T}$, and the weight $\:{C}_{j}\:$of criterion $\:{\omega\:}_{i}$ satisfies $\:{\omega\:}_{1}+{\omega\:}_{2}+\cdots\:+{\omega\:}_{n}=1$ and $\:{\omega\:}_{j}\ge\:0\:(j\in\:N)$. Note $\:M=\left\{\text{1,2},\cdots\:,m\right\}$ and $\:=\left\{\text{1,2},\cdots\:,n\right\}$, $\:L=\left\{\text{1,2},\cdots\:,l\right\}$ based on criterion $\:{C}_{j}$, the evaluation information given to the scheme $\:{A}_{i}$ is expressed by interval Pythagoras fuzzy number $\:{\stackrel{\sim}{Z}}_{ij}^{k}=\left(\left[{\mu\:}_{ij}^{kL},{\mu\:}_{ij}^{kU}\right],\left[{\nu\:}_{ij}^{kL},{\nu\:}_{ij}^{kU}\right]\right)$, of which $\:i\in\:M,j\in\:N,k\in\:L$. Therefore, practical group decision-making problems can be expressed $\:={\left(\stackrel{\sim}{{Z}_{ij}}\right)}_{m\times\:n}(k\in\:L)$ .

Step 1: In order to eliminate the impact of different dimensions on the decision-making results, the criterion value $\:{\stackrel{\sim}{Z}}_{ij}^{k}(i\in\:M,j\in\:N,k\in\:L)$ is normalized to $\:{\stackrel{\sim}{S}}_{ij}^{k}$ using the formula. $\:{C}^{b}$ and $\:{C}^{c}$ are the benefit criterion set and the cost criterion set, respectively.

$$\:\begin{array}{c}\stackrel{\sim}{{S}_{ij}}=\left\{\begin{array}{c}\left[{\mu\:}_{ij}^{kL},{\mu\:}_{ij}^{kU}\right],\left[{\nu\:}_{ij}^{kL}{,\nu\:}_{ij}^{kU}\right],{C}_{j}\in\:{C}^{b}\\\:\left[{\nu\:}_{ij}^{kL},{\nu\:}_{ij}^{kU}\right],\left[{\mu\:}_{ij}^{kL}{,\mu\:}_{ij}^{kU}\right],{C}_{j}\in\:{C}^{c}\left(i\in\:M,j\in\:N,k\in\:L\right)\end{array}\right.\end{array}$$

Therefore, $\:Z={\left(\stackrel{\sim}{{Z}_{ij}}\right)}_{m\times\:n}$can be normalized to $\:{Z}^{\prime }={\left(\stackrel{\sim}{{S}_{ij}}\right)}_{m\times\:n}$ as required.

Step 2: Formula (28) determines $\:{r}^{+}{r}^{-}$ for each risk factor. For criterion $\:{C}_{j}$, it is assumed that the positive ideal distance of the scheme is $\:{r}^{+}={\left({r}_{j}^{1+},{r}_{j}^{2+},\cdots\:,{r}_{j}^{l+}\right)}^{T}$, and the negative ideal distance is $\:{r}^{-}={\left({r}_{j}^{1-},{r}_{j}^{2-},\cdots\:,{r}_{j}^{l-}\right)}^{T}$, where $\:{r}_{j}^{+}$ and $\:{r}_{j}^{-}$ are the positive and negative ideal distances.

Step 3: Determine the distance between each party and the corresponding attribute value of the positive ideal scheme and the distance of the corresponding attribute value of the negative ideal scheme. Please refer to formula (12) for a detailed explanation of the Hamming distance.

Step 4: Select the reference point based on the different conditions of Definition 2. For a neutral decision-maker, select Assumption 1 of Definition 2.

Step 5: Formula (29), (30), and (31) for calculating proximity and expert weights. The specific calculation method is in accordance with to formula. Therefore, the expert weight vector under criterion $\:{C}_{j}(j\in\:N)$ is $\:{{w}_{g}=\left({w}_{g}^{1},{w}_{g}^{2},\cdots\:,{w}_{g}^{l}\right)}^{\text{T}}\left(g\in\:N\right)$. Effectively gather the information given by the experts. The IVPFWA is applied for calculation using the formula (32).

Step 6: Assuming that the comprehensive loss value of $\:{A}_{i}$ relative to $\:{A}^{+}$ is $\:{\varphi\:}^{+}\left({A}_{i}\right)$, and the comprehensive income value relative to $\:{A}^{-}$ is $\:{\varphi\:}^{-}\left({A}_{i}\right)$, use the formula (15) and (16) to Calculate the closeness coefficient and prospect theory value for each alternative.

Step 7: According to the formula (17), compare the benefit-loss ratios of each alternative and rank the alternatives based on their ratios.

Example analysis of risk assessment for prefabricated building construction

Project overview

Project A, a university teaching building initiative, is situated in Shanghai, China. It boasts a significant investment of 90 million yuan and covers a total construction area of 8900 square meters. Scheduled to break ground in May 2021, the project has a targeted completion timeline of 200 days. Aligning with national directives, it will incorporate prefabricated building technology, ensuring that major load-bearing components, including beams, slabs, and columns, are prefabricated. This approach is anticipated to achieve an assembly rate of approximately 70%.

Determination of risk assessment index weights for prefabricated building construction phase

Invite relevant experts and scholars to conduct a pairwise comparison and evaluation of various factors related to the risks during the construction phase of prefabricated buildings, and provide a paired comparison matrix of the Pythagorean fuzzy AHP language terminology form in (Table 3). By calculating the entropy value, the weights of the evaluation index system for prefabricated building construction and the influencing factors are finally obtained as shown in (Table 4).

Table 3 Weights of various influencing factors in the risk assessment indicator system.

Table 4 AHP weights of first-level risk indicators for prefabricated building construction stages.

Pythagoras fuzzy risk evaluation matrix for prefabricated building projects

We extend an invitation to experts and scholars specializing in relevant fields to conduct evaluations on three construction plans for this project, considering the specified risk factors. These evaluations will employ linguistic scoring methods to rate each factor. Expert assessments will be articulated using linguistic terms, with the relationship between these terms and IVPFNs numbers elaborated in Table 5 for the criteria-specific scheme evaluations. This process will not only ensure a comprehensive evaluation of each construction plan but also facilitate a nuanced understanding of each risk factor’s impact, as detailed in (Table 2).

Table 2 lists the language terminology decision matrix provided by experts. Experts and scholars rate the corresponding risk factors based on language and language skills.

Table 5 Correspondence between linguistic terms and IVPFNs numbers.

Convert the language term decision matrix provided by experts into IVPFNs numbers. Due to the identified risk factors including cost and benefit factors, it is necessary to standardize the data in the above table according to the formula in Step 1. Meanwhile, according to Step 2, obtain the IVPFNs positive ideal solution and IVPFNs negative ideal solution under the criterion, respectively. According to step three, determine the distance between each party and the corresponding attribute values of the positive ideal scheme and the corresponding attribute values of the negative ideal scheme.

Calculate the distance between each scheme and the corresponding attribute values of the positive ideal scheme, as well as the distance between the corresponding attribute values of the negative ideal scheme. Afterwards, calculate closeness and expert weights. The specific calculation method is as follows (28) to (31). After obtaining the expert weights, the information provided by each expert and scholar is collected comprehensively and systematically. Following Step 6, the gathered information is aggregated effectively using the IVPFWA operator. Based on the obtained aggregation results, continue to calculate the distance between each scheme and the corresponding attribute values of the positive ideal scheme in Table 6, as well as the distance between the corresponding attribute values of the negative ideal scheme in (Table 7).

Table 6 Distances between alternatives and positive ideal solution attribute values.

Table 7 Distances between alternatives and negative ideal solution attribute values.

Step 4: The expert weights are shown in (Table 8).

Table 8 Expert weights.

Step 5: Effectively gather the information given by the experts in (Tables 9 and 10).

Table 9 Distances between aggregated expert results and positive ideal solution attribute values.

Table 10 Distances between aggregated expert results and negative ideal solution attribute values.

Step 6: The comprehensive income values of each plan are shown in (Table 11).

Table 11 Comprehensive income value of each scheme.

Afterwards, follow step six to calculate the profit and loss values. Take parameters $\:\alpha\:=\beta\:=0.88$ and $\:\theta\:=2.25$. Assuming that the comprehensive loss value of$\:{A}_{i}$ relative to $\:{r}^{+}$ is $\:{\varphi\:}^{+}\left({r}_{i}\right)$and the comprehensive income value relative to $\:{r}^{-}$is $\:{\varphi\:}^{-}\left({r}_{i}\right)$, the ranking result of each scheme is $\:{S}_{3}>{S}_{2}>{S}_{1}$.

Comparison of different decision-makers’ subjective preferences

The results obtained from applying the method proposed in this paper to the aforementioned problem, based on the subjective preferences of different decision-makers, are shown in (Table 12). Based on Table 12, plot the specific evaluation results, as shown in (Fig. 3).

Table 12 The evaluation results of the proposed method in this paper.

Fig. 3

The evaluation results of the proposed method in this paper.

According to the evaluation results shown in Table 12, regardless of whether the weights are adjusted, it can be observed that $\:{S}_{i}^{L}{\ge\:S}_{i}^{Z}{\ge\:S}_{i}^{B}$. For instance, in the case of alternative A₁, without adjusting the weights, the evaluation values from the optimistic, neutral, and pessimistic perspectives are 0.711, 0.633, and 0.559, respectively. After adjusting the weights, the evaluation values from the optimistic, neutral, and pessimistic perspectives become 0.771, 0.744, and 0.623, respectively, thus confirming that $\:{S}_{i}^{L}{\ge\:S}_{i}^{Z}{\ge\:S}_{i}^{B}$. Moreover, without adjusting the weights, the evaluation results from different types of decision-makers show slight variations. For example, under the optimistic perspective, the optimal alternative is A₂, while from the neutral and pessimistic perspectives, the optimal alternative is A₃. This indicates that the subjective preferences of different decision-makers can influence the final evaluation results. To some extent, this finding also demonstrates the necessity of considering different types of decision-makers in the proposed model, as ignoring the variations in subjective preferences may lead to inaccurate conclusions.

However, after adjusting the weights, the optimal alternative selected by different types of decision-makers is consistently A₂, indicating to some extent that weighting adjustments can lead to more stable evaluation results. Nonetheless, there are still slight differences in the specific rankings. At the same time, the excessive subjective preferences of different decision-makers are effectively corrected. Therefore, when conducting a comparative analysis of alternatives, decision-makers may consider the results after weighting adjustments to ensure more accurate and stable evaluation outcomes.

Comparative analysis and discussions

In this section, the proposed method is compared with several existing methods to demonstrate its effectiveness and efficiency. To validate the effectiveness of the proposed method, it is compared with existing methods, including the PT-IVHFS-TOPSIS³⁶, PT-VIKOR³⁷, SVN-PT-TOPSIS³⁸. In a fair context, the same dataset and simulation flowchart are employed to compare the scoring values of each method, allowing the alternatives to be ranked accordingly based on these scores. The comparison results are shown in (Table 13; Fig. 4).

Table 13 Results from different methods.

Fig. 4

Results from different methods.

As shown in Table 13, the ranking results of the proposed method are consistent with the literature. Although there are differences in rankings compared to PT-TOPSIS and PT-VIKOR, the optimal solution remains unchanged. Therefore, the proposed model is feasible and effective.

At the same time, a comparison of the above methods reveals their shortcomings. As fundamental methods, PT-TOPSIS and PT-VIKOR cannot accurately capture expert attitudes and do not account for the impact of hesitation, which may lead to information loss. IVHFs³⁶ cannot directly capture explicit hesitation, resulting in less differentiation between alternatives, which in some cases may reduce the accuracy of evaluations and limit their applicability. SVNs³⁷ represents uncertainty as a fixed single value, which cannot dynamically reflect the degree of hesitation, leading to differences in the final results. Although the aforementioned methods use prospect theory to establish evaluation models, they do not consider the impact of decision-makers’ subjective preferences on the results. Therefore, the model proposed in this paper can provide a more accurate solution.

The prospect theory in this model mainly relies on the setting of the reference point, which is often subjective and may lead to deviations in the entire decision-making process. When combined with interval-valued Pythagorean fuzzy numbers, the fuzziness and uncertainty further increase the complexity of selecting the reference point, thus affecting the accuracy and effectiveness of the model. Although this model is designed for risk evaluation during the construction phase, it can be extended to the risk assessment of the entire prefabricated building process. However, in fields such as dynamic financial markets or energy management, this model cannot accommodate a dynamic adjustment mechanism.

To address the above shortcomings, future improvements can be made in the following aspects: (1) To mitigate the subjectivity of the model, a historical decision data analysis system can be introduced to replace expert evaluations, thereby reducing the subjective influence of different interest-driven decision-makers. (2) A dynamic version of the TOPSIS model can be developed by incorporating a time dimension into the model. This would allow for automatic adjustments of parameters and decision criteria based on data and decision conditions at different time points. In this way, the model can adapt to evolving scenarios over time, making it especially suitable for long-term project evaluations and risk management.

Conclusion

This paper presents an innovative evaluation framework that marries TOPSIS with prospect theory and IVPFNs, specifically designed for risk assessment in prefabricated construction projects. The following conclusion has been drawn:

• (1) A risk assessment index system for assembly construction has been established that comprehensively considers factors such as personnel, materials, machinery, management, and technology. Through the IVPFN - AHP entropy method, it was determined that risk factors C₁ and C₃ are relatively significant. Therefore, companies should enhance management practices during construction to mitigate these risks.

• (2) This paper compares decision-makers’ subjective preferences and adjustment coefficients, demonstrating that decision-makers with different preferences may lead to varying evaluation outcomes. This finding underscores the necessity of adequately considering diverse subjective preferences within prospect theory.

In summary, this study provides a scientific and rational solution to MADM problems and offers guidance and references for selecting prefabricated construction schemes under complex conditions.

Future directions and perspectives

Currently, prefabricated buildings are widely used in various sectors in China, including residential, office buildings, hospitals, and schools. At the same time, the range of prefabricated building products is becoming increasingly diverse, including various types such as PC structures, steel structures, and wooden structures. However, due to the rapid development of prefabricated buildings in China, many risk factors remain difficult to address. Based on the risk factor evaluation results in this paper, the following recommendations are proposed:

• (1) Promotion of industry vocational qualification examinations. Relevant departments, such as the Ministry of Housing and Urban-Rural Development, are advancing the recognition of vocational skill levels, requiring workers in the prefabricated building sector to obtain relevant vocational qualification certificates through examinations.

• (2) Promotion of technical standards and guidance documents. To ensure that professional technical personnel can accurately understand and implement the relevant technologies for prefabricated buildings, the government has issued technical standards and guidance documents to unify industry regulations. This ensures that technical personnel can perform their work according to the standards, thereby improving their operational skills.

• (3) The implementation of full lifecycle safety management. Given the characteristics of prefabricated buildings, the government encourages enterprises to adopt full lifecycle safety management, conducting safety risk assessments and management at every stage, from design and production to construction and usage. In particular, during the construction phase, high-risk activities such as lifting and component installation must be subject to strict safety control measures.

Future research on the evaluation method could investigate the application of extended picture fuzzy sets and Fermatean fuzzy sets in assessing construction risks for prefabricated buildings to improve evaluation accuracy. Furthermore, the methodology proposed in this study could be extended to the evaluation of supply chains^39,40 and bulk material handling technologies⁴¹, thereby broadening the model’s scope of applicability.