Introduction

Electric load forecasting is imperative for the planning and operation of power companies1. The cost savings of load forecasting significantly impact the operation and control of vehicle allocation, fuel allocation, and online network analysis, as reported by Bunn2. Gao et al. quantified the value of predicting short-term electric load forecasting, showing that reducing the average prediction error by 1% can save millions of dollars3.

Electric load forecasting can be divided into three categories: 1) short-term load forecasting (STLF), 2) mid-term load forecasting (MTLF), and 3) long-term load forecasting (LTLF). Typically, STLF forecasts for up to one day, MTLF for 1 day to 1 year, and LTLF for 1–10 years4. In terms of the purpose of electric load forecasting, STLF is utilized for the operation of power systems, such as start-and-stop plans and economic arrangements; MTLF is for operational planning of power systems, such as maintenance schedules and coordination of power supplies; LTLF is for the expansion and planning of power systems, such as the construction of new power plants5,6. A study was conducted on very short-term load forecasting, targeting forecasting less than one day4. Various techniques such as similar-day approach, regression model, time-series, neural network, expert system, fuzzy logic, and statistical learning have been used for STLF7. Several analysis techniques have been employed, namely, trend analysis, which includes a linear trend, polynomial trend, and logarithmic trend. The econometric approach combines economic theories and statistical techniques, and the end-use approach predicts the electric load based on the statistical information collected at the end-use for MTLF and LTLF8.

Electric load forecasting has evolved from statistical methods to artificial intelligence-based techniques using machine learning models. The prediction accuracy of traditional statistical methods is limited because electricity usage data exhibit irregular and nonlinear features9. Machine learning techniques such as support vector machine (SVM)10,11, and fuzzy theory12,13,14 have been proposed for STLF. Neural network-based models such as artificial neural networks (ANN)15,16,17,18, convolutional neural networks (CNNs) and long short-term (LSTM) neural networks have been presented19,20. Studies on STLF have reported that prediction using neural network-based models show higher accuracy than other machine learning-based methods21,22,23. The main distinguishing property is that while sophisticated feature selection is required for machine learning-based models, it is inherent to the process of learning an effective neural network-based model. This means that it is particularly important to compare their performances in a unified framework, especially for forecasting large-scale electricity load datasets24.

There have been various research efforts to compare these methods. Amarasinghe et al.19 compared the performance of CNN, support vector regression (SVR), and ANN to predict energy loads at the individual building level, showing that CNN outperforms SVR and performs similarly to ANN. Kuo et al.20 compared neural network-based models such as CNN and LSTM with machine learning-based models such as SVM, random forest, and decision trees, concluding that CNN performs best in STLF. Dong et al.24 applied k-means clustering to CNN for STLF and showed that this method helps to improve performance. However, these existing studies targeted small datasets, ranging from tens to hundreds of thousands of records. Some previous studies partially compared the performances between neural network-based and machine learning-based models. However, their reported performances are inconsistent for the same dataset with different sizes24. Even the same model shows contradictory results on different datasets19,24,25.

In this study, we aim to study STLF for large-scale electricity usage datasets over 60 million records. To this purpose, we adapt dimensionality reduction and subsequent clustering to the prediction model for the first time. To show the effectiveness of dimensionality reduction and clustering, we use over 60 million records for 4710 households, where each household consists of 12,864 samples measured hourly from July 14th, 2009, to Dec. 31st, 2010. Most previous studies used the total usage in a region for prediction19,26,27,28,29,30,31,32,33,34. Furthermore, less than 100 households were targeted even when individual usages were used25,35. Accordingly, the methodologies for large-scale households have not been considered before.

To this end, we propose a new prediction method for STLF on large-scale electricity usage data through a combination of data clustering and dimensionality reduction schemes. This is the first research effort to incorporate both techniques in the prediction model for STLF. Data clustering can improve prediction accuracy because it allows us to forecast the electric load of a cluster having similar patterns, in particular, for large-scale households. Then, we investigate the effects of applying dimensionality reduction before data clustering to effectively deal with the large data samples. Here, we adopt k-means clustering for data clustering and kernel principal component analysis (kernel PCA), universal manifold approximation and projection (UMAP), and t-stochastic nearest neighbor (t-SNE) for dimensionality reduction. To verify the effectiveness of the proposed model, we extensively apply the proposed model to neural network-based models, i.e., ANN, CNN, and LSTM.

We compare and analyze their performances using electricity usage data for 4710 households. Experimental results show that applying data clustering with dimensionality reduction can clearly improve the performances of the baseline models. We compare the performances of prediction models using two kinds of datasets: (1) individual electricity usage and (2) total electricity usage. As a result, the prediction accuracy of the proposed method outperforms those of the existing methods by 1.01–1.76 times for summer data and by 1.03–1.36 times for winter data in terms of mean absolute percentage error (MAPE).

The remainder of this paper is organized as follows. In “Related Work” Section, we review related work. In “Backgrounds” Section, we introduce background techniques. In “Proposed Method” Section, we propose a new prediction model for STLF targeting large-scale electricity usage datasets. In “Performance Evaluation” Section, we explain the experimental results. In “Conclusions” Section, we conclude the paper.

Related work

There have been various research efforts for STLF. In this section, we classify them into three categories: (1) statistical methods, (2) machine learning-based methods, and (3) neural network-based methods.

Statistical methods

Regression models have been widely used for electric load forecasting because of the convenience of the implementation and ease of analysis. They are used to understand the relationship between electricity usage and other factors such as weather conditions, the day of the week, and customer class. Papalexopoulos et al. proposed a regression-based approach for STLF, focusing on 24-h peak electricity usage and electric load forecasting36. Specifically, a regression model was applied for weighted least squares, temperature modeling using air conditioner temperatures, and holiday modeling using binomial variables. Hyde et al. developed a regression-based model for predicting electric loads from the weather26. Generalized Linear Models (GLMs), an extension of traditional linear regression, are used to model nonlinear relationships between load and influencing factors through a link function, accommodating non-normal response distributions. Wang et al. demonstrated the effectiveness of GLMs for load forecasting by comparing them with various shallow and deep learning models37.

Index smoothing is another method used for load forecasting. Estimated values obtained using exponential smoothing are weighted averages of historical observations, which decrease exponentially over time. Abderrezak et al. used the Holt-Winters index smoothing technique to capture both electric demand trends and seasonal variations38. Taylor et al. proposed an index smoothing method that considers ARIMA, adaptive Holt-Winters index smoothing, and daytime and weekday seasonal cycles for extreme STLF between 10 and 30 minutes39.

Machine learning-based methods

Various machine learning models, such as fuzzy logic, SVMs, decision trees, random forests, and ensemble approaches, have been widely applied to electric load forecasting. The fuzzy set theory-based approach has been used to solve power system problems40. Hsu et al. presented a fuzzy set theory-based expert system for STLF41. Mori et al. used fuzzy inference methods for STLF and presented a nonlinear optimization model to minimize model errors42. Chow et al. demonstrated fuzzy logic to combine the information needed for spatial load forecasting to predict the scale and location of electric loads43 .

SVMs have been widely used for time-series prediction and STLF, which can be classified as nonlinear problems in time-series analysis. Hu et al. proposed a new method for STLF by combining a fuzzy C-mean clustering algorithm and weighted SVM44. Guo et al. presented an SVM-based model for overcoming the general limitations of ANNs, such as recognizing local minima as global minima or difficulty of model convergence29. Sina et al. used support vector regression whose parameters were tuned by social spider optimization45. Zhu et al. proposed a hybrid prediction model based on pattern sequence-based matching for proportional curve and XGBoost for daily extremum of electricity load to forecast holiday load46. Yu et al. proposed a decision tree-based model for predicting building energy demand, demonstrating high accuracy and interpretability by identifying significant factors influencing energy use intensity (EUI)47. Dudek et al. explored the application of random forest to STLF, considering various input pattern definition methods and training modes48. Ensemble methods have also been proposed to improve forecasting accuracy by combining multiple models. Zhang et al. used an ensemble approach that combines the CEEMDAN data preprocessing method with a hybridized quantum dragonfly algorithm (QDA) and support vector regression (SVR)49. This method effectively reduces noise and enhances forecasting performance by optimizing SVR with QDA.

Neural network-based methods

Some research efforts have shown that neural network-based methods outperform the statistical and machine learning methods in STLF21,22,23. Ahmed et al. demonstrated that linear regression models are less accurate for load forecasting on large-scale data25. Nawaz et al. showed that machine learning-based methods such as k-nearest neighbors, decision trees, and random forests are effective for STLF but only on small-sized datasets23. Wang et al. proposed stacked denoising autoencoders for STLF30. The model showed effective predictive results, particularly for the previous day’s forecasts. ANN is one of the most commonly used neural network techniques for predicting electric loads. Various ANNs were adapted for electric load forecasting, such as the feed-forward neural network (FFNN) and radial basis function networks (RBF). Shahidehpour et al. used a different ANN module for each season to reflect different seasonal characteristics in load forecasting50. El et al. compared the performance of multi-layered perceptron (MLP)-based neural networks divided by day or time27. Khotanzad et al. used an adaptive modular ANN using weekly, daily, and hourly modules for predicting hourly loads28. Marino et al. used the LSTM and LSTM-based sequence-to-sequence (S2S) for the load forecasting to 1 h and 1 min31. Kwon et al. used LSTM augmented with a fully-connected layer for the hourly load prediction, where LSTM was used to extract features from past data51. Massaoudi et al. combined CNN, GRU, LSTM, and Autoencoder and provided multiple combined models52. Dong et al. applied k-means clustering to CNN and demonstrated its effectiveness24. In this study, data clustering and dimensionality reduction are incorporated into a prediction model to represent large-scale households and the large-scale data samples for each household effectively. As a result, we apply data clustering and dimensionality reduction not only for CNN but also for neural network-based and other machine learning-based models to show their effect on each prediction model. Wan et al. proposed a hybrid model combining CNN, LSTM, and attention mechanisms to address information loss from excessively long input time series data and improve short-term power load forecasting accuracy53. Yang et al. proposed a hybrid VMD-VAE-LSTM model for power load forecasting, combining variational mode decomposition (VMD) for data decomposition, variational autoencoder (VAE) for noise reduction, and LSTM for prediction54. Acquah et al. combines CNN-GRU with clustering to capture distinct consumption patterns in electric load forecasting55. By grouping the data into patterns like weekday, weekend, and holiday consumption, the model can focus on each pattern separately, ultimately enhancing prediction accuracy. Jiang et al. proposed Deep-Autoformer, an enhanced Autoformer model with added MLP layers to improve feature extraction for very short-term load forecasting56. This model performs state-of-the-art in forecasting fluctuating and irregular load patterns in microgrid systems. Huang et al. demonstrated the performance of the Active Graph Recurrent Network (Ac-GRN) for district heat load forecasting through extensive experiments against 11 state-of-the-art models, including DLinear, LSTNet, and StemGNN57. Park et al. proposed a correlation-guided attention-based learning model for multi-energy consumption forecasting, effectively capturing correlations among different energy sources to improve prediction accuracy58.

Summary

Table 1 Summary of related works.
Full size table

Table 1 summarizes related work by the category. We incorporate both neural network-based and other machine learning-based models, combining both data clustering and dimensionality reduction, and compare their performances by focusing on large-scale individual household usages.

In this study, combining both data clustering and dimensionality reduction is a key technique for electric load forecasting targeting datasets consisting of large-scale households. Table 2 summarizes the coverage of related studies in terms of (1) data scale for electric load usage, (2) dimensionality reduction, and (3) data clustering, which are the three main focuses of this study. As shown in the table, the previous studies only considered dimensionality reduction32,53,54 or clustering24,35,44,55,60 to predict energy consumption, not both. The total data records in the previous studies excluding57 are less than 10 million, and the number of target households is less than 100 at maximum. Huang et al. also mentioned the significant limitations in terms of computational resources and time required to handle large-scale and high-dimensional data57. Dimensional reduction and clustering were not considered as the purpose of effectively handling the large-scale electric load usage data.

As shown in Figure 3 in Section 4.4, the scale of the dataset covered in this study shows a completely different distribution compared to the case of dealing with the small-scale dataset, and a new prediction model is required. In this study, data clustering and dimensionality reduction are incorporated into a prediction model to effectively represent large-scale households and large-scale data samples for each household. In this study, a total of 60,589,440 records of data collected from 4710 households are treated as an electric load forecasting model, which is the large-scale dataset as summarized in Table 2. This study is the first research effort to combine clustering and dimensionality reduction to construct an integrated forecasting model to deal with those large-scale datasets.

Table 2 Comparison between the previous studies and our model.
Full size table

The contributions of our proposed model compared to previous studies are summarized with the following two points:

  • We target to utilize large-scale individual usages for electric load forecasting models. Previous studies considered the total usage in a region or individual usage for less than 100 households. Accordingly, the methodologies to effectively deal with large-scale individual usages have not been considered. In this study, we adapt dimensionality reduction and associated clustering to deal with large-scale individual usages and show its effectiveness using datasets consisting of 4710 households.

  • To verify the effectiveness of the proposed model, we extensively apply it to the various neural network-based models, including state-of-the-art deep learning prediction models by combining dimensionality reduction and clustering. As a result, we show that our model clearly improves the performance of the baseline models for all the models and outperforms the existing models for STLF.

Backgrounds

Dimensionality reduction

The most widely used methods for dimensionality reduction are as follows: (1) principal component analysis (PCA)61, (2) t-SNE62, (3) UMAP63, and (4) SOM64,65. In particular, PCA is the most popular dimensionality reduction method. It finds a hyperplane in which the projected data can minimize data loss by maximally preserving the dispersion of the data before projection. It repeatedly finds the next hyperplane to preserve the variance in as many dimensions as desired. On the other hand, the kernel is a function that maps data into a high-dimensional feature space. A linear decision boundary in high-dimensional space corresponds to a non-linear decision boundary in the original space, allowing more complex projections. The technique applied to PCA is called kernel PCA (kernel PCA). t-SNE has been widely used to reduce the dimension of massive data collected in time-series form in smart grids and other fields and to extract statistical attributes of groups. It maps neighbors in original spaces into reduced dimensional spaces66,67,68,69. UMAP effectively maintains relationships between clusters in the original spaces, even in reduced dimension spaces, and has been shown to outperform the latter in dimensionality reduction. Although both UMAP and t-SNE preserve data similarity in the original spaces, UMAP shows better runtime performance and maintains more global structures than t-SNE. This study uses t-SNE and UMAP as dimensional reduction methods for electricity load forecasting referring to previous studies63,70,71.

Data clustering

In this study, we use k-means clustering for representative data clustering. In particular, in electric load forecasting, research efforts have shown that data clustering, based on k-means clustering of the entire dataset into multiple clusters, is effective in learning the prediction model24. k-means clustering has been widely used for data clustering owing to its advantages, such as ease of application, simplicity, and efficiency. This clustering model clusters the entire dataset into multiple clusters based on similarity. In other words, when \(X = \{x_1, x_2, \ldots , x_n\}\) is given, they are divided into sets \(S = \{S_1,S_2,\ldots ,S_k\}\), minimizing the squared errors in the cluster. If \(\mu _i\) is the center point of the set \(S_i\), the goal is to find a set S that minimizes the square of the distance between the center point of each set and the objects in the set.

Neural network-based forecasting model

Neural network-based models include artificial neural networks (ANN), also called feed-forward neural networks, convolutional neural networks (CNN), and recurrent neural networks (RNN), depending on how they operate. To cover them widely for electric load forecasting, we choose the following three models: 1) ANN, 2) CNN, and 3) long short-term memory (LSTM), which is an improved model of RNN that is capable of handling long-term dependencies.

An ANN is a network of artificial neurons that abstracts neurons72. It can be described as a function, a simple mathematical model consisting of inputs and outputs. Inputs are transferred to the neuron body, which is weighted, summed, and then converted to the neuron’s output through the defined function73. Neural networks can execute tasks that linear programs cannot execute.

CNNs74 were proposed for effective image classification by applying filtering techniques. CNN uses a convolutional layer in at least one layer within the network, where the convolutional operation consists of the multiplication of the input function x and the weight function w62. Here, the weight function is called “kernel,” and the output of convolutional operations is often called “feature map.” According to the number of dimensions of input data, 2D convolution is usually used for image processing; 1D convolution is for sequential data such as time series and natural language75.

LSTM is a variation of recurrent neural networks (RNN) that is effective for time-series data classification and prediction. LSTM was developed to solve the vanishing gradient problem, in which the learning ability is significantly reduced, owing to the gradual decrease in the backward propagated gradients, when the relevant information and the point where the information is used are far apart in temporal distance35,76.

Proposed method

Overall framework

Among the problems related to electric load forecasting, STLF is essential to operating power systems such as activation and shutdown plans and economic arrangements. The economic benefits, owing to the improved prediction accuracy in STLF, have been demonstrated by various existing studies1,63,77. The STLF model can be extended to other forecasting periods. Specifically, it can be extended to mid- or long-term load forecasting by adding metering variables and to very short-term forecasting by adding electric load data for shorter cycles78.

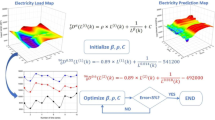
Figure 1 presents the proposed model for electric load forecasting. The inputs are (1) hour-by-hour electricity usage of households, (2) time information including hour, month, day, and holiday, and (3) weather information, i.e., daily minimum and maximum temperature. The entire flow consists of 4 steps: (1) data preprocessing, (2) dimensionality reduction, (3) data clustering, and (4) prediction models. In data preprocessing, we conduct data refining and data normalization. For a refined prediction considering the seasons, we divide the entire dataset into summer and winter datasets. Second, we perform dimensionality reduction to effectively deal with large-scale samples. It reduces the original dimensions for raw datasets by preserving important features as much as possible. We adopt three dimensionality reduction techniques: kernel PCA, UMAP, and t-SNE. Third, we cluster all households into household groups with similar usage patterns in data clustering. We apply dimensionality reduction to reduce the dimensions of each usage and then perform clustering on households showing similar patterns. Here, we use the k-means algorithm and investigate the number of appropriate clusters. Fourth, we build the prediction model for each clustered group to improve prediction performance. We use neural network-based models. For the former, we use ANN, CNN, and LSTM.

Fig. 1
figure 1

The proposed method of electric load forecasting models.

Full size image

Table 3 illustrates the prediction methods in terms of the combination of clustering and dimensionality reduction to consider specific machine learning-based and neural network-based models. We note that the previous studies have applied dimensionality reduction or clustering to forecasting models, but no studies have applied both of them.

Table 3 A combination of components for electric load forecasting models.
Full size table

Input data

The input data consists of three components: household electricity usage data, time data, and weather data. We used the dataset obtained from the Commission for Energy Regulation (CER), which is responsible for regulating the electricity and natural gas sector in Ireland, provided by the Irish Social Science Data Archive (ISSDA)79. The total data size was approximately 2.3 GB, consisting of electricity usage in 6,435 households and businesses between July 14, 2009, and January 1, 2011. Here, we use the data for 4710 households to target only households. The dataset contains 60,589,440 records, each consisting of (1) a meter ID, (2) a five-digit code, and (3) electricity usage. Each record contains electricity usage data for a single time point per household. As input data, we used external variables commonly used in existing studies for STLF. Specifically, we used time data, including hour, day, month, and holiday information and weather data from 2009 to 2012 in the Cork region of Munster, southwestern Ireland, where electricity usage data were collected. Here, the time and weather data were configured to maintain information for the next seven time points, based on the day when electricity usage was measured, to reflect future changes in the prediction model. For example, the electricity usage for January 1 at 1:00 AM for 4710 households is concatenated with the time and weather data from 1:00 AM to 7:00 AM to maintain the consecutive information. Table 4 lists the data composition.

Table 4 The description of input data.
Full size table

Data pre-processing

In this study, we used 4815 variables listed in Table 4 for the prediction model, i.e., electricity usage on 4710 households, 91 times, and 14 weather information points. Data pre-processing is a very important step in extracting meaningful features from raw data effectively. Data preprocessing in this study consisted of 1) data cleaning and 2) data concatenation and splitting.

For data cleaning, we carried out the following four steps. (1) We dealt with missing values in the electricity usage data. Simply removing the missing values would have made it challenging to consider the time-continuous characteristics. To resolve this problem, we substituted those values with the closest measured values. (2) We performed a log transformation for the raw electricity usage data. The distribution of raw usage data was skewed because most data had small values, and a few had large values. We converted the raw data into log transformation to stabilize such distribution and adjust abnormal values. Here, because the usage data included zero values, the log conversion was performed after adding one to the raw data by the equation, \(x^{\prime }=log(x+1)\). (3) For the time data (i.e., hours, days, and months), we applied a trigonometric function to the raw data to eliminate inherent discontinuity in the time (e.g., 11:59 PM to 00:00 AM) by Eq. (1). (4) We represented the day of the week and holiday information as a binary value. (5) We normalized the temperature information based on the maximum and minimum values.

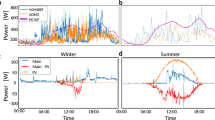
$$\begin{aligned} \begin{aligned} hour_{x}&=sin(2\pi \cdot hour/24)\\ hour_{y}&=cos(2\pi \cdot hour/24)\\ day_{x}&=sin(2\pi \cdot day/days\_of\_month)\\ day_{y}&=cos(2\pi \cdot day/days\_of\_month)\\ month_{x}&=sin(2\pi \cdot month/12)\\ month_{y}&=cos(2\pi \cdot month/12)\\ mon&=0~if~the~day~is~Monday,~otherwise~1\\&\dots \\ sat&=0~if~the~day~is~Monday,~otherwise~1\\ holiday&=0~if~the~day~is~Monday,~otherwise~1 \end{aligned} \end{aligned}$$
(1)

For data concatenation and splitting, we concatenated electricity usage, time, and weather data performed through preprocessing as a single dataset for further analysis. Then, we separated the entire dataset into two sub-datasets to focus on the seasonal analysis. Figure 2 shows the distribution of total electricity usage on the actual dataset we used, where the individual usages for all the households were aggregated per day to see the seasonal trends. As presented, we observed a severely different pattern between summer and winter.

Fig. 2
figure 2

The distribution of total electricity usage by the season.

Full size image

Data clustering

Small-scale load datasets do not require a complicated process because the variation in electricity usage between households is not significant. For example, a load forecasting model is performed for households with similar patterns by excluding users with abnormal patterns35. However, as the number of households increases, the variation in electricity usage and abnormal patterns increase, which causes complexity to the effective prediction model. To confirm this complexity, we randomly selected 40 and 400 households from the entire dataset for 4710 households used in this study. We checked the distribution of electricity usage as the number of households increased. Figure 3 shows the distribution of electricity usage according to the change in the number of households. The y-axis range in Fig. 3a,b was kept the same to clearly show the difference in variability based on the dataset size. Figure 3a shows the distribution of the daily electricity usages for the entire period; Figure 3b shows the distribution of hourly electricity usages for a specific period (i.e., 10 days). As shown in the figure, we confirm that as the number of households increases, the variation of electricity usage and households with abnormal patterns increase significantly. Accordingly, to deal with large-scale individual usages, an effective methodology for identifying households with similar patterns is essential.

Fig. 3
figure 3

Electricity usage patterns as the number of individual households increases (40, 400, 4710 households from top to bottom).

Full size image

We clustered all households into multiple groups with similar electricity usage patterns and predicted at the group level to improve accuracy. Dong et al. also showed that data clustering learned the model more effectively for electric load forecasting24. In this study, we used k-means for a data clustering method. We employed the k-means++ initialization method to set the initial centroids. k-means++ improves the selection of initial centroids by spreading them out, which helps avoid poor local minima and speeds up convergence. This method has been widely adopted in clustering tasks due to its ability to produce more stable and consistent results compared to random initialization. We chose k-means++ because it enhances the clustering performance, especially when dealing with large-scale datasets like ours, by reducing the risk of suboptimal solutions and accelerating the convergence process. Here, we used the Euclidean distance as the similarity metric in the vector spaces of features. Based on the k-means clustering results, we divided the datasets for the entire household into groups of households and then generated a predictive model for each group. We investigated the silhouette scores to evaluate the clustering quality quantitatively on summer and winter data by varying the number of clusters from 2 to 6. We used the silhouette score to evaluate the clustering quality quantitatively. Table 5 lists the results of measuring silhouette scores on summer and winter data by varying the number of clusters from 2 to 6. The results show that the silhouette score was the best when the number of clusters was two. However, as the number of clusters increased, the clustering quality rapidly declined, suggesting the need for additional methods.

Table 5 Silhouette scores for the clustering results.
Full size table

Dimensionality reduction

In the previous section, we observed that data clustering was ineffective for the target large-scale datasets. We analyzed the used datasets, which included large-scale dimensions where the electricity usage data contained data per 1 h for 431 days, resulting in 12,864 dimensions. In this section, we introduce a method that adapts dimensionality reduction before data clustering to improve the effects of data clustering. Specifically, we reduce the original dimensions to two by applying dimensionality reduction. We use kernel PCA, t-SNE, and UMAP as algorithms for dimensionality reduction. Table 6 shows the silhouette score and the distribution after performing the dimensionality reduction in the case using t-SNE and UMAP. In the experiments, clustering with dimensionality reduction was performed on clusters ranging from 2 to 6. Compared to the results from the previous section, where dimensionality reduction was not applied, the performance of the clustering with 2 clusters showed a slight decrease. However, overall improvement in performance was observed when the number of clusters exceeded 2.

Table 6 Silhouette scores after the dimensionality reduction.
Full size table

Prediction model

In this study, we adapt machine learning and neural network-based methods for the prediction model. For machine learning-based methods, we employed linear regression, XGBoost, and SVR, while for neural network-based methods, we utilized ANN, CNN, and LSTM. The input length for training data to generate predictions was set to 192 time points. Specifically, we created individual models for each of the 24-time points (\(y_{1}-y_{24}\)), where each \(y_{n}\) represents the total electricity consumption sum for each household, derived from the training data for machine learning methodologies. We trained the model to fit each target variable \(y_{n}\) with the corresponding training data. Subsequently, we applied the test data to each model to derive the predicted value for each time point. We calculated the prediction error between the predicted and actual values for each time point. These errors were then aggregated for each day to obtain the daily prediction error. Table 7 lists parameters used for the machine learning models.

Table 7 Parameters used in machine learning-based models.
Full size table

For the application of neural network-based models, we constructed the training data in the unit of 3,072 rows (i.e., 3,072 h) as a chunk and constructed a single minibatch by randomly selecting 16 chunks. 3072 h is simply the product of the input length of 192 and the number of chunks of 16. We fed the mini-batch into the neural network-based model as the input for the data loader. We iteratively performed error calculations and updates for every 1 batch and obtained verification errors for every 10 batches. Table 8 lists the parameters used in the neural network-based model. On a CNN basis, we typically downsampled data with multiples of 2. We tried to configure the input and output sizes of all layers to be multiples of 2 as much as possible for the precise matrix operation and adjust them to be maintained at a constant ratio. We configured other models, i.e., ANN and LSTM, to be similar to CNN.

Table 8 Parameters used in neural network-based models.
Full size table

Performance evaluation

Experimental datasets and methods

We used three kinds of attributes for the experimental datasets, as explained in Section 4.2: (1) electricity usage, (2) time information, and (3) weather information. The electricity usage data occupied approximately 2.3 GB and contained 60,589,440 records. Table 9 shows the statistics of the used datasets. The entire dataset includes 4710 individual households. The Total-Usage dataset is constructed by summing individual usages in the entire dataset.

Table 9 Statistics of the used datasets.
Full size table

The collected weather information was hourly temperature information. To collect the information, we used the Python Selenium package. We used approximately 75% of the total data (i.e., data for the front 431 days) for learning and validation and used the remaining 25% (i.e., data for the latter 100 days) for testing. We used four commonly used evaluation metrics: 1) MAPE, 2) RMSE, 3) NMAE, and 4) NRMSE. They are shown in Eqs. (2) \(\sim\) (5). Here, \(A_t\) is the actual value, \(F_t\) is the predicted value, and n is the number of measurements. For evaluating the performance of methods, the experiment was conducted 10 times, and the mean was used. This number of repetitions was chosen based on previous studies in short-term load forecasting (STLF). Previous studies performed up to 10 repetitions with models such as LSTM and CNN-LSTM53, Autoformer and LSTM56, and DLinear and LSTNet57. Based on these precedents, we conducted 10 repetitions to provide reliable measurement and comparison of model performance and showed standard deviations for each experimental result of neural network-based models to confirm the variations of each experiment.

$$\begin{aligned} MAPE= & \frac{1}{n}\sum _{t=1}^{n}\left| \frac{A_{t}-F_{t}}{A_{t}}\right| \end{aligned}$$
(2)
$$\begin{aligned} RMSE= & \sqrt{\frac{1}{n}\sum _{t=1}^{n}(A_{t}-F_{t})^{2}} \end{aligned}$$
(3)
$$\begin{aligned} NRMSE= & \frac{RMSE}{\overline{A_{t}}} \end{aligned}$$
(4)
$$\begin{aligned} NMAE= & \frac{\sum _{t=1}^{n}(A_{t}-F_{t})^{2}}{\sum _{t=1}^{n}(\overline{A_{t}}-A_{t})^{2}} \end{aligned}$$
(5)

We performed this experiment on a machine equipped with Intel(R) Xeon(R) Silver 4210R CPU @ 2.40GHz of 8 cores, NVIDIA RTX A5000, and 8GM RAM running Ubuntu 18.04.4. We used Python version 3.7.12, Pytorch version 1.7.1, and Cuda version 11.6.

Comparision using individual usages and a total usage

Table 10 The accuracy of the prediction model using individual usages and a total usage.
Full size table

Most previous studies used total usage in a region for electricity load forecasting. It is relatively easy and sufficiently effective to forecast the overall electricity usage. However, there is a limitation to constructing a sophisticated prediction model because household usage patterns cannot be considered. To check the effectiveness of using individual household usages, we compare the performance of prediction models using two kinds of datasets: (1) Individual-Usage and (2) Total-Usage. We build two prediction models: (1) one uses individual usage, time, and weather information for 4710 households, and (2) the other uses total usage, time, and weather information for the total households.

Table 10 shows the accuracy of the prediction models using individual usages and total usage. Different trends are observed between neural network-based models and other machine learning-based models for the two datasets. Specifically, machine learning-based models perform better when predicting total usage than individual usage. This is attributed to the significant impact of feature selection on the performance of machine learning-based models23. Effective feature selection becomes challenging when dealing with many features for 4710 households.

On the contrary, neural network-based models, except for ANN in the summer dataset, exhibit better performance in individual usages than total usage. Although in winter, the performance of some models slightly degrades for individual usages, the overall performance shows clear improvement. Notably, LSTM, which demonstrates the best performance, significantly enhances its performance in individual usages. This improvement is due to the effective extraction of essential features by neural network-based models23.

In this study, given the focus on developing a sophisticated prediction model for individual household usages, we utilize datasets related to individual usages for subsequent experiments. It is worth noting that for machine learning models, predicting total usage is more advantageous due to challenges in effective feature selection when dealing with many features for multiple households. However, because we focus on developing accurate individual usage prediction models, it leads us to concentrate on neural network-based models in the subsequent experiments.

Effectiveness of data clustering and dimensionality reduction

Table 11 The performance of machine learning-based forecasting models with data clustering and dimensionality reduction.
Full size table
Table 12 The performance of neural network-based forecasting models with data clustering and dimensionality reduction.
Full size table

We compared the performance of the prediction model that incorporated data clustering and dimensionality reduction. For dimensionality reduction methods, we employed kernel PCA, t-SNE, and UMAP. Tables 11 and 13 list the performance of the prediction model with data clustering and dimensionality reduction for both machine learning-based and neural network-based models. It’s worth noting that the prediction target is the total electricity consumption sum for each household. When applying clustering, the electricity consumption sum for each cluster is considered as the prediction target. Here, only MAPE and RMSE were used, as overall trends are similar in NMAE and NRMSE. Overall, we observe that the prediction models show further performance improvement compared to the basic prediction model due to the application of data clustering and dimensionality reduction. Most prediction models performed best, especially with kernel PCA and clustering (n=4).

Neural network-based models generally performed better when kernel PCA and clustering (n=4) were used in both summer and winter. In the case of LSTM in the summer dataset, the RMSE of the basic prediction model was the lowest, which is similar to the clustering (n=4) with kernel PCA within the standard deviation. Overall, the performance of prediction models in the summer season was better than that in the winter season, indicated by the variation of the winter season for the electricity usage distribution in Fig. 2.

Overall, we note that most methods showed the best performance when data clustering and dimensionality reduction were applied, which shows the effectiveness of data clustering and dimensionality reduction. Specifically, overall, in both summer and winter, the proposed methods combining data clustering and dimensionality reduction outperformed basic models only, except for the case of RMSE in summer with a negligible difference. In both the summer and winter seasons, we observed that LSTM-based models showed the best performance.

Comparison with the existing methods

Table 13 The comparison between the proposed method and the existing methods.
Full size table

Based on the results in Section 5.3, we used kernel PCA and k-means (n=4), which demonstrated the best performance with the proposed dimensionality reduction and clustering methods. In summarizing the experimental results, we compare our proposed method with baseline models and their performance when combined with the proposed dimensionality reduction and clustering techniques. Table 13 presents the comparison results showing how applying our proposed approach improves baseline models. Based on the experimental results, we observed that, with a few exceptions, the proposed method consistently improved the performance of baseline models in predicting both summer and winter.

As outlined in Table 13, compared to existing methods for Short-Term Load Forecasting (STLF), the proposed method demonstrated superior performance in almost all cases and evaluation metrics for both summer and winter. This improvement trend was consistently observed not only in baseline models such as traditional ANN, CNN, and LSTM but also in state-of-the-art deep learning prediction models, including DLinear, Autoformer, and LSTNet. The only exception was observed in the winter results of Autoformer, where the difference was negligible. Furthermore, the significance of the proposed method lies in its ability to substantially enhance the performance of not only traditional neural network-based models but also SOTA deep learning models. Specifically, we demonstrate that the proposed dimensionality reduction and clustering method improved the performance of baseline models in terms of Mean Absolute Percentage Error (MAPE) by a factor of 1.009 to 1.559 in the summer prediction model and by 0.997 to 1.418 in the winter prediction model.

Conclusions

In this study, unlike small-scale household data used in previous studies, it was observed that the distribution changes as the size of households increases in the case of large-scale household data. Dimensionality reduction and clustering were utilized to account for the diverse household distribution in large-scale data. We proposed a new model for STLF on large-scale electricity usage data through a combination of data clustering and dimensionality reduction schemes. Applying the proposed method to neural network-based models on a large-scale household dataset demonstrated the effectiveness of data clustering, and dimensionality reduction followed by data clustering improved the performance compared to the baseline model. As a result, applying the proposed method to the existing models improved their prediction accuracy by 1.009–1.559 times for summer data and by 0.997–1.418 times for winter data in terms of MAPE.

With the development and spread of remote electricity usage detection technologies such as smart meters, the necessity to effectively predict electricity usage on large-scale datasets is increasing. There are distinguishing properties in predicting electric load forecasting because we need to consider various features such as weather and days of the week. Exploratory data analysis (EDA) for feature selection has been an essential part of the success of the prediction because the performance of the existing machine learning models depends on feature selection. In contrast, neural network-based methods integrate the feature selection process into the learning process, even if significant efforts are required to train the model. As a result, we can identify the effects of data clustering and dimensionality reduction on each method based on neural network-based and other machine learning-based prediction models. These properties are also valid in other domains considering various features such as multi-sensor IoT data in smart grids, water quality forecasting, and finance data forecasting, which are affected by several external variables.