Introduction

Additive manufacturing has revolutionized the aerospace and automotive sectors by enabling the production of components on demand and creation of obsolete legacy parts. Nevertheless, the dynamic characteristics of additive manufacturing have concurrently introduced a security vulnerability with distinct supply chain challenges. A taxonomy of security threats, including counterfeit, theft, loss, reverse engineering, sabotage, and blacktopping, are summarized in Yampolskiy et al.1. Of the various threats, counterfeiting stands out as the most pervasive and negatively affects the global economy2. A leading countermeasure is embedded digital codes for component authentication and tracking2,3.

The concept of embedding structures into printed works for authentication has an extensive history. For example, Benjamin Franklin developed an anti-counterfeiting technique of high resolution elm leaf prints on paper currency4,5. Similarly, part marking is widely implemented in the aerospace industry for quality control and part lifecycle management6. Although 2D surface-applied part markings aid in component identification, authentication is at risk due to removal, duplication, or alteration2,3.

A variety of part authentication processes have been proposed such as fingerprinting, watermarking, material biometrics, signatures, and tagging. The implementation method may add a foreign material or may change a processing parameter; the method may yield digital information encoded on the surface or internal to the part. The information readout may be optical7,8, near-infrared9, radio frequency10, magnetic11, or X-ray2,12. And the embedded digital information may be a few bits or longer. An example of embedded digital Quick Response (QR) code in the selective laser melting fabrication of stainless steel 316 L is the work by Sofinowski and co-workers13. Here, the laser power was modulated to affect grain orientation in the surface layer which was then read out with optical reflectance microscopy and mapped to a QR code of 841 bits in an area of 60 mm \(\times\) 60 mm. The risks to the additive manufacturing supply chain have been discussed1,14 and the procedures for information embedding have been reviewed3. The standards organizations—ISO, ASTM, NIST, GS1—are providing cyber security guidance15,16,17,18.

Verification of part identity with the aforementioned readout methods requires technologies to facilitate the process of authentication. These authentication mechanisms in digital environments have been referred to as a “trust anchor”19. A basic process is based on two factors: The first factor is a unique identifier such as a serial number. The second factor is physical features specific to that part, analogous to a human fingerprint, DNA, or retinal scan where we recognize the inspection of physical features is affected by noise. In cyber terminology, the serial number is convertible to a cryptographic hash; then, a physical feature, including its readout noise, is converted to a perceptual hash. Lastly, the hashes are coupled to a blockchain17. We label this hash pair a cyber-physical trust anchor. A cyber-physical trust anchor is a reliable means of authenticating a component throughout a chain. A cyber-physical trust anchor in an additive manufacturing workflow covers several technology domains and three dominating questions: First, how much digital information can be encoded in the anchor? Second, what are the performance implications? Third, how secure is a cyber-physical trust anchor? The technologies used in this paper to answer these questions span cyber security, fractals, additive manufacturing, tensile testing, and advanced X-ray imaging.

Herein, we discuss processes and procedures applicable to embedding digital information in additive manufacturing components for supply chain security. In particular, we address the challenges of verifying the authenticity and quality of additively manufactured components throughout the life cycle. The procedures include embedding digital codes, readout with advanced X-ray imaging, and tensile testing. The procedures are tested to determine data size and ensure readability. The readable digital information uniquely identifies the part and can be used for authentication and tracking. Authentication and tracking help secure the supply chain. The unique identification is tied to the identity of the part, along with other identifiers, and when combined are termed a trust anchor. No empirical study, to the best of our knowledge, has embedded digital codes and tested data size, readout, and included performance analysis. The digital codes are in a format not visible with conventional X-ray inspection, and cryptography techniques are employed after the data size is determined. The challenge of compromising mechanical properties with tensile testing is addressed, as discussed in the following sections and Supplementary Material. The overview of this research can be summarized in the itemized list below.

An overview of the research is posed as a series of questions and answers.

  1. 1.

    How many digits are needed to create a unique identifier? We note the $100 bill uses a letter/number sequence that supports 15,000-fold more unique identifiers than the number of $100 bills in circulation. Figure 2 shows a scheme for encoding large numbers.

  2. 2.

    Can a commercial additive manufacturing printer, without any hardware/software modifications, print information inside a part? Table 1 lists parameters for the selective laser melting prints of ASTM E8/E8M dumbbells and Figs. 5, 6 and 7 show the X-ray tomography of dumbbells with internal digital information. In total, 400 internal features were successfully printed and observed by X-ray tomography.

  3. 3.

    Does printing internal information affect the part integrity? There is a minor effect when the part is under static loading within the elastic range. The worst-case effects for large features and large digital values are described in the tensile data shown in Figs. 3, 4 and 5.

  4. 4.

    What is the impact on workflow, both data embedding and data readout speeds? Figure 1 shows CAD representations, i.e., there is essentially no slow down in print speed. It is true that X-ray tomography, also called CT scanning, is on the order of two hours per part, but Fig. 8 demonstrates a new X-ray technology with potential for two minute readout or faster. To support faster readout, resistance of the coding against read-write errors was tested. Figure 2 shows that part uniqueness can be maintained with up to 20% error rate.

Embedding digital information

The method presented in this work relies upon embedding data in powderbed fusion manufactured parts. The data is added to printed parts by creating voids in patterns inspired by the Cantor dust fractal. A modification of the Cantor dust fractal is used in this work as a structure for encoding digital information. The mathematics, discovery, and applications of fractals are discussed in “Fractals in the Natural Sciences”20. The Cantor dust fractal in 2-D is illustrated in Wolfram MathWorld21. The motivation for choosing fractals is the aesthetic nature, and allows a highly unique and recognizable pattern, which enables the construction of a unique digital identifier as well as ease of detection and decoding using X-ray imaging technologies. Furthermore, the self-similar structure is efficient and enables a usage of surface area to maximize structural integrity. A modified Cantor dust fractal, due to its recursive nature, is ideal for creating distinct, easily identifiable voids. Other methods, such as random dot patterns, holographic markers, and watermarking can require more space, be susceptible to noise and partial data loss, and less structurally integrated.

Cantor dust fractals are also appropriate for this work, as they have been used in the design of RF antenna and X-ray optics22,23. We have used the original Cantor dust fractal in prior work objects printed in stainless steel with selective laser sintering and in polymer resin with stereolithography19. In that work, the Cantor dust fractal was very useful for rapidly determining the print resolution for internal cubic voids. In the present work, the Cantor dust fractal has two modifications: cubes are replaced with ellipsoids and a stagger is introduced between layers. Neighboring ellipsoids have center-to-center distances of twice the major radius. The embedded digital information is based on discrete voids, in this case, ellipsoids with the shape of prolate spheroids with the rotation axis normal to the build plane. Groups of eight ellipsoids were arranged in a staggered Cantor dust fractal where fractal order = 1 contains eight ellipsoids, fractal order = 2 contains 8\(^2\) = 64 ellipsoids, and fractal order = 3 contains 8\(^3\) = 512 ellipsoids. The first and second-order fractals are shown in Fig. 1a,b. The cyber-physical trust anchor is developed with print features in a pattern derived from Cantor dust fractals of order 1 and 2, as shown in Fig. 1a,b, and then embedded in either the gauge or tail section of an ASTM E8/E8M dumbbell, Fig. 1c.

Fig. 1
figure 1

Cantor dust fractals are shown with orders 1 and 2 ellipsoids in a staggered pattern. (a) An order = 1 fractal with eight ellipsoids (prolate spheroids) having a major radius of 300 \(\upmu\)m and two minor radii of 150 \(\upmu\)m. (b) Order = 2 fractal with 64 ellipsoids having a major radius of 400 \(\upmu\)m and two minor radii of 200 \(\upmu\)m. Neighboring ellipsoids have center-to-center distances of twice the major radius. (c) The position along the dumbbell from Table 1 where 55 mm is in the gauge volume and 85 mm is in the tail.

Full size image

A Cantor dust fractal structure in an AM part can incorporate both components of a trust anchor, both the unique identifier such as a serial number and physical features analogous to a fingerprint as will be illustrated conceptually in Fig. 2 and based upon the experimentally realities of AM printing and X-ray tomography described in Results.

Figure 2 will be discussed as nodes and paths in a structure defined by a Cantor dust fractal. Let us define two properties of a node, namely size and color. Furthermore, let the size be deterministic such that three discrete values can be assigned: 0, 1, or 2. As for the color, let it be randomly assigned; later, the color will be mapped from the irregularities of the AM print process onto three possible colors: R, G, or B. The readout errors for node size are rare while the readout error rate for the node properties shown as colors may be significant. The paths will be a function of node size, although mapping errors will occur. For example, two adjacent nodes of size 2 will usually be joined by a thick link and two nodes of size 1 and 2 will be joined by a thin line. Otherwise, a dashed line will be drawn. The node sizes and locations can be mapped onto a base-3 number; a Cantor dust fractal of order 2 can represent \(3^{64}-1 \approx 3 \times 10^{30}\). In practice, a portion of the fractal will suffice as shown in Fig. 2a where 16 nodes can represent over 40 billion unique serial numbers.

The fingerprint component of a trust anchor is derived from the colors and lines. In practice, X-ray imaging of the AM part is used measure the fingerprint and assign three-state values, shown here as colors and line thickness. The noise properties of X-ray imaging will lead to an error rate. If we assume a read error rate of 20%, we get the distribution of measurements shown in Fig. 2b. The three colors represent three different AM prints of a part with the same serial number. Each dot represents one of a thousand X-ray measurements of that part. The result shows an error rate of 20% is acceptable provided there are sufficient features, here 13 nodes and 11 lines contributing to the fingerprint structure.

Fig. 2
figure 2

The 64 locations of a Cantor dust fractal of order 2 are shown in (a). Locations 1 through 16 are printed with ellipsoids both large and small, giving a unique number expressed in base-3 in the plot label and corresponding to 35,427,451 in base-10. The AM print quality of each ellipsoid and the touch or not-touching of adjacent ellipsoids is shown as red, green, or blue ellipsoids and as thick, thin, or dashed lines between ellipsoids. The colors and lines represent the AM print imperfection fingerprint of an AM part. In practice, the fingerprint structure will have a read error rate. Assuming a read error rate of 20% of the ellipsoids AM imperfections and interactions, the effective uniqueness is shown in a principal component analysis in (b) for three simulated AM parts all sharing the same serial number but having unique fingerprints. The separation between clusters can be increased by reducing the read error rate or increasing the digit length of the serial number. An increase of the serial number from 16-digits to 24-digits in base-3 would use one more cube in the Cantor dust fractal.

Full size image

Methods

Sample preparation

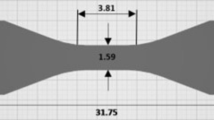
ASTM E8/E8M standard dumbbells were chosen for the evaluation of tensile strength in AM parts with embedded Cantor dust fractals. Mathematica version 14.0 software program was used to create region objects representing the Cantor dust ellipsoids (Fig. 1a,b), a QR or barcode, and a cylinder slightly larger in diameter, 15 mm, than the ASTM dumbbell shown in Fig. 1c. The QR or barcodes were printed to compare performance with Cantor dust ellipsoids. Boolean operations were used to merge the region objects and the results were exported to both standard tessellation language (STL) and Standard for the Exchange of Product Data (STEP) files for printing.

Fifteen pairs of cylinders (30 in total) were fabricated in two batches (one with 1-digit serial numbers and the other with 2-digit serial numbers) using the Direct Metal Laser Sintering method with an EOS M290 before machining into standard ASTM dumbbell shapes. The particle size ranged from 20 to 90 \(\upmu\)m, and the printing was conducted with a layer thickness of 30 \(\upmu\)m under the nitrogen environment. The printing parameters included a laser spot size of 100 \(\upmu\)m, laser power of 370 W, scanning speed of 1300 mm/s, hatch spacing of 0.15 mm, and layer rotation of 67\(^{\circ }\). The build direction was parallel to the dumbbell’s axis. No heat treatment was carried out for these printed samples. The material was aluminum powder EOS AlF357, the beryllium-free form of AlSi7Mg0.6 alloy. The chemical composition in weight percent is24: Al, balance; Si, 6.5–7.5; Fe, 0–0.10; Cu, 0–0.20; Mn, 0–0.10; Mg, 0.40–0.7; Zn, 0–0.10; Ti, 0.04–0.20; Be, 0–0.002; and other, 0–0.15. Sample details are listed in Table 1. We did find that for two print test bars in the same build layer, sample SN = 7 yielded a solid cylinder with no sign of the expected 512 ellipsoids. This print failure was noted, but not investigated any further.

Table 1 ASTM samples imaged and tensile tested (SN Serial Number, ell. ellipsoid; major radius, y-position, and order is illustrated in Fig. 1).
Full size table

The as-printed cylindrical rods were taken to the LSU Advanced Manufacturing and Machining Facility (AMMF) and lathe-machined, conforming to the tensile sample geometry outlined in ASTM E8/E8M25 (Fig. 1c). As the impact of surface quality on tensile strength is minimal, the sample surface was not polished.

Tensile testing

Although mechanical components in action rarely undergo only a uniaxial static tensile loading, this test can establish the grounds for future multiaxial and dynamic loading conditions. The fabricated samples underwent static uniaxial testing to examine how the location of embedded Cantor dust fractals within the specimen affects its strength under static loads. The TestResources hydraulic fatigue tester with a 25 kN load capacity was utilized for the experimental setup, specifically in the static tensile testing mode. Following the ASTM E8/E8M standard25, a strain rate of 0.6 mm/min (0.01 mm/s) was employed, and an Epsilon Technology Corp (USA) model 3541 axial extensometer was mounted on the gauge section for accurate measurement of the strain.

Finite element analysis

To investigate the impact of the prolate ellipsoid alignment in relation to loading direction and the effect of staggering, the Finite Element Method (FEM) using ANSYS Workbench has been employed. The initial validation of the model is carried out using existing experimental data. The part is discretized using quadratic elements, where the average element size is 0.5 mm. In order to conform to the intricate geometry of the Cantor dust, the mesh grid size is progressively reduced to 10 microns on the void surface. The fixed boundary condition is applied to the cylindrical surface on one end, while the other end undergoes a displacement with a constant rate of 0.01 mm/sec, replicating the standard test procedure. The FEM results can be found in Supplementary Information Section S3 “FEM results”.

X-ray tomography

Nine samples were selected from the printed specimens, including sample #94 (Fig. 5), and analyzed using X-ray tomography at the University of Texas High-Resolution X-ray CT Facility with a Zeiss Xradia Versa 620 instrument. The scan parameters were: X-ray source: 100 kV, 12 W; Detection: flat panel with binning = 1, 0.05 s acquisition time, 5 samples per view, projection angle range ± 180, 3201 views, HE1 filter, dithering; Processing: beam hardening 0.25, theta 0, byte scaling [− 0.01, 0.3], recon filter smooth (kernel size = 0.7). Projections were reconstructed by Xradia Reconstructor with (6.0 \(\upmu\)m)\(^3\) voxels and 1637 slices. Tomography acquisition parameters for the other samples were similar with acquisition times in the range of 0.04 to 0.06 s and voxel sizes of (6.0 \(\upmu\)m)\(^3\) to (12.0 \(\upmu\)m)\(^3\), which are one order of magnitude smaller than the smallest void. OTSU filter was used to find the thresholding value with no other filtering.

X-ray interferometry

The Microworks Talint grating-based X-ray interferometer consists of an optical rail fitted with three X-ray optics. The optical rail is sized to fit within the X-ray cabinet of a laboratory X-ray tomography system. The X-ray optics are microfabricated attenuation and phase shift structures on silicon wafers and are typically labeled G0, G1, and G2: G0 and G2 are optics with a linear array of X-ray absorption features and G1 has a linear array of X-ray phase shift features26,27.

Three sample pairs with a range of void sizes with major axis radii of 200 \(\upmu\)m, 300 \(\upmu\)m, and 400 \(\upmu\)m, have been imaged at Microworks GmBH for X-ray interferometry imaging with a Talbot–Lau system operating at 40 keV. Viscom source XT9160-DED at 80 kV and Dexela 1207 detector are used. Period of Gratings are all at 6 \(\upmu\)m. 31 phase stepped images were taken with 1.0 s acquisition time and 1.5 s waiting time between steps per image. Effective pixel size is 33.71 \(\upmu\)m with 2.22 magnification.

The interferometry autocorrelation length is an important parameter for observing porosity in additive manufacturing. There are two equations for calculating the interferometry autocorrelation length, depending on the position of the sample in the grating-based interferometer. If the sample is between G1 and G2, autocorrelation length is28,29,

$$\begin{aligned} \xi _{GI} = \frac{\lambda L_s}{p_g}, \end{aligned}$$
(1)

where \(\lambda\) is the wavelength of the X-rays at the design energy, \(L_s\) is the sample-to-detector distance, and \(p_g\) is the grating period.

If the sample is between G0 and G1, then, replace \(L_s\) with \(L'_s = (L_1+L_2 - L_s) (L_2/L_1)\)

$$\begin{aligned} \xi _{GI} = \frac{\lambda (L_1+L_2 - L_s)(L_2/L_1)}{p_g}, \end{aligned}$$
(2)

where \(L_1\) is the distance between G0 and G1 and \(L_2\) is the distance between G1 and G230.

Microworks reports the energy is 40 keV, \(L_1\) = \(L_2\) = 29 cm, and \(L_s\)=50 cm with the samples 2 to 3 cm downstream of G1, thus Eq. (1) is relevant. The grating period is 6 \(\upmu\)m. The result is an interferometer autocorrelation length \(\xi\)= 2.6 \(\upmu\)m. For comparison, most of our neutron interferometry work on AM test coupons subjected to bending and fatigue was done with \(\xi\) in the range of 0.60 \(\upmu\)m to 1.99 \(\upmu\)m31,32.

Results

The embedded digital codes were assessed with the 15 identical pairs of cylindrical ASTM E8/E8M dumbbell tensile test samples (30 samples in total) in terms of printing accuracy and static structural strength. The samples covered a range of ellipsoid size, location within the ASTM dumbbell, Cantor dust order, and external labeling as listed in Table 1 and illustrated in Fig. 1. The print quality was evaluated using X-ray tomography and X-ray interferometry radiography. Uniaxial tensile testing measured the static strength of the specimens up to the point of failure. The following sections describe the process in detail, including tensile testing and advanced imaging analyses.

Tensile testing for design validation

The tensile specimens from Table 1 were subjected to testing in accordance with ASTM E8/E8M until reaching the point of rupture. In each scenario, two identical specimens were tested. The data in Fig. 3 displays the average values of the Ultimate Tensile Strength (UTS) and yield stress for the two specimens in each pair.

Fig. 3
figure 3

Measured average UTS for various void sizes and Cantor dust fractal locations. All the samples with \(z = 55\) failed due to cracks initiated from the cantor dust voids, as expected. The EOS range represents the range of experimental values for yield and ultimate stress, reported by EOS, the printer manufacturer and powder supplier24.

Full size image

The Cantor dust features embedded inside the gauge section will affect the minimum tensile area. A drop in the effective tensile area of the sample is anticipated by increasing the Cantor dust size and order, which alone leads to higher stress values for a given constant load and early failure.

Analyzing the stress–strain curve (Fig. 4) shows that the material exhibits ductile behavior, with intact samples containing Cantor dust in their tail sections elongating between 8 and 11% before rupture. A slight decrease in stress prior to rupture indicates necking behavior. The elastic yield, with a 95% confidence interval, reduces from \(267.4\pm 1.4\) to \(259.4\pm 7.0\) MPa, reflecting slightly lower yield stress and greater variability. In the plastic region, embedding Cantor dust in the tail section does not affect tensile strength, whereas elongation decreases to 2.1–4.2% for samples with Cantor dust features in their gauge section.

The effect of the cross-sectional areas of the Cantor dust fractals on the tensile strength was further studied with FEM calculations which are included in the supplementary material.

Fig. 4
figure 4

Stress–strain curve for various combinations; some elongation results for certain specimens were not reliable and are not shown, as the grip section slipped during tension.

Full size image

Nondestructive evaluation with X-ray tomography

The X-ray imaging shows good fidelity for ellipsoids 300 \(\upmu\)m and larger and for Cantor dust fractals of order 1 and 2. The X-ray imaging shows, residual powder in the ellipsoids, the expansion of the ellipsoids, as well as the contribution of the ellipsoids in sample failure under uniaxial tensile loading as shown in Fig. 5. The average empty volume of the twelve ellipsoids in the tomography field of view, and unconnected to the fracture, is 89.1 ± 1.6 nL, somewhat larger than the as-designed volume of 67.0 nL for an ellipsoid with a major radius of 400 \(\upmu\)m and two minor radii of 200 \(\upmu\)m. The analytical equation for the volume of a prolate ellipsoid is \(V=\frac{4}{3} \pi a b c\) where a, b, c are the ellipsoid radii.

Fig. 5
figure 5

ASTM samples were typically tensile tested (a), then imaged with X-ray tomography (b,c). Sample #94 with 400 \(\upmu\)m ellipsoids in a Cantor dust order = 2 pattern (64 ellipsoids) shows (b) fracture propagation through the fractal pattern and the contribution of the embedded features in sample failure and (c) ellipsoids partially filled with residual powder. The X-ray tomography voxels are 6 \(\upmu\)m. The 400 \(\upmu\)m scale bar in (c) corresponds to the requested diameter of the ellipsoid showing some expansion of the ellipsoid beyond the size described in the CAD STEP file.

Full size image

Other examples of 400 \(\upmu\)m ellipsoids printed in Cantor dust fractal order 1 (8 ellipsoids) and order 2 (64 ellipsoids) are shown in Fig. 6. The blue regions denote the surface of the ellipsoid inside the aluminum matrix. The as-designed ellipsoid is shown in yellow. Again, the ellipsoids are partially filled with unconsolidated powder, and the ellipsoids are oversized.

Fig. 6
figure 6

Sample #92 (a) with 400 \(\upmu\)m ellipsoids, order = 1, printed at position 55 mm in the gauge volume. The volume calculation is over eight ellipsoids for an average volume of 85.3 ± 1.6 nL versus an as-designed volume of 67.0 nL. Sample #98 (b) with 400 \(\upmu\)m ellipsoids, order = 2, printed at position 85 mm in the tail. The volume calculation over 64 ellipsoids gives an average volume of 96.9 ± 4.8 nL. CT imaging parameters are 0.04 s acquisition time with 6.28 \(\upmu\)m voxel resolution for #92 and 0.06 s with 7.99 \(\upmu\)m for #98.

Full size image

Ellipsoids at the size extremes of Table 1 are shown in Fig. 7. The 200 \(\upmu\)m ellipsoids print poorly, with neighboring ellipsoids merging into each other. The 600 \(\upmu\)m ellipsoids print well, though oversized. Further results from the X-ray tomography can be viewed in Supplemental Information Section S1.

Fig. 7
figure 7

Sample #93 (a) with 200 \(\upmu\)m ellipsoids, order = 2, printed at position 55 mm in the gauge volume. Due to mergers (the center-to-center distance is 400 \(\upmu\)m), the volume calculation is over five ellipsoids for an average volume of 10.6 ± 2.0 nL versus an as-designed volume of 8.4 nL. Sample #99 (b) with 600 \(\upmu\)m and order = 2 with 53 ellipsoids in the lathed tail. The measured volume over 53 ellipsoids is 276.9 ± 8.8 nL versus an as-designed volume of 226.2 nL. CT imaging parameters are 0.04 s acquisition time with 6.28 \(\upmu\)m voxel resolution for #93 and 0.06 s with 9 \(\upmu\)m for #99.

Full size image

X-ray interferometry radiography

Inspection speed is critical for embedded digital codes. The conventional X-ray tomography used above typically requires on the order of 2 h instrument time to acquire roughly 1500 projections. On the other hand, grating-based X-ray interferometry radiography requires on the order of nine images to generate an interferogram. From the interferogram, three imaging modalities can be produced, transmission, scattering, and differential phase contrast, as shown in Fig. 8. The transmission image is equivalent to one projection in a conventional X-ray tomography experiment and lacks the image contrast to easily observe the ellipsoids. However, the scattering image is sensitive to the multiple air-aluminum interfaces in the unconsolidated powder inside the ellipsoids, surfaces with scatter the imaging X-ray beam and produce a strong contrast in the scatter imaging between the homogeneous aluminum metal and the ellipsoids.

Fig. 8
figure 8

X-ray interferometry images of dumbbells with three different size voids and Cantor dust fractals of order = 1 and 2. The transmission images can detect the largest ellipsoids with a major radius of 400 \(\upmu\)m, but not the smaller ellipsoids. The scattering and differential phase contrast images clearly show the 300 \(\upmu\)m and 400 \(\upmu\)m ellipsoids and show faint indications of the 200 \(\upmu\)m ellipsoids. An important parameter for the X-ray scattering image is the sample position within the interferometer. The sample position determines both the X-ray magnification and the interferometer autocorrelation length. The magnification was 2.22 giving an effective pixel size of 33.7 \(\upmu\)m. The sample position between G1 and G2 with a sample-to-detector distance of 50 cm gives an interferometer autocorrelation length of \(\xi\) = 2.6 \(\upmu\)m28, well suited for observing loose powder inside the Cantor dust fractal ellipsoids.

Full size image

Digital information content

The embedded digital information quantity can be as rich as \(n^{8^{O}}\) where n = 2, 3, or 4 corresponding to binary, ternary, or quaternary representation and O is the order of the Cantor dust fractal. The value of n is set by printing voids at different sizes: n = 2 corresponds to a Cantor dust printed at a constant size such as 0 \(\upmu\)m and 250 \(\upmu\)m. Then, n = 4 corresponds to four different sizes such as 0 \(\upmu\)m, 250 \(\upmu\)m, 350 \(\upmu\)m, and 450 \(\upmu\)m.

Consider a Cantor dust fractal of order = 2 with ternary sizes. This structure can encode positive integers up to \(3^{8^{2}} = 3.43\times 10^{30}\). Or, consider a Cantor dust fractal of order = 1 with binary sizes. This structure can encode positive integers up to \(2^{8^{1}} = 64\). Lastly, a Cantor dust fractal of order = 3 with quaternary representation can encode positive integers up to \(4^{8^{3}} = 1.80\times 10^{308}\), vastly exceeding the number of atoms in the universe.

The recommended coding is a Cantor dust fractal of order = 1 with ternary sizes. This structure can encode positive integers up to \(3^{8^{1}}\, = \,6561\). Also recommended is a partial Cantor dust fractal of order = 2 as shown in Fig. 2 which supports over 40 billion unique serial numbers as well as a robust fingerprint structure.

Discussion

These results show that the dumbbells meet the ultimate tensile strength specification for the EOS AlF357 powder, as long as the Cantor dust features are embedded in the sample far away from the high-stress regions. X-ray imaging, both conventional and interferometry, can detect the digital information. X-ray tomography shows the average volume of the ellipsoid is slightly greater than as-designed even with included loose powder in the void. X-ray interferometry had increased void detectability, with a great fractional content of unconsolidated powder. These results suggest a standard selective laser sintering printer with typical metal powders could reasonably expect to print 100 bits of digital information in a gauge volume 6 mm in diameter while still maintaining tensile specifications.

This work shows that embedded digital codes can be printed inside low-stress regions of aluminum ASTM E8/E8M dumbbell test coupons with no effect on the yield tensile strength. Since in standard mechanical design procedures stressing the part up to the yield point and entering the plastic region is considered as the static failure criteria, we can claim that embedding Cantor dust features of order = 1 has no significant negative effect on static strength. Nonetheless, it is recommended to embed the Cantor dust fractals within the areas of the component experiencing minimal stress, with its orientation aligning along the direction of stress flow.

The high-resolution X-ray tomography with the Zeiss Xradia Versa 620 images of the ellipsoids, 400 \(\upmu\)m major radius, show good print quality and powder infilling (Fig. 5). A machine learning algorithm is being developed to fit the ellipsoid size and calculate the percent of the ellipsoid volume occupied by loose powder. More of the samples listed in Table 1 will be examined with X-ray tomography to build up a set of several hundred ellipsoids of various sizes to develop the machine learning algorithm.

The X-ray interferometry with an interferometer autocorrelation length of \(\xi\) = 2.6 \(\upmu\)m proved exceptionally well suited for observing loose powder inside the Cantor dust fractal ellipsoids. The image contrast-to-noise ratio for the scattering image is much greater than for the transmission images. The instrument time of X-ray interferometry versus high-resolution X-ray tomography is quite different, on the order of a minute for interferometry versus two hours for high-resolution X-ray tomography.

Conclusion

The landscape of the secure supply chain for additive manufacturing is quite complex as there are many stakeholders and many attack vectors. ISO/IEC 27002 describes an international approach to access control of sensitive information15,17. Several case studies in the report discuss QR codes on or inside the part2, inherent detail of the part9, and unique additives to the part2,7,11, as steps towards a cyber-physical trust anchor.

In the present work, we have explored one option for a cyber-physical trust anchor, embedded structures within an additive manufactured part. Our constraints have included working with existing additive manufacturing printers, using conventional additive manufacturing supplies, and avoiding additives and foreign components. These self-imposed constraints are derived from the case studies listed in the NIST IR 8419 report; stakeholders report the introduction of additives and foreign components into AM parts creates a barrier to implementation. Cyber-physical trust anchors based upon inherent unique features of a part, analogous to human fingerprints, retina scans or DNA analysis, provide one method to identify an object, but introduce an extra step in the workflow as each part must be inspected and logged into a database. Embedded digital codes as developed in this work strike a balance between an invasive change to the additive manufacturing workflow versus security, part performance, and equipment modifications.

The questions asked and answered in this project are:

  • Design Can digital structures be generated algorithmically and converted into CAD file format? A Mathematica notebook was written to create ellipsoids in the structure of a staggered Cantor dust fractal, then embedded the ellipsoid structure inside a cylinder. This mathematical structure was then surface labeled with either a QR code or barcode for sample tracking, and then converted to STL AM print files and STEP CAD files.

  • Printing Will a standard AM printer print isolated voids? Yes, an EOS M290 printer reliably printed embedded structures of 8 and 64 ellipsoids for a major radius of 300 \(\upmu\)m with center-to-center distance of 600 \(\upmu\)m. It did, however, fail to print 512 embedded structures and the samples with major radius of 200 \(\upmu\)m with center-to-center distance of 400 \(\upmu\)m were not reliably printed as isolated voids.

  • Validation with X-ray tomography How close in size are the measured and as-designed ellipsoids? Most measured volumes are larger than volume of the as-designed ellipsoid, even when accounting for loose powder trapped inside the printed ellipsoid.

  • Validation with X-ray interferometry How does 2-D X-ray interferometry compare to 3-D X-ray tomography? As shown in Fig. 2, projections of cantor dust fractal 1 through 16 onto a plane are not overlapped. 2D interferometry images of embedded cantor dust fractals can be decoded. The expected speed-up of data acquisition and high sensitivity to loose powder was verified.

  • Digital information How much data can be stored? The recommended coding is a Cantor dust fractal of order = 1 with ternary sizes. This structure can encode positive integers up to 6561. Also recommended is a partial Cantor dust fractal of order = 2 as shown in Fig. 2 and supporting over 40 billion serial numbers.

  • Uniaxial tensile strength How does the Cantor dust fractal affect tensile strength? The measured values and FEM calculations show tensile strength is affected proportional to the total cross-sectional area of the ellipsoids. At Cantor dust fractal order = 1, all measured samples had a tensile strength in excess of the powder specifications.

  • Part certification The embedding of features within an existing design will generally lead to the requirement of re-certification of the design for its application. Hence, the procedure described herein is best applied to new designs.