Generalizability of machine learning models for diabetes detection a study with nordic islet transplant and PIMA datasets

Abstract

Diabetes Mellitus (DM) is a global health challenge, and accurate early detection is critical for effective management. The study explores the potential of machine learning for improved diabetes prediction using microarray gene expression data and PIMA data set. Researchers utilizing a hybrid feature extraction method such as Artificial Bee Colony (ABC) and Particle Swarm Optimization (PSO) followed by metaheuristic feature selection algorithms as Harmonic Search (HS), Dragonfly Algorithm (DFA), Elephant Herding Algorithm (EHA). Evaluated the performance of a system by using the following classifiers as Non-Linear Regression—NLR, Linear Regression—LR, Gaussian Mixture Model—GMM, Expectation Maximization—EM, Bayesian Linear Discriminant Analysis—BLDA, Softmax Discriminant Classifier—SDC, and Support Vector Machine with Radial Basis Function kernel—SVM-RBF classifier on two publicly available datasets namely the Nordic Islet Transplant Program (NITP) and the PIMA Indian Diabetes Dataset (PIDD). The findings demonstrate significant improvement in classification accuracy compared to using all genes. On the Nordic islet transplant dataset, the combined ABC-PSO feature extraction with EHO feature selection achieved the highest accuracy of 97.14%, surpassing the 94.28% accuracy obtained with ABC alone and EHO selection. Similarly, on the PIMA Indian diabetes dataset, the ABC-PSO and EHO combination achieved the best accuracy of 98.13%, exceeding the 95.45% accuracy with ABC and DFA selection. These results highlight the effectiveness of our proposed approach in identifying the most informative features for accurate diabetes prediction. It is observed that the parametric values attained for the datasets are almost similar. Therefore, this research indicates the robustness of the FE and FS along with classifier techniques with two different datasets.

Introduction

DM is a significant global health concern, recognized as one of the leading causes of morbidity and mortality worldwide. According to the World Health Organization (WHO), noncommunicable diseases (NCDs) accounted for 74% of global deaths in 2019, with diabetes contributing to approximately 1.6 million fatalities, making it the ninth leading cause of death¹. Projections indicate that by 2035, nearly 592 million people could be affected by diabetes, predominantly driven by the rise of type 2 diabetes, which constitutes 90% of all cases². Once prevalent in affluent nations, type 2 diabetes has become a global pandemic, with rapid increases in low- and middle-income countries due to urbanization, industrialization, unhealthy diets, and sedentary lifestyles³. India exemplifies this crisis, ranking second globally in diabetes prevalence, with over 77 million people affected as of recent estimates⁴. The increasing number of undiagnosed cases, exceeding 50% worldwide, exacerbates the situation, highlighting the urgent need for early detection strategies to manage and prevent complications⁵. This underscores the critical role of advanced methodologies, such as machine learning, in improving the accuracy and reliability of diabetes diagnosis.

Existing research has explored a range of machine learning techniques to enhance diabetes detection, primarily using PIDD. For instance, studies have applied classifiers such as Decision Trees, Random Forests, and SVM, achieving modest accuracies limited by small datasets and imbalanced classes⁶. Approaches leveraging convolutional neural networks (CNNs) and image-based transformations have shown promise but face challenges in computational complexity and potential data biases^7,8. Other works have incorporated omics data⁹ and quantum models¹⁰, demonstrating incremental improvements in accuracy but lacking generalizability across datasets. Recent advancements in metaheuristic optimization have introduced algorithms such as the Parrot Optimizer (PO)¹¹, Educational Competition Optimizer (ECO)¹², Fata Morgana Algorithm (FATA)¹³, Polar Lights Optimization (PLO)¹⁴, and Rime Optimization Algorithm (RIME)¹⁵. These methods address optimization challenges by drawing inspiration from natural and behavioral phenomena, including mimicry, educational competition, and environmental factors. While these algorithms hold great promise, this study leverages well-established optimization methods that are highly suited for high-dimensional gene expression data, leaving the exploration of newer techniques for future work.

In this study, we propose a novel two-stage machine learning framework that combines hybrid feature extraction using ABC and ABC-PSO with metaheuristic feature selection techniques such as HS, DFA, and EHA. This selection was guided by the specific challenges posed by high-dimensional gene expression data in diabetes detection. The proposed approach is validated using two diverse datasets—the NITP Dataset and the PIDD—to ensure robustness and generalizability. Key contributions include significant improvements in classification accuracy, reduced dimensionality for computational efficiency, and enhanced interpretability of features. By bridging the gap in generalizability and accuracy across datasets, this research provides a robust foundation for scalable diabetes detection frameworks. The findings offer potential avenues for broader applications in clinical settings, advancing the fight against this global health challenge. Table 1 presents a comparative analysis of existing research studies, including their methodologies, datasets used, achieved accuracy rates, and the challenges encountered in each article.

Table 1 Summary of related works and identified challenges.

The summarized challenges highlight the limitations of existing methodologies, particularly in generalizability and feature selection. To address these gaps, this study proposes a novel hybrid framework combining ABC-PSO and metaheuristic feature selection techniques, validated on diverse datasets.

Methodology

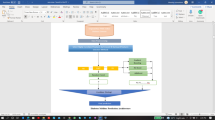
DM poses a significant global health challenge, demanding innovative strategies for early detection and improved management. This study introduces a novel two-stage machine learning approach shown in Fig. 1, for enhanced diabetes prediction using gene expression data. The proposed approach transcends existing methods by offering a flexible framework adaptable to various datasets. Unlike single-stage approaches, this two-stage design separates feature extraction and selection, providing advantages. The first stage employs a hybrid feature extraction method combining the ABC algorithm and PSO²⁶. This unique combination leverages the strengths of both algorithms, ABC’s robust search capabilities and PSO’s efficient information sharing. This stage aims to extract the most informative genes that effectively differentiate diabetic and non-diabetic samples within diverse gene expression datasets. Following feature extraction, the second stage utilizes metaheuristic feature selection algorithms as HS, DFA and EHA. Each algorithm iteratively refines the solution to identify the most relevant gene subsets for classification based on their specific search strategies²⁷. This flexibility allows for the exploration of different feature selection techniques and their impact on the overall prediction performance. The selected genes are then used to train various classifiers such as NLR, LR, GMM, EM, BLDA, SDC and SVM-RBF. To demonstrate the generalizability and robustness of the proposed approach, two publicly available microarray gene expression datasets are employed for evaluation: the NITP and the PIDD. The ability of this approach to effectively predict diabetes using these diverse datasets highlights its potential for broader application²⁸. The model’s performance is assessed using various metrics, including AUC, F1-Score, MCC, Kappa and CSI. Figure 1 represents overall research methodology acquired in this article.

Highlights of the work

• This research addresses the complexity of gene expression data in diabetes diagnosis using PIMA data and feature extraction (ABC, ABC-PSO) for dimensionality reduction and relevant feature selection.

• A new method combines feature extraction and selection (HS, DFA and EHA) to identify the most informative features for improved machine learning classification of diabetes.

• Classifier performance (NLR, LR, GMM, EM, BLDA, SDC and SVM(RBF) with and without feature selection is compared using metrics like accuracy and F1-score to assess the effectiveness of the selection techniques in diabetes detection.

• The system’s performance is validated on two datasets (Nordic transplant & PIMA) to ensure the model and chosen machine learning approaches work across different data characteristics.

Fig. 1

Overall research methodology.

Need for feature extraction

Microarray gene and PIMA diabetes data, despite their wealth of information, present challenges due to high dimensionality which indicates a vast number of features. But it might be irrelevant, redundant, or noisy. This leads to a trifecta of problems: the “curse of dimensionality” with increased computational burden, overfitting of machine learning models that struggle with unseen data, and difficulty in interpreting the key factors influencing model predictions. Feature extraction techniques like ABC and ABC-PSO are crucial tools to address these issues. This helps by selecting the most informative features for diabetes classification, reducing computational complexity for efficient analysis, and enhancing interpretability by focusing on the key factors that drive the model’s predictions. This allows us to extract the most valuable information from these complex datasets, paving the way for effective machine learning models in diabetes diagnosis²⁹.

• a. Role of feature extraction techniques.

• 1. Artificial bee colony.

This study incorporates the ABC algorithm, inspired by the foraging behavior of honeybees, for feature extraction in diabetes prediction. The ABC algorithm³⁰ mimics the process by which honeybees locate and exploit food sources, translating it to the task of identifying informative genes within gene expression data.

The algorithm operates with three essential components:

• 1. Food sources: These represent potential gene subsets within microarray data. Each “food source” is evaluated based on its quality, which in this context translates to the effectiveness of the gene subset in differentiating diabetic and non-diabetic samples.

• 2. Employed bees: These virtual bees represent gene subsets that have already been identified. They carry information about the quality of their associated gene subset and share this information with other “bees” in a virtual “hive.“.

• 3. Unemployed bees: These represent two types of search strategies:

• Scout bees: These bees randomly explore the gene expression data, searching for potentially informative gene subsets.

• Onlooker bees: These bees are drawn to the information shared by employed bees. They evaluate the quality of different gene subsets based on the shared information and may choose to exploit a promising gene subset identified by another employed bee³¹.

The key aspect of the ABC algorithm lies in the information exchange between employed and unemployed bees. Employed bees share information about the quality of their associated gene subsets with a probability proportional to that quality. This means that more informative gene subsets attract a higher number of onlooker bees³². Through this iterative process, the ABC algorithm converges towards identifying the most relevant gene subsets within the gene expression data, ultimately leading to improved diabetes prediction performance³³.

ABC algorithm

• 1. Generate an initial population of solutions $\:{x}_{i}$​ for i = 1. . .SN and each solution is generated randomly within the problem’s search space.

• 2. Assess the fitness of each solution $\:{x}_{i}$ using the objective function.

• 3. Initialize the cycle counter, cycle = 1.

• 4. Repeat until termination,

• Employed Bees Phase.

• For each solution $\:{x}_{i}$, generate a new solution $\:{v}_{i}$ using

$$\:{v}_{ij}\:=\:{x}_{ij\:}+\:{\phi\:}_{ij}\:x\:({x}_{ij}\:-\:{y}_{ij})$$

(1)

• Evaluate the new solution $\:{v}_{i}$.

• Apply the greedy selection process: replace $\:{x}_{i}$ with $\:{v}_{i}$ if $\:{v}_{i}$ has a better fitness.

  • 5. Calculate probabilities.

    • Compute the selection probability $\:{p}_{i}$ for each solution $\:{x}_{i}$ using:

      $$\:{p}_{i}\:=\:\frac{{fitness}_{i}}{{\sum\:}_{j=1}^{SN}{fitness}_{j}}$$

      (2)

• Onlooker Bees Phase.

• Onlooker bees choose solutions $\:{x}_{i}$​ based on probabilities $\:{\text{p}}_{\text{i}}$​.

• Generate a new solution $\:{v}_{i}$​ for the chosen solution and evaluate it.

• Apply the greedy selection process.

• Scout Bees Phase - If a solution$\:\:{x}_{i}$​ has not improved after a predefined number of trials, replace it with a new randomly generated solution.

• Memorize Best Solution - Keep track of the best solution found so far.

• Increment Cycle - Increase the cycle counter by 1 :$\:Cycle\:=\:Cycle\:+\:1$.

• 6. Termination—repeat the above steps until the maximum cycle number (MCN) is reached.

• 7. Output—The best solution found during the algorithm’s execution.

• 2. Artificial Bee Colony–Particle Swarm Optimization.

In many instances, diabetic detection datasets have a lot of characteristics that could be either duplicated or irrelevant which leads to higher complexity and greater risks of overfitting. The ABC-PSO algorithm is a mix of the exploratory strength of ABC and the fine-tuning competence of PSO, balancing exploration and exploitation appropriately³⁴. Ideally, this hybrid method selects the most important features, removes irrelevancies, noise and enhances model’s precision and cost effectiveness.

In the PSO algorithm, particles move within an n-dimensional space to solve optimization problems involving n variables. Each particle determines its next move based on its own experience and the current environment, helping it find the global best position within the neighborhood. The ABC algorithm assists in updating the global position velocity $\:{V}_{ij}$​ for each dimension³⁵.

Hybrid ABC-PSO algorithm

• i. Initialize an empty Rule Set.

• ii. For each Class C, consider training samples from all classes.

• iii. While the number of uncovered training samples of class C exceeds the maximum allowed:

  • a. For each particle $\:i$:

  • b. Update the velocity:

    $$\:{V}_{ij\:}\:=\:w\:{V}_{ij}\:+\:{C}_{1}{r}_{1}({pbest}_{ij}\:-\:{X}_{ij})+{C}_{2}{r}_{2}\:-\:({gbest}_{ij}\:-{X}_{ij})$$

    (3)

    where w is the inertia weight, $\:{C}_{1}$ is the self-confidence factor, ​$\:{C}_{2}$ is the swarm-confidence factor, and $\:{r}_{1}$ and $\:{r}_{2}$ are random variables uniformly distributed between 0 and 1.

  • c. Update the position: $\:{X}_{ij}\:=\:{X}_{ij}\:+\:{V}_{ij\:}$

  • d. If $\:f\:\left(pbest\right)\:\le\:\:f\left({X}_{i}\right)$ then update $\:pbest\:=\:{X}_{i}$​.

  • e. End For.

  • f. Update the $\:gbest$ value.

  • g. For each particle i:

    • 1. Select a random problem variable.

    • 2. Apply the ABC update rule to pbest.

    • 3. Update pbest_i​ and gbest.

  • h. End For.

• iv. Increment the iteration counter.

• v. End while loop.

• vi. End For loop.

• vii. Return $\:gbest$.

Table 2 Statistical analysis for ABC and ABC-PSO FE techniques.

From Table 2, analyzed features selected by ABC and ABC-PSO (Microarray & PIMA) for diabetes diagnosis. According to the mean and variance, moderate values within each class for both techniques suggest informative features without outliers and excessive noise. Corresponding to the skewness and kurtosis, generally minimal skewness indicates symmetrical distributions³⁹. Positive kurtosis are in Microarray with ABC and PIMA with ABC suggests flatter peaks and heavier tails, potentially capturing informative patterns. With PCC of getting low values across datasets suggest minimal linear correlation within each class, indicating potentially complementary information captured by features, which could benefit classification. According to the Sample Entropy, it has constant in Microarray (ABC & ABC-PSO) requires further investigation. For PIMA shows lower entropy in the diabetic class, potentially indicating a more predictable structure for classification. For Kolmogorov Complexity and Hijroth Parameters, the variations observed require further analysis to determine significance and impact on feature selection. According to the Higuchi Fractal Dimension, the minimal differences across techniques and classifications. Needs further research to understand its relevance. CCA: Slight increase in Microarray (ABC-PSO) suggests potentially better class distinction but requires confirmation. Both techniques seem to select informative features with moderate mean/variance and minimal skewness. Positive kurtosis and low PCC suggest potentially useful characteristics for classification. Further analysis is needed for constant sample entropy in Microarray and the additional parameters to understand their role in feature selection for diabetes diagnosis.

Fig. 2

Normal probability plot of FE in both ABC and ABC-PSO for microarray dataset in both diabetic and non-diabetic class.

In Fig. 2, the normal probability plots for both ABC and ABC-PSO which applied FE techniques on diabetic and non-diabetic classes prove that there are significant overlaps in those distributions. This overlap shows a non-linear, non-Gaussianity, and non-separability among the classes.

Fig. 3

Violin plot of FE in both ABC and ABC-PSO for microarray dataset in both classes of diabetic and non-diabetic.

Figure 3 presents violin plots⁴⁰ illustrating the FE performance of ABC and ABC-PSO on a microarray gene dataset for both diabetic and non-diabetic classes. Violin plots, a combination of box plots and kernel density plots, visually depict data distribution and probability density. The width of each violin represents the data point concentration at different values, while its overall shape provides a comprehensive view of the data’s distribution. As shown in Fig. 3a, the ABC-based FE method demonstrates distinct separation between diabetic and non-diabetic classes. The diabetic points range from 0.09 to 1.4, while the non-diabetic points fall within a narrower range of 0.78 to 0.84. Figure 3b depicts the ABC-PSO method, where the diabetic points range from 0.09 to 4, and the non-diabetic points range from $\:-$0.5 to 2.1. This indicates a clear distinction between the two classes.

Fig. 4

Violin plot of FE in both ABC and ABC-PSO for PIMA dataset in both classes of diabetic and non-diabetic.

Figure 4 presents violin plots illustrating the FE performance of ABC and ABC-PSO on the PIMA dataset for both diabetic and non-diabetic classes. The width of each violin represents the data point concentration at different values, while its overall shape provides a comprehensive view of the data’s distribution. As shown in Fig. 4a, the ABC-based FE method demonstrates distinct separation between diabetic and non-diabetic classes. The diabetic points are clustered within a narrow range of 0.82 to 0.83 typically it’s a strip line, while the non-diabetic points exhibit a wider distribution, ranging from $\:-$0.1 to 1.0. Figure 4b depicts the ABC-PSO method, where the diabetic points range from 0.6 to 1.3, and the non-diabetic points range from $\:-$0.1 to 0.7. This indicates a clear distinction between the two classes. The analysis of FE techniques revealed that the data is characterized by non-Gaussian distribution and non-linearity, highlighting its complexity across classes. These findings underscore the importance of further feature selection to enhance classification performance

Need for feature selection methods

We observed a few limitations through visual inspection using violin plots and normal probability plots notwithstanding the success of FE techniques in analyzing microarray gene data. The reduced data still showed non-Gaussian features, nonlinearities and overlapping patterns suggesting that there was need for further investigation⁴¹. While FE is diminishing the dimensionality of data very well, it is important to identify what are the most critical features within this reduced space that can lead to accurate classifications because it is not possible to examine all these features. More specifically, we look at how nature-inspired meta-heuristic algorithms such as HS, DFA and EHA can help us in identifying the hidden most prominent and informative features within the data that can facilitate accurate classification.

• b. Feature selection methods.

  • 1. Harmonic search (HS).

HS is a metaheuristic optimization technique inspired by the process of musical improvisation. It was introduced by Geem et al. in 2001⁴² as a method that mimics how musicians create harmonious melodies. The HS algorithm⁴³ consists of several key steps:

Step 1: First, the optimization problem is defined, typically as minimizing or maximizing an objective function f(x), subject to constraints on the decision variables. The algorithm parameters are then set up, including the number of decision variables and their acceptable ranges.

Step 2: Harmony Memory Setup: A HM is established, which is essentially a collection of potential solutions. Initially, this memory is populated with randomly generated solutions within the defined variable ranges.

Step 3: New Solution Generation: The algorithm creates new potential solutions by combining three strategies:

• Drawing from existing solutions in the HM.

• Making small adjustments to selected values.

• Introducing completely new random values.

Step 4: Solution Evaluation and Update: The newly created solution is evaluated using the objective function. If it outperforms the worst solution currently in the HM, it replaces that solution. Otherwise, it is discarded.

Step 5: Iteration and Termination: Steps 3 and 4 are repeated until a stopping condition is met, such as reaching a maximum number of iterations or achieving a satisfactory solution quality.

HS balances exploring new features and focusing on promising feature combinations. This allows HS to effectively identify relevant features for diabetes diagnosis, even in high-dimensional gene expression data⁴⁴. HS can be easily adapted by defining an appropriate fitness function that evaluates the quality of each feature subset based on your specific feature selection criteria in diabetes diagnosis.

• 2. Dragon Fly Algorithm (DFA).

The DFA is an optimization technique inspired by swarm intelligence and the collective behaviors of dragonflies, introduced by Mirjalili in 2016⁴⁵. This algorithm mimics both the static and dynamic swarming behaviors observed in nature. During the dynamic or exploitation phase, it forms large swarms and moves in a specific direction to confuse potential threats. In the static or exploration phase, the swarms form smaller groups, moving within a confined area to hunt and attract prey⁴⁶. The DA is guided by five fundamental principles: separation, alignment, cohesiveness, attraction, and diversion. These principles dictate the behavior of individual dragonflies and their interactions within the swarm. Figure 5 represents the flow diagram of DFA.

In the equations that follow, K and Ki denote the current position and the $\:{i}^{th}$ position of a dragonfly, respectively, while N represents the total number of neighboring flies.

Separation: Dragonflies avoid colliding with each other The calculation aims to ensure the avoidance of collisions among flies:

$$\:{Se}_{j}=\:-{\sum\:}_{i=1}^{n}k-{k}_{j}$$

(4)

where $\:{Se}_{j}$ represents the motion of the $\:{i}^{th}$ individual aimed at maintaining separation from other dragonflies.

Alignment: Dragonflies within a group synchronize their velocities. It is represented as:

$$\:{Ag}_{j}=\:\frac{{\sum\:}_{i=1}^{n}{Ve}_{i}}{n}$$

(5)

here $\:{Ag}_{j}$ is the velocity of the $\:{i}^{th}$ individual.

Cohesiveness: Dragonflies tend to converge towards the center of their swarm.

$$\:{Co}_{j}=\:\frac{{\sum\:}_{i=1}^{n}{k}_{i}}{N}-k$$

(6)

Attraction: Dragonflies are attracted to food sources

$$\:{H}_{j}=\:{K}^{+}-\:K$$

(7)

where $\:{H}_{j}$ is the attraction of the food source, and $\:{K}^{+}$ represents the position of the food source.

Diversion: Dragonflies try to divert away from enemies, calculated as:

$$\:{D}_{j}={K}^{-}+K$$

(8)

This calculation determines the diversion from the enemy, and it is expressed in terms of the step vector (∆K) and the current position vector K, which are used to update the locations of artificial dragonflies within the search space. The step vector (∆K) can be calculated using the direction of movement of the dragonfly:

$$\:{\varDelta\:K}_{j}^{t+1}=\left(s{Se}_{j}+a{Ag}_{j}+c{Co}_{j}+h{H}_{j}+d{D}_{j}\right)+\omega\:{\varDelta\:K}_{j}^{t}$$

(9)

The behavior of the dragonfly algorithm is influenced by factors such as separation weight (s), alignment weight (a), cohesion weight (c), attraction weight (h), and enemy weight (d). The inertia weight is represented by “ω”, and “t” represents the iteration number [47].

Through the manipulation of these weights, the algorithm can achieve both exploration and exploitation phases. The position of the $\:{i}^{th}$ dragonfly at t + 1 iterations is determined by the following equation:

$$\:{K}_{j}^{t+1}=\:{K}_{j}^{t}+\:{\varDelta\:K}_{j}^{t+1}$$

(10)

Fig. 5

Algorithmic flowchart of the DFA process.

• 3. Elephant Herding Algorithm (EHA).

EHA introduced by Wang et al.,⁴⁸ is a powerful technique inspired by herd behavior in elephants. It excels at identifying the most informative features from a large dataset, making it well-suited for feature selection in diabetes diagnosis using gene expression data. EHA combines global search strategies with local search. This balance allows EHA to effectively identify relevant features for diabetes diagnosis, even in high-dimensional gene expression data⁴⁹. EHA starts by randomly distributing the elephants across the feature space, ensuring a comprehensive exploration from the beginning. Figure 6 represents the flow diagram of EHA.

$$\:{y}_{i}^{new}=\:{y}_{i}^{old}+\:\propto\:\left({Y}_{best}-\:{Y}_{i}^{old}\right)*r$$

(11)

The position of each elephant which is representing a potential feature subset is updated based on a combination of its current position ($\:{y}_{i}^{old}$) and the best position discovered by the herd so far ($\:{y}_{i}^{new}$). A control parameter ($\:\propto\:$) within the range [0, 1] and a random number (r ∈ [0, 1]) are used to determine the extent of this update:

$$\:{Y}_{best}=\:\beta\:*\:{Y}_{centre}$$

(12)

$$\:{Y}_{centre\:}=\:\frac{1}{m}*\:{\sum\:}_{i=1}^{m}{y}_{i}$$

(13)

Each elephant in EHA remembers its best encountered feature subset ($\:{Y}_{best}$). A control parameter (β) between 0 and 1 guides the update of $\:{Y}_{best}$. Higher β values (closer to 1) emphasize the herd’s best-found solution, promoting convergence. Lower β values (closer to 0) allow more exploration by the elephant⁵⁰. This interplay between β and the elephant’s current position helps EHA balance exploration and exploitation during feature selection.

$$\:{Y}_{worst}=\:{Y}_{min}+\left({Y}_{max}-\:{Y}_{min}+1\right)*rand$$

(14)

Fig. 6

Flow diagram of EHA.

Evaluating Feature Selection Performance by using p value significance and t-Test: The effectiveness of the feature selection methods was assessed by analyzing the significance of p-values⁵¹ obtained from t-tests. Lower p-values indicate a stronger rejection of the null hypothesis, suggesting that the feature selection method is not random and has identified informative features (Table 3).

Understanding the t-test: A t-test⁵² is a statistical tool commonly used to compare the means of two groups. In this context, it helps determine if the feature selection method significantly outperforms a random selection process.

Null hypothesis and significance levels: The t-test evaluates the following null hypothesis (H₀): The feature selection method performs no better than random selection. A predefined significance level (α, typically 0.01) is used to assess the evidence against the null hypothesis⁵³.

Interpreting p-values: A p-value less than α indicates statistical significance, suggesting we can reject the null hypothesis and conclude that the feature selection method is effective in identifying relevant features. By comparing gene expression levels between diabetic and non-diabetic individuals. A t-test could be used to see if the feature selection method identifies genes with expression levels that significantly differ between the two groups.

Feature selection and interpretability

Feature selection generally enhances model interpretability by simplifying the feature set, allowing for easier understanding of model predictions. However, when employing advanced metaheuristic methods, the interpretability of the selection process itself may be reduced due to the non-transparent nature of these algorithms. This study acknowledges this trade-off and emphasizes the importance of balancing model performance with process interpretability.

Table 3 Utilizing p-values for feature selection in diabetes detection: a comparison of various FE techniques.

From the Table 3, it is assuming a significance level of 0.05 observe that both ABC and ABC-PSO achieved statistically significant results (p-value < 0.05) for at least one class (diabetic or non-diabetic) in both datasets. This suggests strong evidence that these techniques effectively selected features that differentiate between the two classes. However, HS, DFA, and EHA exhibited higher p-values (often > 0.05) across some classes and datasets. While this might indicate a weaker distinction between their chosen features and those selected by chance, analyzing trends within each technique is crucial. For instance, if a technique consistently exhibits lower p-values for a specific dataset or class, it could suggest some informative feature selection despite not reaching significance for all cases. Ultimately, classification accuracy on a held-out test set is vital for a more comprehensive evaluation of how well these features distinguish between diabetic and non-diabetic individuals.

• c. Classifiers.

  • 1. Non-linear regression.

While linear regression assumes a straight-line relationship between variables, non-linear regression⁵⁴ offers a powerful tool for diabetes detection. It addresses the challenge of capturing complex relationships between features extracted from gene expression data and the presence of diabetes. This method employs a specific mathematical function to model the non-linear connection between these features and the diabetic state.

$$\:{G}_{m}\:=\:y({a}_{m},\:\theta\:)\:+\:{P}_{mm}$$

(15)

The model is optimized to minimize the errors between the predicted diabetic state (based on the function) and the actual diabetic state for each data point. This allows the model to leverage the intricate patterns within gene expression data, potentially leading to improved accuracy in diabetes diagnosis.

Non-linear regression utilizes an expectation function ($\:E\left(y\right|x$)) to represent the predicted⁵⁵ diabetic state for each data point. This function takes the independent variable “$\:x$” as input and outputs the predicted value of the dependent variable denoted by “$\:y$”.

A crucial distinction between non-linear and linear models lies in the parameters. In non-linear regression, at least one parameter ($\:{a}_{m}$) for each data point ($\:m$) must influence one or more derivatives of the expectation function. This allows the model to capture the non-linear relationships between gene expression features and the diabetic state.

• 2. Linear regression.

While linear regression⁵⁶, a foundational statistical method, excels at modeling linear relationships, it has limitations for diabetes diagnosis using gene expression data. It assumes a straight-line connection between gene expression features and the diabetic state, potentially missing the complex, non-linear biological processes involved. Additionally, applying a threshold to the predicted values for binary classification (diabetic or non-diabetic) might not effectively capture the subtleties within the data and the disease itself.

$$\:Z\:=\:p\:+\:qX$$

(16)

• 3. Gaussian mixture model (GMM).

Unlike methods requiring labeled data, GMMs⁵⁷ excel at identifying hidden structures within unlabeled gene expression profiles from diabetes studies. Acting like detectives, GMMs automatically group similar profiles into clusters, potentially revealing subgroups within the diabetic or non-diabetic population. This unsupervised approach is valuable for analyzing readily available gene expression data⁵⁸. Additionally, GMMs employ a softer clustering technique, allowing data points to have some membership in multiple clusters. This flexibility reflects the potential for overlapping gene expression patterns between subgroups, providing a more nuanced view of the underlying biology in diabetes.

$$\:\left(a\right)=\:\frac{1}{{\left(2\pi\:\right)}^{\frac{n}{2}}{\left|{\Sigma\:}\right|}^{\frac{1}{2}}}{e}^{-\left(\frac{1}{2}\right){\left(a-\mu\:\right)}^{T}{{\Sigma\:}}^{-1}\left(a-\mu\:\right)}$$

(17)

• The mean vector (µ) indicates the central tendency of data points in multi-dimensional space.

• The covariance matrix (Σ) quantifies relationships and interactions between different features.

• The determinant of Σ, written as |Σ|, helps measure the overall dispersion of data around the mean.

• The exponential function (exp) is utilized to compute probability densities for specific data points within the distribution.

• 4. Expectation maximum (EM).

The EM algorithm⁵⁹ is a powerful tool for handling incomplete data or hidden variables, making it well-suited for analyzing gene expression data in diabetes research. This algorithm acts like a detective, working in a two-step process:

• 1. Expectation phase: EM first estimates missing data or hidden factors based on the available data and current model parameters.

• 2. Maximization phase: Using these estimates, EM then improves the model’s ability to analyze the data. This iterative process allows EM to progressively gain a deeper understanding of the underlying patterns within the gene expression data. Figure 7 represents the flow diagram of EM.

EM can work effectively with gene expression data that might have missing values or hidden⁶⁰ factors like disease status. The iterative process of estimating missing information and refining the model leads to a more accurate understanding of the data structure and its relationship to diabetes.

Fig. 7

Flow diagram of EM.

• 5. Bayesian linear discriminant analysis (BLDA).

BLDA⁶¹ is a technique well-suited for analyzing high-dimensional gene expression data in diabetes research. It has potentially reduced the influence of noisy signals and improved the model’s focus on the most relevant features for distinguishing diabetic and non-diabetic cases. BLDA can be computationally more efficient compared to other methods when dealing with high-dimensional datasets. A target $\:b$ is related with $\:x$ with the gaussian noise $\:c$.

The following expression of a with the assigned weight t is with x, as $\:a=\:{x}^{T}b+c$

$$\:p\left( {G|\beta \:,\:x} \right) = \:{\left( {\frac{{\beta \:}}{{2\pi \:}}} \right)^{\frac{c}{2}}}{\rm{exp}}\left( { - \frac{{\beta \:}}{2}\left\| {{B^T}x - m} \right\|} \right)$$

(18)

The G representation on the following equations is the combination of B, m. The x of earlier distribution is stated as

$$\:p\left(x|\alpha\:\right)={\left(\frac{\alpha\:}{2\pi\:}\right)}^{\frac{1}{2}}{\left(\frac{\epsilon\:}{2\pi\:}\right)}^{\frac{1}{2}}\text{exp}(-\frac{1}{2}{x}^{T}{H}^{{\prime\:}}\left(\alpha\:\right)x$$

(19)

The square matrix is given as

$$\:{H^{\prime \:}}\left( {\alpha \:} \right) = \:{\left[ {\begin{array}{*{20}{c}}{\alpha \:}&{\: \cdots \:}&{\:0}\\{\: \vdots }&{\: \ddots \:}&{\: \vdots }\\{\:0}&{\: \cdots \:}&{\:\varepsilon \:}\end{array}} \right]_{(l + 1)(l + 1)}}$$

(20)

$\:\alpha\:$ is a hyperparameter derived from data forecasting, and l denotes the assigned vector number. Using Bayes’ theorem, $\:x$ can be determined as follows:

$$\:p\left(x|\beta\:,\:\alpha\:,G\right)=\:\frac{P\left(G|\beta\:,x\right)P\left(x|\alpha\:\right)}{\int\:P\left(G|\beta\:,\:x\right)P\left(y|\alpha\:\right)dy}$$

(21)

The mean vector $\:\upsilon\:$ and the covariance matrix $\:X$ need to satisfy the criteria specified in Equations $\:p\left(x|\alpha\:\right)$ and $\:p\left(x|\beta\:,\:\alpha\:,G\right)$ to conform to the posterior distribution⁶². The posterior distribution is predominantly Gaussian in nature.

$$\:\upsilon\:=\:\beta\:{(\beta\:B{B}^{T}+\:{H}^{{\prime\:}}\left(\alpha\:\right))}^{-1}Ba$$

(22)

$$\:X=\:{(\beta\:B{B}^{T}+\:{H}^{{\prime\:}}\left(\alpha\:\right))}^{-1}$$

(23)

The probability distribution for regression when predicting the input vector $\:\widehat{b}$ can be expressed as follows:

$$\:p\left(\widehat{a}|\beta\:,\alpha\:,\widehat{b,\:G}\right)=\:\int\:p\left(\widehat{a}|\beta\:,\widehat{b,\:x}\right)p\left(x|\beta\:,\alpha\:,G\right)dy$$

(24)

Again, this prediction analysis is primarily Gaussian in nature, with the mean given by $\:\mu\:=\:{\upsilon\:}^{T}\widehat{b}$ and the variance given by $\:{\delta\:}^{2}=\:\frac{1}{\beta\:}+\:\widehat{{b}^{T}}X\widehat{b}$.

• 6. Softmax discriminant classifier (SDC).

The SDC is utilized to verify and identify the group to which a specific test sample belongs⁶³. It measures the distance between the training samples and the test sample within a particular class or data group. Z is represented as follows:

$$\:Z=\left[{Z}_{1,}{Z}_{2},.,{Z}_{q}\right]\in\:{\mathfrak{R}}^{c\times\:d}$$

(25)

Consisting of samples from distinct classes denoted as q, is $\:{Z}_{q}=\left[{Z}_{1}^{q},{Z}_{2}^{q},\:.,{Z}_{dq}^{q}\right]\in\:\:{\mathfrak{R}}^{c\times\:{d}_{q}}$. Each class $\:{Z}_{q}$ contains samples from the $\:{q}^{th}$ class, where $\:{\sum\:}_{i=1}^{q}{d}_{i}=d.\:$ The total number of samples, given a test sample $\:K\:\in\:\:{\mathfrak{R}}^{c\times\:1}$, is evaluated by the classifiers to minimize construction errors, thereby assigning the test sample to class q. The transformation of class samples and test samples in SDC includes nonlinear enhancement values, as described by the following Eq. 

$$\:h\left(K\right)=\text{arg}\text{max}{Z}_{w}^{i}$$

(26)

$$\:h\left( K \right) = {\rm{arg}}\mathop {{\rm{max}}}\limits_i {\rm{log}}\left( {\sum {\:_{j = 1}^{{d_i}}} {\rm{exp}}( - \lambda \:{{\left\| {v - \:\upsilon \:_j^i} \right\|}_2})} \right)$$

(27)

In these equations, $\:h\left(K\right)$ denotes the differentiation of the $\:{i}^{th}$ class, and ${\left\| {v - \:\upsilon \:_j^i} \right\|_2}\:$approaches zero, which maximizes $\:{Z}_{w}^{i}$. This asymptotic behavior results in the highest likelihood that the test sample belongs to a specific class.

• 7. Support vector machine (radial basis function).

SVMs with RBF kernel are a powerful tool for diabetes diagnosis because they can handle complex relationships between gene expression features and the diabetic state⁶⁴. Unlike linear methods, SVMs can transform the data into a higher-dimensional space where a clear separation between diabetic and non-diabetic cases is possible using a hyperplane. The RBF kernel acts like a bridge, measuring similarity between data points in this new space. This allows the SVM to identify the optimal hyperplane that best distinguishes diabetic from non-diabetic data points⁶⁵. Once trained, the SVM can classify new, unseen data points based on their position relative to the hyperplane in the transformed space.

$$\:\text{R}\text{B}\text{F}:\:\text{k}\:\left({\text{x}}_{\text{i}},{\text{x}}_{\text{j}}\right)=\text{exp}\left\{\frac{-{\left|{\text{x}}_{\text{i}}-\:{\text{x}}_{\text{j}}\right|}^{2}}{{\left(2\text{*}\:{\upsigma\:}\right)}^{2}}\right\}$$

(28)

By effectively managing non-linearities and utilizing the RBF kernel for similarity calculations, SVMs provide a robust method for classifying diabetic cases based on gene expression data.

Selection of classifiers parameters through training and testing

Microarray gene data set: To ensure generalizability on unseen data, we employed 10-fold cross-validation, a robust technique that repeatedly splits the data for training and testing. The model was trained on a dataset containing 2870 features per patient for a group of diabetics of 20 patients and non-diabetic of 50 patients’ individuals. This comprehensive training process, combined with k-fold cross-validation, strengthens the reliability of the model’s performance, which will be evaluated using the Mean Squared Error (MSE) metric for further details on training performance included in the methods Sect. 

$$\:MSE=\frac{1}{N}{\sum\:}_{j=1}^{N}{\left({O}_{j}-{T}_{j}\right)}^{2}$$

(29)

Classifiers training and testing

Table 4 exposes the confusion matrix between the real values and predicated values among diabetic and non-diabetic.

Table 4 Confusion matrix of diab and non-diab classification.

Table 5 MSE analysis for FE techniques with different dataset without FS.

From Table 5 the provided table shows MSE values for various classifiers applied to Microarray Gene and PIMA datasets. MSE values range from 2.56 × 10^− 6 SVM(RBF) on PIMA with ABC feature selection to 2.7 × 10^− 5 (NLR on Microarray Gene with ABC). Generally, lower MSE indicates better performance. Classifiers like SVM(RBF) and EM consistently achieve low MSE across both datasets, suggesting strong performance. NLR and LR also show promise on the Microarray Gene data with generally low MSE values. However, some classifiers like BLDA and SDC on the PIMA Dataset exhibit higher testing MSE compared to training MSE, which might indicate struggles with generalizing to unseen data. It’s important to note that this analysis is based solely on MSE and further evaluation with other metrics like accuracy and F1-score is recommended for a more complete understanding.

Table 6 MSE for two FE techniques with different dataset in HS FS.

From Table 6, it is analyzing the MSE values for various classifiers applied to Microarray Gene and PIMA datasets with FS reveals some key trends. MSE values range from a low of 1 × 10^− 7 as SVM(RBF) on PIMA with ABC to a high of 9.6 × 10^− 6 (NLR on Microarray Gene with ABC), with generally lower MSE indicating better performance. Classifiers like SVM(RBF) and EM shine across both datasets, consistently achieving low MSE values (often below 10^− 6) suggesting strong performance for both training and generalizing to unseen data. On the Microarray Gene data, NLR and LR also show promise with MSE typically below 8 × 10^− 6. However, BLDA and SDC on the PIMA Dataset might have challenges with generalizability based on some higher testing MSE compared to training MSE. It’s important to remember that MSE is just one piece of the puzzle, and a more comprehensive evaluation with other metrics is recommended for final model selection.

Table 7 MSE for two FE techniques with different dataset in DFA FS.

From Table 7, it is analyzing the MSE values for various classifiers applied to Microarray Gene and PIMA datasets with dimensionality reduction using feature selection (DFA FS) reveals some key insights. MSE values range from a low of 1.6 × 10^− 7 SVM(RBF) on PIMA with ABC to a high of 1.22 × 10^− 5 (LR on Microarray Gene with ABC-PSO). Generally, lower MSE indicates better performance. SVM (RBF) stands out as a strong contender across both datasets, achieving consistently low MSE values (often below 10^− 6) for both training and testing data. This suggests its ability to learn the data effectively and generalize well to unseen examples.

For the Microarray Gene data, NLR and LR also show promise with MSE typically below 6.5 × 10^− 6, indicating good performance in both learning and generalizing. On the PIMA Dataset, BLDA and SDC achieve some very low MSE values but might have limitations with generalizability based on some configurations where testing MSE is higher than training MSE. EM exhibits consistent performance across datasets, with MSE values typically below 3.5 × 10^− 6. GMM performs well on the Microarray Gene data but might not be the best choice for PIMA based on the MSE values. This analysis highlights promising options based on MSE, but further investigation is recommended for a definitive conclusion.

Table 8 MSE for two FE techniques with different dataset in EHA FS.

Table 8, it is analyzing the MSE values for various classifiers applied to Microarray Gene and PIMA datasets with EHA feature selection reveals some key trends. MSE values range dramatically, from an exceptional low of 1 × 10^− 8 (SVM(RBF) on PIMA with ABC) to a high of 1.3 × 10^− 5 (LR on Microarray Gene with ABC-PSO). As always, lower MSE indicates better performance. SVM(RBF) emerges as the star performer across both datasets, achieving remarkably low MSE values (often below 10^− 7) for both training and testing data. This suggests its exceptional ability to learn the underlying patterns in the data and generalize well to unseen examples. For the Microarray Gene data, NLR and LR show promise with MSE values typically below 6.76 × 10^− 6, indicating good training performance and generalizability. However, on the PIMA Dataset, BLDA and SDC, while achieving some very impressive MSE values (around 10^− 7), might have limitations with generalizability based on some configurations where the testing MSE is higher than the training MSE.

EM exhibits consistent performance across datasets, with MSE values typically below 4 × 10^− 6. GMM performs well on the Microarray Gene data but might not be the best choice for PIMA based on the MSE values. This analysis highlights promising options based on MSE, but further investigation is recommended for a definitive conclusion.

Feature extraction and selection rationale

The feature extraction techniques utilized in this study, ABC and ABC-PSO were chosen due to their well-established reliability in handling high-dimensional data. These methods are extensively studied and have consistently demonstrated their ability to identify key features effectively. The hybridization of ABC and PSO leverages their respective strengths—ABC’s robust exploration capabilities and PSO’s efficient convergence—addressing the limitations of individual methods such as premature convergence in PSO and slower convergence in ABC.

The metaheuristic-based feature selection algorithms, including HS, DFA, and EHA, were selected for their ability to refine extracted features with precision. These techniques are specifically designed to navigate complex, non-linear optimization landscapes, ensuring the selection of the most prominent features. Their adaptability reduces the risk of overfitting during classifier training, even with high-dimensional data.

The combination of these feature extraction and selection methods provides a robust framework for training classifiers using a ten-fold cross-validation approach. This approach ensures model generalizability while avoiding overfitting, leading to superior classifier performance. The results achieved in this study, with classifiers showing the highest accuracies across multiple datasets, underscore the effectiveness of the chosen methods.

Datasets details

Nordic islet transplant program

Microarray gene expression analysis plays a crucial role in deciphering the molecular mechanisms of diabetes by enabling researchers to compare gene expression levels between healthy and diabetic individuals. These comparisons can potentially identify genes involved in disease development, progression, or complications. In this study, we leverage publicly available microarray data from the Nordic Islet Transplantation program (https://www.ncbi.nlm.nih.gov/bioproject/PRJNA178122) [66]. The data accessed on 20 august 2021. This dataset encompasses gene expression profiles from human pancreatic islets of 57 non-diabetic and 20 diabetic donors, totaling 28,735 genes which is represented in Table 9. Preprocessing involved selecting the 22,960 genes with the highest peak intensity per patient, followed by a base-10 logarithmic transformation to standardize individual samples with a mean of 0 and a variance of 1.

Table 9 Pancreatic microarray gene dataset for non-diabetic and diabetic classes.

PIMA dataset

The Pima Indians Diabetes Dataset (PIDD), a benchmark for diabetes diagnosis, is available from the UCI Machine Learning Repository. This dataset consists of information on 768 Pima Indian women, categorized as either diabetic (268) or non-diabetic (500) [67]. Eight key physiological measurements relevant to diabetes are included: number of pregnancies, plasma glucose concentration at a 2-hour oral glucose tolerance test, diastolic blood pressure, triceps skin fold thickness, 2-hour serum insulin level, body mass index, diabetes pedigree function, and age. The final column indicates the presence (1) or absence (0) of diabetes. This readily available dataset allows researchers to evaluate the effectiveness of feature selection techniques in identifying the most informative features for diabetes classification. Table 10 depicts the specification of the PIMA dataset with all 9 parameters in the dataset followed by Table 11 representing the missing value details and attributes in the dataset.

Table 10 Specification of PIMA dataset.

Table 11 Missing value details in the attributes of the pima dataset.

Selection of targets

The non-diabetic class has target values ranging from 0 to 1, with a tendency towards lower values. This range is dictated by a specific constraint [68].

$$\:\frac{1}{N}{\sum\:}_{i=1}^{N}{\mu\:}_{i}\le\:{T}_{Non-Dia}$$

(30)

In classification, the non-diabetic class is represented by a mean target value ($\:{\mu\:}_{i}$) calculated from N features describing non-diabetic samples. This value typically falls on the lower end of the 0-to-1 scale. Similarly, the diabetic class is represented by a mean target value ($\:{\mu\:}_{o}$) positioned near the upper end of the scale. This alignment reflects the principle that

$$\:\frac{1}{M}{\sum\:}_{j=1}^{N}{\mu\:}_{j}\le\:{T}_{\text{D}\text{i}\text{a}}$$

(31)

Within our classification task, µ₁ represents the average value calculated across the input feature vectors for the M diabetic samples we’re considering. It’s important to note that the target value assigned to the diabetic class ($\:{\mu\:}_{j}$) is intentionally set higher than the average values of both the non-diabetic class ($\:{\mu\:}_{i}$) and the individual diabetic feature vectors. This choice ensures a minimum difference of 0.5 between $\:{\mu\:}_{i}$ and $\:{\mu\:}_{j}$, as expressed in the following equation: Δµ ≥ 0.5.

$$\:\left|\right|{T}_{\text{D}\text{i}\text{a}}-{T}_{\text{N}\text{o}\text{n}-\text{D}\text{i}\text{a}}\left|\right|\ge\:0.5$$

(32)

To distinguish between diabetic and non-diabetic cases, our classification model assigns target values of 0.1 and 0.85 to the non-diabetic ($\:{\mu\:}_{i}$) and diabetic ($\:{\mu\:}_{j}$) classes, respectively. Following this target assignment, by using MSE to evaluate the model’s performance. The results of the training and testing phases are presented in Table 12, which highlights the optimal parameter settings for the classifiers.

Table 12 Classifiers optimal parameters.

Findings

To ensure a robust assessment of the models’ effectiveness in classifying diabetic patients, we employed tenfold cross-validation. This technique divides the data into ten equal sets, using nine for training and one for testing to prevent overfitting and evaluate real-world performance. Beyond simple accuracy, we utilized a confusion matrix to calculate comprehensive performance metrics, including accuracy, F1 score, MCC, Jaccard Metric, Error Rate, and Kappa statistic. These metrics provide insights into the models’ strengths and weaknesses in distinguishing between diabetic and non-diabetic cases.

Table 13 Performance metrics.

In Table 13 outlines the methods used to calculate these metrics, ensuring transparency in the evaluation process. By comparing the performance of the models on both datasets, it can be derived as their generalizability and robustness.

Table 14 Analysis of different parameters with seven classifiers through two FE techniques without FS methods.

From Table 14 compares the performance of two feature extraction techniques (ABC, ABC-PSO) and classifiers (NLR, LR, GMM, EM, BLDA, SDC, SVM(RBF)) on both microarray gene data and the PIMA Indians Diabetes Dataset. Performance is evaluated using seven metrics: Accuracy (Acc), F1 Score (F1S), Matthews Correlation Coefficient (MCC), Jaccard Metrix (Jacc Met), Classifier Success Index (CSI), and Kappa Statistic (Kappa).

Notably, SVM(RBF) achieved the highest overall performance across both datasets. On the microarray data, SVM(RBF) with ABC-PSO feature extraction yielded the best results, reaching an Accuracy of 88.57%, F1 Score of 81.82%, MCC of 0.7423, Jaccard Similarity of 69.23%, Markedness of 65%, and Kappa of 0.7358. For the PIMA dataset, SVM(RBF) maintained strong performance with all feature extraction techniques, achieving an Accuracy range of 88.31–89.74%, F1 Score range of 84.12–86.12%, MCC range of 0.7521 to 0.7831, Jaccard Similarity range of 72.59–75.62%, Markedness range of 68.37–72.74%, and Kappa range of 0.7581 to 0.7801. These observations suggest that SVM(RBF) might be a powerful classifier for both datasets without FS, particularly when combined with feature extraction using ABC-PSO for microarray data. However, the effectiveness of feature extraction techniques appears to be data-dependent, as all techniques yielded comparable performance with most classifiers on the PIMA dataset.

Table 15 Analysis of different parameters with seven classifiers through two FE techniques with HS FS methods.

From Table 15 this analysis investigates the effectiveness of Harmonic Search as a feature selection method compared to the previously explored feature extraction techniques (ABC and ABC-PSO). The results demonstrate that Harmonic Search is particularly advantageous for SVM(RBF) on microarray data. On this dataset, SVM(RBF) with Harmonic Search achieves a significant improvement over both ABC and ABC-PSO, reaching an Accuracy exceeding 91% (compared to 88% with feature extraction techniques) and an F1 Score exceeding 86%. This suggests that Harmonic Search effectively selects informative features, leading to superior classification performance for SVM(RBF) on high-dimensional data like microarray gene data. While Harmonic Search offers some improvements for other classifiers on the microarray data, its impact seems less pronounced compared to SVM(RBF).

For the PIMA Indians Diabetes Dataset, with potentially lower dimensionality, SVM(RBF) remains the strongest performer across all feature selection and extraction techniques, achieving an Accuracy exceeding 93% and an F1 Score exceeding 90%. Harmonic Search does offer some advantages for specific classifiers like BLDA, leading to a higher Accuracy (over 91%) and MCC (over 0.8) compared to ABC or ABC-PSO. However, overall, the impact of feature selection on the PIMA data appears less substantial, with most classifiers exhibiting comparable performance regardless of the technique used (Accuracy ranging from 88 to 91% for most classifiers). HS emerges as a valuable tool for feature selection, particularly for high-dimensional datasets where selecting informative features can significantly improve classification performance, especially for classifiers like SVM(RBF). However, the effectiveness of feature selection appears to be data-dependent, with potentially less impact on datasets with lower dimensionality like the PIMA data.

Table 16 Analysis of different parameters with seven classifiers through two FE techniques with DFA FS methods.

From the Table 16 it is analyzed that the effectiveness of the DFA for FS compared to the previously explored feature extraction techniques. For the microarray gene data, DA with SVM(RBF) achieves the best performance, reaching an Accuracy of 91.43%, F1 Score of 85.71%, MCC of 0.7979, Jaccard Similarity of 75%, Markedness of 71.82%, and Kappa of 0.7961. This suggests that DFA effectively selects informative features for SVM(RBF) on this high-dimensional data. However, for other classifiers on the microarray data, DFA’s impact seems less significant compared to feature extraction techniques. On the PIMA Indians Diabetes Dataset, SVM(RBF) remains the strongest performer across all feature selection and extraction methods, achieving an Accuracy exceeding 95% and an F1 Score exceeding 93%. While DFA offers some improvements for specific classifiers like SDC (reaching a Kappa of 0.8783), the overall impact of feature selection on the PIMA data appears less substantial. Most classifiers with DFA as FS in ABC, or ABC-PSO exhibit comparable performance. DFA demonstrates potential as a feature selection method, particularly for high-dimensional data like microarray gene data where it can improve the performance of classifiers like SVM(RBF). However, like the previous observations, the effectiveness of feature selection appears to be data dependent. For datasets with potentially lower dimensionality like the PIMA data, the impact of DFA might be less pronounced.

Fig. 8

Performance analysis of different parameters with classifiers through FE techniques with DFA FS methods.

From Fig. 8 the graph reveals the exceptional performance of SVM with an RBF kernel in diabetes detection across both the Microarray Gene and PIMA datasets. On the Microarray Gene Data, SVM (RBF) consistently achieves accuracy rates of approximately 90–95% and F1 scores between 85 and 90%, significantly outperforming other classifiers. While GMM and BLDA also demonstrate strong results, their performance generally falls within the 80–90% range for accuracy and 75–85% for F1 score. On the PIMA Dataset, SVM (RBF) maintains its superiority, with accuracy rates around 85–90% and F1 scores between 80 and 85%. Other classifiers like GMM and BLDA exhibit similar performance levels on the PIMA Dataset. The choice of feature extraction technique can influence results, with ABC and ABC-PSO showing varying effectiveness across datasets. Overall, SVM (RBF) emerges as a robust and effective approach for diabetes detection, consistently outperforming other classifiers on both datasets.

Table 17 Analysis of different parameters with seven classifiers through two FE techniques with EHA FS methods.

From Table 17, the analysis examines the effectiveness of the Elephant Herding Algorithm (EHA) for feature selection compared to the previously explored techniques (ABC, ABC-PSO, and DA). For the microarray gene data, EHA with SVM(RBF) achieves the most significant improvement, reaching an Accuracy of 97.14%, F1 Score of 95%, MCC of 0.93, Jaccard Similarity of 90.48%, Markedness of 90%, and Kappa of 0.93. This suggests that EHA excels at selecting informative features for SVM(RBF) on this high-dimensional data. Compared to DFA and feature extraction techniques, EHA leads to a substantial performance boost for SVM(RBF). However, for other classifiers on the microarray data, EHA’s impact seems less pronounced.

On the PIMA Indians Diabetes Dataset, SVM(RBF) remains the strongest performer across all feature selection and extraction methods, achieving an Accuracy exceeding 98% and an F1 Score exceeding 97%. Interestingly, EHA with SVM(RBF) reaches similar performance levels (Accuracy of 98.57%, F1 Score of 97.95%) compared to ABC-PSO. While EHA offers some improvements for specific classifiers like SDC and GMM, the overall impact of feature selection on the PIMA data appears less substantial. Most classifiers with EHA as FS in ABC, ABC-PSO, and DFA exhibit comparable performance.

In conclusion, EHA demonstrates promise as a feature selection method, particularly for high-dimensional data like microarray gene data where it can significantly enhance the performance of classifiers like SVM(RBF). Like previous observations, the effectiveness of feature selection appears to be data dependent. For datasets with potentially lower dimensionality like the PIMA data, the impact of EHA might be less significant compared to high-dimensional scenarios.

Table 18 Comparison of accuracy achieved by different combinations of feature extraction (ABC and ABC-PSO), feature selection methods (HS, DFA, and EHA), and classifiers (SVM with RBF kernel) on NITP and PIDD datasets.

Table 18 presents a detailed comparison of the classification accuracies achieved by various combinations of feature extraction methods (ABC and ABC-PSO), feature selection techniques (HS, DFA, and EHA), and classifiers (SVM with RBF kernel) on the NITP and PIDD datasets. The results highlight the significant impact of combining ABC-PSO for feature extraction with metaheuristic feature selection methods, demonstrating consistent improvements in accuracy across both datasets. Notably, the ABC-PSO with EHA combination achieved the highest accuracies of 97.14% and 98.57% on the NITP and PIDD datasets, respectively, outperforming other methods. These findings emphasize the complementary roles of hybrid feature extraction and metaheuristic selection in optimizing predictive performance. The consistent improvement across datasets validates the generalizability and robustness of the proposed approach.

Analysis of results

Across all analyses, SVM(RBF) consistently proves to be the most powerful classifier for both the microarray gene data and the PIMA Indians Diabetes Dataset. Feature selection methods such as Harmonic Search (HS), DFA, and EHA significantly improve performance, particularly for high-dimensional data. EHA stands out for its substantial impact on microarray data, achieving the highest Accuracy and F1 scores. However, for lower-dimensional datasets like PIMA, the differences between feature selection techniques are less significant, with SVM(RBF) performing well regardless of the method used.

Fig. 9

False positive rate vs. negative predicted value.

This scatter plot of Fig. 9, visualizes the relationship between False Positive Rate (FPR) and Negative Predicted Value (NPV). FPR, on the x-axis ranging from 0 to 25, represents the likelihood of the model mistakenly classifying a negative sample as positive. NPV, on the y-axis between 0 and 100, indicates the probability of a sample being negative when the model predicts it as such. The data points form a loose cloud, suggesting a weak positive correlation. As the FPR increases, the NPV also tends to rise, but not in a strict linear fashion. This implies that a higher false positive rate might be associated with a higher probability of correctly predicting negative cases, but the connection isn’t very strong. To gain deeper insights, it’s important to consider the specific domain and the significance of a high NPV. Additionally, exploring for outliers, the strength of a fitted linear model, and potential influences beyond FPR on NPV would provide a more comprehensive understanding.

Conclusion, limitations and future work

Conclusion

This study explored the potential of machine learning for diabetes prediction by employing a hybrid feature extraction method (ABC, ABC-PSO) combined with metaheuristic feature selection algorithms (HS, DFA, and EHA). The proposed approach demonstrated significant improvements in classification accuracy on the NITP and PIDD. Notably, ABC-PSO with EHA selection achieved the highest accuracies of 97.14% and 98.13% on the respective datasets, outperforming individual techniques. These findings underscore the effectiveness of the hybrid method in identifying informative features for more accurate diabetes prediction, contributing to advancements in machine learning-driven diabetes diagnostics.

Limitations and future work

Despite promising results, the study has certain limitations that warrant further exploration. First, the datasets used for evaluation, while diverse, are limited in size and demographic scope, which may impact the generalizability of the findings. Future studies should incorporate larger and more diverse datasets to validate the approach across a wider range of populations. Additionally, while the hybrid methodology balances computational efficiency and predictive performance, the computational costs associated with the iterative nature of ABC-PSO and metaheuristic algorithms could pose challenges for real-time clinical applications. To address this, future research will focus on optimizing algorithmic efficiency through parallelization and lightweight feature selection methods.

Furthermore, the model currently does not address interpretability, which is crucial for clinical decision-making. Exploring techniques for improving model explainability could enhance its adoption in practice. Lastly, practical strategies for integrating machine learning models into clinical workflows and addressing ethical considerations surrounding the use of genetic data are essential to ensure the responsible application of this research in real-world scenarios.