Introduction

Ship identification is essential for detecting illegal vessels and pinpointing unauthorized activities by ship type. In the realm of fishing vessel management, the identification of fishing vessels plays a crucial role in enhancing sea area management and safeguarding marine resources1. Small fishing vessels, typically with a displacement of less than 50 tons, are prevalent in offshore and inland waterways worldwide. As shipping and fisheries rapidly develop, the management of waterways and fisheries faces significant challenges, highlighting the urgent need for informatization and automation in the management and monitoring of small fishing vessels. Currently, fishing vessel target detection primarily employs methods and technologies based on radar scanning, the Automatic Identification System (AIS), and optical imaging, each presenting limitations.

The radar system, which operates by transmitting electromagnetic waves, can detect vessels in all weather conditions. However, due to their minimal reflective cross-section and low height, small fishing vessels often evade detection by conventional radar. The AIS, an automatic tracking system equipped with transceivers on ships, collects and provides information such as position, heading, and speed. This system necessitates open and cooperative sharing of information, rendering it ineffective for vessels that cannot share their data2. Optical imaging systems, which include visible light CCTV and infrared systems, frequently suffer from interference caused by reflections in the water or adverse weather conditions, leading to poor detection results. With the application and development of laser sensors, different feature information of fishing boat types can be collected through laser sensors, breaking the dependence on optical system image data samples and having stronger data stability and environmental resistance to interference. In fishing boat classification and recognition, different data of small fishing boats with different materials and outlines can be collected through laser sensors, achieving a high-quality data set collection, which is beneficial to the learning and training process of deep learning models. Therefore, this study introduces a new method for the classification and recognition of diverse ship hull contours using infrared laser sensors. This approach, based on varied data models, aims to enhance the robustness of the detection system.

Laser sensors are currently widely utilized in various applications including obstacle detection and recognition, environmental reconstruction, and the recognition of unmanned vehicles or ground mobile robots3. With the ongoing advancement and refinement of deep neural network algorithms, deep learning technologies based on laser data have reached a mature stage4,5. Consequently, this study explores the use of deep learning models that utilize laser sensors for the identification of small fishing boats. As illustrated in Fig. 1, different types of fishing boats exhibit variations in size, shape, and materials. These distinct characteristics influence the shape and distribution of laser spots produced during ship scans. This research introduces a recognition method for small fishing vessels based on the Gramian Summation Angular Field (GASF) sequence diagram and the EMPViT model.

Fig. 1
figure 1

Four different types of small fishing boats. (a) Small alloy fishing boats (b) wooden fishing boats (c) rubber inflatable fishing boats (d) PE plastic fishing boats.

Full size image

In this approach, sequence laser points are encoded using the Gramian Summation Angular Field (GASF), resulting in the generation of GASF two-dimensional color time series images. GASF encoding expands the scale and dimension of one-dimensional contour data features of small fishing boats, enhancing the neural network model’s sensitivity to varying fishing boat contour features6. Additionally, this paper introduces an improved MPViT neural network model, the EMPViT, which not only enhances the classification and recognition effectiveness of fishing boats but also reduces the complexity and training time of the model.

Research on fishing boat recognition is broadly categorized into two main approaches: traditional machine learning methods and deep learning methods for ship recognition7. Xia et al.8 developed a ship detection algorithm for optical remote sensing images based on a dynamic fusion model that utilizes multiple features and variance features, employing a Support Vector Machine (SVM) based on geometric features for training and prediction. Damastuti et al. conducted an experiment using a real-time AIS database, classifying fishing vessels in Indonesian waters based on tonnage, length, and width using KNN and neighborhood component analysis9. To ensure reliable and timely identification of ship targets in maritime battlefields, Guo et al. proposed a ship identification method based on the entropy of optical remote sensing data. This method constructs a decision tree based on hierarchical discriminant regression according to information entropy to identify different small fishing boats in optical remote sensing data10.

Compared to conventional machine learning techniques, some researchers have integrated traditional algorithms with machine learning to enhance benefits and boost target recognition performance. Han et al. introduced a hierarchical target recognition method based on fractal analysis of evidence, addressing the challenge of incomplete images11. Zhu et al. developed a ship detection approach that utilizes shape and texture features for optical image recognition of ships, employing a novel semi-supervised hierarchical classification method to distinguish between small and non-small fishing vessels, significantly reducing false positives12. Khan introduced a recognition method for small fishing boats using histograms of oriented gradients and bag of words for infrared images, demonstrating its superiority over other algorithms through empirical testing.

Furthermore, various researchers have devised effective small fishing boat recognition models using diverse algorithms, yielding commendable results13. Zhang et al. proposed a ship recognition method based on Bayesian inference and evidence theory, validated in simulated battle scenarios, showing notable performance advantages in recognition accuracy over other methods14. Wang et al. introduced a support vector regression (SVR) recognition method enhanced by an improved particle swarm optimization (PSO) algorithm to address issues of model inaccuracy.

Beyond machine learning, deep learning has rapidly advanced, with numerous methods applied to ship imagery for target recognition15. Liu et al. enhanced a convolutional neural network (CNN) to improve ship detection under varying weather conditions16. Chen et al. introduced a new deep learning framework for small fishing boat type recognition, termed coarse-fine cascade CNN, and validated the model’s performance through experimental analysis17. Huang et al. developed a ship detection method based on deep learning to address the challenge of detecting ships of various sizes and types in complex sea conditions, enhancing the convolutional network18. As Synthetic Aperture Radar (SAR) image resolution has improved, Dong et al. proposed a high-resolution SAR image ship classification framework based on a deep residual network19. Lang et al. designed a neural network-based method for infrared intrusion target detection and classification, tailored to the characteristics and detection difficulties of small fishing boats in infrared images20. Ma et al. introduced a novel concept utilizing an improved YOLO v3 and KCF algorithm for accurate identification and authenticity verification of water targets21. Deep learning methods often provide superior accuracy and efficiency but typically require extensive labeled data and substantial computational resources. Addressing the challenges of inadequate labeled data, unoptimized polarimetric images, and noise interference in ship classification, Jeon et al. combined CNN and KNN models to enhance the classification efficiency of small fishing boats, particularly useful for datasets of limited size22. Mishra et al. explored transfer learning in CNNs, applying it to AlexNet, VGGNet, and ResNet architectures for ship classification tasks on the Miracle dataset23. Li et al. proposed a small fishing boat recognition method using a ResNet neural network and transfer learning24.

The Transformer, a novel deep learning model, surpasses traditional convolutional neural networks (CNNs) in performance despite its relatively recent development. Initially dominating the field of natural language processing (NLP) due to its high-performance recognition capabilities, the Transformer model has gained prominence in Computer Vision (CV), challenging the long-established dominance of CNNs. Researchers have started investigating Transformers for applications in small fishing boat detection. For instance, Wang et al. utilized the Vision Transformer (ViT) model for small fishing boat recognition, creating an image dataset comprising four distinct classes. Pre-training on ImageNet addressed the issues of model complexity and data scarcity, resulting in a 4.45% improvement in verification accuracy. Exploring the scalability of Transformers, Gao et al. introduced an enhanced architecture, the variant Swin Transformer, which incorporates a novel window shifting scheme to improve feature transformation between windows, enhancing the framework’s efficacy in defect detection. The comprehensive framework, named Cas-VSwin Transformer, outperforms most existing models25. Lee et al. developed the multi-path Vision Transformer (MPViT) model, which diverges from conventional Transformers by incorporating multi-scale path embedding and a multi-path structure, addressing the limitations of models that overlook local features and enhancing overall performance26.

In this study, the one-dimensional contour of a small fishing boat is captured using a high-precision laser sensor, with the data subsequently fitted using polynomial methods. The Gramian Summation Angular Field (GASF) coding method then generates GASF two-dimensional time series images, enhancing feature differentiation in terms of scale and dimension. This study further refines the MPViT model into the EMPViT model, achieving superior accuracy and reduced computational demands. “Introduction” introduces the research background and methodology. “Model approach” section details the proposed image recognition method for small fishing boats.  “Experiment” section elaborates on the experimental process and results, including the setup of the experimental environment, data preparation, and analysis of the findings. “Conclusion” section concludes the paper.

Model approach

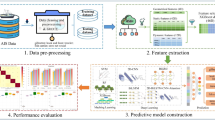
The SICK laser contour sensor is utilized to capture the contour data of various small fishing boats, which are then encoded into time series images using the Gramian Summation Angular Field (GASF) method. These images serve as input for the EMPViT neural network model during pre-training. Subsequently, the trained EMPViT model is employed to enhance the recognition of small fishing boats. This study is conducted in three distinct phases. Initially, the contour data of different fishing vessels are collected using SICK laser contour scanning equipment and are modeled into one-dimensional curves through polynomial fitting. In the second phase, the fitted curve data are treated as one-dimensional time series and transformed into GASF two-dimensional time series images. In the final phase, the MPViT neural network model is advanced to the EMPViT model, facilitating rapid classification and recognition of small fishing boats via GASF two-dimensional time series images. The efficacy of this methodology is substantiated through experimental validation. The workflow of this study is depicted in Fig. 2.

Fig. 2
figure 2

Flow chart of our method.

Full size image

Polynomial fitting to 1D contour data

Since the contour data of fishing boats encompass a full 360-degree range, the surround data from different directions are concatenated into one-dimensional contour data. This approach maximizes the retention of the distinctive characteristics of various fishing boats.

Due to the dispersion in the original ship contour data, which includes substantial amounts of invalid information, the data must undergo fitting and cleaning. To ensure the accuracy of the fitting results, isolated scattering points that are distant from the main contour are removed prior to fitting. The contour data of the cleaned small fishing boat is then fitted using a polynomial curve fitting algorithm. The specific process of fitting is detailed as follows27:

The polynomial curve fitting method was used to fit the scattered data close to the curve. For a set of data \(\:A=\left\{\left({u}_{0},{v}_{0}\right),\left({u}_{1}.{v}_{1}\right),\:\:\ldots\:\left({u}_{k-1},{v}_{k-1}\right)\right\},k\in\:{\text{N}}^{\text{*}}\), the polynomial that best fits the data is:

$$\:u={c}_{0}+{c}_{1}v+\cdots\:+{c}_{m}{v}^{m},m\in\:N$$
(1)

The sum of squares of errors is expressed as:

$$\:{R}^{2}=\sum\:_{i=1}^{k}{\left[{y}_{i}-\left({c}_{0}+{c}_{1}{v}_{i}+\cdots\:+{c}_{m}{v}_{i}^{m}\right)\right]}^{2}$$
(2)

By calculating the partial derivatives of the equation and using the Van der Monde matrix for simplification, we obtained the bounding values, resulting in Eq. (3).

$$\left[ {\begin{array}{*{20}l} 1 \hfill & {v_{0} } \hfill & \ldots \hfill & {v_{{k - 1}}^{m} } \hfill \\ 1 \hfill & {v_{1} } \hfill & \ldots \hfill & {v_{{k - 1}}^{m} } \hfill \\ \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \\ 1 \hfill & {v_{k} } \hfill & \ldots \hfill & {v_{{k - 1}}^{m} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {c_{0} } \\ {c_{1} } \\ \vdots \\ {c_{{k - 1}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {u_{0} } \\ {u_{1} } \\ \vdots \\ {u_{{k - 1}} } \\ \end{array} } \right]$$
(3)

Equation (3) can be abbreviated as Eq. (4):

$$\:V*C=U$$
(4)

In Eq. (4), V, Cand U represent the three matrices in Eq. (3), and the coefficient matrix is derived from the desired fitting curve. After applying the fitting algorithm to fit the original contour data, as shown in Fig. 3, all fitting results were obtained.

Fig. 3
figure 3

Data of four types of small fishing boats. (a) Small alloy fishing boats (b) wooden fishing boats (c) rubber inflatable fishing boats (d)PE plastic fishing boats.

Full size image

Polynomial fitting data stitching

After fitting all segments of the fishing boat contour data, the results are concatenated and treated as a one-dimensional time series suitable for encoding. The fitted results are stitched together in the sequence that matches the actual contour of the fishing vessel. During the splicing process, the intersection points of the fitting result equations serve as connection points, ensuring that the fitted segments are seamlessly joined into a continuous result28. The specific effect of this connection is illustrated in Fig. 4.

Fig. 4
figure 4

The stitching effect of all fitting results with the intersection point of the fitting function equation as the stitching point.

Full size image

GASF 2D time series images encoded by 1D stitching data

Gramian Angular Field (GAF) method is to encode the time series into a pole-based representation rather than Cartesol coordinates. It looks into the angle and poor triangle function transformation. The image is considered a Gramian matrix in the GAF method, each of which is a triangle and (i.e., superimposed) between different time intervals. The data is then processed as a one-dimensional time series using the Gramian Summation Angular Field (GASF) method. This can well preserve the time dependence of fishing vessel profile data, and encode one-dimensional data features into two-dimensional image features, which is conducive to strengthening the sensitiViTy of neural network models.

Suppose all vectors are in units, the Gram matrix can be written as the following formula:

$$G_{1} = \left( {\begin{array}{*{20}l} {\cos \left( {\phi _{{1,1}} } \right)} \hfill & {cos\left( {\phi _{{1,1}} } \right)} \hfill & \ldots \hfill & {\cos \left( {\phi _{{1,1}} } \right)} \hfill \\ {\cos \left( {\phi _{{1,1}} } \right)} \hfill & {cos\left( {\phi _{{1,1}} } \right)~} \hfill & \ldots \hfill & {\cos \left( {\phi _{{1,1}} } \right)} \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {\cos \left( {\phi _{{1,1}} } \right)} \hfill & {\cos \left( {\phi _{{1,1}} } \right)} \hfill & \ldots \hfill & {\cos \left( {\phi _{{1,1}} } \right)} \hfill \\ \end{array} } \right)$$
(5)

where \(\:{\varphi\:}_{m,n}\) is an angle of two vectors. Single variable time sequences cannot explain data characteristics and potential status to some extent. The Gram matrix can not only show the features of the data but also reflect the close link between different features.

In a given time series \(X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}\), in order to make the inner spot not bias toward the maximum observation, we normalize \(\:X\) to make all values in the time series at intervals [-1,0] or [0,1]:

$$\:{\stackrel{\sim}{x}}_{-1}^{m}=\frac{({x}_{m}-{max}\left(X\right)+({x}_{m}-min\left(X\right))}{{max}\left(X\right)-min\left(X\right)}$$
(6)
$$\:{\stackrel{\sim}{x}}_{0}^{m}=\frac{{x}_{m}-min\left(X\right)}{{max}\left(X\right)-min\left(X\right)}$$
(7)

By encoding the value as the angle cosine and the as a radius, we mark the time series \({\stackrel{\sim}{x}}\), and the equation is as follows:

$$\left\{ {\begin{array}{*{20}l} {\Phi = \arccos \left( {\tilde{x}_{m} } \right), - 1 \le \tilde{x}_{m} \le 1,\tilde{x}_{m} \in \tilde{X}} \hfill \\ {r = \frac{{\tau _{m} }}{N},\tau _{m} \in N} \hfill \\ \end{array} } \right.$$
(8)

In Eq. (8), \(\tau _{m}\) is a timestamp, and \(\:\text{N}\) is a constant factor that standardizes polar coordinate span. This conversion has two advantages.

After converting the time series into a pole coordinate form, it is possible to consider the triangular and defiance between each point to exhibit time dependence of different time intervals with an angle view angle. The Gramian Summation Angular Field (GASF) are defined as follows:

$$\:GASF=\left[{COS}\left({\varphi\:}_{m}+{\varphi\:}_{n}\right)\right]$$
(9)
$$G_{2} = \left( {\begin{array}{*{20}l} {\cos \left( {\phi _{1} + \phi _{1} } \right)} \hfill & {cos\left( {\phi _{1} + \phi _{1} } \right)} \hfill & \ldots \hfill & {\cos \left( {\phi _{1} + \phi _{n} } \right)} \hfill \\ {\cos \left( {\phi _{2} + \phi _{1} } \right)} \hfill & {cos\left( {\phi _{2} + \phi _{1} } \right)} \hfill & \ldots \hfill & {\cos \left( {\phi _{2} + \phi _{n} } \right)} \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {\cos \left( {\phi _{m} + \phi _{1} } \right)} \hfill & {\cos \left( {\phi _{m} + \phi _{1} } \right)} \hfill & \ldots \hfill & {\cos \left( {\phi _{m} + \phi _{n} } \right)} \hfill \\ \end{array} } \right)$$
(10)

In the above formula, \(\:{G}_{2}\) is a Gram matrix of the GASF method. The one-dimensional time series is encoded as a GASF matrix by the above algorithm. The GASF encoding process is shown in Fig. 5.

Fig. 5
figure 5

The stitching effect of all fitting results with the intersection point of the fitting function equation as the stitching point.

Full size image

EMPViT neural network model

Overall architecture of EMPViT neural network model

We introduce a novel small fishing boat detection framework called the Efficient Multipath Vision Transformer (EMPViT), building upon the latest advancements in the MPViT model. This new framework is designed to enhance training speed and accuracy while effectively handling local and multi-scale features. In EMPViT, an efficient multi-stage transformer structure is developed, incorporating new convolutional embeddings that significantly enhance the model’s capability to capture local features, addressing a common shortfall in transformers when compared to convolutional networks. Furthermore, by integrating multi-scale features at each stage into a transformer, the redundant paths typically present in the original framework are minimized, reducing the model’s complexity and boosting its performance efficiency.

As illustrated in Fig. 6, the EMPViT architecture extends the multipath approach of the ViT and XCiT models29, adding a local convolution module to augment detection performance and precision. While the MPViT model offers substantial improvements in these areas, it also increases in complexity and demands more extensive training resources. This poses challenges for smaller datasets, where MPViT models can be overly cumbersome and difficult to train. To mitigate these challenges, we implement a streamlined transformer path stacking framework that incorporates convolutional modules30,31, optimizing the EMPViT model for faster inference speeds and reduced computational costs.In our design, a four-stage feature hierarchy is constructed to generate feature maps at various scales, addressing the high computational demands of MPViT models by implementing strategies to simplify the model’s structure. To curb the model’s linear complexity, a single transformer structure is used at each stacking stage. Additionally, the decomposed self-attention transformer encoder from CatCoaT32 is utilized alongside the convolution module from LeViT33, ensuring that no critical information is lost during processing. This holistic approach not only streamlines the model but also preserves its effectiveness in capturing essential features.

Fig. 6
figure 6

Efficient multipath vision transformer EMPViT neuralnetwork model architecture.

Full size image

In the realm of object detection, excessive model complexity can give rise to a host of challenges. Typically, datasets feature a limited number of samples, making data augmentation a time-intensive and resource-heavy aspect of model training. Furthermore, employing transfer learning for small datasets can complicate the training process even further. Large models are often prone to overfitting and instability during training. Given these issues, there is a crucial need to strike a balance between reducing model complexity and maintaining accuracy.

To address these challenges, this paper introduces a newly designed, more efficient model named the Efficient Multipath Vision Transformer (EMPViT). This model is predicated on a single Transformer structure that boasts reduced complexity while still prioritizing high accuracy. The EMPViT model leverages the strengths of the Transformer architecture to ensure a streamlined yet effective approach to object detection, particularly for small fishing boats where conventional models may falter due to the aforementioned issues. This design philosophy not only simplifies the training process but also enhances the practical applicability of the model in real-world scenarios.

Our modifications to the original MPViT model, particularly the reduction of the Transformer three-path module, have significantly improved the performance of the EMPViT model. By consolidating multi-scale features into a single-path Transformer module, the EMPViT model demonstrates enhanced classification capabilities with faster training speeds and greater accuracy. This adaptation indicates that integrating multi-scale features into a single Transformer pathway is an effective strategy.

To further explore the potential of the EMPViT framework, we developed three distinct versions of the model, each varying in complexity and depth:

  1. (1)

    EMPViT-Base(*M): The baseline model that establishes the core architecture.

  2. (2)

    EMPViT-Base+: This version includes an additional two layers of EMS-PatchEmbedded and two EMP-Transformer modules, designed to enhance the model’s feature extraction and processing capabilities.

  3. (3)

    EMPViT-Base++: The most complex version, incorporating four layers of EMS-PatchEmbedded and four layers of EMP-Transformer modules, aiming for even more refined feature integration and classification performance.

All versions of the EMPViT model employ eight Transformer encoder heads, enabling efficient data processing and feature extraction across different scales. The varying layers and modules in each version are tailored to accommodate different levels of computational resources and performance requirements. Detailed specifications and performance metrics of each EMPViT model version are provided in Table 1, facilitating a comprehensive comparison and analysis of their effectiveness in practical applications.

Table 1 EMPViT model version configuration.
Full size table

Efficiency multi-scale patch embedding

To address the challenge of overfitting due to the small sample size in small fishing boat datasets, it is crucial to reduce the complexity of the model. Our approach leverages a multi-level Transformer architecture with low complexity, where we eliminate all redundant Transformer structures from the original model and introduce an efficient multi-scale patch embedding module. This module uses various convolution embedding layers—specifically 3 × 3, 5 × 5, and 7 × 7—to integrate the convolution results of different sizes into the Transformer structure through patching.

To optimize the utilization of both fine-grained and coarse-grained visual tokens, we employ a convolution operation with overlapping patches, similar to techniques used in CNN34 and CvT35. The convolutional patch embedding layer is designed to adjust the token sequence length by varying the stride length and the amount of padding, enabling it to produce feature outputs of the same size across different patch sizes. As depicted in Fig. 7, this method generates visual tokens of uniform sequence length, with patch sizes of 3 × 3, 5 × 5, and 7 × 7.

In practice, to expand the receptive field while maintaining reduced complexity, we use three consecutive 3 × 3 convolutions with the same channel size, a padding of 1, and a stride (S) where S is 2 for reduced spatial resolution, and 1 otherwise. This approach mimics the effects of larger convolution kernels: two 3 × 3 operations equate to a 5 × 5, and three 3 × 3 operations equate to a 7 × 7.

Given the multi-path structure of the MPViT, which includes numerous embedding layers, we propose a novel multi-scale aggregation method. During the embedding process, as shown in Fig. 8, the output feature matrix sizes of the three convolution kernels (3 × 3, 5 × 5, and 7 × 7) are standardized through padding. These outputs are then linearly combined by matrix addition. The aggregated features are subsequently fed into a single Transformer module, achieving early token aggregation and minimizing computational load while ensuring that the multi-path and multi-scale convolution features are preserved.

Fig. 7
figure 7

Efficient multi-scale patch embedding process.

Full size image

Additionally, we incorporate a 3 × 3 depthwise separable convolution36 to further reduce the model’s parameters and computational burden. This involves a combination of 3 × 3 depthwise convolution and a 1 × 1 point convolution, effectively streamlining the model without sacrificing the integrity of the multi-scale features. This strategic reduction in complexity and enhancement of feature processing capabilities positions the modified EMPViT model as a robust solution for the efficient and accurate detection of small fishing boats.

Assuming that the input size before padding is \(\:(H,W)\), the filter size is \(\:({F}_{H},{F}_{w})\), the output size is \(\:({O}_{H},{O}_{w})\), the padding is \(\:P\), and the step size is \(\:S\), the output size after padding can be calculated using Eqs. (11) and (12) :

$$\:{O}_{H}=\frac{H+2P-{F}_{H}}{S}+1$$
(11)
$$\:{O}_{W}=\frac{H+2P-{F}_{W}}{S}+1$$
(12)

After adjusting the output matrices \(\:A\), \(\:B\) and \(\:C\) of the three distinct pathways (3 × 3, 5 × 5, 7 × 7) to a uniform size by zero-padding, the final aggregated matrix \(\:D\) is obtained through summation. The formula is as follows:

$$\:D=A+B+C$$
(13)

Due to the multipath structure of EMPViT with many embedding layers, a 3 × 3 depth-separated convolution and a 1 × 1 point convolution are used to reduce the model parameters and computational overhead.

Local-to-global feature interaction

While the self-attention mechanism in Transformers captures long-term dependencies (i.e., global context), it overlooks the structural and local relational features within patches. Conversely, CNNs exploit local connectiViTy and translation invariance, processing images uniformly. This inductive bias leads CNNs to rely heavily on texture in visual object classification. To synergize the local strengths of CNNs with the global context capabilities of Transformers, this paper introduces a local to global feature interaction module. We employ a deep residual bottleneck block comprising 1 × 1 convolutions, two layers of 3 × 3 deep convolutions, and 1 × 1 convolutions with identical channel sizes and residual connections. The integration of local and global features is achieved through concatenation, using the specified formula.

$$\:{M}_{i}=Concat\left(\right[{F}_{i},{T}_{i,0},{T}_{i,1},\dots\:,{T}_{i,j}\left]\right)$$
(14)
$$\:{X}_{i+1}=P\left({M}_{i}\right)$$
(15)

In Eq. (9), \(\:{T}_{i,j}\in\:{\mathbb{R}}^{{H}_{i}\times\:{W}_{i}\times\:{C}_{i}}\) represents the two-dimensional reshaped global feature of each transformer, \(\:{F}_{i}\in\:{\mathbb{R}}^{{H}_{i}\times\:{W}_{i}\times\:{C}_{i}}\) denotes the local feature, where \(\:j\) is the path index and \(\:i\) is the stage number. \(\:{M}_{i}\) is the aggregated feature, and \(P(\cdot)\) is the learning and feature interaction function. The final feature \(\:{X}_{i+1}\in\:{\mathbb{R}}^{{H}_{i}\times\:{W}_{i}\times\:{C}_{i+1}}\) is obtained through calculation, and its size is the channel dimension \(\:{C}_{i+1}\) of the next stage.

Convolution local feature

As depicted in Fig. 8, to enhance the model’s ability to capture local features, a 3 × 3 convolution kernel has been added to the local convolution module. It is recognized that two 3 × 3 convolution kernels can perform equivalently to one 5 × 5 kernel. While 3 × 3 kernels involve a higher computational load, they require significantly fewer parameters compared to 5 × 5 kernels, and computers process them more rapidly during convolution operations. This optimization approach was commonly utilized in early VGG networks. Additionally, substituting a 5 × 5 kernel with two 3 × 3 kernels not only increases the network’s depth, thereby enhancing the non-linear expression of features, but this benefit is also supported by subsequent experimental validations. Furthermore, research indicates that replacing [CLS] labels with global average pooling (GAP) of the final feature map does not compromise performance; thus, for simplicity, we implement Global Average Pooling (GAP). The model’s parameters and computational demands are further reduced by using 3 × 3 depthwise separable convolutions, which consist of 3 × 3 depthwise convolutions and 1 × 1 point convolutions in the embedding layer.

Fig. 8
figure 8

EMPViT neural network model local convolutional module.

Full size image

Experiment

Experiment environment

In the training process of deep learning, the neural network requires substantial computational resources; hence, an all-in-one computer equipped with an Intel i9 processor and an RTX 3090 graphics card serves as the hardware environment for running the neural network model in this experiment.

Python is widely favored by deep learning researchers due to its simplicity, open-source nature, portability, object-oriented features, and extensive third-party libraries. The software environment for this study is established using the PyCharm development tool, which is based on the Python language. Within this environment, the Python frameworks employed are Torch GPU 2.2 and Keras 2.2.4.

Experimental dataset

Datasets play a crucial role in the training and validation of models. In this study, we used the SICK LMS511, an LMS series infrared laser scanner, to collect small fishing boat profile data in local rivers, lakes and coastal waters during spring and summer, when fishing vessels are at their peak.We concentrated on four distinct types of small fishing boats: alloy, wooden, rubber-filled, and PE plastic. After securing the necessary authorization, we employed a 360-degree surround sampling method using an infrared laser sensor to capture the contours of these boats.

Due to restrictions imposed by epidemic policies, the data collection and sampling process extended over approximately six months, resulting in a total of 3,268 distinct profile datasets of fishing boats. The breakdown of the sampling data was as follows: 1,063 datasets from small alloy fishing boats, 918 from small wooden fishing boats, 726 from PE plastic small fishing boats, and 561 from small pneumatic rubber fishing boats. Among these, the small alloy fishing boats constituted the largest proportion of the data, while the small inflated rubber fishing boats represented the smallest.

The same fitting method was applied across all the collected contour data to concatenate the results into one-dimensional time series data, which was then used for subsequent image coding. A uniform two-dimensional time series image coding method (GASF) was employed to encode all one-dimensional time series, generating reliable samples of time series image datasets. Four distinct types of GASF time series images were produced, as illustrated in Fig. 9.

Fig. 9
figure 9

GASF 2D time series images corresponding to four different types of small fishing boats, (a) GASF images of small alloy fishing boats, (b) GASF images of wooden fishing boats, (c) GASF images of rubber inflated fishing boats, and (d) GASF images of PE plastic fishing boats.

Full size image

To enhance the model’s performance, we augmented the dataset of four small fishing vessels through various data augmentation techniques, including flipping, scaling, and noise addition. Specifically, the images of the fishing boats were flipped horizontally. During the scaling process, the images were adjusted using scale factors of 0.75 and 1.5. Overfitting, which often occurs when a neural network excessively learns high-frequency features that are not beneficial for its tasks, was addressed. To mitigate the influence of these high-frequency features on the low-frequency ones, Gaussian noise and salt-and-pepper noise were randomly introduced to the image samples upon completion of the data augmentation.

Following all augmentation steps, we meticulously cleaned the dataset by selectively removing several poor-quality image samples. This process resulted in an adjusted total of 3,600 samples per image type.

Experimental procedure

Data augmentation and setup

Sample size significantly influences the learning capabilities of neural networks. To enrich the feature learning of the network, we expanded the number of time-series images by incorporating various sample types. Dataset expansion techniques such as rotation, scaling, and translation were employed to maximize the diversity of sample types available in the dataset.

To simplify the processing complexity, we ensured a balanced distribution of the dataset during the preparation phase. The enhanced and expanded dataset samples are detailed in Table 2. The complete dataset includes four different types of small fishing boats, totaling 14,400 Gramian Summation Angular Field (GASF) time series images, with each type—small alloy fishing boats, wooden fishing boats, rubber inflated fishing boats, and PE plastic fishing boats—contributing 3,600 images.

The dataset was segmented in a 3:1:1 ratio for training, testing, and validation, respectively. For imaging, the GASF method was used to generate pseudo-color images. In this process, each value in the Markov matrix was mapped to a color to produce RGB-channel time series images. Additionally, to meet the neural network model’s requirements, all images were standardized to a uniform size of 3 × 224 × 224.

Experimental parameter settings

During the experimental training process, through multiple training iterations, we refined the parameters that best suit the classification and recognition of small fishing boat datasets, such as the number of training iterations and batch size parameters. Additionally, we selected an optimal Adam optimizer to mitigate network overfitting. Based on the data presented in Table 2, we established that an initial learning rate of 0.01, a batch size of 32, a momentum of 0.9, and 300 training iterations constitute the optimal parameter configuration for the model. This setup was determined to effectively enhance the model’s performance in recognizing and classifying small fishing boats.

Table 2 EMPViT neural network model training parameter settings.
Full size table

We assessed the performance of the EMPViT model on a dataset composed of 2D GASF time-series images, which were derived from fitting and concatenating contour data of various small fishing boats. The dataset includes GASF images of small alloy fishing boats, wooden fishing boats, rubber inflated fishing boats, and PE plastic fishing boats. To demonstrate the advantages of the proposed EMPViT model, we conducted a comparative experiment using well-established models from both the convolutional neural network and visual Transformer domains. The mainstream convolutional neural network models utilized include VGG-16, ResNet5037, GoogleNet38, DenseNet39, and MobileNet40.

For visual Transformer models, we included ViT41, Swin42, LocalViT43, DeepViT44, CaiT45, CrossViT46 and MPViT26 in the comparison.

All models underwent training for 300 iterations, employing the Adam optimizer with a batch size of 32 and an initial learning rate of 0.01. Image scaling was managed using a cosine decay learning rate scheduler, and each image was cropped to a size of 224 × 224. Parameter details were maintained consistently with those outlined in Table 3. This experimental setup aimed to ensure a fair and comprehensive evaluation of EMPViT’s performance relative to other prominent models in the field.

The experimental results and analysis

The experimental comparison results, presented in Table 4, delineate two primary experimental pathways: the CNN convolutional neural network models and the Transformer neural network models. Within the mainstream CNN model pathway, the accuracy of the 2D GASF time series image dataset corresponding to small fishing boats shows a progressive improvement with increasing model complexity and parameter count. The MobileNet network achieves the highest accuracy in this category at 89.67%, which falls slightly below 90%.

Table 3 Comparison results of different models in the experiment.
Full size table

Conversely, in the mainstream Transformer model pathway, the highest recorded accuracy is an impressive 99.67% Notably, the EMPViT neural network model not only exhibits a substantial improvement in accuracy but also demonstrates a significant reduction in model complexity. Compared to other models, EMPViT stands out with its remarkable balance of high accuracy and reduced complexity, highlighting its substantial advantages in both aspects.

In the model comparison experiments, the EMPViT-Base model stands out with the highest performance results. The experimental conditions and network model parameters were standardized across all tests to ensure comparability. As detailed in Table 3, while the parameters of the Transformer series models are generally more complex than those of the CNN series models, they also achieve significantly higher accuracy and GFLOPs (Giga Floating Point Operations per Second). Within the Transformer model family, the EMPViT model distinguishes itself with an exceptional performance, achieving an accuracy of 99.67%. It not only delivers the highest accuracy and GFLOPs but also maintains the least parameter complexity among its counterparts, underscoring its efficiency and effectiveness in processing.

Experimental results and analysis of EMPViT ablation

In Table 4, the EMPViT-Base + and EMPViT-Base + + model versions, which feature added layers in two and four-layer stack modules respectively, underwent fusion experiments with different layer configurations as detailed in the table. These experiments utilized a dataset of 2D GASF time series images corresponding to small fishing boats for comparative analysis.

The data presented in Table 4 indicates that the EMPViT-Base + + model, which has more layers, tends to be more accurate but also possesses a higher number of parameters, thus increasing the model’s complexity. Conversely, the EMPViT-Base version maintains fewer model parameters and lower complexity, while the accuracy gap between it and the higher-stack version remains modest. This characteristic is particularly advantageous for reducing model training time.

Further analysis of the experimental data in Table 4 reveals that the EMPViT models exhibit a 2–3% improvement in accuracy over the MPViT models. Despite the significant boost in accuracy, all versions of the EMPViT model maintain a smaller size and faster inference speed. This combination of improved performance metrics robustly confirms the practical effectiveness and application value of the EMPViT models.

Table 4 EMPViT Melting models experiment analysis.
Full size table

Ablation experiments were conducted on EMPViT models featuring different configurations to evaluate enhancements proposed in the method. The two key configurations tested include the addition of a new 3 × 3 local convolution module and an improvement involving multi-scale, multi-path convolutions aggregated into a single Transformer module. The results of these ablation experiments are displayed in Table 5.

As indicated in Table 5, both configuration improvements significantly enhance the accuracy and efficiency of the EMPViT models compared to the MPViT models. The introduction of the local convolution module markedly influences the model’s performance; however, it also increases the consumption of model parameters. Conversely, the strategy of aggregating individual Transformer modules in advance not only boosts the model’s performance but also substantially reduces the number of model parameters and the computational resources required. This demonstrates the effectiveness of the improvements in optimizing both the operational efficiency and the computational economy of the EMPViT models.

Table 5 Analysis of ablation experiments for the EMPViT Model.
Full size table

Conclusion

This paper introduces a novel method for recognizing small fishing boats based on GASF time series images and the EMPViT model, aiming to enhance the classification and recognition of four distinct types of small fishing boats. Unlike traditional approaches, this method initially employs an infrared laser sensor to capture one-dimensional contour data of the boats. These data are then fitted using a polynomial fitting function and gradually assembled into one-dimensional time series data, which are subsequently encoded into two-dimensional time series images. The enhanced EMPViT model is then utilized for training and learning, with the neural network classification and recognition model undergoing fine-tuning and improvements throughout the experimental process. This method is based on laser sensors, combined with GASF encoding method and improved optimized EMPViT model, which has lower cost and higher performance in classification recognition, and has good implementation and applicability.

The experimental results demonstrate that this method achieves the highest average accuracy across the dataset of four types of boats, with the EMPViT-Base + + model reaching an accuracy of 99.95%. These findings effectively validate the proposed method and clearly illustrate its advantages over traditional convolutional neural network models and one-dimensional CNNs. This paper presents a novel method for classifying and detecting small fishing boats. The method has a lower deployment cost and possesses good application prospects. By GASF encoding of small fishing boat contour data in combination with an improved EMPViT model, the method reduces model complexity while further enhancing the accuracy of small fishing boat and recognition. In the future, we will try different fishing boat contour data coding and model improvement methods to better improve the classification and recognition performance of small fishing boats.