Introduction

Epilepsy is a life-threatening chronic neurological disorder. Whether manifesting as overt symptoms or as subtle pre-seizure states, epilepsy represents one of the most critical conditions within the realm of neurology1,2. Severe seizures can have a profound impact on patients, potentially leading to injury3. Furthermore, patients with epilepsy and their families may also experience stigma and discrimination, which can have a detrimental effect on their quality of life. The World Health Organization (WHO) estimates that approximately 180,000 new cases of epilepsy are reported globally each year4. The prevalence of active epilepsy in the general population at a given time is estimated to range from 4 to 10 per 1,000 individuals. Although anti-epileptic drugs are an effective treatment for the condition, one third of patients continue to experience seizures despite receiving treatment5. Moreover, approximately 75% of seizures are not preventable. Accurately detecting seizures is pivotal in ensuring patient safety, enhancing quality of life, and determining long-term prognosis. Therefore, this represents not only a significant technical advancement but also a beacon of hope for numerous individuals6. The distinctive patterns (i.e., three-phase waves, biphasic waves, whole-body sharp and slow waves, and multi-spike) observed in electroencephalogram (EEG) signals serve as indicators for various seizure types and play an essential role in identifying seizure-related brain abnormalities, diagnosing specific seizure categories, and pinpointing treatment targets7,8. In conventional epilepsy treatment, the identification of seizure fragments is primarily conducted by epilepsy specialists through the observing of long-term EEG recordings and subsequent manual labeling. However, this artificial method is constrained by limitations in detection time when dealing with long-term continuous EEG. Furthermore, fatigue increases the risk of misjudgment by experts. Consequently, the development of automated and expedient seizure detection algorithms needs exploration.

Despite the extensive research conducted over the past two decades on automated seizure detection using EEG, a significant challenge persists: the imbalance between seizure and non-seizure categories. This imbalance arises because the duration of seizures is considerably shorter than that of non-seizure periods9. This phenomenon of class imbalance is not exclusive to seizure detection. It is also commonly observed in large real-world datasets, leading to the development of numerous methods for addressing unbalanced label distribution. These classical methods can be divided into two categories: algorithm level and data level. Siddiqui et al.10 employed a cost-sensitive learning method with random forest, representing the most classical of the algorithm-level methods. However, both the method proposed by Siddiqui et al. and the sensitive-specificity weighted cross-entropy (SSWCE) method proposed by Ingolfsson et al.11, which allows for higher specificity or sensitivity based on cross-entropy loss, require domain experts to construct a cost matrix or loss function based on task-specific prior knowledge. It is imperative to acknowledge that the cost matrix or loss function, designed for a particular problem, is exclusively applicable to that specific task and may not ensure optimal performance when applied to other tasks. Moreover, reweighting methods have been developed that assign distinct weights to distinct categories. These include weighted extreme learning machine (ELM) and penalty strategies12,13. Compared with the aforementioned methods that only improve the recognition ability of the model for the minority class, Yanna Zhao et al.14 used the focal loss to redefine the loss function of the linear graph convolutional network (LGCN) in the seizure detection model based on LGCN, which allowed paying more attention to those samples that were difficult to classify or misclassified.

Besides oversampling-based methods, such as K-means synthetic minority oversampling technique (SMOTE)15,16, SMOTE + TomekLinks17, ADASYN18, and borderline nearest neighbor synthetic minority oversampling technique (BNNSMOTE)19, the random channel ordering (RCO) method, as proposed by Xuyang Zhao et al.20, generated EEG images by randomly shuffling the order of channels. The EEGAug method employed time frequency conversion to transform data comprising disparate frequency bands from disparate samples into time-domain samples21. Furthermore, the method developed by Bin Gao et al.22 employed a generative adversarial network (GAN) to enhance the data. These methods can be classified as minority generation methods. However, when applied to large datasets, they may result in increased computational overhead, a slower training speed, and the potential for overfitting. Consequently, the strategy of reducing samples from the majority of categories is a favorable approach, such as undersampling23,24 or using anomaly sampling to transform non-seizure data into outlier samples, as demonstrated by Nizar Islah et al.25. Furthermore, Xiaoshuang Wang et al.26 employed sliding window segmentation to enhance seizure data and to randomly select non-seizure data. Zhen Jiang et al.27 combined the TomekLink technique with undersampling to address the imbalance ratio between seizure and non-seizure data. Nevertheless, this mixed-class method may exhibit shortcomings inherent to both types of data-level methods.

The traditional imbalanced learning methods often rely on heuristic assumptions derived from the training data. They typically assume that instances with higher training errors provide more valuable information for learning, as demonstrated by the focus loss and RUSBoost algorithm used in K-double cross-validation by Nipun Bhanot et al.28. Another commonly held assumption is that generating synthetic samples around a small number of instances facilitates the learning process. However, the former outliers may result in the generation of false reinforcement, whereas the latter cannot accommodate excessive overlap between a minority class sample and a majority class sample. Meta-learning can be employed to address complex practical tasks without the need for heuristic assumptions. Therefore, a framework combining meta-learning and ensemble learning is introduced for solving the issue of imbalance existing in seizure detection. Indeed, some studies have demonstrated the potential of ensemble learning to address imbalances in seizure detection. Yao Guo et al.29 employed the EasyEnsemble algorithm within the supervised learning framework to enhance robust seizure detection for uncertain subjects, potentially mitigating the generalization error associated with seizure-free segments. Tiejia Jiang et al.30 introduced the Ensemble Classification Model (ECM) method, which partitions data into several relatively balanced subsets based on the imbalance ratio, trains an independent classifier for each subset, and integrates the output results via vote-based decision-making. Despite these advancements, both methods remain rooted in heuristic design, which may limit their overall performance. Additionally, EasyEnsemble utilizes AdaBoost as its base classifier; however, boosting-class methods are known to be sensitive to noise, which could adversely affect classification accuracy. The proposed framework combining meta-learning and ensemble learning can avoid these problems. In recent years, numerous seizure detection algorithms based on deep learning have emerged. Xu et al.31 introduced a method for labeling cross-period samples with soft labels and integrated this approach with a three-dimensional convolutional neural network (3D-CNN) architecture. They further developed a multi-scale feature extraction technique utilizing the short-time Fourier transform (STFT). In addition to traditional CNN models, hybrid models have also become prevalent. These include combinations such as CNN + long short-term memory networks (LSTM)32, LSTM + multi-scale Atrous-based deep convolutional neural networks (MSA-DCNN)33, as well as graph neural network (GNN)-based hybrids like graph attention networks (GAT) + Transformer34, graph convolutional networks (GCN) + Transformer35, and attention-based GNNs36. However, machine learning methodologies offer distinct advantages in terms of model universality and feature interpretability compared with deep learning. Using interpretable features as inputs enables medical experts to map features to corresponding biological or chemical factors, thereby facilitating the formulation of appropriate treatment plans9.

In this study, epileptic seizures were detected based on meta-learning and ensemble learning to address the imbalanced classification in this field. On the one hand, a meta-sampler was employed to autonomously identify and implement adaptive undersampling strategies from EEG data, with the aim of mitigating the instability and high computational cost. And the non-differentiable optimization issue associated with the meta-sampler was addressed by using the soft Actor-Critic algorithm. On the other hand, this method distinguished between model training and meta-training processes, rendering it broadly applicable to a diverse array of classifiers. And the use of task-independent meta-states kept high robustness in the face of EEG data tag corruption. Besides, the EEG features were extracted in the five frequency bands (δ, θ, α, β, and γ) and from the three distinct perspectives, i.e., time domain analysis, nonlinearity assessment, and entropy-based measurement. Subsequently, Semi-JMI was employed to select EEG features that were fed into this classification framework. The proposed seizure detection system demonstrated superior classification performance compared with other published methods based on two publicly accessible EEG databases, resulting in encouraging outcomes.

The remaining content of this article is organized as follows: section “Materials and methods” elaborates on data sets, data preprocessing, a proposed framework for imbalanced classification based on meta-learning and ensemble learning, and experimental settings. Then, in section “Results”, we clarify the results of the experiment. Finally, sections Discussion” and “Conclusion” are the objects of discussion and conclusions, respectively.

Materials and methods

Experimental datasets

TUSZ dataset

The Temple University Hospital (TUH)-EEG Corpus (TUEG) is publicly available from the Neural Engineering Data Consortium (NEDC) website (www.nedcdata.org). The TUEG Seizure Corpus (TUSZ) is a subset of the TUH clinical EEG signal database, which is notable for its extensive patient population and diverse configurations37. These files comprise male and female (51% women) patients with an average age of 1–90 years (mean age 51.6). The data frequency range is 250–1024 Hz, with 250 Hz data accounting for 87% of the total. The electrodes are arranged on the scalp in a standard 10–20 format. The EEG has 23 or 22 channels available, although, in rare cases, it may contain 20 channels.

A randomly selected subset of the data, comprising channel numbers 23 and 22 from the latest version (v2.0.1) of TUSZ, was employed as the dataset in this study. The data were then uniformly downsampled to 250 Hz. Subsequently, all data were transformed into a temporal central parasagittal (TCP) montage of 22 channels (Fig. 1)38. Due to the extensive volume of data, it was necessary to divide it into 4-second, non-overlapping segments. Single-channel data were employed as samples, ensuring that each segment consisted of 22 samples of 1,000 data points. The examination of the seizure and non-seizure data revealed that the majority of the records in the validation set consisted of a single seizure or non-seizure, exhibiting distinct characteristics. Accordingly, the validation set data of TUSZ was employed as the training set of the experiment, and the training set data of TUSZ was used as the validation set of the experiment. TUSZ’s non-seizure signal duration was considerably longer than any seizure type duration, rendering it an appropriate choice for the algorithm. The selected dataset exhibited an imbalance ratio of 10 for both the training and validation sets. This indicates that the majority class (non-seizure) data is ten times more than the minority class (seizure) data. Table 1 lists some details of the experimental dataset.

Table 1 Statistical overview of the TUSZ dataset used in our seizure detection experiments.
Full size table
Fig. 1
figure 1

Representation of the temporal central parasagittal (TCP) montage of 22 channels.

Full size image

SWEZ dataset

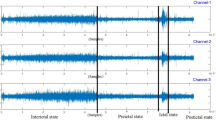
The SWEC-ETHZ (SWEZ) short-term dataset comprised 100 intracranial EEG (iEEG) recordings from 16 patients with drug-resistant epilepsy, which are available for download at http://ieeg-swez.ethz.ch/. The data had undergone digital band-pass filtering between 0.5 and 150 Hz and were sampled at a rate of 512 Hz39. Each seizure was stored as a record, beginning 3 min after the start of the record and ending 3 min before the end, as shown in Fig. 2. The number of seizures in these patients ranged from 2 to 14, with durations ranging from 10 to 1002 s. Patient 14 was removed because his non-seizure data were inadequately provided. The specific information of the experimental dataset is provided in Table 2. The duration of seizures exhibited by different patients varied considerably, which necessitated the use of a K-fold cross-validation approach. In this method, one record was designated as the test set for each patient (with k records), whereas the remaining records were divided equally into training and validation sets. The data were divided into non-overlapping 5-second intervals, with the data from a single channel serving as the sample.

Table 2 Information on 15 patients from the SWEC-ETHZ short-term dataset.
Full size table
Fig. 2
figure 2

Intracranial partial channel EEG of patient 7’s first episode in the SWEZ dataset, with seizure data inside the red line.

Full size image

Data preprocessing

Butterworth filter

The EEG signals in the database were removed with a sixth-order Butterworth band-pass filter for signal components below 1 Hz or above 60 Hz40. Setting the low frequency to 0.5 Hz could effectively eliminate the direct current (DC) component noise present in the EEG signal. Furthermore, a high frequency of 60 Hz was employed to ensure that the filtered signal contained the typical rhythms observed in EEG signals, including δ (0.5–4 Hz), θ (4–8 Hz), α (8–13 Hz), β (13–30 Hz), and γ (30–60 Hz)41.

Feature extraction

Following the application of a filter, the EEG data of the δ, θ, α, β, and γ waves were obtained in five distinct frequency bands. For each band of data, 29 classical statistical features were extracted and organized in the order of δ, θ, α, β, and γ bands, resulting in a feature vector comprising a total of 29\(\:\times\:\)5=145 features. This process transforms EEG signals into informative features, thereby achieving the objective of data dimensionality reduction. EEG signals were inherently nonlinear and irregular, necessitating the inclusion of nonlinear features in the analysis of EEG activity. The 29 univariate features were selected from three categories: time domain, nonlinear features, and entropy-based features. The numbering followed the order of the δ-γ bands (e.g., 30 was θ-1). Table 3 provides further details on these features. Additionally, Table 4 presents the mathematical foundation of these measures and provides descriptions.

Table 3 List of all the 29 extracted features and their respective abbreviations.
Full size table
Table 4 More details about some of the features used in this work.
Full size table

Feature selection

Mutual information is widely adopted in the field for feature selection49. This study presented a comparative analysis of four filter-based feature selection methods, including maximum mutual information (MIM), joint mutual information (JMI), and their semi-supervised variants (Semi-MIM and Semi-JMI)50. The features were ranked based on the scoring metric, and those with higher scores were selected due to feature selection. The MIM criterion was as follows:

$$\:{J}_{MIM}\left({X}_{j}\right)=\widehat{I}\left({X}_{j};Y\right)$$
(1)

Although mRMR is a widely used criterion that considers redundancy between features, Brown et al. (2012) found it to be quite unstable in an extensive empirical study. Accordingly, we elected to use the JMI criterion:

$$J_{{JMI}} \left( {X_{j} } \right) = \mathop \sum \nolimits_{{X_{k} \in {\mathbf{X}}_{\theta } }} ~\hat{I}\left( {X_{j} ;Y\mid\:X_{j} } \right)$$
(2)

The binary random variable s is used to annotate the original EEG dataset D, thereby constructing a semi-supervised EEG dataset containing both labeled and unlabeled instances. The true label value y was only recorded when s = 1; otherwise, it was marked as “missing.” The proportion of labels was controlled by ps1. Therefore, what could be observed was not really Y but a “surrogate” variable \(\:\stackrel{\sim}{\text{Y}}\). The “soft” prior knowledge was employed to determine the optimal proxy for ranking the features to decide whether the label marked as missing was all assumed to be positive for the agent \(\:{\stackrel{\sim}{\text{Y}}}_{1}\:\)or all assumed to be negative for the agent \(\:{\stackrel{\sim}{\text{Y}}}_{0}\). Once the most influential agent was identified, the ranking could be conducted using either the MIM or the JMI criterion for this variable. The Semi-MIM and Semi-JMI scoring metrics were as follows:

$$\:Semi-\text{M}\text{I}\text{M}:{J}_{MIM}^{{\stackrel{\sim}{Y}}_{0}/{\stackrel{\sim}{Y}}_{1}}\left({X}_{j}\right)=\widehat{I}({X}_{j};{\stackrel{\sim}{Y}}_{0})or\:\:\widehat{I}({X}_{j};{\stackrel{\sim}{Y}}_{1})$$
(3)
$$\:Semi-\text{J}\text{M}\text{I}:{J}_{JMI}^{{\stackrel{\sim}{Y}}_{0}/{\stackrel{\sim}{Y}}_{1}}\left({X}_{j}\right)={\sum\:}_{{X}_{i}\in\:{X}_{\theta\:}}\:\widehat{I}({X}_{j};{\stackrel{\sim}{Y}}_{0}\mid\:{X}_{i})\text{o}\text{r}{\sum\:}_{{X}_{i}\in\:{X}_{\theta\:}}\:\widehat{I}({X}_{j};{\stackrel{\sim}{Y}}_{1}\mid\:{X}_{i})$$
(4)

Imbalanced classification framework

The framework was divided into two distinct parts: meta-training for the purpose of optimizing the meta-sampler, and meta-sampling and ensemble training for the training of integrated models. The aforementioned elements will be described in this section. The specific structure and overview of the seizure detection system are depicted in Fig. 3(a).

Meta-state

Inspired by the concept of gradient/hardness distributions51,52, we used the histogram distribution of prediction errors on both the training and validation sets as a meta-state representation of the entire framework. This representation was agnostic to specific task properties (e.g., dataset size and feature space) and not only provided ensemble training information to the meta-sampler but also enabled adaptive resampling across tasks. The prediction error was defined as the absolute difference between the predicted probability of the ensemble classifier G and the true label. It was approximated by a histogram of n positions. Specifically, the \(\:i\)-th component of the error histogram E for the dataset D was calculated as follows:

$$\:{\text{E}}_{\text{D}}^{\text{i}}=\frac{\left|\right\{(x,y)\mid\:\frac{i-1}{n}\le\:abs\left({G}_{j}\right(x)-y)<\frac{i}{n},(x,y)\in\:\mathcal{D}\left\}\right|}{\left|\mathcal{D}\right|}*n,1\le\:i\le\:n.$$
(5)

The concatenated prediction error histograms of the training and validation sets formed the meta-state S=[Etr,Ev]. It intuitively reflected the fit of the model to the training set and its generalization on unseen data. When n > 2, the histogram provided a finer granularity in showing the distribution of “easy” samples (errors close to 0) and “hard” samples (errors close to 1) and thus contained more information to guide the resampling process. In addition, the size of the meta-state near the hard sample indicated bias, whereas the level of histogram aggregation indicated variance. The combination of the training and validation set histograms revealed whether the model was underfitting or overfitting to some extent, providing decision support for the sampling process. Since the meta-state provided input to the meta-sampling, the prediction probability and label were calculated for the majority (non-seizure) of the dataset.

Meta-sampling

We employed the Gaussian function technique to streamline both the meta-sampling process and the sampler itself. Specifically, let \(\:\widehat{s}\) be defined as a meta-sampler that produces the scalar a∈[0,1] based on the input meta-state S. For a sample with a current model prediction error of x, the (unnormalized) probability of being sampled is:

$$\:{g}_{a,\sigma\:}\left(x\right)=\frac{1}{\sigma\:\sqrt{2\pi\:}}\text{e}\text{x}\text{p}(-\frac{1}{2}{\left(\frac{x-a}{\sigma\:}\right)}^{2})$$
(6)

where \(\:\sigma\:\) is a hyperparameter. The majority of data (non-seizure) in the training set was sampled as much as the minority of data (seizure), and the sampling weight was expressed as:

$$\:{w}_{i}=\frac{{g}_{a,\sigma\:}\left(\right|G\left({x}_{i}\right)-{y}_{i}\left|\right)}{\sum\:_{({x}_{j},{y}_{j})\in\:{M}_{a}}\:{g}_{a,\sigma\:}\left(\right|G\left({x}_{j}\right)-{y}_{j}\left|\right)}$$
(7)

The process of combining the resampled majority data (non-seizure) with the minority data (seizure) resulted in a balanced training subset. In essence, this meant that the sampler tended to retain samples with prediction errors close to a. For instance, as a approached 1, our sampling behavior pattern resembled hard example mining, whereas as a approached 0, it resembled robust learning. Additionally, two modes of action existed for a in the meta-training process: the “rand” mode involved randomly selecting a from the action space, and the “mesa” mode involved outputting a from the Gaussian strategy network45. For details on the specific network output process, refer to section “Meta-training”.

Ensemble training

The ensemble training procedure trained multiple base classifiers in a serial manner. With the meta-sampler \(\:\widehat{s}\) and the meta-sampling strategy, we could iteratively train the new base classifier using a balanced training set after meta-sampling. Specifically, at the j-th iteration we had the unbalanced original dataset and the current ensemble model Gj() to get the meta-state S. The sampler then dynamically undersampled the original data according to the current S to obtain a balanced training set Dj + 1, tr. We performed an update to train a base classifier gj+1() with this balanced training set and added it to the ensemble model to obtain Gj+1(). Finally, an ensemble model consisting of m base classifiers was obtained. The prediction probability of the new ensemble model was obtained by a weighted average between the ensemble model Gj() and the base classifier gj + 1() to maintain the consistency of the prediction probability and prevent the old prediction probability from having an excessive influence on the new ones. The first base classifier G1() was trained with random undersampling. At the same time, the ensemble training was not only part of the meta-training; but also the training of the ensemble model after obtaining the optimal meta-sampler.

Meta-training

As mentioned earlier, we aimed for a framework to learn the most appropriate sampling strategy (sampler parameters) directly from the data so as to optimize the final generalization performance of the ensemble model53. An interaction between the meta-sampler and the external environment was observed in each iteration of ensemble training, where the environment provided a meta-state S, the meta-sampler took an action a based on the current S, and the ensemble model was updated to obtain a new meta-state \(\:{S}^{{\prime\:}}\). We wanted the sampler to learn from its own interaction with the ensemble training process, so the non-differentiated optimization problem of training the meta-sampler could naturally be solved by reinforcement learning (RL).

Specifically, the ensemble training system could be considered as an environment (ENV) in our RL setting. Within each episode (EPI), the environment was initialized and the meta-state S was obtained. Subsequently, through meta-sampling and ensemble training at each environment step, the action a, the new state\(\:\:{S}^{{\prime\:}}\), and the reward r were determined based on the difference in the performance measure function of G on the verification set before and after the update. At the same time, Soft Actor-Critic (SAC) was used to optimize the parameters of our meta-sampler. This process continued until the number of base classifiers in the ensemble model reached m (d = 1), at which point it moved on to the next episode.

The SAC algorithm is a non-strategic actor-critic deep RL algorithm based on the maximum entropy RL framework54. It consists of 1 actor network, 2 Q critic networks, and 2 target soft Q-networks. The actor policy network of the meta-sampler consists of a fully connected layer of 55 neurons, followed by 2 branches that output the mean and log standard deviation, respectively. The Gaussian distribution was used to extract a∈[0,1] and logπ() through the reparameterization technique and the tanh function. The critic network consisted of two identical Q-networks, each of which was a multilayer perceptron (MLP) of {2n + 1,55,55,1}. The parameters for the target soft Q network were obtained by exponentially moving average Q network parameters. In addition, the tuple of information (S, a, r, \(\:{S}^{{\prime\:}}\), d) was stored in the experience replay buffer B to reduce the correlation between previous and subsequent actions55. During neural network training, a batch of experiences is randomly selected from the B pool to increase training efficiency. As a standard practice in network training, we used the ADAM optimizer to optimize policy and critic networks, as shown in Fig. 3(b).

Fig. 3
figure 3

Seizure detection system structure diagram. (a) System flow chart, including the specific process for training the ensemble model of the framework. (b) Soft Actor-Critic(SAC) update parameter process in meta-training.

Full size image

Channel decision fusion

The output result of a sample is the predicted label of a channel in the fragment. The results of all the channels were summed and compared with a predefined threshold to obtain the predicted label of the fragment. If the sum was greater than or equal to the threshold, the segment was labeled as a seizure; otherwise, it was labeled as a non-seizure. The range of values for the dataset threshold was defined as (\(\:0.5\times\:C-C\times\:0.25\),\(\:0.5\times\:C+C\times\:0.25\)), where C represents the number of channels in the data. The schematic figure for channel decision fusion is shown as Fig. 4.

Fig. 4
figure 4

Explanation of channel decision fusion.

Full size image

Evaluation method

In this study, we employed sensitivity, specificity, accuracy, and F1 score as performance metrics for the model.

Sensitivity (sen) represents the proportion of correctly identified attacks:

$$\:SEN=\frac{TP}{TP+FN}$$
(8)

Specificity (spe) represents the proportion of correctly identified non-seizures among all non-seizures:

$$\:SPE=\frac{TN}{TN+FP}$$
(9)

Accuracy (acc) is defined as the proportion of correctly classified samples:

$$\:ACC=\frac{TP+TN}{TP+FN+FP+TN}$$
(10)

The F1 score represents a composite evaluation metric that integrates sensitivity and specificity to provide an overall assessment:

$$\:F1=\frac{2TP}{2TP+FN+TN}$$
(11)

The Matthews correlation coefficient (MCC) is a crucial metric for evaluating the performance of binary classification models, especially in the context of imbalanced datasets. MCC values range from − 1 to + 1, with the following interpretations: +1 indicates a perfect prediction, 0 denotes a random prediction, and − 1 signifies a complete inconsistency between the prediction and the actual observation:

$$\:\text{MCC}=\frac{TP\times\:TN-FP\times\:FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}$$
(12)

where TP is the seizure sample correctly classified as seizure, FN is the seizure sample incorrectly classified as non-seizure, TN is the non-seizure sample that is correctly classified as non-seizure, and FP is the non-seizure sample incorrectly classified as seizure.

The experiment’s preprocessing was conducted using MATLAB R2021b, while the algorithm was implemented in Python using the PyTorch framework with Python version 3.7. The system ran on the Windows 10 operating system and was equipped with an Intel(R) Core i7-7700 CPU @ 3.60 GHz. A portion of the settings for the hyperparameters used in the experiment are presented in Table 5. The TUSZ dataset employed a fixed entropy regularization coefficient (α) of 0.1, whereas the SWEZ dataset employed an automatic adjustment of α to enforce the entropy constraint.

Table 5 Partial hyperparameter settings for TUSZ dataset and SWEZ dataset.
Full size table

Results

Feature selection experiment

The results of the four feature selection methods exhibited little difference, leading to the selection of six features for comparative experiments on the TUSZ dataset. In addition, a fifth method (mixture) was created by integrating common features from the four selections. The experimental results of these five methods demonstrated minimal disparity, with the Semi-JMI method showing superior effectiveness. The detailed results are presented in Table 6. The Semi-JMI feature selection method was used in all subsequent experiments.

Table 6 Performance results for the sensitivity, specificity, accuracy, and F1 score of the features selected according to the five feature selection methods.
Full size table

Scalp EEG(sEEG) dataset experiment

We conducted cross-patient experiments using a sEEG dataset. Five experiments were performed on the model using a decision tree as the base classifier, with the number of features set at 6, 9, 12, 30, and 60. The results of the experiment are depicted in Fig. 5. The figure also illustrates a notable decline in experimental outcomes when the number of features was 30 and 60, accompanied by an increase in both running time and model complexity with the increase in the number of features. Following a comprehensive evaluation of the time cost and performance metrics, it was concluded that the model achieved optimal performance with 6 features. This resulted in sensitivity, specificity, accuracy, and F1 score of 92.58%, 92.51%, 92.52%, and 75.54%, respectively.

Fig. 5
figure 5

A comparison of the sensitivity (sen), specificity (spe), accuracy (acc), and F1 score of the five feature quantities in the model based on the decision tree classifier.

Full size image

Our model decoupled model training and meta-training, thereby enabling its application to a diverse range of machine learning models. Consequently, when dealing with 6 features, we employed four distinct classifiers, that is, the k-nearest neighbor classifier (KNN), Gaussian naive bayes (GNB), decision tree (DT), and adaptive boosting (AdaBoost), as base classifiers for conducting experiments. At the conclusion of meta-training, the experiment’s EPI was set to 70 due to the longer execution time required by KNN compared with the other three methods. When the DT was employed as the base classifier, the model attained optimal performance, as illustrated in Fig. 6. The sensitivity, specificity, accuracy, F1 score, and MCC were 92.58%, 92.51%, 92.52%, 75.54%, and 0.7303, respectively. It is paramount to note that all classifier parameters used the default settings preset by the SCISKIT-LEARN package. In the case of the ensemble classifier (AdaBoost), the value of N_ESTIMATOR was set to 10.

Fig. 6
figure 6

Comparison of sensitivity (SEN), specificity (SPE), accuracy (ACC), F1 score, and Matthews correlation coefficient (MCC) of a classifier based on decision tree, k-nearest neighbor, Gaussian naive Bayes and adaptive boosting at episode = 70.

Full size image

Intracranial EEG(iEEG) dataset experiment

The iEEG dataset experiment was a patient-specific study that evaluated the sensitivity, specificity, accuracy, and F1 score of a model using a DT as the base classifier for fifteen patients. The average sensitivity of the model was 98.56%, with an average specificity of 98.82%, an average accuracy of 98.7%, and an average F1 score of 96.85%. The experiment results for each patient are illustrated in Fig. 7. The sensitivity, specificity, and accuracy for fourteen patients exceeded 95%, while their F1 score surpassed 90%. Notably, all metrics for patient 3, patient 7, patient 8, patient 10, and patient 11 achieved optimal performance. Conversely, patient 13 exhibited suboptimal outcomes, which might be attributed to a combination of frontal lobe epilepsy and an excessive number of electrode channels during channel decision fusion56. Consequently, the final prediction label was determined by combining the threshold value with the five adjacent detection results.

Fig. 7
figure 7

Performance of the respective cross-validation experiments on sensitivity, specificity, accuracy, and F1 score in fifteen SWEZ patients.

Full size image

Concurrently, the more prolonged episode is divided into two segments due to the disparate durations of each patient’s record. An additional experiment was conducted to enhance the overall detection effect, such as the 5th fold of patient 6 (see Fig. 8). The results of the 14-fold cross-validation for patient 4 are presented in Fig. 9. All indices for the 3rd and 4th folds reached 100%, indicating that Semi-JMI selected the most representative features and accelerated the convergence process of the model.

Fig. 8
figure 8

The 5-fold cross-validation result for patient 6, with the fifth fold being the one fold added by splitting the excessively long record into two parts.

Full size image
Fig. 9
figure 9

The 14-fold cross-validation result for patient 4.

Full size image

Discussion

Robustness to corrupted labels

In practice, label contamination and damage are unavoidable occurrences in the preprocessing of large raw datasets and in real-world medical applications. The absence of label data represents a significant challenge to the algorithmic process. The ps1 values were set to three distinct levels with the objective of creating semi-supervised datasets with labeled proportions of 75%, 50%, and 25% under the condition of missing completely at random (MCAR). The unlabeled data were considered to be corrupted label data, whereas the training subsets comprised labeled data with proportions of 75%, 50%, and 25%, respectively. Subsequently, these subsets were employed to assess the robustness of the algorithm. The experimental results of the GNB classifier, which served as the base classifier, are depicted in Fig. 10. The 25% training subset exhibited the worst performance, with sensitivity, specificity, F1 score, and accuracy at 0.9053, 0.9061, 0.7062, and 0.9061, respectively. Nevertheless, this outcome was deemed acceptable. The F1 score can only reach 70–75% due to the imbalance ratio of the test set approaching 7. In contrast, the sensitivity and specificity of the four datasets showed minimal disparity. The results of the 75% training subset exhibited the most pronounced imbalance, which was the reason for the positive number in the performance loss. The performance degradation of 11/12 of the three subsets was below 2.5%, while that of the 50% and 75% subsets was significantly less than 1%. This evidence demonstrated the robustness of the algorithm in labeling corruption. Furthermore, the meta-sampler effectively mitigated overfitting in the ensemble classifier by optimizing for generalized performance.

Fig. 10
figure 10

(a) Performance of 25%, 50%, 75%, and full training sets on sensitivity, specificity, accuracy, and F1 score. (b) Performance loss of 25%, 50%, 75%, and full training sets on sensitivity, specificity, accuracy, and F1 score.

Full size image

Comparisons

Table 7 presents a summary of seizure detection studies conducted in recent years using the TUSZ dataset. It demonstrates the benefits of our study and provides comprehensive information on the study years, methodologies, and performance metrics. It is important to note that these methodologies are fragment-based cross-patient experiments. Compared with 13 distinct methodologies, our algorithm demonstrated the most accurate results and the highest F1 score, ranking second and third in sensitivity and specificity, respectively. The method employed by Tsiouris et al.38 demonstrated a notable sensitivity of 93.94%. This method was designed to detect absence seizures exclusively, which resulted in the use of only absence seizure data in the patient-independent assessment. Golmohammadi et al.57 employed a deep learning method with a mixed deep structure to achieve optimal specificity; however, the sensitivity was only 30.83%, representing the most imbalanced result in the table. The results of the five methods in the recent study were all imbalanced, with our sensitivity and specificity differing by only 0.07%. This indicated the effectiveness of our method in the face of class-imbalanced data. In a related study, Abou-Abbas et al.5 employed 44 features extracted from disparate fields and subjected them to random forest analysis following feature selection. This approach yielded 94.12% sensitivity and 91.55% accuracy, which was comparable to our findings. This suggested that, in the case of the TUSZ dataset, manual feature extraction might prove to be a more effective approach than automatic feature extraction, which would entail the direct input of data into the network.

Table 7 Comparison of existing methods for detecting epileptic seizures using scalp electrical signals in TUSZ dataset.
Full size table

Table 8 presents the classification performance of this study and the four most recent algorithms on the SWEZ dataset. It was evident that the average sensitivity and average specificity in this study exhibited superior performance, at 98.56% and 98.82%, respectively, surpassing the second-place scores of 96.81% (sen, MIX + HD67) and 98.78% (spe, MIX + SVM67). Concurrently, our algorithm exhibited the most balanced performance among the five results, with a difference of only 0.26% in sensitivity and specificity. Once the optimal sampler was identified, the considerable discrepancies in feature representativeness and data volume across each fold of each patient collectively resulted in a significant variation in ensemble training latency. Consequently, the maximum latency of 7.14 s was selected as the final outcome. The average sensitivity and specificity of the four algorithms resulted from the recalculation of fifteen patients from the original text.

Table 8 Comparison of existing epileptic seizure detection methods using iEEG signals in SWEZ dataset.
Full size table

Table 8 also presents the cross-validation results for each individual patient. The algorithm demonstrated superior performance in six patients, with patient 4 diagnosed with parietal lobe epilepsy56. The sensitivity and specificity of our algorithm exceeded 96%, thereby demonstrating superior performance compared with other algorithms. The specificity of the MIX + SVM method in patient 12 was 99.54%, while the sensitivity was 90.5%. This represented an unbalanced result in comparison to the 99.31% and 98.47% reported in this study. Patient 6 and patient 16 were lower than the rest of the algorithms due to the imbalance ratio of one fold being much larger than the others, which affected the final result. The suboptimal performance of patients 13 and 1 could be attributed to the excessive number of electrode channels, which impaired the decision-making process of channel fusion, as previously discussed.

Two experiments were conducted on TUSZ and SWEZ datasets. The first was a cross-patient study to assess the model’s performance with previously unseen patient data. The second was a patient-specific investigation to develop a highly tailored model for individual patients. The results of both experiments were favorable, demonstrating the model’s capacity for generalization and personalization. The minimal difference in sensitivity and specificity indicated that the model could accurately identify both seizure and non-seizure samples. Concurrently, our algorithm exhibited a total delay of 16–18 s in the extensive TUSZ dataset after determining the optimal meta-sampler, which was sufficient for real-time seizure monitoring.

Yuzhe Yang et al.69 proposed that the availability of a greater quantity of unlabeled data reduced label bias in a semi-supervised manner, thereby significantly enhancing the performance of the final classifier. Our future objective was to identify a task-independent meta-state suitable for semi-supervised EEG data with the intention of significantly enhancing the final classification results. Concurrently, the recent study has indicated that burst energy70, an emerging engineering characteristic, exerts a substantial influence on classification performance. By distinguishing between abnormal and normal EEGs across various energy levels, accurate brain activity information can be extracted from the continuous wavelet transform scale map. This approach demonstrates significant potential in enhancing the accuracy of epilepsy recognition. In future work, this approach and other methods for addressing imbalanced data classification, such as stratified sampling, will be incorporated to further improve the accuracy of seizure detection. Besides, both Baghersalim et al.64 and Sabor et al.61 introduced electrocardiogram (ECG) signals to aid in the detection of seizures by the brain, thus providing another clear direction for future research.

Conclusion

In this study, the framework of meta-sampling in conjunction with an ensemble classifier was developed to address the issue of class imbalance between seizure and non-seizure in epileptic EEG datasets. This framework optimized the sampling strategy of the meta-sampler through the meta-training process, adaptively selected training data, and learned effective cascaded ensemble classifiers from imbalanced EEG data. The proposed method has been successfully implemented on both scalp and intracranial EEG datasets. For the TUSZ dataset, the sensitivity, specificity, and accuracy were 92.58%, 92.51%, and 92.52%, respectively. In the case of the SWEZ dataset, the average sensitivity, specificity, and accuracy were 98.56%, 98.82%, and 98.7%, respectively. A comparative analysis with existing methods demonstrated that this method exhibited superior performance in terms of sensitivity, specificity, and accuracy for both scalp and intracranial EEG datasets. Additionally, the method demonstrates robustness in the presence of label damage, as evidenced by the TUSZ dataset with 25% label loss. In future work, deep learning models will be incorporated within this framework to automatically generate EEG feature for further improvement of seizure detection.