Small traffic sign recognition method based on improved YOLOv7

Abstract

As autonomous and assisted driving technologies progress rapidly, the significance of traffic sign recognition intensifies. Currently, the detection accuracy of algorithms for traffic sign recognition remains suboptimal, particularly when identifying small traffic signs amid complex backgrounds and under inadequate lighting, leading frequently to errors in detection. This paper introduces an enhanced method for small traffic sign recognition, underpinned by an improved version of YOLOv7. Initially, The Spatial Pyramid Pooling Fast and Cross-Stage Partial Connection (SPPFCSPC) strategy was used to improve the feature extraction of small targets. Subsequently, a Shuffle Attention-CARAFE (S-CARAFE) up-sampling operator is crafted. S-CARAFE refocuses on key features within the input data, boosting the information detail and improving feature recombination. Finally, the introduction of a new Normalized Wasserstein Distance (NWD) method resolves the traditional IoU measurement’s sensitivity to small-target traffic signs. Experimental results show that the mAP@0.5 and mAP@0.5:0.9 values of the model trained on the TT100K dataset are increased by 3.48% and 2.29%, respectively. In the comparison with algorithms of a similar type, the proposed method achieved improvements of 2.61% and 2.12% in mAP@50 and mAP@50:95, respectively. Additionally, the algorithm’s improvements are validated on the small-target characteristics of the CCTSDB dataset and the sorted foreign traffic sign dataset, effectively elevating the recognition of small traffic signs across varying environments, consequently advancing the traffic sign recognition capacity of autonomous driving systems.

Introduction

With the increasing number of vehicles and the rapid development of driverless technology and intelligent driving assistance systems, there is a growing demand for accurate and rapid detection of traffic signs^1,2. The use of deep learning technologies to advance transportation has become increasingly prevalent^3,4,5. Traffic signs in actual driving scenarios usually occupy only a small part of the image, which brings a lot of challenges to traffic sign recognition when the vehicle is actually moving. Therefore, in order to reduce the possibility of accidents and improve the safety of drivers, it is of great significance to solve the problem of traffic sign recognition in the scene with complex background and insufficient light.

To enhance the detection accuracy of detectors, numerous researchers have conducted a series of studies addressing the aforementioned issues. Jiang et al.⁶ achieved higher accuracy in small object detection by introducing a context-aware local feature enhancement mechanism, which yielded promising results in marine debris recognition tasks. Zi et al.⁷ improved the YOLO framework by incorporating a channel attention mechanism, effectively addressing the challenge of detecting ocean eddies. Wang et al.⁸ developed a spatiotemporal traffic flow prediction network based on a multi-head attention mechanism, achieving remarkable performance and demonstrating the effectiveness of multi-head attention in neural networks. Similarly, Wang et al.⁹ achieved more precise traffic flow prediction by integrating multiple visual quantization features. An et al.¹⁰ achieved more accurate traffic sign recognition through the introduction of a cascaded attention mechanism.

Although progress has been made in traffic sign recognition, the recognition of small target traffic signs still faces the following three challenges:

• 1. Small target traffic signs often occupy a small space in the image, which leads to the feature information of small traffic signs is very limited, and it is easy to be disturbed by the surrounding background, resulting in the lack of feature expression ability of small traffic signs, making it difficult for detection algorithms to accurately identify them.

• 2. When the feature recombination is carried out, information may be lost or lost due to the incomplete problem of the features of small targets, which makes the reconstituted features unable to accurately represent the key information of small targets. At the same time, the background information around the small traffic sign has similar features to the small traffic sign itself, especially in dense scenes, the background information may be mixed with the features of the small target, resulting in the background interference of the features in the process of feature reorganization, thus affecting the detection and recognition accuracy of the small target traffic sign.

• 3. The overlap between the predicted boundary box and the real boundary box of the small target traffic sign is very limited, and even a small part of the offset will lead to a significant decrease in the IoU¹¹ value. This makes the traditional IoU metric very sensitive to the detection results of small targets, which can easily lead to misdetection or missing detection problems.

In order to solve the above problems, this paper proposes a small traffic sign recognition method based on improved YOLOv7¹².

• 1. A new spatial pyramid pool structure SPPFCSPC is proposed to replace SPPCSPC and multi-scale spatial pyramid pool is carried out on the input feature map to optimize the original algorithm and improve the algorithm’s receptive field and feature expression ability.

• 2. A Shuffle Attention- CARAFE up-sampling operator was designed, which introduced Shuffle Attention¹³ attention mechanism into the CARAFE¹⁴ up-sampling operator structure, and improved the up-sampling of the feature fusion layer in the model, so as to better capture the correlation and importance among features. And enhance the details of small targets to improve the accuracy and pertinence of feature recombination, so as to further improve the effect of up-sampling operation.

• 3. Aiming at the problem that the detection task of small target traffic signs has high requirements on positioning performance, an NWD¹⁵ method based on interframe distance measurement is adopted to solve the problem that traditional IoU indicators are too sensitive to small targets, and improve the performance of non-maximum suppression module and loss function.

Specifically, the main contributions of this paper are as follows:

• 1. A SPPFCSPC space pyramid pool structure is proposed to extract multi-scale features from the input feature map to improve the algorithm’s receptive field and small target traffic sign feature expression ability.

• 2. A Shuffle Attention-CARAFE up-sampling operator is designed to capture the correlation between features, enhance the details of small targets, and improve the accuracy and pertinence of feature recombination.

• 3. An NWD method of interframe distance measurement is used to solve the problem that traditional IoU metrics are too sensitive to small targets, and improve the performance of non-maximum suppression modules and loss functions.

Related work

The traditional traffic sign recognition algorithm mainly extracts and classifies the features of color, shape, edge and so on through image processing technology. A detection algorithm for training adaptive enhancement (Adaboost) classifier in HSV¹⁶ (Hue, Saturation, Value) space is proposed. This method has good robustness and high precision, but the detection speed is relatively slow. A histogram feature training support vector machine¹⁷ (SVM) for CIELab and YCbCr¹⁸ spaces is proposed, but the generalization ability of this method is weak. By considering the color and shape of traffic signs¹⁹, an intelligent traffic sign detection method is proposed. First, the image is converted into the hue subspace of the HSI color model, and specific colors are extracted. The standard LOG template is then used for edge detection on the extracted red areas. Finally, the vertices are discriminated and located, and the recognition accuracy is improved. Although the accuracy of the traditional algorithm has been improved, the detection accuracy of traffic signs still needs to be improved. In addition, due to the diversity of changes and interference of the target to be measured in the imaging, the traditional target detection algorithm usually adopts the features of manual selection, which is easy to make its robustness low. Therefore, the traditional algorithm can not well complete the traffic sign detection task which requires high precision and speed. In contrast, the object detection algorithm based on deep learning far exceeds the traditional algorithm, with higher detection accuracy and efficiency.

The object detection algorithm based on deep learning utilizes multi-layer convolutional neural network²⁰ (CNN) to gradually extract image features, thereby improving the accuracy of traffic sign detection and reducing the detection time. Common methods include R-CNN²¹, Faster R-CNN²², SSD²³, YOLOv3²⁴, YOLOv4²⁵, YOLOv5, YOLOv6²⁶, YOLOX²⁷, etc. This deep learning-based object detection algorithm has been widely used in the field of traffic sign detection.

Spatial pyramid can enhance the expression ability of features, and obtain more robust, rich and context-aware feature representation through multi-scale observation and analysis. SPP²⁸ spatial pyramid provides an effective feature extraction method through the capture of scale invariance and context information, but it also has problems of computational complexity and memory consumption, and has certain limitations for processing small target objects. However, SPP-Fast spatial pyramid provides more powerful feature expression ability through feature fusion, reduces the computational complexity and alleviates the problem of computational complexity and memory occupation, but the information beyond the receptive field is limited. SPPCSPC spatial pyramid pooling structure obtains different receptive fields through the maximum pooling structure, and divides the features into two parts, one part of which is processed by routine, the other part is processed by SPP structure, and finally the two parts are combined together, although the calculation amount is reduced to some extent. But its structure can not better extract more levels of features.

The up-sampling operation converts low-resolution images into high-resolution images, making small targets or details more clearly visible, enhancing the ability of feature recombination, and providing higher-resolution feature maps as inputs to obtain more expressive and adaptive feature representations. PixelShuffle²⁹ realizes efficient up-sampling by rearranging the input feature maps, and can also convert low-resolution feature maps into high-resolution images. However, during the sampling process of PixelShuffle, some details of small targets are likely to be lost, which may result in the quality of the generated images being inferior to other methods. Transposition convolution is a classical up-sampling method, which can realize fine pixel interpolation through learning parameters and generate high-resolution images. It has the flexibility to accommodate different up-sampling multiples, but transposed convolution introduces the problem of checkerboard artifacts³⁰, where the resulting images can appear grid-like pseudo-structures that can adversely affect the boundaries and details of small targets. DUp-sampling³¹ is a subpixel convolution method based on depth separable convolution³², which can effectively improve the resolution of images, but DUp-sampling is relatively new and its performance on some specific tasks and data sets needs more research and validation. Meta-Upscale³³ is a general upscale method that is upscale at any scale, so you can have a higher quality image with different up-sampling multiples to a certain extent. Meta-Upscale³⁴ is a method that is learned to upscale the images. However, the Meta-Upscale may not be accurate in traffic sign detection, because the details and shapes of the small target may not be accurately reconstructed, which affects the detection performance. At the same time, the Meta-Upscale model is relatively large, so more computational resources and training samples are required to upscale.

The relatively small target in the target detection task requires the localization ability of the algorithm very much. Traditional IOU metrics and improved CIOU³⁵ and GIOU³⁶, etc., are calculated based on the overlap area and union area of the bounding box. When the size of the traffic sign is small, even if there are subtle positioning errors, the value of these indicators may decrease significantly, and they are more sensitive to the positioning performance of small targets. Mean Euclidean Distance and boundary frame offset error are also commonly used to evaluate the positioning performance of small targets. Mean Euclidean distance and bounding frame offset error are intuitive metrics that can be used to measure the position difference and positioning accuracy between the target prediction box and the real labeled box. And the calculation of these indicators is relatively simple, only need to calculate the average distance or offset, easy to understand and implement. But for small target detection, there are still some problems, such as scale sensitivity, location accuracy insensitivity, threshold selection and ignoring target shape.

Although the above research methods have improved the accuracy of traffic sign recognition to a certain extent, in the real driving environment, the continuous scale change of vehicles from small targets in the distance to medium-scale targets and then to large targets in the near place, and the detection under complex background and insufficient illumination still face great challenges, and the relevant solutions need to be studied.

Theoretical analysis

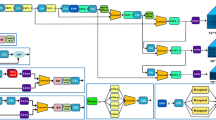
YOLOv7 is one of the latest YOLO series algorithms, which consists of a backbone network, neck, and prediction module. The backbone network includes the Convolutional, E-ELAN, MPConv and SPPCSPC modules. The E-ELAN module improves the original ELAN and enhances the learning ability of the network. SPPCSPC module avoids image distortion through multiple parallel MaxPool³⁷ operations, and solves the problem of repeated feature extraction. The MPConv module extends the receptive field of the feature layer by fusing with the feature information of normal convolution processing. The neck module adopts the path aggregation feature pyramid network³⁸ (PAFPN) structure to effectively integrate features at different levels. The prediction module uses the REP network structure to adjust the number of channels for the different scale features of PAFPN output and make the final prediction. Although YOLOv7 performs well in general target detection tasks, there are some problems of misdetection and missing detection during the detection of small target traffic signs in real driving environments such as complex background and insufficient light. Therefore, this paper makes improvements on the basis of YOLOv7 algorithm. The improved YOLOv7 network structure is shown in Fig. 1. Firstly, SPPFCSPC is used to replace SPPCSPC used in the model to optimize the training model, improve the accuracy of the algorithm, and realize more accurate target recognition. Then, S-CARAFE up-sampling operator is used to generate up-sampling kernel adaptively through input features, which can effectively increase the model’s sensory domain and make better use of the surrounding information. Finally, a new NWD method of interframe distance measurement is adopted to solve the problem that the traditional IoU measurement is too sensitive to small targets, and improve the ability to recognize traffic signs with small features in the actual traffic scene.

Fig. 1

Network structure diagram of improved YOLOv7.

SPPFCSPC

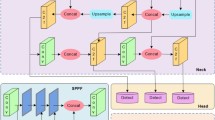
SPP(Spatial Pyramid Pooling) is a spatial pyramid pooling method that uses maximum pooling to obtain different receptive fields, enabling the algorithm to adapt to images with different resolutions. SPP-Fast (SPPF) is a new spatial pyramid structure proposed on the basis of SPP. The calculation quantity of SPPF is much smaller and the calculation speed is faster. In YOLOv7, SPPCSPC space pyramid pool is adopted. Although its performance is better than SPP-Fast, the number of parameters is increased a lot. Inspired by the idea of SPP-Fast maximum pooling structure ordering, a new optimized SPPFCSPC space pyramid pool structure is proposed by adjusting the maximum pooling module structure of SPPCSPC and rearranging the maximum pooling module.

In the parallel operation of maximum pooling of the original SPPCSPC, the feature graphs of different scales are directly connected in channel dimension after maximum pooling. Although such operation retains the features of each scale feature map, there is no direct interaction between the features of different scales, and at the same time, the model is limited to model a larger receptive field, so it may not be able to effectively capture broader context information.

The SPPFCSPC as shown in Fig. 2 divides the input feature map into blocks, then carries out maximum pooling operations within each block, and finally concatenates the results after maximum pooling in series according to the location of the original block, and carries out convolution operations.

Fig. 2

Space pyramid pool structure. (a) SPPF (b) SPPCSPC (c) SPPFCSPC.

Maximum pooling is to divide the input image into a number of matrix regions, and output a maximum value for each subregion. Its definition formula (1) is shown:

$${y_{kij}}=\mathop {\hbox{max} }\limits_{{\left( {p,q} \right) \in {\Re _{ij}}}} {x_{kpq}}$$

(1)

Where${y_{kij}}$, represents the maximum pooled output value in the matrix region ${\Re _{ij}}$related to the k-th feature map, and ${x_{kpq}}$ represents the element located at $\left( {p,q} \right)$ in the matrix region ${\Re _{ij}}$.

As shown in Fig. 3, if the input image size is 5 × 5, randomly set the size of each element value, move the window size is 2 × 2, step size is 1, carry out the first maximum pooling operation, select the maximum value to output to the next layer, and obtain the feature map size of 4 × 4. And on the basis of this feature graph, the second maximum pooling operation is carried out to obtain the feature graph with the size of 3 × 3. Finally, the third maximum pooling operation is carried out to obtain the feature graph with the size of 2 × 2. Three consecutive maximum pooling operations can obtain three different scale feature map information of 4 × 4, 3 × 3 and 2 × 2 respectively, which can enlarge the features of small targets, thus enhancing the feature extraction ability of small targets. However, according to the original parallel operation method of maximum pooling, only the feature map with size of 4 × 4 can be extracted, and the features of small target traffic signs are easily submerged in the background features.

Fig. 3

Three maximum pooling operations.

The maximum pooling of the SPPFCSPC is able to extract deeper features and integrate them into a longer feature vector, increasing the diversity of features. At the same time, feature maps of different scales can also complement and strengthen each other’s feature representation. Smaller scale feature maps can capture detailed information, while larger scale feature maps can provide broader context information, making feature expression richer. In addition, compared with SPPCSPC, SPPFCSPC can also increase the feature dimension and make the feature vector longer on the basis of keeping the number of parameters unchanged. Longer feature vector can provide more information capacity, better express the features of input data, enhance its feature expression ability and receptive field size, and improve the accuracy of the model.

S-CARAFE

In the YOLOv7 algorithm, the up-sample operation is performed using the nearest neighbor interpolation, that is, the up-sample operation. Although this method can realize the amplification of high-level feature maps in the feature pyramid network³⁹ (FPN), in the small target detection task, due to the small target size and low resolution, it lacks the required rich semantic information. The CARAFE up-sampling operator is introduced, which can match the output size of the input feature map with the original image, and realize the fusion of features of different scales. Through CARAFE up-sampling, the receptive field of the model is enlarged, which can make better use of the information around the target, improve the accuracy of small target detection, positioning accuracy and classification effect, and enhance the adaptability of the algorithm to complex scenes, and the extra parameters and calculation amount are relatively small. At the same time, the introduction of Shuffle Attention into CARAFE operator can better capture the correlation between features, enhance the details of small targets, improve the accuracy and specificity of feature recombination, and further improve the effect of up-sampling operation.

The up-sampling method of the feature fusion layer in the algorithm is improved, and the improved CARAFE operator is used to replace the up-sampling of the original algorithm. The network structure of CARAFE up-sampling module is shown in Fig. 4, which is mainly divided into two parts: prediction part and feature recombination part, as shown in Fig. 4.

Fig. 4

S-CARAFE up-sampling network structure.

• 1. Up-sampling prediction part: Firstly, the number of channels is compressed, assuming that a feature map with the shape $H \times W \times C$ is input, the number of channels is compressed to ${C_m}$ by a 1 × 1 convolution. The size of the up-sampled kernel is represented by ${k_{up}} \times {k_{up}}$, the size of the up-sampled ratio is represented by $\sigma$, the number of channels is changed from $H \times W \times {C_m}$ to ${\sigma ^2} \times k_{{up}}^{2}$ by convolution operation. Then the number of channels is expanded in the spatial dimension to obtain the up-sampled kernel of size $\sigma H \times \sigma W \times k_{{up}}^{2}$, and then the softmax normalization process is carried out, so that the weight sum of the convolution kernel is 1.

• 2. Feature recombination part: Map each position in the output feature map back to the input feature map, take the original feature map region of ${k_{up}} \times {k_{up}}$ centered on it and the predicted up-sampled kernel of the point as the point product to get the output value. Different channels in the same position share the same up-sampled kernel, and finally get the new feature map of $\sigma H \times \sigma W \times C$.

NWD

The current mainstream target detection performance evaluation metric is Average Precision (AP), which uses the IoU value between the prediction box (P) and the true box (G) to determine the accuracy of the prediction box⁴⁰. In the two images (a) and (b) in Fig. 5, it is assumed that rectangular box A is the real box and rectangular boxes B and C are the prediction boxes. When the prediction box B is translated by four pixels to get C, the IoU values between the prediction box and the real box in (a) and (b) are reduced from 0.85 to 0.00 and 0.85 to 0.65, respectively. This indicates that the IoU metric is sensitive to targets of different scales. When the target scale is very small, the attenuation rate of IoU is very fast, and when the target scale is normal, the attenuation rate of IoU is normal. Therefore, the object detection algorithm designed based on IoU is not suitable for small target detection task, because IoU is more sensitive to the sensitivity of small target or the positioning error of small target.

Fig. 5

Sensitivity analysis of IoU metrics to targets at different scales. (a) Small target (4 × 4)  (b) Ordinary target (32 × 32).

In view of the above problems, a measurement index using the distribution distance is proposed. Specifically, the method models the rectangular box as a Gaussian distribution and uses the distributed distance to measure the similarity between the rectangular boxes. First, the boundary box (bbox) is re-modeled as a two-dimensional Gaussian distribution to better fit the characteristics of the small target, converting the IoU of the predicted box and the real box into the similarity between the two distributions. Second, a new evaluation index NWD (Normalized Wasserstein Distance) is introduced to measure the similarity between the two distributions. The NWD metric can be applied to target detectors that use the IoU metric, and the IoU can be directly replaced with NWD. For small traffic signs, in most cases, they are not standard rectangles, so it is inevitable that there will be many background pixels in their bbox. In order to better describe the weights of different pixels in the bbox, the bbox is modeled as a two-dimensional Gaussian distribution, in which the weight of the center pixel of the bbox is the highest, and the weight size gradually decreases from the center to the border. Two-dimensional Gaussian distribution modeling: where bbox is a rectangle and bbox is $\left( {cx,cy,w,h} \right)$, the coordinates of the center point of the rectangular box and the width and height, formula (2) is the expression of the internal ellipse Eq. 

$$\frac{{{{\left( {x - {\mu _x}} \right)}^2}}}{{\sigma _{x}^{2}}}+\frac{{{{\left( {y - {\mu _y}} \right)}^2}}}{{\sigma _{y}^{2}}}=1$$

(2)

Where, $\left( {{\mu _x},{\mu _y}} \right)$ is the central coordinate of the ellipse in formula (2) ${\sigma _x},{\sigma _y}$ are the length of the semi-axis of x and y. Formula (3) two-dimensional Gaussian distribution probability density function.

$$f\left( {x|\mu ,\sum } \right)=\frac{{\exp \left( { - \frac{1}{2}{{\left( {x - \mu } \right)}^T}{\sum ^{ - 1}}\left( {x - \mu } \right)} \right)}}{{2\pi {{\left| \sum \right|}^{\frac{1}{2}}}}}$$

(3)

In formula (3)$x,\mu ,\sum$, respectively, mean vector and Gaussian distribution covariance matrix. $coordinate\left( {x,y} \right)$When in the numerator of formula (3)${\left( {x - \mu } \right)^{\rm T}}{\sum ^{ - 1}}\left( {x - \mu } \right)=1$, the ellipse in formula (2) is the density contour of the two-dimensional Gaussian distribution. So, as shown in expression (4), bbox $\left( {cx,cy,w,h} \right)$ can be modeled as a two-dimensional Gaussian distribution $N\left( {\mu ,\sum } \right)$.

$$N\left( {\mu ,\sum } \right)|\mu =\left( {\begin{array}{*{20}{c}} {cx} \\ {cy} \end{array}} \right),\sum =\left( {\begin{array}{*{20}{c}} {{{{w^2}} \mathord{\left/ {\vphantom {{{w^2}} 4}} \right. \kern-0pt} 4}}&0 \\ 0&{{{{h^2}} \mathord{\left/ {\vphantom {{{h^2}} 4}} \right. \kern-0pt} 4}} \end{array}} \right)$$

(4)

In addition, the similarity between the prediction box and the real box A and B can be translated into the distribution distance between the 2 Gaussian distributions. Use Wasserstein distance to calculate the distribution distance. For two Gaussian distributions and, the ${\mu _1}=N\left( {{m_1},{\sum _1}} \right)$${\mu _2}=N\left( {{m_2},{\sum _2}} \right)$. Wasserstein distance between ${\mu _1}$ and is ${\mu _2}$ represented by the expression (5) :

$$\begin{gathered} W_{2}^{2}\left( {{\mu _1},{\mu _2}} \right)=\left\| {{m_1} - {m_2}} \right\|_{2}^{2}+ \\ Tr\left( {{\sum _1}+{\sum _2} - 2{{\left( {\sum _{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}{\sum _1}\sum _{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}} \right) \\ \end{gathered}$$

(5)

$\parallel \cdot {\parallel _F}$Is the Frobenius norm, and $\parallel \cdot {\parallel _F}$ is a matrix norm defined as the sum of the absolute squares of the elements in a matrix. The $Tr\left( {{\sum _1}+{\sum _2} - 2{{\left( {\sum _{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}{\sum _1}\sum _{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}} \right)$ in formula (5) simplifies the $\left\| {\sum _{1}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} - \sum _{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}} \right\|_{F}^{2}$ form in the expression (6).

$$W_{2}^{2}\left( {{\mu _1},{\mu _2}} \right)=\left\| {{m_1} - {m_2}} \right\|_{2}^{2}+\left\| {\sum _{1}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} - \sum _{2}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}} \right\|_{F}^{2}$$

(6)

Predict box and real box are $A=\left( {c{x_a},c{y_a},{w_a},{h_a}} \right)$ and $B=\left( {c{x_b},c{y_b},{w_b},{h_b}} \right)$, and are modeled as Gaussian distribution ${N_a}$ and ${N_b}$ to further simplify the expression (6) to expression (7).

$$\begin{gathered} W_{2}^{2}\left( {{N_a},{N_b}} \right)= \\ \left\| {{{\left[ {c{x_a},cy{}_{a},\frac{{{w_a}}}{2},\frac{{{h_a}}}{2}} \right]}^T},{{\left[ {c{x_b},cy{}_{b},\frac{{{w_b}}}{2},\frac{{{h_b}}}{2}} \right]}^T}} \right\|_{2}^{2} \\ \end{gathered}$$

(7)

But $W_{2}^{2}\left( {{N_a},{N_b}} \right)$ is a distance measure and cannot be used directly as a similarity measure (i.e. values between 0 and 1 as IoU). So, using its exponential form to normalize, we get the new metric NWD:

$$NWD\left( {{N_a},{N_b}} \right)=\exp \left( { - \frac{{\sqrt {{W^2}\left( {{N_a},{N_b}} \right)} }}{C}} \right)$$

(8)

In formula (8), C is a constant, determined by the average size of the target in the data set. When NWD = 1, the two rectangular boxes overlap completely, and when NWD = 0, the distance between the two rectangular boxes does not overlap, so it has the nature of IoU to a certain extent. At the same time, it can solve the sensitivity problem of measurement index to small target scale.

Experimental verification

Experimental environment and parameter setting

Table 1 shows the basic environment and parameter Settings of the experiment, and the other parameters of the experiment remain unchanged.

Table 1 Experimental environment and parameter settings.

Data sets

In this experiment, the TT-100 K(Tsinghua-Tencent 100 K Tutorial, TT-100k)⁴¹ small traffic sign data set was experimentally verified. Meanwhile, CSUST Chinese Traffic Sign Detection Benchmark (CCTSDB)⁴² data set and collated foreign traffic sign data set to verify the universality and robustness of the improved algorithm.

TT100K is a road traffic sign data set jointly marked by Tsinghua University and Tencent Road traffic sign data set, which contains different small traffic signs. In this experiment, the data sets of the top 42 categories of entity number are sorted out for experiment.

The Chinese traffic data set CCTSDB contains 15,734 images of different sizes and large scale changes, which are divided into three categories: warning, prohibitory and mandatory.

The sorted foreign traffic sign data set is marked on the basis of street view panoramic pictures. This traffic sign data set is a single category of data set, with a total of 8820 data sets.

Figure 6 shows the styles of three data sets, among which (a) is TT100K data set, (b) is CCTSDB data set, and (c) is organized foreign data set. The red box in the Fig. 6 is a small traffic sign board.

Fig. 6

Three data set styles. (a) TT100K data set. (b) CCTSDB dataset. (c) collated foreign datasets.

Evaluation indicators

In this experiment, Precision (P), Recall (R) and mean average precision (mAP) were selected as evaluation indexes to measure the model performance. The recall rate refers to the proportion of correct predictions that are positive in all actual positive, and the precision rate refers to the proportion of correct predictions that are positive in all predictions. The calculation formula is shown in Eq. (9):

$$\left\{ \begin{gathered} R=\frac{{TP}}{{TP+FN}} \hfill \\ P=\frac{{TP}}{{TP+FP}} \hfill \\ AP=\int {PdR} \hfill \\ mAP=\frac{{\sum AP}}{N} \hfill \\ \end{gathered} \right.$$

(9)

Where, TP (True Positive) means that the correct category is judged as the correct category, FN (False Negative) means that the correct category is judged as the wrong category, FP (False Positive) means that the wrong category is judged as the correct category, The P-R curve is drawn with R as the horizontal coordinate and P as the vertical coordinate. The area surrounded by the P-R curve and the coordinate axis is called AP, and N represents the total number of categories of traffic signs.

The Frames Per Second (FPS) metric is the number of images detected per second. Generally, the larger the FPS value, the better the real-time performance of the algorithm. Generally, when the FPS value is greater than 30, it indicates that the algorithm can meet the real-time requirements of detection.

Experimental results and analysis

To verify the superiority of the proposed algorithm, a comparison experiment was conducted with mainstream target detection algorithms including Deformable DETR⁴³, DINO⁴⁴, DAMO-YOLO⁴⁸，YOLOv3, YOLOv5, YOLOv6, RFB Net⁴⁵, ScratchDet⁴⁶ and CAB Net⁴⁷ on TT100K data set. The experimental results are shown in Table 2. It can be seen that the improved model is superior to Deformable DETR, DINO, DAMO-YOLO, YOLOv3, YOLOv5 ,YOLOv6, RFB Net, ScratchDet and CAB Net al.gorithms in the detection of accuracy rate (P), recall rate (R), mAP@0.5, mAP@0.5:0.95. The accuracy rate of the improved YOLOv7 algorithm is 88.69%, the size of the recall rate is 88.41%, mAP@0.5 is 92.74%, mAP@0.5:0.95 is 72.67%. Therefore, the algorithm in this study can well improve the accuracy. The superiority of the proposed method is verified.

Table 2 Experimental results of TT-100 K dataset in mainstream model.

To further present the accuracy of the proposed model in detecting different traffic signs, Table 3 shows the specific values of various metrics across different classes. In the table, the performance of most classes is outstanding, particularly the il60 class, which achieves an impressive accuracy of 98.5%. Additionally, the recall rate for the il60 class reaches 100%, further confirming the model’s strong recognition ability for this category. On the other hand, the pl20 class exhibits relatively low accuracy, with only 78.8%, indicating potential challenges the model faces when handling this category. This discrepancy may stem from various factors, such as the difficulty of the samples in different classes, data distribution differences, or similarities between classes. Categories with high recall rates include il60 (100%) and pg (100%), indicating that the model can efficiently identify samples from these classes. The recall rate for the i2 class is 83.5%, suggesting that although the accuracy is high, there are still some false negatives (samples not correctly predicted as positive). The recall rate for the pl20 class is relatively low (67.6%), which may indicate that the samples of this category are difficult to distinguish in the dataset, leading to the model’s inability to capture all instances comprehensively. Mean Average Precision (mAP) is a commonly used evaluation metric in multi-object detection tasks, reflecting the overall performance of the model in detection tasks. The i5 class stands out with an mAP of 97.5%, indicating that the model not only achieves high precision and recall but also performs excellently in the object detection task. In contrast, the pl20 class has an mAP of 77.3%, which suggests that the object detection performance for this class is relatively inadequate.

Table 3 Experimental results of TT-100 K dataset in different classes.

Ablation experiment

In order to verify the effectiveness of the three proposed improvement methods, ablation experiments were conducted on the TT100K dataset, and the results are shown in Table 4.

Where, “√” indicates that this module is used for the design, and “×” indicates that this module is not used. Where SPPFCSPC, NWD and S-CARAFE indicate whether the improvements proposed in this paper are used. After the introduction of SPPFCSPC, mAP@0.5 and mAP@0.5:0.95 have increased by 2.24% points and 2.05% points respectively. After the introduction of S-CARAFE, mAP@0.5 and mAP@0.5:0.95 have increased by 3.12% points and 2.23% points respectively; And mAP@0.5 and mAP@0.5:0.95 increased by 3.10% points and 1.77% points respectively after the introduction of NWD. After the combination of SPPFCSPC and S-CARAFE, mAP@0.5 and mAP@0.5:0.95 increased by 3.21% points and 2.08% points respectively; Finally, when the three improvement strategies are combined, mAP@0.5 and mAP@0.5:0.95 increase by 3.48% points and 2.29% points respectively. The feasibility of the proposed scheme is further verified.

Table 4 Results of ablation experiment.

Comparison results of CARAFE up-sampling operators before and after improvement

Table 5 shows the comparison of experimental results between CARAFE and S-CARAFE. It can be seen that the recognition rate of mAP@0.5 and mAP@0.5:0.95 using S-CARAFE up-sampling operator is increased by 0.30% points and 0.03% points, respectively, compared with that of CARAFE up-sampling operator.

Table 5 Comparison results of the improved CARAFE.

Figure 7 is a graph of the changes of the improved algorithm and mAP@0.5 of the original YOLOv7 with the number of iterations on the TT100K data set. In the early stage of network training, compared with the original YOLOv7 algorithm, under the condition that the same training times were consistent, the improved algorithm achieved higher accuracy, faster promotion speed and more stable model training by mAP@0.5. Meanwhile, in the later stage of network training, when the algorithm before and after the improvement is convergent in the model, the number of training iterations of the improved algorithm is obviously much less than that of the original YOLOv7 algorithm, and the improved algorithm speeds up the model convergence speed.

Fig. 7

Improved comparison of mAP@0.5 curves before and after.

Figure 8 show the graphs of the mAP@0.5 indicators of different algorithms on the TT100K small target traffic sign dataset with the number of training iterations. It can be clearly seen that compared with other algorithms, our algorithm(SSN-YOLOv7) has higher mAP@0.5 value, faster improvement speed, and more stable model training.

Fig. 8

Comparison of the curves of mAP@0.5 with the number of iterations for different algorithms.

Figure 9 is the heat map after the small traffic sign is cropped. The original traffic sign is represented by Fig. 9 (a), Fig. 9 (b) the heat map of the original YOLOv7 algorithm, Fig. 9 (c) the output heat map after adding SPPFCSPC, Fig. 9 (d) the output heat map after adding S-CARAFE, and Fig. 9 (e) the output heat map after adding NWD. Figure 9(f) is the output heat map after adding SPPFCSPC + S-CARAFE, and Fig. 9 (g) is the output heat map of the improved algorithm in this paper.

Fig. 9

Heat map visualization results for each module of the improved algorithm. (a) Original image (b) Original YOLOv7 (c) SPPFCSPC (d) s-CARAFE (e) NWD (f) SPPFCSPC + NWD (g) Ours.

From the perspective of regional attention: with the improvement of each module, it can be seen that the highlighted area of the heat map pays more attention to the area related to the actual location of the traffic sign more accurately, and is related to the target features of the traffic sign.

From the perspective of the shape of the heat map: with the improvement of each module, the shape and distribution of the heat map can capture the edge and shape of the traffic sign more accurately.

Through the visual comparison of the features of traffic signs through the heat map, it can be concluded that with the improvement of each module, its heat map is more in line with the characteristics of the traffic sign target itself, enhancing the extraction of traffic sign feature maps, making the features of traffic signs more accurate than those extracted by the original algorithm, and verifying that the improved modules are effective in extracting the features of traffic signs.

Improved algorithm feasibility verification experiment

In order to further verify the universality and robustness of the improved algorithm, the validation was carried out on the CCTSDB traffic sign dataset and the collated foreign traffic sign dataset. Tables 6 and 7 are the experimental results verified on the CCTSDB data set and the collated foreign traffic sign data set respectively.

• 1. Experimental results are shown in Table 6: In the CCTSDB dataset of the improved YOLOv7, on the premise that the number of parameters of the improved algorithm is slightly reduced, its accuracy rate, recall rate, mAP@0.5 and mAP@0.5:0.95 are increased by 0.90, 1.16, 3.32 and 2.32% points respectively, with obvious accuracy improvement effect. The universality and robustness of the improved algorithm are verified.

• 2. The experimental results are shown in Table 7: The improved YOLOv7 in the sorted foreign traffic sign data set, the experimental results show: Under the premise of slightly reducing the number of parameters of the improved algorithm, its accuracy rate, recall rate, mAP@0.5 and mAP@0.5:0.95 increase by 3.97, 1.15, 2.44 and 1.15% points respectively. The accuracy improvement effect is obvious, which further verifies the universality and robustness of the algorithm.

Table 6 Experimental results of the improved algorithm verified on the CCTSDB dataset.

Table 7 Experimental results of the improved algorithm on sorted foreign traffic sign data sets.

Identify the results of the visualization

Figures 10, 11 and 12 are the comparison of recognition results of YOLOv7 algorithm on TT100K, CCTSDB and sorted foreign traffic sign data sets before and after the improvement. As can be seen from the figures, the visualization results includes small traffic signs under complex background and insufficient illumination.

Fig. 10

Comparison of the recognition results of the YOLOv7 algorithm before and after the improvement. (a) Original drawing (b) YOLOv7 (c) Ours.

Fig. 11

Comparison of recognition results of YOLOv7 algorithm in CCTSDB data set before and after improvement. (a) Original (b) YOLOv7 (c) Ours.

Fig. 12

Comparison of recognition results of foreign traffic sign data set organized by YOLOv7 algorithm before and after the improvement. (a) Original image (b) YOLOv7 (c) Ours.

The recognition results before and after the improvement are shown in Figs. 10, 11 and 12. Through comparison, it is found that the improved YOLOv7 algorithm can detect traffic signs well and classify traffic signs more accurately, no matter it is traffic signs in complex background or small traffic signs in under-illuminated scenes. As shown in the first row of images in Fig. 10 the detection confidence of the improved YOLOv7 algorithm in the low-light scene is higher than that of the original YOLOv7 algorithm. As shown in the second row of images in Fig. 10 although the improved algorithm before and after the improvement can detect pne type small traffic signs in the complex background, the detection confidence of the improved YOLOv7 algorithm is higher. As shown in the third row of images in Fig. 10 the original YOLOv7 algorithm failed to detect pr40 small traffic signs, but the improved YOLOv7 could detect them very well. As shown in Fig. 11, in a relatively complex background, although the algorithm before and after the improvement can detect small traffic signs, the improved YOLOv7 has a higher detection confidence. As shown in the first row of images in Fig. 12, the original YOLOv7 algorithm failed to detect traffic signs, but the improved YOLOv7 can detect them very well. In addition, the detection effect of traffic signs in the second and third rows in the dark environment in Fig. 12 is better than that of the original YOLOv7 algorithm. The visual experiment results of the improved algorithm on three traffic sign data sets at home and abroad show that the algorithm proposed in this paper has a good improvement effect on small traffic sign recognition in complex driving scenarios. It can effectively reduce the missing situation of traffic sign detection, and has a good generalization effect.

Conclusion

Aiming at the problem of low accuracy of traffic sign detection, this paper improves YOLOv7 algorithm. SPPFCSPC space pyramid pool is used to improve the expression ability of image features. The S-CARAFE lightweight up-sampling operator is introduced to improve the up-sampling of the feature fusion layer in the algorithm, so as to enlarge the receptive field of the feature map and enhance the capability of feature recombination. Finally, an NWD method based on interframe distance measurement is used to solve the problem that the traditional IoU measurement is too sensitive to small targets. Through the analysis of experimental data, it can be seen that the improved YOLOv7 verifies the feasibility of the improved algorithm on three traffic sign data sets while reducing the number of algorithm parameters, and the correct recognition rate of traffic signs has been greatly improved. At the same time, the correct recognition rate of the improved algorithm is also much higher than that of other mainstream algorithms. The algorithm proposed in this paper still needs to be improved in many aspects, and the recognition speed has great room for improvement. How to further improve the detection accuracy and speed of the model will be the next research direction.