A novel Hadamard matrix based hybrid compressive sensing technique for enhancing energy efficiency and network longevity

Abstract

Wireless Sensor Networks (WSN)-based Internet of Things (IoT) are made up of many tiny sensor nodes that are assigned specific tasks to sense, data process, communicate and control in predetermined areas. These networks are used in many different domains, including military operations, security, disaster relief, and habitat monitoring. However, there are various challenges and design issues in WSN like node deployment, routing, energy consumption, computational power, bandwidth, clustering, fault tolerance, coverage, connectivity and QoS. Such issues complicating protocol design and reducing network efficiency. While various clustering protocols exist, a critical gap still remains in effectively balancing these limitations, to optimize energy consumption, memory efficiency, data accuracy, and network longevity. To address these challenges, integrating excellent data compression and reconstruction methods with high-quality clustering algorithms can be the ideal solution. The proposed approach, NHM-HCS (Novel Hadamard Matrix-based Hybrid Compressive Sensing) introduces a collaborative method incorporating data compression, efficient cluster head selection, and optimal routing. By adopting improved versions of Particle Swarm Optimization (PSO), Grey Wolf Optimization (GWO), and novel Hadamard matrix-based hybrid compressed sensing techniques, NHM-HCS enhances the network’s lifespan and improves other performance metrics. Compared to the existing and traditional methods, the proposed NHM-HCS approach improves the network lifetime by 13%, percentage of alive nodes by 17%, residual energy by 16% and the throughput by 43%. It also reduces energy consumption by half and End-To-End delay by 39%. The simulation results also reveal that the proposed strategy can reduce energy costs while ensuring reliable performance. Furthermore, the strategy can be easily implemented with existing hardware, making it a viable option for WSNs.

Introduction

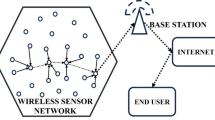
The IoT is a noteworthy technical advancement that enables practically any object to be connected to the internet. WSN-based IoT¹ are mainly utilized in numerous applications to gather network data and periodically transmit it to a central base station, which makes decisions based on the data, as shown in Fig. 1. The combination of IoT with WSNs reduces latency and has enormous potential for a variety of smart applications. When WSNs are used in healthcare settings, for instance, sensor nodes affixed to patients’ bodies gather vital information that is subsequently transferred to IoT gadgets like smartphones or Raspberry Pi. Subsequently, this data is forwarded to healthcare centers following specific communication protocols². Typically, IoT devices need more hardware resources, including energy, storage, and processing capabilities, which can restrict the lifespan of a network. Therefore, there is a critical need for efficient data compression schemes in sensor networks that minimize energy consumption during processing and communication, thereby reducing overall energy demands. This method addresses the problem of energy usage by concentrating on reducing data size before transmission and employing efficient techniques for sending data over the network to its final destination or sink³. Effective routing strategies and the use of compressed sensing are used to achieve this. Reduced data size and resource consumption are the goals of an effective compressed sensing algorithm. When compressing data, it is important to consider the characteristics of data consumers since irrelevant data may be excluded depending on the user’s capacity to rebuild and utilize it.

Fig. 1

General structure of WSN-based IoT network.

Nevertheless, most of the attention in CS-WSN research is focused on improving CS and WSN routing algorithms, frequently ignoring the real effect of lossy networks on CS data reconstruction performance. This error results from the fact that, in the CS signal-gathering procedure, the original signal X is converted into a sparse coefficient α via a sparse basis. The accuracy of the reconstructed signal Y is determined by the precision of the sparse coefficient α. Because of the sparsity of the signal vector, every non-zero compressed datum inside the sparse coefficient has a significant weight. Therefore, throughout the data reconstruction process, faults in the sparse coefficient α are magnified and harm each rebuilt signal if it contains mistakes or is lost owing to lossy network packet loss⁴. Large inaccuracies in the rebuilt data are the end outcome, and this leads to subpar network performance.

Cluster-based routing is an energy-efficient method that works by dividing sensor nodes into clusters and assigning a cluster head (CH) and cluster members (CM) to each cluster. As an aggregator, the CH gathers data from CMs in its cluster and transmits it either directly to the base station (BS) or via many CHs in a multi-hop manner⁵. At some point, the BS uses an IoT platform to send the combined data to the cloud for additional analysis. The advantages of cluster-based routing techniques include lower energy consumption, increased network longevity, and scalability. The integration of compressed sensing with routing mechanisms represents a novel approach aimed at minimizing the transmission count during data collection. This integration directly correlates with reduced energy consumption and enhanced lifetime of the WSN.

Literature survey

Nguyen et al.⁶ proposed an integrated approach that combines clustering and compressed sensing to lower power consumption and memory usage in WSNs. In order to optimize energy use, they compared several matrix architectures and adopted random Gaussian coefficients for data transmission. The potential of CS in reducing power consumption and minimizing memory usage is shown in this method. Devika et al.⁷ proposed LEACH-PWO, a hybrid algorithm that enhances the LEACH protocol in WSNs through combining Wolf Search with Particle Swarm Optimization. In terms of network lifetime and throughput, this technique overcomes standard protocols by enhancing cluster head selection and energy-efficient communication. Subramanyam et al.⁸ proposed a hybrid Grey Wolf and Crow Search Optimization (HGWCSOA-OCHS) for the ideal selection of cluster head. This strategy defeats existing optimization strategies like Firefly and Grey Wolf in terms of reducing energy usage, decreasing delay, and maintaining node lifespan.

Nigam et al.⁹ contemplated a CS-based clustering technique for efficient data compression in WSNs. Their manner decreases data transmissions by up to 60% and increases energy efficiency by up to 30% non-CS based methods. Yuan et al.¹⁰ proposed the CS-CARDG scheme, which combines CS and cluster formation with a two-level routing technique to minimize data loads in nodes. Their method remarkably enhances energy efficiency and lengthens network lifetime. Manchanta et al.¹¹ proposed an energy-efficient clustering framework (ECSCF) for WSN-based IoT, accounting node energy heterogeneity and network conditions. This method optimizes cluster head selection and data transmission in a way to outperform existing methods in network lifetime and energy consumption.

Prabha et al.¹² proposed the Improved Hierarchical Compressive Sensing (IHCS) approach, combining clustering and CS with Block Tri-Diagonal Matrices (BDM). This method minimizes energy consumption and develops data recovery accuracy, achieving 70% energy efficiency and 93% recovery rate. Aziz et al.¹³ suggested the EMCA-CS scheme, which integrates CS and routing protocols to optimize network lifetime and decrease reconstruction error. The method uses Grey Wolf-based path selection, smashing existing techniques in energy consumption and network performance. Pacharaney et al.¹⁴ proposed a data aggregation scheme for WSNs that integrates CS with spatially correlated clustering for reducing transmission costs. This method uses hexagonal topology to enhance energy efficiency and increasing network lifetime by avoiding unwanted intra-cluster communication.

Zhang et al.¹⁵ proposed a method for reconstructing heterogeneous networks by imposing CS with clustering. This approach speeds up optimization using linear programming relaxation, thus improves precision in network reconstruction. Ghaderi et al.¹⁶ proposed a strategy to analyze energy consumption in CS-based data gathering by taking different signal models. Their model, evaluated with Compressive Data Gathering (CDG) and Hybrid Compressive Sensing (HCS), improves energy savings in sensor networks. Kaur et al.¹⁷ proposed the GSTEB protocol by combining ACO with PSO for clustering and routing. This hybrid technique reduces data redundancy and congestion and considerably enhancing network lifetime compared to other methods. Ahmed et al.¹⁸ proposed a Block Sparse Bayesian Learning (BSBL) technique for recovering speech signals from limited samples. The technique, compared with ℓ1-norm minimization and achieved signal intelligibility, particularly for unstructured speech datasets.

Xue et al.¹⁹ proposed an image compression-encryption scheme integrating CS and bit-level XOR operations for security improvement. This approach improves image reconstruction quality and security over real-valued matrices, providing better performance in transmission of encrypted image. Canh et al.²⁰ suggested the Restricted Structural Random Matrix (RSRM) for compressive sensing, which improves sensing efficiency while maintaining measurement integrity. RSRM combines block-based and frame-based CS, ensuring successful reconstruction without giving up Restricted Isometry Property. Sekar et al.²¹ proposed the Compressed Tensor Completion (CTC) approach for signal reconstruction in WSNs. CTC utilizes spatio-temporal correlations and reduces energy usage by reconstructing signals at sampling rates less than Nyquist rate, overcoming existing methods in accuracy and efficiency. Li et al.²² proposed the Tail-Hadamard Product Parametrization (Tail-HPP) technique for sparse signal recovery in CS. This technique combines Hadamard product efficiency with tail-ℓ1-minimization, ensuring to be more efficient than direct solutions for sparse recovery.

The Literature review conducted above, addresses various methods combining Compressed Sensing with clustering and optimization techniques to improve energy efficiency and network lifetime in WSNs. Main approaches include hybrid algorithms (PSO-Wolf Search, ACO-PSO), clustering with compressive sensing, energy-efficient routing, and novel sensing matrices like RSRM. These techniques lower data transmissions, avoids data redundancy and optimize routes for effective energy usage. However, they may encounter challenges in scalability, complexity, and ensuring robustness in dynamic network environments. While they outperform conventional techniques in energy efficiency and lifetime, their practical implementation could need high end computational resources or specialized hardware setups. At the outset, these techniques show best ways in improving WSN performance, but still need further improvement as need grows. The comparison between various literatures cited above is given Table 1.

Table 1 Comparison between various methodologies.

Problem statement

The primary goal of this work is to develop a novel cluster-based compressed sensing technique that achieves balanced energy consumption, improved residual energy, reduced end-to-end delay, increased throughput, extended network lifetime and enhanced percentage of alive nodes that observed as gaps in previous works. To achieve this goal, we propose a novel approach called NHM-HCS (Novel Hadamard Matrix-based Compressive Sensing). This work addresses the energy, network lifetime and memory issues by selecting appropriate cluster heads and make meaningful transmission across nodes using hybridized PSO-GWO algorithms. Also, the Hadamard matrices used here will ensure the effective reconstruction of data, since it is the heart of any compressive sensing method. The computational complexity, which arises during the reconstruction of data will be reduced by using a novel and simple Hadamard matrices, that enable effective sparse recovery with reduced computations. Even though, we have collaborated various algorithms and techniques in the proposed work, carefully simplifying or removing the unnecessary co-efficient and selection of appropriate methods for signal recovery, reduces the computational complexity. In such a way, it helps the proposed approach to work effectively with reduced computational complexities, thus improves energy and memory efficiency related parameters.

Principles and methods

Energy model

The first order radio model²³ is given in Fig. 2. The energy requirements of the transmitter for delivering the $\:m$-bit message over a distance $\:l$ between a transmitter $\:{E}_{tsr}\left(m,l\right)$ and a receiver $\:{E}_{rcr}\left(m\right)$ is given in Eqs. 1 and  2 as

$$E_{{tsr}} \left( {m,l} \right) = \left\{ {\begin{array}{*{20}l} {m*E_{{tx}} + m*\varepsilon _{{fs}} *l^{2} } \hfill & {~if\;~l \le l_{o} } \hfill \\ {m*E_{{tx}} + m*\varepsilon _{{mp}} *l^{4} } \hfill & {if\;~l \ge l_{o} } \hfill \\ \end{array} } \right.$$

(1)

$$\:{l}_{o}=\sqrt{{\epsilon\:}_{fr}/{\epsilon\:}_{2r}}$$

(2)

where,

${E}_{tx}$ is the amount of energy used by electronics to transmit a bit

$\:{E}_{rx}$ is the amount of energy used by electronics to receive a bit

$\:{\epsilon\:}_{fs}$ and $\:{\epsilon\:}_{mp}$ is the energy dissipation for free-space transmission and multi-path fading

$\:{\epsilon\:}_{fr}$ and $\:{\epsilon\:}_{2r}$ indicate the free state amplifier and the two ray model parameters, respectively

$\:{l}^{2}$ and $\:{l}^{4}$ refer to transmissions over short and long distances, respectively

$\:{l}_{o}$ is the threshold distance

Fig. 2

First order radio.

The multipath model takes into account the reflection of the signals off different objects in the environment, such as the walls and floors of a building and this model is applied when $\:{l}^{2}<\:{l}_{o}.$ The free space model, on the other hand, assumes that the signals are traveling in free space, with no obstacles or reflections is applied otherwise. Equation 3 provides the expression for the energy need of the receiver, $\:{E}_{rcr}\left(m\right).$

$$\:{E}_{rcr}\left(m\right)=m*{E}_{rx}$$

(3)

Furthermore, we go over the model energy structure of a sensor network in which sensor node energy is dispersed at random. The subsequent Eq. 4 expresses the initial energy for every sensor node in total.

$${E}_{tot}=\sum\limits_{i=1}^{n}{E}_{in}\left(1+{a}_{i}\right)$$

(4)

where,

$\:n$ is the number of sensor nodes and $\:{E}_{in}\:$is the initial energy of a node.

The energy of the cluster is given in Eq. 5

$$\:{E}_{CH}=m*\frac{n}{k}*\left({E}_{el}+{E}_{ag}\right)+m*{\epsilon\:}_{2r}*{l}_{toS}^{4}$$

(5)

where,

${E}_{CH}$ is cluster head’s energy level

$n$ is node count

$k$ is cluster count

${E}_{el}$ is energy required for a bit transaction

${E}_{ag}$ is energy required for data aggregation

$m$ is data packet size in bits

${\epsilon}_{2r}$ is long-distance to BS amplification parameter

Likewise, Eq. 6 expresses the energy dissipated by nodes other than CHs.

$$\:{E}_{nCH}=m*{E}_{el}+l*{\epsilon\:}_{fr}*\:{l}_{toCH}^{2}$$

(6)

where,

$\:{\epsilon\:}_{fr}$ is short-distance to CH amplification parameter.

The distance that can be represented as both long and short lengths is found using the Eqs. 7 and 8,

$$\:{l}_{toS}^{4}=\:\frac{M}{\sqrt{2\pi\:k}}\:\:$$

(7)

$$\:{l}_{toCH}^{2}=0.765\frac{M}{2}$$

(8)

where,

$\:M$ is the dimension of the sensor field,

$\:{l}_{toCH}^{2}$ is a shorter distance to head of a cluster,

$\:{l}_{toS}^{4}$ is the longer distance to sink.

Therefore, Eqs. 9 and 10 express the energy $\:{E}_{tot}$ spent by a cluster and the network in total.

$$\:{E}_{Ctot}={E}_{CH}\left(\frac{n}{k}-1\right){E}_{nCH}\approx\:\:{E}_{CH}+\frac{n}{k}{E}_{nCH}$$

(9)

$$\:{E}_{tot}=k*{E}_{Ctot}$$

(10)

where,

$\:N{W}_{lt\:}$is the total network lifetime.

Consequently, each round’s energy consumption by the network is indicated by Eq. 11 and the number of rounds can be calculated by Eq. 12 as

$$\:{E}_{ro}=m*2*n*{E}_{el}+n*{E}_{ag}+k*{\epsilon\:}_{2r}*{l}_{toS}^{4}+n*{\epsilon\:}_{fr}*{l}_{toCH}^{2}$$

(11)

$$\:R=\:\frac{{Ec}_{tot\:}}{{E}_{ro}}$$

(12)

where,

$\:R$ is the number of rounds

$\:{Ec}_{tot\:}$ is the total energy

Particle swarm optimization(PSO) algorithm

PSO functions as a population-based technique in which a large number of particles assemble into a swarm, each of which represents a possible solution. These solutions exist in a search space and work together collaboratively. Every particle in the swarm searches for the best answer as it moves over the search region. All possible solutions are included in the search area, and the growing set of possible solutions is represented by the particle swarm. Every particle keeps track of both its own best solution and the best solution in the swarm during iterations. It modifies position and velocity, two important characteristics, according to its own experiences and those of nearby particles. While position changes take into account information about the particle’s present state, proximity to its own best solution, and the best solution for the swarm, as shown in Fig. 3, velocity adaptation reacts to prior flight experiences. The cluster continues to navigate toward favorable areas until it converges to the global optimum, which solves the optimization problem²⁴. Next, we will outline the mathematical models that are necessary to build the PSO algorithm. These models are defined by relevant parameters and equations.

Two main equations are involved in the PSO algorithm. Equation 13, also referred to as the velocity equation, specifies how each particle in the swarm updates its velocity according to its current position and the individual and global best solutions. The so-called acceleration factors, denoted by the coefficients $\:{c}_{1}$ and $\:{c}_{2}$, are trust parameters that show how much a particle trusts its surroundings (the social component) and itself (the cognitive aspect), respectively. These coefficients add randomness to the algorithm, capturing the interaction between social and cognitive actions, together with the random numbers $\:{r}_{1}$ and $\:{r}_{2}.$

$$v_{{{\text{i}}j}}^{{t + 1}} = \omega v_{{{\text{i}}j}}^{t} + c_{1} r_{{1j}}^{t} [P_{{b{\text{e}}st,i}}^{t} - x_{{ij}}^{t} ]{\text{ }} + c_{2} r_{{2j}}^{t} [G_{{best}} - x_{{ij}}^{t} ]$$

(13)

Equation 14 explains how each particle’s position is updated by taking into account the velocity that was determined in the preceding step.

$$\:{p}_{i}^{t+1}={p}_{i}^{t}+\:{v}_{i}^{t+1}$$

(14)

Fig. 3

Velocity and position updation in PSO.

Grey wolf optimization(GWO) algorithm

The social organization and hunting techniques of grey wolves in the wild served as inspiration for the development of the Grey Wolf Optimization algorithm. There is a hierarchy in this algorithm, as seen in Fig. 4, where the hunters are usually led by leaders represented by α.

Fig. 4

GWO hierarchy.

The hunting method, which includes team searches, tracking, chasing, and approaching the target, mimics the coordinated actions of wolves. They then surround and torment their prey until it stops moving. When the enclosure is small enough, the wolves that are closest to the prey—designated as β and δ—attack first, with assistance from other wolves. If the victim tries to get free, the pursuing wolves reposition the trap to guarantee that they will not let up until they are caught.

The top three search agents (α, β, and δ) in the GWO algorithm represent the greatest, second-best, and third-best individuals²⁵, respectively. The location of the prey represents the optimization problem’s global ideal solution. To start the optimization process, a set of grey wolves is randomly generated within the search space. α, β, and δ estimate the prey’s location throughout each iteration and direct other wolves to adjust their locations accordingly. The wolves keep doing this until they have surrounded and approached their prey, at which point they attack when the victim stops moving. The α, β, and δ wolves have a better awareness of possible prey places than the grey wolves. Therefore, they imitate their cooperative hunting style. They determine where the prey is in the search space, and other wolves, indicated by ω, scatter themselves randomly about the prey. As a result, ω wolves are positioned based on the integration of the top three places (α, β, and δ) into the population²⁶.

Fig. 5

Workflow of GWO.

This algorithm works on the phases as presented in Fig. 5. The prey will be encircled during the prey-encircling phase by applying the following Eqs. 15, 16, 17 and 18:

$$\:{D}_{gwo}=\left|{C}_{gwo}\times\:\:{X}_{prey}\left(t\right)-{X}_{wolf}\left(t\right)\right|$$

(15)

$$\:{X}_{wolf}\left(t+1\right)={X}_{prey}\left(t\right)-{A}_{gwo}.\:{D}_{gwo}$$

(16)

$$\:{C}_{gwo}\:=\:2\times\:{r}_{and}$$

(17)

$$\:{A}_{gwo}\:=\:2\times\:a\times\:{r}_{and}-a$$

(18)

where,

$\:t$ - the present iteration,

$$\:{A}_{gwo}\:\text{a}\text{n}\text{d}\:{C}_{gwo}\:-\:\text{c}\text{o}\text{e}\text{f}\text{f}\text{i}\text{c}\text{i}\text{e}\text{n}\text{t}\text{s},$$

$\:{X}_{prey}$ – position of prey,

$\:{X}_{wolf}$ – position of the wolf,

$\:{r}_{and}$ – random value,

$\:a$ – value linearly decreasing from 2 to 0.

The hunting phase will be governed by the following Eqs. 19, 20, 21, 22, 23, 24 and 25,

$$\:{D}_{gwo\alpha\:}=\left|{C}_{gwo1}\:\times\:\:{X}_{prey\alpha\:}\left(t\right)-{X}_{wolf}\left(t\right)\right|$$

(19)

$$\:{D}_{gwo\beta\:}=\left|{C}_{gwo2}\:\times\:\:{X}_{prey\beta\:}\left(t\right)-{X}_{wolf}\left(t\right)\right|$$

(20)

$$\:{D}_{gwo\delta\:}=\left|{C}_{gwo3}\:\times\:\:{X}_{prey\delta\:}\left(t\right)-{X}_{wolf}\left(t\right)\right|$$

(21)

$${X}_{wolf1}={X}_{prey\alpha}-{A}_{gwo1} \cdot {D}_{gwo\alpha}$$

(22)

$${X}_{wolf2}={X}_{prey\beta}-{A}_{gwo2} \cdot {D}_{gwo\beta}$$

(23)

$${X}_{wolf3}={X}_{prey\delta}-{A}_{gwo3}\cdot{D}_{gwo\delta}$$

(24)

$$\:{X}_{wolf}\left(t+1\right)=\:\frac{{X}_{wolf1}+\:{X}_{wolf2}+\:{X}_{wolf3}}{3}$$

(25)

The wolves will attack the prey during the attacking phase once it stops moving. The co-efficient $\:{A}_{gwo}$ has a value between − 1 and 1. The wolves will begin attacking the victim if the value of $\:{A}_{gwo}$ satisfies the criterion | $\:{A}_{gwo}$ | < 1²⁷.

Compressive sensing

A cutting-edge new method in data and signal processing is called compressive sensing. This broad method is used to reconstruct signals that have been sampled much below the Nyquist rate²². It can produce compression that lowers the needed bandwidth utilization of communication networks to a small portion of the original transmission needs by taking advantage of the inherent sparsity in signals. In compressive sensing, we simplify the sensing system by immediately performing a compact set of measurements. A key component of compressive sensing is the measurement matrix, which establishes the compression ratio and the original signal’s reconstructive accuracy. The steps involved in the compressive sensing technique are exhibited in Fig. 6.

Fig. 6

Compressive sensing scheme.

In general, the information signal is represented as given in Eq. 26

$$\:x=\:{\Psi\:}\theta\:$$

(26)

where,

$\:x\:$ is original signal and $\:x\:\in\:{\mathbb{R}}^{n},$ assumed as compressible and sparse,

$\:\theta\:$ – Sparse signal with k non-zero elements,

$\:{\Psi\:}$ - sparsifying matrix and $\:{\Psi\:}\:\in\:{\mathbb{R}}^{n*n},\:$

The compressed measurement vector is modeled as given in Eq. 27

$$\:y={\Phi\:}x\:=\:{\Phi\:}{\Psi\:}\theta\:=S\theta\:$$

(27)

where,

$\:y$ is the compressed measurement vector, and $\:y\:\in\:{\mathbb{R}}^{m},$

$\:{\Phi\:}$ is the sensing matrix, and $\Phi \in \mathbb{R}^{{m*n}}$ ($m^{\prime\prime}n$)

The reconstruction of the original information is obtained by the Eq. 28

$$\:\widehat{x}=\:{\Psi\:}\widehat{\theta\:}$$

(28)

The success of compressed sensing relies on two main principles²⁸:

• 1. Sparsity: The desired signal should be able to be described with a small number of basis functions or coefficients in a given domain or have a sparse representation.

• 2. Incoherence: The sparse representation of the signal should be “incoherent” with the rows of the sensing matrix. Incoherence guarantees that sufficient information is captured in the measurements for reconstruction.

Hadamard matrices

A Hadamard matrix is a n*n matrix with elements ± 1 and mutually orthogonal columns. This matrix has been widely used in signal and data recovery processing and error correction codes due to its minimal cross-correlation and maximal determinant property. In general, it is expressed in Eqs. 29, 30, 31, 32 and 33 represent the Hadamard matrices for various values of $\:k.$

$$H_{K} = ~\left( {\begin{array}{*{20}c} {H_{K} } & {H_{K} } \\ {H_{K} } & { - H_{K} } \\ \end{array} } \right)\;{\text{Where}}~ = {\text{ }}0,{\text{1}},{\text{2}},{\text{3}} \ldots ..$$

(29)

$${\text{when}}\;k = {\text{ }}0,~H_{o} = + \left( 1 \right)$$

(30)

$$\:\text{For}\:k>0,\:{H}_{K}=\:\left(\begin{array}{cc}{H}_{K-1}&\:{H}_{K-1}\\\:{H}_{K-1}&\:-{H}_{K-1}\end{array}\right)$$

(31)

$${\text{Then}}\;H_{1} = \left( {\begin{array}{*{20}c} 1 & 1 \\ 1 & { - 1} \\ \end{array} } \right)$$

(32)

Algorithm 1

CH selection

$$H_{2} = \left( {\begin{array}{*{20}l} {\quad 1} & {\quad 1} & {\quad 1} & {\quad 1} \\ {\quad 1} & {\quad - 1} & {\quad 1} & {\quad - 1} \\ {\quad 1} & {\quad 1} & {\quad - 1} & {\quad - 1} \\ {\quad 1} & {\quad - 1} & {\quad - 1} & {\quad 1} \\ \end{array} } \right)$$

(33)

The Hadamard measurement matrix is an exceptional matrix, particularly when the compression ratio is the same. It has been noted that the Hadamard matrix exhibits superior reconstruction accuracy compared to all other proposed matrices²⁹. It results from the row and column vectors of the Hadamard matrix’s orthogonal and non-linear related properties. For example, the row vectors of the matrix remain orthogonal and non-linearly related even after taking M rows out of it, which satisfies the measurement matrix properties of compress sensing. Compared with other matrices such as Gaussian, Bernoulli, Toeplitz, etc., the Hadamard measurement matrix has outstanding reconstruction accuracy, and its hardware deployment complexity is acceptable.

Algorithm 2

Hybridized methodology

Novel Hadamard matrix-based hybrid compressive sensing technique (NHM-HCS)

PSO and GWO are working together to achieve more optimal outcomes with fewer iterations. With this method, the strong points of both algorithms may be effectively combined for increased efficiency. This algorithm has several benefits, including simplicity, quick convergence³⁰, and excellent exploitation potential. Increased performance and stability with more ideal solutions are possible when the advantages of PSO work in tandem with GWO’s strong exploration capacity. GWO and PSO, however, have unique qualities.

• 1. There is a distinct search process for each of the two algorithms. In PSO, $\:{PER}_{best}$ and $\:{GLO}_{best}$ serve as the guides, while the three best grey wolves lead GWO. It follows that they are both highly exploitable. PSO’s exploration capabilities need to be improved in comparison to GWO’s. The GWO exploration approach can be applied in PSO to get rid of this obstacle.

• 2. The GWO updating equations lack velocity characteristics and have a complicated calculating method, whereas the PSO updating equations have. Consequently, the computational complexity grows.

• 3. During the search, GWO only keeps the top three results. PSO saves the velocity in addition to $\:{P}_{best}$ and $\:{G}_{best}$, as a result, PSO has a larger spatial complexity.

This research suggests a novel collaborative GWO algorithm with PSO that uses a high-level hybridization method to get over the problems addressed in the literature. First, we reduce the computational complexity in the suggested method by eliminating either the co-efficient $\:{A}_{gwo}$ or the co-efficient $\:{C}_{gwo}$. The co-efficient $\:{C}_{gwo}$ can be eliminated as given in Eqs. 34, 35 and 36. Because it has no particular influence on the outcomes, but the co-efficient $\:{A}_{gwo}$ must be retained because it manages the trade-off between exploitation and exploration capacities.

$$\:{D}_{gwo\alpha\:}=\left|\:{X}_{prey\alpha\:}\left(t\right)-{X}_{wolf}\left(t\right)\right|$$

(34)

$$\:{D}_{gwo\beta\:}=\left|\:{X}_{prey\beta\:}\left(t\right)-{X}_{wolf}\left(t\right)\right|$$

(35)

$$\:{D}_{gwo\delta\:}=\left|\:{X}_{prey\delta\:}\left(t\right)-{X}_{wolf}\left(t\right)\right|$$

(36)

Fig. 7

Flowchart of proposed methodology.

Second, by employing GWO in the first phase and PSO in the second, the suggested algorithm’s exploration capability was enhanced, as displayed in Fig. 7. Algorithm 1 explains the procedure conducted for the selection of cluster heads and algorithm 2 explains the hybridized methodology. The measurement matrix determines the precision of signal reconstruction and the acquisition of the measurement vector. In order to ensure that the measurement vector retains the essential information from the original signal, one of the core tasks of compressive sensing is to generate a measurement matrix. As a result, the development and use of compressive sensing are greatly aided by the measurement matrix design. We use a novel Hadamard matrix, as given in Eq. 37, in the suggested technique.

$$\:{\Phi\:}\left(\text{i},\text{j}\right)=\:{H}_{o},\:\:\:\:when\:i=j\:$$

(37)

where $\:{\Phi\:}\:\in\:{\mathbb{R}}^{m\times\:n},i\:\in\:\left(1,m\right),j\in\:\left(i,n\right)$

The proposed equation satisfies the Restricted Isometry Property³¹ as given in Eqs. 38,

$$\:(1-\delta\:)\parallel\:x{\parallel\:}_{2}^{2}\:\le\:\parallel\:{\Phi\:}\text{x}{\parallel\:}_{2}^{2}\le\:(1+\delta\:)\parallel\:x{\parallel\:}_{2}^{2}$$

(38)

Table 2 Specification of Simulation parameters.

Additionally, it meets the mutual coherence condition because the columns of the sparsity basis orthonormal matrix and the rows of the measurement matrix are incoherent. During this execution procedure, the cluster head uses innovative Hadamard base compressive sensing to construct its necessary measurement matrix. The sink node receives measurement values from the cluster heads. With the associated compressive sensing reconstruction algorithm, the sink node reconstructs the original signal. We examined how much energy the suggested algorithm used for node communications. The outcomes of the trial demonstrate that this strategy can successfully lower the network’s energy usage.

Experimental results and discussions

The simulation parameters³² listed in Table 2, are used to assess the performance of the suggested algorithm. The performance metrics like throughput, energy consumption, residual energy, end-to-end delay, percentage of alive nodes and network lifetime were calculated and compared with standard protocols as well as protocols suggested by other researchers, such as SFA-CHS, ABC-CHS, FCGWO-CHS, HGWCSOA-OCHS³³ for number of rounds. These strategies were selected due to that they provide numerous optimization methodologies for cluster head selection and energy efficiency, which are important in prolonging network lifetime and decreasing energy consumption over thousands of rounds. These methods also show efficient balancing of exploration and exploitation, which is crucial for dynamic, long-term network operations. The motivation is to compare these different strategies to evaluate their impact on the network’s overall endurance and performance over multiple communication rounds.

The methods like Cross layer_RSA, BiHCLR, and CL-NDRECT³⁴ chosen for number of nodes, due to their competencies at optimizing data transmission and routing across different network layers, which is essential for managing the number of nodes efficiently. They help in ensuring that energy consumption and computational overhead are reduced when dealing with varying node densities. The selection is driven by their proven capability to deal with large-scale networks effectively and minimize network traffic. The techniques like ACEAMR, AntChain, EMCBR, and IACR²⁵ accounted for simulation time, because of their relevance in optimizing routing and data compression, which directly dominates the overall simulation time. The aim was to include techniques that help minimization in end-to-end delays, improvement in throughput, and enables faster data reconstruction, all of which led to reducing the simulation time. Through the evaluation of these techniques, the comparison effectively offers insights into how each techniques impacts the simulation. Since, we have used metaheuristic algorithms, which are naturally random based, multiple number of experiments were conducted and average value of the results are given to meet our objective results.

Fig. 8

Throughput obtained from various models.

Throughput

Throughput is a measure of the amount of data that can be transferred in a given period of time. The simulation with proposed model has been conducted and results are obtained for different data sizes, different simulation times and variety of data rates. The average value rounded to nearest integer is taken as the final value of the model. From the given Fig. 8, beyond Cross layer_RSA, BiHCLR, and CL-NDRECT, the proposed technique reveals the best performance for every network configuration, ranging from 515 Kbps at 100 nodes to 845 Kbps at 1000 nodes. As the number of nodes rises, its performance increases faster than that of the other approaches, suggesting more efficient scalability. As the number of nodes rises, the suggested strategy continues to work well than competing methods by a greater margin. For instance, it outperforms other techniques by 95 Kbps at 100 nodes and by 145 Kbps at 1000 nodes. The suggested approach shows improved efficiency and efficacy in high-node situations and is noticeably better adapted to handle higher numbers of nodes. The proposed technique consistently overcomes other approaches across the whole range of nodes, while other approaches exhibit different degrees of improvement and smaller performance gaps. At the outset, the proposed technique outperforms cross layer_RSA by about 21%, BiHCLR by 11%, and CL-NDRECT by 9%, according to our evaluation of the results for up to 1000 nodes.

Energy consumption

Energy consumption is the entire amount of energy used by the CH and nodes in order to maintain successful communication. The energy model provided in Fig. 2. with per bit characteristics that transmission and reception take 5 nJ, amplification takes 40 pJ and the non-reporting nodes take 3 nJ is considered for calculating the energy consumption. The relation between energy consumption and number of nodes is depicted in Fig. 9.

Fig. 9

Energy consumption of different models for different node configurations.

As given in Fig. 9, as more nodes are added, the network’s energy consumption rises as well since the energy used by each node is accumulated together. As a result of using far fewer sensors, the compressed sensing approach included in our proposed method minimizes the energy consumption of the network. Being the most efficient, the proposed technique continuously has the lowest energy consumption. It is substantially lower than the consumption of Cross layer_RSA, BiHCLR, and CL-NDRECT, for example, starting at 2.9 mJ for 100 nodes and reaching 21.2 mJ for 1000 nodes. The given approach exhibits more effective performance growth with an increase in nodes, proving improved scalability. Compared to previous approaches, it manages large network configurations more effectively. The proposed technique is more dependable and smoother in terms of performance enhancement because, it shows a consistent and progressive gain in performance values with increasing nodes, while the other ways frequently show more abrupt increase in energy consumptions. The proposed technique consistently achieves the highest performance values across all node counts, defeating the other approaches in terms of efficiency and scalability. Our suggested solution saves 52% of the energy when compared to the cross-layer RSA algorithm, 50% when compared to BiHCLR, and 42% when compared to CL-NDRECT. The average value of per node energy consumption during each method is given Fig. 10. These values are obtained by simulating the network with 1000 nodes for the simulation duration of 25 s.

Fig. 10

Average energy consumption per node of different models for network with 1000 nodes and simulation duration of 25 s.

Residual energy

Residual energy is the quantity of energy that remains in a sensor node after it has finished its. It has an important role in maximizing network lifetime and minimizing energy consumption. The Fig. 11 shows the residual energy results as a function of simulation time. The residual energy of the network drops as computational complexity and simulation duration increase, as illustrated. This is because the network requires more energy to function when computational complexity rises, which lowers the network’s residual energy. Using a novel hybrid optimization technique that balances the characteristics of exploration, exploitation, and velocity updation, the suggested scheme lowers the computing complexity of sensor nodes. With an energy balance rate of 99.80% for 25 s and 89.10% for 150 s, the suggested approach consistently achieves the highest performance throughout all simulation times. Including ACEAMR, AntChain, EMCBR, and IACR, this plays better than all the methods mentioned. With an increase in simulation time, the residual energy decreases the least in the proposed method. For instance, the measure of the proposed technique stays greater across the range of 25 to 150 s, whereas other techniques see a notable decrease in effectiveness with respect to residual energy during this time. When compared to the other techniques, the proposed method consistently maintains better performance, suggesting improved stability over a range of simulation times.

Fig. 11

Residual energy of different models with various simulation duration.

The recommended approach continues to lead in performance at longer simulation times (e.g., 150 s), proving higher long-term efficiency than other methods whose energy reduces more significantly. The average value of residual energy is given Fig. 12. Our suggested method saves 16% of the energy over ACEAMR, 14%, 12%, and 11% on AntChain, EMCBR, and IACR, respectively.

End to end delay

The overall time needed to send a packet across a network is referred to as the end-to-end delay. The parameters like propagation delay, transmission delay and delay due queues and processing, also considered in number of iterations, then the average value is considered for results. The results generated from various models are given in Fig. 13 gives the corresponding relation between End-To-End delay and number nodes in network. It is clear from Fig. 13 that End-To-End delay increases with increase in number of nodes in network. Our suggested approach incorporates sparsity based compressive sensing scheme for minimizing node usage and hybrid optimization algorithm for appropriate node selection and routing. Thus makes our proposed approach performs well over other existing techniques taken for comparison. Across all node counts, the proposed technique consistently yields the lowest delay. For example, it excels Cross layer_RSA, BiHCLR, and CL-NDRECT, starting at just 7.4 ms for 100 nodes and very minimal of 24.1 ms for 1000 nodes.

Fig. 12

Average residual energy after simulating the network for 150 s.

Fig. 13

End-to-end delay of various models for different node configurations.

When compared to the other methods, the recommended technique operates, most efficiently. This suggests that it can handle the increasing number of nodes more effectively. The performance of the proposed method increases gradually than other approaches as the number of nodes advance. When the number of nodes increases, every strategy exhibits increase in delay, however, the proposed technique has the low rise in delay, suggesting that it manages higher node counts more efficiently with the highest amount of performance. As per the simulation results our proposed outperforms CL-NDRECT by 39%, BiHCLR by 37%, and cross layer_RSA by 35%.

Network lifetime

The sum of the remaining lifespans of all the sensor nodes that make up the network is known the network’s lifetime. The direct relationship between network lifetime and number of nodes for the simulation time of 10 s is given in Fig. 14. Reducing energy consumption is the main idea for maximizing network lifetime. Our proposed methodology, involves a novel optimization approach which eliminates unwanted co-efficients for reducing computation complexity, thus contributes for less energy consumption and increased network lifetime. The proposed technique continues the very best network lifetime values throughout all variety of node sets, 9.4 s for 200 nodes and 8.5 s for 1000 nodes, which displays advanced overall performance in network lifetime as compared to Cross layer_RSA, BiHCLR, and CL-NDRECT. The proposed technique has higher lifetime indicates the best performance in overall even the quantity of nodes increases. This shows that it handles scalability effectively, retaining pretty better overall performance degrees. The proposed technique demonstrates higher performance as compared to the alternative algorithms, which has less performance throughout specific node counts, indicating a extra strong and dependable overall performance.

Fig. 14

Network lifetime of different models for simulation time of 10 s.

The relation between network lifetime and number of nodes for the simulation duration of 50 s is given in Fig. 15. According to Fig. 15. the proposed technique overcome the other alternative techniques (Cross layer_RSA, BiHCLR, and CL-NDRECT) throughout all network configurations, indicating its superiority in dealing with growing community sizes. The proposed technique indicates a substantive development over CL-NDRECT. For example, with 200 nodes, the proposed approach defeats CL-NDRECT through significantly good network lifetime, and this benefit.

Fig. 15

Network lifetime of different models for simulation time of 50 s.

stays tremendous throughout all examined sizes. As the range of nodes will increase from 200 to 1000, the overall performance of all techniques barely decreases, however the proposed technique nonetheless keeps the very best lifetime. This shows that the proposed technique scales higher or degrades much less in comparison to others.

.

Fig. 16

Network lifetime of different models for simulation time of 100 s.

The relation between network lifetime and number of nodes for the simulation duration of 100 s is given in Fig. 16. The proposed technique has a clean margin of development over CL-NDRECT and other methods. For instance, with 200nodes, the proposed approach survives 99 s, that is better than CL-NDRECT and other methods. As the quantity of nodes will increase from 200 to 1000, all techniques display a lower in overall performance, however the proposed technique declines much less. This suggests that the proposed method keeps higher overall performance whilst the node configuration scales up. As the simulation period increases, the sensors experience a steady degradation in energy rather than rapid. Most of the time, the sensor nodes stay idle due to applied compressive sensing scheme and consume minimal energy. Even when active, they may only be operating for short periods of time, resulting in a slow, cumulative energy consumption over the simulation period. On the whole, our suggested technique offers 13% efficiency over cross layer_RSA, 9% improvement over BiHCLR, and 7% efficiency over the CL-NDRECT algorithm, according to simulation data obtained for 1000 nodes.

Percentage of alive nodes

The instantaneous measurement of the proportion of nodes that have not yet used up all of their energy is known as the “percentage of alive” nodes. The relationship between the total number of rounds and the percentage of alive nodes is depicted in Fig. 17.

Fig. 17

Percentage of alive nodes of different models against number of rounds.

In this, an increase in the number of rounds will result in a fall in the percentage of alive nodes. It makes sense that as increase in number of rounds, the node’s energy will be used more, and eventually it will run out and die. When compared with other methods, sampled at a rate less than the Nyquist rate, the suggested approach prevents or decreases the repeated use of nodes, especially cluster heads. All techniques begin 100%, the proposed technique fast starts off evolved to outperform the others, keeping a near-best overall performance while early as 200 rounds. By 600 rounds, it holds a big lead, with a 96% as compared to HGWCSOA-OCHS at 95% and others trailing behind. When compared with our technique, SFA-CHS suggests the steepest decline, with its overall performance losing to 42% through 600 rounds. The proposed technique maintains to hold advanced overall performance, scoring 80% at 800 rounds and 55% at 1000 rounds, properly in advance of the alternative methods. Other models, especially SFA-CHS and ABC-CHS, display fast degradation, with nodes losing to 24% and 30% through 800 rounds, respectively. By 1400 rounds, it nonetheless plays higher than others with 30% nodes, at the same time as maximum different models have almost collapsed, with SFA-CHS and ABC-CHS at 0. By 2000 and 2200 rounds, only the proposed technique has living nodes, indicating its advanced resilience and network lifetime.

Conclusion

For the purpose of optimizing energy in fast computing applications, this paper introduced a novel Hadamard matrix-based compressive sensing technique along with hybridized bio-inspired approaches named as NHM-HCS. By taking into account solely the non-zero values from installed sensors within a network, the suggested technique reduced the amount of transmission data. In the compressive sensing approach, we have added a novel Hadamard-based sensing matrix that is backed by sparsity to enable this feature. The hybridized optimization method demonstrated superior performance compared to other metaheuristic algorithms. It achieved a higher convergence rate and improved solution quality, making it a promising approach for solving complex optimization problems. Enhancements in network metrics like throughput, energy consumption, residual energy, network lifetime, End-To-End delay and percentage of alive nodes were made possible by our suggested algorithm. In contrast to the current and conventional techniques, the suggested NHM-HCS method enhanced the network lifetime by 13%, percentage of alive nodes by 17%, residual energy by 16% and throughput by 43%. Additionally, it cuts down on end-to-end delays by 39% and energy consumption by half. Future enhancements include, optimize the framework to adapt in all network conditions as the current algorithm struggles to perform well in few conditions, a large number of nodes with various energy requirements will be carried out to compare the effectiveness of the suggested approach with other algorithms inspired by nature and addition of security features will enhance the system further. Additionally, since it is conceivable for nodes with higher energy to run out of power and cease operating on the network, research should concentrate on finding a solution to this problem.