Improved optimization based on parrot’s chaotic optimizer for solving complex problems in engineering and medical image segmentation

Abstract

Metaheuristics, which are general-purpose algorithms, are commonly used to solve complex optimization problems. These algorithms manipulate multiple potential solutions to converge on the optimum, balancing the exploration and exploitation phases. A recent algorithm, the Parrot Optimizer (PO), is inspired by the behavior of domestic parrots to improve the diversity of solutions. However, while promising, the PO may encounter difficulties such as convergence to sub-optimal solutions or slow convergence speed. This paper proposes an improvement to the PO algorithm by integrating chaotic maps to solve complex optimization problems. The improved algorithm, called Chaotic Parrot Optimizer (CPO), is characterized by a better ability to avoid local minima and reach globally optimal solutions thanks to a dynamic diversification strategy based on chaotic maps. The effectiveness of the CPO algorithm has been rigorously evaluated through in-depth statistical analysis, using 23 benchmark functions as well as IEEE CEC 2019 and CEC 2020 benchmarks, covering a wide range of optimization challenges. The results show that CPO outperforms not only the original PO algorithm, but also six recent metaheuristics in terms of convergence speed and solution quality. In addition, it has been successfully applied to three complex engineering illustrating its ability to solve real-world, multi-constraint problems. Its integration with Kapur entropy also enabled precise segmentation of medical images, underlining its strong potential for critical biomedical applications. The CPO source code will be available on the Github account: adil.sayyouri@etu.uae.ac.ma after acceptance.

Introduction

Optimization is a vibrant and continually evolving field that intersects with various disciplines such as engineering, logistics, operations management, economics, biology, medicine, and the environment. It plays a crucial role in addressing the growing demands of artificial intelligence, machine learning, and computing, where the main objective is to enhance effectiveness and reduce costs^1,2,3.

Metaheuristics are general-purpose algorithms specifically designed to solve difficult optimization issues. They work by gradually getting closer to the optimal solution by adjusting one or more viable solutions^4,5. Their iterative approaches consist of gradually improving initial solutions that are often imperfect, adjusting their parameters until a predetermined condition is met. This condition can be based on the elapsed time, the iterations number, or the accomplishment of a certain level of precision^6,7,8. The capacity of these algorithms to effectively handle a variety of real-world optimization issues sets them apart⁹, often marked by complex nonlinearity and multimodality¹⁰. Their success relies on a fine balance between two crucial phases: the exploration phase, which uses randomization to traverse the entire solution space, and the exploitation phase, which refines solutions by focusing on promising specific regions^10,11.

There are two basic groups into which metaheuristics fall. The initial category comprises algorithms that concentrate on the iterative enhancement of a solitary answer, like Simulated Annealing¹¹, which replicates the cooling procedure of materials to escape local minima and the Taboo method¹² which uses a memory to avoid revisiting the same solutions. The second category brings together algorithms which simultaneously explore a set of solutions such as genetic algorithms^13,14 are inspired by the mechanisms of natural selection, Particle Swarm Optimization (PSO)¹⁵ mimics the group behavior of fish or birds, while the Bee Colony Algorithm (ABC)¹⁶ restricts the bees’ ability to forage. By allowing for a more thorough investigation of the solution space, these parallel techniques raise the likelihood of discovering ideal or nearly ideal solutions.

There are four primary categories into which metaheuristic algorithms can be further classified: (i) Evolutionary algorithms, including genetic algorithms (GA), which draw inspiration from biological processes of evolution like natural selection and mutation¹³ and Ebola Optimization Search Algorithm (EOSA)¹⁷. (ii) Algorithms inspired by human behavior that attempt to reproduce human social behaviors to solve complex problems such as the Running City Game Optimizer (RCGO)¹⁸, Teaching Learning Based Optimization (TLBO)¹⁹, the Exchange Market Algorithm (EMA)²⁰, and Harmonic Search Optimization (ORH)²¹ are examples of algorithms used for optimization. Additionally, physics-based algorithms, which emulate physical laws and phenomena to navigate the solution space, include the Gravitational Search Algorithm (GSA)²², the Special Relativity Search (SRS)²³, and the Kepler Optimization Algorithm (KOA)²⁴. (iv) Inspired by the collective behavior of animals and insects, swarm-based algorithms use individual collaboration and communication to identify optimal solutions, like PSO¹⁵, Siberian Tiger Optimization (STO)²⁵, the Orca Optimization Algorithm (OOA)²⁶ and the Remora Optimization Algorithm (ROA)²⁷.

Recent work on optimization algorithms, including hybrid and improved versions of the Moth Flame Optimizer (MFO) and Whale Optimization Algorithm (WOA), has shown significant advances²⁸. These variants incorporate strategies such as dynamic opposed learning²⁹, arithmetic and geometric averaging³⁰, Fibonacci search³¹, and mutualism mechanisms³², thus improving robustness, accuracy, and exploration capability in global, multidimensional and multi-objective optimization problems³³. These approaches have been successfully applied to a variety of fields, such as medical image segmentation (COVID-19 CT images) and the resolution of complex engineering problems, demonstrating their effectiveness and relevance to current challenges^34,35.

Recently, an innovative swarm-based metaheuristic optimization algorithm named Parrot Optimizer (PO) was introduced, which is inspired by the behaviors of domestic parrots Pyrrhura Molinae when searching for food, staying, communication and fear of strangers. In this algorithm, each Parrot adopts one of these behaviors randomly at each iteration, which increases diversity within the population unlike conventional metaheuristic algorithms, which distinguish between the stages of exploration and exploitation³⁶.

However, although the PO algorithm performs well, it has certain limitations, such as premature convergence and limited exploration of the search space. To address these shortcomings, researchers have proposed integrating chaos theory, a mathematical discipline that analyzes the complex behavior of dynamic systems sensitive to initial conditions. This approach has been successfully applied in various contexts, including the hybridization of chaos theory with the Dragonfly Algorithm (DA) to maximize robot spatial coverage³⁷, and chaos control for theoretical and practical applications³⁸. Additionally, parameter optimization using Meixner functions for signal and image analysis through the Arithmetic Optimization Algorithm (AOA) has shown promising results³⁹. Other works include a whale optimization algorithm combined with a quasi-opposition-based chaotic mechanism for global optimization problems⁴⁰, and chaotic game optimization to solve complex mathematical and engineering problems^41,42. The Archimedes algorithm has also been improved using chaotic dynamics for real-world engineering problems and signal feature extraction⁴³, while a binary horse herd optimization algorithm integrates chaotic mechanisms for feature selection⁴⁴. These studies highlight the effectiveness of chaos theory in enhancing metaheuristic algorithms for a wide range of complex applications.

Accordingly, we introduce the Chaotic Parrot Optimizer (CPO), an innovative fusion of the standard Parrot algorithm (PO) with various chaotic maps to increase the variety of solutions and the search space’s capacity for exploration. This hybrid approach takes advantage of the unpredictability and sensitivity to initial conditions of chaotic systems to improve the optimization process, aiming to overcome the limitations of conventional methods through enhanced exploration and exploitation of Parrot’s four behaviors. To assess the effectiveness of the ten CPO variants, we tested them on twenty-three fixed-dimension test functions, including unimodal, multimodal and complex multimodal functions, as well as on the CEC 2019 and CEC 2020 benchmarks, in addition to three distinct real-world problems⁴⁵. This evaluation began with a comparison between their performance and that of the original Parrot algorithm. Having identified the best-performing variant of the CPO, we set it against six others recently developed metaheuristic algorithms, namely Gray Wolf Optimizer (GWO)⁴⁶, Whale Optimization Algorithm (WOA)⁴⁷, Gazelle Optimization Algorithm (GOA)⁴⁸, Sine Cosine Algorithm (SCA)⁴⁹, COOT natural bird (COOT)⁵⁰ and Polar Lights Optimizer (PLO)⁵¹.

Table 1 provides a comparison of metaheuristics and their application domains, highlighting the algorithms selected for our experiments. These algorithms were chosen for their relevance and representativeness in the field of metaheuristics. They cover various paradigms and methodologies, reflecting the latest advances in the field. This selection provides a solid basis for positioning our proposed algorithm CPO in various optimization contexts, guaranteeing a rigorous and balanced comparison. This enables us to assess the robustness and performance of CPO against widely recognized approaches.

Table 1 Comparison of metaheuristics and their fields of application.

Finally, we tested the capability of our method on three concrete engineering design problems with specific constraints: the tension-compression spring problem⁵², the welded beam problem⁵³ and the pressure vessel problem⁵⁴. In addition, we have integrated it with Kapur entropy to achieve accurate segmentation of medical images.

The main contributions of this manuscript are as follows:

• Introduction of the CPO algorithm, combining 10 chaotic maps with the PO algorithm to improve the diversity and accuracy of solutions by avoiding the pitfalls of local minima.

• Performance evaluation of the ten CPO variants on 23 test functions, as well as on CEC 2019 and CEC 2020 benchmarks.

• Validation of CPO on three engineering problems to demonstrate its optimization capabilities in real-life contexts.

• Segmentation of medical images using a combination of CPO and Kapur entropy.

The structure of this document is as follows: First, the original version of the Parrot optimization algorithm is shown in “Standard Parrot optimizer (PO)”. “Chaotic maps” presents the ten chaotic maps that will be used to improve the PO algorithm. “The proposed Chaotic-Parrot Optimization algorithm (CPO)” provides an in-depth explanation of the CPO algorithm that we propose in this work. “Simulation results and discussion” evaluates the performance of the CPO algorithm on a benchmark set consisting of twenty-three functions, the CEC2019 and CEC2020 functions, three real engineering problems and a medical image segmentation problem, while comparing the CPO algorithm to other recent metaheuristic algorithms. The conclusion is given in “Conclusion” along with recommendations for further study directions.

Standard parrot optimizer (PO)

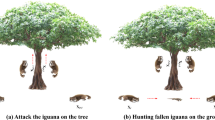
The Parrot Optimization (PO) algorithm draws inspiration from the social behavior and feeding techniques observed in domesticated Pyrrhura Molinae parrots³⁶. It combines the four behaviors of foraging, staying, communicating, and fearing strangers (Fig. 1) to solve complex optimization problems. In the initial phase the potential solutions, represented by the positions of the parrots in a search space, are randomly generated. Then, through successive iterations, the parrots adjust their positions based on several factors, such as the quality of neighboring solutions, communication with other individuals, and their tendency to avoid regions of the search space associated with less promising solutions. This approach allows PO to converge to optimal or near-optimal solutions in a relatively short time, making it a valuable tool in various fields, including engineering, data science, and optimization of complex systems. A detailed explanation of the main PO steps is given in the following section:

Fig. 1

The four behaviors of a domestic parrot Pyrrhura Molinae. The parrot illustrations shown in this figure were generated using the ChatGPT artificial intelligence tool and organized using version 25.0.3 of the Draw.io platform (https://www.drawio.com).

Population initialization

For a large population N and a maximum number of iterations $Max\_iter$, the initialization of PO in a search space defined by lower bounds ${l_b}$ and upper bounds ${u_b}$ is expressed by Eq. (1) :

$$X_{i}^{0}={l_b}+rand(0,1) \times ({u_b} - {l_b})$$

(1)

with $X_{i}^{0}$ signifying the starting point of the ith Pyrrhura Molinae and $rand(0,1)$ representing a random number in the interval [0, 1].

Foraging behavior

In the PO algorithm’s foraging phase, the parrots determine the food’s approximate location mostly by looking at it or by taking their owner’s position into account. They then proceed in the direction of this place. Therefore, the displacement of their position is represented by the subsequent Equation:

$$X_{i}^{{t+1}}=(X_{i}^{t} - {X_{best}}) \times Levy(\dim )+rand(0,1) \times {(1 - \frac{t}{{Max\_iter}})^{\frac{{2t}}{{Max\_iter}}}} \times X_{{mean}}^{t}$$

(2)

with:

$X_{i}^{t}$: indicates current location.

$X_{i}^{{t+1}}$: indicates the location of the upcoming update.

$X_{{mean}}^{t}$: indicates the present population’s average situation.

${X_{best}}$: designates the best position found from initialization to the current position.

$Levy(\dim )$: The host’s current position is represented by the Levy distribution, which is used to simulate the flight movements of parrots.

t : indicates the count of iterations underway.

The first term in Eq. (2) $(X_{i}^{t} - {X_{best}}) \times Levy(\dim )$ represents the Parrot’s movement based on its position relative to the owner. while the second term

$rand(0,1) \times {(1 - \frac{t}{{Max\_iter}})^{\frac{{2t}}{{Max\_iter}}}} \times X_{{mean}}^{t}$

shows an assessment of the population’s overall location to further improve the direction toward feeding, taking into account the average position of the current swarm, noted $X_{{mean}}^{t}$, is calculated using the formula presented in Eq. (3)

$$X_{{mean}}^{t}=\frac{1}{N}\sum\nolimits_{{k=1}}^{N} {X_{k}^{t}}$$

(3)

The Levy distribution for $\gamma =1,5$ is calculated by Eq. (4)

$$Levy(\dim )=\frac{{\mu \times \sigma }}{{{{\left| \upsilon \right|}^{\frac{1}{\gamma }}}}};{\text{ with }}\left\{ \begin{gathered} \mu \sim N(0,\dim ) \hfill \\ \upsilon \sim N(0,\dim ) \hfill \\ \end{gathered} \right.{\text{ and }}\sigma \sim {\left[ {\frac{{\Gamma (1+\gamma ) \times \sin (\frac{{\pi \gamma }}{2})}}{{\Gamma (\frac{{1+\gamma }}{2}) \times \gamma \times {2^{\frac{{1+\gamma }}{2}}}}}} \right]^{\gamma +1}}$$

(4)

Staying behavior

Winging to its gregarious disposition, the Pyrrhura Molinae takes up a resting posture that primarily entails abrupt leaps to any area of its owner’s body, where it stays still for a while. The following describes this dynamic:

$$X_{i}^{{t+1}}=X_{i}^{t}+{X_{best}} \times Levy(\dim )+rand(0,1) \times ones(1,\dim )$$

(5)

with:

$ones(1,\dim )$: denotes the dimension vector.

${X_{best}} \times Levy(\dim )$: designates flight to host.

$rand(0,1) \times ones(1,\dim )$: symbolizes the process of haphazardly pausing on a certain area of the host’s body.

Communication behavior

Close communication throughout their communities is a defining characteristic of the highly sociable Pyrrhura Molinae parrot species. There are two components to this communication pattern: flying in the direction of the flock and communicating without flying. The mean position of the current population is utilized to represent the flock center, and these two behaviors are believed to occur with equal probability for optimization purposes. The following is a description of this procedure:

$$X_{i}^{{t+1}}=\left\{ {\,\begin{array}{*{20}{c}} {0.2 \times rand(0,1) \times (1 - \frac{t}{{Max\_iter}}) \times (X_{i}^{t} - X_{{mean}}^{t}),}&{P \leqslant 0.5} \\ {0.2 \times rand(0,1) \times \exp ( - \frac{t}{{rand(0,1) \times Max\_iter}}),}&{P \geqslant 0.5} \end{array}} \right.$$

(6)

The mechanism by which an individual joins a group of parrots to commence communication is explained in the first half of the equation, and the procedure by which an individual immediately flies away after communicating is described in the second portion. In the interval [0, 1], both alternative actions are determined by a randomly generated probability value P.

Fear of strangers’ behavior

Pyrrhura Molinae parrots are no different from other birds in that they are naturally wary of strangers. An explanation of their actions, which include avoiding unfamiliar people and running to their owners for safety, is provided below:

$$\begin{gathered} X_{i}^{{t+1}}=X_{i}^{t}+rand(0,1) \times \cos \left( {\frac{{0.5\pi t}}{{Max\_iter}}} \right) \times \left( {{X_{best}} - X_{i}^{t}} \right) \hfill \\ {\text{ }} - \cos \left( {rand(0,1) \times \pi } \right) \times \mathop {\left( {\frac{t}{{Max\_iter}}} \right)}\nolimits^{{\frac{2}{{Max\_iter}}}} \times \left( {X_{i}^{t} - {X_{best}}} \right) \hfill \\ \end{gathered}$$

(7)

recognizing that $\cos (rand(0,1) \times \pi ) \times {(\frac{t}{{Max\_iter}})^{\frac{2}{{Max\_iter}}}} \times (X_{i}^{t} - {X_{best}})$ depicts the process of moving away from unknown people and $ran(0,1) \times \cos (0.5\pi \times \frac{t}{{Max\_iter}}) \times ({X_{best}} - X_{i}^{t})$ shows the reorientation procedure to fly to the owner.

The PO algorithm uses uniformly distributed random variables to initialize and update the position. However, this approach often leads to local optima, which reduces the efficiency of the search. In order to solve this issue, we describe the values of previously allocated randomly generated sequences produced by chaotic systems. The application of chaotic maps in the initialization phase improves the quality of the initial population, making it easier to obtain global optima. In addition, chaotic position updating for all four behaviors optimizes the algorithm’s search performance.

Chaotic maps

Lately, chaos theory is widely applied in many disciplines, including physics, mathematics, computer security, encryption, and signal and image coding. In fact, dynamic behavior, sensitivity to beginning conditions, and unpredictable nature of chaotic systems are their defining characteristics. Several optimization algorithms, such as Moth Flame Optimization (MFO)⁵⁵, Firefly Algorithm (FA)⁵⁶, Artificial Bee Colony (ABC)⁵⁷, Biogeography-Based Optimization (BBO)⁵⁸, Particle Swarm Optimization (PSO)⁵⁹, and GWO⁴⁶, have been able to incorporate them more easily thanks to these particular traits. Chaotic maps and metaheuristic algorithms together have demonstrated efficacy in resolving challenging optimization issues by enhancing the quality of solutions and removing roadblocks to local optima. As seen in Table 2; Fig. 2, we provide 10 popular one-dimensional chaotic maps in the literature in this part. These maps can be utilized to create chaotic sequences that can be used to enhance and alter optimization techniques. It should be noted that the starting values are selected at random within the interval [0, 1], or in accordance with the chaotic maps’ domain of definition. The incorporation of these dynamic data is essential for enhancing an optimization algorithm’s search performance, particularly the PO algorithm, which permits the exploration of a greater range of potential solutions and, consequently, a controlled increase in search efficiency. This novel method expands on the range of solutions that have been researched, providing exciting potential to optimize difficult situations.

Table 2 Chaotic maps.

Fig. 2

Chaotic map values.

Chaotic maps add another level of complexity to the PO algorithm’s search process by including a controlled random exploration element. This can prevent local optimum stagnation and promote a more varied search space exploration. The parrots’ search paths can be varied due to the chaotic qualities of the maps they employ, which can enhance their capacity to discover globally optimal solutions to a variety of engineering issues and enable a more effective study of the solution space.

The proposed chaotic-parrot optimization algorithm (CPO)

In this section, we propose an improved chaos-based OP algorithm called Chaos-Parrot Optimization Algorithm (CPO), in which the chaotic sequences generated by the various chaotic maps are used to avoid local optima, increase the probability of finding the global optimum in a limited number of iterations, and improve the search for global solutions to various problems. There are several benefits of using chaotic variables in the search for the best solutions as compared to a random method. More specifically, we exploit the ergodic characteristics of chaotic maps to circumvent local minima and increase search efficiency. As a result, the chaos-based approach shows to be a creative, incredibly effective, and outstanding optimization technique. For each behavior, both initialization and position updating will be performed using the 10 chaotic maps given in Table 2. Algorithm 1 provides specifics for each step in the CPO algorithm.

Chaotic maps for population initialization

The original PO algorithm uses a method of generating initial solutions based on uniformly distributed sequences of random numbers. However, in our algorithm (CPO), we have substituted this standard random generation $rand(0,1)$with an innovative technique utilizing chaotic sequences (CCi). The following formula is applied to initialize the position using these chaotic sequences:

$$X_{i}^{0}={l_b}+C{C_i} \times ({u_b} - {l_b})$$

(8)

where CCi stands for a chaotic sequence produced by a particular chaotic map.

Chaotic maps for updating the position of the four behaviors

At each iteration, every member of the PO algorithm population randomly chooses one of these four behaviors, unlike traditional metaheuristic algorithms, which alternate between separate phases of exploration and exploitation. The position update for all four behaviors in the standard PO algorithm is performed according to Eqs. (2), (5), (6), and (7). It is worth noting that the values of $rand(0,1)$, required in these equations, are generally generated at random in the interval [0, 1]. Nevertheless, we make a crucial advancement within the CPO method with every iteration: we define these parameters using chaotic maps rather than random values. This novel method creates new avenues for enhancing the algorithm’s performance and identifying the best answers. Consequently, the position update in our algorithm is defined as follows:

• a. Foraging behavior.

$$X_{i}^{{t+1}}=(X_{i}^{t} - {X_{best}}) \times Levy(\dim )+C{C_i} \times {(1 - \frac{t}{{Max\_iter}})^{\frac{{2t}}{{Max\_iter}}}} \times X_{{mean}}^{t}$$

(9)

• b. Staying behavior.

$$X_{i}^{{t+1}}=X_{i}^{t}+{X_{best}} \times Levy(\dim )+C{C_i} \times ones(1,\dim )$$

(10)

• c. Communication behavior.

$$X_{i}^{{t+1}}=\left\{ {\begin{array}{*{20}{c}} {0.2 \times C{C_i} \times (1 - \frac{t}{{Max\_iter}}) \times (X_{i}^{t} - X_{{mean}}^{t}),\,\,P \leqslant 0.5} \\ {0.2 \times C{C_i} \times \exp ( - \frac{t}{{rand(0,1) \times Max\_iter}}),\,\,P \geqslant 0.5} \end{array}} \right.$$

(11)

• d. Fear of strangers behavior.

$$\begin{gathered} X_{i}^{{t+1}}=X_{i}^{t}+C{C_i} \times \cos (0.5\pi \times \frac{t}{{Maxiter}}) \times ({X_{best}} - X_{i}^{t}) - \hfill \\ \cos (C{C_i} \times \pi ) \times {(\frac{t}{{Max\_iter}})^{\frac{2}{{Max\_iter}}}} \times (X_{i}^{t} - {X_{best}}) \hfill \\ \end{gathered}$$

(12)

Figure 3 displays the proposed CPO algorithm’s flowchart.

Fig. 3

CPO algorithm flowchart.

Algorithm 1. The pseudo-code for the CPO algorithm.

Complexity of the CPO algorithm’s computation

Given that the standard PO algorithm primarily relies on three key elements: solution initialization, fitness function computation, and solution updating, this section analyzes the computational complexity of the proposed CPO algorithm. Specifically, assuming there are N solutions, the computational cost of initializing all of them, including chaotic sequences, is determined by the complexity C of generating a chaotic sequence.

Update processes present additional complexity due to the integration of chaotic sequences into foraging and resting behaviors. These behaviors add O(C) complexity for each chaotic sequence generation, which occurs for every solution and dimension during the update process. The overall complexity of the updating process therefore includes:

$$O(CPO)=O\left( {T \times N} \right)+O\left( {T \times N \times dim} \right)+O\left( {T \times N \times logN} \right)+O\left( {T \times N \times dim \times 2C} \right)$$

(13)

Note that the O(T×N×dim×2 C) term reflects the additional computations of chaotic sequences during foraging and resting behaviors.

Then, by combining these components, the overall computational complexity of the CPO, including the chaotic sequences, is as follows:

$$O\left( {CPO} \right)=O\left( {N \times \left( {1+C} \right)} \right)+O\left( {T \times N \times \left( {1+dim+logN+2 \times dim \times C} \right)} \right)$$

(14)

This new complexity reflects the additional operations introduced by the integration of chaotic sequences in the initialization, foraging and resting behaviors of the algorithm.

Simulation results and discussion

In order to evaluate the effectiveness of the CPO algorithm presented in this work, we selected 23 test functions including unimodal, multimodal and fixed-dimension multimodal functions, as well as functions from the CEC 2019 and CEC 2020 packages, in addition to four real-world problems: a tension and compression spring design problem, a pressure vessel problem, a welded beam design problem and a medical image segmentation problem. By using this wide range of examples and tasks, we hope to demonstrate the adaptability and efficiency of the CPO algorithm in resolving a variety of optimization and practical issues. It should be noted that there are 10 different variants of the suggested algorithm CPO, each based on a different chaotic map as follows: The chebyshev map (CPO-1), the circle map (CPO-2), the mouse map (CPO-3), the iterative map (CPO-4), the logistic map (CPO-5), the piecewise map (CPO-6), the sine map (CPO-7), the singer map (CPO-8), the sinusoidal map (CPO-9), and the tent map (CPO-10). The performance of the proposed CPO algorithm is then compared with that of six other well-known algorithms that have already been published in the literature as part of a comparative analysis. These include GWO⁴⁶, WOA⁴⁷, GOA⁴⁸, SCA⁴⁹, COOT⁵⁰ and PLO⁵¹. We evaluated and contrasted the results of the suggested CPO algorithm for the different chaotic maps and on the different optimization problems in order to assess the caliber of the solutions produced. Two performance measures were used in this respect: mean and standard deviation (STD). All experiments were carried out with MATLAB R2021a on a Windows 11-64-bit PC equipped with an Intel(R) Core (TM) i7-1165G7 processor running at 2.8 GHz and 16 GB RAM.

Reference functions

This section compares the results of the proposed CPO algorithm with those of the standard PO algorithm in order to evaluate the algorithm’s performance. Twenty-three reference functions (F1–F23) presented in Table 3 are tested with a population size of 30 and a number of iterations up to 1000.

Table 3 Test functions for multimodal, unimodal, and multimodal with fixed dimensions.

Tables 4 and 5, and 6 show the mean and standard deviation (STD) findings for the PO and suggested CPO algorithms in comparison. The ten suggested algorithms’ convergence performances are also depicted in Figs. 4 and 5, and 6.

For the ten chaotic maps, the standard algorithm PO and the suggested CPO algorithm yielded solutions for twenty-three functions. The means and standard deviations of these solutions are displayed in Tables 4 and 5, and 6. In light of the fact that the CPO-10 algorithm, which incorporates the chaotic Tent map, stands out for its exceptional accuracy in comparison to the other algorithms and solidifies its position as the best option for the optimization of a variety of multidimensional problems, the analysis of these results demonstrates that the CPO algorithms outperform the PO algorithm for all tested functions (F1–F23). These findings show that the use of chaotic maps in optimization algorithms significantly increases their effectiveness in avoiding local optima and achieving quick convergence and accurate solutions. Being aware that convergence is a crucial factor in determining how well algorithms perform in achieving the global optimum. The convergence curves of the test functions employing the PO and suggested CPO algorithms are shown in Figs. 4 and 5, and 6. These graphs show how the CPO algorithms are remarkably good at locating the best answers for the twenty-three reference functions. They differ from the standard PO algorithm in their reliability, stability and ability to explore search areas in depth. What’s more, compared with the PO algorithm, they reach optimal solutions much more quickly.

In addition, we also observe that some CPO and PO algorithms converge very quickly for some functions: F9 and F11 in less than 50 iterations, F14, F17, F21, F22 and F16 in less than 100 iterations, and F10 and F23 in less than 100 iterations. These findings demonstrate that the performance of these algorithms is greatly enhanced by the inclusion of chaotic maps in metaheuristic optimization, leading to increased efficiency and a discernible decrease in the amount of time required to find optimal solutions.

Table 4 Findings on unimodal reference functions (F1 to F7).

Table 5 Outcomes for multimodal reference functions (F8 to F13).

Table 6 Outcomes on multimodal benchmark functions with fixed dimensions (F14 to F23).

From the ranking of proposed algorithms based on ten chaotic maps (see Tables 4, 5 and 6), we can see that the choice of chaotic map 10 proved to be the most efficient compared with the other chaotic maps used in our study. After a rigorous comparative analysis carried out in Table 7, it became clear that the chaotic map 10 offers an optimal combination of diversity and convergence, two essential criteria for an efficient search for global solutions. In particular, the Tent chaotic map delivered more stable and accurate results on the variety of benchmarks of the 23 functions, reinforcing its robustness and reliability in various application scenarios. This choice is therefore based on a thorough evaluation of its overall performance, making the CPO algorithm the preferred choice for our optimization algorithm for external comparison with other metaheuristic algorithms and for other applications.

Table 7 Ranking result for all algorithms.

Fig. 4

Unimodal function convergence curves (F1–F7).

Fig. 5

Multimodal function convergence curves (F8–F13).

Fig. 6

Convergence curves for fixed-dimension multimodal functions (F14–F23).

Diversity test

Population diversity is an essential criterion for optimization algorithms, as it determines their ability to efficiently explore the search space and escape the traps of local optima.

Figure 7 illustrates the comparison of diversity between the CPO-10 and PO algorithms on several test functions (F1, F4, F8, F12, F16, F18), highlighting marked differences in their performance. CPO-10 stands out for its enhanced stability and optimized diversity management, enabling balanced exploration and efficient use of the search space. This behavior is particularly visible in functions F1, F4 and F18, where CPO-10 manages to maintain stable diversity, essential for avoiding local optima while guaranteeing reliable convergence. Conversely, PO is generally more diverse, especially for functions F8 and F12, but with large variations reflecting a more extensive, but less coherent, exploration. These fluctuations may limit its ability to converge rapidly on optimal solutions. In conclusion, CPO-10 stands out as the best-performing algorithm in this context, thanks to its optimal balance between exploration and stability, whereas PO, although offering broader exploration, seems less suited to problems requiring robust convergence. These results confirm that integrating chaotic maps, such as Tent’s map, into the optimization process not only improves performance in terms of fitness, but also the algorithm’s ability to preserve high diversity within the population.

Fig. 7

Convergence diversity comparison between CPO-10 and PO algorithms on different test functions.

Tests on CEC 2019 and CEC 2020 functions

In this section, we present the results of the comparison between the CPO algorithm, incorporating ten chaotic maps, and the PO algorithm, applied to the CEC 2019 and CEC 2020 test functions⁵⁹. Tables 8 and 9 provide a description of the reference functions chosen for this comparison.

Table 8 CEC 2019 benchmark functions.

Table 9 CEC 2020 benchmark functions.

Table 10 shows the means and standard deviations of the results obtained by the PO algorithm and the proposed CPO algorithm. The data reveal that the CPO algorithms perform significantly better than the PO algorithm on the CEC2019 test functions. In particular, the CPO-10 algorithm stands out for its accuracy and consistency, reaching rank 1 six times, making it an optimal solution for multidimensional optimization. In addition, the CPO-3 and CPO-5 algorithms performed exceptionally well on specific functions, reinforcing the overall superiority of the CPO algorithms. Finally, these results highlight that the integration of chaotic maps into the PO algorithm significantly improves its performance, enhancing its ability to avoid local optima, accelerate convergence and deliver accurate solutions.

Table 10 Results of CEC 2019 functions.

Table 11 summarizes the performance of the PO algorithm and the proposed CPO algorithms, presenting the means and standard deviations obtained on the CEC2020 test functions. The results unambiguously demonstrate the superiority of CPO algorithms over PO, both in terms of solution accuracy and result stability. Among them, the CPO-10 algorithm particularly stood out, achieving rank 1 eight times, making it the solution of choice for multidimensional optimization thanks to its remarkable consistency and ability to produce accurate solutions. In addition, the CPO-6 and CPO-9 algorithms also stand out for their solid performance on a variety of functions, highlighting their versatility and robustness in the face of diverse optimization problems. These observations underline the significant contribution of the chaotic maps integrated into CPO algorithms, which significantly improve their ability to avoid local optima, a major challenge in the optimization of complex functions. Unlike PO, which struggles on certain functions, CPO algorithms succeed in accelerating convergence while maintaining a balance between exploration and exploitation of search spaces. This mechanism for integrating chaotic maps promotes superior performance, both in terms of convergence speed and accuracy of final solutions, making CPO algorithms particularly well-suited to complex multidimensional environments. These results testify to the striking evolution of modern metaheuristic approaches, where the use of chaotic elements is proving to be an effective strategy for tackling the challenges posed by global optimization.

Table 11 Results of CEC 2020 functions.

External comparison with other metaheuristic optimization algorithms

After validating the performance of the proposed CPO algorithm for optimizing various reference functions and the CEC2019 and CEC2020 benchmark functions, we proceed with a comprehensive comparison between the CPO algorithm and six recent optimization algorithms: GWO⁴⁶, WOA⁴⁷, GOA⁴⁸, SCA⁴⁹, COOT⁵⁰ and PLO⁵¹. The detailed control parameters of these algorithms are presented in Table 12. The evaluation focuses on the performance of the CPO-10 algorithm applied to various complex optimization problems to assess the quality of the solutions produced. Two main metrics will be used for this analysis: the mean, which reflects the overall accuracy of the solutions obtained, and the standard deviation (STD), which evaluates the stability and robustness of the results. This comparison aims to demonstrate the superiority of the CPO-10 algorithm in terms of accuracy, convergence, and its ability to solve multidimensional problems in complex optimization environments.

Table 12 Parameter values for the algorithms used for $N=30$and $Max\_iter=1000$

We ran tests on a sample of nine functions, including unimodal, multimodal, and multimodal with fixed dimension types, to compare the Tent chaotic map-based CPO-10 algorithm with other metaheuristic optimization algorithms including GWO, WOA, GOA, SCA, COOT and PLO. With a population size of 30, the maximum number of evaluations was set at 500 iterations. Table 8 presents the comparison’s findings, including each algorithm’s mean and standard deviation. Furthermore, Fig. 8 shows the assessment of the convergence behavior of every method in resolving the different problems.

Table 13 clearly shows that the CPO-10 algorithm outperforms all the others for optimizing any type of function. Convergence curves in Fig. 8 further demonstrate how quickly CPO-10 converges in comparison to other algorithms across all cases. While other algorithms find it difficult to enhance the quality of solutions, even after multiple exploratory stages, the suggested CPO-10 approach exhibits impressive convergence from the very first search rounds. These outcomes highlight the advantages of the CPO-10 algorithm, whose chaotic initialization method dramatically speeds up the beginning stages of the search. Moreover, CPO-10 increases the likelihood of avoiding local optimal solutions significantly, which facilitates the search for global optimal solutions.

Table 13 Results of comparison with other algorithms for functions F1; F6; F7; F10; F12; F13; F15; F16 and F18.

Fig. 8

Convergence curves of all algorithms for functions F1; F6; F7; F10; F12; F13; F15; F16 and F18.

Optimization of real-world problems

This section assesses the optimization performance of the suggested CPO10 algorithm using three actual engineering design issues. These issues include pressure vessel design, welded beam construction, and tension-compression spring design. To tackle each of these challenges, which are all subject to certain limitations, an external penalty mechanism must be used. For a population of thirty, 1000 iterations are the maximum number of times any problem may be solved. A comparison of the suggested CPO10 algorithm with other optimization methods found in the literature includes GWO⁴⁶, WOA⁴⁷, GOA⁴⁸, SCA⁴⁹, COOT⁵⁰ and PLO⁵¹.

Problem with tension compression spring design

The goal of the problem of designing tension/compression springs is to create a spring with the lowest possible weight⁵². Some of the restrictions of this minimization problem are depicted schematically in Fig. 9, including breaking stress, ripple frequency, and minimum deviation. The wire diameter (d) (x₁), average coil diameter (D) (x₂), and number of active turns (N) (x₃) are the three choice variables in the tension/compression spring problem. Appendix 1 provides a mathematical formulation of this topic. Table 14 displays the comparison findings for this problem. The optimal cost and decision-making factors for the tension compression spring design problem are displayed in this table. Figure 10 illustrates the higher performance of the CPO10 algorithm over the standard PO algorithm and the other competing algorithms mentioned above, based on a review of the literature and testing results. The decision factors provide a thorough analysis of the best results produced by each algorithm.

Fig. 9

Design problem for a tension-compression spring. This model was created using version 25.0.3 of the Draw.io platform (https://www.drawio.com).

Table 14 Results of comparison for the tension compression spring design issue.

Fig. 10

Convergence curves for the tension compression spring design problem.

Design problem for welded beams

The main objective of the welded beam design problem is to create a beam at the lowest possible cost while complying with specific constraints⁵³. Figure 11 illustrates a welded beam design where beam A is connected to element B by a welding process. This design problem comprises five non-linear inequality constraints and four decision variables. The design parameters are weld thickness h (x₁), weld joint length l (x₂), element width t (x₃) and element thickness b (x₄). The mathematical formulation of this problem is detailed in Appendix 2.

Table 15 shows the results obtained when optimizing the welded beam design problem, including best cost and relevant decision variables, using the CPO10 algorithm as well as those of other algorithms as shown in Fig. 12. The test results show that the CPO10 algorithm performs significantly better than the standard PO and the other comparison algorithms in terms of the efficiency of optimizing the design cost of welded beams while complying with the specified constraints.

Fig. 11

Welded Beam Design Problem created using version 25.0.3 of the Draw.io platform (https://www.drawio.com).

Table 15 Comparison results of the welded beam design problem.

Fig. 12

Convergence curves for the welded beam design problem.

Pressure vessel problem

The main objective of this problem is to optimize vessel design, material utilization and welding costs⁵³. The objective function is formulated using four variables: shell thickness (x₁), head thickness (x₂), inner radius (x₃) and length (x₄), without taking the vessel height into account. This problem has four constraints that must be respected. Figure 13 illustrates the schematic structure of the pressure vessel design problem. The mathematical representation of this problem is detailed in Appendix 3.

Table 16 shows the best obtained cost and decision variables relevant to the pressure vessel problem, using the CPO10 algorithm as well as those suggested by other researchers (see Fig. 14). Examination of the results reveals that the CPO10 algorithm delivers superior performance compared with the standard PO algorithm and other competing methods. These results demonstrate the increased effectiveness of the CPO10 method in cost optimization for pressure vessel design.

Fig. 13

The design of pressure vessel problem. created using version 25.0.3 of the Draw.io platform (https://www.drawio.com).

Table 16 Comparison findings for the pressure vessel issue.

Fig. 14

Convergence curves for the pressure vessel problem.

Application of CPO in the medical field

Image-based medical data systems are attracting growing interest due to their essential influence on improving diagnostic accuracy, developing therapeutic plans and improving all-encompassing patient care in the field of medical management. Thus, it is crucial that the optimizer can play an essential role in optimizing solutions to medical problems. In this section, we examine how the CPO algorithm is used in medical applications, highlighting its enhancement capabilities for solving medical image segmentation problems.

Segmentation of medical images

The effective method of segmenting an image into distinct sections using several thresholds is called multi-threshold image segmentation (MTIS)⁶⁰. With respect to photos with multiple objects or discontinuous fluctuations in color and light power, MTIS provides an effective method as opposed to standard binary segmentation. It uses a set of criteria to assess pixel intensity to affect them in various areas. Even though MTIS calculation is straightforward, traditional techniques may overlook spatial information, which increases the risk of segmentation mistakes, especially when objects are small in relation to the image⁶¹. We propose an MTIS paradigm to handle this dilemma. Non-local mean filtering reduces noise in images, allowing for more precise segmentation. Using 2D histograms and Kapur entropy makes it easier to identify locations and set thresholds that maximize relevant data⁶⁰. The CPO algorithm makes it possible to find optimal thresholds quickly, which lowers computational expenses while first, the input image is converted to grayscale, and noise is then reduced using non-local average filtering⁶². Next, a two-dimensional histogram is built, and the information content is assessed for different threshold combinations using Kapur entropy⁶¹. The goal is to choose thresholds that promote information retention by maximizing entropy. Metaheuristic methods are utilized to do this. The picture is sliced using the optimal thresholds, which are then determined, to provide a finely tuned segmented image.

It is essential to select suitable image data to validate the methods, which requires a thorough evaluation of several essential elements. Six medical images extracted from the Radiopedia database⁶³ were used in this section (see Fig. 15). To illustrate how MTIS works, a flow chart is shown in Fig. 16. The aim was to evaluate CPO segmentation results on various images, considering that each image presents a specific challenge in terms of selecting the optimal segmentation threshold.

Segmentation tests were carried out on images with two threshold levels: 3 thresholds for low-dimensional scenarios and 7 thresholds for high-dimensional scenarios. These segmentation levels were used to assess the algorithms’ ability to handle optimization problems of increasing complexity. Each test was run over 1000 iterations with a population of 30 individuals and repeated independently 10 times to minimize random interference and ensure reliability of results. The main objective of these tests was to maximize entropy, an essential criterion for identifying the thresholds that best preserve the original data and guarantee accurate segmentation.

Once the optimum thresholds had been determined, they were applied to segment the images, producing precisely calibrated results. The performance of the proposed algorithm (CPO) was compared with that of six well-established algorithms, namely GWO, WOA, SCA, GOA, COOT and Polar lights optimizer (PLO)⁵¹. Tables 17 and 18 summarize this comparison, illustrating the performance obtained for image segmentation with 3 and 7 thresholds, respectively.

Fig. 15

Original and segmented images.

Fig. 16

Flowchart of the proposed segmentation method using the CPO algorithm.

It can be clearly seen that for a low number of thresholds 3, the CPO algorithm achieves the highest PSNR value (10.8690), indicating that it better preserves image quality compared to other methods. It also achieves the highest values for SSIM (0.3400) and FSIM (0.5547) compared with the other algorithms. Since both SSIM and FSIM are indicators of perceived image quality⁵⁴, it can be stated that the evaluation results are statistically consistent with those of the researchers. This highlights the effectiveness of the CPO algorithm in preserving structural detail and similarity between segmented and original images. However, for a high number of thresholds 7, the proposed CPO algorithm returns superior values for the parameters PSNR, SSIM and FSIM, which are 13.9959, 0.3971 and 0.6143 respectively, and outperforms the other methods with the exception of PSNR, which comes in second after CPO with a small difference.

Table 17 Comparison results of the CPO algorithm and other algorithms with 3-threshold image segmentation.

Table 18 Comparison results of the CPO algorithm and other algorithms with 7-threshold image segmentation.

Conclusion

In this paper, we have proposed an improved version of the PO algorithm, called CPO, incorporating chaotic maps to solve complex optimization problems. CPO stands out for its ability to avoid local minima and reach global optimal solutions thanks to a dynamic diversification strategy based on these chaotic maps. To evaluate its effectiveness, we carried out extensive statistical analyses on a set of twenty-three test functions. Experimental results show that CPO outperforms not only the original PO, but also five other recent optimization algorithms, in terms of convergence speed and solution quality. In addition, CPO has been successfully applied to three complex engineering problems and to a medical image segmentation problem, confirming its robustness and practical effectiveness. In the future, we plan to extend its use to other areas of optimization, including multi-criteria optimization with conflicting objectives. We also plan to develop and evaluate binary and multi-objective variants of CPO to solve even more complex optimization problems in practical contexts.

Despite its performance, there are several limitations that need to be considered. Parameter sensitivity and the computational complexity associated with chaotic maps can pose challenges, especially for real-time applications or on large datasets. Furthermore, although CPO outperforms many metaheuristics, it has not been compared to modern approaches such as deep neural networks. Finally, its applicability to more diverse contexts remain to be explored. These limitations underline the potential and value of our approach, while opening interesting prospects for future improvements.