Intelligent evaluation of coal mine solid filling effect using fuzzy logic and improved D-S evidence theory

Abstract

Addressing the inherent fuzziness and uncertainty in filling outcomes, this paper proposes a novel method for evaluating the effectiveness of solid filling operations in coal mines by integrating Interval Type-2 Fuzzy Logic Systems (IT2FLS) with an improved Dempster-Shafer (D-S) evidence theory. Initially, local data fusion is conducted using IT2FLS-Adam, where interval type-2 fuzzy sets are employed to fuzzify input features, and the Adam optimizer is utilized for parameter optimization. This allows for preliminary judgments on filling effects from various perspectives based on local features. To overcome the limitations of local fusion, an improved D-S evidence theory is adopted, which effectively handles conflicting evidence by incorporating the Wasserstein distance and Deng entropy to combine the judgments from local features, achieving global data fusion. Experimental results demonstrate that the proposed method attains a remarkable accuracy of 92.9% in global fusion tasks, surpassing traditional methods. This study provides a data fusion framework for filling workfaces, integrating multi-sensor data and addressing the complexities and uncertainties associated with filling processes, thereby making a significant contribution to the intelligent monitoring and management of coal mine filling operations.

Introduction

To mitigate the environmental issues arising from coal mining and enhance coal extraction rates, solid waste filling mining technology has emerged¹. This technique involves injecting solid filling materials into mined-out areas during the extraction process, thereby providing support for the roof of the mined-out space², which prevents surface subsidence and reduces the environmental impact of coal mining³. As demands for filling efficiency and safety continue to rise, precision and automation in solid filling mining have become new development directions for this technology⁴. For precision and automated filling operations, comprehensive and accurate acquisition of the filling work face status is fundamental, while real-time evaluation of filling performance is crucial⁵.

The effectiveness of solid filling operations refers to the ability of the compacted fill material formed during the filling process to provide effective support for the roof of the mined-out area, thereby preventing ground subsidence^6,7. To accurately predict the impact of waste filling mining on dynamic surface settlement and to assess the damage caused by mining activities, Zhu et al. developed a dynamic settlement model using Knothe time function⁸. Xu Kai and others analyzed the relationship between equivalent mining height and fill density in the context of solid filling and comprehensive mining principles, further investigating how fill density and mining height influence surface settlement⁹. Huang Yanli used numerical simulations to analyze the effect of fill density on strata movement control and surface subsidence, proposing that maintaining a fill density of 15% keeps surface subsidence within acceptable limits¹⁰. JiaZ studied the influence of fill width on stability, suggesting that increasing fill width can enhance overall stability and improve filling efficiency¹¹. However, most recent studies have only analyzed individual indicators affecting the mechanical properties of fill materials, and the standards in filling operations have not been addressed in relation to the ecological impact assessment following completion of filling work. Thus, the focus of these studies has been on the protective role of filling operations in the environment, leaving a gap in the ability to make real-time judgments about filling operation effectiveness during the filling mining process.

In practical filling operations, it is challenging to establish clear boundary conditions to assess whether the filling work meets standards. Consequently, quantifying and evaluating filling effectiveness based solely on precise sensor outputs is difficult. Fuzzy logic systems, however, can describe filling work faces influenced by multiple factors. By applying fuzzification to the various factors affecting filling effectiveness and normalizing them into semantic expressions, fuzzy logic reasoning can facilitate the information fusion of heterogeneous sensors, ultimately providing a quantitative description of filling effectiveness through defuzzification¹².

In recent years, fuzzy logic systems have garnered significant attention for their ability to handle uncertainty and imprecision. Type-1 Fuzzy Logic Systems (T1FLS) have been widely applied in fields such as data classification, decision support, and control optimization within various engineering and complex systems. For instance, Hagras et al. proposed an adaptive fuzzy logic control system tailored for dynamic environments. This system enhanced the stability and robustness of control mechanisms in nonlinear dynamic settings by optimizing the fuzzy rule base in real time¹³. Despite demonstrating the potential of fuzzy logic systems in dynamic applications, the scalability of its rule base remains a notable challenge as the number of input variables increases. Wu and Mendel conducted an in-depth investigation into the key differences between T1FLS and Interval Type-2 Fuzzy Logic Systems (IT2FLS), establishing that IT2FLS outperforms T1FLS in highly uncertain situations¹⁴. However, their study did not adequately address the efficient construction of fuzzy rule bases adaptable to varying scenarios, particularly in tasks involving multi-source data fusion. Montazeri-Gh and Yazdani combined IT2FLS with deep learning for fault diagnosis in complex industrial equipment, achieving high diagnostic accuracy through the optimization of fuzzy rule parameters¹⁵. Nevertheless, this approach relied heavily on large-scale labeled datasets and underutilized the interpretability of fuzzy logic, thereby diminishing model transparency.

In recent years, scholars have explored integrating theories such as Intuitionistic Fuzzy Sets (IFSs), Fuzzy Soft Sets (FSSs), Multi-Fuzzy N-Soft Sets (MFNSS), and Weighted Hesitant Bipolar Fuzzy Soft Sets (WHBFSS) with fuzzy logic systems, leading to innovative methodologies. For example, Das et al. introduced Intuitionistic Fuzzy Parameterized Multi-Fuzzy N-Soft Sets (IFPIMFNSS) and Hesitant N-Soft Sets (IFPHNSS), which significantly enhanced group decision models in expressing uncertainty and handling imprecision¹⁶. Additionally, a fuzzy multi-criteria decision-making model (FMCDM) was developed to tackle the complexity of urban river water quality assessment, effectively integrating multi-source judgment information and improving evaluation accuracy¹⁷.

In the domain of decision support, Das et al. proposed an improved adjustable group decision-making method (GDMM) to address the limitations of Mohammed-Azam GDMM in group decision-making problems (GDMPs) based on fuzzy soft sets (FSSs)¹⁸. Furthermore, they defined and operationalized WHBFSS, incorporating operators such as the root mean square difference and weighted score matrix to create a flexible and robust decision-making method (DMM). This approach substantially enhanced the applicability and efficiency of decision-making in complex scenarios¹⁹. They also developed a decision model based on fuzzy-parameterized intuitionistic fuzzy soft multiset (p-sets), overcoming the limitations of traditional fuzzy soft sets in multi-decision-maker evaluations and providing greater expressiveness and practical value for real-world group decision problems²⁰.

Despite these advancements in optimizing and extending fuzzy logic systems, traditional approaches still face several limitations: 1. Complexity of Rule Base Generation: Traditional fuzzy logic systems rely on manually designed rule bases, where the number of rules grows exponentially with the input dimensions, leading to significant computational burdens²¹. 2. Single-Source Design: Existing methods are often tailored for single data sources, rendering them ineffective at integrating data from multiple sensors, which limits their applicability in real-time decision-making²². 3. Limitations in Handling Conflicting Evidence: While IT2FLS excels in managing imprecision, it struggles to achieve global judgments independently when faced with conflicting evidence, necessitating more efficient data fusion mechanisms¹⁴.

Numerous factors influence the effectiveness of filling operations²³. However, when the input variables in a fuzzy logic system become excessive, the system’s structure can become overly complex, complicating parameter tuning¹⁵. To address this, the factors affecting filling effectiveness can be categorized into several relatively independent groups, allowing for the establishment of multiple fuzzy logic systems that assess filling effectiveness from different perspectives. Yet, each fuzzy logic system is only capable of evaluating filling effectiveness locally, and discrepancies may arise among the results of these systems. This necessitates an effective decision-level fusion method to reconcile the judgment outcomes. Dempster-Shafer (D-S) evidence theory can be employed to merge independent pieces of evidence based on their confidence levels, yielding a comprehensive global assessment that integrates the results from various local sensors. Consequently, it has been widely applied in multi-level data fusion²⁴. One significant advantage of D-S evidence theory in merging independent evidence is that it does not require prior knowledge, but this can also lead to inefficiencies when handling highly conflicting evidence²⁵. As a result, numerous researchers have focused on improving D-S evidence theory in the context of conflict. Current enhancement methods can generally be classified into two categories: modifying the combination rules directly and weighting evidence before combining.

Some researchers argue that the traditional combination rules of D-S evidence theory are flawed, leading to significantly erroneous and counterintuitive results when faced with conflicting evidence, thus necessitating improvements to these rules. Smets has modified the D-S evidence combination rules based on the open-world assumption, which posits that if a statement has not been explicitly defined as true or false within the system, it cannot be assumed to be false. This approach permits trust functions to be assigned to conflicting evidence²⁴. Voorbraak focused exclusively on single-element propositions, utilizing Bayesian approximation methods to transform hypotheses containing multiple elements into single-element hypotheses, thereby reducing computational complexity and circumventing situations involving conflicting evidence²⁶. Yager introduced a novel combination rule to address issues related to conflicting evidence. Unlike traditional rules, this new combination rule allocates the total trust conflict across all elements using a normalization factor $K$, rather than solely distributing it to the focal elements²⁷. However, altering the combination rules may compromise beneficial computational properties, such as commutativity and associativity, thereby increasing computational time and potentially failing to eliminate counterintuitive results caused by erroneous original evidence.

Conversely, some researchers opt to preprocess evidence before combination to avoid counterintuitive outcomes. Murphy proposed and demonstrated the effectiveness of evidence preprocessing methods²⁸. Deng considered evidence distance to determine the weights of evidence²⁹. Zhang derived evidence weights based on cosine theory³⁰. Yuan proposed a method for modifying evidence weights based on information quantity³¹. Xiao and Song optimized the calculation of evidence weights based on different measures of evidence distribution^32,33. These methods not only address issues related to merging conflicting evidence but also avoid the complications associated with modifying combination rules.

Based on the above analysis, traditional Dempster-Shafer (D-S) evidence combination theory exhibits the following limitations: 1. The conventional Dempster combination rule may yield counterintuitive results when handling highly conflicting evidence, potentially leading to outcomes that deviate from actual scenarios. 2. While the D-S theory is sensitive to evidence uncertainty, it lacks effective tools to quantify and balance the uncertainty between pieces of evidence. 3. In multi-sensor scenarios, the computational complexity of D-S theory grows exponentially, restricting its applicability in real-time systems. Additionally, traditional fuzzy logic systems typically rely on manually designed rule bases, where complexity increases exponentially with the dimensionality of input variables. Furthermore, these systems are often limited to single data sources and struggle to achieve global integration of multidimensional features in multi-sensor data fusion contexts.

To address these shortcomings, this paper proposes a novel fusion method combining Interval Type-2 Fuzzy Logic Systems (IT2FLS) with an improved D-S evidence combination theory. The proposed approach addresses gaps in existing research through the following enhancements: 1. Leveraging the Adam optimization algorithm from deep learning frameworks to adaptively adjust fuzzy rule parameters, significantly improving the efficiency and adaptability of rule generation. 2. Utilizing fuzzy logic systems for local fusion of multi-source data, followed by D-S evidence theory for global decision-making, thereby enhancing the model’s performance in real-time decision-making scenarios. 3. Integrating the improved D-S evidence combination theory with Wasserstein distance and Deng entropy, improving its adaptability to highly conflicting and uncertain data.

The remainder of this article is structured as follows. Initially, an analysis of the factors influencing the efficiency of the filling operation is conducted. Subsequently, recommended methodologies for assessing the effectiveness of the fill are presented. This is followed by a presentation and examination of the experimental results. Lastly, a comprehensive summary of the entire article is provided.

Analysis of factors affecting filling effects

To assess the effectiveness of filling operations, it is essential to analyze the features that influence this effectiveness and to determine how to position sensors in the filling work face to perceive these features in real time. The primary objective of solid fill with gangue is to insert filling materials into the mined-out area, allowing the filling materials to provide support to the roof of the mined-out space, restrict rock layer movement, and prevent roof collapse. Ultimately, this process aims to keep the subsidence of the roof and surface within acceptable limits³⁴. Therefore, the effectiveness of filling operations is fundamentally based on the supportive capacity of the dense fill formed during the operation³⁵. Before analyzing the factors that influence filling effectiveness, it is crucial to examine the load-bearing and supportive process of the fill body on the roof.

As illustrated in Fig.1, the load-bearing support process of the fill body is depicted. Prior to coal mining, the coal seam and surrounding rock layers are in a state of stress equilibrium. Once the working face begins to mine deeper coal seams, the roof of the mined-out area loses the supportive capacity provided by the coal seam, leading to a disruption of the original stress balance. This results in stress redistribution, causing the roof to experience a tendency to subside and collapse³⁶. Immediately following coal extraction, when filling operations are initiated, the bulk gangue filling materials are compacted, forming a dense fill that can provide support. Consequently, the surrounding rock stress is redirected to the roof of the mined-out area, interacting with the newly formed dense fill and transferring part of the stress to the fill body, thus establishing a new state of stress equilibrium³⁷.

Fig. 1

The schematic diagram of the filling body bearing support process.

Fig.2illustrates the relationship between the operational state of the filling work face and the effectiveness of the fill. The degree of insufficient contact with the roof and the density of the fill determine whether the fill can effectively support the roof under stress, thereby influencing the extent to which subsidence of the roof and surface can be limited³⁸. Consequently, the insufficient contact with the roof and the centroid position of the filling material can be used to gauge whether the filling operations will achieve their intended goals and outcomes. Numerous studies have indicated that the state of the filling material, the spatial positioning of filling equipment, and the operational status of the compaction mechanism directly affect the insufficient contact with the roof and the centroid position of the filling material after compaction^39,40,41. Therefore, these three aspects of the filling work face’s operational status significantly impact filling effectiveness. By employing a sensor network within the filling work face, specific values of these influencing factors can be obtained, allowing for quantitative analysis through mathematical tools such as fuzzy logic, thereby enabling objective and accurate assessments of filling effectiveness.

Fig. 2

Filling hydraulic support structure diagram.

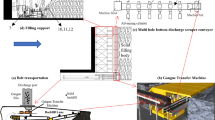
Fig.3presents the structural diagram of the filling hydraulic support, which primarily consists of a hydraulic support, a compaction mechanism, and a scraper conveyor⁴². The hydraulic support provides temporary support to the mined-out area, while the scraper conveyor is responsible for delivering filling materials. The compaction mechanism pushes the delivered materials into the filling area, creating a dense fill body. The specific sensors installed are detailed in Tab.1. Weight sensors and radar distance sensors mounted on the scraper conveyor measure the volume of material dispensed and the height of the accumulation, while an ultrasonic sensor positioned at the base can detect the distance between the filling material and the hydraulic support. Angle sensors installed on the base and the four-link structure capture the posture data of the hydraulic support, allowing for the acquisition of posture characteristics that affect filling effectiveness, including the inclination angle of the work face, compaction distance to the roof, and compaction distance to the void. Additionally, sensors installed on the compaction mechanism can gather data regarding the pushing angle, number of pushes, and the extension of the compaction mechanism.

Fig. 3

The schematic diagram of the filling body bearing support process.

Table 1 Sensor installation scheme.

To obtain the dataset necessary for generating fuzzy rules, data collection was conducted at an experimental filling work face in a mine located in Hebei Province, following the sensor arrangement designed in this study. This data captured the features influencing filling effectiveness during each filling operation, as well as the evaluations made by field engineers regarding the effectiveness of these operations after completion. Engineers classified the filling effectiveness into three categories: good, average, and poor. A “good” filling effectiveness indicates that no further filling operations are necessary, allowing for the next round of filling to proceed. An “average” filling effectiveness suggests that additional simple operations are required in the area yet to be filled. A “poor” filling effectiveness indicates that the current result is unsatisfactory, necessitating several repetitions of the filling action. For the purpose of training the fuzzy logic system, filling effectiveness labels were stored in a one-hot encoding format: (1,0,0) for good, (0,1,0) for average, and (0,0,1) for poor. After excluding outliers and missing values, a total of 500 data sets were compiled, containing nine features influencing filling effectiveness along with their respective labels.

Local-Global data fusion method for filling working faces

Fusion framework

Based on the perception of filling material, hydraulic support attitude and driving mechanism of filling face, the characteristics that affect filling operation effect are obtained. Then, filling material characteristics, filling equipment attitude characteristics and pushing mechanism characteristics are input into three independent fuzzy logic systems. The corresponding membership degree of filling effect is calculated, and the criterion of local working effect of filling surface is obtained. Finally, the D-S evidence combination theory is used to integrate the criteria at the global level, and the final filling effect judgment is obtained. The block diagram of the filling effect judgment method is shown in Fig.4.

Fig. 4

Local-global fusion framework.

Local data fusion for filling working faces based on IT2FLS-Adam

The characteristics that influence the filling operation are numerous, and directly fusing all feature quantities would greatly increase the parameter count of the fusion model. Therefore, this paper designs a local data fusion method for the filling working face. As shown in Fig.5, the system consists of three subsystems that evaluate the operational effects based on the state of filling materials, the spatial position of equipment, and the state of the pushing and compacting mechanism. Each subsystem inputs the corresponding feature data, performs fuzzification, and then uses a preset fuzzy rule base for inference, outputting membership values for good, moderate, and poor filling effects.

Fig. 5

Local data fusion schematic diagram.

Specifically, the filling material state subsystem evaluates based on features such as pile height, pile volume, and pile position; the equipment spatial position subsystem judges based on parameters like working face inclination, pushing and compacting distance to the roof, and distance from the roof; the pushing mechanism state subsystem infers from mechanical state features such as pushing angle range, pushing speed, and number of pushes. To achieve adaptive optimization of system parameters, the Adam algorithm is used to identify parameters in the fuzzy logic system. This process inputs training data and adjusts the parameters of the interval type-2 membership functions of the antecedents and the consequent functions in the fuzzy rule base through forward computation and error backpropagation, ensuring the accuracy of the system’s assessment of filling effects. Finally, the outputs of the three subsystems are globally fused using D-S evidence combination theory, further enhancing the accuracy and reliability of filling effect judgments.

Structure of the interval type-2 fuzzy logic system

The proposed interval type-2 fuzzy filling effect assessment system consists of three first-order TSK fuzzy logic systems, each responsible for fuzzy judgment of the state information of the filling materials, the relative spatial position information of the filling equipment, and the information of the filling actions. Each logic system includes a three-dimensional input vector and a three-dimensional output vector, where the inputs are the influencing factors of the filling effect presented in Section 2, and the output vector represents the classification of the filling effect. The i-th fuzzy rule is as follows:

$$\begin{aligned} R_{i}:IF\ x_{1}\ is\ {\widetilde{A}}_{i,1}\ and\ x_{2}\ is\ {\widetilde{A}}_{i,2}\ and\ x_{3}\ is\ {\widetilde{A}}_{i,3}, \ THEN\ \textbf{y}_{\textbf{i}}\mathbf {\ is\ }{\widetilde{\textbf{Y}}}_{\textbf{i}} \end{aligned}$$

(1)

where i = 1, 2, ..., C. $x_{i}$ represents the factors that affect the filling effect, ${\widetilde{A}}_{i,j}$ is the corresponding membership interval ranges for the features of the filling working face, $\left[ \underline{\mu }_{\widetilde{A}_{i,j}}, \overline{\mu }_{\widetilde{A}_{i,j}} \right]$, indicating the corresponding filling feature range under this filling operation mode. The specific memberships are calculated using the upper and lower membership functions, and this paper selects the Gaussian membership function:

$$\begin{aligned} & {\overline{\mu }}_{{\widetilde{A}}_{i,j}}\left( x_{j} \right) = \exp \left( - \left( x_{j} - {\overline{c}}_{i,j} \right) ^{2}\text {/}2{\overline{\sigma }}_{i,j}^{2} \right) \end{aligned}$$

(2)

$$\begin{aligned} & \quad {\underline{\mu }}_{{\widetilde{A}}_{i,j}}\left( x_{j} \right) = \exp \left( - \left( x_{j} - {\underline{c}}_{i,j} \right) ^{2}\text {/}2{\underline{\sigma }}_{i,j}^{2} \right) \end{aligned}$$

(3)

where, ${\overline{c}}_{i,j}$ and ${\underline{c}}_{i,j}$ represent the central values of the Gaussian membership function and are used for the upper membership function and the lower membership function respectively. ${\overline{\sigma }}_{i,j}$ and ${\underline{\sigma }}_{i,j}$ are the standard deviations of the Gaussian membership function, used for the upper and lower membership functions respectively. $\textbf{y}_{\textbf{i}}$ is the output filling effect vector, where the elements represent the degree to which the filling effect falls into the categories of good, moderate, and poor when the influencing features of the filling effect are x in the i-th mode.${\widetilde{\textbf{Y}}}_{\textbf{i}} = [{\underline{\textbf{y}}}_{\textbf{i}}{\textbf{,}\overline{\textbf{y}}}_{\textbf{i}},]$is the output interval:

$$\begin{aligned} & {\underline{\textbf{y}}}_{\textbf{i}}\mathbf {=}{\underline{\textbf{a}}}_{\textbf{0}\textbf{i}} \mathbf {+}{\underline{M}}_{i}\textbf{x} \end{aligned}$$

(4)

$$\begin{aligned} & \quad {\underline{\textbf{a}}}_{\textbf{0}\textbf{i}} = \left[{\underline{a}}_{i0}^{1},{\underline{a}}_{i0}^{2},{\underline{a}}_{i0}^{3} \right]^{T} \end{aligned}$$

(5)

$$\begin{aligned} {\underline{M}}_{i} = \begin{bmatrix} {\underline{a}}_{i1}^{1} & {\underline{a}}_{i2}^{1} & {\underline{a}}_{i3}^{1} \\ {\underline{a}}_{i1}^{2} & {\underline{a}}_{i2}^{2} & {\underline{a}}_{i3}^{2} \\ {\underline{a}}_{i1}^{3} & {\underline{a}}_{i2}^{3} & {\underline{a}}_{i3}^{3} \end{bmatrix} \end{aligned}$$

(6)

$$\begin{aligned} & \quad {\overline{\textbf{y}}}_{\textbf{i}}\mathbf {=}{\overline{\textbf{a}}}_{\textbf{0} \textbf{i}}\mathbf {+}{\overline{M}}_{i}\textbf{x} \end{aligned}$$

(7)

$$\begin{aligned} {\overline{\textbf{a}}}_{\textbf{0}\textbf{i}} = \left[{\overline{a}}_{i0}^{1},{\overline{a}}_{i0}^{2},{\overline{a}}_{i0}^{3} \right]^{T} \end{aligned}$$

(8)

$$\begin{aligned} & \quad {\overline{M}}_{i} = \begin{bmatrix} {\overline{a}}_{i1}^{1} & {\overline{a}}_{i2}^{1} & {\overline{a}}_{i3}^{1} \\ {\overline{a}}_{i1}^{2} & {\overline{a}}_{i2}^{2} & {\overline{a}}_{i3}^{2} \\ {\overline{a}}_{i1}^{3} & {\overline{a}}_{i2}^{3} & {\overline{a}}_{i3}^{3} \end{bmatrix} \end{aligned}$$

(9)

where, ${\underline{\textbf{a}}}_{\textbf{0}\textbf{i}}$ and ${\overline{\textbf{a}}}_{\textbf{0}\textbf{i}}$ represent the offset vectors of the lower and upper output intervals, ${\underline{M}}_{i}$ and ${\overline{M}}_{i}$ represent the coefficient matrices of the lower and upper output intervals. After completing the construction of the fuzzy rule base, the fuzzy logic system can perform fuzzy inference on the input data through fuzzy rules, mapping the input features to probabilities that measure the quality of the filling effect. The key to fuzzy inference lies in how to combine the values of the membership functions calculated from the rule antecedents to determine the strength of the input features triggering the fuzzy rules. Common calculation methods include the minimum t-norm method and the product t-norm method. Although both methods perform similarly, using the product t-norm reduces the computational load in subsequent parameter optimization. Therefore, this paper adopts the product t-norm for fuzzy inference. For interval type-2 fuzzy systems, the product t-norm is computed separately at the left boundary (LMF) and right boundary (RMF):

$$\begin{aligned} & F^{i}\left( \textbf{x} \right) = \left[{\underline{f}}^{i}\left( \textbf{x} \right) ,{\overline{f}}^{i}\left( \textbf{x} \right) \right]\end{aligned}$$

(10)

$$\begin{aligned} & \quad {\underline{f}}^{i}\left( \textbf{x} \right) = {\underline{\mu }}_{{\widetilde{A}}_{i,1}}\left( x_{1} \right) \times {\underline{\mu }}_{{\widetilde{A}}_{i,2}}\left( x_{2} \right) \times {\underline{\mu }}_{{\widetilde{A}}_{i,3}}\left( x_{3} \right) \end{aligned}$$

(11)

$$\begin{aligned} & \quad {\overline{f}}^{i}\left( \textbf{x} \right) = {\overline{\mu }}_{{\widetilde{A}}_{i,1}}\left( x_{1} \right) \times {\overline{\mu }}_{{\widetilde{A}}_{i,2}}\left( x_{2} \right) \times {\overline{\mu }}_{{\widetilde{A}}_{i,3}}\left( x_{3} \right) \end{aligned}$$

(12)

In the equation, $F^{i}(x)$ represents the triggering strength interval of the input vector for the i-th fuzzy rule, while ${\underline{f}}^{i}\left( \textbf{x} \right) ,{\overline{f}}^{i}\left( \textbf{x} \right)$denote the lower and upper bounds of the triggering strength, respectively. The values ${\underline{\mu }}_{{\widetilde{A}}_{i,m}}\left( x_{m} \right)$ and ${\overline{\mu }}_{{\widetilde{A}}_{i,m}}\left( x_{m} \right)$ indicate the lower and upper intervals of the membership functions.

After computing the triggering strength intervals for the rule antecedents, the inference engine must utilize the rule consequents to calculate the outputs. A type-1 fuzzy system can directly use the triggering strengths as weights and compute a weighted average of the outputs of the rule consequents as the final output. However, in an interval type-2 fuzzy system, the triggering strength obtained from the rule antecedents forms an interval that cannot be directly averaged.Instead, it requires the use of a reduction algorithm to derive the left and right endpoint values $y_{r}$ and $y_{r}$, followed by calculating the average as $\frac{y = (y_{r} + y_{r})}{2}$. This paper employs the EIASC algorithm for the reduction process, with the algorithm workflow outlined in Tab.2. The specific steps are as follows:

• 1. Initialization: Calculate the variables a and b, where a is the sum of the products of all left endpoint values of the triggering strength intervals with their corresponding outputs $y^{n}$, and b is the sum of all left endpoint values of the triggering strength intervals.For the left endpoint $y_{l}$, initialize L to 0; for the right endpoint $y_{r}$ , initialize R to N (the number of fuzzy rules).

• 2. Calculation Process: For the left endpoint $y_{l}$, increment L by 1 after each calculation, update the values of a and b, and compute the new $y_{l}$, If the newly calculated $y_{l}$ is less than or equal to the next computed value, stop; otherwise, continue iterating. For the right endpoint $y_{r}$, decrement R by 1 after each calculation, similarly update a and b, and compute the new $y_{r}$. If the newly calculated $y_{r}$ is greater than or equal to the next computed value, stop; otherwise, continue iterating.

• 3. Termination Condition: When the stopping conditions are satisfied, the algorithm terminates, outputting the final reduced fuzzy values $y_{l}$ and $y_{r}$.

Table 2 EIASC algorithm.

Through the EIASC reduction algorithm, three sets of endpoint values $y_l$ and $y_r$ can be obtained. By averaging each set, the outputs $y^1$, $y^2$ and $y^3$ are derived, which represent the final output results. The complete calculation process is illustrated in Fig.6.

Fig. 6

The operation process of fuzzy logic system.

Parameter identification of interval type-2 fuzzy logic systems

The structure of the fuzzy logic system and the fuzzy inference engine have been established; however, the linear functions in the consequent of the fuzzy rules remain undetermined. Therefore, it is necessary to utilize the input and output data from the training set to identify the unknown parameters in the consequent function by minimizing the loss function.

The principle of parameter identification is to determine the optimal parameters by minimizing the loss function. Adaptive Moment Estimation (ADAM) is a commonly used method for accelerating stochastic gradient descent in deep learning frameworks. It is built on the foundations of the AdaGrad and RMSprop algorithms, combining the advantages of AdaGrad’s ability to handle sparse gradients and RMSprop’s effectiveness in managing non-stationary objectives. Due to its high computational efficiency, low deployment complexity, and minimal memory usage, the ADAM algorithm is widely employed for model optimization. This paper employs the ADAM algorithm to optimize the gradient of the composite loss function, facilitating the identification and optimization of the parameters of the TSK-type fuzzy rule consequents.

When using the ADAM algorithm for parameter identification, the loss function during the training process must first be defined. Given a specific input, the fuzzy logic system outputs a vector containing three elements, each representing the probabilities of achieving good, average, and poor filling operation effects, respectively. Thus, the problem of assessing filling effectiveness can be viewed as a classification problem, where the category with the highest probability constitutes the judgment of the fuzzy logic system. The training data utilized consists of labeled data that reflect actual operational outcomes, allowing for the use of the cross-entropy loss function to measure the accuracy of the fuzzy logic system’s judgment regarding filling operation effects:

$$\begin{aligned} L\left( y,\widehat{y} \right) = - \sum _{i = 1}^{C}y_{i}\log \left( \widehat{y_{i}} \right) \end{aligned}$$

(13)

where C is the number of categories, $y_{i}$ and $\widehat{y_{i}}$ represent the true labels and predicted probabilities, respectively.

The gradient can be expressed in matrix form as the partial derivatives of the loss function with respect to all parameters:

$$\begin{aligned} g = \begin{bmatrix} \frac{\partial L}{\partial c_{11}^{1}} & \cdots & \frac{\partial L}{\partial a_{1D}^{1}} \\ \vdots & \ddots & \vdots \\ \frac{\partial L}{\partial c_{c1}^{M}} & \cdots & \frac{\partial L}{\partial a_{cD}^{M}} \end{bmatrix} \end{aligned}$$

(14)

where $c$ denotes the number of fuzzy rules, $D$ is the number of input data points within each fuzzy rule, and $M$ represents the dimensionality of the output vector.

After determining the gradient of the composite loss function, the Adam algorithm first calculates two moment estimates, initializing them as zero matrices to correct for their initial bias. The corresponding parts of these corrected estimates are then used to update the parameters. The parameter update process is as follows:

First, the first moment estimate is computed through the exponentially weighted average of the gradients:

$$\begin{aligned} h_{t} = \beta _{1} \cdot h_{t - 1} + (1 - \beta _{1}) \cdot g_{t} \end{aligned}$$

(15)

where $h_{t}$ represents the first moment estimate at the current time step, $g_{t}$ represents the gradient at the current time step, and $\beta _{1}$ represents the parameter controlling the decay of $h_{t}$.

Next, the second moment estimate is updated through the exponentially weighted average of the squared gradients:

$$\begin{aligned} s_{t} = \beta _{2} \cdot s_{t - 1} + (1 - \beta _{2}) \cdot g_{t}^{2} \end{aligned}$$

(16)

where $s_{t}$ is the second moment estimate at the current time step, and $\beta _{2}$ is the parameter controlling the decay of $s_{t}$.

Subsequently, bias correction is applied to both the first and second moment estimates to mitigate the impact of the initial small estimates:

$$\begin{aligned} & {\widehat{h}}_{t} = \frac{h_{t}}{1 - \beta _{1}^{t}} \end{aligned}$$

(17)

$$\begin{aligned} & \quad {\widehat{s}}_{t} = \frac{s_{t}}{1 - \beta _{2}^{t}} \end{aligned}$$

(18)

Finally, the parameters are updated as follows:

$$\begin{aligned} \theta _{t} = \theta _{t - 1} - \frac{a{\widehat{h}}_{t}}{\sqrt{{\widehat{s}}_{t}} + \epsilon } \end{aligned}$$

(19)

where, ${\widehat{h}}_{t}$ represents the first moment estimate after correction for deviation, ${\widehat{s}}_{t}$ represents the second moment estimate after correction for deviation, $\theta _{t}$ is the parameter value at the current time step, $\theta _{t - 1}$ is the parameter value at the previous time step, $a$ is the learning rate, and $\epsilon$ is a small constant to prevent division by zero. Once the identification of the consequent parameters is complete, the construction of the fuzzy logic system is finalized. The system can then make fuzzy judgments on the filling effect level based on the input local data from the working face. By normalizing the output results, these can be interpreted as the degrees of membership of the current filling effect across various levels.

Global fusion based on improved D-S evidence combination theory

When assessing the operational effectiveness of solid filling working faces, multiple sensors collect information regarding the filling material, equipment positions, and the status of the pushing mechanism from different perspectives. As illustrated in Fig.7, the raw data from the sensors are processed through a fuzzy logic system, resulting in several basic probability assignments (BPA) concerning the filling effect: BPA $m_1$ from the state of the filling material, BPA $m_2$ from the spatial position of the filling equipment, and BPA $m_3$ from the status of the pushing mechanism. Each of these reflects a unilateral judgment on the filling effect derived from local information sources.

Fig. 7

Global data fusion process of filling working face.

Since each sensor and the fuzzy logic system can only assess the filling effect from a specific angle, there may be instances of incomplete or uncertain local information. To achieve a comprehensive and more accurate assessment of the filling effect that incorporates global information, this study employs D-S evidence combination theory for hierarchical data fusion. By applying Dempster’s combination rule, the BPAs of the filling effect from various sources are fused, synthesizing the support from different information sources to arrive at the final global assessment of the filling effect. This final outcome not only considers the information from individual local sensors but also reduces the impact of uncertainty from single systems through evidence fusion, thereby enhancing the accuracy and reliability of the filling effect judgment.

Traditional D-S evidence theory provides an effective theoretical framework for integrating uncertain and incomplete information in solid filling working faces. However, it exhibits certain limitations when handling conflicting evidence, often resulting in counterintuitive outcomes, particularly when there is significant conflict among the pieces of evidence. This can ultimately lead to fusion results that deviate from the true situation, affecting the accuracy of decision-making.

To overcome this limitation, this paper proposes an improved method based on Wasserstein distance and Deng entropy. Wasserstein distance effectively measures the differences between different BPAs (basic probability assignments), offering a novel approach to assessing the credibility of evidence. Simultaneously, Deng entropy serves as a tool for measuring uncertainty, aiding the data fusion system in comprehensively understanding the relationships among pieces of evidence. Building on this foundation, the improved D-S evidence theory can more accurately allocate evidence weights by integrating Wasserstein distance and Deng entropy, thereby enhancing the accuracy and reliability of the final global fusion results.

Measuring evidence conflict degree

Wasserstein distance, also known as Earth Mover’s Distance, is a metric used to quantify the difference between two probability distributions. The fundamental concept of Wasserstein distance, as illustrated in Fig.8, treats one distribution as a pile of earth and calculates the distance to another distribution by minimizing the cost of moving this earth. The computation of Wasserstein distance involves finding an optimal transport plan to transfer the mass of one distribution to another while minimizing the overall transportation cost. The calculation of Wasserstein distance W is expressed as follows:

$$\begin{aligned} W(P,Q) = \inf _{\gamma \sim \prod {(P,Q)}}{E_{x,y\sim \gamma }[\left\| x - y \right\| ]} \end{aligned}$$

(20)

where, $\prod \left( \text {p},\text {q} \right)$ denotes the set of all possible joint distributions formed by P and Q. For each possible joint distribution $\gamma$, one can sample a pair $(x,y) \sim \gamma$ to obtain a sample pair x and y and compute the distance for this pair $\left\| x - y \right\|$. Consequently, one can compute the expected value of the sample pair distances under this joint distribution $\gamma$, $E_{x,y\sim \gamma }[\left\| x - y \right\| ]$. The Wasserstein distance represents the lower bound of this expected value across all possible joint distributions, reflecting the minimal distance cost to transform P into Q under “optimal path planning.”

Fig. 8

The basic idea of Wasserstein distance.

Wasserstein distance effectively captures the differences between different BPAs and reflects these as values between (0,1). For example, consider a set of BPAs under a certain recognition framework, with the functional expressions as follows:

$$\begin{aligned} \left\{ \begin{array}{c} m_1(\alpha )=0.5,m_1(\beta )=0.5\\ m_2(\alpha )=x,m_2(\beta )=1-x\\ \end{array} \right. \end{aligned}$$

(21)

let $x$ increase from 0 to 1. The variation of the Wasserstein distance between $m_1$ and $m_2$ is shown in Fig.9. When $x$ increases from 0 to 0.5, the difference between the two probability distributions decreases, and the degree of conflict diminishes, resulting in a lower Wasserstein distance. Conversely, when $x$ increases from 0.5 to 1, the difference between the two basic probability distributions increases again, leading to a higher degree of conflict and an increase in Wasserstein distance.

Fig. 9

The variation trend of Wasserstein distance with $x$.

Measuring evidence uncertainty

Deng entropy is a metric used to quantify the uncertainty of BPA during the D-S evidence combination process. As a generalization of Shannon entropy, Deng entropy $Ed(\cdot )$ overcomes the limitations of traditional information theory when applied to complex systems. Its calculation is expressed as follows:

$$\begin{aligned} Ed(m) = - \sum _{A \subseteq \Theta } {m(A)}\log _{2}\frac{m(A)}{2^{|A|} - 1} \end{aligned}$$

(22)

here, $|A|$ denotes the number of elements in set $A$. When the number of elements in $A$ is one, Deng entropy is equivalent to Shannon entropy.

Improved evidence combination rule

To address the issue of traditional D-S evidence combination theory producing counterintuitive results when handling conflicting evidence, this study integrates Wasserstein distance and Deng entropy theory. Prior to evidence combination, the credibility and information content of each piece of evidence are calculated. The weights are then determined based on the credibility and information content, followed by a weighted summation of the original evidence. This results in a weighted average that is subsequently combined to produce a final comprehensive global assessment of the filling effect. The computational process of the improved D-S evidence combination rule based on Wasserstein distance and Deng entropy is illustrated in Fig.10, with the specific steps as follows:

(1) Calculate the Wasserstein Distance Matrix:

$$\begin{aligned} WDM = \begin{bmatrix} 0\cdots & W_{1i}\cdots & W_{1k} \\ W_{i1}\cdots & 0\cdots & W_{ik} \\ W_{k1} & W_{ki} & 0 \end{bmatrix} \end{aligned}$$

(23)

where, $W_{ki}$ represents the Wasserstein distance between $m_{k}$ and $m_{i}$.

(2) Calculate the Credibility of Evidence. When the Wasserstein distance of a certain evidence $m_{i}$ is low in relation to other evidences, it indicates that this evidence has a lower degree of conflict with the others and therefore possesses higher credibility. The credibility ${Sup}_{i}$ of $m_{i}$ is defined as the inverse of the average distance to other evidences:

$$\begin{aligned} {Sup}_{i} = \frac{1}{\frac{\sum _{j = 1,j \ne i}^{k}W_{ij}}{k - 1}} \end{aligned}$$

(24)

(3) Calculate the Information Content of Evidence. The uncertainty measured by Deng entropy reflects its information content. When the Deng entropy of evidence is low, it indicates lower uncertainty, thus implying a higher information content. Therefore, information content $Iv(\cdot )$ is defined as:

$$\begin{aligned} Iv(i) = e^{{- E}_{d}} \end{aligned}$$

(25)

(4) Calculate the Weight of Evidence. For each piece of evidence $m$, its weight ${Wg}_{i}$ is related to both its credibility and information content, defined as the product of credibility and information content:

$$\begin{aligned} {Wg}_{i} = {Sup}_{i} \times {I}_{vi} \end{aligned}$$

(26)

The normalized weight ${We}_{i}$ is then calculated as:

$$\begin{aligned} {We}_{i} = \frac{{Wg}_{i}}{\sum _{j = 1}^{k}W_{j}} \end{aligned}$$

(27)

(5) Weighted Combination of Evidence. The evidence is adjusted based on its weight, and the average BPA of the modified evidence is computed. This average BPA replaces all original BPAs for D-S evidence combination:

$$\begin{aligned} \widetilde{m} = \sum _{i} {m_{i}(A_{j})}W_{i} \end{aligned}$$

(28)

where, $\widetilde{m}$ represents the weighted average of evidence, $m_{i}(A_{j})$ represents the fundamental probability copy of evidence $m_{i}$ to hypothesis $A_{j}$.

Fig. 10

Improved D-S evidence combination theory algorithm.

This paper proposes an improved D-S evidence combination theory that, by introducing the Wasserstein distance and Deng entropy, optimizes the computational efficiency of the traditional Dempster combination rule in multi-sensor data fusion scenarios. The improved method involves the following main steps, with their respective complexities as follows:

(1) Wasserstein Distance Matrix Calculation: For kk pieces of evidence (BPA vector length N), a $k \times k$ distance matrix needs to be calculated. Each Wasserstein distance calculation has a complexity of $O(N \log N)$. Therefore, the complexity of this step is:

$$\begin{aligned} O(k^2 , N \log N) \end{aligned}$$

(29)

(2) Deng Entropy Calculation and Evidence Weight Generation: Deng entropy is calculated for each piece of evidence, with a complexity of O(k, N). Subsequently, a weight vector is generated based on the weights and credibility, resulting in a total complexity of approximately: O(k, N)

(3) Weighted Average Fusion and D-S Combination: The complexity of weighted averaging is O(k, N) , while the improved D-S combination has a complexity of $O(N^2)$ per calculation. Since the proposed method performs the D-S combination twice, the complexity of this step is:

$$\begin{aligned} 2 \times O(N^2) =O(N^2) \end{aligned}$$

(30)

Combining the above steps, the total time complexity of a single run of the improved method is:

$$\begin{aligned} O(k^2 , N \log N + k , N + N^2) \end{aligned}$$

(31)

The traditional D-S combination rule employs the Dempster combination formula and enumerates the power set of evidence. Its complexity grows exponentially with the number of evidence k and the size of the frame of discernment $\Theta$. When the frame of discernment has a size $|\Theta |$, its time complexity is:

$$\begin{aligned} O(4^{|\Theta |}) \end{aligned}$$

(32)

In contrast, the proposed method directly treats the BPA as a vector of length N, utilizing the Wasserstein distance and Deng entropy to optimize evidence weighting and conflict resolution, thus avoiding the enumeration of the power set. The complexity is significantly reduced to a polynomial level, achieving higher computational efficiency in common application scenarios.

To intuitively demonstrate the advantages of the improved D-S evidence theory over traditional D-S evidence theory in handling conflicting evidence, a specific set of data from local fusion is selected for illustration, as shown in Tab.3:

Table 3 Filling effect judgment evidence conflict situation.

In this scenario, the fuzzy logic system derives the filling effect judgment $m_1$ based on local information of the filling material, concluding that the filling effect is good, with a credibility of 0.73. From the local information regarding the spatial position of the filling equipment, the judgment $m_2$ indicates an average filling effect, with a credibility of 0.91. Based on the working status of the pushing mechanism, the judgment $m_3$ concludes a good filling effect, with a credibility of 0.79. At this point, evidence $m_1$ and $m_3$ exhibit a significant conflict with $m_2$. When using traditional D-S evidence theory for evidence combination, the conflict coefficient results in:

$$\begin{aligned} \begin{aligned} K&= m_{1}\left( \theta _{1} \right) \cdot m_{2}\left( \theta _{1} \right) \cdot m_{3}\left( \theta _{1} \right) + m_{1}\left( \theta _{2} \right) \cdot m_{2}\left( \theta _{2} \right) \cdot m_{3}\left( \theta _{2} \right) \\ &~~~ + m_{1}\left( \theta _{3} \right) \cdot m_{2}\left( \theta _{3} \right) \cdot m_{3}\left( \theta _{3} \right) \\ &= 0.73 \cdot 0.01 \cdot 0.79 + 0.16 \cdot 0.91 \cdot 0.14 + 0.11 \cdot 0.08 \cdot 0.07 \\&= 0.0268 \end{aligned} \end{aligned}$$

(33)

The BPA indicating a good filling effect is:

$$\begin{aligned} m\left( \theta _{1} \right) = \frac{m_{1}\left( \theta _{1} \right) \cdot m_{2}\left( \theta _{1} \right) \cdot m_{3}\left( \theta _{1} \right) }{K} = 0.2155 \end{aligned}$$

(34)

The BPA indicating an average filling effect is:

$$\begin{aligned} m\left( \theta _{2} \right) = \frac{m_{1}\left( \theta _{2} \right) \cdot m_{2}\left( \theta _{2} \right) \cdot m_{3}\left( \theta _{2} \right) }{K} = 0.7615 \end{aligned}$$

(35)

The BPA indicating a poor filling effect is:

$$\begin{aligned} m\left( \theta _{3} \right) = \frac{m_{1}\left( \theta _{3} \right) \cdot m_{2}\left( \theta _{3} \right) \cdot m_{3}\left( \theta _{3} \right) }{K} = 0.0230 \end{aligned}$$

(36)

Thus, according to traditional D-S evidence theory, the final fusion result suggests an average filling effect, which contradicts intuition and the actual situation. When applying the improved D-S evidence theory proposed in this paper for global fusion, the steps are as follows:

Step 1-1: Construct the Wasserstein distance matrix:

$$\begin{aligned} WDM = \begin{bmatrix} 0 & 0.12 & 0.04 \\ 0.12 & 0 & 0.08 \\ 0.04 & 0.08 & 0 \end{bmatrix} \end{aligned}$$

Step 1–2: Calculate the credibility of the filling effect judgments, yielding $Sup_{1} = 12.5$, $Sup_{2} = 10$, and $Sup_{3} = 16.7$.

Step 2-1: Calculate the Deng entropy of the filling effect judgments: $H_{1} = 3.91$, $H_{2} = 3.29$, and $H_{3} = 3.47$.

Step 2-2: Compute the information content based on Deng entropy, resulting in ${IV}_{1} = 0.02$, ${IV}_{2} = 0.37$, and ${IV}_{3} = 0.24$.

Step 3-1: Calculate the normalized weights of the evidence, yielding $W_{1} = 0.25$, $W_{2} = 0.37$, and $W_{3} = 0.38$.

Step 3-2: Calculate the weighted evidence, resulting in $\widetilde{m}(\theta _{1}) = 0.49$, $\widetilde{m}(\theta _{2}) = 0.43$, and $\widetilde{m}(\theta _{3}) = 0.08$.

Step 3-3: Perform evidence combination on the weighted evidence twice, yielding the final result {[0.59953338, 0.39749423, 0.00297239]}, indicating that the highest credibility corresponds to a good filling effect. This demonstrates that the global fusion method based on the improved D-S evidence combination theory can effectively handle conflicts in local evidence and make accurate judgments regarding the filling effect.

Experimental results and discussion

Data description

To validate the performance of the proposed method for assessing filling effects, a dataset was utilized for testing and verification. The dataset was divided into training, testing, and validation sets in a ratio of 50%, 30%, and 20%, respectively. To prevent an excessive number of parameters in the fuzzy logic system, the number of fuzzy rules was preset to 8. Following recommendations from the literature, the parameters for the Adam algorithm were set to $\beta _{1} = 0.9$, $\beta _{2} = 0.999$, and $\epsilon = 10^{-8}$. To enhance algorithm efficiency and prevent overfitting, an early stopping mechanism was introduced during training; training was halted if the loss function did not decrease for several consecutive iterations. The maximum number of iterations, batch size, and early stopping patience values were set to 1500, 64, and 50, respectively.

Accuracy testing

The proposed method for assessing filling effects comprises three independent fuzzy logic systems, each handling local sensory information from the state of the filling material, the spatial position of the filling equipment, and the filling actions. For the fuzzy logic system evaluating the state of the filling material, the inputs include the drop position, the amount of material dropped, and the height of the pile; for the fuzzy logic system assessing the spatial position of the filling equipment, the inputs are the distance to the top during compaction and the distance to the empty top during compaction; for the fuzzy logic system evaluating the filling actions, the inputs include the pushing angle and pushing speed. The outputs of all three systems are normalized three-dimensional vectors $y$, representing the probabilities of the filling effect being good, average, or poor.

Each fuzzy logic system generates 3 $\times$ 8 = 24 rule antecedent functions. Each rule’s antecedent function represents a filling equipment spatial position pattern learned by the fuzzy logic system under the optimization of the Adam optimizer. One of the rules from the parameter-identified fuzzy logic system is illustrated in Fig.11, which indicates that when the input features conform to the patterns set in the rule antecedent, the corresponding probabilities of the filling effect being good, average, or poor are calculated according to the functions in the rule consequent.

Fig. 11

One of the fuzzy rules of FLS.

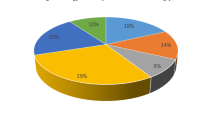
Since the fuzzy logic systems can only assess the filling effect based on local characteristics of the filling working face, they cannot comprehensively reflect the operational status of the filling working face, resulting in relatively low accuracy in assessing the filling effect. After local data fusion is completed by the fuzzy logic systems, the three independent filling effect judgments are further fused to obtain a comprehensive global assessment of the filling effect. The final experimental results are shown in Figure X. Fig.12, 13, and 14 present the local fusion results of the three fuzzy logic subsystems. Due to the inputs of the subsystems only including certain operational information from the filling working face, the accuracy of the filling operation assessments is relatively low, at 77%, 74%, and 79%, respectively, and they struggle to correctly assess cases where the filling effect is average. Fig.15 shows the confusion matrix of the filling effect judgment after global data fusion. By further combining the judgment results of each subsystem using the improved D-S evidence combination theory, the accuracy of the filling effect assessment was significantly improved, achieving an overall accuracy of 92.9%. This indicates that the proposed improved D-S evidence combination theory can effectively integrate information from different parts of the filling working face to assess the filling effect from a global perspective.

Fig. 12

Confusion matrix of filling material FLS.

Fig. 13

Confusion matrix of equipment attitude FLS.

Fig. 14

Confusion matrix of filling action FLS.

Fig. 15

Confusion matrix of global fusion.

Comparative experiments

To evaluate the performance of the proposed IT2FLS-improved D-S combination method, comparisons were made with different fuzzy logic systems and D-S evidence combination theories. These included the T1TFLS-D-S evidence combination method, the T1FLS-improved D-S method, the T2FLS (C0)-D-S method, the T2FLS (C0)-improved D-S method, and the IT2FLS-D-S evidence combination method. The membership functions of the fuzzy logic systems were all chosen to be Gaussian, and the parameters in the fuzzy rules were identified using the Adam optimizer. The model performance was ultimately evaluated using accuracy, precision, recall, and F1 score, with the results presented in Tab.4 and Fig. 16.

Table 4 Comparison of global fusion method results.

Fig. 16

Comparsion of global fusion method results.

The experimental results demonstrate that methods based on fuzzy logic systems and D-S evidence combination theory can effectively assess the filling effects. The recognition accuracy for T1TFLS-D-S and T1FLS-improved D-S was 87.18% and 86.41%, respectively, both of which were lower than the accuracy of the methods based on the interval type-2 fuzzy logic system. Furthermore, a comparison was made between the proposed method and the IT2FLS (C0) method, yielding accuracies of 87.75% and 89.31%, respectively. Additionally, the precision, recall, and F1 score for the proposed method surpassed those of the other methods. This indicates that the proposed improved method can accurately capture the complex operational patterns of filling tasks during the local fusion phase, utilizing fuzzy rules to describe the uncertainties and fuzziness within the filling operation system. The improved D-S evidence combination theory can address conflicts in judgments from different subsystems, thereby synthesizing various assessments of the filling effect during the global fusion phase and correctly evaluating the outcome of filling operations.

Conclusion

This study implements an assessment method for the effects of solid filling operations in coal mines, based on interval type-2 fuzzy logic systems and improved D-S evidence combination theory. By analyzing the mechanized and automated filling operations, observable information from the filling working face was summarized and its relationship with the filling operation effects was discussed. Building upon this, the perceptual information from the filling working face was categorized into three types based on the different observed objects, and a multi-level data fusion framework for assessing filling operation effects was proposed. Through local data fusion based on fuzzy logic systems and global data fusion based on D-S evidence theory, associative information among different variables was extracted to achieve assessments of the filling operation effects. The main contributions of this paper are as follows:

• (1) Addressing the issue of isolated sensor operations in filling working faces, where information does not interconnect, this study aims to provide a comprehensive assessment of filling operation effects. By analyzing the mechanized filling operation process, high-level features affecting the filling operation were identified, and the potential for utilizing multiple sensors to collectively represent these high-level features was analyzed, enabling information interoperability among multiple sensors.

• (2) To tackle the ambiguity and uncertainty of filling operation effects, this study proposes a local data fusion method based on fuzzy logic systems. First, features affecting the filling operation effects were categorized into filling material features, spatial position features of the filling equipment, and operational features of the pushing mechanism. Local fusion was performed on features with substantial correlations reflecting the same object state to obtain preliminary judgments on filling operation effects. To enhance the ability of the fuzzy logic system to represent the fuzziness of filling operation effects, an IT2FLS-Adam fuzzy judgment system was introduced, applying interval type-2 fuzzy sets to fuzzify input features and using the Adam optimizer within a deep learning framework to identify and optimize system parameters.

• (3) In response to the issue that local fusion results cannot comprehensively reflect the filling operation effects, this study proposed a global data fusion method based on improved D-S evidence theory. Probabilities for good, average, and poor filling effects from local fusion results were used as the BPA required by D-S evidence theory for evidence combination, yielding the final assessment of filling effects. Since traditional D-S evidence theory can fail in the presence of highly conflicting evidence, this study combined Wasserstein distance and Deng entropy to evaluate the support and information content of the evidence. Before combining evidence, a weighting preprocessing step was applied to assign higher weights to credible evidence. Experimental results indicate that the proposed method achieved an accuracy of 93% in global fusion tasks within the filling working face, demonstrating superior performance compared to traditional methods.

In summary, fuzzy logic systems exhibit significant advantages in modeling systems characterized by uncertainty and imprecision, particularly through the innovative integration of Interval Type-2 Fuzzy Logic Systems with Dempster-Shafer evidence theory. In the foreseeable future, our objective is to harness the strengths of fuzzy logic systems by fine-tuning sensor network configurations, constructing fuzzy rule bases, and implementing evidence combination strategies. These advancements aim to enable adaptive applications across diverse domains such as manufacturing, energy management, urban planning and ecological conservation. By integrating these systems with target recognition algorithms and independent diagnostic analysis and evaluation frameworks, we aspire to deliver intelligent solutions for assessing complex systems in industrial and environmental contexts, thereby enhancing intelligence and decision-making capabilities across various industries.