Introduction

Automatic Generation Control (AGC) plays a pivotal role in ensuring the smooth functioning of a deregulated energy system, ultimately upholding system reliability1,2. The deregulated system was introduced to prevent the monopolization of utility companies and promotes a more competitive environment. In this deregulated setup, various entities are involved, including Generating Companies (GENCOs), Transmission Companies (TRANSCOs), Distribution Companies (DISCOs), and the Independent System Operator, collectively managing the entire system. Within this framework, GENCOs have the option to take part, while DISCOs possess the autonomy to opt the contract with GENCOs from different areas to meet their load demands. The overarching administration of the system is under the supervision of the Independent System Operator. Several authors have provided insights into the mechanisms of energy trading, which encompasses bilateral transactions, pool-based systems, and contractual compliance. Bhatt and colleagues have expounded on the control of output power variations in individual areas through the utilization of the Area Participation Factor (APF). Additionally, researchers like Parida have described the formation of the DPM depend on Contract Participation Factors (CPFs), highlighting its impact in conjunction with area participation factor(APFs). Furthermore, Donde and others have undertaken an analysis of AGC issues within a deregulated system that primarily relies on thermal units for power generation3. This diverse body of research contributes significantly to our understanding of AGC within the context of a deregulated energy system1,4,5,6,7.

Renewable Energy Sources (RES) are more sustainable, produce less carbon emissions, and minimize air pollution compared to energy sources based on fossil fuel. Solar and wind energy are more cost-effective. Implementation of RES into the grid provides a more stable and secure source of energy. Using RES, power can be provided to rural and remote areas where installation of a centralized grid may not be possible or economical. By incorporating RES into the grid, the stability of grid can be improved. In this article, a robust efficient controller is incorporated in a three area deregulated energy system consisting of RES and non-renewable energy sources.

The organization of the rest of the article can be summarized as follows: The state-of-art review of the proposed work has been explained in Sect. "State of the art". The proposed controller configuration, and the design procedures for the controller are outlined in Sect. "Literature survey". The Sect. "Research gap and motivation" outlines the hybrid model, incorporating both conventional and renewable sources. The Coatis optimization algorithm (COA) has been discussed in Sect. "Proposed TID + IDN controller for LFC". Section "Deregulated hybrid three area test system" provides an analysis of the performance of the COA with simulation results and discussions. Section "Objective function for automatic generation control (AGC)" concludes the paper. Different system parameters used in this paper have been included in supplementary material file in the form of appendix.

State of the art

This section represents the recent literature analysis regarding load frequency control considering various energy sources with separate power systems along with distinct controllers for maintaining stability of automatic generation control. Second part of this section represents the research gap and motivation.

Literature survey

Various authors have reported performance assessments on multi area hybrid power systems within a deregulated scenario. Demiroren et al.8 investigated a deregulated three-area system, analyzing its performance by implementing a continuous parameter Genetic Algorithm (GA) based on real values. However, it is noteworthy that their analysis did not consider any non-linearities in the system. In a separate study, Bhatt et al. explored the response of a deregulated four-area system using hybrid particle swarm optimization9. Notably, they did not incorporate non-linearities into their analysis either. The DISCO participation matrix concept was implemented in both three-area and four-area systems within a bilateral scenario. Nasiruddin10 et al. focused on analyzing AGC in a system with two control area in which the bacteria foraging optimization technique is implemented. Similar to previous studies, they did not incorporate system nonlinearities. To enhance the realism of their analysis, other authors introduced non-linearities such as the generation rate constraint (GRC) and governor dead band (GDB). In a comprehensive examination, Mohanty11 et al. studied the dynamic of a multi-area system under deregulation, specifically considering the impact of the GRC effect. Their analysis included thermal, nuclear, and hydropower units in each area, incorporating GRC and AC/DC links. The study further conducted sensitivity analysis using different controllers, such as integral-double derivative (IDD) and proportional-integral-double derivative (PIDD). Sekhar et al.12 analyzed a multi-area system, considering GDB and GRC. This research highlights the fruitfulness of the novel Firefly Algorithm-tuned hybrid fuzzy PID controller with a derivative filter in a multi-area, multi-source system in a deregulated environment. In this paper the nonlinearities are taken into account while examining the controller’s response under varying loads, different parameters, and random load disturbances. In a separate study, Rosaline et al.13 scrutinized a restructured two-area system that involved GRC and GDB nonlinearities along with boiler dynamics. Their paper introduces a structured H-infinity controller and a redox flow battery implemented in a deregulated power system. The purpose is to showcase the robustness of the controller considering the effects of time delay, generation rate constraint and governor dead band.

Expanding on optimization techniques, Aribowo et al.14 introduced a modified mountain gazelle optimizer for tuning PID parameters in DC motor control, achieving enhanced system responsiveness and stability. In a subsequent study, Aribowo et al.15 employed a gradient-based optimizer for PID parameter tuning in DC motors, emphasizing the importance of precise parameter adjustment in control systems. These studies underscore the critical role of optimization algorithms in refining controller performance across various applications. Addressing the challenges of hybrid power systems, Premkumar et al.16 investigated the optimal operation and control of systems incorporating stochastic renewable energy sources and Flexible AC Transmission Systems (FACTS) devices. They employed an intelligent multi-objective optimization approach to balance operational efficiency and system reliability. Complementing this, Pandya et al.17 proposed a multi-objective RIME algorithm for techno-economic analysis in security-constrained load dispatch and power flow, accounting for uncertainties in hybrid power systems. Their work provides a comprehensive framework for managing the complexities associated with renewable integration and system security. In the realm of control system simplification, Alsmadi et al.18 presented a model order reduction technique that preserves substructure and incorporates fuzzy logic control. This method effectively reduces system complexity while maintaining essential dynamic characteristics, facilitating more efficient control strategies. Focusing on aerospace applications, Abualigah et al.19 designed a filtered PID controller for aircraft pitch control using the sinh-cosh optimizer, achieving improved stability and response times. Their approach demonstrates the applicability of advanced optimization techniques in critical control scenarios. In power quality enhancement, Alrashed et al.20 improved the control strategy of Dynamic Voltage Restorer (DVR) compensators by integrating an adaptive notch filter with an optimized proportional-derivative (PD) controller, utilizing the Improved Grey Wolf Optimizer (IGWO) algorithm. This integration effectively mitigates voltage disturbances, ensuring consistent power delivery. Addressing frequency regulation in multi-microgrid systems, Fadheel et al.21 proposed a hybrid sparrow search optimized fractional virtual inertia control, enhancing system resilience to frequency deviations. Their work highlights the importance of adaptive control mechanisms in maintaining grid stability amidst fluctuating renewable inputs. In the context of aircraft control systems, Abualigah et al.22 introduced an artificial rabbits optimizer integrated with a PID-F controller for optimizing aircraft pitch control, resulting in superior handling of dynamic changes and disturbances. Furthering advancements in voltage regulation, Izci et al.23 utilized a refined sinh-cosh optimizer to design controllers that enhance the stability of automatic voltage regulators, demonstrating improved transient response and robustness. In a subsequent study, Izci et al.24 developed a novel control scheme for automatic voltage regulators using a modified artificial rabbits optimizer, achieving notable improvements in voltage stability and control precision. Focusing on renewable energy integration, Altawil et al.25 optimized fractional-order PI controllers for regulating grid voltage in PV systems using the slap swarm algorithm, effectively managing the variability inherent in solar power generation. In automotive control, Abualigah et al.26 employed a modified elite opposition-based artificial hummingbird algorithm to design fractional-order PID controllers for cruise control systems, achieving enhanced speed regulation and adaptability. Lastly, Sarayrah et al.27 studied a damping control strategy based on predictive approaches for inter-area power systems, contributing to improved system stability and reduced oscillations in large-scale power networks. Collectively, these studies underscore the critical role of advanced control strategies and optimization algorithms in addressing the complexities of modern power systems, particularly in the integration of renewable energy sources and the enhancement of system stability and performance.

Kalyan et al.28 proposed a coordinated strategy integrating a supercapacitor and Static Synchronous Series Compensator (SSSC) to enhance the performance of interconnected power systems with diverse energy sources, demonstrating improved power oscillation damping and stability under load variations. Building on the theme of system stability, Kalyan et al.29 investigated frequency regulation in geothermal power plant-integrated systems using a 3DOFPID controller, highlighting its adaptability to renewable energy variability. Gopi et al.30 introduced the V-Tiger PID controller for automatic voltage regulators, achieving superior transient response and robustness compared to traditional PID controllers, emphasizing its applicability for voltage control. Further advancing optimization techniques, Kalyan et al.31 utilized the Squirrel Search Algorithm (SSA) to design an intelligent controller for interconnected systems, which effectively managed dynamic complexities and improved system robustness. In a similar vein, Goud et al.32 applied a Gravitational Search Algorithm (GSA)-tuned Fractional Order PID controller within a Current-Controlled Voltage Source Inverter (CC-VSI) to address power quality issues in photovoltaic (PV)-integrated systems, ensuring stable operation. Begum et al.33 developed an intelligent fuzzy logic-based sliding mode controller for frequency stability in deregulated systems, validated through real-time simulation using the OPAL-RT platform. Mohapatra et al.34 optimized grid-connected PV systems with a super-twisting sliding mode controller, addressing uncertainties and enhancing real-time power management. Kalyan et al.35 assessed the effectiveness of open-loop and closed-loop Generation Rate Constraint (GRC) models in maintaining frequency stability in three-area thermal systems. Further, Kalyan et al.36 introduced a Seagull Optimization Algorithm-based Fractional Order Fuzzy Controller for multi-source systems with realistic constraints, achieving significant improvements in frequency control. Their subsequent work37 applied a Water-Cycle Algorithm to tune an intelligent fuzzy controller for multi-fuel systems, effectively managing time delays and ensuring stability. In38, Kalyan et al. conducted a comparative analysis of energy storage devices in combined Load Frequency Control (LFC) and Automatic Voltage Regulation (AVR), offering insights into their contributions to system stability. Finally, Kalyan et al.39 proposed a Type-II fuzzy controller optimized with the Water Cycle Algorithm for LFC in multi-area, multi-fuel systems with communication delays, demonstrating robustness and reliability in diverse operating conditions. These studies collectively highlight advancements in controller designs and optimization techniques to address challenges like renewable energy integration, system stability, and real-time control in hybrid power systems, offering complementary insights to existing solutions.

Arya et al.4 conducted an investigation on a multi-area system interconnected through AC/DC parallel links in a restructured environment. The analysis focused on a two-area non-reheat thermal system, considering GDB. Optimal control theory was employed to design a Proportional-Integral (PI) controller, and the system’s output was differentiated with a single-source thermal unit in a deregulated scenario. In a related study5, a two-area system with AC/DC parallel links under a restructured environment was analysed. Optimum Control Methods were implemented, and optimal control theory was implemented to configure a PI-tuned Automatic Generation Control. The response of this system was correlate with a system consisting a thermal unit in a deregulated structure. Furthermore, the analysis was done to investigate the impact of GDB in a system consisting of two control area with non-reheat thermal system.

Demiroren et al. analysed a restructured 3-area system without considering any non-linearities. Mohanty et al. examined a deregulated multi-area system, incorporating generation rate constraints. Sekhar et al. explained a restructured multi-source system, considering non-linearities such as generation rate constraints (GRC) and governor dead band (GDB). More recently, Rosaline et al. analyzed a deregulated 2-area system, incorporating GDB and GRC non-linearities along with boiler dynamics. Papers40,39,40,43 have investigated load frequency control, primarily focusing on conventional energy sources like coal. However, these studies have not analyzed systems comprising Renewable Energy Sources (RESs) based power plants. The decline rate of conventional energy sources and emissions of carbon components have turned the researchers towards renewable energy sources such as wind power plants, Solar Thermal Power Plants (STPP), Distributed Solar Thermal Systems (DSTS), and Gas Turbine Power Plants (GTPP). In44, the authors analyzed a system incorporating wind plants, solar photovoltaic, along with thermal, hydro, diesel plants, and gas turbines. Papers45,46 investigated a three-area system, including thermal, wind, GTPP, STPP, and hydro plants. In45, a combined differential evolution artificial electric field algorithm-based PID controller was presented to examine the robustness and sensitivity analysis of a hybrid system incorporating both RES and non-renewable energy sources. This paper also addresses the effects of communication time delays and GRC on the load frequency control of the hybrid system. In46, the authors made a pioneering attempt to implement an artificial flora algorithm (AFA) optimized cascade CPDN-PIDN controller in the united Automatic Load Frequency Control & Automatic Voltage Regulator (AVR) system. It is observed that the dynamic responses of CPDN-PIDN are significantly better than those of PI and PIDN controllers. From the investigation it is observed that as compared to the wind plant the geothermal power plant is more reliable. It is justified by using a real-time simulation with the OPAL-RT OP4510 real-time setup.

In a study the authors in47, analyzed the response of a three-control area system incorporating diesel unit, thermal unit and Solar Thermal Power Plants (STPP). DSTS units were introduced in a three-area system comprising hydrothermal units48. R. Rajbanshi49 et al. incorporated a dish-Stirling solar thermal system into a multi-area system, considering GRC and GDB with thermal and hydro units44,43,44,45,46,49. The analysis reveals that the implementation of renewable energies in the power system tends to decrease system stability. To address this issue and improve power transfer capability between interconnected control areas, FACT (Flexible AC Transmission System) controllers are introduced50. Different authors in50,49,50,53 have incorporated various FACT devices, such as the Thyristor Control Series Capacitor (TCSC), Unified Power Flow Controller (UPFC), Thyristor Control Series Capacitor (TCSC), Thyristor Control Phase Shifter (TCPS), Static Synchronous Series Compensator (SSSC) and Inter-line Power Flow Controller (IPFC), aiming to enhance system stability. Dhundhara et al.52 proposed a 2-area interconnected system incorporated with a Capacitor Energy Storage (CES) device in a deregulated scenario. Their paper validates the effect of the united action of thyristor-controlled phase shifter units and capacitive energy storage by implementing a sine-cosine algorithm-optimized controller under different operating conditions. Shankar et al.53 examined Automatic Generation Control (AGC) issues under a deregulated environment, incorporating Unified Power Flow Controller (UPFC) and AC/DC links. Designing a dynamic controller is essential to solve AGC problems in electrical energy systems. The oscillation states of the test system were evaluated through small signal stability analysis of each area, incorporating a robust controller optimized by the Fruit Fly Algorithm.

Addressing both scheduled and unscheduled power transactions between different control areas causes a shift in stable operating points within the deregulated system. A robust controller becomes essential to navigate these challenges, as a simple Proportional-Integral-Derivative (PID) controller often falls short. Researchers have developed non-integer PID controllers to enhance controller responses. In a restructured system, a significant concern is the design and application of robust control strategies for Automatic Generation Control (AGC) issues. Various authors have employed different controllers for this purpose. Sahu et al.54 implemented a Teaching-Learning-Based Optimization (TLBO) tuned Fuzzy-PID controller. Robustness analysis was conducted under wide changes in system parameters, comparing it with other optimization algorithms. Rahman et al.55 explored AGC in a deregulated scenario incorporating a Three Degrees of Freedom (3-DOF) based Integral-Derivative (ID) controller. The performance was compared with single-degree-of-freedom controllers such as integral (I), integral-derivative (ID), and two-degree-of-freedom integral-derivative (2DOF-ID) controllers. Bio-geography-Based Optimization (BBO) technique was applied for optimizing governor parameters and controller gains, demonstrating superior performance of the 3DOF-ID controller. Nayak et al.56 proposed a Fuzzy-based PID controller to enhance AGC performance. A Two Degree of Freedom Optimal Fuzzy-Aided PID controller was applied in both two and three-area systems as a secondary controller. The proposed controller’s performance was validated through a comparative study with other controllers, introducing a new optimization algorithm. Saha et al.57 addressed controller performance by integrating non-integer and integer based PID controllers in the AGC of system having two control area in a deregulated scenario. A novel controller cascaded PIDN-FOID was introduced and outperformed other controllers. Tasnin et al.58 presented the performance of a FOPI–FOPD cascaded controller compared to a conventional PID in a deregulated three-area system. The study involved a comparison of various energy storage devices and introduced a new fractional-order cascade controller. S lalngaihawma et al. presented an interconnected system in deregulated environment incorporating electric vehicle59. S. Rangi analysed a multi area system with an optimal controller in deregulated scenario incorporating energy storage devices60.

Literature analysis reveals a trend among researchers to implement different fractional-order controllers due to their flexible configuration and higher degree of freedom. Fractional-order PID61,60,61,62,63,66 and fractional-order fuzzy PID controllers67 have been incorporated to achieve better dynamic responses. Additionally, various cascade controllers, such as CPDN-PIDN, FOI-FOPDF, PDN-PIDN, FOPDN-FOPIDN, and fuzzy FOPI-FOPID, have been designed and incorporated in Load Frequency Control (LFC) studies. Several meta-heuristic optimizations have been employed to minimize Automatic Generation Control (AGC) issues. Different methodologies, including Particle Swarm Optimization (PSO)8, Teaching-Learning Based Optimization Algorithm, Firefly Optimization Algorithm (FOA)47, OFF Algorithm50, Fruit Fly Optimization51, Quasi-Oppositional Harmony Search Algorithm52, and Improved Squirrel Search Algorithm68, have been incorporated to analyze Load Frequency Control (LFC) performance. The analysis suggests that the integration of a robust controller using a novel meta-heuristic optimization methodology is crucial to enhance time response characteristics.

Research gap and motivation

Despite extensive research in Load Frequency Control, several key gaps remain unaddressed, particularly with the increasing complexity of modern power systems. Many traditional controllers such as PI and PID controllers often struggle with nonlinearity, time-varying parameters, and the inherent uncertainty of renewable energy sources. The adaptive and intelligent controllers like Fuzzy Logic, Neural Networks, and Fractional Order PID (FOPID) controllers often face challenges in balancing adaptability, robustness and computational efficiency. The incorporation of renewable energy in deregulated environments introduces uncertainties and disturbances which are not fully captured by already existing control techniques.

It has been observed that till date no attempt has been made to implement a COA tuned controller for LFC study in deregulated scenario. Hence a novel controller TID + IDN tuned with COA optimization has been proposed.

This study focuses on a multi-source system that includes hydro unit, thermal unit, dish-Stirling solar thermal system, geothermal power plant and solar thermal power plant. Geothermal energy is considered more reliable than wind because the output power of geothermal power plant can be easily predicted with very good accuracy. In case of wind power plant, power production is unpredictable as weather plays an important role in power generation. The actual power output in Geothermal power plant is close to total installed capacity. The analysis takes into consideration both Governor Dead Band (GDB) and Generation Rate Constraint (GRC) non-linearities. GRC and GDB are the most common non-linearities present in load frequency control. The rate of fluctuation of output power of thermal power plant is restrained by thermodynamics and mechanical limitations on steam turbines. To maintain the safety of equipment, large deviations can be avoided by imposing rate limits by variables such as temperature and pressure. GDB deals with the governor sustaining to speed changes for which the valve’s position remains unchanged. For this analysis, a backlash of 0.05% is chosen.

The system is examined with a Redox Flow Battery (RFB). An innovative algorithm known as the Coati Optimization Algorithm (COA), developed by Mohammad et al. in69, is introduced. However, it has yet to be implemented to address the LFC problem in a deregulated scenario. In this methodology, a newly developed Coati Optimization Algorithm has been implemented to fine tune the parameters of a novel TID + IDN controller. This COA optimization has a faster converging characteristic as compared to other algorithms like ISSA, SSA and PSO. The performance indices of the response obtained using this proposed technique is better as compared to ISSA optimized TID + IDN controller, SSA optimized TID + IDN controller, PSO optimized TID + IDN controller and COA tuned TID and IDN controller.

The main contributions of this work are outlined as follows:

  1. (i)

    To endorse a newly developed COA optimized TID + IDN controller to solve LFC problem of interconnected three-area multi-source system in deregulated scenario.

  2. (ii)

    To determine the advantages of the proposed controller in comparison to ISSA/SSA/PSO optimized TID + IDN, COA tuned IDN/ TID controllers.

  3. (iii)

    To solve the problems related to LFC by applying Coati Optimization Algorithm (COA) tuned TID + IDN controller in a three-area interconnected power system consisting of renewable and non-renewable units.

  4. (iv)

    A three-area system with different generating units is mathematically modelled using MATLAB/ Simulink environment.

  5. (v)

    To enhance the dynamic performance of the suggested system, TID + IDN controller is implemented.

  6. (vi)

    The response of the TID + IDN controller is compared with the output response of the controllers such as TID and IDN controller to prove its supremacy over other controllers.

  7. (vii)

    To illustrate the validity of the suggested work, different variations in load have been considered in the system.

  8. (viii)

    This research has been further continued to validate the dominance of the applied optimization technique by comparing the response with the responses of optimization algorithms such as PSO, SSA and ISSA.

Proposed TID + IDN controller for LFC

A proposed novel TID + IDN controller is the parallel combination of Tilt Integral Derivative (TID) controller and Integral Derivative Filter (IDN) controller. The advantages of a parallel combination of these two controllers include flexibility and adaptability for tuning the controller to different operating conditions along with the improved system reliability and redundancy, hence reducing the risk of failure. Proposed controller reduced sensitivity to parameter variations or changes in the controlled process. Figure 1 shows the block diagram of TID controller, IDN controller and proposed TID + IDN controller. Output of the proposed controller has been given in Eq. 3 which is the combination of TID (Eq. 1) and IDN (Eq. 2) controllers.

Fig. 1
figure 1

(a). Block diagram of TID controller (b). IDN controller. (c). TID + IDN controller.

Full size image
$$\frac{{U(s)}}{{E(s)}}=\frac{{{K_{i1}}}}{{{s^n}}}+\frac{{{K_{i2}}}}{s}+{K_{d1}}s$$
(1)
$$\left. {\frac{{U(s)}}{{E(s)}}} \right|=\left( {\frac{{sN{K_{d2}}}}{{s+N}}+\frac{{{K_i}}}{s}} \right)$$
(2)

Output of the proposed TID + IDN controller can be given by Eq. (3)

$$\left. {\frac{{U(s)}}{{E(s)}}} \right|=~~~~\frac{{{K_{i1}}}}{{{s^n}}}+\frac{{{K_{i2}}}}{s}+{K_{d1}}s+\left( {\frac{{sN{K_{d2}}}}{{s+N}}+\frac{{{K_i}}}{s}} \right)$$
(3)

Where, Ki1, Ki2, & Kd1 represent the gain for TID controller whereas Ki& Kd2 represent the gain of IDN controller and N is the filter constant.

Deregulated hybrid three area test system

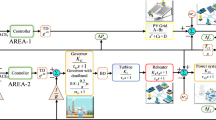
Figure 2 depicts the transfer function model of a three-area system designed for automatic generation control in a restructured scenario. This three-area multi-source system serves as the basis for analyzing Automatic Generation Control (AGC) in a deregulated environment70. The diagram illustrates the overall multi-area system featuring various generation units. To enhance system performance, Thyristor-Controlled Series Compensator (TCSC) and Redox Flow Battery (RFB) are integrated. This paper specifically considers GRC and GDB in a deregulated scenario71. Area 1 is comprised of three generation units, including a hydro power unit, Solar Thermal Power Plant (STTP), and a reheat thermal unit, all while considering generation rate constraints. Area 2 consists of three Generation Companies (GENCOs), a Dish-Stirling Solar Thermal System (DST), a hydro power unit, and a reheat thermal unit with GRC. Area 3 includes a thermal reheat unit with GRC, a Geothermal Power Plant (GTPP), and a hydro power unit. Each control area is provided with three different Distribution Companies (DISCOs). The mathematical model of this system is presented in Fig. 2. ∆f1, ∆f2 and ∆f3 are the system frequency deviations in Hz. For the thermal unit the GDB of 0.06% (0.036 Hz) and GRC of 3% p.u MW/min is considered72. For the hydro-plant GDB of 0.02%(0.012 Hz) is taken. The GRC of 270% p.uMW/min raising and 360% p.u MW/min lowering power generation are considered for the hydro unit. The solar insolation of the STPP and DSTS units are taken as 0.008puMW/m2. The pertinent parameters are provided in Appendix A (supplementary material file). The interconnected system under a deregulated scenario involves a total of nine Generation Companies (GENCOs) and nine Distribution Companies (DISCOs). When there is a power contract between DISCOs and GENCOs within the same control area, it is termed as a “poolco-based transaction.” On the other hand, if the transaction occurs between GENCOs and DISCOs from two different areas, it is referred to as a “bilateral transaction.” The term “contract violation” is used when the load demand exceeds the contracted value.

Objective function for automatic generation control (AGC)

The system consists of nine Generation Companies (GENCOs) and nine Distribution Companies (DISCOs). When there is a power contract between DISCOs and GENCOs within the same control area, it is termed as a “poolco-based transaction.” On the other hand, if the transaction occurs between GENCOs and DISCOs from two different areas, it is referred to as a “bilateral transaction.” The term “contract violation” is used when the load demand exceeds the contracted value. DISCO Participation Matrix (DPM) is used to specify the power contract between DISCOs and GENCOs. The total rows in DPM is same as the total number of generation companies and the total columns represent the number of distributed companies in the system. The summation of all the values in any column of a DPM is always one.

GENCO1, GENCO2, GENCO3, DISCO1, DISCO2 and DISCO3 are in area (1) GENCO4, GENCO5, GENCO6, DISCO4, DISCO5 and DISCO6 are in area (2) GENCO7, GENCO8, GENCO9, DISCO7, DISCO8 and DISCO9 are in area (3) Then the corresponding DPM is written as9.

\(DPM=\left[ {\begin{array}{*{20}{c}} {cp{f_{11}}}&{cp{f_{12}}}&{cp{f_{13}}}&{cp{f_{14}}}&{cp{f_{15}}}&{cp{f_{16}}}&{cp{f_{17}}}&{cp{f_{18}}}&{cp{f_{19}}} \\ {cp{f_{21}}}&{cp{f_{22}}}&{cp{f_{23}}}&{cp{f_{24}}}&{cp{f_{25}}}&{cp{f_{26}}}&{cp{f_{27}}}&{cp{f_{28}}}&{cp{f_{29}}} \\ {cp{f_{31}}}&{cp{f_{32}}}&{cp{f_{33}}}&{cp{f_{34}}}&{cp{f_{35}}}&{cp{f_{36}}}&{cp{f_{37}}}&{cp{f_{38}}}&{cp{f_{39}}} \\ {cp{f_{41}}}&{cp{f_{42}}}&{cp{f_{43}}}&{cp{f_{44}}}&{cp{f_{45}}}&{cp{f_{46}}}&{cp{f_{47}}}&{cp{f_{48}}}&{cp{f_{49}}} \\ {cp{f_{51}}}&{cp{f_{52}}}&{cp{f_{53}}}&{cp{f_{54}}}&{cp{f_{55}}}&{cp{f_{56}}}&{cp{f_{57}}}&{cp{f_{58}}}&{cp{f_{59}}} \\ {cp{f_{61}}}&{cp{f_{62}}}&{cp{f_{63}}}&{cp{f_{64}}}&{cp{f_{65}}}&{cp{f_{66}}}&{cp{f_{67}}}&{cp{f_{68}}}&{cp{f_{69}}} \\ {cp{f_{71}}}&{cp{f_{72}}}&{cp{f_{73}}}&{cp{f_{74}}}&{cp{f_{75}}}&{cp{f_{76}}}&{cp{f_{77}}}&{cp{f_{78}}}&{cp{f_{79}}} \\ {cp{f_{81}}}&{cp{f_{82}}}&{cp{f_{83}}}&{cp{f_{84}}}&{cp{f_{85}}}&{cp{f_{86}}}&{cp{f_{87}}}&{cp{f_{88}}}&{cp{f_{89}}} \\ {cp{f_{91}}}&{cp{f_{92}}}&{cp{f_{93}}}&{cp{f_{94}}}&{cp{f_{95}}}&{cp{f_{96}}}&{cp{f_{97}}}&{cp{f_{98}}}&{cp{f_{99}}} \end{array}} \right]\)

Where\(cp{f_{ij}}\) is known as “contract participation factor” i.e. p.u.

$$cpf_{{ij}} = \frac{{j^{{th}} {\text{ }}DISCOs{\text{ }}power{\text{ }}demand{\text{ }}from{\text{ }}i^{{th}} {\text{ }}GENCO}}{{j^{{th}} {\text{ }}DISCO's{\text{ }}total{\text{ }}power{\text{ }}demand}}$$
(4)

Power flow between control area-1 &area-2 can be computed based on the values of the cpf using the Eq. (5).

$$\Delta {P_{tie1 - 2scheduled}}=\sum\limits_{{i=1}}^{3} {\sum\limits_{{j=4}}^{6} {cp{f_{ij}}\Delta {P_{Lj}} - } } \sum\limits_{{i=4}}^{6} {\sum\limits_{{j=1}}^{3} {cp{f_{ij}}\Delta {P_{Lj}}} }$$
(5)

Tie-line power flow for interconnected lie between area-2 &area-3 can be determined applying the Eq. (6).

$$\Delta {P_{tie2 - 3scheduled}}=\sum\limits_{{i=4}}^{6} {\sum\limits_{{j=7}}^{9} {cp{f_{ij}}\Delta {P_{Lj}} - } } \sum\limits_{{i=7}}^{9} {\sum\limits_{{j=4}}^{6} {cp{f_{ij}}\Delta {P_{Lj}}} }$$
(6)

Tie-line power flow for interconnected lie between area-3 &area-1 can be calculated based on the values of the cpf employing the Eq. (7).

$$\Delta {P_{tie3 - 1scheduled}}=\sum\limits_{{i=7}}^{9} {\sum\limits_{{j=1}}^{3} {cp{f_{ij}}\Delta {P_{Lj}} - } } \sum\limits_{{i=1}}^{3} {\sum\limits_{{j=7}}^{9} {cp{f_{ij}}\Delta {P_{Lj}}} }$$
(7)

The actual tie line power flow through tie line between control area-1 and control area-2 is described by Eq. (8)

$$\Delta {P_{tie1 - 2actual}}=\frac{{2\pi {T_{12}}}}{s}\left( {\Delta {F_1}\left( s \right) - \Delta {F_2}\left( s \right)} \right)$$
(8)

The power flow through tie line between area-2 and area-3 is expressed by Eq. (9)

$$\Delta {P_{tie2 - 3actual}}=\frac{{2\pi {T_{23}}}}{s}\left( {\Delta {F_2}\left( s \right) - \Delta {F_3}\left( s \right)} \right)$$
(9)

The actual tie line power flow through connected line between area-3 and area-1 is represented by Eq. (10)

$$\Delta {P_{tie3 - 1actual}}=\frac{{2\pi {T_{31}}}}{s}\left( {\Delta {F_3}\left( s \right) - \Delta {F_1}\left( s \right)} \right)$$
(10)

The difference between actual power of the tie-line should be equal to zero at steady-state. This error is applied to evaluate area control error and can be expressed as Eq. (11).

Area control error of area-i can be expressed

$$AC{E_i}={B_i}\Delta {F_{ierror}}+\Delta {P_{ierror}}$$
(11)

The objective function is represented by:

$$J=ITAE=\int\limits_{0}^{{{t_{sim}}}} {(\left| {\Delta {F_1}} \right|+\left| {\Delta {F_2}} \right|+\left| {\Delta {F_3}} \right|+\left| {\Delta {P_{tie12}}} \right|+\left| {\Delta {P_{tie23}}} \right|+\left| {\Delta {P_{tie31}}} \right|).t.dt}$$
(12)
Fig. 2
figure 2figure 2

Multi area multi machine power system in deregulated system. (a) Power system. (b) GRC of thermal unit. (c) GRC of hydro unit. (d) TCSC controller. (e) Contract participation factor (cpf) of DISCOs for with GENCOs.

Full size image

Coatis optimization algorithm (COA)

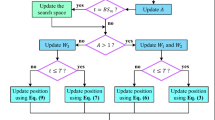
Mohammad Dhegihan developed a new algorithm in 202369 named coatis optimization technique. The proposed COA approach is inspired by the escaping behavior of the predators and the procedure of the coatis to attack iguanas. Flow chart of COA algorithm is depicted in Fig. 3. The location of the coatis is randomly created using Eq. (13):

$$\begin{gathered} X_{i} :x_{{i,j}} = lb_{j} + r.(ub_{j} - lb_{j} ), \hfill \\ i = 1,2,.....N, \hfill \\ j = 1,2,.....m \hfill \\ \end{gathered}$$
(13)

Where,\({X_i}\)is the location of the\({i^{th}}_{{}}\) coati in exploration zone, \({x_{i,j}}\)is the value of the \({j^{th}}_{{}}\) decision variable, N represent the sum total number of coatis,\({m_{}}\) is the number of decision variables & r is a real number generated randomly between [0, 1], \(l{b_j}\)and\(u{b_j}\)are the minimum and maximum value of the\({j^{th}}_{{}}\) variable, respectively.

The repositioning of coatis relies on two distinct behaviours: their approach towards attacking iguanas and their instinct to evade predators. As a result, the population undergoes updating in two distinct phases.

Phase1: The mathematical modelling of coatis’ population updating is depending on their action plan to encounter iguanas. A subset of coatis ascends a tree to arrive at iguana, intimidating it. Simultaneously, another subset of coatis remains beneath the tree, anticipating the iguana’s fall to the ground. Once the iguana descends, these coatis engage in the attack and capture. This strategic behaviour prompts coatis to explore diverse locations within the search area. The position of the member with best objective function represent the iguana’s location. The mathematical expression for the location of coatis ascending from the tree is defined in Eq. (13).

$$\begin{gathered} X_{i}^{{P1}} :X_{{i,j}}^{{P1}} = X_{{i,j}} + r.(iguana_{j} - I.X_{{i,j}} ), \hfill \\ i = 1,2,....(N/2)\& \hfill \\ j = 1,2,....m \hfill \\ \end{gathered}$$
(14)

Upon falling from the tree, the iguana undergoes a random change in location. Depending on the iguana’s new position, coatis adjust their ground locations, as indicated by the mathematical models presented in Eqs. (15) and (16).

$$\begin{gathered} iguana_{j}^{G} :iguana_{j}^{G} = lb_{j} + r.(ub_{j} - lb_{j} ), \hfill \\ j = 1,2,....m \hfill \\ \end{gathered}$$
(15)

\(\begin{gathered} X_{i}^{{P1}}:X_{{i,j}}^{{P1}}=\{ {X_{i,j}}+r.(iguana_{j}^{G} - I.{X_{i,j}})\} ,{F_{iguan{a^G}}}<{F_i} \hfill \\ else \hfill \\ X_{i}^{{P1}}:X_{{i,j}}^{{P1}}=\{ {X_{i,j}}+r.({X_{i,j}} - iguana_{j}^{G})\} \hfill \\ \end{gathered}\)

$$\begin{gathered} i = \left[ {\frac{N}{2}} \right] + 1.\left[ {\frac{N}{2}} \right] + 2....N\& \hfill \\ j = 1,2,....m \hfill \\ \end{gathered}$$
(16)

The assessment of a new location for each coati is permissible for an update only if the objective function value improves; otherwise, the coati maintains its current location. This updating condition, applicable for i = 1, 2,. . ., N is represented by Eq. (17).

$$\begin{gathered} {X_i}=\{ X_{{_{{i,}}}}^{{P1}},F_{{_{i}}}^{{P1}}<{F_i} \hfill \\ else \hfill \\ {X_i}={X_i} \hfill \\ \end{gathered}$$
(17)

Here \(X_{{_{{i,}}}}^{{P1}}\) is the updated location evaluated for the \({i^{th}}_{{}}\)coati, \(X_{{i,j}}^{{P1}}\) is its \({j^{th}}_{{}}\) dimension, \(F_{{_{i}}}^{{P1}}\) is its objective value, r is a random real number in between [0, 1], Iguana represents the iguana’s location, which actually refers to the position of the best member, \(iguan{a_j}\) is its \({j^{th}}_{{}}\)dimension, \({I_{}}\) is an integer, which is randomly selected from the set {1, 2}, \(iguana_{{}}^{G}\) is the position of the iguana on the ground, which is randomly generated, \(iguana_{j}^{G}\)is its \({j^{th}}_{{}}\)dimension, \({F_{iguan{a^G}}}\) is its value of the objective function.

Phase 2: The second phase, named as the exploitation phase, signifies the mathematical modelling of coatis’ behaviour to escape from their location when under attack by predators. This behaviour is mathematically characterized by generating a random position in proximity to each coati’s current location, as outlined in Eqs. (18) and (19).

$$lb_{j}^{{local}} = \frac{{lb_{j} }}{t},ub_{j}^{{local}} = \frac{{ub_{j} }}{t},where\,{\mkern 1mu} t = 1,2,......T$$
(18)
$$X_{i}^{{p2}} :x_{{i,j}}^{{P2}} = x_{{i,j}} + (1 - 2r).(lb_{j}^{{local}} + r.(ub_{j}^{{local}} - lb_{j}^{{local}} )),{\mkern 1mu} i = 1,2,....,N\& j = 1,2,....m$$
(19)

The new updated location is considered if the objective function corresponding to new position is better, which is represented by Eq. (20).

$$\begin{gathered} {X_i}=\{ X_{{_{{i,}}}}^{{P2}},F_{{_{i}}}^{{P2}}<{F_i} \hfill \\ else \hfill \\ {X_i}={X_i} \hfill \\ \end{gathered}$$
(20)

Here \(X_{i}^{{P2}}\) is the updated location evaluated for the \({i^{th}}_{{}}\)coati, \(x_{{i,j}}^{{P2}}\) is its \({j^{th}}_{{}}\) dimension, \(F_{{_{i}}}^{{P2}}\) is its objective function value, r is a number generated randomly between [0, 1]. For the\({j^{th}}_{{}}\) decision variable \(lb_{j}^{{local}}\) and \(ub_{j}^{{local}}\) are the lower and upper bounded value respectively.‘T’ is maximum number of iteration.

Fig. 3
figure 3

Flow chart of COA algorithm.

Full size image

Results and discussions

Case study I (Poolco agreement)

In this scenario, all Generation Companies (GENCOs) across the three areas are equally participating in Automatic Generation Control. A load disturbance of 0.03 per unit (p.u.) is introduced specifically in area 1, and this load perturbation is evenly distributed among the three Distribution Companies (DISCOs) operating in the same area. Importantly, the remaining DISCOs in the different control areas are not drawing load from the GENCOs. In this particular case, the Demand Participation Matrix (DPM) is represented in the following manner. Load change in all the DISCOs of area 1 are: DISCO1 = 0.01, DISCO2 = 0.01, DISCO3 = 0.01.

\(DPM=\left[ {\begin{array}{*{20}{c}} {0.333}&{0.333}&{0.333}&0&0&0&0&0&0 \\ {0.333}&{0.333}&{0.333}&0&0&0&0&0&0 \\ {0.333}&{0.333}&{0.333}&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \\ 0&0&0&0&0&0&0&0&0 \end{array}} \right]\)

Notably, in the DPM matrix, the presence of null values in the corresponding cells indicates the absence of contractual agreements between a DISCO and a GENCO of two separate control area. Powers generated by different GENCOs are evaluated as.

ΔPg1=0.0099, ΔPg2=0.0099, ΔPg3=0.0099, ΔPg4=0, ΔPg5=0, ΔPg6 = 0, ΔPg7= 0, ΔPg8= 0, ΔPg9 = 0.

Under steady-state conditions, it is essential that the power generated by Generation Companies (GENCOs) matches the load demanded by Distribution Companies (DISCOs) within their respective regions. The variations in frequencies across different regions and the power flow through three tie-lines are illustrated in Fig. 1. We have also compiled various time domain specifications, including undershoot (Ush), overshoot (Osh), and settling time (Ts), along with values of ITAE performance index while considering an error margin of 0.02% for these dynamic responses, as detailed in Tables 1 and 2. Optimal values of controller’s parameters tuned with different optimization algorithm have been given in Table 3.

Table 1 Transient performance indices for frequency variation in three areas for case study I.
Full size table
Table 2 Transient performance indices for Tie-line power in three areas for case study I.
Full size table
Table 3 Optimally tuned parameters of different controllers with different optimization techniques for case study I.
Full size table

Figure 4 clearly demonstrates that the TID + IDN controller outperforming TID and IDN controllers when tuned with COA optimization technique. Cascaded TID + IDN controller exhibits faster and smoother responses compared to the other controllers, with regards to the dynamic relationship between frequency and tie-line power. The proposed controller effectively minimizes the peaks and troughs in the transient responses of area frequency deviation (Δf) and tie-line power deviation (ΔPtie). Furthermore, it is worth noting that the controller based on the COA outperforms controllers based on PSO, SSA and ISSA as shown in Fig. 5. Convergence characteristics of SSA, PSO, ISSA and COA with proposed controller has been shown in Fig. 6 which validates the defectiveness of the optimization techniques in terms of speed and efficiency. Figure 7 represents the power generation output for case study I.

Fig. 4
figure 4

Comparison of different controllers with COA optimization techniques-case study I. (a) Frequency deviation in area-1. (b) Frequency deviation in area-2. (c) Frequency deviation in area-3. (d) Tie-line power deviation between areas 1–2. (e) Tie-line power deviation between areas 2–3. (f) Tie-line power deviation between areas 3 − 1.

Full size image
Fig. 5
figure 5

Comparison of perturbed response of variables with different optimization techniques based TID + IDN controller case study I. (a) Frequency deviation in area-1. (b) Frequency deviation in area-2. (c) Frequency deviation in area-3. (d) Tie-line power deviation between areas 1–2. (e) Tie-line power deviation between areas 2–3. (f) Tie-line power deviation between areas 3 − 1.

Full size image
Fig. 6
figure 6

Convergence characteristics of SSA, PSO, ISSA and COA with proposed controller.

Full size image
Fig. 7
figure 7

Power generation output in case study I. (a) Power generation output of area-1. (b) Power generation output of area-2. (c) Power generation output of area-3.

Full size image

Case study II (bilateral agreement)

In this scenario, Distribution Companies in any region have the autonomy to request power from Generating Companies located in any region. Each GENCO adjusts its power generation to meet the requirements of DISCOs based on the transaction allocated by the administrator. For bilateral transactions, the DPM matrix is provided as follows.

Load change in all the DISCOs of area 1 are: DISCO1 = 0.01, DISCO2 = 0.01, DISCO3 = 0.01.

\(DPM=\left[ {\begin{array}{*{20}{c}} {0.1}&{0.1}&{0.2}&{0.1}&{0.1}&{0.1}&{0.2}&{0.2}&{0.3} \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.2}&0 \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.2}&{0.1}&{0.1}&{0.1}&{0.1} \\ {0.2}&{0.1}&{0.1}&{0.2}&{0.1}&{0.2}&{0.1}&{0.1}&{0.0} \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.0}&{0.2} \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.05}&{0.2} \\ {0.1}&{0.2}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.05}&{0.0} \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1} \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.2}&{0.1} \end{array}} \right]\)

In this particular context, we are focusing on a bilateral agreement that has been established between three area power systems. All the DISCOs in each area are currently undergoing shifts in their electrical load, with an aggregate load change of 0.03 per unit (pu) occurring in area 1, which is mirrored by an equivalent change in area 2. To delve into the specifics of individual demands from Distribution Companies (DISCOs), in area 1, DISCO1 has a requirement of 0.01, DISCO2 necessitates 0.01, and DISCO3 demands 0.01. On the other side, in area 2, DISCO4 requires 0.01, DISCO5 has a need for 0.01, and DISCO6 has a substantial demand of 0.01. In area-3, DISCO7 requires 0.01, DISCO8 has a need for 0.01, and DISCO9 has a substantial demand of 0.01. The formulation of the Demand Participation Matrix (DPM) has been significantly shaped by the agreements that have been forged between these DISCOs and Generation Companies (GENCOs).

Powers supplied by different GENCOs are calculated.

ΔPg1 = 0.014, ΔPg2 = 0.009, ΔPg3 = 0.01, ΔPg4 = 0.011, ΔPg5 = 0.009, ΔPg6 = 0.0095, ΔPg7 = 0.0085, ΔPg8 = 0.009, ΔPg9 = 0.01.

The power generated in three separate control areas are0.033 p.u,0.0295p.u. and 00.0275p.u., respectively. Consequently, the demand power by all DISCOs is matched to the generated power by all the GENCOs.

Tables 4 and 5 compile the time domain parameters of the responses along with values of ITAE performance index, clearly demonstrating that the proposed controller significantly reduces both overshoots and undershoots. Optimal values of controller’s parameters tuned with four separate optimization algorithm have been given in Table 6.

Table 4 Settling time and overshoot/ undershoot for frequency variation in three areas for case study II.
Full size table
Table 5 Settling time and Overshoot/ undershoot for tie-line power variation in three areas for case study II.
Full size table
Table 6 Optimally tuned parameters of different controllers with different optimization for case study II.
Full size table

Figure 8 displays the responses in terms of tie-line power and frequency oscillation. It is evident that the TID + IDN controller, utilized in the existing system during bilateral transactions, exhibits outstanding performance when compared to other controller designs. This is achieved by effectively constraining the amplitudes of peaks and valleys while also reducing the settling times. Furthermore, the COA tuned controllers have yielded superior outputsas compared to those based on PSO, SSA and ISSA based controllers, as observed in Fig. 9. Figure 10 Shows the power generation of each unit in case study II.

Fig. 8
figure 8

Comparison of different controllers with COA optimization techniques-case study II. (a) Frequency deviation in area-1. (b) Frequency deviation in area-2. (c) Frequency deviation in area-3. (d) Tie-line power deviation between areas 1 & 2. (e) Tie-line power deviation between areas 2 & 3. (f) Tie-line power deviation between areas 3 & 1.

Full size image
Fig. 9
figure 9

Comparison of perturbed response of variables with different optimization techniques based TID + IDN controller -case study II. (a) Frequency deviation in area-1. (b) Frequency deviation in area-2. (c) Frequency deviation in area-3. (d) Tie-line power deviation between areas 1 & 2. (e) Tie-line power deviation between areas 2 & 3. (f) Tie-line power deviation between areas 3 & 1.

Full size image
Fig. 10
figure 10

Power generation output in case study II. (a). Power generation output of area-1 in case-2. (b) Power generation output of area-2 in case-2. (c) Power generation output of area-3 in case-2.

Full size image

Case study III (contract violation)

In the context of contract violations, any increase in the contracted power size is covered by the excess power demanded by DISCOs within the same area. In this study, DISCOs in area-1 breach the contract by requesting an additional 0.1p.u power as local load for that area.

$$DPM=\left[ {\begin{array}{*{20}{c}} {0.1}&{0.1}&{0.2}&{0.1}&{0.1}&{0.1}&{0.2}&{0.2}&{0.3} \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.2}&0 \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.2}&{0.1}&{0.1}&{0.1}&{0.1} \\ {0.2}&{0.1}&{0.1}&{0.2}&{0.1}&{0.2}&{0.1}&{0.1}&{0.0} \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.0}&{0.2} \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.05}&{0.2} \\ {0.1}&{0.2}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.05}&{0.0} \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1} \\ {0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.1}&{0.2}&{0.1} \end{array}} \right]$$

Figure 11 illustrates the superior performance of TID + IDN controller in terms of both speed and smoothness compared to its competitors. Tables 7 and 8 provide a summary of the transient specifications, confirming that COA driven TID + IDN controller significantly reduces both undershoot and overshoot. Optimal values of controller’s parameters tuned with four separate optimization algorithm have been given in Table 9. Figure 12 displays generation output of generating units in case study III.

Fig. 11
figure 11

Response of different controllers with COA optimization techniques-case study III. (a) Frequency deviation in area-1. (b) Frequency deviation in area-2. (c) Frequency deviation in area-3. (d) Tie-line power deviation between areas 1 & 2. (e) Tie-line power deviation between areas 2 & 3. (f) Tie-line power deviation between areas 3 & 1.

Full size image
Fig. 12
figure 12

Power generation output in case study III. (a) Power generation output of area-1 in case-3. (b) Power generation output of area-2 in case-3. (c) Power generation output of area-3 in case-3.

Full size image
Table 7 Time domain parameters for frequency variation in three areas for case study III.
Full size table
Table 8 Settling time and Overshoot/ undershoot for tie-line power variation in three areas for case study III.
Full size table
Table 9 Optimized parameters of different controllers for case study III.
Full size table

Case study IV: analyzing the robustness of proposed controller with varying step load demand and with sinusoidal input

In this study, we investigate the robustness of the proposed COA based TID + IDN controller for LFC under conditions of frequent load changes. The adaptability of the proposed concept is examined through load variations in all the three areas, each occurring after a 30-second interval. Figure 13 illustrates the step load changes in all the areas over time. Figure 14 displays the deviations in the frequency of areas 1, 2 and 3, along with corresponding changes in tie-line power. The system is simulated using the TID + IDN controller optimized by the COA algorithm for the initial load change.

From Fig. 15, it is evident that the perspective way for addressing the LFC problem results in improved system dynamics, constancy, and resilience of the power system when subjected to dynamic load changes at regular intervals. These findings highlight the efficacy of the COA-driven TID + IDN controller in enhancing the system response in the face of varying and challenging load scenarios.

Fig. 13
figure 13

Dynamic operational shift (Load change) in the area 1, area 2 and area 3.

Full size image
Fig. 14
figure 14

Transient response due to random change in load demand. (a) Frequency deviation in area-1. (b) Frequency deviation in area-2. (c) Frequency deviation in area-3. (d) Tie-line power deviation between areas 1 & 2. (e) Tie-line power deviation between areas 2 & 1. (f) Tie-line power deviation between areas 3 & 1.

Full size image
Fig. 15
figure 15

Response due to sinusoidal input in case study I. (a) Sinusoidal input in area-1 in case study I. (b) Frequency deviation in area-1 due to sinusoidal input.

Full size image

Figure 15 represents the frequency response of area1 due to application of sinusoidal input in area 1 in poolco transaction.

Case study V: sensitivity ANALYSIS

The efficacy of the suggested load frequency control concept has been confirmed through testing under varying parameters within the system’s dynamics. These parameters, including the thermal turbine time constant (Tt) and power system time constant (Tps), were subjected to a 25% change in both positive and negative directions. Figure 12 illustrates the perturbed frequency response across areas 1, 2, and 3 and the fluctuation in the power flow in different tie-line with a 25% variation in Tt. Similarly, Fig. 16 demonstrates the perturbed frequency response across the same areas alongside variations in tie-line powers due to a 25% change in Tps. The figures collectively demonstrate the system’s stability despite fluctuations in various parameters, thus validating the proposed concept’s sensitivity and robustness in addressing load frequency control challenges within power systems.

The suggested control theory for load frequency control has undergone rigorous verification to assess its sensitivity under varying conditions within the system’s dynamics. This validation process involved testing the concept while systematically changing different parameters of the test system. These parameters include the time constants associated with the turbine (Tt) and time constant of generator (Tps). Each of these parameters was subjected to a 25% change in both positive and negative values to simulate real-world operational shifts. To analyse the impact of these parameter variations, dynamic response of frequencies and tie-line power have been shown. Figure 12 displays the perturbed frequency responses observed across areas 1, 2, and 3 of the test system, as well as the resulting fluctuations in tie-line power, due to a 25% variation in the turbine time constant (Tt). Figure 12 illustrates similar perturbed frequency responses across the same areas along with the variations in tie-line powers resulting from a 25% change in the power system time constant (Tps). Despite these parameter variations, the test system consistently demonstrated stability, as depicted in the figures. This resilience justifies the sensitivity and fitness of the suggested concept in effectively addressing the challenges associated with LFC in the system. In essence, the findings validate the concept’s capability to adapt and maintain system stability even under dynamic shifts in various system parameters.

Fig. 16
figure 16

Dynamic response of the system with change in system parameters (Tt &Tps). (a) Frequency deviation in area (1) (b) Frequency deviation in area (2) (c) Frequency deviation in area (3) (d) Tie-line power deviation between areas 1 & 2. (e) Tie-line power deviation between areas 2 & 3. (f) Tie-line power deviation between areas 3 & 1. (g) Frequency deviation in area (1) (h) Frequency deviation in area (2) (i) Frequency deviation in area (3) (j) Tie-line power deviation between areas 1 & 2. (k) Tie-line power deviation between areas 2 & 3. (l) Tie-line power deviation between areas 3 & 1.

Full size image

Case study VI: Effect of TCSC FACTS controller

The incorporation of renewable energy sources and diverse control mechanisms introduces complexity and non-linearity to the system. The perturbed responses observed in cases I and II clearly indicate heightened the variation in power flow in the tie-line. To mitigate these oscillations, the implementation of a FACT controller, such as the Thyristor-Controlled Series Capacitor (TCSC), is proposed. The TCSC is adept at swiftly and steadily controlling power, offering the potential to mitigate oscillations within a short time frame.

Figure 17 illustrates the output response of the system employing TCSC controller for the Poolco agreement between Generation Companies (GENCOs) and Distribution Companies (DISCOs). The visualization depicts the efficacy of a COA -driven TID_IDN controller in conjunction with an integrated TCSC in minimizing oscillations in tie-line power.

Figure 18 represent the stability of the controller. Gain margin with value 7.02dB and phase margin of 27.5 degree justify the stability of the proposed controller.

Fig. 17
figure 17

Perturbed response for the system with TCSC for Poolco agreement. (a) Frequency deviation in area (1) (b) Frequency deviation in area (2) (c) Frequency deviation in area (3) (d) Tie-line power deviation between areas 1 & 2. (e) Tie-line power deviation between areas 2 & 3. (f) Tie-line power deviation between areas 3 & 1.

Full size image
Fig. 18
figure 18

Frequency response graph of TID + IDN controller.

Full size image

Conclusion

The study introduces a novel Coatis Optimization Algorithm (COA) for a TID + IDN controller structure, aiming to manage the disturbances in frequency of a system having three separate control area. The research demonstrates the superiority of the proposed algorithm over existing PSO, SSA, and ISSA algorithms in a deregulated area. Results indicate a notable decrease in performance indices when applying the COA algorithm compared to other techniques. Consequently, the application of the proposed COA-based TID + IDN controller approach is justified. This approach is implemented for frequency regulation in a three-area power system, and simulation outputs reveal its superior efficiency compared to other controllers. The study concludes that the COA-based TID + IDN controller significantly minimizes the maximum peak overshoot and undershoot of the system following small disturbances. Lastly, a sensitivity analysis, performed on system parameters, underscores the efficacy of the suggested technique. Finally, the fruitfulness of the proposed control theory has been tested by incorporating TCSC FACTS controller in the system. While the current work incorporates only a few renewable energy sources in the hybrid system, future research could explore the application of additional sources and different controllers, testing new algorithms in distributed systems. Additionally, hardware validation remains a potential avenue for future investigation. This proposed technique can not be implemented in case of fault analysis because the disturbance applied to the system under analysis is very small as compared to the fault magnitude which is more. This is the limitation of the proposed technique.