Introduction

Concrete is currently consumed in enormous quantities by the building industry, with global consumption reaching up to 10 billion tons per year1,2. Due to the increasing global population, it is anticipated that by 2050, the demand for concrete would increase significantly and may reach up to 18 billion tons yearly3,4 and a sizable portion of this concrete production led to the significant generation and emission of CO2, which harms the environment5. Studies show that the cement industry alone accounts for roughly 8% of global CO2emissions6,7,8, highlighting the urgent need for sustainability in the construction sector9. Consequently, research into alternative materials, particularly supplemental cementitious materials (SCM), has become a major area of focus10,11,12,13,14. Among these, the use of waste products with high pozzolanic reactivity has been explored as a potential solution to reduce environmental impact in concrete mixtures13,15,16,17,18. One such material, palm oil fuel ash (POFA), has recently gained attention as an environmentally friendly option for producing more sustainable concrete19,20,21,22,23.

POFA is a byproduct of producing palm oil that is produced in reactors by burning waste materials such as fiber, palm oil shells, and empty fruit bunches24. POFA’s increased pozzolanic reactivity, which is the result of heat treatment, justifies its use in concrete mixes in place of cement25,26. Because of the growing demand for POFA, palm oil factories eventually produce a significant amount of fuel ash15. While Thailand produces more than 100,000 tons of POFA year on average, the Malaysian sector produces almost 3 million tons of POFA annually27. A maximum of 2 kg of palm oil can be generated for every 8 kg of raw palm oil batch; the remaining material is classified as dry biomass14,28. When this waste residue is disposed of in an untreated manner into open space and used as landfill material, it might harm people by producing various illnesses28. When compared to standard materials, POFA is more energy-efficient and environmentally benign due to its geopolymer properties29. Thus, it is possible to achieve sustainability and cost-effectiveness by substituting POFA for a portion of cement, which may also lower transportation costs and the amount of waste dumped in landfills30,31.

The most important aspect influencing concrete’s strength and durability attributes is thought to be the fineness of POFA32. Numerous scholars are investigating the relationship between concrete strength and POFA fineness and pozzolanic reactivity33,34. Several research with varying outcomes improved the characteristics of concrete35,36,37. According to the findings of Chindaprasirt et al.'s study38, 20% OPC replacement with POFA improved workability and mechanical performances. The research additionally documented the pattern of strength degradation resulting from the elevated water consumption requirement at 40% cement replacement by POFA. Tangchirapat et al.'s39likewise recommended an increase of 8% using a comparable type of replacement. In 10–20% of POFA replacements, the ideal strength increase pattern was assessed. When compared to cement-based concrete, high-volume POFA concrete decreased production costs by 8–12% and CO2 emissions by 32–45%. It results in lower natural resource usage and energy consumption, which causes the concrete industry to refocus on more ecologically friendly and sustainable manufacturing practices40,41,42.

It is found that, the utilization of POFA with other SCMs or high pozzolanic43,44in high strength concretes (HSC)13,33such as geopolymer45, self-compacting46, and lightweight concrete47, it greatly increases the durability and some other properties of concrete. To produce high-strength concrete, POFA was employed as a supplemental binder by Zayed et al.26. The treatment of POFA resulted in the creation of treated POFA (T-POFA) or ultrafine POFA (UPOFA), which had positive impacts on the concrete’s strength, workability, and fluid transport characteristics. According to the study, UPOFA-infused high-strength concrete had better fluid transport characteristics and greater compressive strength26,33. In separate research, Zayed et al.48 found that when HSC containing ground POFA (GPOFA) and OPC was compared, the latter included inferior strength, shorter setting periods, less workability, and worse physical features. This study demonstrated that the POFA’s carbon content and particle size had almost no impact on the CS of HSC provided OPC replacement was limited to a maximum of 40%. Alsubari et al.40 further suggested that treated POFA could improve the newly discovered properties of SCC in place of OPC. However, when compared to the control mix that contained 100% OPC, SCC mixtures containing 50 to 70% treated POFA initially showed reduced compressive strength. Another study by Alsubari et al.49 looked at the use of modified treated POFA (MT-POFA) in SCC at several percentages (0%, 30%, 50%, and 70%) as a cement substitute. The result analysis showed that the mechanical qualities of MT-POFA concrete declined over time, but that these properties significantly improved as the cure period has risen. Moreover, in studying the effect of fineness degree of POFA, Philip et al.50 used 45 and 150 μm particle sizes of POFA with 20% OPC replacement and found that found the optimal value of 45 μm particle size which increased the CS. Notably, the results imply that POFA fineness optimization and its absorption into concrete greatly improve strength and durability, which makes it a perfect fit for environmentally friendly building methods.

Advances in artificial intelligence (AI) have led to the application of machine learning (ML) techniques for the prediction of diverse mechanical and physical characteristics of concrete51. Many machine learning techniques, like as clustering, regression, and classification, can be applied to quantify a variety of additional features to produce dependable compressive strength estimates52,53,54. Gene expression programming (GEP) was employed by Javed et al.55 to forecast the CS of concrete composed of sugarcane bagasse ash. Moreover, ANN was used by Getahun et al.56to forecast the lifespan of concrete that contains leftover components. Moreover, ANNs, ANNs with combined inputs and ANNs with nature inspired optimizers such as particle swarm optimization (PSO), genetic algorithms (GA), beetle algorithms and ant colony optimization have been proposed in the literature in recent years. Combining several soft computing techniques can result in the development of better prediction models, such as artificial bee colony algorithms, PSO, imperialist competitive algorithm, and ANN mixed with GA. These combinations have demonstrated encouraging outcomes in resolving challenging issues, suggesting that these methods could be applied to tasks involving prediction and optimization57,58,59,60. In this regard, Yasmina et al.61used hybrid models that included ANN with additional optimization approaches including PSO and GA to forecast the CS of POFA concrete. Their findings demonstrated that the hybrid ANN models performed better than standalone ANN and other optimization strategies, delivering increased predicted accuracy. Furthermore, a few well-known machine learning techniques, like bagging, support vector machines, Extreme Gradient boosting (XGB), and hybrid machine learning models, are frequently employed extensively in huge amounts of data of CS prediction of SCMs materials62. These tree-based machine learning models are popular ensemble techniques63,64. The mechanical properties of many recently developed advanced concrete types and HSC65,66such as self-healing concrete67, fiber-reinforced rubberized recycled aggregate concrete68,69, UHPC70, and RCA71,72, have been predicted by several studies. Thus, creating a trustworthy database containing pertinent training and test cases is essential. This first step ensures that pertinent data is available for model training and performance evaluation. Data preprocessing, regression analysis and correlation analysis are statistical investigations carried out by gathering datasets from previous studies and extracting important information that directs the creation of sophisticated ML models73.

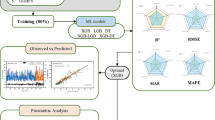
Therefore, to perform optimization and predictive modeling, this study offers a comparative examination of advanced machine learning and deep learning models such as Bagging, improved version of SVM i.e., LSSVM, XGB, LGBM, ANN with advance structure of BPNN optimized with Adam, GEP and hybrid XGB-LGBM model. It examines and evaluates prior studies to determine the main variables affecting POFA concrete’s compressive strength, such as the amount of POFA and cement, aggregate ratios, water-to-binder ratios, dose of superplasticizer, and curing time. The study investigates the link between these characteristics and compressive strength using a heatmap to graphically represent the associations, using a vast dataset of 407 samples with six input features. The results yield five performance indices: coefficient of determination (R2), root mean squared error (RMSE), normalized root mean squared error (NRMSE), Willmott index (d), and mean absolute error (MAE). In addition, the model’s interpretability and performance are evaluated using SHAP analysis and Taylor diagrams to confirm the results and offer a thorough comprehension of the significant parameters.

Existing literature

Predicting the characteristics of POFA concrete, particularly its compressive strength, has not received much attention in literature. Most of the research that is now accessible has created models using their own experimental datasets, which usually include less than 100 data points. The use of ML models in various concrete types is briefly covered in this section, with particular attention paid to POFA or comparable concrete types. Table 1 presents in detail the models utilized on concrete type by researchers with obtained performance metrics.

Table 1 Existing literature about ML models utilization in concrete properties prediction.
Full size table

The CS of concrete incorporating steel slag was predicted using ANN, full quadratic (FQ) models, multi-logistic regression (MLR), and M5P-tree. It is found that ANN proved to be the most accurate predictor of CS, while the FQ model was most useful in estimating the electrical resistivity of the concrete74. In the case of metakaolin-containing concrete, the M5P-tree model performed better in CS forecasting rather than LR, NLR, and MLR75. In a different investigation, the FEM was used to forecast the ultimate strength of columns, and the results were compared to both GEP model and actual data. GEP produced results that were more in line with the experimental findings than FEM76. Also, while forecasting the CS of rubber modified concrete, models such as MEP, ANN, MARS, and NLR were applied, with ANN appearing as the most successful77. The M5P-tree model outperformed LR, MLR, FQ, and other techniques in terms of predicted accuracy for rubberized SCC78. Models including LR, FQ, M5P-tree, and ANN were created to estimate the CS of HSC; the findings showed that the ANN model produced the most accurate forecasts79. To estimate the CS of fly ash-modified concrete, ANN model was improved by adding PSO and the imperialist competitive algorithm (ICA); the ANN-PSO model yielded the most accurate findings in this regard80.

Recently, researchers have tended to utilize advanced AI techniques. In this regard, ANN, ANNX, PSO, GA, and other machine learning algorithms were used by Kellouche Y et. al61. utilized 249 sample dataset and employed ANN, ANNX, PSO, and GA to forecast the CS of POFA enriched concrete. They found that the ANN models outperformed PSO and GA achieving the best predictive accuracy. Moreover, Alahmari et al.68 used bagging, GEP, and ANN models to predict the air-cooled CS of rubberized concrete while taking temperature, exposure time, rubber fiber content, and W/C ratio into account. ANN outperformed bagging and GEP in terms of R2 value (0.984), and it also showed the lowest RMSE and MAE of all the models. Using a dataset of 626 compressive strength and 317 flexural strength data points, Das et al.81 employed ML and hybrid ML models, especially XGB, LGBM, and a hybrid XGB—LGBM, to predict the CS and FS of UHPC. The hybrid XGB-LGBM model achieved the maximum accuracy in forecasting both CS and FS, with the best R2 values and lowest RMSE, exceeding the separate models.

Based on a thorough review of existing literature, this study utilized advanced AI techniques, including LSSVM, Bagging, XGB, LGBM, Hybrid XGB-LGBM, BPNN, and GEP models. These models were selected due to their proven effectiveness in handling complex, non-linear relationships and their superior performance in similar predictive tasks, particularly in the context of concrete and material property prediction. LSSVM was chosen for its enhanced ability to manage non-linear data patterns in regression tasks82, while Bagging was included to improve model stability and reduce variance68. XGB and LGBM are well-known for their high accuracy and efficiency with large, structured datasets, making them ideal for predicting material properties62. The Hybrid XGB-LGBM model was selected to combine the strengths of both boosting algorithms, maximizing predictive performance. BPNN with the Adam optimizer was incorporated for its capacity to model highly non-linear relationships82, while GEP was chosen for its symbolic regression capabilities, offering interpretable results68. The selection of these models was based on their demonstrated success in similar studies and their suitability for the task of predicting compressive strength in POFA-based concrete. The details about the dataset, used parameters and models are explained in detail in the subsequent sections.

Research methodology

Description of the dataset.

This study tries to forecast the compressive strength of POFA concrete, given the availability of experimental data on the material and its advantages to the environment and economy. Figure 1 illustrates the overall framework of the research, presenting the systematic process that includes several fundamental stages of the study pipeline. For this, a dataset of 407 samples is utilized, collected from 18 journal articles (as sourced in Table 2). Complete details, including the data sources with URLs/DOIs for accessing the original studies, are provided in the Supplementary file (S1-2). Concrete’s compressive strength depends on several elements, mainly on its composition and curing conditions. Cement content, POFA dosage, water-to-binder (W/B) ratio, aggregate (CA/FA) ratio, superplasticizer, and curing time (age) are the six important variables used as model inputs. The desired output variable is the compressive strength.

Fig. 1
figure 1

Research framework outlining the key stages of the study pipeline, from dataset collection to model development and SHAP analysis.

Full size image
Table 2 Collected experimental data sources.
Full size table

To ensure the study’s reproducibility, additional details about the dataset are provided in Table 3, which presents key statistics for each variable, including the minimum, maximum, average, and standard deviation. Figure 2 illustrates the distribution and range of the variables, offering insights into the data’s spread and facilitating the identification of any unusual data points or patterns.

Table 3 Statistical characteristics of dataset.
Full size table
Fig. 2
figure 2

Statistical range of dataset.

Full size image

To evaluate the robustness and dependability of the experimental results, it is imperative that the dataset spreads over the parameter values as demonstrated by Fig. 2's well-distributed frequency. Most data points for the input variables fall into one of the following ranges: [200–600] kg/m3 for Cement, [0–200] kg/m3 for POFA, [1.0–1.5] for CA/FA, [0.2–0.9] for W/B, [0–40] kg/m3 for SP, and [0–100] days for Age. This suggests that when forecasting results for fresh data that falls between these intervals, the machine learning model will perform better. Because the distribution of data is sparse in such areas, it is anticipated that the accuracy of the model would decline for values outside of these ranges.

Training and testing data

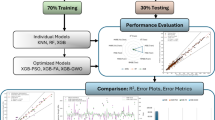
A total of 284 data points, or 70% of the dataset, are used to train the models; the remaining 123 data points or 30%, are set aside for testing.

Moreover, the occurrence of multicollinearity in machine learning models is a significant issue that arises when two or more predictor variables exhibit high levels of correlation95. Among the issues it may lead to unstable and more variance in coefficient estimates, less interpretability of the model, and a higher chance of overfitting96,97,98,99. It is intimated that the R (correlation coefficient) be maintained less than 0.8 to reduce multicollinearity100,101,102. Moreover, when there is a positive correlation (+ 1), the target variable rises together with the input variable. On the other hand, when there is a negative correlation (−1), the target variable decreases as the input variable increases96,97,103. To find strongly linked predictors, Pearson and Spearman correlation heatmap (Fig. 3) is used. This demonstrated that there was no chance of multicollinearity in the models as all the variables had R < 0.8. Notably, as shown in Fig. 3, strong positive correlations found between cement and SP with CS (0.65 and 0.7, respectively) show that these two variables significantly affect the target variable. W/B and CS have a somewhat negative association (−0.59). POFA has a negligible impact on CS; this finding may be explained by POFA’s large particle size and sluggish pozzolanic activity104. Furthermore, curing time has a weakly positive connection with CS at 0.25, suggesting that although curing time affects strength, its influence is not particularly great in this instance. Although POFA and curing have a very minimal effect in this dataset, the combination of their delayed response and longer curing time implies that the compressive strength might increase over time.

Fig. 3
figure 3

Multicollinearity heat map.

Full size image

Data preprocessing

The main goal of data preprocessing is to guarantee data integrity by eliminating duplicates, blank cells and fixing mistakes. Data transformation is a crucial step in this process that entails standardization to match the scales of various variables and reduce bias in machine learning models105,106. Data normalization is a crucial preprocessing procedure that sets the input feature scale’s mean to zero and standard deviation to one. By preventing any one feature from having an excessively large impact on the model due to its size, this procedure helps to increase the stability and performance of ML models107. “Standard Scaler” method from python library “scikit-learn” was used to normalize the dataset used in this investigation. This method scales each variable to have a unit variance and centers the data around the mean. Potential biases are reduced, and the model’s performance is improved by standardizing the data. For machine learning algorithms that are vulnerable to feature scaling, this standardization is essential since it keeps any one feature from controlling the learning process because of its size. More accurate and dependable predictions are produced when the model examines all characteristics equally, which is especially crucial for algorithms that employ gradient-based techniques or distance measures108,109,110.

Advanced modeling techniques

The research uses advanced modeling techniques LSSVM, Bagging, XGB, LGBM, Hybrid XGB-LGBM, BPNN and GEP models due to their superior performance to predict the CS of POFA based concrete. The working process of these utilized models with their parameters used in study are explained below.

Bagging algorithm

Bagging is one of the most often used techniques for ensemble learning111. By choosing random subsets of the original dataset and combining the predictions of each individual regressor through voting or averaging, bagging regression produces a final estimate. By adding unpredictability to the model-building process, this meta-predictor technique significantly reduces variation—which often arises in black-box estimations112. It has been demonstrated through experiments on both simulated and real datasets that bagging can lead to appreciable performance gains when regression trees are employed for subset selection in linear regression and classification. The model’s estimate instability is a crucial element; bagging functions best when slight modifications to the training data result in appreciable variations to the estimator68. Although bagging can be used with any approach, it is most used in connection with decision trees and is a specific type of model averaging113. By training on a range of data subsets, bagging lessens the effect of data fluctuations, improving the performance of unstable estimators like regression trees. Combining predictions increases the model’s resiliency and accuracy112,114. The ensemble approach is a well-established tactic because it stabilizes predictions by combining many estimators, particularly in cases when there is significant model heterogeneity115.

The equation is presented below having a dataset \(D=\left\{\left({x}_{1},{y}_{1}\right),\left({x}_{2},{y}_{2}\right),\dots ,\left({x}_{n},{y}_{n}\right)\right\},\) where \({x}_{i}\) represents the input features and \({y}_{i}\)​ is the corresponding target value. Bagging works by creating \(B\) different subsets of data \({D}_{1}{,D}_{2},\dots , {D}_{B}\) ​, each sampled with replacement from the original dataset \(D\). For each subset \({D}_{b}\) (where \(b=\text{1,2},\dots , B\)), a regressor \({f}_{b}\left(x\right)\) is trained, and the final prediction \(\widehat{y}\) is the average of all individual predictions from each regressor:

$$\widehat{y}=\frac{1}{B}\sum_{b=1}^{B}{f}_{b}\left(x\right)$$

where:

  • \(B\) is the number of bootstrap samples (ensemble models).

  • \({f}_{b} \left(x\right)\) is the prediction of the \(b-th\) regressor trained on the \(b-th\) bootstrap sample \({D}_{b}\).

  • \(\widehat{y}\) is the final prediction, which is the averaged result of all \(B\) individual predictions.

The process flow of bagging is represented in Fig. 4.

Fig. 4
figure 4

Process flow visualization of bagging algorithm.

Full size image

Least Square Support Vector Machine (LSSVM)

Suykens and Vandewalle116introduced the Least Squares Support Vector Machine (LSSVM) technique to improve Support Vector Machine (SVM) performance. LSSVM simplifies computation by addressing linear matrix problems with fewer restrictions82. One of LSSVM’s main advantages over regular SVMs is its capacity to lower computing costs and minimize uncertainty when selecting structural parameters. When applied to nonlinear and small-data issues, LSSVM outperforms regular SVMs in terms of processing power. It is frequently used for jobs involving both regression and classification117,118.

But one significant disadvantage of LSSVM is that the regularization parameter (γ) and the kernel function parameter (σ), which is the kernel width, are critical decisions that affect the accuracy of the model. Although the model performance can be enhanced by using reconstructed input datasets with appropriate parameters, this method may induce bias when the data trends. The procedure can also be laborious and frequently necessitates prior knowledge, which can have a detrimental effect on the accuracy of the model119. The working process of LSSVM is represented on Fig. 5.

Fig. 5
figure 5

Process flow visualization of LSSVM algorithm.

Full size image

Light Gradient Boosting machine (LGBM)

One well-respected machine learning architecture is the Light Gradient Boosting Machine (LGBM), which processes huge datasets quickly and effectively while retaining excellent accuracy and powerful prediction powers120. As illustrated in Fig. 6, LGBM discretizes continuous data by building decision trees based on a histogram-based method. It uses leaf-wise growth techniques, building the tree leaf by leaf and dividing the dataset at the leaves according to the highest data gain. By choosing the leaf with the greatest loss reduction, this technique improves the prediction accuracy of the tree121,122,123.

Fig. 6
figure 6

Process flow visualization of LGBM algorithm.

Full size image

LGBM has achieved great popularity because of its effectiveness in managing enormous volumes of data while generating very accurate forecasts53.

Extreme Gradient Boosting (XGB)

Guestrin and Chen124refined and customized the LGBM technique for classification and regression tasks and called Extreme Gradient Boosting (XGB). It utilizes ensemble learning based on regression trees, which allows it to handle both regression and classification problem125. XGB significantly outperforms commonly used LGBM models in terms of overfitting and wasteful calculation since it has distributed leverages and parallel computing62.

XGB is now widely used in many different sectors because of its remarkable capacity for problem-solving and low processing overhead126,127. The models in this study were forecasted using the XGB algorithm. The final prediction is produced by combining the outputs of multiple learners, and the total prediction function is calculated using the given equations. Moreover, XGB integrates techniques to reduce overfitting while maintaining high computational efficiency, allowing the algorithm to evaluate its “goodness” based on its core competencies and ultimately enhancing model performance127.

Hybrid XGB-LGBM model

The advantages of both LGBM and XGB are combined in a hybrid XGB-LGBM model to improve accuracy and performance, especially when dealing with complicated datasets81. This hybrid model was created in Google Colab using Python code and several machine learning modules. By training a first level boosting model (XGB) and using its predictions as inputs to train a second level boosting model (LGBM), for example, the two algorithms can be stacked or blended in this way. This allows one model to remedy the deficiencies of the other, enhancing overall predictive performance. The grid search technique was used to discover the optimal values for these hyperparameters, which were modified because they are critical to the accuracy and efficiency of the algorithm in this hybrid approach81. This method finds the best estimated hyper-parameters by evaluating efficacy for each possible combination of the supplied hyper-parameter. The hyperparameters used in this investigation are listed in Table 4.

Table 4 Configuration of XGB, LGBM and Hybrid model.
Full size table

Artificial Neural Network (ANN)

A computer model known as an artificial neural network (ANN) simulates the structure and functions of the human mind. This potent machine learning method is flexible and useful for problems including regression, pattern recognition, and classification. An important feature of ANN that makes them versatile in processing many kinds of data is their ability to learn complex patterns and correlations128. An ANN is made up of linked nodes arranged in layers, often known as neurons. After the input layer gets the data, it processes them through one or more hidden layers to provide the required prediction in the final output layer. Every neuron receives inputs, converts them mathematically, and produces an output that is sent to the layer next to it129. The influence of one neuron on another is determined by the connections between neurons, or weights. To minimize the discrepancy between expected and actual outputs, optimization methods are used to iteratively alter the weights during the training phase130,131. The ANN can generalize from training data and generate precise predictions on fresh, unseen data because of this learning process. Large dataset requirements, computational complexity, and the possibility of overfitting are the main issues with ANNs. When a model is overfitted to the training set, it captures noise and particular patterns that are poorly generalized to new data, which results in subpar performance on datasets that have not been seen before132. Furthermore, the quantity and quality of data have a significant impact on how effective an ANN is; inadequate or low-quality data might result in less-than-ideal model performance133.

As illustrated in Fig. 7, the input layer of the ANN model contains six variables and the output indicates CS. The subsequent values of the ANN parameters are shown in Table 5. To build a network, this study employed backpropagation, a deep learning approach.

Fig. 7
figure 7

Process flow visualization of ANN algorithm.

Full size image
Table 5 Configuration of ANN model.
Full size table

This study employed backpropagation, a popular training strategy called BPNN; to improve ANN model’s learning from input data and help it produce correct predictions. It can move both forward and backward during passes. The neural network processes the input data to produce the anticipated output during the forward pass. The gradients of the model’s parameters with respect to the loss function are computed during the backward pass. To lower prediction errors, optimization methods are guided by these gradients while modifying the model’s parameters83. During training, this study employed the Adaptive Moment Estimation (ADAM) which dynamically modifies the learning rate for every parameter over time ensuring quick convergence and efficiently managing sparse gradients134. To further speed up learning, the ReLU function is employed as the transfer function in the internal hidden layers of the network since it helps prevent the vanishing gradient issue135.

Gene expression programming

The genetically enhanced population methodology was created by Ferreira134. based on The genetically enhanced population methodology was created by Ferreira136. based on GA and GP methodologies. The main applications of GA are in the optimization domain. Darwin’s theory of the survival of the fittest served as the basis for this 1960 publication by John Holland68,136. Using GP, a computer may be trained to solve issues by being informed what must be done, rather than how to execute it. This methodology creates computer programs that automatically solve problems by utilizing biological evolution theory and techniques68.

The GP approach has evolved because of three basic genetic algorithms: crossover, mutation, and reproduction. At the replication stage, a strategy for selecting which apps should discontinue use has to be put into place. During implementation, a minuscule percentage of the trees with the lowest resistance are eliminated99,137,138,139. GEP considerably progresses by crossing a crucial evolutionary threshold by separating the genotype and phenotype. The term “phenotype threshold” is another name for this threshold137,138.

Although GEP is a simple system, its translation mechanism is sophisticated and reliable, making it unique among artificial genotype/phenotype systems. The fact that just one gene could be passed over to the following generation was a significant constraint on GEP; since all changes occur inside a straightforward, linear framework, it was not necessary to replicate and alter the complete structure113. It is possible to evolve more complex solutions than GP because of GEP’s unique encoding method, which preserves genetic information in a linear fashion. The reason for this is that evolving programs that grow too quickly often cause GP to encounter issues. In many different fields, when traditional approaches may not be able to find the best solutions, GEP is a useful tool for predictive modeling and optimization. This can be attributed to its more straightforward depiction and evolutionary process140. Symbolic regression is one of the main advantages of GEP; it finds the optimal geometric expression to match the data without having a pre-established model structure. When the correlations between the variables are complicated or unclear, GEP’s flexibility allows it to study a larger variety of options141. Figure 8 shows a thorough flow of the genetic procedures.

Fig. 8
figure 8

Process flow visualization of GEP genetic procedures.

Full size image

Performance assessment

Every model undergoes a thorough evaluation procedure that computes many performance indicators to determine its reliability and efficacy. The Willmott index of agreement (d), coefficient of determination (R2), root mean square error (RMSE), normalized root means square error (NRMSE) and mean absolute error (MAE) are among these metrics. Consequently, as can be seen from the equations in Table 6, which give the mathematical formulas for these measurements with standard range, offer perceptive examination of the model’s predicting skills under various conditions.

Table 6 Performance Metrics.
Full size table

Results and discussion

Prediction accuracy

The reliability, effectiveness, and predictive capacity of ML models may all be evaluated with the use of regression analysis. A high linear connection between expected and actual values is shown by a regression coefficient (R2) that is close to 1 (especially around 0.8), which shows that the model’s predictions closely match the observed data142,143. The R2 values of the models that were assessed in this study provide insight into the predictive power of each model.

With a R2 value of 0.976, the Hybrid XGB-LGBM model performs the best, showing the highest level of predicted accuracy and dependability. XGB model alone also shows good predictive power with an R2 value of 0.962, indicating a high degree of agreement between anticipated and actual values. With an R2 of 0.966, the BPNN (Backpropagation Neural Network) model outperforms the XGB model in accuracy. The LGBM model produces an R2 of 0.956, suggesting strong performance however it lags hybrid and BPNN. In the same manner, bagging model also produce good accuracy of 0.950.

It’s interesting to note that the LSSVM model did not perform as well as the other models in this study, although still showing good predictive potential with an R2 of 0.849. Also, the GEP model performs the worst, with an R2 of 0.499, which suggests that the model’s predictions and the actual data are not as well correlated. This may be due to non-linear relationships and the challenge of optimizing its evolutionary process, making it less suited for high-dimensional or intricate datasets compared to Hybrid and ANN model, which are better at capturing such complexities.

Regression graphs illustrating testing phase results are shown in Fig. 9 (a-g). By using normalized data, deviations originating from variations in the size or magnitude of variables are successfully addressed, allowing for an accurate assessment of the model’s performance.

Fig. 9
figure 9

Prediction Accuracy (a) LSSVM, (b) Bagging, (c) LGBM, (d) XGB, (e) Hybrid XGB-LBGM, (f) ANN (BPNN), (g) GEP.

Full size image

Comparative analysis of models

Comprehensive insights into the prediction power of several predictive models are obtained by evaluating them using a variety of measures. Table 7 displays the models’ comparison with respect to accuracy and error metrics.

Table 7 Models accuracy with respect to performance indicators.
Full size table

The hybrid XGB-LGBM model is the best performer, showing greater predictive accuracy across all parameters, with the greatest R2 value of 0.976 and the lowest NRMSE (0.080) and MAE (3.11). Likewise, XGB and ANN (BPNN) exhibit outstanding performance, displaying R2 values of 0.962 and 0.968, respectively, and comparatively low MAE and NRMSE values. Based on these findings, it can be concluded that the models have good predictive power and low error rates throughout training and testing. With R2 values of 0.955 and 0.950 and low NRMSE values of 0.117 and 0.121, respectively, the LGBM and Bagging models likewise exhibit excellent performance. They nonetheless have strong predictive performance with minimal error margins, while being marginally less accurate than the Hybrid XGB-LGBM, XGB, and ANN models.

Interestingly, the GEP model, despite having a relatively low R2 value of 0.499, exhibits a very low MAE of 0.11. This paradox can be attributed to the nature of the GEP model’s learning process. While the MAE suggests that GEP produces predictions with small average absolute deviations from the observed data, its low R2 and high NRMSE (0.464) indicate that these predictions do not capture the variance and overall distribution of the dataset as effectively as the other models. This suggests that while GEP may predict small deviations accurately, it struggles with more complex relationships in the data, leading to poorer overall accuracy and performance. Moreover, Fig. 10 presents a detailed comparison of the forecast and experimental CS for all models throughout with the help of error metrics. The accuracy of the Hybrid followed by ANN in predicting the CS is clearly dominant in this graphic representation, which confirms their suitability for POFA incorporated concrete CS prediction.

Fig. 10
figure 10

Comparison of models with error representation: (a) LSSVM, (b) Bagging, (c) LGBM, (d) XGB, (e) Hybrid XGB-LBGM, (f) ANN (BPNN), (g) GEP.

Full size image

Moreover, the spider graph (Fig. 11) illustrates a comparative prediction power analysis of multiple models across four evaluation metrics: R2, NRMSE, MAE, and Willmott’s Index of Agreement (d) which clearly indicates that Hybrid model performs better than other models followed closely by ANN.

Fig. 11
figure 11

Comparison of models with respect to performance indicators (Spider Graph).

Full size image

Performance assessment

The Taylor diagram, which shows variances in standard deviation, correlation coefficient (R), and RMSE, offers a brief yet simple evaluation of each machine learning model’s performance with respect to the reference dataset. These discrepancies are represented by points in Fig. 12, and the centered RMSE is indicated by contour lines, which facilitates the evaluation and ranking of the models144. The Hybrid XGB-LGBM model, which is positioned close to the ideal correlation coefficient of 1.0 and has low RMSE and standard deviation, suggesting its higher prediction accuracy, shows the closest agreement with the reference data in the diagram.

Fig. 12
figure 12

Performance assessment of models in terms R, RMSE and Standard deviation.

Full size image

In terms of overall prediction accuracy, the ANN model falls closely behind Hybrid XGB-LGBM, but it matches standard deviation well, as indicated by its placement on the dotted line, which represents a measured standard deviation of 30. According to this location, the ANN performs well in matching the measured data’s range and variability, but it is less accurate in terms of other parameters of accuracy. Conversely, the GEP model performs the worst, with a location that is farthest from the optimal line of 30, a higher predicted standard deviation, and a poorer correlation value. When compared to GEP, models such as LSSVM and Bagging exhibit intermediate performance, but still closer to reference. The models’ accuracy can be ordered as follows using the Taylor diagram: Hybrid XGB-LGBM > ANN > XGB > LGBM > Bagging > LSSVM > GEP.

SHAP Interpretation

SHAP analysis helps explain the outputs of machine learning models by assigning a value to each feature, indicating its contribution to the prediction. These values reveal how different features influence the model’s outcome, providing insight into the model’s decision-making process. By examining SHAP values, it becomes clear which features have the most significant impact and how they interact109. This method aids in understanding, interpreting, and validating the model through both qualitative and quantitative means (Illustrated in Fig. 13 and 14). With a mean absolute SHAP value of roughly 0.065, the water-to-binder ratio (W/B) is the most significant of the six parameters taken into consideration. This suggests that W/B has the largest influence on the anticipated CS, with larger W/B ratios (shown by red spots in the SHAP summary plot) typically translating into estimates of higher compressive strengths. W/B has a crucial role in influencing the workability and strength of concrete, which is consistent with its substantial influence.

Fig. 13
figure 13

Feature importance using SHAP analysis.

Full size image
Fig. 14
figure 14

Summary plot of SHAP analysis.

Full size image

Age has a mean absolute SHAP value of 0.060, making it the second most influential attribute. According to the SHAP analysis, age is a crucial factor in non-linear relationships, contrary to earlier heatmap correlation studies which claimed age had little effect on the CS. Though its linear correlation is smaller, it is possible that longer curing times lead to stronger concrete. Cement ranks third, demonstrating its noteworthy contribution to CS with a mean absolute SHAP value of 0.055. As indicated by the positive SHAP values, a higher cement content increases the expected compressive strength which is an essential function in the process of concrete hydration. Furthermore, CA/FA and SP, with typical SHAP values of roughly 0.035 and 0.025, respectively, are ranked fourth and fifth in significance. Higher values (shown by red dots) increase compressive strength, indicating that SP has a role in both reducing water content and enhancing workability. Lower values, on the other hand, exhibit varying effects. The effects of CA/FA are inconsistent; in some situations, larger ratios increase strength, but in other situations, they decrease it. The balance between aggregate size and total mix design, which is dependent on cement content and W/B, may be the cause of this heterogeneity.

Finally, with a mean absolute SHAP value of about less than 0.01, POFA has the least influence on the model’s predictions. The SHAP summary plot indicates that POFA has a largely neutral effect, with the majority of SHAP values falling close to zero which was also confirmed by correlation heat map. This suggests that the compressive strength predictions are not significantly affected by changes in POFA content. This finding may be explained by POFA’s comparatively large particle size and slow pozzolanic activity, which may limit their ability to contribute to the early development of strength in the concrete mix.

Conclusion

This study effectively addresses the challenges of incorporating POFA into concrete by utilizing advanced machine learning models such as Hybrid XGB-LGBM, ANN with structure of BPNN optimized with Adam, LSSVM, XGB, LGBM and Bagging to predict its compressive strength. These models were developed and assessed using an extensive dataset of 407 samples, demonstrating the efficacy of machine learning approaches in capturing complex correlations within the input parameters. The study divided the dataset into training and testing in the ratio of 70:30 with six inputs and validated the prediction performance of models based on R2, RMSE, NRMSE, MAE and d. Furthermore, the model output was validated and interpreted with the assistance of SHAP analysis, which offered more insight into the feature contributions. The study’s principal conclusions are summarized as follows:

  • Among the evaluated models, the Hybrid XGB-LGBM emerged as the most effective, achieving the highest R2 value of 0.976, followed closely by ANN with an R2 of 0.968. XGB demonstrated good performance but marginally lesser accuracy, with an R2 of 0.962.

  • While the Hybrid XGB-LGBM and ANN models showed strong predictive accuracy, GEP (R2 = 0.495) and LSSVM (R2 = 0.865) performed poorly. Specifically, GEP struggled to capture complex relationships, which made the model less effective in forecasting the compressive strength of POFA-based concrete.

  • The Taylor diagram further validates the superior performance of the Hybrid XGB-LGBM model, as it is closest to the ideal correlation coefficient of 1.0 with low RMSE and standard deviation. While the ANN model closely follows, it matches the measured standard deviation well but is slightly less accurate overall. In contrast, the GEP model performs the worst, showing the highest deviation from the optimal line.

  • SHAP analysis highlighted the water-to-binder (W/B) ratio as the most influential factor in determining compressive strength, followed by curing age and cement content. In contrast, POFA content showed minimal impact on the CS, aligning with its slow pozzolanic activity and larger particle size.

By using advanced ML algorithms to precisely estimate the CS of POFA-based concrete, this research greatly improves the capacity of the construction sector to use POFA in concrete. These prediction models contribute to the creation of more affordable and environmentally friendly building materials by providing a dependable framework for evaluating POFA concrete in practical applications thus reducing the need for extensive and costly experimental testing. Future research should focus on expanding the dataset and incorporating additional predictors to improve the accuracy of the models such as type of concrete and POFA particle size. Exploring advanced techniques such as hybrid models of ANN and LSSVM with nature inspired optimizers is recommended to enhance predictive performance. Additionally, applying these models to investigate other properties of concrete, beyond compressive strength, will provide a more comprehensive understanding of POFA-incorporated concrete in various construction applications.