Optimizing sustainable energy management in grid connected microgrids using quantum particle swarm optimization for cost and emission reduction

Abstract

The global shift towards decentralized energy systems, driven by the integration of distributed generation technologies and renewable energy sources, underscores the critical need for effective energy management strategies in microgrids. This study proposes a novel multi-objective optimization framework for grid-connected microgrids using quantum particle swarm optimization (QPSO) to address the dual challenges of minimizing operational costs and reducing environmental emissions. The microgrid configuration analyzed includes renewable energy sources like photovoltaic panels and wind turbines, along with conventional energy sources and battery storage. By incorporating quantum-inspired mechanics, QPSO overcomes limitations such as premature convergence and solution stagnation, often seen in traditional methods. Simulation results demonstrate that QPSO achieves a 9.67% reduction in operational costs, equating to savings of €158.87, and a 13.23% reduction in carbon emissions, lowering emissions to 513.70 kg of CO₂ equivalent in the economic scheduling scenario. In the environmentally constrained economic scheduling scenario, the method delivers a balanced solution with operational costs of €174.11 and emissions of 401.63 kg of CO₂. The algorithm’s performance is validated across various microgrid configurations, including standard low-voltage setups. These results highlight QPSO’s potential as an efficient tool for optimizing microgrid energy management, promoting both economic and environmental sustainability. This study provides a robust framework for achieving practical solutions in real-world applications, emphasizing the role of advanced optimization techniques in sustainable energy systems.

Introduction

The India’s electricity demand surged significantly in 2022, notably surpassing the typical annual growth rate of previous years, highlighting an urgent need for robust and adaptable energy solutions. Microgrids, as decentralized energy systems, play a critical role in addressing these challenges. Particularly during the summer months of 2022, which saw record high temperatures, the surge in electricity consumption highlighted the vulnerability of the national grid. In such scenarios, microgrids provide localized power generation and distribution, alleviating the pressure on the main grid and reducing the risk of widespread outages. The 12% increase in electricity demand between March and July 2022, compared to the same period in the previous year, further emphasizes the need for scalable energy systems¹. The shift toward microgrids aligns with the growing demand for more resilient infrastructure, capable of adapting to fluctuating consumption patterns and mitigating the impact of climate extremes and system stress. Although India’s energy demand is projected to grow at a slightly slower pace in the coming years, the adoption of microgrid technology is critical for strengthening energy security and supporting sustainable recovery in the post-pandemic era. With an increasing focus on renewable energy, the importance of effective energy management in microgrids cannot be overstated. These systems are particularly valuable for improving grid resilience during natural disasters, power outages, or cyberattacks, given their ability to operate autonomously and integrate renewable sources efficiently. As the reliance on renewable energy sources expands, optimizing microgrid operations becomes increasingly challenging, especially due to the uncertainties associated with both renewable power generation and fluctuating demand patterns. The implementation of advanced energy management strategies in microgrids is vital to ensure reliable, cost-effective, and sustainable energy solutions². Moreover, microgrids facilitate the integration of renewable resources like solar and wind energy, which are often dispersed and variable, supporting the development of cleaner and more sustainable energy systems. Given their capacity to enhance the reliability and resilience of the grid, microgrids are essential in addressing issues like grid failures, natural disasters, and cyber threats, thanks to their ability to generate power locally and operate independently from the main grid. The conceptual framework of microgrids is depicted in Fig. 1. Over recent years, there has been a notable increase in the integration of renewable energy sources (RES), such as wind and solar power, into microgrid systems. However, these sources present challenges due to their intermittent and unpredictable nature, which introduces variability that can affect the stability and efficiency of microgrid operations. Additionally, the variation in load demands adds another layer of complexity to energy management, necessitating the development of advanced strategies to ensure grid reliability³.

Fig. 1

Conceptual representation of a typical microgrid.

Forecasting plays a pivotal role in electrical engineering, especially in optimizing energy system configurations for short-term periods. Accurate forecasts are essential for effective renewable energy integration, enabling better planning and reducing reliance on fossil fuels. By enhancing forecast accuracy, it is possible to lower costs and CO₂ emissions from conventional power generation. Inaccurate predictions, on the other hand, may result in system inefficiencies or failures. Hybrid energy systems (HES), which combine various renewable energy sources such as solar and wind, depend on precise forecasting due to the fluctuating and nonlinear characteristics of these resources. Factors such as weather patterns, power production, and demand significantly influence the performance of HES. For instance, knowing weather conditions can help predict the availability of solar and wind energy, which in turn determines the energy production capacity of the system. The depletion of fossil fuel reserves and the continuous rise in global energy consumption have made it essential for researchers to explore alternative energy sources. Furthermore, environmental pollution caused by traditional fossil fuel-based power plants is a growing concern due to its link to global warming. Integrating renewable sources such as solar, wind, and hydro energy into hybrid systems can significantly reduce environmental pollution, while also improving the efficiency and reliability of energy systems. However, the variability in energy production from renewable sources, particularly due to weather conditions, remains a major challenge. The unpredictability of solar energy, in particular, exacerbates this issue. To address these challenges, microgrids that incorporate a variety of distributed energy resources (DERs) such as energy storage systems, fuel cells, wind turbines, and solar panels offer a reliable and environmentally sustainable alternative. Microgrids have gained considerable attention due to their flexibility and efficiency in integrating diverse renewable energy sources to meet local energy demands. These systems can operate both in grid-connected and islanded modes, providing increased energy security^4,5. The benefits of microgrids extend beyond energy generation. They can reduce greenhouse gas emissions, enhance voltage stability through reactive power support, and provide decentralized power generation. Additionally, microgrids facilitate demand response, improve the reliability of energy supply, and reduce transmission losses. In the United States, the development of microgrids has been driven by the need to increase resilience and reliability in critical infrastructure sectors such as healthcare, transportation, and emergency services. This is particularly evident in regions like the Northeastern U.S., where aging infrastructure and frequent extreme weather events have caused significant economic losses. As a result, there is growing interest in expanding microgrid technology beyond critical facilities to cover entire communities. Several states are now funding demonstration projects to explore the feasibility of such initiatives⁶. The maximum electrical energy can be harvested from renewable energy sources (i.e., up to 70%), and the corresponding statistics are represented in Fig. 2, respectively.

Fig. 2

Global electricity demand statistics.

The dispersion of energy supply across a decentralized network, integration of heat demands for cogeneration, the provision of ancillary services, the enhancement of demand response (DR) capabilities, reduction of GHG emissions, support for reactive power to enhance voltage profiles, and many more benefits are provided by microgrids. They also help keep transmission and distribution system outages and line losses to a minimum. Renewable energy resources (RERs) have significant investment prices, which is one of the microgrids’ many constraints. Other drawbacks include control problems, an absence of system safeguards and regulatory frameworks, worries about consumer privacy, and difficulties in optimizing energy source use. Scientists are focusing on energy management difficulties because of the increasing integration of probabilistic controllable loads into microgrids and the large deployment of RERs, which are fundamentally intermittent. To ensure efficient, long-term, and dependable operation, microgrids use energy management systems (EMS) that cover both the supply and demand sides of the system. In addition to generation dispatch and energy savings, reactive power support, frequency regulation, improved reliability, reduced loss costs, optimized energy balance, reduced greenhouse gas emissions, and customer participation with privacy protection are just a few of the many benefits offered by the EMS. This study introduces a quantum particle swarm optimization (QPSO)-based framework to address the dual challenges of operational cost minimization and emission reduction in grid-connected microgrids. Unlike conventional optimization methods such as GA, PSO, or MILP, QPSO integrates quantum mechanics principles, enabling enhanced exploration and exploitation of the solution space. This approach avoids premature convergence and stagnation, often seen in traditional methods, by leveraging quantum-inspired operators like the mean best and quantum probability distributions. These mechanisms improve the algorithm’s ability to identify globally optimal solutions efficiently, even in the presence of complex, non-linear, and multi-modal optimization problems. The integration of QPSO into microgrid energy management represents a novel and robust tool for simultaneously optimizing economic and environmental objectives, addressing a significant gap in existing literature.

Literature review

Extensive studies have been conducted in recent years, the primary focus of which is the operation of microgrids (MGs). To meet the difficulty of optimal operation scheduling under a variety of loading situations and a wide range of objectives, numerous optimization strategies have been utilized. Within the context of⁷, the emphasis is placed on the distributed microgrid that is equipped with a significant quantity of Renewable Energy Sources (RES) and demand side management. The primary objective of a microgrid (MG) is to minimize the overall cost, which encompasses expenses related to Distributed Generation (DG), distributed energy storage, and the use of flexible or dispatchable loads. The MG operates in tandem with the main grid, ensuring that it remains connected for seamless energy management. Furthermore, the system is designed to account for the worst-case scenario in terms of transaction costs, arising from the inherent uncertainties of renewable energy sources (RES). This approach aims to mitigate the financial risks associated with the variability and unpredictability of RES, optimizing the economic performance of the microgrid. When it comes to microgrids (MGs) that are fueled by renewable energy sources, the issue of scheduling their operations has been successfully overcome⁸. This involves determining the unit commitment (UC) and the corresponding dispatch that minimizes costs while meeting the system’s demand and operational requirements. It is important to stress that the publications listed above have only employed a framework that focuses on a single purpose without considering the problems related to greenhouse gas emissions. Although research has been conducted in the field, there is still a need for more detailed models of MG operation. A lot of research has gone into how MGs work, and researchers have used metaheuristic optimization techniques to tackle the environmental and economic issues that arise from MGs’ multi-objective operation. The search capabilities and fast convergence time of metaheuristic approaches make them well-suited to tackle multi-objective optimization problems, including the economic and environmental functioning of MGs⁹. The authors in¹⁰ have analyzed the techno-economic aspect of Distributed Energy Resources (DERs) by examining how their generation affects network losses. They also aim to reduce operational costs and emissions. Research on microgrid (MG) optimization focuses on economic dispatch and unit commitment to minimize costs while considering RESs and DSM.

Khosravi et al.¹¹ introduce a novel control strategy for hybrid AC/DC microgrids, emphasizing voltage and frequency stability to support renewable energy integration. This highlights the importance of robust control strategies for maintaining power quality. Choudhury et al.¹² employ a modified water wave optimization algorithm, focusing on energy management and power quality improvement in microgrids, which aligns with the need for advanced heuristic techniques to enhance microgrid reliability and operational efficiency. Hematian et al.¹³ address robust optimization for microgrid management, incorporating renewable energy sources, energy storage, EVs, and demand response, showcasing a comprehensive approach to tackling uncertainties inherent in energy systems. Sahoo et al.¹⁴ propose a prairie dog-based meta-heuristic optimization algorithm for improving transient response and power quality in hybrid microgrids. This work emphasizes dynamic response and control optimization, a key aspect of resilient microgrid operations. Ma et al.¹⁵ focus on demand-side energy management, particularly addressing price oscillations for residential heating and ventilation systems, offering strategies that complement broader energy optimization frameworks. Sahoo et al.¹⁶ further develop a scaled conjugate-artificial neural network-based framework for power quality enhancement in grid-tied systems, which supports improved energy distribution and integration with renewable sources. Panda et al.¹⁷ present a comprehensive review of demand-side management and market design for renewable energy integration, highlighting critical aspects of consumer engagement and demand response in microgrid configurations. Mu et al.¹⁸ introduce a deep reinforcement learning-based optimization framework for multi-objective interval dispatch in microgrids, demonstrating advanced AI-based approaches to handling system uncertainties and achieving cost-efficiency. Nagarajan et al.¹⁹ propose an enhanced cheetah-inspired algorithm for dynamic economic dispatch in integrated renewable energy and demand-side management, illustrating the value of bio-inspired optimization techniques in achieving economic sustainability. Majeed et al.²⁰ emphasize dynamic resource management in microgrids, optimizing efficiency through renewable penetration and resource allocation. This work aligns with strategies for achieving efficient energy distribution while minimizing losses. Sharma et al.²¹ explore modeling and sensitivity analysis of grid-connected hybrid green microgrid systems, which provides insights into parameter optimization for hybrid configurations. Ma et al.²² delve into cost modeling, game strategies, and algorithms for demand response in smart grids, highlighting the role of communication and decision-making strategies in achieving energy management goals. Abdalla et al.²³ optimize the economic operation of microgrids, integrating combined cooling, heating, power, and hybrid energy storage systems to enhance operational flexibility and sustainability. Zhang et al.²⁴ present a resilient distributed energy management framework under cyber-attack scenarios, leveraging homomorphic encryption and event-triggered mechanisms to enhance security and robustness. Dashtdar et al.²⁵ design an optimal energy management system for residential microgrids, focusing on smart control to achieve economic and operational efficiency. Sharma et al.²⁶ investigate the optimal sizing and cost assessment of off-grid hybrid microgrid systems, emphasizing cost-effectiveness in rural electrification. Zhang et al.²⁷ employ a multi-objective optimization approach using deep reinforcement learning for microgrid dispatch, showcasing advancements in AI-driven optimization techniques. Vennila et al.²⁸ propose a tournament selection-based ant lion optimization algorithm for static and dynamic environmental economic dispatch, addressing the dual challenges of environmental sustainability and cost efficiency. Akarne et al.²⁹ perform experimental analysis on dual-layer energy management and power control in AC microgrid systems, contributing valuable experimental validation of energy management frameworks. Finally, Panda et al.³⁰ provide an exhaustive review of residential demand-side management models, optimization techniques, and future perspectives, underscoring the importance of consumer-centric approaches in renewable energy systems. Nadimuthu et al.³¹ explore the feasibility of renewable energy microgrids integrated with vehicle-to-grid (V2G) technology for rural electrification in India. Their study emphasizes systematic rural energy planning to achieve peak shaving and optimize renewable resource utilization, directly addressing challenges of energy access in underdeveloped areas. Wang et al.³² propose distributed predefined-time optimization for DC microgrids, offering advanced control mechanisms to manage power distribution efficiently across multiple buses, aligning with efforts to improve distributed control in energy systems. Kumar³³ conducts a techno-economic analysis of off-grid hybrid renewable energy systems, highlighting sustainable energy solutions for rural communities in India. This work underscores the importance of cost-effective and resilient microgrid designs for remote applications. Yi et al.³⁴ investigate collaborative planning of multi-energy systems integrating a complete hydrogen energy chain, offering insights into the integration of hydrogen energy within microgrid frameworks to enhance sustainability. Nagarajan³⁵ introduces an enhanced wombat optimization algorithm for multi-objective power flow in systems integrating renewable energy and electric vehicles, presenting an innovative bio-inspired approach to optimization. Pramila et al.³⁶ discuss integrating hybrid intelligent algorithms for microgrid energy optimization, emphasizing the role of smart grid management in achieving operational efficiency. Davoudkhani et al.³⁷ propose a mountaineering team-based optimization algorithm for load frequency control in islanded microgrids, illustrating its application in enhancing frequency stability in renewable-integrated microgrids. Fatima et al.³⁸ focus on enhancing power dispatch efficiency in grid-connected microgrids through bio-inspired optimization, emphasizing improvements in computational techniques for energy scheduling. Karthik et al.³⁹ present a chaotic self-adaptive sine cosine algorithm for solving optimal energy scheduling problems in microgrids, showcasing the application of advanced algorithms for effective energy management. Terada et al.⁴⁰ examine multi-objective microgrid sizing, addressing both environmental and economic optimization challenges in achieving sustainable energy systems. Singh et al.⁴¹ leverage machine learning-based energy management and power forecasting to enhance the operational reliability of grid-connected microgrids with distributed energy sources. Long and Liu⁴² propose an optimal green investment strategy for grid-connected microgrids, considering renewable energy endowment and incentive policies to maximize economic and environmental benefits. Rajagopalan et al.⁴³ introduce a multi-objective energy management strategy using a self-adaptive crystal structure algorithm for renewable and EV-integrated microgrids, offering innovative solutions for handling complex scheduling problems. Khan et al.⁴⁴ apply a novel modified artificial rabbit optimization algorithm for stochastic energy management in grid-connected microgrids, showcasing its effectiveness in addressing uncertainties in renewable generation. Adiche et al.⁴⁵ propose a hybrid ANN-based adaptive PI controller for advanced control in AC microgrids, integrating droop control and virtual impedance to enhance power quality. Al-Quraan and Al-Mhairat⁴⁶ introduce predictive control-based sizing and energy management for hybrid renewable systems, focusing on economic and operational optimization. Selvaraj et al.⁴⁷ employ the crow search algorithm for optimal power scheduling in real-time distribution systems, improving microgrid performance under variable conditions. Singh et al.⁴⁸ utilize price-elastic demand response and greedy rat swarm optimization to achieve economic and environmental efficiency in advanced microgrid optimization frameworks. Saleem et al.⁴⁹ optimize energy management in solar battery microgrids with a focus on economic approaches toward voltage stability. Li et al.⁵⁰ propose a hierarchical improved marine predators algorithm for operational scheduling of grid-connected multi-microgrid systems, emphasizing scalability and efficient energy flow management. Kushwaha et al.⁵¹ conduct a techno-economic analysis of load scheduling in standalone hybrid microgrid systems, utilizing HOMER Pro to optimize power generation costs and reduce load shedding. Their integration of photovoltaics, wind power, and battery energy storage highlights efficient load management strategies that resonate with sustainable energy objectives. In another study, Kushwaha et al.⁵² propose integrated load and source-side management for hybrid renewable systems, aiming to improve techno-economic-environmental performance for rural electrification. Their approach emphasizes balancing load demands with renewable generation capabilities, offering a comprehensive framework for rural energy access. Furthermore, Kushwaha and Bhattacharjee⁵³ explore integrated techno-economic-enviro-socio designs of hybrid renewable energy systems, addressing domestic and telecommunication load requirements in India. By incorporating a suitable dispatch strategy, their work showcases how hybrid systems can meet diverse energy demands while ensuring sustainability. Finally, Kushwaha and Bhattacharjee⁵⁴ focus on socio-techno-economic-environmental sizing of hybrid renewable energy systems using metaheuristic optimization approaches. These studies collectively demonstrate advancements in algorithmic approaches, control strategies, and integration techniques for enhancing microgrid operations in diverse scenarios.

Existing models often overlook the environmental impact of microgrid operations, particularly regarding greenhouse gas emissions. This highlights the necessity for more inclusive frameworks that address both economic and ecological objectives. Metaheuristic optimization techniques are widely used in microgrid (MG) operations because of their efficiency in balancing multiple goals, such as minimizing operational costs while reducing emissions. However, these methods have limitations, especially when dealing with complex system dynamics and the uncertainties introduced by renewable energy sources (RES). In analysing Distributed Energy Resources (DERs) within microgrids, the aim is to lower both costs and emissions while factoring in the effects on network losses. Despite the advantages, challenges remain in integrating DERs into the current energy infrastructure and managing their variable nature. A model for minimizing operational costs in residential microgrids (MG) is presented in⁵⁵, focusing on optimal energy management. The model incorporates various factors, including the cost of energy trading, penalties for adjustable load shedding, wear-and-tear costs on electric vehicle (EV) batteries. The model differentiates between three types of loads: critical, adjustable, and shiftable loads. The study explores three scenarios, each with different risk levels, to evaluate the trade-offs between operational costs and the typical state of charge (SOC) of EV batteries, specifically addressing the issue of range apprehension. Furthermore, a revenue maximization model for microgrid energy management systems (EMS) that integrates demand-responsive loads is discussed in⁵⁶. This model includes an application for peak shaving from the main grid. The authors of this study assume that the microgrid’s load demand consistently exceeds its generating capacity, emphasizing the need for smart energy management to ensure reliability and profitability. The authors assumed that the microgrid (MG) would consistently have a load demand greater than its generating supply. An analysis is conducted on the performance and effectiveness of the proposed Mixed Integer Linear Programming (MILP) optimization model in the CPLEX program. This analysis includes two case studies: one involving a single bus and another using an IEEE 14-bus Microgrid (MG) system. The authors of reference⁵⁷ introduced a highly effective energy management strategy in their study to reduce the operational costs of a microgrid (MG). This approach also considers curtailable and shiftable loads into demand response (DR) strategies. Maintenance and operation expenses, startup and shutdown charges, energy trading with the main grid, and load shedding are all part of the goal function. Table 1 shows the results of the evaluation of MG EMSs utilizing various optimization methods, including linear and nonlinear programming, dynamic programming, and optimization inspired by nature. Every one of these MG EMSs is designed with centralized supervisor control. Previous coverage in this field has covered the main findings of the research works, with most of the studies concentrating on microgrids (MG) energy resource optimization.

Table 1 MG-EMS-based optimization approaches literature survey.

The existing literature on microgrid energy management primarily emphasizes single-objective optimization, such as minimizing operational costs or emissions, often relying on methods like Mixed-Integer Linear Programming (MILP). While MILP can provide optimal solutions under specific assumptions, it is computationally intensive and struggles with uncertainties inherent in renewable energy sources. Dynamic Programming, while well-suited for sequential decision-making, is significantly constrained by exponential computational complexity. Heuristic approaches like Genetic Algorithms (GA) and Particle Swarm Optimization (PSO) are effective in navigating large search spaces but often encounter challenges such as premature convergence to local optima and require meticulous parameter tuning. Similarly, rule-based methods, while straightforward, lack the flexibility to adapt to complex systems. This review identifies a significant gap in the literature a lack of comprehensive multi-objective optimization strategies that balance economic and environmental goals while addressing the uncertainties and complexities of renewable energy integration^{74,86,87,88,89,90,91,92}. The overall literature survey of the previous research works is tabulated in Table 1 respectively. To bridge this gap, this research proposes a quantum particle swarm optimization (QPSO)-based approach, leveraging QPSO’s unique attributes, such as rapid convergence, resilience to local optima, and superior handling of multi-objective functions. By integrating QPSO into microgrid energy management frameworks, this methodology aims to optimize operations while simultaneously addressing economic and environmental factors, such as cost efficiency, emissions reduction, and penalty minimization. QPSO combines principles of quantum mechanics with swarm intelligence, enabling enhanced exploration of solution spaces and efficient optimization of multiple objectives. Its dynamic swarm behavior and quantum-inspired operators mitigate common challenges faced by traditional algorithms, such as handling non-linear, multi-modal, and complex objective functions. By avoiding entrapment in local optima, QPSO delivers a diverse set of Pareto-optimal solutions, allowing decision-makers to analyze trade-offs between conflicting objectives effectively. This diversity facilitates informed decision-making, providing stakeholders with tailored solutions that align with specific priorities and constraints. The proposed QPSO framework demonstrates its potential to address the dual challenges of economic and environmental scheduling in microgrid management. Its ability to explore complex optimization landscapes with precision establishes QPSO as a promising tool for advancing sustainable energy practices in microgrids. This innovative approach not only expands the scope of current literature but also offers practical solutions for reducing emissions and minimizing the carbon footprint of microgrid operations. By achieving superior performance compared to traditional methods, this study highlights the transformative potential of QPSO in enhancing the sustainability and operational efficiency of microgrids. In this research work introduces a comprehensive multi-objective framework aimed at optimizing the day-ahead scheduling of a microgrid (MG). The proposed framework effectively incorporates both cost and emission factors, ensuring a balanced approach to economic and environmental objectives. The contributions of this research work as follows.

• This study introduces a comprehensive multi-objective framework aimed at optimizing the day-ahead scheduling of a microgrid (MG). The proposed framework effectively incorporates both cost and emission factors, ensuring a balanced approach to economic and environmental objectives.

• The quantum-inspired particle swarm optimization (QPSO) approach is employed to achieve simultaneous minimization of costs and emissions, leading to optimal outcomes. This method leverages quantum-inspired mechanisms within the particle swarm to thoroughly explore the solution space, enabling convergence towards Pareto-optimal solutions that effectively balance economic and environmental objectives.

• The proposed approach demonstrates outstanding performance by delivering superior results in terms of cost efficiency, emission reduction, and computational time when compared to other recently published methodologies.

The structure of this paper is organized as follows: In “Problem formulation” section outlines the problem formulation, detailing the objectives and constraints associated with the optimization challenge. In “Model description” section explores the utilization of quantum-inspired particle swarm optimization (QPSO) as a novel approach to address these objectives, providing a detailed explanation of its principles and implementation for achieving optimal cost and emission minimization. In “Development of the proposed algorithm and methodology” section presents the simulation results obtained through the QPSO method, offering a thorough analysis of its performance and effectiveness in generating high-quality solutions. This section also identifies the most optimal outcomes. Finally, “Conclusion and future research directions” section concludes the study by summarizing the findings and discussing the broader implications of adopting QPSO for tackling multi-objective optimization issues in the realm of sustainable energy management.

Problem formulation

The main objective of microgrid optimization with distributed energy sources (DERs) is to determine the most efficient power generation operating points within a given timeframe. This optimization aims to minimize both the cost of operation, and the amount of emissions produced simultaneously. Therefore, the challenge might be defined as having two conflicting objectives: the reduction of running costs and the simultaneous reduction of emissions. The microgrid is considered to consist of distributed renewable energy sources like solar PV, wind, fuel cells, microturbine, battery, and utility.

$$F_{toc} \left( {{P}_{gm} } \right) = \mathop \sum \limits_{t = 1}^{T} OC = \mathop \sum \limits_{t = 1}^{T} \left\{ {\mathop \sum \limits_{{\mathcalligra{i} \,= 1}}^{NDG} \left[ {{\text{DG}}_{{\mathcalligra{c}}} } \right] + \mathop \sum \limits_{{\mathcalligra{j} \, = 1}}^{NBS} \left[ {{\text{BES}}_{{\mathcalligra{c}}} } \right] + {p}_{ut}^{t} {\mathcal{M}}_{ut}^{t} } \right\}$$

(1)

$${P}_{g}^{i} = \left[ {{\mathcal{P}}_{DG1}^{t} ,{\mathcal{P}}_{DG2}^{t} ,..{\mathcal{P}}_{NDG}^{T} ,{\mathcal{P}}_{BES1, }^{t} {\mathcal{P}}_{BES2,}^{t} ..{\mathcal{P}}_{NBS}^{T} , {p}_{ut}^{1} , p_{ut}^{2} , {p}_{ut}^{3} , \ldots , {p}_{ut}^{T} } \right]$$

(2)

$$DG_{{\mathcalligra{c}}} = \left[ {u_{{\mathcalligra{i}}}^{t} {\mathcal{P}}_{{DG\mathcalligra{i}}}^{t} \,{\mathcal{M}}_{{DG\mathcalligra{i}}}^{t} + {\mathcal{S}}_{{DG\mathcalligra{i}}}^{on} \, max\left\{ {0,u_{{\mathcalligra{i}}}^{t} - u_{{\mathcalligra{i}}}^{t - 1} } \right\} + {\mathcal{S}}_{{DG\mathcalligra{i}}}^{off} \, max\left\{ {0,u_{{\mathcalligra{i}}}^{t - 1} - u_{{\mathcalligra{i}}}^{t} } \right\}} \right]$$

(3)

$$BES_{{\mathcalligra{c}}} = \left[ {u_{{\mathcalligra{j}}}^{t} {\mathcal{P}}_{{BES\mathcalligra{j}}}^{t} \, {\mathcal{M}}_{{BES\mathcalligra{j}}}^{t} + {\mathcal{S}}_{{BES\mathcalligra{j}}}^{on} \, max\left\{ {0,u_{{\mathcalligra{j}}}^{t} - u_{{\mathcalligra{j}}}^{t - 1} } \right\} + {\mathcal{S}}_{{BES\mathcalligra{j}}}^{off} \, max\left\{ {0,u_{{\mathcalligra{j}}}^{t - 1} - u_{{\mathcalligra{j}}}^{t} } \right\}} \right]$$

(4)

The main goal of the function F(${P}_{gm}$) in Eq. (1) is to reduce the running expenses (OC) throughout a 24-h time (T). The system includes the operational expenses of DG units $DG_{{\mathcalligra{c}}}$, BES units $BES_{{\mathcalligra{c}}}$, and the costs associated with exchanging power with the utility. The items in the vector ${P}_{gi}$, as denoted by (2), serve as choice variables for the optimization problem. The variables NDG and NBS denote the total count of distributed generation (DG) units and behind-the-meter energy storage (BES) units, resctively, that are connected in the microgrid (MG) network. The terms specified in (3) include the power output of the ith DG unit, denoted as P_DGi^t, the bid cost M_DGi^t, and the startup/shutdown expenses represented by ${\mathcal{S}}_{{DG\mathcalligra{i}}}^{on} \, max$ and ${\mathcal{S}}_{{DG\mathcalligra{i}}}^{off} \, max$ Likewise, the terms mentioned in (4) include the capacity output of the jth BES unit, the bid cost ${\mathcal{M}}_{{BES\mathcalligra{j}}}^{t}$, and the startup/shutdown charges ${\mathcal{S}}_{{BES\mathcalligra{j}}}^{on} \, max$ and ${\mathcal{S}}_{{BES\mathcalligra{j}}}^{off} \, max$.

Emission

The second purpose is to reduce the overall emission of the system by including non-RESs such as Micro-Turbine, FC, and BES into the microgrid being studied. This can be mathematically represented as:

$$E\left( {{P}_{gm} } \right) = \mathop \sum \limits_{t \in T} \mathop \sum \limits_{j \in et} \left\{ {\mathop \sum \limits_{m \in \mu t} {P}_{g\mu } \left( t \right)*E_{gm} \left( t \right) + \mathop \sum \limits_{m \in FC} {P}_{gF} \left( t \right)*E_{gF} \left( t \right) + \mathop \sum \limits_{m \in BS} {P}_{gB} \left( t \right)*E_{gB} \left( t \right) + {P}_{gGrid} \left( t \right)*E_{gGrid} \left( t \right) } \right\}$$

(5)

The formula for $E({P}_{gi} )$ involves calculating the total emissions, which comprise various pollutants emitted from different sources. In this context, we focus on three key pollutants: Carbon dioxide (CO₂), Sulphur dioxide (SO₂), and Nitrogen oxides (NO_x). The emissions from three specific sources are denoted as $E_{gm} \left( t \right),$ $E_{gF} \left( t \right),$ and $E_{gB} \left( t \right)$ for Micro-Turbine, FC, and battery. Additionally, $E_{gGrid} \left( t \right)$ represents emissions resulting from power obtained from the utility grid.

System constraints

The management of a microgrid for optimal functioning involves solving a constraint optimization issue. In this investigation, various practical constraints are considered. The primary constraint while solving the microgrid energy management problem is the power balance constraint. The total power generated by the distributed energy resources and renewable energy sources should meet the total demand, including losses. The mathematical representation of the equality constraint is represented as follows.

$$\mathop \sum \limits_{m \in \mu t} {P}_{g\mu } \left( t \right) + \mathop \sum \limits_{m \in FC} {P}_{gFC} \left( t \right) + \mathop \sum \limits_{m \in WT} P_{gWT} \left( t \right) + \mathop \sum \limits_{m \in PV} P_{gPV} \left( t \right) + \mathop \sum \limits_{m \in BS} P_{gBS} \left( t \right) + \mathop \sum \limits_{m \in grid} P_{gGrid} \left( t \right) + P_{l} \left( t \right) = P_{D} \left( t \right)$$

(6)

In this context, $P_{D} \left( t \right)$ signifies the aggregate energy demand during the hour t., while $P_{l} \left( t \right)$ represents the aggregate loss during that time. For this study, we consider a low-voltage, 3-feeder system where losses are minimal; thus, we neglect them for simplicity. During the evaluation of the decision variables, they must be restricted to the upper bound and lower bound values. To maintain the decision variables within the permissible ranges, the mathematical representation of the upper bound and lower bound of the decision variables are represented in Eqs. (7) to (11) and as follows.

$$P_{gWT}^{min} \left( t \right)*S_{WT} \left( t \right) \le P_{gWT} \left( t \right) \le P_{gWT}^{max} \left( t \right)*S_{WT} \left( t \right)$$

(7)

$$P_{gPV}^{min} \left( t \right)*S_{PV} \left( t \right) \le P_{gPV} \left( t \right) \le P_{gPV}^{max} \left( t \right)*S_{PV} \left( t \right)$$

(8)

$$P_{gFC}^{min} \left( t \right)*S_{FC} \left( t \right) \le P_{gFC} \left( t \right) \le P_{gFC}^{max} \left( t \right)*S_{FC} \left( t \right)$$

(9)

$$P_{{g\upmu t}}^{min} \left( t \right)*S_{{\upmu t}} \left( t \right) \le P_{{g\upmu t}} \left( t \right) \le P_{{g\upmu t}}^{max} \left( t \right)*S_{{\upmu t}} \left( t \right)$$

(10)

$$P_{gBS}^{min} \left( t \right)*S_{BS} \left( t \right) \le P_{gBS} \left( t \right) \le P_{gBS}^{max} \left( t \right)*S_{BS} \left( t \right)$$

(11)

$$P_{gGrid}^{min} \left( t \right) \le P_{gGrid} \left( t \right) \le P_{gGrid}^{max} \left( t \right)$$

(12)

In this scenario, the minimum and maximum power outputs from the wind turbine (WT) and photovoltaic (PV) sources are denoted by ${P}_{gWT}^{min} \left( t \right)$ and ${P}_{gWT}^{max} \left( t \right)$, and ${P}_{gPV}^{min} \left( t \right)$ and ${P}_{gPV}^{max} \left( t \right)$ respectively, for each scheduling period. Additionally, ${P}_{{g\upmu t}}^{min} \left( t \right)$ and ${P}_{{g\upmu t}}^{max} \left( t \right)$ represents the min and max constraints of total power generation by the microturbine (MT), while $P_{gFC}^{min} \left( t \right)$ and $P_{gFC}^{max} \left( t \right)$ specifies the corresponding metrics for the fuel cell. (FC). The minimum and maximum power constraints of the battery are indicated by $P_{gBS}^{min} \left( t \right)$ and $P_{gBS}^{max} \left( t \right)$ respectively. Furthermore, the power transaction limits of the microgrid (MG) with the utility grid are represented by $P_{gGrid}^{min} \left( t \right)$ and $P_{gGrid}^{max} \left( t \right)$ as the lower and upper constraints.

Model description

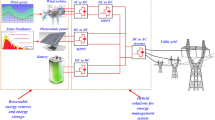
The illustration in Fig. 2 depicts a prototypical low-voltage grid-connected microgrid, serving as the basis for evaluating the proposed framework. Central to this setup is the microgrid central controller (MGCC), which is responsible for the supervision and regulation of power exchange between the microgrid (MG) and the utility. Its principal function lies in the allocation of power references to local controllers, thereby ensuring compliance with linear constraints throughout the scheduled period T. Supporting this endeavor are the micro-source controller and load controller, tasked with fulfilling power requirements by either absorbing or supplying excess or deficit energy, respectively. This approach incorporates storage devices to address uncertainties in forecasting, ensuring stable and reliable system performance. The architecture includes various distributed generation (DG) units, such as photovoltaic (PV) systems, wind turbines (WT), fuel cells (FC), and microturbines (MT), along with multiple energy storage solutions. A schematic representation of a typical low voltage microgrid setup is provided in Fig. 3. This study also incorporates mathematical models for distributed energy resources, including Solar PV, WT, FC, MT, battery energy storage, and market bid prices, as referenced in⁷⁴.

Fig. 3

Typical LV microgrid system.

Development of the proposed algorithm and methodology

Microgrid optimum functioning under environmental restrictions is addressed in the following section by outlining the algorithm that has been proposed. An accurate portrayal of people and their components is crucial to the performance of any algorithm that relies on population-based data. Optimization techniques inspired by quantum mechanics present a fundamental departure from conventional heuristics, meta-heuristics, and other optimization methods when it comes to problem-solving strategies.

These methodologies are motivated by quantum mechanical principles, including entanglement, tunneling, and superposition, to more effectively explore and exploit search spaces. In contrast to conventional optimization algorithms, quantum-inspired methods possess the capability to investigate numerous potential solutions concurrently. This results in enhanced global optimization and accelerated convergence. Furthermore, they exhibit resilience when confronted with intricate, high-dimensional optimization challenges involving non-linear and discontinuous objective functions, which conventional approaches may encounter difficulties with because of computational inefficiencies or local optima traps. A prominent optimization technique that draws inspiration from quantum mechanics is quantum particle swarm optimization (QPSO). QPSO integrates concepts from quantum mechanics with the collective intelligence of particle swarm optimization. QPSO utilizes particles as representations of potential solutions to the optimization problem, with their movements being influenced by a combination of classical and quantum behaviors. QPSO utilizes quantum-inspired operators, such as the quantum rotation gate and quantum probability measurement, to explore the solution space and preserve variety among the particles. The hybrid technique employed by QPSO allows for the efficient handling of multi-objective optimization problems by successfully balancing the exploration and exploitation processes. This results in the discovery of a wide range of Pareto-optimal solutions. Furthermore, the capability of QPSO to flexibly modify its settings and actively manage the search process improves its efficiency in discovering optimal trade-off solutions for multi-objective optimization tasks.

PSO stands out as a widely embraced swarm intelligence-based algorithm, effectively addressing essential electrical domain issues like ED and OPF problems respectively⁶⁹. Inspired by quantum mechanics theory and particle dynamics analysis, Sun et al. introduced quantum particle swarm optimization (QPSO)⁷⁰. The conventional PSO exhibits limitations, particularly when a small subset of particles fails to converge towards the global optimum, leading to their exclusion from the swarm during subsequent iterations. This exclusion adversely impacts the algorithm’s global search capability. To address this, QPSO introduces the concept of mean best, reincorporating lagged particles into the swarm. Additionally, QPSO streamlines parameter adjustments compared to the canonical PSO, as it doesn’t necessitate a velocity vector model for particles and relies on a minimal number of parameters. In QPSO, a particle’s state is denoted by a wave function, ψ(x,t). The position of the particle at each iteration undergoes updates according to Eqs. (13) and (14). The rest of the algorithm-related information is considered from the^69,70 respectively.

$$x_{p,q} \left( {t + 1} \right) = p_{p,q} \left( t \right) \pm \xi \cdot \left| {Mb_{p,q} \left( t \right) - x_{p,q} \left( t \right)} \right| \cdot \ln \frac{1}{u}$$

(13)

$$p_{p,q} \left( t \right) = \left( {\varphi \cdot p_{p,q} \left( t \right) + \left( {1 - \varphi } \right)G_{q} \left( t \right)} \right),\;\; \left( {1 \le p \le N,\;1 \le q \le M} \right)$$

(14)

$$\varphi = \frac{{c_{1} r_{1} }}{{c_{1} r_{1} + c_{2} r_{2} }}$$

(15)

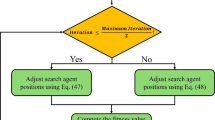
The parameters of the microgrid system are initially established in accordance with the prescribed framework. The fitness of each solution is subsequently assessed for a maximum of 200 iterations to ascertain the personal and global finest. To avert premature convergence, the contraction-expansion coefficient must be meticulously adjusted. The mean-best, which is determined during each iteration, aids in the preservation of population diversity. In the case where a randomly generated number is less than 0.5, a positive sign is appended to (14); otherwise, a negative sign is appended. The algorithm’s stopping criteria rely on either convergence or reaching the maximum iteration count. Once the algorithm has converged, the updated personal best and global best values provide the optimal set points for distributed generation units, along with the calculated cost over a 24-hour period. The overall methodology of the proposed QPSO optimizer flowchart is represented in Fig. 4 respectively.

Fig. 4

Implemented methodology.

Methodology

QPSO offers an effective approach for managing energy in microgrids by optimizing the configuration of distributed generators (DGs) to reduce operational costs and minimize emissions. Its quantum-inspired algorithms are particularly well-suited for multi-objective optimization, as they allow for efficient exploration of complex solution spaces while striking a balance between exploration and exploitation. Additionally, QPSO effectively addresses both equality and inequality constraints, making it a robust choice for solving intricate energy management problems.

Initialization

The QPSO algorithm begins by generating a population of particles, each representing a potential solution to the microgrid scheduling problem. The position of each particle within the solution space reflects a unique combination of scheduling parameters for distributed generators (DGs), including power output, start/stop timings, and fuel consumption.

Fitness evaluation

A fitness function is designed to evaluate multiple objectives, typically balancing operational costs and emissions. This function accounts for costs associated with fuel, maintenance, and other operational factors, alongside the environmental impact of emissions. The goal is to minimize these variables while meeting the required energy demands.

Quantum-inspired operations

QPSO incorporates concepts from quantum mechanics, such as superposition, to perform a comprehensive and efficient exploration of the solution space. The “mean best” strategy is employed to guide particles toward improved solutions while maintaining diversity within the swarm. These quantum-inspired mechanisms enable the algorithm to explore a wide array of possible solutions concurrently, reducing the chances of premature convergence to suboptimal points.

Handling constraints

The microgrid scheduling problem involves both equality and inequality constraints, such as meeting energy demands, adhering to operational limits, and maintaining system stability. QPSO addresses these constraints by incorporating penalties into the fitness function for violations, thereby steering the optimization process toward feasible solutions.

Iterative optimization

Through multiple iterations, QPSO refines particle positions by considering personal bests, global bests, and quantum-inspired adjustments. This iterative process ensures convergence toward an optimal solution that balances cost minimization and emission reduction while meeting the defined constraints.

Simulated results

The final output of QPSO is the optimal scheduling for the microgrid, which minimizes operating costs and emissions. The solution provides specific recommendations for DG scheduling, including when to operate each generator, how much power to produce, and how to manage fuel consumption effectively. This optimal solution contributes to a more efficient and environmentally friendly operation of the microgrid.

Quantum particle swarm optimization (QPSO) presents a versatile and resilient method for addressing intricate multi-objective optimization challenges in microgrid energy management through the integration of quantum principles.

Simulation results with different test systems

The implemented QPSO optimizer is employed on two different test systems to show the ability and efficacy of the optimization approach. It is implemented and tested under the MATLAB environment with the configuration of 1.4 GHz,12 GB RAM System ModelHP Laptop 15t-dy100, respectively.

Test system 1

As an initial step toward a direct comparison, the recommended method is implemented on a test system comprising three plants and six thermal generators. The system is illustrated in Fig. 5 as a schematic diagram. The system’s theoretical maximum load demand is 900 MW. In this instance, two competing objectives, the achievement of fuel cost reduction while minimizing operating expenses, are also considered.

Fig. 5

Test system 1.

The initial solution is focused solely on optimizing the economic schedule, where minimizing fuel costs is the primary goal. The suggested method utilizes a quantum-inspired particle swarm optimization (QPSO) algorithm to optimize a sample test system consisting of 3 plants and a total of 6 thermal generators. This configuration enables a direct comparison with different optimization techniques. The QPSO algorithm’s performance can be evaluated by considering load demand, which is set at 900 MW. Emission and cost coefficients of Test System-1 are depicted in Table 2.

Table 2 Emission and cost coefficients of test system-1.

The number of particles (num_particles = 50) represents the swarm size, striking a balance between solution diversity and computational efficiency. A smaller swarm may limit solution quality, while a larger one could unnecessarily increase computation time. The maximum number of iterations (max_iter = 500) is set to allow sufficient opportunity for convergence while ensuring practical computational feasibility for real-world scenarios. The contraction-expansion coefficient (beta = 1.5) plays a pivotal role in controlling the search behavior of particles. It balances global exploration, which prevents premature convergence to suboptimal solutions, with local exploitation, which refines the search around promising areas. The convergence criterion (epsilon = 1e−6) ensures the algorithm halts when there is negligible improvement in solution quality, avoiding unnecessary computations during the stable convergence phase. These include the power balance constraint, which ensures total generation meets demand, and generation limits for various distributed energy resources, ensuring feasible solutions. Penalty terms are introduced in the fitness function to steer the optimization toward feasible regions of the search space. These parameter choices and constraint-handling methods are pivotal in achieving the dual objectives of microgrid energy management: Fig. 5 depicts the schematic diagram of the test system, emphasizing the arrangement and interconnections of the three plants and the six thermal generators. The primary objective is to optimize the scheduling of the generators to satisfy the 900 MW load demand while minimizing fuel expenditures. The simulated results of pure economic scheduling that were obtained are tabulated in Table 3. Taking emission objectives exclusively into account, the issue is now resolved. Table 3 contains a comparison of the optimal outcomes to those of alternative approaches. As shown in Table 4, improved outcomes are achieved with regard to petroleum expenditure, emissions, and losses. Economic and emission factors are currently considered concurrently. With the obtained simulated results regarding the pure emission scheduling problem, the QPSO optimizer shows superiority and is compared with other implemented optimization approaches. The market bid costs, market prices, load demand and the real-time power generation of solar PV and wind power values have been taken from⁹², respectively.

Table 3 Simulated test results for test system 1 only economic scheduling.

Table 4 Simulated test results for test system 1 only emission scheduling.

A comparison of the costs and emissions for three distinct scenarios is displayed in Table 5. These scenarios are economically constrained economic scheduling (ECES), which prioritizes emission reduction over cost minimization, and emission scheduling, which focuses on cost minimization alone. As shown in Table 5, emission scheduling produces the highest level of emissions, while economic scheduling produces the least amount of fuel. A mutually agreeable resolution is reached when ECES occurs. The inherent contradiction between the objectives of pollution reduction and economic efficiency is illustrated in Table 5.

Table 5 Simulated test results for test system 1 environmentally constrained economic emission (ECES) scheduling.

Test system II

A typical microgrid consisting of a battery, fuel cell, wind turbine, and microturbine (MT) has been investigated for this scenario. All data and components of the system are identical to those in Reference⁸⁸ to allow for a direct comparison. The microgrid that was taken into account for this case study is depicted in Fig. 3. Through the PCC, the microgrid is linked to the utility grid, allowing for the exchange of power as required. A typical microgrid is illustrated schematically in Fig. 3. The acronyms for various parts are shown in Fig. 3: The acronyms MV for medium voltage, LV for low voltage, MT for the microturbine, WT for the wind turbine, MC for the microcontroller, LC for local controller, and MGCC for microgrid central controller are all capitalized. Microturbines (MT) are connected to AC–AC controllers to meet grid criteria, whereas photovoltaic (PV) and fuel cells (FC) are connected to DC–AC converters. Every hour, new generation schedules are set up, and the scheduling horizon is set at 24 h. At any given hour, it is anticipated that all units, including the utilities, are operating within their designated boundaries and fulfilling the essential limits. The main goal of this challenge is to provide a 24-hour scheduling technique that reduces emissions and operating expenses.

The power generated by photovoltaic (PV) and wind turbine (WT) systems is intermittent in nature. Consequently, given the present conditions, the amount of electricity that can be obtained from these sources the following day must be calculated. Microgrids require precise forecasts of wind and solar power generation throughout the entire scheduling timeframe to operate efficiently. The microgrid considered for this case study is taken from⁸⁸ and includes all the parameters associated with low voltage microgrids. Three distinct instances are examined in this study, each contingent upon specific aims. Initially, the primary focus is on the economy, with the outcomes being presented solely in terms of economic planning. Subsequently, the sole focus is on emissions, disregarding the economy, resulting in a schedule that is purely based on emissions. In the final scenario, both the economy and emissions are the principal objectives. The outcomes are categorized under the acronym ECES (ecologically constrained economic scheduling). To evaluate the robustness of the proposed algorithm, fifty iterations were performed for each case, yielding an approximate success rate of 100%. Table 6 displays the optimal outcomes attained through pure economic scheduling. The minimal operational cost is 158.87 Euro, as shown in Table 6, and it corresponds to an emission of 513.7017 kg. From hour one to hour eight, the active power output of most DG units is either zero or negligible, as shown in Table 6. Thus, electricity is procured from the power grid to satisfy the demand. It is evident from Table 7 that the anticipated electricity generation of PV and WT systems is either non-existent or significantly diminished throughout the specified time periods. Power could be supplied by MT at its maximum capacity during those hours; however, the expense would be considerably elevated because of elevated price proposals and SUC/SDC costs (refer to Table 6). Hence, contingent upon the price proposed, the battery and the grid provide the maximum amount of power necessary. Equal validity can be attributed to additional temporal epochs. The convergence characteristics that correspond to each other are illustrated in Fig. 6.

Table 6 Outcomes for pure economic scheduling (test system II).

Table 7 Comparative results of ECES test system-II.

Fig. 6

Convergence characteristics of QPSO on test system-II.

From the observations the QPSO techniques outperform when compared to other algorithms. The optimal cost obtained by implementing the QPSO technique is 158.87 €ct, while DE is found to be 174.2450 €ct. The significant improvement in cost reduction is around 9.67%, which is comparable to other algorithms like DE and TMDE approaches when solving the microgrid energy management problem. In this work, the problem is resolved by solely focusing on emissions as the primary objective, which is referred to as pure emission scheduling. In this case, the study reveals that the emission amounts to 97.6597 kg and incurs a cost of 1365.3095 euros, which is significantly greater than the cost associated with pure economic scheduling. The sole purpose of this scenario is to minimize emissions without considering economic factors. In this scenario, the power generated by the MT is zero for every hour. This occurs due to the elevated emission coefficients, particularly for CO₂, associated with MT. Consequently, to ensure minimal emissions, no power is sourced from MT. This rationale also applies to fuel cells. During the intervals of hours 1–5, 11–13, and 24, power extraction from the fuel cell is zero, again due to its high emission coefficients. As a result, energy is obtained from alternative sources. The convergence characteristics for this scenario are illustrated in Fig. 7.

Fig. 7

Convergence characteristics of QPSO on test case study 2.

The considered problem is solved by taking the economy and emissions into consideration concurrently in this third case study, which is a crucial and final case study. To put it another way, minimizing emissions and operating costs are equally important. Ecological constraints economic scheduling (ECES) is the name given to this effort. According to the obtained simulation results, the emission of 401.063 kg and an ideal operational cost of 174.1129 euros are found. The load requirement is satisfied every hour according to the necessary demand from the end users. During hours 1–4, there is no electricity drawn from microgrid elements. Although capable of generating power during these periods, neither MT nor FC are used due to higher emission coefficients and higher price bids. When compared to alternative power sources like batteries and the utility grid, the price bid for power from WT is also greater. Power is, therefore, taken from the utility grid and battery to meet the load requirement. For further hours, a similar conclusion might be made. During hours 18–24, for instance, very little power is taken from WT, and no power is drawn from the PV system due to the forecasted power output being zero. The suggested method, which is based on quantum theory, can yield better outcomes in the aspects of overall cost and emission. The corresponding convergence characteristics of the third case study are represented in Fig. 8 respectively. The overall obtained simulated results of three different case studies were tabulated in Table 7, respectively. The simulated results presented in Tables 3, 4, 5, 6 and 7 highlight the exceptional performance of the proposed quantum particle swarm optimization (QPSO) framework in optimizing microgrid operations. Specifically, QPSO consistently achieves superior results in terms of cost reduction and emission minimization compared to other optimization methods. For instance, the economic scheduling scenario demonstrates a significant reduction in operational costs, with QPSO achieving approximately 9.67% lower costs than traditional approaches, reflecting its efficiency in resource allocation. Additionally, the environmentally constrained economic scheduling (ECES) scenario showcases QPSO’s ability to balance economic and environmental objectives effectively, achieving a notable decrease in emissions while maintaining competitive operational costs. These results underscore QPSO’s robustness in addressing multi-objective optimization challenges. Furthermore, the algorithm demonstrates remarkable computational efficiency, completing optimization tasks in significantly less time compared to alternative methods, which enhances its practical applicability in real-time energy management systems. By combining these insights, the results validate the transformative potential of QPSO in advancing sustainable and efficient microgrid operations.

Fig. 8

Convergence characteristics of QPSO on test case study 3.

Conclusion and future research directions

In this research work the primary objective is to investigate a conventional six-generator test system and a microgrid energy management framework incorporating renewable energy sources such as photovoltaics (PV), wind turbines (WT), fuel cells (FC), and batteries. A novel quantum particle swarm optimization (QPSO) algorithm was proposed, leveraging quantum-inspired mechanisms to overcome limitations like premature convergence and solution stagnation commonly encountered in traditional methods. The results demonstrate the effectiveness of QPSO in achieving significant improvements in energy management outcomes. Specifically, the proposed approach achieved a 9.67% reduction in operational costs, lowering costs from €174.25 to €158.87 in the economic scheduling scenario, while also reducing carbon emissions by 13.23%, from 592.13 to 513.70 kg of CO₂ equivalent. In the environmentally constrained economic scheduling (ECES) scenario, the method balanced economic and environmental objectives, achieving operational costs of €174.11 and emissions of 401.63 kg of CO₂ equivalent. Compared to conventional optimization techniques such as differential evolution (DE) and TMDE, QPSO demonstrated superior performance in cost reduction, emission minimization, and computational efficiency. These results underscore the algorithm’s robustness and practicality in addressing the dual challenges of economic efficiency and environmental sustainability in microgrid energy management. Future research can focus on developing hybrid quantum-inspired optimization methods to enhance the efficiency and scalability of microgrid energy management. Integrating advanced energy resources like hydrogen fuel cells and next-generation storage technologies can improve resilience, especially in high renewable energy penetration scenarios. Real-world implementation and testing of QPSO systems are essential to validate performance and address deployment challenges. Expanding the framework to interconnected multi-microgrid systems can enable scalable and collaborative resource management. Incorporating real-time forecasting tools for renewable energy uncertainties and aligning QPSO solutions with dynamic electricity markets and policies will further improve reliability and adoption in sustainable energy systems. QPSO is scalable for interconnected microgrids, optimizing energy flows and storage across diverse distributed resources. Additionally, its compatibility with emerging technologies, such as bidirectional electric vehicle charging and advanced hybrid storage systems, highlights its relevance in managing renewable energy intermittency. With the capability to leverage real-time data and predictive analytics, QPSO provides dynamic, resilient, and sustainable solutions for modern energy systems.