Constrained search space selection based optimization approach for enhanced reduced order approximation of interconnected power system models

Abstract

Metaheuristic search-based optimization strategies have recently emerged to obtain approximated models for interconnected complex power systems. However, these algorithms are frequently criticized for randomly selecting lower and upper search space boundaries and taking longer to simulate. The incorrect selection of suitable boundaries for each unknown decision variable may result in an inaccurate or unstable reduced model. This proposal introduces an interim reduced model (IRM) concept to select a tight solution space for the optimization algorithm. The balanced residualization method (BRM) obtains the IRM, and the geometric mean optimization (GMO) algorithm tunes the reduced model coefficients. The proposed method has an appealing feature: the IRM obtained by the BRM structures the solution space selection of the GMO algorithm rather than leaving it completely arbitrary. The GMO method finds the ideal reduced model coefficients by minimizing a weighted error index. The primary benefit of employing IRM-based search space limitations is that they guarantee a focused search with viable answers and lower model stability. Furthermore, maintaining the transient gain mitigates the BRM’s high-frequency spectrum error disadvantage. Three complex interconnected power system models from the literature support the proposed method, contrasting with the state-of-the-art MOR methodologies.

Introduction

Currently, dynamic structures are used for diverse analysis objectives in various fields of technological and physical phenomena. Consequently, the need for greater accuracy and correct interpretation of events gives rise to a dynamic system with larger dimensions and more sophisticated computing intricacy. Due to its immense complexity, the contemporary power system is challenging to model for planning, controlling, and operating purposes. As a result, fast simulation is essential for better evaluation and safety. The architectures of power systems are interrelated, and their system order has enhanced the complexity of systems¹. Simulating such an ample system takes a lot of memory and computing power. However, due to the power system’s massive scale and intricacy, numerical calculations are time-consuming and memory-intensive. In power system analysis, control design, and model order reduction (MOR) are the main focus of the current study. Thus, to have affordable alternatives, the approximation for the MOR approach of the higher-order systems (HOS) becomes increasingly important as the requirement for system accuracy rises. The MOR method ought to maintain the intrinsic properties of the HOS in the reduced order system (ROS), such as stability, transient responsiveness, and steady-state error. In addition to being useful for the parametric study of system behavior, ROS are motivated to get a more profound knowledge of the underlying physical phenomena. Furthermore, applying contemporary control methods to a complex power system model (PSM) necessitates reducing the system model to a lower degree of freedom.

A method for MOR of intricate power systems was proposed in². It necessitates a priori knowledge of the time behavior of the state variable. In³⁴, the singular perturbation technique is discussed for MOR; nevertheless, this approach requires eigenvalue decomposition, which might be a costly computer procedure. For MOR of complex power system models, the balanced truncation approach is frequently employed in the literature^5,6,7,8. For DFIG-based wind turbines, a unique technique⁵, the balanced realization of the approach and frequency-weighted and restricted Grammians, is discussed. An approximation of the controllability and observability of Grampians is provided using modal information in⁶, where a truncated balanced realization approach is described to compute the ROSs of linked power systems. The application of balanced realization to produce ROSs for dynamic electric power networks is discussed in⁷. The balanced truncation method employs an expanded Krylov subspace methodology for the ROS approximation of large-scale power systems⁸. A streamlined single-machine infinite bus (SMIB) PSM was created using the Routh table and matching moments⁹.

Studying algorithms inspired by nature is a necessary discipline that continuously helps with optimization issues¹⁰. It is among the categories of metaheuristic algorithms that have caught the interest of scholars in the last few decades. Finding the optimum option among all workable options for decision-making and physical system analysis is the primary goal of optimization¹⁰. The optimization process finds the ideal values for particular system features to complete the design at the lowest feasible cost. The key to determining the optimal goal among the resources at hand is the collection of factors related to the difficulties. The conventional optimization methods have shortcomings, such as premature convergence, an unknown search space, and convergence to local optima. In recent years, researchers have been focusing increasingly on metaheuristic algorithms that draw inspiration from nature to tackle these challenges and solve intricate optimization problems Li et al.¹². In many domains, including science and engineering, metaheuristic algorithms are important for resolving optimization issues Chen et al.¹¹. Metaheuristics is a popular method for resolving several challenging real-world and multi-objective optimization issues. Meta heuristics are recurrent generation processes that employ comparable intelligent strategies to explore the exploration space. They learn rules that help them put together information in a way that is effectively near to the best answers. Compared to other iterative approaches, optimization algorithms, and heuristic methods, metaheuristics frequently take less computation time to get the optimal or nearly optimal solution¹⁰. Figure 1 illustrates how metaheuristic optimization algorithms may resolve various optimization problems in the context of practical power systems.

The idea of optimizing the performance of contemporary power systems through the use of metaheuristics is appealing. Optimization techniques for MOR applications to assess HOSs have developed dramatically due to recent developments in metaheuristic methods^{13,14,15,16,17,18,19,20,21}. In^13, Gallehdari et al. employed the particle swarm optimization (PSO) method to reduce the PSM by minimizing the frequency-weighted Hankel norm. In^14, Salma and Vaisakh used multi-objective optimization to minimize an SMIB PSM using the interlacing feature and the PSO and differential evolution (DE) algorithms. In^15,16,17, Vasu et al. used the enhanced DE algorithm, the enhanced PSO-DV algorithm, and the enhanced DE algorithm with the improved multi-point Pade approximation (IMPPA) approach to estimate complex power system models utilizing ROS. In¹⁸, load frequency management is implemented using the grasshopper optimization technique. In^19,20, Meena et al. employed the Harris Hawks optimization method for MOR of linked wind turbine systems and modified student psychology-based optimization. In²¹, Singh et al. employed the grey wolf optimization (GWO) with Proximity Index Value to achieve ROS for linked PMS. These techniques provide the best-reduced models that fulfill accuracy requirements regarding error values. However, in these methods, the search space bounds are selected randomly based on trial and error by simulating the algorithm multiple times. Nassef et al.²² have thoroughly investigated using metaheuristic optimization approaches to address power system issues and ensure sustainable environments. Tian et al.²³ investigated a multi-objective optimization model for heavy-haul railroad traffic to lower carbon emissions and increase transportation effectiveness. Salgotra et al.²⁴ addressed the categorization of metaheuristic methods published in the literature, including MATLAB and Python source online links. Rani et al.¹⁰ reviewed the recently developed nature-inspired algorithm from 2019 to 2023. This study aims to identify the best nature-inspired algorithms to tackle constrained and other optimization problems. Pan et al.²⁵ investigated improved pigeon-inspired optimization using the Taguchi technique to track maximum power points and estimate parameters for numerous solar arrays. Tian et al.²⁶ explored the snow geese technique for constrained engineering optimization issues. Table 1 provides a brief overview of the adaptation of metaheuristic techniques for MOR of power systems.

Fig. 1

Metaheuristic-based algorithms adaptation in MOR of practical systems.

The metaheuristic techniques are criticized for random solution space selection and ample simulation time^{27,28,29,30,31}. Any optimization technique must consider exploitation and exploitation equally because these concepts significantly influence the optimization process. The incorrect selection of suitable boundaries for each unknown decision variable may result in an inaccurate or unstable ROS^27,29,30,31. For example, if the starting search region is too broad, convergence may slow down; if it is too limited, it may lock in a local optimum^27,29. The authors^{27,28,29,30,31} have recently established unique approaches to choosing a compact solution space for optimizing the simplified model numerator coefficients. The literature still needs to provide a straightforward procedure for obtaining the lower and upper bound values for the soft computing technique to generate optimal de-creased model numerator and denominator coefficients. By limiting the search region selection, the total number of necessary generations and the time required for their execution decrease. It is the motivation behind the current study.

This paper uses GMO³² to develop a reduced-order approximation for intricate PSM. The HOS Hankel singular values (HSV) discriminate the reduced model order. The proposed method is appealing because the GMO algorithm’s solution space selection is structured by the interim reduced model built using the BRM^33,34 rather than entirely random. The proposed technique is appealing because it enables a novel strategy for integrating soft computing technologies into control applications, reducing the unpredictability and longer simulation time often associated with heuristic approaches. The ROS coefficients are obtained by minimizing a multi-objective optimization function built using integral and root mean square errors. The proposed approach is evaluated using three PSMs to ensure high efficiency and accuracy. The suggested technique produces system approximations substantially comparable to their higher-level counterparts. The suggested approximated system retains the HOS transient, steady-state, and frequency response features, has the lowest ISE and RMSE values, and preserves stability.

The rest of the article is decomposed: "Problem description and model order reduction"Sect. discusses the problem description and preliminaries. "Proposed reduction algorithm" Section discussed adapting the geometric mean optimization algorithm for model order reduction. "Case studies and discussion of outcomes" Section demonstrates the efficacy of the proposed algorithm through simulation. "Conclusion and future scope" Section concludes with possible future directions.

Main contributions:

• i) Develop a new MOR strategy for reduced order approximation of intricate power system models.

• ii) Validate the feasibility of the GMO algorithm and analyse the test system’s frequency and step response results.

• iii) Demonstrate the comparative analysis of the obtained results with the state-of-the-art methods regarding time domain characteristics and various performance metrics.

Table 1 Overview of metaheuristic-based model reduction methods for power systems.

Problem description and model order reduction

Let us consider the dynamics of a minimal, asymptotically stable LTI SISO system with a minim or non-minimum phase nature are represented by

$$\left. \begin{gathered} \dot {x}(t)={A_{orig}}x(t)+{B_{orig}}u(t) \hfill \\ y(t)={C_{orig}}x(t)+{D_{orig}}u(t) \hfill \\ \end{gathered} \right\}$$

(1)

Where $x \in {\Re ^n}$is the state vector.

In the frequency domain, the system (1) dynamics are described as follows:

$${G_{orig}}(s)={C_{orig}}{(sI - {A_{orig}})^{ - 1}}{B_{orig}}+{D_{orig}}=\frac{{\sum\limits_{{j=0}}^{m} {{\beta _j}{s^j}} }}{{\sum\limits_{{i=0}}^{n} {{\alpha _i}{s^i}} }}$$

(2)

Where $m<n$;$({\beta _j},{\alpha _i}) \in {\Re ^2}$.

The MOR aims to find a kth-order reduced system for (1) with the following form.

$$\left. \begin{gathered} {{\dot {x}}_{red}}(t)={A_{red}}{x_{red}}(t)+{B_{red}}u(t) \hfill \\ {y_{red}}(t)={C_{red}}x(t)+{D_{red}}u(t) \hfill \\ \end{gathered} \right\}$$

(3)

where ${x_{red}} \in {\Re ^k}$is the state vector.

In the frequency domain, the system (1) dynamics are described as:

$${R_{red}}(s)={C_{red}}{(sI - {A_{red}})^{ - 1}}{B_{red}}+{D_{red}}=\frac{{\sum\limits_{{j=0}}^{{k - 1}} {{a_j}{s^j}} }}{{\sum\limits_{{i=0}}^{k} {{d_i}{s^i}} }}$$

(4)

Where$({a_j},{d_i}) \in {\Re ^2}$.

For further analysis, we establish three fundamental assumptions about the system.

Assumption 1

The system’s dynamics are at least proper$(n>m)$, and it is known.

Assumption 2

No common factors exist between the polynomials in (1)’s numerator and denominator. It indicates no pole-zero cancellation, assuring the plant’s controllability and observability.

Assumption 3

in the denominator of (1). It says the system is not subject to integrating dynamics.

Preliminaries

Definition 1

Assume that ${G_{orig}}(s):u \to {y_{orig}}$is any generic, stable HOS of order n, and then MOR approaches attempt to find a ROM ${R_{red}}(s):u \to {y_{red}}$of order k such that $k<n$and ${y_{red}}(t) \approx {y_{orig}}(t)$for the same input $u(t)$.

Definition 2

Using an optimization approach, MOR outlines the task of obtaining the reduced-model ${R_{red}}(s)$ from the full-order plant ${G_{orig}}(s)$ as follows:

Let${y_{orig}}(t)$and${y_{red}}(t)$are the output of a HOS and a simplified model for the input$u(t)$; respectively, then, $e(t)={y_{orig}}(t) - {y_{red}}(t)$gives the estimation of error between them. Minimizing $e(t)$within the allowable tolerance band obtains the reduced model.

Optimal reduced model order

The simplified model order in this article is not chosen at random. The HSVs of the HOS establish the order of the ROS. These are necessary for distinguishing which states are obligatory and which ones may be eliminated without substantially influencing the input-output characteristic of the system.

The HSVs of HOS are defined as^29,35,,36,37.

$${\sigma _i}({G_{orig}}(s))=\sqrt {{\lambda _i}({P_c}{Q_o})}$$

(5)

here ${P_c} \in {\Re ^{n \times n}}$ and ${Q_o} \in {\Re ^{n \times n}}$ are the controllability and observability Gramians of the HOS.

The HSVs calculate the energy contribution of each system state. To maintain stability and provide a reliable approximation of the system, the more significant energy states of the system must be maintained in the simplified model. Select the simplified model-order k such that

$${\sigma _k}>\sum\limits_{{i=k+1}}^{n} {{\sigma _i}},$$

(6)

here ${\sigma _i}$is the i^th HSV of HOS.

Balanced residualization method

The kth order reduced model determined using the BRM^33,34 has the following form

$${R_{BRM}}\left( s \right)=\frac{{{{\hat {a}}_k}{s^k}+{{\hat {a}}_{k - 1}}{s^{k - 1}}\cdots \cdots +{{\hat {a}}_1}s+{{\hat {a}}_0}}}{{{{\hat {d}}_k}{s^k}+{{\hat {d}}_{k - 1}}{s^{k - 1}}\cdots \cdots+{{\hat {d}}_1}s+{{\hat {d}}_0}}}$$

(7)

Transient gain (TG)

It is the ratio of numerator and denominator polynomials of a transfer function when$s=\infty$

TG of (7) is

$${R_{BRM}}\left( {s=\infty } \right)=\frac{{{{\hat {a}}_k}+\frac{{{{\hat {a}}_{k - 1}}}}{s}\cdots \cdots+\frac{{{{\hat {a}}_1}}}{{{s^{k - 1}}}}+\frac{{{{\hat {a}}_0}}}{{{s^k}}}}}{{{{\hat {d}}_k}+\frac{{{{\hat {d}}_{k - 1}}}}{s}\cdots \cdots+\frac{{{{\hat {d}}_1}}}{{{s^{k - 1}}}}+\frac{{{{\hat {d}}_0}}}{{{s^k}}}}}=\frac{{{{\hat {a}}_k}}}{{{{\hat {d}}_k}}}$$

(8)

The TG of the original system (2) is

$${G_{orig}}(s=\infty )=0$$

(9)

Remark 1

From (8) and (9), it is evident that the transient gain of the HOS and the ROM obtained via the balanced residualization method are different.

Limitations of the balanced residualization method.

• i. It gives a poor approximation at high frequencies. This discrepancy exists since balanced residualization establishes a direct feed-forward relationship between the system input and output.

• ii. The simplified model did not maintain the higher-order system’s transient gain (TG). i.e. $G{\left. {\left( s \right)} \right|_\infty } \ne {R_{BRM}}{\left. {\left( s \right)} \right|_\infty }$.

• iii. The balanced residualized model has a non-zero gain at the frequency$w=\infty$Moreover, it fails to preserve the passivity property of the HOS in the ROM, resulting in infinite impulse response energy.

Proposed reduction algorithm

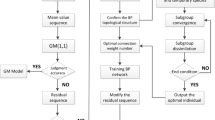
A newly generated meta-heuristic algorithm, geometric mean optimization, is used for the MOR of continuous-time LTI systems. First, a simplified interim model is retrieved for the given HOS using the BRM. The balanced residualized model’s coefficients are considered an initial guess to select the search space bounds for applying the GMO algorithm to obtain the proposed reduced model optimal coefficients. The performance requirements (12) are scaled down in the second stage using the GMO algorithm to obtain the optimal simplified model.

Search space selection for GMO

Let the interim k^th-order simplified model derived employing the BRM while preserving the transient gain have the following transfer function:

$$R_{{Interim}}^{{BRM}}\left( s \right)=\frac{{{{\hat {a}}_{k - 1}}{s^{k - 1}}\cdots \cdots+{{\hat {a}}_1}s+{{\hat {a}}_0}}}{{{{\hat {d}}_k}{s^k}+{{\hat {d}}_{k - 1}}{s^{k - 1}}\cdots \cdots+{{\hat {d}}_1}s+{{\hat {d}}_0}}}$$

(10)

Take into consideration the following as a set of decision factors that need to be optimized:

$$Q=\left[ {\begin{array}{*{20}{c}} {{a_{k - 1}}}&{\cdots}&{{a_1}}&{{a_0}}&{{d_k}}&{\cdots}&{\begin{array}{*{20}{c}} {{d_1}}&{{d_0}} \end{array}} \end{array}} \right],$$

(11)

where ${a_{k - 1}},\cdots.{a_0};{d_k},\cdots.{d_0}$ are the unknown coefficients of the proposed simplified system numerator and denominator, respectively.

The object is to obtain the optimal Q such that the simplified model approximates the actual system adequately. This study aimed to minimize the ISE between step responses and the RMSE between the HOS’s Bode magnitude plot and ROM. The SISO case’s fitness function has the following form:

$$J={x_1} \times {J_{ISE}}+{x_2} \times {J_{RMS{E_{Gain}}}}.$$

(12)

where ${x_1}$ and ${x_2}$ are weighting factors. ${J_{ISE}}$Represent the ISE between step responses of HOS and ROM; ${J_{RMS{E_{Gain}}}}$Represent the RMSE between the Bode magnitude responses of HOS and ROM.

The interim k^th-order balanced residualized model coefficients should be used to determine the solution space for the GMO technique. The interim model’s coefficients are designated as follows:

$$\hat {Q}=\left[ {\begin{array}{*{20}{c}} {{{\hat {a}}_{k - 1}}}&{\cdots}&{{{\hat {a}}_1}}&{{{\hat {a}}_0}}&{{{\hat {d}}_k}}&{\cdots}&{\begin{array}{*{20}{c}} {{{\hat {d}}_1}}&{{{\hat {d}}_0}} \end{array}} \end{array}} \right].$$

(13)

The solution space for the GMO method may be calculated by considering (13) as the starting point. Choose the following lower and higher search space bounds for the SISO instance:

$$\left. \begin{gathered} {{\tilde {Q}}_{lb}}=\left[ {\begin{array}{*{20}{c}} {{\delta _{D - 1}}}&{\cdots}&{{\delta _{k+2}}}&{{\delta _{k+1}}}&{{\delta _k}}&{\cdots}&{\begin{array}{*{20}{c}} {{\delta _1}}&{{\delta _0}} \end{array}} \end{array}} \right].*\left[ {\begin{array}{*{20}{c}} {{{\hat {a}}_{k - 1}}}&{\cdots}&{{{\hat {a}}_1}}&{{{\hat {a}}_0}}&{{{\hat {d}}_k}}&{\cdots}&{\begin{array}{*{20}{c}} {{{\hat {d}}_1}}&{{{\hat {d}}_0}} \end{array}} \end{array}} \right] \hfill \\ {{\tilde {Q}}_{ub}}=\left[ {\begin{array}{*{20}{c}} {{\phi _{D - 1}}}&{\cdots}&{{\phi _{k+2}}}&{{\phi _{k+1}}}&{{\phi _k}}&{\cdots}&{\begin{array}{*{20}{c}} {{\phi _1}}&{{\phi _0}} \end{array}} \end{array}} \right].*\left[ {\begin{array}{*{20}{c}} {{{\hat {a}}_{k - 1}}}&{\cdots}&{{{\hat {a}}_1}}&{{{\hat {a}}_0}}&{{{\hat {d}}_k}}&{\cdots}&{\begin{array}{*{20}{c}} {{{\hat {d}}_1}}&{{{\hat {d}}_0}} \end{array}} \end{array}} \right] \hfill \\ \end{gathered} \right\},$$

(14)

where${\tilde {Q}_{lb}}$ and ${\tilde {Q}_{ub}}$denotes the lower and upper limits of the solution space; D is the number of decision variables, and ${\delta _i}<1;$ ${\phi _i}>1$ investigate the available options in the solution space.

Remark 2

The intermediate reduction model notion presented in this article may be used for compact search space selection with any generalized soft computing method. It offers an organized depiction of the first solution space selection, ultimately decreasing the degrees of randomness and longer simulation time that any soft computing method experiences.

Geometric mean optimizer (GMO)

The GMO was proposed in 2023; it draws on the characteristics of the geometric mean operator in mathematics²⁴. It allows the GMO algorithm to simultaneously handle search agent diversity and fitness by examining a single straightforward index, the dual-fitness index (DFI). Each search agent creates a local guide using this index, which is evaluated for each agent in the population. The creation of the DFI index in GMO is the main advancement of this algorithm over earlier meta-heuristics²⁴. In GMO, many different guides are chosen for the search agents at the appropriate distances from them to prevent them from being caught in local optima and from participating in a drift that would cause them to lose a lot of reasonable solutions while quickly approaching their guides. Also, the guides in the GMO undergo a Gaussian mutation to add a stochastic element to the search process of this method and better explore the solution space of any optimization issue. The GMO’s results are likewise quite reliable, as there are no adjustable factors.

The following stages may be used to describe the mathematical formulation of the geometric mean optimizer:

Step 1

Randomly initialize a set of search agents’ X and their velocity V in the population.

${P_i}=({p_{i1}},{p_{i2}},\cdots,{p_{iD}})$ and ${V_i}=({v_{i1}},{v_{i2}},\cdots,{v_{iD}})$are the position and velocity of agent ‘i’, respectively.

Step 2

Calculate a search agent’s dual fitness index (DFI) using the following formula.

$$DFI_{i}^{t}=\prod\limits_{\begin{subarray}{l} j=1 \\ j \ne i \end{subarray} }^{Q} {MF_{j}^{t}}$$

(15)

where Q is the population size and $DFI_{i}^{t}$is the DFI of agent ‘i’ at the generation ‘t,’ $MF_{j}^{t}$is the fuzzy membership function (MF) value of the jth personal best so-far agent.

The fuzzy MF value for this agent may be determined by following the formula in (16).

$$MF_{j}^{t}=\frac{1}{{1+exp\left[ { - \frac{4}{{{\sigma ^t}\sqrt e }} \times \left( {{\text{Z}}_{{best,j}}^{t} - {\mu ^t}} \right)} \right]}};j=1,2,.Q$$

(16)

Where ${\text{Z}}_{{best,j}}^{t}$ is the jth individual best-so-far agent’s objective function value at generation ‘t,’ ${\mu ^t}$and ${\sigma ^t}$are the average and standard deviation of all agents’ fitness function values at generation ‘t,’ respectively.

Step 3

The global guide agent’s position vector for the agent ‘i’ at generation ‘t’ is.

$$Y_{i}^{t}=\frac{{\sum\nolimits_{{j \in Qbest,j \ne i}} {DFI_{j}^{t} \times P_{j}^{{best}}} }}{{\sum\nolimits_{{j \in Qbest}} {DFI_{j}^{t}+\varepsilon } }}$$

(17)

where $DFI_{j}^{t}$ is the DFI of the search agent ‘j’ at the generation ‘t,’ $P_{j}^{{best}}$ stands for the search agent ‘j’ personal best position vector up to this point in the search, $\varepsilon$is a minimal positive number, and Qbest is used to obtain each guide agent’s elite individual best-so-far agent with its initial value equal to the population size during the first generation and two during the final generation³².

Step 4

The mutated position vector to guide the search agents evaluated for the agent ‘i’ at generation ‘t’.

$$Y_{{i,{\text{mut}}}}^{t}=Y_{i}^{t}+w \times randn \times \left( {Std_{{\hbox{max} }}^{t} - St{d^t}} \right)$$

(18)

where randn is a random vector that is created based on the normal distribution of the standard;$St{d^t}$ is the vector representing the standard deviation of the agents’ best-so-far performance at the generation ‘t’; $Std_{{\hbox{max} }}^{t}$ is a vector that contains the highest standard deviation values of the personal best-so-far agents’ dimensions at the generation ‘t’ and $\omega$ is a parameter that decreases the mutation step size by the lapse of generations determined using (18).

Step 5

The velocity vector of search agent ‘i’ at the generation (t + 1) is updated using.

$$V_{i}^{{t+1}}=\omega \times V_{i}^{t}+\varphi \times \left( {Y_{{i,mut}}^{t} - P_{i}^{t}} \right)$$

(19)

with

$$\varphi =1+\left( {2 \times rand - 1} \right) \times \omega\, ;\, \omega =1 - \frac{t}{{{t_{\hbox{max} }}}}.$$

where $\omega$ is a control parameter, t is the current, and t_max is the maximum number of generations³². $V_{i}^{t}$ Represents the velocity vector of the ith search agent during the generation ‘t,’ $Y_{{i,mut}}^{t}$ is the location vector for the agent i’s specific global guide at generation ‘t,’ and $P_{i}^{t}$ is the agent ‘i’ location vector at generation ‘t.’ In addition, $\varphi$ is a scaling parameter vector that indicates the steps the agent ‘i’ takes to reach its guide, and the rand is a random number produced in the range [0, 1].

Note 1

The size of the vector $\varphi$is diminishing, as it is asserted in the spectra [0, 2], [0.1, 1.9], [0.2, 1.8] … [0.8, 1.2], [0.9, 1.1], and [1, 1] = {1}, as the number of iterations increases. It can improve the GMO’s exploration capabilities in the first iterations while significantly increasing the emphasis on exploitation in the last iterations to ensure a well-balanced exploration and exploitation transition³².

Step 6

The position vector of search agent ‘i’ at the generation (t + 1) is updated using.

$$P_{i}^{{t+1}}=P_{i}^{t}+V_{i}^{{t+1}}$$

(20)

The GMO’s ability to address various challenges in the optimization tasks was examined by comparing it with PSO. Table 2 outlines these algorithms’ parameter configurations. 150 was the population size and the maximum number of iterations these algorithms could perform on four test issues. Thirty separate runs of each approach were conducted.

Table 2 Parameter settings of the GMO and its peers.

The geometric mean optimization algorithm’s potential benefits and computational complexity³²

• It can assess the fitness and diversity of the search agents to assign them a higher priority, enhance the search space’s diversity, and grant access to areas with a high degree of fitness.

• It reduces the guide agents’ uncertainties by modifying them to avoid the GMO being caught in local optima detected early on and by lessening the chance of drift occurring when the search agents are heading toward their guides.

• Adding an elitism feature to the GMO increases its capacity for exploitation and hastens its convergence to the global best solution.

• Considering each search agent’s velocity will encourage the agents to continue exploring the solution space.

• It does not have any parameters to tune.

Performance measures

We determined the IAE, the ISE between the step responses, the RMSE between the Bode magnitude plot, and the IRE of the HOS and its ROM to evaluate the suggested method’s effectiveness.

The ISE is described as follows:

$${J_{ISE}}=\int\limits_{{t=0}}^{{{t_{sim}}}} {{e^2}(t)dt}.$$

(21)

The IAE is described as follows:

$${J_{IAE}}=\int\limits_{{t=0}}^{{{t_{sim}}}} {\left| {e(t)} \right|dt}$$

(22)

The impulse response energy (IRE) is defined as the L² energy norm of the impulse response of a stable system. In state space form, IRE is defined as follows:

$${J_{IRE}}=\left\| H \right\|_{{{L^2}}}^{2}=tr\left[ {\int\limits_{0}^{\infty } {{H^T}Hdt} } \right]$$

(23)

where $H=C{e^{At}}B$is the impulse response of a stable system.

In transfer function form, IRE is defined as follows:

$${J_{IRE}}=\int\limits_{0}^{\infty } {h{{(t)}^2}dt}$$

(24)

where $h(t)$is the impulse response of a stable system.

The RMSE between the Bode magnitude plot of the HOS and its simplified model is:

$${J_{RMS{E_{Gain}}}}=\sqrt {\frac{{\sum\limits_{{i=1}}^{{{N_\omega }}} {{{\left( {{{\left| {{G_{orig}}(j{\omega _i})} \right|}_{dB}} - {{\left| {{R_{red}}(j{\omega _i})} \right|}_{dB}}} \right)}^2}} }}{{{N_\omega }}}}$$

(25)

where${\left| {{G_{orig}}(j{\omega _i})} \right|_{dB}}$ the original system’s magnitude; ${\left| {{R_{red}}(j{\omega _i})} \right|_{dB}}$ the magnitude of the k^th-order simplified model.

Flow chart of the proposed reduction algorithm (Fig. 2).

Fig. 2

Flow chart of the proposed algorithm.

Case studies and discussion of outcomes

Here, we use three case studies of power system models from the academic literature to show the efficacy of the proposed method.

Case Study 1 Let us examine the transfer function model of the single-area reheated hybrid thermal power system²³.

$$G(s)=\frac{{ - 6{s^6} - 119.4{s^5} - 663.3{s^4} - 1438{s^3} - 1145{s^2} - 124.2s - 2.343}}{{{s^7}+19.96{s^6}+109.2{s^5}+262.1{s^4}+352.6{s^3}+364.8{s^2}+66.83s+1.972}}$$

(26)

Step 1

Use the HSVs of (26) and (6) to select the reduced model order.

The system (26) has HSVs: [5.0005 3.6738 0.6909 0.0776 0.0362 0.0018 0.0015].

Choose the simplified model’s order; for k = 3 now by using (6).

$$\sum\limits_{{i=k+1}}^{7} {{\sigma _i}=} (0.0776+0.0362+0.0018+0.0015)=0.1171<{\sigma _3}=0.6909$$

Remark 3

The importance of the first three singular values is much greater than that of the remaining ones. Although the states corresponding to the fourth through seventh singular values change and decay more swiftly, those corresponding to the first three are simple to identify and regulate. It is possible that the third-order simplified model, which truncates the states corresponding to these unique values, adequately captures the whole system.

Using the balanced residualization method, the third-order interim decreased model is obtained as follows:

$$R_{3}^{{BRM}}(s)=\frac{{0.08324{s^3} - 6.006{s^2} - 6.709s - 0.245}}{{{s^3}+0.8703{s^2}+2.307s+0.2062}}$$

(27)

Step 2 The presented system is strictly proper; hence, the HOS’s transient gain equals zero. The transient gain of ROS (27) is calculated as 0.08324, which denotes the addition of a zero at high frequency and causes poor approximation in high-frequency areas. The following is the suggested simplified model, which was created while keeping the original system’s transient gain:

$$\hat {R}_{3}^{{BRM}}(s)=\frac{{ - 6.006{s^2} - 6.709s - 0.245}}{{{s^3}+0.8703{s^2}+2.307s+0.2062}}$$

(28)

Let us assume that the suggested simplified model has the following transfer function:

$$R_{3}^{{\Pr op}}(s)=\frac{{{a_2}{s^2}+{a_1}s+{a_0}}}{{{d_3}{s^3}+{d_2}{s^2}+{d_1}s+{d_0}}}$$

(29)

where $[{a_2},{a_1},{a_0},{d_3},{d_2},{d_1},{d_0}]$ are unknown decision factors that the GMO algorithm seeks to optimize.

Step 3 For the GMO algorithm, choose a limited search space based on the coefficients (28).

$${\tilde {Q}_{lb}}=\left[ {\begin{array}{*{20}{c}} { - 6.006 \times {\delta _6}}&{\begin{array}{*{20}{c}} { - 6.709 \times {\delta _5}}&{\begin{array}{*{20}{c}} { - 0.245 \times {\delta _4}}&{1 \times {\delta _3}}&{0.8703 \times {\delta _2}}&{\begin{array}{*{20}{c}} {2.307 \times {\delta _1}}&{0.2062 \times {\delta _0}} \end{array}} \end{array}} \end{array}} \end{array}} \right],$$

$${\tilde {Q}_{ub}}=\left[ {\begin{array}{*{20}{c}} { - 6.006 \times {\phi _6}}&{\begin{array}{*{20}{c}} { - 6.709 \times {\phi _5}}&{\begin{array}{*{20}{c}} { - 0.245 \times {\phi _4}}&{1 \times {\phi _3}}&{0.8703 \times {\phi _2}}&{\begin{array}{*{20}{c}} {2.307 \times {\phi _1}}&{0.2062 \times {\phi _0}} \end{array}} \end{array}} \end{array}} \end{array}} \right],$$

where ${\tilde {Q}_{lb}}$and ${\tilde {Q}_{ub}}$ indicate the solution space’s lowest and upper boundaries;${\delta _i}$and${\phi _i}$, which serve as multiplicative factors.

Remark 4

For base values with negative coefficients, choose${\delta _i}>1$and${\phi _i}<1$; for base values with positive coefficients, select${\delta _i}<1$and ${\phi _i}>1$ to prevent concerns with uneven bounding. Where$i=0,1,2,3,\cdots,D - 1$; is the dimension of the decision variable vector.

For test system 1, we chose ${\delta _i}(i=6,5,4)=1.5;{\delta _i}(i=0,1,2,3)=0.5$ and ${\phi _i}(i=6,5,4)=0.5;{\phi _i}(i=0,1,2,3)=1.5$since the base values for choosing a small solution space are negative from (27). Hence, the GMO algorithm’s compact solution space falls between

$${\tilde {Q}_{lb}}=\left[ {\begin{array}{*{20}{c}} { - 9.009}&{\begin{array}{*{20}{c}} { - 10.0635}&{ - 0.3675}&{0.5}&{\begin{array}{*{20}{c}} {0.43515}&{1.1535}&{0.1031} \end{array}} \end{array}} \end{array}} \right],$$

$${\tilde {Q}_{ub}}=\left[ {\begin{array}{*{20}{c}} { - 3.003}&{\begin{array}{*{20}{c}} { - 3.3545}&{ - 0.1225}&{1.5}&{\begin{array}{*{20}{c}} {1.30545}&{3.4605}&{0.3093} \end{array}} \end{array}} \end{array}} \right].$$

Step 4 After performing multiple tests runs in the neighborhood of the search space computed in Step 3, the following is the simplified model of the third order obtained using the suggested technique:

$$R_{3}^{{\Pr op}}(s)=\frac{{ - 5.9337{s^2} - 6.8337s - 0.2806}}{{{s^3}+0.87103{s^2}+2.3127s+0.2269}}$$

(30)

Comparing the proposed simplified model (30) to reduced models of the other methods^{15,23,27,28,29,30,31,32,33} to assess the usefulness of the suggested simplified technique. Figure 3 gives the convergence of the proposed algorithm compared with other techniques. The GMO method converges to the optimum point of all functions in this category much more quickly. Figure 4 (a & b) display the step reaction and Bode plot of (26), as well as its offered simplified model (30) and the models set up in the recent literature^29,30,31,33. Figure 5 (a & b) display the step error and magnitude error responses. For better comprehension and visualization of the proposed results bar charts were provided in Fig. 6 which compare the proposed model performance error measures with other methods. Table 3 exhibits the time domain needs and error measurements for the proposed model (30), the system (26), and other scaled-down versions^{17,29,35,36,37,38,39,40,41}. From Fig. 4(a), the proposed decreased model (30) has a step response that is more comparable to the system’s (26) than the lowered models^37,38,39,41. Figure 4(b) illustrates the Bode diagram and simplified representations of the system.

Fig. 3

Convergence plot.

Fig. 4

Comparison of the step and frequency responses of the reduced systems.

Fig. 5

Comparison of the step and frequency error responses of the reduced systems.

Fig. 6

Comparison of various performance measures of different reduced models for example 1.

Table 3 A qualitative evaluation of reduced model performance characteristics.

This graph shows that the suggested model (30) produces noticeably superior results than those^37,38,39,41. Compared to the models35,36,37,38,41, the proposed simplified model (30) closely matches the system’s (26) time domain criteria. In addition, the proposed simplified model’s (30) ISE, IAE, and RMSE values are better than the models17,29,35,36,37,38,39,40,41. Compared to the models37,38,39,41, the suggested method gives a close approximation of a single-area reheated hybrid thermal power system from the step reaction and Bode plot in Fig. 4(a) and 4(b), the time domain characteristics in Table 3, and the performance measures.

Test system 2 In this case, a sixth-order hydropower system is used to demonstrate the effectiveness of the suggested technique. The following model represents the transfer function of the system^15,29

$$G(s)=\frac{{ - 0.1{s^5} - 2.61{s^4} - 7.3434{s^3} - 4.8751{s^2} - 0.0417s}}{{{s^6}+26.0999{s^5}+73.4331{s^4}+32.0833{s^3}+6.2497{s^2}+1.1666s+0.0417}}$$

(31)

The system (41) has HSVs: [1.1611 1.1391 0.0786 0.0552 0.0014 0.0000].

Choose the simplified model’s order; for k = 2 using (6).

$\sum\limits_{{i=k+1}}^{6} {{\sigma _i}=} 0.1352<{\sigma _2}=1.1391$

The balanced residualization procedure yielded the interim second-order reduced model, which can be described as:

$${R_{BRM}}(s)=\frac{{0.04405{s^2} - 0.1618s+1.55 \times {{10}^{ - 16}}}}{{{s^2}+0.07115s+0.0422}}$$

(32)

The transient gain and steady-state gain of the system (31) are retained in the interim simplified model (32) as

$${R_{Interim}}(s)=\frac{{ - 0.1618s}}{{{s^2}+0.07115s+0.0422}}$$

(33)

Assuming that the recommended second-order simplified model has the following form:

$$R_{2}^{{\Pr op}}(s)=\frac{{{a_1}s+({a_0}=0)}}{{{d_2}{s^2}+{d_1}s+{d_0}}}$$

(34)

where $[{a_1},{d_2},{d_1},{d_0}]$ are unknown decision factors that the GMO algorithm seeks to optimize.

Step 3 Select a constrained search area for the GMO algorithm about the numerator coefficients of (33) as.

follows:

$${\tilde {Q}_{lb}}=\left[ {\begin{array}{*{20}{c}} { - 0.1618 \times {\delta _4}}&{\begin{array}{*{20}{c}} { - 0 \times {\delta _3}}&{\begin{array}{*{20}{c}} {1 \times {\delta _2}}&{\begin{array}{*{20}{c}} {0.07115 \times {\delta _1}}&{0.0422 \times {\delta _0}} \end{array}} \end{array}} \end{array}} \end{array}} \right],$$

$${\tilde {Q}_{ub}}=\left[ {\begin{array}{*{20}{c}} { - 0.1618 \times {\phi _4}}&{\begin{array}{*{20}{c}} { - 0 \times {\phi _3}}&{\begin{array}{*{20}{c}} {1 \times {\phi _2}}&{\begin{array}{*{20}{c}} {0.07115 \times {\phi _1}}&{0.0422 \times {\phi _0}} \end{array}} \end{array}} \end{array}} \end{array}} \right],$$

where ${\tilde {Q}_{lb}}$and ${\tilde {Q}_{ub}}$ indicate the solution space’s lowest and upper boundaries;${\delta _i}$and${\phi _i}$, which serve as multiplicative factors.

For test system 2, we chose ${\delta _4}=1.5;{\delta _i}(i=0,1,2,3)=0.5$ and ${\phi _4}=0.5;{\phi _i}(i=0,1,2,3)=1.5$ since the base values for choosing a compact solution space are negative from (33). Hence, the GMO algorithm’s compact solution space falls between

$${\tilde {Q}_{lb}}=\left[ {\begin{array}{*{20}{c}} { - 0.2427}&{\begin{array}{*{20}{c}} 0&{0.5}&{0.035575}&{0.0211} \end{array}} \end{array}} \right],$$

$${\tilde {Q}_{ub}}=\left[ {\begin{array}{*{20}{c}} { - 0.0809}&{\begin{array}{*{20}{c}} 0&{1.5}&{0.106725}&{0.0633} \end{array}} \end{array}} \right],$$

Step 4 After performing multiple test runs in the neighborhood of the search space computed in Step 3, we derive the following simplified models of the second and third orders using the suggested technique:

$$R_{2}^{{\Pr op}}(s)=\frac{{ - 0.1553s}}{{{s^2}+0.06906s+0.04129}}$$

(35)

$$R_{3}^{{\Pr op}}(s)=\frac{{0.095867{s^2} - 2.0393s}}{{{s^3}+13.54{s^2}+1.002s+0.5691}}$$

(36)

The simplified model (36) for Test System 2 is compared to lowered models obtained in various ways previously available to evaluate the suggested reduction strategy’s efficiency^{15,29,35,36,37,39,40,42}. Figure 7 (a) and (b) show the step and bode response for the system (31), its recommended simpler model (36), and a few previously published models. Figure 7 (a) depicts that the step reaction of the simpler model (36) is closely approximated (31) compared to other reduction methods^{15,29,35,36,37,39,40,42}.

Fig. 7

Comparison of the step and frequency responses of the reduced systems.

Fig. 8

Comparison of various performance measures of different reduced models for example 2.

Table 4 The qualitative evaluation of error indices for test system 2.

Figure 7 (b) depicts that the bode reaction of the simpler model (36) is closely approximated (31) compared to other reduction methods^{15,29,35,36,37,39,40,42}. The error indices for the simple models in the literature and the simplified model (36) suggested for the system (31) are shown in Table 4. The model (36) performs ISE, IAE, and RMSE values much better than the simple models^{15,29,35,36,37,39,40,42}. Similarly, the IRE values are better than reduced models^{27,28,29,31,32,34}. Because of this, the suggested simplified model’s (36) step reaction and Bode plot are very similar to those of (31) and its improved performance, as shown by the step reaction and Bode plot in Fig. 7 (a) and 7 (b) and the performance measure values in Table 4. For better comprehension and visualization of the proposed results, bar charts were provided in Fig. 8, which compare the proposed model performance error measures with other methods.

Test case 3: In this instance, a ninth-order boiler system²⁹ is considered to demonstrate the effectiveness of the suggested reduction technique. The boiler system’s transfer function is represented as follows:

$$G(s)=\frac{\begin{gathered} 3.063 \times {10^{15}}+3.971 \times {10^{15}}s+1.154 \times {10^{15}}{s^2}+1.113 \times {10^{14}}{s^3}+3.582 \times {10^{12}}{s^4}+ \hfill \\ 3.206 \times {10^{10}}{s^5}+5.999 \times {10^7}{s^6}+9.81 \times {10^4}{s^7}+146.4{s^8} \hfill \\ \end{gathered} }{\begin{gathered} 2.406 \times {10^{14}}+3.636 \times {10^{14}}s+1.221 \times {10^{14}}{s^2}+1.523 \times {10^{13}}{s^3}+8.737 \times {10^{11}}{s^4}+2.422 \times {10^{10}}{s^5}+ \hfill \\ 2.13 \times {10^8}{s^6}+4.136 \times {10^5}{s^7}+659.8{s^8}+{s^9} \hfill \\ \end{gathered} }$$

(37)

The system (37) has HSVs: [6.2141 0.8283 0.6794 0.0602 0.0576 0.0184 0.0096 0.0032 0.0007]

Choose the simplified model’s order; for k = 3 using (6).

$$\sum\limits_{{i=k+1}}^{9} {{\sigma _i}=} 0.149<{\sigma _3}=0.6794$$

The third-order ROS obtained by the proposed method is

$${R_{prop}}(s)=\frac{{153.0001{s^2}+4675.0253s+5053.1019}}{{{s^3}+33.8382{s^2}+451.2026s+396.9622}}$$

(38)

The ROSs acquired using the methods^{35,37,38,43,44,45,46,47} for the system (37) are compared to the suggested ROS (38). The step response, Bode diagram, and suggested ROS (38) for the system (37), as well as the ROSs from the methods^{35,38,43,45,46}, are displayed in Fig. 9 (a) and 9 (b). Table 5 shows the ROSs of the methods^{35,37,38,43,44,45,46,47}, the system (37), the recommended ROS (38), and their error indices and time domain requirements. The resultant model (38) and the system’s step response are identical, as shown in Fig. 9 (a). There is an improvement over previous models^{35,38,43,45,46}with the step response matching. Similarly, the bode diagram of the created model performs better (38), as shown in Fig. 9 (b), than the models^{35,38,43,45,46}. The system and its approximants are shown in Table 5, together with time-domain data and several performance error indices. The time domain data of the proposed simplified model (38) closely suits the system (37). The proposed reduced model has enhanced ISE, IAE, ITAE, and RMSE more than the simple model^{35,37,38,43,44,45,46,47}. Table 5’s performance error and time domain data values demonstrate how well the model created with the suggested approach resembles model reduction methods in the literature. For better comprehension and visualization of the proposed results bar charts were provided in Fig. 10 which compare the proposed model performance error measures with other methods. Hence, the reduced model of the suggested approach performs better at modeling the boiler system operation than previous reduction methods.

Fig. 9

Comparison of the step and frequency responses of the reduced systems.

Fig. 10

Comparison of various performance measures of different reduced models for example 3.

Table 5 Qualitative comparison of reduced model performance parameters.

Test case 4: Consider the dynamics of an interconnected hybrid power system model⁴⁹

$$G(s)=\frac{\begin{gathered} 260.4{s^{10}}+5.629 \times {10^4}{s^9}+3.44 \times {10^6}{s^8}+4.611 \times {10^7}{s^7}+4.731 \times {10^8}{s^6}+1.515 \times {10^9}{s^5} \hfill \\ +1.971 \times {10^9}{s^4} - 2.231 \times {10^9}{s^3} - 5.561 \times {10^8}{s^2} - 7.418 \times {10^6}s+3.245 \times {10^{ - 10}} \hfill \\ \end{gathered} }{\begin{gathered} {s^{13}}+232{s^{12}}+1.674 \times {10^4}{s^{11}}+4.178 \times {10^5}{s^{10}}+7.04 \times {10^6}{s^9}+7.377 \times {10^7}{s^8} \hfill \\ +5.499 \times {10^8}{s^7}+2.514 \times {10^9}{s^6}+7.489 \times {10^9}{s^5}+1.453 \times {10^{10}}{s^4}+1.686 \times {10^{10}}{s^3} \hfill \\ +1.005 \times {10^{10}}{s^2}+2.433 \times {10^9}s+1.985 \times {10^8} \hfill \\ \end{gathered} }$$

(39)

The system (39) has HSV: [0.6779 0.5795 0.2328 0.1236 0.0313 0.0310 0.0123 0.0018 0.0001 0.0000 0.0000 0.0000 0.0000]

Choose the simplified model’s order; for k = 3 using (6).

$$\sum\limits_{{i=k+1}}^{{13}} {{\sigma _i}=0.2001<{\sigma _3}=0.2328}$$

The third-order proposed reduced model is

$${R_{\Pr op}}(s)=\frac{{2.733{s^2} - 2.087s+2.454 \times {{10}^{ - 13}}}}{{{s^3}+4.122{s^2}+6.973s+6.183}}$$

(40)

The ROSs acquired using the methods^{29,35,38,48,49,50,51,52,53} for the system (39) are compared to the suggested ROS (40). The step response, Bode diagram, and suggested ROS (40) for the system (39), as well as the ROSs from models^29,35,48,49, are displayed in Fig. 11 (a) and 11 (b). Table 6 shows the ROSs for the system (39), the recommended ROS (40), and their error indices and time domain requirements. The resultant model (40) and the system’s step response are identical, as shown in Fig. 11 (a). There is an improvement over previous models^29,35,48,49 with the step response matching. Similarly, the bode diagram of the created model (40) performs better, as shown in Fig. 11 (b), than the models^29,35,48,49. The system and its approximants are shown in Table 6, together with time-domain data and several performance error indices. The time domain data of the proposed simplified model (40) closely suits the system (39).

Fig. 11

Comparison of the step and frequency responses of the reduced systems.

Fig. 12

Comparison of various performance measures of different reduced models for example 4.

Table 6 Qualitative comparison of reduced model performance parameters.

The proposed reduced model has enhanced ISE, IAE, ITAE, and RMSE more than the simplified models^{29,35,38,48,49,50,51,52,53}. Table 6’s performance error and time domain data values demonstrate how well the model created with the suggested approach resembles model reduction methods in the literature. For better comprehension and visualization of the proposed results bar charts were provided in Fig. 12 which compare the proposed model performance error measures with other methods. Hence, the reduced model of the suggested approach performs better at modeling the interconnected power system operation than previous reduction methods.

Advantages of the proposed algorithm

• Simplified cost-effective control design.

• We might employ the recommended strategy to reap the advantages of sub-optimality that cuts down simulation time and the random search space selection of soft computing methods while still allowing us to satisfy the control goals.

• It chooses a narrow search area that reduces randomness in search space selection and, thereby, the simulation time.

• It eliminates the requirement for a complex, higher-order power system model to facilitate control design, analysis, and simulation.

• It yields an appropriately simplified model and offers an enhanced approximation of bode diagrams and step responses.

• The suggested technique creates a ROS with enhanced ISE, IAE, ITAE, and RMSE values for stable higher-order LTI systems.

• The ROS with low error measures generates reliable models and shares most characteristics with the HOS.

The aforementioned advantages will advance the adoption of the proposed algorithm for fuel cells, modern power systems, power electronic converters, robotics, biomedical, aerospace, wind and solar systems, and so on for quick comprehension and simple control design.

Conclusion and future scope

This paper proposes a novel approach for constructing a robust, accurate reduction model for a hybrid interconnected power system model. The HSVs of the original system are used to select the optimal order of the simplified model. An interim reduced model (IRM) concept was implemented to select a compact search space to apply the optimization algorithm. The geometric mean optimization (GMO) algorithm is adopted for model order reduction. The recommended method is appealing because the IRM produced by the balanced residualization technique structures the GMO algorithm’s solution space selection rather than being completely random. It enables a fresh way to incorporate soft computing techniques into control applications, reducing the randomness and lengthier simulation times often associated with heuristic methods. Minimizing a weighted multi-objective function obtains reduced model numerator and denominator coefficients. Four practical power system models verify the suggested technique’s efficiency and accuracy. It is shown that the suggested approximated system preserves the original system time and frequency response characteristics. Compared to other simplified systems, the recommended system delivers the lowest values of ISE and RMSE and keeps the IRE. The suggested technique may be applied in further research to generate the reduced-order model for MIMO and interval systems. This approach may also address practical issues that arise in real time, such as controller design and parameter optimization.

Possible future directions:

• It can be extended to reduce fractional-order and interval systems’ order.

• According to no free-launch algorithm, no single algorithm can give accepted results for all kinds of systems. Hence, integrating two or more metaheuristic algorithms may be a good bet.

• There is a connection between weights and fitness functions. Weight ascertainment techniques can be used to calculate these weights to produce a better-reduced model. The methods for determining weights that are often used include the equal-weight (EW), reciprocal weight (RW), rank-sum weight (RSW), rank-order-centroid (ROC), rank-exponent (RE), and so on.

• It can be extended for order reduction and control design of discrete-time systems.

• The technique may be expanded to MIMO systems and controller design for interval systems.

• The potential industrial significance of our work in reducing orders in power systems, power electronics, wind turbines, fuel cells, robotics, biomedical, aerospace, electric vehicles, and controller design.