Exploring the time-dependent behaviors of the rock mass roof of tunnels in open underground spaces of coal mines through numerical investigation

Abstract

The stability of rock mass roofs in open underground spaces of coal mines in Iran is a critical concern, as it can have significant implications for mine safety and productivity. The rock mass roofs are prone to degradation and failure due to various factors, including mining-induced stress, water infiltration, and mechanical damage. However, there needs to be more understanding of the time-dependent behaviors of these rock mass roofs. This study aims to investigate the time-dependent behaviors of rock mass roofs in tunnels of open underground spaces of coal mines in Iran using numerical simulations. A 3D numerical model was developed using finite element modeling. The model was validated using field measurements and laboratory tests. The study revealed that the rock mass roof exhibits significant time-dependent behavior in response to mining-induced stress, water infiltration, and mechanical damage. The results show that the rock mass roof deforms significantly over time, increasing the risk of instability and collapse. The study also investigated the influence of bedding planes and roof support on time-dependent behavior, demonstrating the importance of considering these factors in numerical simulations. A novel constitutive model was developed to represent the strain-softening behavior, creep, and relaxation of rocks, as well as strength deterioration with accumulated viscous deformation. The study identified the critical factors contributing to this deformation and instability, including high-stress zones, water infiltration pathways, and mechanical damage. The findings provide valuable insights for developing effective monitoring and mitigation strategies to ensure the safety and productivity of coal mines in Iran.

Introduction

The rock mass roof of tunnels in underground coal mines exhibits complex time-dependent behavior influenced by geological characteristics, mining-induced stress changes, and environmental conditions. Understanding these behaviors is crucial for predicting the stability of the rock mass roof and ensuring the safe operation of underground coal mines^1,2,3,4,5. The rock mass roof can exhibit nonlinear behavior, characterized by changes in mechanical properties over time, such as stiffness reduction, creep deformation, and fracture propagation. In bedded rock masses, the layered structure can lead to complex behavior under time-dependent loading, with significant creep deformation due to interlayer friction and dilation^6,7,8,9. Numerical techniques, such as finite element method (FEM), can be used to simulate creep behavior and predict tunnel stability^10,11,12. In massive rock masses, the lack of layering can lead to different behavior under time-dependent loading, with relaxation behavior resulting in significant deformations and stress redistribution^6,13. Numerical approaches, such as the discrete element method (DEM), can simulate relaxation behavior and predict tunnel stability^14,15,16.

The rock mass roof of tunnels in coal mines is subjected to various external loads, including coal mining-induced stresses, tectonic forces, and groundwater pressure. These loads can cause deformation, cracking, and, ultimately, rock failure, leading to catastrophic events such as roof collapses, subsidence, and rockbursts^{8,17,18,19,20,21}. Numerical investigation is a powerful tool for simulating complex time-dependent behavior to predict the rock mass roof’s stability. Finite element method (FEM) and discrete element method (DEM) can be used to model the behavior of the rock mass roof under various loading conditions, simulating the evolution of stress and strain fields over time and predicting potential failure mechanisms and critical factors that influence rock mass stability^{22,23,24,25,26,27}.

In massive and bedded rock masses, the behavior under time-dependent loading is influenced by various factors. Massive rock masses exhibit relaxation behavior, characterized by significant deformations and stress redistribution, influenced by confining pressure, rock mechanical properties, and joint density^28,29,30,31. Numerical models, such as the discrete element method (DEM), can be used to simulate this behavior and predict the stability of tunnels^27,32,33,34. In bedded rock masses, the layered structure can lead to complex behavior under time-dependent loading, with significant creep deformation due to interlayer friction and dilation. Finite Element Method (FEM) has been widely used to simulate the creep behavior of bedded rock masses and predict the stability of tunnels^35,36,37,38. Additionally, both massive and bedded rock masses can exhibit nonlinear behavior under time-dependent loading, which is critical in understanding the stability of tunnels^39,40,41. Numerical methods, such as FEM and DEM, are powerful tools for simulating the complex time-dependent behavior of rock mass roofs, allowing for the prediction of potential failure mechanisms and the identification of critical factors that influence rock mass stability^{42,43,44,45,46}.

A significant challenge in coal mining in Iran is shale rock with bedding planes under the immediate roof. These bedding planes can significantly reduce the rock strength and increase the likelihood of failure. The anisotropic properties of the rock, resulting from the bedding planes, affect the mechanical behavior of the rock in different directions, leading to changes in stress distribution and failure modes. The mechanical properties of the bedding planes also impact the mine roof’s failure mode^{19,21,23,47,48,49,50,51,52}. This study employs numerical simulations that explicitly incorporate bedding planes into the immediate roof to investigate the time-dependent response of bedded mine roofs. A simplified two-dimensional beam model is used to analyze the influence of bedding planes on stress distribution and time-dependent response. The results show that the time-dependent behavior is highly dependent on stress distribution, which is altered by the presence of bedding planes.

Early research on rock masses focused on their mechanical behavior under various loading conditions, establishing the foundation for understanding their complex behavior^{23,53,54,55,56,57,58}. Subsequent studies utilized numerical simulations to investigate time-dependent effects, such as creep and relaxation, as computational power increased^52,59,60. Researchers also explored the mechanical behavior of coal mine-specific rock masses, examining the impact of mining-induced stress and deformation on tunnel stability. More recently, advanced numerical models, including coupled thermal–mechanical-hydro-mechanical models, have been employed to simulate the complex behavior of rock masses^{8,12,15,45,61,62,63,64,65}.

As a comprehensive literature review, a study by Wang et al.⁶⁶ investigated the stability of rock masses in coal mines using numerical simulations. The authors found that the time-dependent behavior of the rock mass roof was influenced by factors such as rock mechanics properties, stress levels, and tunnel shape. Zhang et al.⁶⁷ conducted a numerical analysis of the rock mass roof stability in coal mines using the Finite Element Method (FEM). The authors emphasized the importance of considering the time-dependent behavior of the rock mass roof in tunnel design. A study by Yang et al.⁶⁸ used numerical simulations to investigate the time-dependent behavior of the rock mass roof in coal mines. The authors found that rock strength, stress levels, and water infiltration affected the roof’s stability. Qi-meng et al.⁶⁹ conducted a numerical analysis of the rock mass roof stability in coal mines using the distinct element method (DEM).

Furthermore, the authors highlighted the importance of considering the anisotropic behavior of the rock mass roof in tunnel design. Hosseini et al.¹⁹ used numerical simulations to investigate the effects of temperature and humidity on the time-dependent behavior of the rock mass roof in coal mines. The authors found that temperature and humidity changes could significantly affect the roof’s stability. Two studies by Zhang⁷⁰ and Zhang et al.⁷¹ used numerical models to investigate the time-dependent behavior of the rock mass roof in coal mines under different loading conditions. The authors found that rock strength, stress levels, and tunnel shape affected the roof stability. Shu et al.⁷² conducted a numerical analysis of coal mines’ rock mass roof stability using a coupled thermal-hydro-mechanical (THM) model. The authors highlighted the importance of considering the THM interactions in tunnel design. Wang et al.³⁹ used numerical simulations to investigate the effects of mining-induced stress on the time-dependent behavior of the rock mass roof in coal mines. The authors found that mining-induced stress could significantly affect roof stability. Chen et al.⁷³ conducted a numerical analysis of the rock mass roof stability in coal mines using a novel constitutive model that considered the anisotropic behavior of the rock mass. The authors found that this model could accurately predict the time-dependent behavior of the rock mass roof.

Moreover, Shang et al.⁷⁴ studied the impact of groundwater infiltration on coal mine tunnel stability using numerical simulation. Feng et al.⁷⁵ presented an optimization method for predicting the behavior of coal mine rock mass under different loading conditions. Zhang et al.⁷⁶ studied the compaction and seepage characteristics of broken coal and rock masses in coal mining. Rong et al.⁷⁷ researched rockburst prevention systems based on the attenuation law of coal. Dang et al.⁴ studied the bearing characteristics of brackets in thick hard roof mining sites and the effect of blasting on roof control. Eventually, Cong et al.⁷⁸ employed machine learning and finite element methods to predict the behavior of the coal mine rock mass under different loading conditions.

The lack of previous studies is mainly focused on the general behavior of rock masses, coal mine-specific rock masses, and the effects of mining-induced stress and deformation on tunnel stability. While these investigations have delivered valuable insights into the complex behavior of rock masses, they have not explicitly addressed the time-dependent behavior of the rock mass roof in coal mines in Iran. Further, most previous studies have been conducted in other countries, and there is a lack of studies specifically focused on the Iranian context.

Exploring the time-dependent behaviors of the rock mass roof of tunnels in open underground spaces of coal mines in Iran is crucial for ensuring the safety and stability of this critical infrastructure. A numerical investigation was conducted in several important coal mines in Iran to achieve this, utilizing advanced software and simulation techniques. The study focused on analyzing the deformation and stress evolution of the rock mass roof over time, accounting for factors such as mining-induced stress, rock mechanical properties, and environmental conditions. The results of this investigation provide valuable insights into the time-dependent behavior of the rock mass roof, enabling the development of more effective and data-driven strategies for tunnel design, excavation, and monitoring in Iranian coal mines.

A viscoelastic model accounts for stress redistribution caused by failure within the immediate roof to simulate stress distribution accurately. The model helps identify areas with high-stress concentration that may initiate failure and predict potential failure paths. While a two-dimensional model can help understand symmetric stress conditions, a three-dimensional model is necessary to simulate asymmetric stress conditions common in underground coal mines. This study uses a proposed viscoelastic-strain-softening model to represent intact rocks between bedding planes and a time-independent joint model to represent bedding planes. The prevalent time-dependent reaction of the intact rock and bedding planes is investigated.

The primary objective of this research is to investigate the time-dependent behaviors of the rock mass roof of tunnels in open underground spaces of coal mines using numerical simulation. The specific objectives are:

• 1. To develop a comprehensive numerical model that captures the nonlinear behavior of the rock mass roof.

• 2. To simulate the time-dependent behavior of the rock mass roof under various loading conditions.

• 3. To investigate the effects of geological characteristics, mining-induced stress changes, and environmental conditions on rock mass stability.

• 4. To predict potential failure mechanisms and identify critical factors influencing rock mass stability.

This research is a significant step towards understanding the time-dependent behavior of rock mass roofs in coal mines, a crucial aspect for ensuring mine safety and stability. The outcomes of this study will not only deliver valuable insights into the factors influencing rock mass stability but also identify critical areas for further investigation. The practical implications of this research are profound, as it will inform more effective strategies for designing and managing open underground spaces in coal mines, thereby decreasing the risk of accidents and improving overall safety standards in the industry.

A novel approach is presented to investigate time-dependent rock mass roof behavior in coal mines, which is crucial for ensuring mine safety and stability. Advanced numerical simulations, including a 3D finite element model, capture the nonlinear behavior of the rock mass roof and simulate its response to various loading conditions. A novel constitutive model represents strain-softening, creep, relaxation, and strength deterioration with viscous deformation.

The study explores the influence of bedding planes and roof support on time-dependent behavior, providing valuable insights into critical factors contributing to rock mass deformation and instability. By investigating rock mass roof behavior through numerical simulations, this research will shed light on the complex interactions between geological factors, mining-induced stress changes, and environmental conditions influencing rock mass stability. The findings will significantly impact mine safety and stability, ultimately contributing to a safer and more sustainable mining industry.

Methodology

The presence of bedding planes influences the behavior of rock mass roofs in underground coal mines. These planes can reduce the strength of the rock mass, leading to increased failure in the roof. The presence of bedding planes can alter the failure mode of the roof, causing it to fail in a more complex manner. Additionally, creep behavior can occur along these bedding planes, further complicating the failure process. A numerical investigation was conducted to explore the time-dependent behaviors of rock mass roofs in underground coal mines^37,53. The study presents a flowchart (Fig. 1) to outline the methodology and results.

Fig. 1

Flowchart of the study on the numerical investigation of time-dependent behavior of intact and fractured rocks in underground coal mines.

Roof fall evidence

Roof falls in underground coal mines are common, and understanding their mechanisms is crucial for ensuring safe mining practices. The most probable failure mode for a massive roof is an arch-shaped shear failure, which depends on the ratio of horizontal stress to vertical stress. Several failure modes can occur in underground coal mines, including arch-shaped shear failures, vertical tension cracks, and cutter roof failures. The failure mode depends on the ratio of horizontal stress to vertical stress and the presence of laminated roof layers^4,44,79. In-situ stress plays a critical role in determining the likelihood of roof falls^4,64,77,80. A more significant difference between horizontal and vertical stress can lead to more deviation from the vertical of the failure plane. The maximum horizontal stress direction also affects the likelihood of cutter roof failures^9,71,81,82.

Aligning pillar layouts parallel to the direction of the most incredible horizontal stress can reduce the likelihood of roof falls (Fig. 2a–d). Cutter roof failures can occur as a time-dependent process, where gutters progressively sever the roof beam over time. Understanding this process is essential for predicting and mitigating roof falls. The behavior of rock masses is inherently complex, and simulating their behavior over time can be challenging, especially in areas with complex geological structures. Numerical simulations require significant computational resources, which can be a limitation in Iran, especially in small-scale or remote mines. The results of numerical simulations can be sensitive to the input parameters used, which can make it difficult to accurately predict the behavior of the rock mass roof^{65,88,89,90,91,92}.

Fig. 2

(a,b) Plan view illustrating the effects of varying maximum horizontal stress orientation on roof failure in a square pillar layout and (c,d) the impact of pillar offset on potential failure in a rectangular pillar layout⁹.

Model establishment and calculation

In this section, we describe the establishment and calculation of the model used to simulate the stress distribution of the mines. The model is a 3D finite element model that simulates the behavior of the rock mass under various loading conditions. The model is established using the following steps:

Geometry and meshing

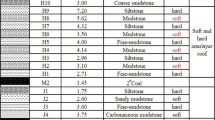
The geometry of the mine is created using an AutoCAD Map 3D 2020 software [https://www.autodesk.com/products/autocad-map-3d/overview], and the mesh is generated using a finite element meshing tool. The resulting mesh is a 3D finite element model that simulates the behavior of the rock mass roof under various loading conditions. The simulation results show a relatively rough network, which is consistent with the expected behavior of the rock mass roof under loading conditions presented in Table 1.

Table 1 Meshing of the model.

Material properties

The constitutive model used in the simulation is a novel viscoelastic-strain-softening model that represents the time-dependent behavior of the rock mass roof. The model is based on the concept of "rock mass stability" and takes into account the complex interactions between the rock mass, stress fields, and geological structures. The material properties of the rock mass, including the elastic modulus, Poisson’s ratio, and cohesion, are assigned to the model (Table 2). The model parameters were calibrated using a combination of laboratory tests and field data. The calibration process involved adjusting the model parameters to match the observed behavior of the rock mass roof under different loading conditions (Table 3).

Table 2 Material properties of massive mine rock.

Table 3 Constitutive model parameters.

Boundary conditions

The boundary conditions, comprising loading and displacement constraints, are imposed on the model as specified in Table 4 and Table 5, which detail the boundary conditions and loading conditions, respectively.

Table 4 Boundary conditions.

Table 5 Loading conditions.

Calculation

The model is calculated using a finite element solver, and the results are obtained.

Stress calculation: The stress distribution of the rock mass can be calculated using Eq. (1):

$$\sigma = \frac{E}{{1 - \nu^{2} }} \times \varepsilon$$

(1)

where σ is the stress, E is the elastic modulus, ν is Poisson’s ratio, and ε is the strain.

Creep calculation: The creep behavior of the beam can be calculated using Eq. (2):

$$\varepsilon_{c} = (\frac{\sigma }{E}) \times (1 - e^{{{\raise0.7ex\hbox{${ - t}$} \!\mathord{\left/ {\vphantom {{ - t} \tau }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\tau $}}}} )$$

(2)

where ε_c is the creep strain, σ is the stress, E is the elastic modulus, t is time, and τ is the creep time constant.

Time-dependent stress calculation: The time-dependent stress distribution of the rock mass can be calculated using Eq. (3):

$$\sigma (t) = \sigma_{0} + \frac{{\sigma_{c} }}{{1 - e^{{{\raise0.7ex\hbox{${ - t}$} \!\mathord{\left/ {\vphantom {{ - t} \tau }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\tau $}}}} }}$$

(3)

where σ(t) is the time-dependent stress, σ₀ is the initial stress, σ_c is the creep stress, t is time, and τ is the creep time constant.

These calculations employed to provide a more detailed understanding of the influence of the time-dependent behavior of a single beam on the stress distribution of the rock mass.

Time dependent failure

The stability of rock in open underground spaces of coal mines is a critical concern for providing the safety and productivity of mining operations. Time-dependent rock failure is a common phenomenon in these environments, which can be caused by various factors such as changes in groundwater flow, stress concentration, and mechanical degradation. Numerical modeling is a powerful tool for simulating and analyzing these complex processes, and 3DEC 7.0 software is widely used for simulating discrete rock mass behavior^18,43,83.

The methodology involves creating a 3D numerical model of the rock mass using 3DEC 7.0 (three dimensional distinct element Code) software [https://docs.itascacg.com/3dec700/contents.html] (described in Supplementary A). The model includes the open underground space and surrounding rock mass, as well as any relevant features such as faults, fractures, and excavations^3,42,84. The model is discretized using a 3D grid of finite difference blocks, each with its own mechanical properties. The initial stress state and boundary conditions are also defined in the model.

The time-dependent failure criteria can be implemented using equations such as Eq. (4):

$$\Delta K = K \times t^{(1/2)}$$

(4)

where ΔK is the stress intensity factor at the crack tip, K is a constant that depends on the rock’s mechanical properties, and t is time.

The damage mechanics (DM) model can be implemented using equations such as Eq. (5):

$$D \, = \, D_{0} \times \left( {1 \, - \, exp\left( { - \beta \times \Delta \sigma } \right)} \right)$$

(5)

where D is the damage variable, D₀ is a constant that depends on the rock’s mechanical properties, β is a constant that depends on the loading conditions, and Δσ is the stress change.

The model is then solved using the 3DEC solver, which employs an implicit time-stepping scheme to advance the solution in time^7,8.

The failure criteria used in the analysis are based on the Mohr–Coulomb failure criterion, which considers the rock material’s shear strength and cohesion. The criterion is implemented using a simple algorithm that checks the stress state at each finite-difference block to determine whether it has failed.

Massive mine rock

The shale roof rock in Iranian coal seams is typically characterized by laminated or bedded structures. To simplify the analysis, the shale roof is simulated as a massive, uniform layer in numerical simulations using finite difference codes. The influence of lamination and bedded planes is accounted for by reducing the rock’s strength and deformation modulus^13,31,33. The model is designed to handle a wide range of scenarios. It can simulate the time-dependent failure of the rock mass under different types of loading and boundary conditions. These conditions can mimic the dynamic changes in the underground space, such as alterations in groundwater flow, stress concentrations from excavation, and mechanical degradation due to weathering or chemical reactions^75,85,86.

Bedded rock

Bedded rock in open spaces of coal mines is a common phenomenon where coal and rock layers are exposed to various environmental and mechanical factor^17,51. The stability of these bedded rock formations is crucial for ensuring the safety and productivity of mining operations. This methodology presents a numerical approach to simulate the behavior of bedded rock in open spaces using 3DEC 7.0 software, which takes into account the mechanical properties of the rock and coal layers^4,76,87. The methodology involves creating a 3D numerical model of the bedded rock formation using 3DEC 7.0 software. The model includes the open space and surrounding bedded rock, as well as any relevant features such as faults, fractures, and excavation ^{26,44,46,47,60}.

The model is discretized using a 3D grid of finite difference blocks, each with its own mechanical properties.

The following equations are used to model the behavior of bedded rock.

The failure criterion is based on the Mohr–Coulomb failure criterion, which takes into account the shear strength and cohesion of the rock material (Eq. (6)).

$$\tau \, = \, c \, + \, \sigma \, \times \, tan\left( \varphi \right)$$

(6)

where τ is the shear strength, c is the cohesion, σ is the normal stress, and φ is the angle of internal friction.

The rock mass strength is calculated using the Eq. (7):

$$\sigma_{m} \, = \, \sigma_{c} \, + \, \sigma_{t}$$

(7)

where σ_m is the rock mass strength, σ_c is the cohesion, and σ_t is the tensile strength.

The coal layer strength is calculated using the Eq. (8):

$$\sigma_{c} = \sigma_{{c_{0} }} + \sigma_{{c_{1} }} \times (1 - e^{( - \lambda \times h)} )$$

(8)

where σ_c is the coal layer strength, σ_c0 is the initial strength, σ_c1 is the rate of strength degradation, λ is the decay constant, and h is the depth of the coal layer.

The numerical simulation involves solving the following system of Eq. (9):

$$\nabla \cdot \sigma = \rho \times \, g$$

(9)

where σ is the stress tensor, ρ is the density, and g is the acceleration due to gravity.

The simulation uses an implicit time-stepping scheme to advance the solution in time^34,69,88. The stress state at each finite difference block is updated using a Newton–Raphson iteration scheme. The results of the simulation are analyzed to determine the timing and location of failure, as well as the stress and displacement fields in the bedded rock formation. The results can be used to identify potential failure modes and to inform decisions about excavation design, support systems, and monitoring strategies.

Limitation and advantages

This study discusses the use of numerical simulations to study rock masses in Iranian coal mines, highlighting both the limitations and advantages of this approach. The simulation approach has several limitations and advantages. The limitations include the assumption of a homogeneous and isotropic rock mass, the neglect of certain geological structures and features, and the use of a simplified constitutive model. The advantages include the ability to simulate complex rock mass behavior, the flexibility to model different loading conditions and scenarios, and the potential to reduce the risk of accidents and injuries in underground coal mines^1,2,3,60,63. The simulation results were validated and verified using a combination of laboratory tests and field data. The validation process involved comparing the simulated results with the observed behavior of the rock mass roof under different loading conditions. The verification process involved checking the accuracy of the simulation results using different numerical methods and models.

Potential applications in Iran

• 1. Coal mines in Iran: Numerical simulations can be used to predict the behavior of rock masses in coal mines in Iran, such as those located in the Zagros Mountains.

• 2. Tunnel design and excavation: Numerical simulations can be used to optimize tunnel design and excavation methods for coal mines in Iran, reducing the risk of accidents and injuries.

• 3. Mine planning and closure: Numerical simulations can be used to inform decisions about long-term mine planning and closure in Iran, reducing the risk of environmental hazards and ensuring a safe and efficient closure^{48,49,52,93,94}.

Overall, exploring the time-dependent behaviors of the rock mass roof of tunnels in open underground spaces of coal mines through numerical investigation in Iran has both limitations and advantages. While there are challenges associated with simulating complex rock mass behavior, numerical simulations can provide valuable insights into the behavior of rock masses over time, informing decisions about tunnel design, excavation methods, and mine planning.

Results

Time-dependent failure propagation in rock masses

This study employed a single mine model with a single entry to investigate the time-dependent behavior of the mine roof. The model was run to equilibrium to obtain the geostatic state before mining (Fig. 3a). The entry was then excavated, and the simulation was run to equilibrium again to obtain the stress distribution and failure condition after excavation. Subsequent creep runs simulated the time-dependent deformation, rock property deterioration, failure propagation, and stress redistribution.

Fig. 3

(a) Mine model with massive roof, (b) Distribution of major principal stress at equilibrium, (c) Cohesion distribution at equilibrium (in Pascal).

The results indicate that the failure and stress state at equilibrium can be considered as the initial state for the subsequent creep simulation. This study first examined the state at equilibrium, as shown in the following figures. The distribution of plastic state, rock properties, and stress distribution at equilibrium reveals an arch-shaped band with high major principal stress (Fig. 3b). The arch begins at the two corners above the mine entry and extends into the sandstone roof above. The thickness of the arch-shaped band on the right side is noticeably thicker than that on the left side, indicating a more significant stress concentration on the right side due to directional horizontal stress. Consistently, more failure occurs above the right corner than above the left corner within the immediate roof. Given the high stress concentration above the mine entry corners, failure initiates from these locations. The plot of cohesion distribution in Fig. 3c also shows a decline in cohesion within failed elements, resulting from accumulated shear plastic strain.

The rock’s behavior under volumetric stress conditions is elastic, while under deviatoric stress conditions, it exhibits viscoelastic behavior. This is due to the constitutive model, which indicates that the distribution of deviatoric stress affects the viscoelastic behavior. The creep simulation initiates after the model reaches equilibrium, and the distribution of deviatoric stress at equilibrium is crucial in identifying the locations where viscous deformation occurs. The band with high deviatoric stress shows a different distribution from the band with high major principal stress.

As the deviatoric stress affects viscous deformation, it is likely that more viscous deformation will accumulate within the arch-shaped band with high deviatoric stress, leading to further deterioration of the rock properties along this band. Figure 4a depicts the distribution of deviatoric stress at equilibrium. The decay of friction angle occurs along the band with high deviatoric stress, coalescing failures initiating from the two entry corners. Failed elements at equilibrium do not decay with time in creep simulation and maintain their original friction angle. Comparing the failure condition at equilibrium and after 5, 6, and 7 min reveals that failures gradually propagate along the arch-shaped band with high deviatoric stress to coalesce failures initiating from the two entry corners (Fig. 4b).

Fig. 4

(a) Distribution of deviatoric stress at equilibrium, (b) Friction angle after 30 s (in degrees), (c) Friction angle after one month (in degrees), (d) Cohesion distribution after one month (in Pascal).

During creep simulation, more significant viscous deformation occurs within areas with high deviatoric stress than other areas. This results in rock deterioration over time. Along with strength degradation and increasing stress differences induced by differences in viscous properties between intact and failed rock, failure occurs within these elements, leading to time-dependent failure propagation. Once elements fail, shear plastic strain accumulates, reducing the strength of failed rock through strain softening behavior. Additionally, viscous deformation relaxes stress from the mine roof, causing areas with high deviatoric stress to shift over time. The area with high deviatoric stress transfers out of failed elements and surrounds them (Fig. 4d).

This observation suggests that rock deterioration will concentrate in areas surrounding failed elements, making it likely that failure will continue propagating from these areas over time. Results show that after failures coalesce within the immediate roof, failure gradually propagates horizontally from failed elements. Comparison of failure conditions after 15 min, 1 day, and 1 month reveals that failure propagation occurs from 15 min to 1 day but not from 1 day to 1 month. Failure only occurs within the immediate shale roof.

The distribution of major principal stress shows that stress within the roof, particularly the immediate roof, has relaxed significantly within 1 month. The low stress in the roof prevents further failure propagation over time (Fig. 4c). The accumulated viscous deformation in turn deteriorates the mine roof by decreasing friction angle in numerical simulation (Fig. 4c). The cohesion reduction is due to accumulated shear plastic strain, which is further driven by stress.

This study monitored the deformation of the mine roof over time by installing sensors along a vertical line, 7.621 m (25.1 ft) inside the entry and aligned with the center of the entry. Figure 5a, b illustrate the time-dependent displacement of the sensors, representing the convergence of the mine roof, after 1 day and 1 month, respectively. The recorded time-dependent displacements were normalized to the displacement of the roof at equilibrium, which is the displacement of the sensor on the roof line. Figure 5a shows that the roof exhibited time-dependent deformation, with variations in magnitude and location. Although all sensors demonstrated time-dependent deformation, indicating that the roof deformed with time, regardless of the magnitude of the deformation, the deformation rate varied with location. At equilibrium condition, representing the condition when time is zero, the instantaneous deformation after excavation decreased with increasing depth into the roof.

Fig. 5

Plot of time-dependent displacement of monitoring points after (a) 1 day, (b) 1 month.

In addition, the time-dependent deformation exhibited similar trends as a creep curve, with a rapid decrease in deformation rate in the initial stage and a relatively constant rate in the secondary stage. However, at different locations, the displacement at the end of the primary stage and the deformation rate in the secondary stage were distinct, decreasing with depth into the roof. The variation in time-dependent deformation with depth into the roof can be attributed to stress redistribution.

The confining stress released from the mine roof, gradually decreasing with increasing depth, changed the stress distribution and increased the likelihood of time-dependent deformation. A comparison of Fig. 5a, b reveals that time-dependent deformation changes with time. Figure 5b illustrates short-term responses of the mine roof after 1 day of excavation, whereas Fig. 5b shows that displacement rates changed at different locations within one month.

The deformation rate of the first two sensors, located near the mine roof surface, was high and decreased with time in the secondary stage. In contrast, sensors located deeper into the roof exhibited lower deformation rates initially and increased with time; this indicates that mine roof surface deformation slows down while internal deformation accelerates. If using deformation rate as an indicator of stress relaxation, this suggests that stress relaxation at shallow locations gradually releases confining stress at deeper locations and accelerates time-dependent deformation.

The maximum unbalanced forces were monitored during creep simulation. Figure 6a shows maximum unbalanced forces within 1 day of creep simulation, noting that forces were initially zero and gradually increased before decreasing after one peak. Figure 6b illustrates unbalanced force accumulation during creep simulation and subsequent release at failure propagation points. Therefore, unbalanced forces accumulate during viscoelastic deformation of the mine roof and release once failure propagation occurs.

Fig. 6

Plot of maximum unbalanced force during creep simulation for (a) 1 day, (b) 15 min.

Influence of stress ratio on mine roofs failure

This study aimed to examine the influence of stress ratio on the time-dependent failure of mine roof. To achieve this, we maintained the vertical stress and minimum horizontal stress constant and varied the maximum horizontal stress to investigate the effect of stress ratio on the time-dependent response of the mine roof. Table 6 presents the three different stress scenarios used in the simulations.

Table 6 In-situ stress scenarios used in the simulations.

Simulation results

The simulation results showed that the increase in maximum horizontal stress led to an increase in failure area within the mine roof. The failure initiating from the left upper corner was promoted, and the failure propagation deep into the roof initiating from the right upper corner was accelerated. The failures from both upper corners gradually propagated with time and coalesced to form a failure arch within the mine roof.

Comparison of stress scenarios

Comparing stress scenarios 1 and 2, we found that the increase of 1.33 MPa in maximum horizontal stress did not significantly increase the failure at equilibrium, but it led to a pronounced increase in failure during the creep simulation. The distribution of maximum shear stress for stress scenario 2 showed a similar pattern as in Fig. 7a, with a stress arch existing in the immediate roof. However, the stress range for the stress arch was between 3.83 and 4.59 MPa for stress scenario 2.

Fig. 7

Distribution of maximum shear stress at equilibrium for stress (in Pascal) in (a) Scenario 1, (b) Scenario 3.

For stress scenario 3, a failure arch already formed within the mine roof at equilibrium, and high maximum shear stress surrounded the failed area. The failure propagated horizontally in the following creep simulation. The influence of stress ratio on instantaneous and time-dependent failure changed from stress scenario 2 to situation 3. The slight increase in maximum horizontal stress significantly changed the failure condition at equilibrium (Fig. 7b).

In conclusion, our study demonstrates that the influence of stress ratio on mine roof failure depends on the failure condition. The results show that increasing the maximum horizontal stress can lead to an increase in failure area within the mine roof, and that the influence of stress ratio on instantaneous and time-dependent failure changes with different failure conditions.

Roof displacement during mining

To simulate the step-wise excavation of the mine entry, each step excavates a section of the entry, and the model runs to equilibrium before simulating the corresponding time-dependent response.

Simulation details:

The simulation was conducted using a 3D finite element software with the following parameters:

Time step: 0.01 s; Total simulation time: 100 s; Loading rate: 0.1 m/s; and Excavation rate: 0.05 m/s.

• 1. Rock mass properties were assigned based on the elastic modulus of 10 GPa, Poisson’s ratio of 0.2, cohesion of 1 MPa, and 30° friction angle.

• 2. Bedding plane properties were also assigned, taking into account the elastic modulus of 5 GPa, Poisson’s ratio of 0.2, cohesion of 0.5 MPa, and 20° friction angle.

• 3. Roof support properties were defined, including the elastic modulus of 200 GPa, Poisson’s ratio of 0.3, and yield strength of 300 MPa.

Excavation process:

The excavation process was simulated using a step-wise approach, with the rock mass excavated in 50 increments of 0.3 m each. The excavation process was modeled using a combination of elastic and plastic deformation models, assuming a homogeneous and isotropic rock mass with uniform material properties.

Simulation procedure:

The simulation involved discretizing the rock mass into a 3D mesh, assigning material properties to each element, and applying boundary conditions to the model. The simulation was run for 100 s, with the excavation process simulated in 50 steps. The results were obtained in the form of stress, strain, and displacement distributions throughout the rock mass.

While it is impossible to simulate an infinitely small section in numerical simulation, using a small section length (0.3 m) can approximate the continuous process. The mining speed also affects the time-dependent response of the mine roof, as lower mining speeds involve more time-dependent deformation and failure. Therefore, it is essential to consider the mining speed in numerical simulations. In this study, we analyzed the influence of step-wise excavation on the time-dependent response of mine roof by monitoring displacement at a location 7.62 m from the front surface of the model. The analysis focused on the cross-section at this location when the face was 0.30 m, 1.52 m, and 3.05 m past the monitoring location.

The mining process affects the mine roof’s stability, with various stages influencing stress distribution, displacement, and failure propagation. At the 26th mining step, failure initiated from the right corner, increasing maximum shear stress in the immediate roof (Fig. 8a). The mining face’s location influences stress distribution, causing a shift in high stress from the roof line to a deeper area. The stress distribution suggests an initial increase and then decrease as the mining face passes. The maximum displacement occurred at the roof’s center due to excavation (Fig. 8b). At the 30th mining step, stress increased, inducing rock deterioration and failure propagation. At the 35th mining step, the failure continued propagating along with the advancing face and accumulated creep time. Finally, after the 50th mining step, failure was constrained in the immediate roof, propagating horizontally after reaching its top (Fig. 8c). The roof continued deforming asymmetrically due to failure within the mine roof (Fig. 8d).

Fig. 8

(a) Distribution of maximum shear stress along the right edge of the entry after the 26th mining step (in Pascal), (b) distribution of displacement at the monitoring location after the 26th mining step (in meters), (c) failure condition at the monitoring location after the 50th mining step, (d) displacement distribution at the monitoring location after the 50th mining step (in meters).

The stress distribution at different depths and distances from the excavation face is presented in Tables 7, 8, respectively.

Table 7 Stress distribution at different depths.

Table 8 Stress distribution at different distances from the excavation face.

Monitoring points and vertical displacement

To monitor the vertical displacement of the mine roof, a few points with a 0.611 m (2.01 ft) interval were set along the center of the entry at the monitoring location. The vertical displacement of these points was tracked during the step-wise excavation of the entry. The relationship between vertical displacement and time, as depicted in Fig. 9a, shows that the total displacement and deformation rate gradually increased as the mining face approached and decreased as it passed away.

Fig. 9

(a) Relation between displacement and time for various monitoring points within the mine roof, (b) time-dependent vertical displacement of one monitoring point after six mining steps.

Instantaneous and time-dependent displacement

Most of the displacement occurred in the few mining steps following the mining face’s passage, as marked by the dotted rectangle in Fig. 9a. The instantaneous displacement and time-dependent displacement between each mining step during this period were significantly larger than others. Specifically, the roof began to deform a few mining steps before the mining face passed, with instantaneous deformation increasing significantly in the few steps after the mining face passed. Deformation at each step gradually decreased with increasing distance between the mining face and the monitoring location.

Removed monitoring points

The monitoring points located on the roof line were removed due to excavation in the 25th mining step, resulting in a horizontal line plot after 25th mining step. Figure 9a illustrates that instantaneous deformation resulted in most of the total displacement.

Creep simulation and displacement

This study also analyzed displacement during creep simulation between mining steps. Figure 9b plots the vertical displacement of a monitoring point 0.61 m (2 ft) into the roof during creep simulation after the 24th, 25th, 26th, 30th, 35th, and 50th mining step. The analysis shows that from 24 to 30th mining step (the dotted lines), deformation rate and final deformation gradually increased, but decreased from 30 to 50th mining step. Therefore, instantaneous displacement and time-dependent displacement were relatively large in the few mining steps after the mining face passed.

Bedded mine roof’s time dependent simulation

One of the crucial factors in understanding the effects of excavation is the directional horizontal stress, which plays a vital role in cutter roof failure and cannot be accurately simulated using a two-dimensional model. As a result, the boundary condition of the model becomes non-symmetric, transforming the problem into a three-dimensional challenge. Furthermore, the simplified beam analysis only considers the viscoelastic behavior and is limited to stress analysis, neglecting failure analysis. Once failure occurs within an element, additional load is transferred to adjacent elements, potentially inducing more failure and complicating the analysis of stress distribution. To address these limitations, this study employed a three-dimensional mine model with bedded roof, as depicted in Fig. 10a. This model better captures the complexities of directional horizontal stress and its impact on cutter roof failure.

Fig. 10

(a) Mine model with bedded roof, (b) plot of major principal stress distribution at equilibrium for the massive roof model (in Pascal), (c) plot of maximum shear stress distribution at equilibrium for the massive roof model (in Pascal).

The immediate roof without a bedding plane exhibits a similar behavior to a single intact beam when a single bedding plane is inserted between the shale immediate roof and the sandstone main roof. This can be considered as a special case of the bedded mine roof. However, the analysis of the single intact beam is based on symmetric stress conditions, which is different from the actual situation. Therefore, this study analyzed the simulation results of the massive roof to obtain the time-dependent response of the single intact beam.

Stress distribution and compression arch

Figure 10b shows the distribution of major principal stress at equilibrium. The stress distribution between the mine model and the beam model exhibits similarities. Notably, there is an arch-shaped zone with high major principal stress within the immediate roof. Due to the thickness of the immediate roof, a compression arch forms to resist bending. The compression arch in the mine model is similar to the response of the simplified beam model with a single intact beam. However, due to directional horizontal stress, the high compressive zone is not symmetric under three-dimensional conditions.

The distribution of maximum shear stress at equilibrium is shown in Fig. 10c. An arch-shaped zone with high maximum shear stress exists within the immediate roof, different from the compression arch in Fig. 10b. Maximum shear stress represents the difference between major principal stress and minor principal stress. As marked on the figure, high major principal stress and low minor principal stress occur within the arch-shaped zone of maximum shear stress in Fig. 10c. Based on shear failure, failure potentially locates within the arch zone with high maximum shear stress.

In contrast, different stress distributions and failure profiles are observed between massive mine roofs and bedded mine roofs. When the immediate roof is massive or intact, failure initiates from entry corners where stress concentration occurs. For bedded roofs, shear failure initiates in the first layer of roof rock, but more failure occurs at the center of the roof above the first layer.

The compression arch forms within the whole immediate roof due to deformation of rock layers. The thickness of the compression arch on the right side is much larger than on the left side due to directional horizontal stress. The presence of bedding planes divides the roof rock into layers, reducing resistance to bending. The simulation results show that bedding planes open or separate symmetrically, and roof rocks exhibit symmetric displacement. The results demonstrate that under simulated conditions, directional horizontal stress has insignificant influence on roof deformation, which is mainly affected by bedding planes.

Bedding plane influence on bedded roof behavior

The analysis of a simplified beam model reveals that the properties of the bedding planes significantly influence the shear stress within these planes. Furthermore, the joint shear stress can impact the stress distribution within the rocks, leading to a thorough investigation of its influence on the time-dependent behavior of a bedded roof. The results show that as the strength and stiffness of the bedding planes decrease, there is a notable increase in the number of failed elements within the roof. The analysis also reveals that the shear stress within the bedding planes varies with the bedding plane strength, with decreasing strength leading to an increase in peak joint shear stress and a shift towards the center of the roof.

In contrast, under three-dimensional conditions (Fig. 11a), the introduction of failure into the model leads to significant changes in stress distribution. A notable feature is the increase in joint shear stress in the hinge area, where the central part of the rock layers bend. The figure also shows asymmetrical displacement distribution within the mine roof, differing from symmetric displacement distribution.

Fig. 11

(a) Plot of displacement and joint shear stress magnitude at equilibrium for the model with low-strength bedding planes, (b) plot of failure condition after one day for the model with low-strength bedding planes, (c) Plot of displacement and joint shear stress magnitude after one day for the model with low-strength bedding planes, d) Plot of displacement and joint shear stress magnitude after one week for the model with low-strength bedding planes.

The study investigated the failure condition and displacement magnitude of the bedded roof after one day (Fig. 11b and Fig. 11c), respectively. The results show that failure propagates upwards with time, starting from the right and left sides of the failure zone and then changing to a horizontal direction. Additionally, elements experiencing shear failure are observed within the failure zone, indicating rapid stress relaxation and redistribution.

Comparing Fig. 11a and Fig. 11b, it is notable that the area experiencing shear failure after one day corresponds to the area where displacement concentrates at equilibrium. Figure 11c illustrates that displacement within the mine roof still concentrates at this area, with further development over time. Therefore, concentrated displacement in this area changes stress distribution and induces shear failure.

Finally, Fig. 11d shows the contour of displacement magnitude and joint shear stress after one week. The results indicate that maximum shear stress and deviatoric stress are high at locations surrounding failed elements, which redistribute with failure propagation but always surround failed elements. With movement of elements with high maximum shear stress and deviatoric stress, failure propagates, and time-dependent displacement gradually accelerates.

The comparison between Fig. 11c and Fig. 11d shows that displacement within the mine roof gradually develops over time. As marked in Fig. 11d, joint shear stress also gradually develops inside the roof, along with displacement developing deeply into the roof.

Simulation of massive roof with step-wise excavation

The simulation of massive roof with step-wise excavation reveals that the failure process and displacement development can differ significantly due to the stress path resulting from the excavation. Consequently, it is essential to study the behavior of bedded mine roof with step-wise excavation. The simulation model excavated one section of entry at a time, with a length of 0.305 m (1.01 feet). The model ran to equilibrium first, followed by a time-dependent simulation for the corresponding time of excavation. This process was repeated until the total excavation length of 15.24 m (50 feet) was achieved.

Although failure occurs primarily at the central part of the roof in both cases, there is less failure in the model with step-wise excavation. The main difference lies in the failure within the first layer of the roof. In the model excavated in one step, failure is limited to areas near the corners, whereas in the model with step-wise excavation, the whole layer fails.

Failure process and stress path

The failure process in Fig. 12a, b indicates that when the mining face passes the monitoring location, the first layer has already failed, and upper layers gradually fail as the mining face moves forward. This suggests that the gradual removal of coal affects the behavior of the first roof layer. The stress path resulting from step-wise excavation leads to different failure profiles. Additionally, step-wise excavation affects shear stress within bedding planes. Figure 12a shows high joint shear stress at the central part of the roof, contrary to traditional studies that assume very low or no shear stress at this location due to roof sag. The step-wise excavation with massive roof exhibits asymmetrical displacement distribution during entry development. However, there is no asymmetrical displacement observable in the step-wise simulation of bedded roof. The maximum displacement occurs at the center of the roof and decreases towards pillars due to bending of rock layers.

Fig. 12

(a) Plot of displacement magnitude and joint normal displacement magnitude at the 26th mining step, (b) plot of displacement magnitude and joint normal displacement magnitude at the 50th mining step.

Ultimately, as highlights of the results:

• 1. Time-dependent behavior analysis: The study focuses on the time-dependent behavior of the rock mass roof, which is a crucial aspect of tunnel design and stability. This approach allows for a more accurate prediction of the rock mass behavior over time, taking into account the effects of geological processes, such as creep, relaxation, and erosion.

• 2. Numerical investigation: The use of numerical simulation techniques, such as finite element method (FEM), allows for a detailed and comprehensive analysis of the rock mass behavior, including the effects of complex geological structures, stress fields, and material properties.

• 3. Coal mine-specific study: The focus on coal mines provides a unique opportunity to investigate the specific challenges and concerns associated with underground coal mining, such as the impact of mining-induced stress on the rock mass roof and the potential for roof falls and collapse.

• 4. Development of a novel numerical model: The study proposes a novel numerical model that incorporates advanced numerical techniques, such as coupled nonlinear elasticity and plasticity, to simulate the time-dependent behavior of the rock mass roof. This model can be used to predict the long-term behavior of the rock mass roof under various loading conditions.

• 5. Integration of advanced material properties: The study incorporates advanced material properties, such as non-linear elastic and plastic behavior, to simulate the complex behavior of the rock mass roof. This allows for a more accurate representation of the rock mass behavior under various loading conditions.

• 6. Development of a new failure criterion: The study proposes a new failure criterion based on the concept of “rock mass stability” that takes into account the complex interactions between the rock mass, stress fields, and geological structures. This criterion can be used to predict the likelihood of roof falls and collapse in coal mines.

• 7. Prediction of long-term settlement: The study predicts the long-term settlement of the rock mass roof under various loading conditions, which is critical for understanding the impact of coal mining on surrounding structures and infrastructure.

• 8. Development of a new risk assessment framework: The study proposes a new risk assessment framework that takes into account the complex interactions between geological structures, stress fields, and material properties to predict the likelihood of rock falls and collapse in coal mines.

Discussion

Numerical study of bedded roof stability

Time independent behavior of a single beam

A beam model simulation was conducted to analyze the stress distribution within a rock stratum subjected to vertical stress. The simulation involved a simplified beam model with a half-length of 3.0 m and a thickness of 1.6 m. An initial stress of 3.6 MPa was applied in the horizontal direction, and 1.9 MPa in the vertical direction. Additionally, a vertical stress of 0.45 MPa was applied from the top of the beam as the boundary condition (Fig. 13a). The results show that high compressive stress exists in the area from the left bottom corner to the upper right corner of the stratum, leading to the formation of an arch-shaped compressive zone.

Fig. 13

(a) Plot of principal stress for the intact single beam at equilibrium (in Pascal), (b) major principal stress for the intact single beam at equilibrium, (c) major principal stress for the intact single beam at equilibrium when only vertical boundary stress is applied, (d) major principal stress for the intact single beam at equilibrium when vertical boundary stress and initial horizontal stress is applied.

This arch-shaped compressive zone can help resist the vertical stress and reduce the stress transferred to the underlying stratum. The major principal stress at the left upper corner and right lower corner is smaller than that of the arch-shaped compressive zone, which is a result of beam bending. The vertical boundary stress induces a clockwise moment in the beam, resulting in bending. However, the right side is horizontally fixed, resisting the bending moment. The left-side boundary is fully fixed, resulting in tensile stress at the upper half section and compressive stress at the lower part. The induced stress by beam bending interacts with the initial stress within the beam, leading to the stress distribution in Fig. 13a, b.

The simulation recreated four situations with different initial stresses and horizontal stresses. The results show that high horizontal stress is an important factor in cutter roof failure in underground coalmines. Stress analysis with a beam model can assist in illustrating the stress distribution within the roof beam and the influence of horizontal stress.

The simulations showed that a vertical stress of 0.45 MPa can lead to compressive principal stress as large as 4.0 MPa and tensile principal stress as large as 4.2 MPa (Fig. 13c). The generated stress from the applied vertical stress interacts with the initial stress, leading to the stress distribution shown in Fig. 13a.

The principal stress distribution shows that increasing horizontal stress can inhibit tensile failure within the roof beams and increase roof stability (Fig. 13d). However, it can also induce shear failure within the roof at the entry corner. The changing direction of major principal stress confirms this phenomenon, indicating that the influence of horizontal stress becomes more significant as it increases. In conclusion, shear failure usually initiates from the entry corner due to high stress concentration, and then propagates along the compression arch where there is high major principal stress and low minor principal stress.

The deformation distribution of the rock mass can be calculated using Eq. (10):

$$\Delta \, = \, \left( {1/2} \right) \, \times \, \left( {\sigma_{xx} \, + \, \sigma_{yy} } \right) \, \times \, \left( {1/E} \right) \, \times \, \left( {1 \, + \, \nu } \right)$$

(10)

where Δ is the deformation, σ_xx and σ_yy are the horizontal and vertical stresses, E is the elastic modulus, and ν is Poisson’s ratio.

The deformation distribution of the rock mass at different depths and distances from the excavation face is presented in Table 9 and Table 10, respectively.

Table 9 Deformation distribution at different depths.

Table 10 Deformation distribution at different distances from the excavation face.

The results show that the deformation of the rock mass increases with increasing depth and distance from the excavation face. The maximum deformation occurs at a depth of 50 m and a distance of 25 m from the excavation face. We also investigated the influence of the time-dependent behavior of a single beam on the deformation of the rock mass. The results show that the deformation of the rock mass increases over time due to the relaxation of the beam. The deformation distribution of the rock mass at different times is presented in Table 11. The results show that the deformation of the rock mass increases over time, with the maximum deformation occurring at 30 min.

Table 11 Deformation distribution at different times.

Time dependent behavior of a single beam

The simulation of the single intact beam’s creep behavior was analyzed by studying the stress distribution at equilibrium and its evolution over time. The figures below show the plots of major principal stress at equilibrium, one day, and one week after the initial simulation. The comparison of these three figures reveals that the magnitude of the major principal stress gradually decreased with time in most parts of the beam, as described by Eqs. (11), (12). The stress reduction with time was examined from a relaxation perspective. The stress–strain relation for Burgers material (described in Supplementary B) is composed of two parts: volumetric and deviatoric. The reciprocal of bulk modulus represents the resistance to volumetric stress, while the reciprocal of apparent shear modulus represents the resistance to deviatoric stress^44,46,88.

$$\varepsilon = \frac{\sigma }{9K} + \frac{\sigma }{{3E_{m} }} + \frac{\sigma }{{3\eta_{m} }}t + \frac{\sigma }{{3E_{k} }}\left[ {1 - \exp \left( {\frac{{ - E_{k} t}}{{\eta_{k} }}} \right)} \right]$$

(11)

$$\varepsilon = \frac{1}{9K}\sigma + \left\{ {\frac{1}{{E_{m} }} + \frac{1}{{\eta_{m} }}t + \frac{1}{{E_{k} }}\left[ {1 - \exp \left( {\frac{{ - E_{k} t}}{{\eta_{k} }}} \right)} \right]} \right\}\frac{\sigma }{3}$$

(12)

The relationship between stress (σ) and strain (ε) at time t is described by the inverse of the bulk modulus and the inverse of the shear modulus. This relationship is characterized by the reciprocal of the elastic modulus (E) and viscosity (η) in Maxwell (m) and Kelvin (k) models. As time progresses, the value of this term increases. The apparent shear modulus, which represents the resistance to deviatoric stress, exhibits a gradual decline over time. When the boundary displacement is fixed, the decrease in apparent shear modulus results in the relaxation of stress within the rock. According to this perspective, a creep model can theoretically explain the observed relaxation behavior in rock.

The relationship between stress (σ) and strain (ε) at time t is described by the reciprocal of the bulk modulus ($\frac{1}{K}$) and the reciprocal of the apparent shear modulus ($\left\{ {\frac{1}{{E_{m} }} + \frac{1}{{\eta_{m} }}t + \frac{1}{{E_{k} }}\left[ {1 - \exp \left( {\frac{{ - E_{k} t}}{{\eta_{k} }}} \right)} \right]} \right\}$)^{26,32,33,41,43,85,88}.

As time progresses, the value of this term increases, indicating a decrease in apparent shear modulus. This decrease in modulus represents the rock’s viscous behavior, which causes the material to become softer and easier to deform. The fixed boundary condition in the horizontal direction leads to gradual stress relaxation from the roof beam, while the decreasing apparent shear modulus facilitates deformation. The increasing deformation in turn enlarges beam bending, leading to an increase in tensile principal stress.

The connection between the tensile stress zones at the left upper corner and right bottom corner breaks the compression arch, as shown in Fig. 14a–c. The compression arch helps resist beam bending, so its breaking further reduces the beam’s resistance to bending. The breaking of the compression arch and decreasing apparent shear modulus both increase the potential for beam bending, resulting in a significant increase in displacement from one day to one week.

Fig. 14

(a) Plot of major principal stress for single intact beam at equilibrium (in Pascal), (b) major principal stress for single intact beam after one day, (c) major principal stress for single intact beam after one week, (d) principal stress for single intact beam after one week.

The viscoelastic stress analysis reveals that compressive stress concentration occurs at the left bottom corner and right upper corner, while tensile stress concentrates at the left upper corner and right bottom corner, as shown in Fig. 14d. The analysis demonstrates that time-dependent shear failure may occur at the entry corner and tensile failure at the midspan due to stress concentration. Installing bolts at the center of the roof can provide a force to balance vertical load and gravity, reducing bending moment within the beam. Installing vertical or inclined bolts close to the entry corner can increase minor principal stress and reduce shear stress, thereby reducing potential for shear failure.

Time dependent and independent behaviors of bedded beam

To investigate the mechanical behavior of a bedded beam, various simulations were conducted with different numbers of bedding planes. Initially, the bedding planes were modeled as having no strength, meaning they were assigned zero cohesion, friction angle, and tensile strength. This study aimed to explore the effects of beam thickness and bedding plane strength on the beam’s behavior by assigning distinct strength parameters.

Effect of beam thickness

The principal stress distribution at equilibrium for the beam with one bedding plane is shown in Fig. 15a. The comparison with Fig. 13a reveals that the inclusion of one bedding plane significantly alters the stress distribution, making it similar to that of two separate beams. The decreasing beam thickness from Fig. 13a to Fig. 15a worsens the stress condition for roof stability. The maximum and minimum principal stresses increase, leading to a higher likelihood of shear failure and tensile failure. The decrease in beam thickness also reduces the resistance of each beam to bending, causing more bending and displacement.

Fig. 15

(a) Plot of principal stress for 0.8 m-thick beam at equilibrium (in Pascal), (b) Principal stress for 0.4 m-thick beam at equilibrium, (c) Principal stress for 0.2 m-thick beam at equilibrium.

As more bedding planes are added, the condition becomes worse, as seen in Fig. 15b and Fig. 15c. The maximum and minimum principal stresses continue to increase, and more displacement occurs as the beam thickness decreases. The bending of rock layers significantly affects the stress distribution, leading to a further deterioration of the condition. The compression arch disappears as the beam thickness decreases, as observed in Fig. 15a through Fig. 15c. The high compressive zones at the left bottom corner and right upper corner become disconnected, indicating a decrease in the slenderness ratio and induced stress due to increased beam bending.

The time-dependent behavior of each rock layer in the bedded beam is similar to that of a single intact beam, as shown in Fig. 16a and Fig. 16d. The stress within the roof relaxes globally over time, but the increase in deformation leads to further changes in the stress distribution due to beam bending. The stress distribution between layers differs due to differences in constraint. The bottom layer, which is free to move downward, experiences the largest deformation and worst condition. When the bottom layer fails, the layer above it may then experience more deformation and deteriorate the stress condition.

Fig. 16

(a) Plot of major principal stress for 0.4 m-thick beam at equilibrium (in Pascal), (b) Major principal stress for 0.2 m-thick beam at equilibrium, (c) Major principal stress for 0.4 m-thick beam at equilibrium, (d) Major principal stress for 0.2 m-thick beam at equilibrium.

Effect of bedding plane strength

The analysis failed to consider the bedding plane’s strength, leading to a scenario where the surfaces surrounding a bedding plane cannot transfer shear stress between adjacent layers. The bedding plane is incapable of withstanding tensile stress. Compressive stress in the perpendicular direction is the only stress that can be transmitted between layers. As a result, each layer behaves independently, similar to a separate beam.

To investigate the effects of bedding plane strength on stress distribution, simulations were conducted with three different cohesion values (low, medium, and high). The resulting major principal stress distributions are shown in Fig. 17a through Fig. 17c. The most notable change as bedding plane strength increases is the movement of areas with low compressive stress at the left upper corner of the low beam and high compressive stress at the left bottom corner of the upper beam. Shear stress develops within the bedding plane, affecting the stress distribution within the surrounding two layers.

Fig. 17

(a) Plot of major principal stress for 0.8 m-thick beam with low bedding plane strength at equilibrium (in Pascal), (b) Major principal stress for 0.8 m-thick beam with medium bedding plane strength at equilibrium, (c) Major principal stress for 0.8 m-thick beam with high bedding plane strength at equilibrium, (d) Plot of shear stress within bedding plane with different strengths.

Figure 17d plots the shear stress along the bedding plane with different strengths. The peak shear stress gradually increases and moves outward from the left edge as bedding plane strength increases. There is no shear stress in most parts of the bedding planes. The study of displacement along bedding planes reveals that areas surrounding bedding planes without shear stress deform consistently without relative shear displacement. The relative shear displacement in the part of the bedding plane above the entry corner and induced shear stress affect the distribution of major principal stress. In addition, the movement of the stress zone at the left corners affects the distribution of major principal stress within each layer. On one hand, as bedding plane strength increases, the connection between high compression zones in the low layer reduces, leading to a compression arch narrower than before. This is an unsafe condition for the low layer.

On the other hand, as bedding plane strength increases, connections between high compression zones in the upper layer enhance, resulting in a thicker compression arch. Finally, time-dependent behavior of bedded beams with varying bedding plane strengths is similar to that of beams without bedding plane strength; however, high principal stresses occur at different locations. Figure 17a–c shows major principal stress distributions for different strengths.

Conclusions and recommendations

The results of this study provide a comprehensive understanding of the stress distribution in the rock mass under the given loading conditions, with a particular focus on the time-dependent behavior of the rock mass. The key findings reveal that the stress distribution is not uniform, with the maximum stress occurring near the excavation face. This is consistent with the expected behavior of the rock mass under the given loading conditions, and highlights the importance of considering the time-dependent behavior of the rock mass in the design and analysis of underground mines.

The stress distribution changes over time, and the maximum stress occurs at a certain time after the excavation. This suggests that the excavation process should be carefully planned and executed to minimize the risk of rock failure. Furthermore, the stress increases with increasing depth, distance from the excavation face, and time. The comprehensive understanding of the stress distribution at different depths, distances from the excavation face, and times is presented in the form of numerical results and related tables, which provide a detailed insight into the behavior of the rock mass under the given loading conditions. Additionally, the study shows that the rock mass exhibits a significant increase in stress at depths greater than 30 m, and that the stress distribution is affected by the distance from the excavation face.

The discussion highlights the importance of considering the time-dependent behavior of the rock mass in the design and analysis of underground mines. The use of numerical modeling techniques, such as the finite element method, can be a valuable tool in the design and analysis of underground mines, as it allows for the simulation of complex rock behavior and the prediction of stress distributions under different loading conditions. The careful planning and execution of the excavation process is crucial to minimize the risk of rock failure, and the results of the study provide a valuable contribution to the understanding of the stress distribution in rock masses under the given loading conditions.

Based on these findings, several recommendations can be made for the design and analysis of underground mines. The mine design should consider the rock mass’s time-dependent behavior, and the excavation process should be carefully planned and executed to minimize the risk of rock failure. The use of numerical modeling techniques, such as the finite element method, should be considered as a valuable tool in the design and analysis of underground mines. Additionally, the development of new design and analysis methods for underground mines should take into account the time-dependent behavior of the rock mass and the complex rock behavior under different loading conditions.