Temporal representation learning enhanced dynamic adversarial graph convolutional network for traffic flow prediction

Abstract

Accurate traffic flow prediction serves as the foundation for urban traffic guidance and control, playing a crucial role in intelligent transportation management and regulation. However, current methods fail to fully capture the complex patterns and periodic characteristics of traffic flow, leading to significant discrepancies between predicted and actual values. This gap hampers the achievement of high-precision forecasting. To address this issue, this paper proposes a temporal representation learning enhanced dynamic adversarial graph convolutional network (TRL-DAG). Our approach utilizes a temporal representation learning strategy with masked reconstruction for pre-training, aiming to extract temporal representations from contextual subsequences in historical traffic data. We further introduce a dynamic graph generation network to enhance the flexibility of graph convolution, enabling the model to capture dynamic spatiotemporal correlations by integrating both current and historical states. Additionally, we design an adversarial graph convolutional framework, which optimizes the loss through adversarial training, thereby reducing the trend discrepancy between predicted and actual values. Experiments conducted on six real-world datasets demonstrate that TRL-DAG outperforms existing state-of-the-art methods, achieving superior performance in traffic flow prediction.

Introduction

In recent years, with advancements in information technology and the increasing number of vehicles, intelligent transportation systems have undergone rapid development. Accurate traffic prediction plays a crucial role in reflecting traffic conditions and assisting urban management in formulating effective scheduling strategies¹. Moreover, various downstream tasks, such as travel time estimation, heavily rely on the accuracy of traffic prediction. As a result, traffic forecasting has emerged as one of the most prominent research directions in the field of intelligent transportation systems.

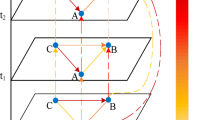
Traffic flow is a typical time series data characterized by complex temporal dependencies and dynamic spatial correlations. First, the complexity of temporal dependencies is primarily reflected in the periodicity and trends of traffic flow. For instance, traffic patterns at the same location on the same day of the week or at the same time of day tend to exhibit certain similarities. On the other hand, dynamic spatial correlations are observed in the mutual influence of traffic flow between different locations. As shown in Fig. 1, the relationships between nodes in the traffic network evolve over time in response to changing traffic conditions. A static graph structure fails to accurately capture the actual relationships between nodes. The correlations between nodes should dynamically change over time, depending on real-time data. For example, traffic nodes near schools and offices may show high spatial correlation during peak hours, while this correlation may significantly decrease during other times. This highlights the presence of complex nonlinear spatiotemporal relationships in traffic flow.

Fig. 1

Complex spatiotemporal correlations.

(a) A road network with loop detectors. (b) The corresponding spatiotemporal correlations of the loop detectors in (a). Although sensor 2 and sensor 4 are physically distant in the road network, at time step $t + \xi + 1,$ sensor 2 and sensor 4 are closely correlated, illustrating the dynamic long- and short-term spatial relationships in traffic flow. Furthermore, the traffic flow at sensor 4 during time step $t + \xi + 1$ might be more closely related to a distant time step (e.g., $t - 1$) than a nearby one (e.g., $t + \xi$), indicating the presence of complex nonlinear temporal relationships in traffic flow.

Early traditional traffic flow prediction methods, such as the historical average (HA) method² and the autoregressive integrated moving average (ARIMA) model³, rely heavily on idealized mathematical assumptions and are limited to linear modeling. However, real-world traffic data is highly complex, dynamic, and nonlinear, making these approaches inadequate for capturing the intricate nonlinear temporal features of traffic flow. Moreover, they fail to account for the dynamic spatial relationships within traffic networks, rendering these methods largely unsuitable for practical applications. As research progressed, grid-based methods were introduced, where urban areas were divided into regular grids to extract spatiotemporal correlations within the traffic network^4,5. However, these methods linearize the nonlinear spatial features and overlook the actual topological structure of the road network, leaving the challenge of extracting nonlinear dynamic spatial features unresolved.

With the continuous development of deep learning, graph convolutional networks (GCNs)^6,7 have been applied to handle non-Euclidean structures, as they can learn latent spatial features by aggregating information from neighboring nodes. Many studies have proposed combining GCNs with models such as recurrent neural networks (RNNs) and convolutional neural networks (CNNs) to develop traffic flow prediction models^8,9. However, GCNs based on predefined graphs lack the ability to model the dynamic spatial dependencies between nodes¹⁰. For example, the dependencies between nodes change over time, meaning that predefined graph structures cannot capture the real-time variations in network topology and traffic flow fluctuations. Additionally, determining temporal and spatial dependencies solely based on geographical distance between nodes is problematic, as nodes that are not directly connected may still influence each other¹¹. Consequently, many existing models that rely on static predefined^12,13 or adaptive adjacency matrices (spatial graphs)^14,15 are inadequate for effectively modeling spatiotemporal dependencies, limiting their practical accuracy and applicability. Moreover, capturing the trends and periodicity of traffic flow remains challenging. For instance, models like diffusion convolutional¹⁶ or temporal graph convolutional networks (T-GCN)¹⁷ may suffer from error accumulation and issues such as vanishing or exploding gradients when extracting long-term spatiotemporal features.

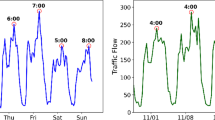
Figure 2 illustrates traffic speed time series data from June 7 to June 14, 2017, highlighting both long-term trends and cyclical variations in traffic flow. The main graph depicts traffic speed data from two sensors (400,236 and 400,240), exhibiting clear cyclical fluctuations likely tied to daily peak and off-peak traffic hours, along with long-term trends that may reflect broader traffic pattern shifts. An inset graph provides a detailed view of the short-term trend from 00:00 to 12:00 on June 14, 2017, showcasing more granular cyclical fluctuations, such as those occurring during morning and evening peak periods. Dashed lines and arrows denote periodicity and specific events, like the notable drop on June 14, 2017, aiding in the identification of key patterns and anomalies for enhanced traffic management and planning.

Fig. 2

Historical time series visualization of sensor 400,236 and sensor 400,240 on the PEMS-BAY dataset.

However, many existing models are constrained by their reliance on short time series inputs, which may not fully encapsulate the intricate temporal characteristics inherent in historical traffic data. For instance, using only 6 h of historical data from 00:00 to 06:00 to predict traffic flow after 06:00 may not offer sufficient short-term trend information for accurate forecasting, given the similar trends and values recorded by the two sensors. In contrast, incorporating long-term trends and periodicity from extended historical sequences can better guide the model in anticipating future traffic patterns. The model can more readily infer various future traffic flow trends based on the distinct long-term trend features of the two sequences and the recurring temporal features indicated by magenta circles. This is a primary reason why many current methods struggle to maintain consistent overall trends and correlations across time series for all nodes, leading to discrepancies between predicted and actual values. Moreover, directly inputting each time step from an extended historical sequence into the model is inefficient, as traffic flow sequences display a degree of continuity and long historical sequences often include redundant information. Thus, efficiently extracting key representations from long sequences is crucial for enhancing model performance.

To address the aforementioned issues, we propose a novel model, the temporal representation learning enhanced dynamic adversarial graph convolutional network (TRL-DAG). This framework simultaneously considers short-term traffic flow trends and captures long-term trends and periodicity from core temporal information in historical sequences through the construction of a temporal representation learning block. Additionally, it leverages dynamic graph generation and adversarial graph convolution networks to model dynamic spatial dependencies, ensuring consistency in the overall trends and correlations of predicted time series. The main contributions of this work are summarized as follows:

• 1. We propose a novel traffic flow prediction model that constructs dynamic graphs and employs an adversarial graph convolutional network to learn dynamic dependency graphs. By integrating a temporal representation learning strategy, the model effectively captures long-term trends and periodic features of traffic flow, enabling accurate traffic flow prediction.

• 2. We design a temporal representation learning block, which is pre-trained through a masked reconstruction task to obtain compressed and contextual temporal representations of subsequences, enabling efficient extraction of key information from long historical sequences by considering long-term trends and periodicity.

• 3. We construct a dynamic graph generation mechanism, which utilizes dynamic graphs and stacked graph convolutional networks to capture dynamic spatiotemporal features. Additionally, we propose an adversarial graph convolution network that reduces the trend discrepancies between predicted and actual traffic flows through adversarial training and loss optimization.

• 4. We evaluate the proposed framework on six real-world traffic datasets, and experimental results demonstrate that the model achieves superior predictive performance compared to popular baseline methods.

Related works

Traffic flow prediction

Traffic prediction has been studied for many years. In the early stages, traditional machine learning models such as autoregressive integrated moving average (ARIMA)³ and support vector regression (SVR)¹⁸ were commonly used for traffic forecasting. These models largely rely on handcrafted features and only model the temporal dimension of traffic flow data, making it difficult to capture complex nonlinear spatiotemporal information. In recent years, with the rapid development of deep learning, recurrent neural networks (RNNs)^12,19,20 have emerged as powerful techniques for time series learning tasks due to their ability to accurately capture dependencies in temporal data. However, the iterative design of RNNs can lead to issues such as error accumulation and loss of temporal correlations in long-term learning. To overcome this limitation, Yao et al.²¹ developed a deep multi-view spatiotemporal network (DMVST), which divides traffic regions into regular grids and utilizes convolutional neural networks (CNNs) to learn the Euclidean spatial distribution of traffic networks. Despite recent advances, CNNs still fail to capture the actual spatial information of road networks, as they rely on Euclidean distance to represent spatial data. Subsequently, numerous studies introduced graph convolutional networks (GCNs)^6,9,22 into the traffic flow prediction domain to handle the graph-structured nature of traffic networks and non-Euclidean data. Wu et al.¹⁴ generated a static graph based on the similarity between two roads’ representations, while Kong et al.²³ employed an attention mechanism¹⁶ to learn data dependency graphs. STSGCN²⁴ and AGCRN¹⁵ also explored similar attention-based graph structure learning methods²⁵. Unfortunately, these approaches overlook the complexity of road network topology and lack consideration of uncertainty in the underlying graph structures when modeling the traffic flow network.

Graph convolution networks

In recent years, graph convolutional networks (GCNs) have been widely used for modeling non-Euclidean data. Particularly in the field of traffic flow prediction, GCNs-based models have demonstrated superior predictive performance compared to traditional methods. GCNs can be broadly categorized into spectral-based and spatial-based approaches. Spectral-based models perform convolution in the spectral domain. For example, Bruna et al.²⁶ introduced a spectral graph convolutional kernel based on the Fourier domain, computed via the eigen-decomposition of the graph Laplacian operator. Subsequently, ChebNet²⁷ proposed approximating the convolutional kernel using a K-order polynomial of the graph Laplacian operator. Defferrard et al.²⁸ and Kipf et al.²⁹ further simplified the GCNs by introducing a renormalization trick. Most spatial-based methods, on the other hand, perform convolution directly on the graph itself. For instance, Diffusion CNN³⁰ uses the graph diffusion process as a convolutional kernel, while GraphSAGE³¹ generates embeddings by sampling and aggregating features from neighboring nodes. In this paper, we adopt a spatial-based approach and construct a dynamic graph generation network to learn the road adjacency matrix, allowing us to model dynamic spatial dependencies in traffic networks.

Generating adversarial networks

Generative adversarial networks (GANs) have demonstrated exceptional performance in time series prediction by generating forecasted data that shares the same trends and global properties as the true values through adversarial learning. Yoon et al.³² were the first to model time series using GANs, employing a GAN based on a learned embedding space to generate dynamic time series data. Wu et al.³³ used GANs to construct a time series prediction model, utilizing a sparse transformer to generate sparse attention graph and a discriminator to mitigate error accumulation during training. Zhang et al.³⁴ embedded convolutional neural networks and long short-term memory (LSTM) networks into a GAN to learn the dynamic spatiotemporal features of traffic flow. More recently, TFGAN³⁵ combined GANs with graph convolutional networks for traffic time series prediction, where the GANs learns the distribution of time series data. The generator constructs multiple static graphs internally to model spatial correlations, while the discriminator builds real and fake samples at the sequence level by connecting inputs with both predicted values and ground truths.

These models typically use GANs to learn the distribution of time series data from a static perspective, which falls short of fully capturing the dynamic spatial dependencies during the generation or discrimination process. Additionally, these approaches rarely explicitly consider the global properties of traffic data, such as the overall trends in each time series and the correlations between different sensors (or channels). These global attributes are critical for extracting trend-related features of traffic flow and for reducing the trend discrepancies between predicted and actual values, which are essential for achieving accurate traffic flow prediction.

Methodology

Problem definition

We represent the traffic road network as a graph $G = \left( {V,E,A} \right)$, where $\left| V \right| = N$ is the set of nodes, with each node representing an observation sensor in the road network, and $E$ is the set of edges between nodes, with edge weights determined by the distance between nodes. $A \in {\mathbb{R}}^{N \times N}$ is the initial adjacency matrix generated from graph $G$, where $A_{ij}$ if $v_{i} ,v_{j} \in V$ and $\left( {v_{i} ,v_{j} } \right) \in E$, 0 otherwise. Using this initial adjacency matrix $A$, derived from the original traffic network as prior knowledge, the goal is to predict future traffic flow $\hat{X}^{T + 1:T + H} = \left\{ {X^{\left( t \right)} ,X^{{\left( {t + 1} \right)}} , \cdots ,X^{\left( H \right)} } \right\} \in {\mathbb{R}}^{H \times N \times O}$ based on the historical time series $X^{1:T} = \left\{ {X^{\left( 1 \right)} ,X^{\left( 2 \right)} , \ldots ,X^{\left( t \right)} , \ldots ,X^{\left( T \right)} } \right\} \in {\mathbb{R}}^{T \times N \times F}$. Here, $X^{\left( t \right)} \in {\mathbb{R}}^{N \times F}$ represents the observed values of $N$ nodes with $F$ features at time step $t$, and $X_{i}^{\left( t \right)}$ denotes the value at node $i$ at time $t$. $T$ represents the length of the historical time series, $H$ is the length of the future traffic sequence to be predicted, and $O$ is the output feature dimension for each node. The mapping relationship for the traffic flow prediction problem can be expressed as follows:

$$\hat{X}^{T + 1:T + H} = f\left( {X^{1:T} ;\Theta } \right)$$

(1)

where $f$ denotes the prediction function and $\Theta$ is all the learnable parameters in the TRL-DAG model.

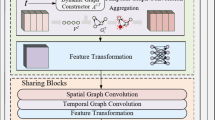
Framework of TRL-DAG

Figure 3 illustrates the overall framework of TRL-DAG, which consists of the temporal representation learning module (TRL), dynamic graph generation (DGG), adversarial graph convolutional network (AGCN), and a discriminator. The TRL module leverages known historical data and temporal context to enhance the model’s ability to capture trend-related features in traffic data, thereby improving TRL-DAG’s understanding of complex traffic patterns. DGG constructs a dynamic graph generation network to extract dynamic spatial dependencies and eliminate the model’s reliance on prior or domain-specific knowledge, enabling multi-step sequence-to-sequence traffic flow prediction. AGCN captures the temporal dependencies in traffic flow and optimizes the loss through adversarial training, reducing trend discrepancies between predicted and actual values, with the final output refined by the Discriminator.

Fig. 3

General framework of TRL-DAG model.

Temporal representation learning

The objective of temporal representation learning (TRL) is to infer the content of masked subsequences based on a small number of subsequences and their temporal context, allowing the model to extract key information. This enables the model to effectively learn compressed, contextually rich representations of subsequences from time series data. We divide the traffic flow sequence into equal-length subsequences, each containing multiple time steps, which serve as the basic units of input for the model. Since traffic flow data exhibits temporal continuity with relatively low information density, a relatively high masking rate is necessary. In this study, we apply a 75% random mask rate, and in TRL, the input at each time step is directly connected to one another. Regardless of how the time steps increase, the model incorporates prior temporal features when learning representations.

The TRL consists of two components: the temporal representation learner and the self-supervised task head. The former learns the temporal representations of subsequences, while the latter reconstructs the complete traffic flow sequence based on the temporal representations of the unmasked subsequences and the masked tokens. Specifically, the sequence $X^{1:T}$ is divided into $N = {T \mathord{\left/ {\vphantom {T S}} \right. \kern-0pt} S}$ non-overlapping subsequences, each containing $S$ time steps. We randomly mask 75% of these subsequences, with the set of masked subsequences denoted as $X_{masked}$. The remaining data, represented as $X_{unmasked}$, is used as input for the temporal representation learner.

$$S_{unmasked} = TRLearner\left( {X_{unmasked} } \right)$$

(2)

where $S_{unmasked}$ denotes the representation of $X_{unmasked}$ and is the output of the temporal representation learner.

The self-supervised task head consists of a transformer layer and a linear output layer, which can reconstruct the complete long sequence based on the given $S_{unmasked}$ and the learnable masked tokens $S_{{\left[ {mask} \right]}}$, as follows:

$$\left[ {\hat{X}_{masked} ,\hat{X}_{unmasked} } \right] = TaskHead\left( {S_{unmasked} ,S_{{\left[ {mask} \right]}} } \right)$$

(3)

The objective is to minimize the error between the reconstructed sequence and the true values of the masked subsequences $\hat{X}_{masked}$. This ensures that the model accurately reconstructs the masked parts of the sequence, improving its ability to capture and predict traffic flow patterns.

Dynamic graph generation

Due to the heterogeneity, dynamism, and uncertainty of information between nodes in the road network, we designed the dynamic graph generation (DGG) module to further capture the dynamic spatiotemporal dependencies of traffic flow. The DGG employs a spatiotemporal embedding network and stacked GCNs to automatically learn hidden dynamic spatial features. The specific structure of the spatiotemporal embedding network is shown in Fig. 4.

Fig. 4

Spatiotemporal embedding networks.

First, the DGG randomly initializes a spatial node embedding $E_{node} = \left\{ {e_{node}^{\left( 1 \right)} ,e_{node}^{\left( 2 \right)} , \ldots ,e_{node}^{\left( N \right)} } \right\} \in {\mathbb{R}}^{{N \times d_{n} }}$ for each node in the traffic flow, where each row of $E_{node}$ represents the embedding of a node, and $d_{n}$ is the dimension of the node embedding. To extract time-varying information from the traffic flow, we use time-varying node embeddings $E_{time} = \left\{ {e_{time}^{\left( 1 \right)} ,e_{time}^{\left( 2 \right)} , \ldots ,e_{time}^{\left( T \right)} } \right\} \in {\mathbb{R}}^{{T \times d_{t} }}$, where $e_{{_{time} }}^{t}$ represents the node embedding at each time step $t$, and $d_{t}$ is the hidden dimension of the time-varying node embedding. To ensure dimensional consistency in the TRL-DAG model during the prediction process, we define $d = d_{n} = d_{t}$. The time-varying graph is constructed by effectively coupling the spatial node embeddings and time node embeddings through a gate module, and this process can be expressed as:

$$A_{ij}^{\left( t \right)} = \lambda \left\{ {Dpt\left( {LN\left( {e_{node}^{\left( i \right)} \Delta_{1} e_{time}^{\left( t \right)} } \right)} \right),Dpt\left( {LN\left( {e_{node}^{\left( j \right)} \Delta_{2} e_{time}^{\left( t \right)} } \right)} \right)} \right\}$$

(4)

where $e_{node}^{i}$ and $e_{time}^{t}$ represent the spatial node embedding and time-varying embedding of the $i$-th node at time step $t$, respectively. The operations $\Delta_{1}$, $\Delta_{2} \in \left\{ { + ,||, \odot } \right\}$, where $||$ and $\odot$ represent concatenation, Hadamard product, respectively. $\left\{ { \cdot , \cdot } \right\}$ represents inner product, $\lambda$ denotes the importance weight of each information item. Additionally, $LN$ and $Dpt$ represent layer normalization and dropout operations, respectively. When $\Delta_{1} = +$ and $\Delta_{2} = +$, Eq. (4) can be expressed as follows:

$$\begin{aligned} A_{ij}^{d} & = \lambda \left\{ {Dpt\left( {LN\left( {e_{node}^{\left( i \right)} + e_{time}^{\left( t \right)} } \right)} \right),Dpt\left( {LN\left( {e_{node}^{\left( j \right)} + e_{time}^{\left( t \right)} } \right)} \right)} \right\} \\ & = \lambda_{1} \underbrace {{\left\{ {e_{node}^{\left( i \right)} ,e_{node}^{\left( j \right)} } \right\}}}_{{\text{spatial homologous terms}}} + \lambda_{2} \underbrace {{\left\{ {\left\{ {e_{node}^{\left( i \right)} ,e_{time}^{\left( t \right)} } \right\} + \left\{ {e_{node}^{\left( j \right)} ,e_{time}^{\left( t \right)} } \right\}} \right\}}}_{{\text{spatial - temporal homologous terms}}} + \lambda_{3} \underbrace {{\left\{ {e_{time}^{\left( t \right)} ,e_{time}^{\left( t \right)} } \right\}}}_{{\text{temporal homologous terms}}} \\ \end{aligned}$$

(5)

The spatiotemporal embedding not only enables homogeneous interactions within the spatial and temporal domains but also allows direct interaction between the i-th node and the j-th time step. As a result, the constructed graph can simultaneously represent spatial, temporal, and spatiotemporal interactions, providing greater expressive power compared to static adaptive graphs that focus solely on spatial interactions.

Additionally, TRL-DAG replaces the graph convolution process with node-aware parameters using a first-order Chebyshev polynomial. In this case, the operation of the DGG network is defined as follows:

$$Z_{{}}^{\left( 0 \right)} = X^{\left( t \right)} ,E_{nt} = E_{node} \Delta_{1} E_{time}^{\left( t \right)}$$

(6)

$$Z_{{}}^{{\left( {l + 1} \right)}} = \left( {I_{N} + softmax\left( {A^{\left( t \right)} } \right)} \right)Z_{{}}^{\left( l \right)} E_{nt} W_{{}}^{\left( l \right)} + E_{nt} b_{{}}^{\left( l \right)}$$

(7)

where $E_{nt}$ represents the combination of spatial and temporal embeddings, and $I_{N}$ is the identity connection for the N nodes. The function $softmax$ is the activation function used to normalize $A^{\left( t \right)}$. $W_{{}}^{\left( l \right)} \in {\mathbb{R}}^{d \times F \times O}$ and $b_{{}}^{\left( l \right)} \in {\mathbb{R}}^{F \times O}$ represent the weight pool and bias pool, respectively. l is the number of graph convolution layers. The DGG updates $E_{node}$ and $E_{time}$ to learn the dynamic spatiotemporal correlations between different nodes at the same time step. This mechanism ensures that the model effectively captures both spatial and temporal interactions, adapting dynamically to the changing relationships between nodes in the traffic network.

Adversarial graph convolutional network

The adversarial graph convolutional network (AGCN) integrates the DGG network into a gated recurrent unit (GRU) and stacks multiple GRU layers, followed by a multi-layer perceptron (MLP) for output. This architecture enables efficient sequence-to-sequence multi-step traffic flow prediction, significantly reducing the prediction time cost. The process can be mathematically expressed as follows:

$$\begin{aligned} & z^{\left( t \right)} = \sigma \left( {g\left( {\left[ {X^{\left( t \right)} ,h^{{\left( {t - 1} \right)}} } \right];\Theta_{z} } \right)} \right) \\ & r^{\left( t \right)} = \sigma \left( {g\left( {\left[ {X^{\left( t \right)} ,h^{{\left( {t - 1} \right)}} } \right];\Theta_{r} } \right)} \right) \\ & c^{\left( t \right)} = tanh\left( {g\left( {\left[ {X^{\left( t \right)} ,r^{\left( t \right)} \odot h^{{\left( {t - 1} \right)}} } \right];\Theta_{c} } \right)} \right) \\ & h^{\left( t \right)} = z^{\left( t \right)} \odot h^{{\left( {t - 1} \right)}} + \left( {1 - z^{\left( t \right)} } \right) \odot c^{\left( t \right)} \\ & \hat{X}^{T + 1:T + H} = Dpt\left( {LN\left( {h^{\left( t \right)} } \right)} \right)W + b \\ \end{aligned}$$

(8)

where $X^{\left( t \right)}$ and $h^{\left( t \right)}$ represent the input and output at time step $t$, respectively. $z^{\left( t \right)}$ and $r^{\left( t \right)}$ denote the reset gate and update gate at time $t,$ respectively. $g$ represents the DGG network with learnable parameters $\Theta_{z},$ $\Theta_{r},$ and $\Theta_{c}$.

The AGCN module reduces trend discrepancies between predicted and actual values through adversarial training, further improving prediction accuracy. It constructs a generator network and introduces two discriminators, $\zeta_{{D_{1} }}$ at the sequence level and $\zeta_{{D_{2} }}$ at the graph level. The AGCN module not only utilizes a network of generators to reduce the trend difference between predicted and actual values, but is also able to capture both trend changes and spatial correlations between nodes in traffic flow sequences by setting discriminators at the sequence level and the graph level, respectively. This design allows the model to learn spatio-temporal features more comprehensively, thus improving the accuracy of traffic flow prediction. Both discriminators consist of three fully connected linear layers and $LeakReLU$ activation functions. Specifically, $\zeta_{{D_{1} }}$ learns the changing trends in the traffic flow sequence, while $\zeta_{{D_{2} }}$ captures the spatial correlations between nodes. The loss function associated with the AGCN module is expressed as follows:

$$\zeta_{{D_{1} }} = - E_{{x_{r}^{1} \sim P}} \left[ {\log \left( {D_{1} \left( {x_{r}^{1} } \right)} \right)} \right] - E_{{x_{f}^{1} \sim Q}} \left[ {\log \left( {1 - D_{1} \left( {x_{f}^{1} } \right)} \right)} \right]$$

(9)

$$\zeta_{{D_{2} }} = - E_{{x_{r}^{2} \sim P}} \left[ {\log \left( {D_{2} \left( {x_{r}^{2} } \right)} \right)} \right] - E_{{x_{f}^{2} \sim Q}} \left[ {\log \left( {1 - D_{2} \left( {x_{f}^{2} } \right)} \right)} \right]$$

(10)

$$\begin{aligned} \zeta_{{D_{G} }} & = \alpha \left( { - E_{{x_{r}^{1} \sim P}} \left[ {\log \left( {1 - D_{1} \left( {x_{r}^{1} } \right)} \right)} \right] - E_{{x_{f}^{1} \sim Q}} \left[ {\log \left( {D_{1} \left( {x_{f}^{1} } \right)} \right)} \right]} \right) \\ & \quad + \beta \left( { - E_{{x_{r}^{2} \sim P}} \left[ {\log \left( {1 - D_{2} \left( {x_{r}^{2} } \right)} \right)} \right] - E_{{x_{f}^{2} \sim Q}} \left[ {\log \left( {D_{2} \left( {x_{f}^{2} } \right)} \right)} \right]} \right) \\ \end{aligned}$$

(11)

$${\text{Sequence level:}}\left\{ {\begin{array}{*{20}l} {x_{r}^{1} = \left( {X^{1:T} ||X^{T + 1:T + H} } \right)} \hfill \\ {x_{f}^{1} = \left( {X^{1:T} ||\hat{X}^{T + 1:T + H} } \right)} \hfill \\ \end{array} } \right.$$

(12)

$${\text{Graph level:}}\left\{ {\begin{array}{*{20}l} {x_{r}^{2} = softmax\left( {\left( {X^{T + 1:T + H} } \right)^{T} X^{T + 1:T + H} } \right)} \hfill \\ {x_{f}^{2} = softmax\left( {\left( {\hat{X}^{T + 1:T + H} } \right)^{T} \hat{X}^{T + 1:T + H} } \right)} \hfill \\ \end{array} } \right.$$

(13)

where $x_{r}^{1} = \left( {X^{1:T} ||X^{T + 1:T + H} } \right)$ and $x_{r}^{2} = \delta \left( {\left( {X^{T + 1:T + H} } \right)^{\rm T} X^{T + 1:T + H} } \right)$ represent values sampled from the true distribution $P$, while $x_{f}^{1} = \left( {X^{1:T} ||\hat{X}^{T + 1:T + H} } \right)$ and $x_{f}^{2} = \delta \left( {\left( {\hat{X}^{T + 1:T + H} } \right)^{\rm T} \hat{X}^{T + 1:T + H} } \right)$ denote the predicted values obtained from the distribution Q. The symbols T and $||$ refer to the transpose and concatenation operations, respectively, and $\delta \left( \cdot \right)$ represents the normalization operation. The terms $\alpha$ and $\beta$ are the balancing weights for the sequence-level discriminator $\zeta_{{D_{1} }}$ and graph-level discriminator $\zeta_{{D_{2} }}$, respectively.

Multivariate time series forecasting

We utilize the $L1$ loss as the training objective and jointly optimize it with the adversarial training loss to enable the generator to perform multi-step predictions. Therefore, the overall loss function for the TRL-DAG model is expressed as:

$$L = L_{P} \left( \Theta \right) + L_{G} ,L_{P} \left( \Theta \right) = \sum\limits_{t = T + 1}^{T + H} {\left| {X^{\left( t \right)} - \hat{X}^{\left( t \right)} } \right|}$$

(14)

where $X^{\left( t \right)} \in {\mathbb{R}}^{N \times O}$ and $\hat{X}^{\left( t \right)} \in {\mathbb{R}}^{N \times O}$ represent the true values and predicted values of all nodes at time step t, respectively. $\Theta$ denotes all the learnable parameters in the model.

Experiment

Data description

Six publicly available traffic datasets were used in the experiments: METR-LA, PEMS-BAY, PEMS03, PEMS04, PEMS07, and PEMS08. These datasets were collected using loop detectors on highways to capture traffic data for the corresponding road segments. The METR-LA dataset contains traffic speed data from highways in Los Angeles, while PEMS-BAY records traffic speed data from the San Francisco Bay Area. PEMS03, PEMS04, PEMS07, and PEMS08 are real-world traffic datasets collected in real-time every 30 s by the California Department of Transportation’s Performance Measurement System (PeMS). These datasets include information such as detection locations, dates, and data types. The detailed information of the experimental datasets is shown in Table 1.

Table 1 Detailed information of the datasets.

In the experiments, missing values were filled using linear interpolation. Additionally, all data were normalized using z-score normalization to eliminate the influence of different scales, making the data comparable and transforming it into a standard normal distribution, thereby providing better feature representation. The normalization formula is as follows:

$$X_{i}^{norm} = \frac{{X_{i} - \mu }}{\vartheta }$$

(15)

where $X_{i}$ represents the $i$-th raw data point, $\mu$ is the mean, and $\vartheta$ is the standard deviation of the dataset.

Experimental settings

In the experiments, the datasets were split into training, validation, and test sets in chronological order. For METR-LA and PEMS-BAY, the ratio was 7:1:2, while for PEMS03, PEMS04, PEMS07, and PEMS08, the ratio was 6:2:2. We used one hour of historical data ($T = 12$) to predict the next hour of traffic data ($H = 12$). For hyperparameters, we set the default number of hidden units in the GRU cells to 64, the number of GRU layers to 2, and the number of GCN layers to 2. The number of input features was set to 2 (speed and timestamp) for METR-LA/PEMS-BAY and 1 (flow) for PEMS03/04/07/08. The number of output features for all datasets was 1. In Eq. (5), we used $\lambda_{1} = \lambda_{2} = \lambda_{3} = 1$, setting $\alpha = 0.01$ and $\beta = 1$ to balance the importance of sequence-level and graph-level adversarial training. The spatial and temporal embedding dimensions for the PEMS03, PEMS04, PEMS07, PEMS08, METR-LA, and PEMS-BAY datasets were set to 4, 6, 10, 4, 10, and 10, respectively. All experiments were conducted on a computer with an Intel Core i7-11700 CPU @ 3.6 GHz and a GeForce RTX 3080Ti GPU. The network was implemented using the Pytorch framework, and training was carried out with the Adam optimizer and a batch size of 64 for a maximum of 200 epochs. Model performance was evaluated using mean absolute error (MAE), root mean squared error (RMSE), and mean absolute percentage error (MAPE).

$${\text{MAE}} = \frac{1}{K}\sum\limits_{k = 1}^{K} {\left| {X_{true(k)} - X_{pred(k)} } \right|}$$

(16)

$${\text{MAPE = }}\frac{1}{K}\sum\limits_{k = 1}^{K} {\left| {\frac{{X_{true(k)} - X_{pred(k)} }}{{X_{true(k)} }}} \right|}$$

(17)

$${\text{RMSE}} = \sqrt {\frac{1}{K}\sum\limits_{k = 1}^{K} {\left( {X_{true(k)} - X_{pred(k)} } \right)}^{2} }$$

(18)

where $X_{true}$ represents the true values $X_{pred}$ represents the predicted values, and $K$ denotes the number of samples. The smaller the values of MAE, RMSE, and MAPE, the better the predictive performance of the model.

Baselines

We compared the proposed TRL-DAG with several traffic prediction methods, including VAR (Vector Autoregression)³⁶, SVR (support vector regression)¹⁸, ARIMA (autoregressive integrated moving average)³, LSTM (long short-term memory)³⁷, GCRN (graph convolutional recurrent network)³⁸, STGCN (spatio-temporal graph convolutional network)⁹, DCRNN (diffusion convolutional recurrent neural network)⁸, ASTGCN(r) (attention-based spatio-temporal graph convolutional network with recent component)³⁹, OGCRNN (optimized graph convolutional recurrent neural network)⁴⁰, STSGCN (spatio-temporal synchronous graph convolutional network)²⁴, Graph WaveNet (GWN)¹⁴, Z-GCNETs (time zigzags at graph convolutional networks)¹⁵, and AGCRN (adaptive graph convolutional recurrent network)⁴¹.

Experimental results

Performance comparisons

We evaluated the proposed TRL-DAG model on two different types of traffic datasets: traffic speed and traffic flow. For the METR-LA and PEMS-BAY datasets, we conducted traffic speed prediction experiments for 15-min, 30-min, and 60-min intervals. Meanwhile, for the PEMS03, PEMS04, PEMS07, and PEMS08 datasets, we performed average traffic flow predictions within a 1-h timeframe. Tables 2, 3 and 4 present the performance comparison of TRL-DAG with several baseline models on these datasets. The best results are highlighted in bold, and the second-best results are underlined.

Table 2 Traffic speed prediction results of different methods on METR-LA and PEMS-BAY.

Table 3 Traffic flow prediction results of different methods on PEMS03 and PEMS07.

Table 4 Traffic flow prediction results of different methods on PEMS04 and PEMS08.

Firstly, in the traffic speed prediction datasets METR-LA and PEMS-BAY, TRL-DAG significantly outperformed other baseline models, particularly in the 60-min long-term prediction task. Specifically, on the METR-LA dataset, the prediction results showed that TRL-DAG achieved an MAE of 3.55, RMSE of 7.37, and MAPE of 10.28%. Compared to baseline models such as DCRNN, the error was notably reduced. This demonstrates the effectiveness of TRL-DAG’s dynamic graph generation mechanism in handling dynamic correlations between nodes, significantly reducing errors caused by data sparsity and spatiotemporal variations. Moreover, the results on the PEMS-BAY dataset further validated the advantages of TRL-DAG in an environment with relatively complete data. This dataset has an extremely low missing rate (0.003%) and a stable traffic network, yet TRL-DAG, through its dynamic adversarial network and temporal representation learning modules, still captured subtle spatiotemporal features. In the 60-min prediction task, TRL-DAG achieved an MAE of 1.92 and RMSE of 4.50, both outperforming other baseline models, further validating its broad applicability across different datasets.

Secondly, TRL-DAG also demonstrates outstanding performance across multiple large-scale datasets. Notably, in complex and large-scale networks such as PeMS07, TRL-DAG achieves the best results in the 60-min prediction, with an MAE of 20.83, RMSE of 34.19, and MAPE of 8.65%. While other baseline models tend to exhibit a drop in performance when dealing with such complex spatiotemporal dependencies, TRL-DAG, through its dynamic graph generation mechanism, is able to establish dynamic correlations between large-scale nodes, maintaining both prediction accuracy and stability. For multidimensional datasets, such as PeMS04 and PeMS08, which include multiple data types like traffic flow, speed, and occupancy, some existing methods, like DCRNN and AGCRN, perform well on smaller datasets but experience significant performance degradation on large-scale datasets like PEMS07. This suggests that they struggle to handle complex dynamic spatiotemporal variations effectively. In contrast, TRL-DAG successfully addresses the spatiotemporal variations across different data types. For example, in the 60-min prediction on the PeMS08 dataset, TRL-DAG achieved the best results with an MAE of 19.05, RMSE of 31.29, and MAPE of 12.30%. Similarly, on the PeMS04 dataset, TRL-DAG maintained excellent performance, achieving the best results in the 60-min prediction with an MAE of 15.14, RMSE of 24.42, and MAPE of 9.63%. These results indicate that, regardless of the dataset size, TRL-DAG is capable of effectively capturing spatiotemporal dependencies through dynamic modeling, maintaining high prediction accuracy.

To further evaluate the effectiveness of our method, we visualized the prediction results of the TRL-DAG model, alongside the STSGCN and ASTGCN methods, over 12 time steps on the PEMS04 and PEMS08 datasets, as shown in Fig. 5. It is evident that the MAE, MAPE, and RMSE values of STSGCN and ASTGCN significantly increase as the prediction time step lengthens, particularly when the prediction reaches 12 steps, where the error shows a substantial rise. This phenomenon reflects the difficulty of most methods in capturing the complex long-term trends and periodic characteristics of traffic flow, leading to error accumulation and reduced prediction accuracy. In contrast, TRL-DAG demonstrates a remarkable improvement in MAE, MAPE, and RMSE metrics, maintaining a stable error growth rate as the time steps increase, highlighting its superior long-term prediction performance. This further validates the effectiveness of temporal representation learning, dynamic spatiotemporal modeling, and the adversarial training strategy in addressing the complexity and dynamic nature of traffic flow.

Fig. 5

Comparison of prediction results for different methods across various horizons.

Ablation experiments

To further investigate the impact of different modules in TRL-DAG on prediction performance, we designed five variants and compared the average MAE, RMSE, and MAPE values of these variants with TRL-DAG on the PeMS03, PeMS04, PeMS07, and PeMS08 datasets. The specific descriptions of these variants are as follows:

• w/o temporal representation learning: This variant directly removes the temporal representation learning module from our framework.

• w/o dynamic graph generation: This variant uses a single adaptive graph without the mechanism for evolving across time.

• w/o generating adversarial network: This variant removes the generating adversarial network from our framework.

• w/o adversarial training for graphs: This variant directly removes the adversarial training mechanism for graphs.

• w/o adversarial training for sequences: This variant directly removes the adversarial training mechanism for sequences.

As shown in Fig. 6 the complete TRL-DAG model demonstrates the best performance across all metrics, including MAE, RMSE, and MAPE. Notably, removing the temporal representation learning and dynamic graph generation modules significantly increased prediction errors, indicating that these two components are crucial for effective spatiotemporal modeling. Furthermore, the absence of the generative adversarial network also led to a decline in model performance. The introduction of adversarial graph training at both the sequence and graph levels provided significant improvements across all variants, with graph-level adversarial training outperforming sequence-level training. This suggests that the correlations among traffic sequences across all nodes may contain more valuable information about the traffic system, underscoring the importance of adversarial training in enhancing the model’s robustness and generalization capabilities. Therefore, the synergy of all components is critical to the overall performance of the TRL-DAG framework, with each module contributing significantly to improving the accuracy and stability of traffic flow prediction.

Fig. 6

Ablation study of key components in the TRL-DAG.

Visualization

To better understand the effectiveness of the TRL-DAG model, we visualized the true traffic flow values and the predicted values across different datasets. Figures 7 and 8 present a comparison between the true and predicted values at two prediction horizons (horizon 3 and horizon 12) for various datasets.

Fig. 7

Visualization of true and predicted values.

Fig. 8

Visualization of true and predicted values.

It is evident that the predictions generated by the TRL-DAG model closely align with the true values across different time spans. In particular, the predictions accurately capture peak periods and overall traffic patterns, showcasing the model’s understanding and adaptability to the dynamics of the traffic network. In the PeMS03, PeMS04, and PeMS07 datasets, TRL-DAG effectively models the sharp increases in traffic flow during morning and evening peak hours, which are often challenging to predict due to rapid fluctuations. For longer prediction horizons (horizon 12), although prediction errors slightly increase during periods of high fluctuation, the model maintains a high level of accuracy. This behavior is consistent across various datasets, such as METR-LA and PEMS-BAY, where the model successfully tracks long-term patterns but occasionally underestimates sudden spikes or dips in traffic flow. Notably, the dynamic adversarial training and temporal representation learning components of TRL-DAG help minimize trend discrepancies between predicted and true values over longer horizons, demonstrating the model’s excellent ability to capture both short-term variations and long-term dependencies. This is particularly evident in the predictions on the PeMS08 dataset, which strongly validate this conclusion. These visualization results confirm that TRL-DAG is not only effective at modeling periodic patterns but also performs exceptionally well in adapting to irregularities, ensuring accurate traffic flow predictions across a variety of scenarios.

Spatial complexity study

To explore the spatial efficiency of TRL-DAG, we compared it with several representative baseline models. Table 5 presents the total number of parameters for each model, while Fig. 9 shows the relationship between the number of model parameters and RMSE on the PEMS08 dataset. As shown, TRL-DAG has a total parameter size of 1,022,592 bytes, which is significantly lower than ASTGCN(r) and STGCN, and slightly lower than DCRNN. This reduced parameter count highlights the spatial efficiency advantage of TRL-DAG. Additionally, the point representing TRL-DAG in Fig. 9 is positioned towards the lower left, indicating that it achieves high prediction accuracy while maintaining a relatively small number of parameters. This further demonstrates the model’s advantage, showing that TRL-DAG can achieve excellent RMSE performance with a comparatively low parameter count.

Table 5 Comparison of total parameters.

Fig. 9

Comparison of total model parameters and RMSE.

Computational efficiency study

Table 6 presents a comparison of the training time (per epoch) and inference time for different models. Overall, TRL-DAG demonstrates a notable advantage in computational efficiency. For the METR-LA dataset, the training time of TRL-DAG is 210.25 s/epoch, showing a significant improvement compared to traditional models like DCRNN (650.64 s/epoch) and STGCN (251.35 s/epoch). Moreover, the inference time is only 10.81 s, far lower than DCRNN’s 110.52 s, and, while slightly higher than Graph WaveNet (6.27 s), TRL-DAG obtains better prediction performance. Similarly, in the PeMS04 dataset, TRL-DAG shows superior computational efficiency, with a training time of 158.98 s/epoch, significantly outperforming DCRNN (394.67 s/epoch) and STGCN (172.27 s/epoch). During inference, TRL-DAG’s time is 4.23 s, slightly higher than Graph WaveNet (3.45 s), but it still maintains a low inference cost compared to other models. Therefore, TRL-DAG achieves a balance between training and inference efficiency, with significantly lower computational time across multiple datasets, indicating its excellent predictive performance in various traffic forecasting tasks.

Table 6 Computation time compared with other modes.

Conclusion

This paper proposes an innovative traffic flow prediction model, the temporal representation learning enhanced dynamic adversarial graph convolutional network (TRL-DAG). By integrating temporal representation learning, adaptive dynamic graph generation, and adversarial graph convolutional networks, TRL-DAG effectively captures the complex dynamic spatiotemporal characteristics of traffic flow. First, the temporal representation learning module employs self-supervised pretraining through a masked reconstruction task to extract long-term trends and periodic features, enhancing the model’s generalization capability and robustness. The dynamic graph generation module adapts to the time-varying relationships between nodes in the traffic network by combining current and historical states, dynamically modeling spatiotemporal dependencies. Additionally, the adversarial graph convolutional network module optimizes model performance through adversarial training at both the sequence and graph levels, allowing TRL-DAG to not only capture complex traffic flow features but also reduce trend discrepancies between predicted and actual values. Experimental results on multiple real-world datasets demonstrate that TRL-DAG significantly outperforms existing state-of-the-art methods, showing exceptional performance on traffic networks of various scales, including smaller datasets like PEMS-BAY and larger networks like PEMS07. Notably, TRL-DAG maintains low error rates even in long-term prediction tasks.

Future research will focus on developing more complex dynamic graph generation networks and incorporating external factors (e.g., weather, traffic incidents, holidays) to further enhance prediction accuracy and applicability.