Introduction

The escalating global desertification and the rapid decline of arable land resources1, particularly in northwest China, have led to the emergence of continuous soil cropping obstacles that are a critical challenge hindering the efficient development of agriculture2. In response, facility agriculture in desert areas has been widely promoted as an innovative approach, especially in arid and semi-arid regions. This approach depends on modern facility technologies, including greenhouses, drip irrigation systems, and sand-based substrate cultivation3, optimizing the use of limited water resources and sunlight. By integrating efficient water and fertilizer management, as well as environmental control, facility agriculture has been shown to significantly enhance crop yield and quality. Greenhouse facilities, such as fully enclosed greenhouses and high tunnels, provide effective protection against extreme weather and a stable growing environment for crops, while the drip irrigation system ensures precise water distribution. In recent years, China has actively encouraged the adoption of facility agriculture in non-cultivated areas4, with particular emphasis on the comprehensive cultivation model based on sand substrates, using river sand as the primary substrate. Sand-based substrates are characterized by excellent air permeability, chemical stability, and drainage properties, which help reduce root diseases and soil-borne diseases, promote healthy plant growth, and maintain nutrient balance. The use of sand-based substrates effectively contributes to the promotion of green agriculture5,6. However, despite the widespread application of sand-based substrates, challenges remain in terms of water and fertilizer efficiency, as well as the compatibility of mechanized operations. These issues arise due to the unique physical properties and texture differences between sand substrates and traditional soils. Therefore, parameter calibration of river sand substrates is of crucial significance to optimizing equipment design and improving the application efficiency of the substrates in facility agriculture.

The particle microcharacteristics of river sand substrates, particularly contact parameters such as recovery coefficient, static friction coefficient, and rolling friction coefficient, are critical for both machinery operations and crop growth7. These parameters are difficult to measure directly due to the complexity of particle morphology and size. However, they are essential for modeling the interactions between the substrate, root systems, and machinery. While previous studies based on the discrete element method (DEM) have investigated the parameterization of various soil types, research focused on the calibration of river sand substrate parameters remains limited. Notably, the successful application of numerical simulation methods in hydraulic engineering provides valuable interdisciplinary insights for agricultural substrate research. For instance, Rahmani Firozjaei et al.8,9 utilized FLOW-3D software to optimize lateral water intake structures, demonstrating that a 45° intake angle and submerged deflection plates significantly improved water flow efficiency and reduced sediment accumulation. This approach, which focuses on fluid-particle interaction-based parameter optimization, offers valuable inspiration on substrate flow properties. Similarly, Aghazadeh et al.10,11,12 applied a multi-physics coupling model to analyze the effects of pipeline diameter and temperature gradients on steam transmission efficiency in desalination systems. Their sensitivity analysis methodology provides an important theoretical framework for calibrating contact parameters.

The calibration of discrete element parameters for soils and similar materials has been the subject of various studies. For example, Moriasi13 and Iwema14 demonstrated that the high fluidity, air permeability, and porosity of substrates increase the complexity of model simulations and parameter calibration. Salavat Mudarisov et al.15,16 calibrated soil parameters and optimized the Hertz-Mindlin contact model using DEM, revealing the influence of particle size on slope angles. Chinese scholars have also made significant progress in this field: Zeng et al.17 employed the area difference method to calibrate soil contact parameters, while Yan et al.18 integrated DEM with the EEPA model to improve the simulation accuracy of sandy loam. Furthermore, Zeng et al.19 developed a DEM simulation model for soil-tool-straw residue interactions, conducting soil bin tests with four different types of tools. The model’s accuracy was validated using various indicators such as soil cutting force, displacement of soil and straw residue, and residue coverage. The seed-soil interaction model developed by Lu et al.20 achieved a tractive resistance error of only 2.22%, and Dai et al.21 optimized membrane-covered soil DEM parameters through repose angle tests, providing a diverse experimental framework for river sand substrate parameter calibration. Additionally, Yu et al.22 developed a two-dimensional DEM analysis model for chip plows and seed-fertilizer openers interacting with soil particles, studying the working process and resistance of the openers, thus demonstrating the feasibility of using DEM to analyze opening resistance. Song et al.23 applied the Hertz-Mindlin no-slip contact model for soil contact and optimized parameters for soil particle interactions and soil-fertilizer equipment using stacking and slope methods, offering a reference for DEM simulation parameter settings in no-till cotton fields. These studies highlight the significant application potential of DEM in soil and agricultural machinery interaction research, providing essential support for soil parameter calibration and equipment optimization design.

Although existing research has predominantly focused on traditional soils or specific engineering materials, such as sediment in hydraulic structures or steam flow in desalination systems, the discrete element modeling of sand-based substrates in desert facility agriculture remains underexplored. Therefore, this study integrates the Hertz-Mindlin contact model with the Johnson-Kendall-Roberts (JKR) contact model and uses the river sand angle of repose as a response parameter. Contact parameters are calibrated utilizing sensitivity experiments and regression optimization methods, and an interaction model between river sand and the tillage equipment is developed to validate simulation accuracy. This research aims to establish a reliable, discrete element parameter system for the optimization design of sand-based substrates and agricultural equipment, thereby advancing the mechanization of facility agriculture.

Materials and methods

Source and collection of river sand matrix samples

River sand samples were collected on June 20, 2024, from the Aksu Naida Agricultural Technology Co., Ltd. in the Xinjiang Uygur Autonomous Region (40.97680°N, 80.12610°E, 1106 m altitude). The substrate exhibited a pH of 8.2. The facility employs a sand-based cultivation system, primarily for greenhouse tomatoes. Although the optimal pH range for tomato growth is between 6.0 and 6.8 (slightly acidic to neutral)24, the pH value in this system is maintained between 7.5 and 8.0 through the addition of sulfur and organic acids. To address deficiencies in essential elements such as iron and zinc, trace element fertilizers (e.g., EDTA-Fe) are applied under high pH conditions25. Additionally, the high aeration of the sand substrate, combined with irrigation-fertilization systems, optimizes the root zone environment, supporting healthy tomato growth and high yields.

Measurement of the physical and chemical properties of river sand matrix

Density determination method and experimental procedure

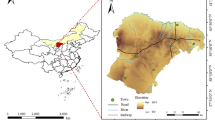
Density was determined according to GB/T 50123-1999 “Standard for Soil Testing Methods”26. A cutting ring with a capacity of 200 cm3 volume was used for sampling, with its mass measured as 165.5 g prior to the test. This study employed the five-point sampling method27, collecting samples from different locations within the greenhouse (including the center, sides, near irrigation equipment, and drainage outlets) and from different depths (0–10 cm, 10–20 cm, 20–30 cm) to ensure spatial and depth representativeness of the data. This approach allowed for a comprehensive assessment of the physical and chemical properties of the river sand substrate (see Fig. 1). After collection, the samples were sealed and labeled for subsequent analysis. The total mass of the cutting ring and soil sample was measured using an electronic balance. The test was repeated five times, and the average value was taken as the final result. The calculation formula for the river sand density (ρ) is:

$$\rho =\frac{{{m_1} - {m_0}}}{V}$$
(1)

Where m1 is the total mass of the ring knife and soil sample (kg), m0 represents the mass of the cutting ring (kg), and V denotes the volume of the cutting ring (cm3).

Fig. 1
figure 1

Schematic of five-point river sand sample collection.

Full size image

Measurement of moisture content and experimental method

The moisture content of the river sand was determined in accordance with the national environmental protection standard HJ613-2011, “Determination of Soil Dry Matter and Moisture by Gravimetric Method.” Initially, an aluminum box and lid were dried at (105 ± 5)°C for 1 h, then slightly cooled. The lid was replaced before the box was cooled in a desiccator for 45 min. The mass of the container with the lid (m2) was measured to an accuracy of 0.01 g. Subsequently, the sample was placed into the aluminum box, and the mass of the aluminum box containing the sample (m3) was accurately measured using an electronic balance. The aluminum box was placed in a forced air drying oven at 105 °C ± 2 °C for 8 h. After drying, the box was allowed to cool to room temperature and weighed again to determine the total mass (m4). The entire procedure was repeated five times, and the average moisture of each river sand sample was calculated. The moisture content (ω) was computed using the following formula:

$$\omega =\frac{{{m_3} - {m_4}}}{{{m_4} - {m_2}}} \times 100\%$$
(2)

Where m2 represents the weight of the aluminum box (kg), m3 denotes the total mass of the aluminum box and wet soil (kg), and m4 represents the total mass of the aluminum box and dry soil (kg).

Sieve analysis and method for particle size distribution

A 2 kg sample of dried river sand was obtained, from which a 1000 g sample was selected using the quartering method, which was accurate to 0.1 g. Standard test sieves with mesh sizes of 5, 2.5, 1, 0.6, and 0.25 mm were set to vibrate for 20 min (see Fig. 2g). After sieving, the river sand particles of different sizes on each sieve were weighed, with the experiment repeated three times, accurate to 0.1 g. The sieved river sand particles and experimental apparatus are shown in Fig. 2. The particle size distribution and mass fraction of the river sand are presented in Table 1.

Table 1 River sand particle size distribution and mass fraction.
Full size table
Fig. 2
figure 2

Different particle sizes of river sand after sieving (a) Particle size > 5 mm (b) Particle sizes between 2.5–5 mm (c) Particle sizes between 1–2.5 mm (d) Particle sizes between 0.6–1 mm (e) Particle sizes between 0.25–0.6 mm (f) Particle sizes between 0–0.25 mm (g) Vibrating screen.

Full size image
Fig. 3
figure 3

Mechanism of bulk angle measurement. (1) Funnel, (2) Funnel opening, (3) Accumulated material, (4) Bulk angle, (5) Base. (a) Side view of the concept for measuring the angle of repose. (b) Front view of the concept for measuring the angle of repose (2D plane diagram).

Full size image

Measurement and testing method of bulk angle

During machinery operations, the interaction between the ground-contact components and the river sand results in sand deformation. As a critical parameter reflecting the mechanical properties of river sand, the angle of repose significantly influences its strain behavior. Therefore, this factor was chosen as a key experimental parameter in this study28. The angle of repose was determined using the funnel method, as illustrated in Fig. 3, where θ represents the measured angle of repose. The experimental setup, shown in Fig. 4, consists of a triangular frame, funnel, retaining plate, and base. In the experiment, river sand was allowed to fall freely from the funnel onto a horizontal surface. Once the sand ceased to flow, the angle θ between the cone’s slope and the horizontal surface was measured, representing the angle of repose.

The funnel used in the experiment had a cone angle of 120°, and the diameter of the bottom hole was 10 mm. The vertical distance from the bottom hole to the horizontal surface of the testing platform was 80 mm, and the diameter of the receiving plate was 200 mm. In the experiment, the river sand sample was gradually poured into the funnel, and once the retaining plate was removed, the sand flowed out through the bottom hole. Once all the sand had fallen from the funnel, the funnel was removed. The angle between the cone’s slope and the horizontal surface was measured using a high-precision universal level. Each set of experiments was repeated five times, and the average value was used to determine the river sand’s angle of repose, with a measurement accuracy of 0.01°.

Fig. 4
figure 4

Test setup for stacking angle measurement.

Full size image

In addition to the traditional measurement method, image processing technology was employed to measure the angle of repose. Image processing involves the use of computers to analyze, manipulate, and process images to meet specific requirements. It is a form of signal processing applied to the image domain and is widely used in fields such as medical imaging, satellite remote sensing, and industrial inspection29,30. The image processing procedure, outlined in Fig. 5, includes image acquisition, grayscale processing, binarization processing, denoising, edge extraction, and linear fitting. After performing 10 angles of repose tests and averaging the results, the final measured angle of repose was 31.91°.

Fig. 5
figure 5

Accurate measurement of river sand matrix (a) Image acquisition (b) Binarization process (c) Image denoising (d) Edge extraction (e) Linear fitting.

Full size image

Measurement method for river sand matrix contact parameters

Collision coefficient of restitution measurement test and method

The collision coefficients of restitution for interactions between river sand or river sand and steel were measured through free-fall experiments31, which assess the ability of objects to recover their original shape after impact. The experimental setup and schematic diagram are shown in Fig. 6. Boards made of sand and steel plates were selected as collision plates, and pre-cut river sand blocks were freely dropped from a vertical height of 200 mm above the collision plate. Upon impact, the sand block followed a parabolic trajectory before eventually landing on the receiving plate. A high-speed camera recorded the rebound height of the sand block, with the camera activated prior to the fall and turned off after the block landed.

The FUJIFILM XT-4 high-speed camera, equipped with a 26-megapixel lens, was used for recording, with Camera Raw software for image processing. The experimental settings included a frame rate of 240 fps, a capture area of 1920 mm × 1080 mm, and a shutter speed of 1/2000 s.

Fig. 6
figure 6

Schematic diagram of collision recovery coefficient measurement. (1) Collision plate (2) River sand block (3) The collision point (4) Splice plate.

Full size image

The collision recovery factor is calculated using the following formulas:

$${C_r}=\frac{{{v_n}}}{{v_{n}^{\prime }}}$$
(3)
$${v_n}={v_1}cos\left( {\frac{\pi }{2} - {\theta _1}+arctan\frac{{{v_y}}}{{{v_x}}}} \right)$$
(4)
$$v_{n}^{\prime }={v_0}sin\left( {\frac{\pi }{2} - {\theta _1}} \right)$$
(5)
$${v_1}=\sqrt {v_{x}^{2}+v_{y}^{2}}$$
(6)
$$v_{0} = \sqrt {2gh_{1} }$$
(7)

When the block of river sand collides with the collision plate in an oblique projectile motion, it can be obtained:

$${H_1}={v_y}t+\frac{1}{2}g{t^2}$$
(8)
$${L_1}={v_x}t$$
(9)

Where Cr is the collision recovery coefficient, vn represents the normal velocity before the collision between the river sand block and the collision plate (m/s). \(v_{n} ^{\prime }\) denotes the normal velocity after the collision between the river sand block and the collision plate (m/s). v0 represents the velocity of the river sand block when it reaches the collision point (m/s). h1 is the vertical distance between the initial position of the river sand block and the collision plate (mm). H1 represents the vertical distance between the collision point of the river sand block and the receiving plate (mm). L1 is the horizontal distance between the collision point of the river sand block and the falling point of the receiving board (mm).

After multiple experiments and 10 repeated measurements, the collision coefficient of restitution between river sand ranged from 0.15 to 0.75, while the coefficient between river sand and steel ranged from 0.2 to 0.8. The final results are the average values of 10 experiments to ensure accuracy and reliability.

Static friction coefficient measurement test and method

The static friction coefficients between river sand and between river sand and steel were measured using the inclined plane method32. Multiple measurements were conducted to ensure the accuracy, reliability, and statistical representativeness of the data, with each measurement repeated 10 times. The working principle of this method is shown in Fig. 7, and the experimental setup is set up in Fig. 8.

Fig. 7
figure 7

Principle of static friction factor determination test (1) Test plate. (2) River sand block.

Full size image
Fig. 8
figure 8

(a) Calibration and initial setup of static friction angle measuring instruments. (b) Critical angle measurements of river sand sliding.

Full size image

In the test, river sand that had been thoroughly wetted, sieved, and evenly spread was applied to the test surface. The surface was then leveled, solidified, and dried for later use. A steel plate was affixed to another inclined surface for the experiment. During the test, the river sand board and the steel plate were placed horizontally, and a river sand block was positioned at one end of the contact surface. The plate was gradually raised until the material being tested began to slide along the inclined surface. The angle at which the sliding occurred was recorded33.

The static friction coefficient (µ1) is calculated as:

$${\mu _1}=\frac{{{f_1}}}{{{N_1}}}=\frac{{{G_1}sin{\theta _2}}}{{{G_1}cos{\theta _2}}}=tan{\theta _2}$$
(10)

Where f1 is the sliding friction force (N), N1 denotes the support force of the flat plate on the river sand block (N), G1 represents the gravity of the river sand block (N), µ1 is the static friction factor, and θ2 denotes the tilt angle of the flat plate at the moment when the sand block starts to move (°).

After multiple experiments with 10 repeated measurements, the static friction coefficient between river sand ranged from 0.2 to 1, and the static friction coefficient between river sand and steel ranged from 0.3 to 0.9, as calculated using Eq. (10). Each measurement result represents the average of 10 experiments to ensure accuracy and reliability.

Rolling friction coefficient measurement test and method

The rolling friction coefficients between river sand and between river sand and steel were measured using the setup shown in Fig. 9. A river sand ball was placed on the test plate, and the angle θ3 between the plate and the horizontal surface was adjusted until the ball rolled down from a certain height and came to rest on the horizontal surface. The test plate matched the surface material used in the static friction measurement, and the connection between the two plates was smoothed to minimize friction34. After the test, the rolling distance of the sand ball was measured. The experiment was repeated 10 times.

Fig. 9
figure 9

Test setup for determining rolling friction. (1) Coefficient test plate. (2) River sand ball. (3) Horizontal plate. (4) River sand ball stationary position.

Full size image

According to the law of conservation of energy, the rolling friction factor µ2 is calculated as:

$${G_2}{H_3}={\mu _2}{G_2}\left( {{G_2}cos{\theta _3}+{L_3}} \right)$$
(11)

Where G2 is the gravity of the river sand ball (N), H3 represents the vertical distance between the river sand ball and the horizontal plate (N), µ2 denotes the rolling friction factor, θ3 represents the angle between the test plate and the horizontal plate (°), and L3 denotes the rolling distance of the sand ball on the horizontal plate (mm).

After multiple experiments, with each test repeated 10 times, the rolling friction coefficient between river sand ranged from 0.1 to 0.4, while between river sand and 65Mn steel, it ranged from 0.1 to 0.5, as calculated using Eq. (11). Each result represents the average of multiple experiments to ensure accuracy and reliability.

Particle analysis and discrete element model construction of river sand matrix

Profile model acquisition

To investigate the shape of river sand particles and facilitate the establishment of their geometric model, the XS-2100 image acquisition system was employed to scan and analyze the river sand particles, as shown in Fig. 10.

Fig. 10
figure 10

Image analysis system.

Full size image

The test procedure involves placing river sand particles with sizes ranging from 0 to 0.25 mm on the slide of the image analysis system. Thirty river sand particle samples were selected, and the shape of each particle was observed on the computer after magnification. Using the same method, magnified images of river sand particles in the size ranges of 0.25–0.6 mm, 0.6–1 mm, 1–2.5 mm, and 2.5–5 mm were obtained. Figure 11a-f shows the 2D scanned images of representative river sand particles selected from different particle size ranges in this study. The river sand substrate primarily exhibited circular, sub-circular, elliptical, and partially angular shapes.

Fig. 11
figure 11

Enlarged view of river sand particles with different size ranges (a) 0–0.25 mm, (b) 0.25–0.6 mm, (c) 0.6–1 mm, (d) 1–2.5 mm, (e) 2.5–5 mm, (f) > 5 mm.

Full size image

Discrete element model construction

Creating an accurate particle model is the primary step in parameter calibration, as it directly influences the accuracy of discrete element simulations35. To closely match the characteristics of actual river sand particles, representative particle shapes (near-circular and elliptical) were selected for modeling based on particle size distribution. The 3D models were created using 3D modeling software before being imported into finite element software for mesh generation and coordinate extraction, ultimately resulting in simulation models for different particles in discrete element software.

As illustrated in Fig. 12, the particles were simulated by filling spheres of different radii. It is observed that as the radius of the filling spheres decreases, the number of spheres increases exponentially, leading to a better fit for the model. However, increasing the number of filling spheres significantly raises the simulation time36, which reduces efficiency. Therefore, it is essential to strike a balance between simulation accuracy and computational efficiency, optimizing the number of filling spheres to achieve the best performance.

Fig. 12
figure 12

Modeling of particle shapes with different particle sizes (a) 0–0.25 mm, (b) 0.25–0.6 mm, (c) 0.6–1 mm, (d) 1–2.5 mm, (e) 2.5–5 mm, (f) > 5 mm.

Full size image

Discrete element simulation testing and parameter calibration experimental design

Discrete element simulation testing

For the discrete element simulation study, the funnel was modeled in complete restoration using SolidWorks software to ensure that the geometric model precisely matched the structure of the experimental setup. The funnel model was then imported into EDEM software, where a virtual surface was created above the funnel as a particle generation source. Particles were generated based on the particle size distribution and mass fraction ratios outlined in section “Sieve analysis and method for particle size distribution”, allowing the simulated particles to closely replicate the actual conditions, thereby enhancing the accuracy of the model.

The Hertz-Mindlin and JKR combined contact model was used to simulate inter-particle interactions, which is particularly suitable for scenarios with significant adhesion effects37,38. Gravitational acceleration was set to -9.81 m/s², with all other parameters set to their default values in EDEM to optimize computational efficiency and model stability while ensuring reliable simulation results. Specific parameters are detailed in Table 2.

Table 2 Parameters required for discrete element simulation.
Full size table

The simulation tests began with meshing the particle flow in the funnel using the DEM (see Fig. 13a), which optimized computational efficiency and simulation accuracy. Subsequently, Fig. 13b demonstrates the flow and gradual accumulation of particles in the funnel, visualizing the settling and accumulation process under the influence of gravity. Figure 13c illustrates the simulation of velocity field changes during the particle flow process using EDEM software. Different colors indicate the distribution of particle velocity and its accumulation in the funnel, allowing for analysis of the velocity and direction of particles at various locations, thus facilitating the analysis of the particle flow characteristics.

Fig. 13
figure 13

(a) Discrete element simulation and meshing optimization of particle flow in the funnel. (b) Simulation and model demonstration of particle flow behavior. (c) Simulation study of particle velocity distribution and flow behavior.

Full size image

Parameter calibration experimental design and testing plan

Design of Experiments (DOE) is a statistical method used to systematically examine the effects of multiple factors on a response variable by appropriately planning experimental conditions to optimize process or product performance. In this study, we employed the Box-Behnken Design (BBD), a method commonly used in Response Surface Methodology (RSM). BBD conducts experiments on combinations of factor levels, effectively fitting quadratic models, evaluating factor interactions, and determining optimal conditions39. This research follows the methodologies suggested by El-Shobery, Klaraplu, Miller, and others40,41, utilizing a multi-stage experimental design process that includes Plackett-Burman experimental design, steepest ascent experiments, and Box-Behnken RSM. These three methods are applied for parameter screening, determining optimal intervals, and parameter optimization, respectively. The Plackett-Burman design was used for the initial screening of key parameters affecting the bulk angle, and statistical analysis was conducted to assess the importance of these parameters. The steepest ascent experiment was used to identify the optimal range for these key parameters, providing a foundation for subsequent optimization. Finally, the Box-Behnken RSM was applied for multi-factor optimization. These experimental approaches complement each other and progressively achieve the systematic calibration of the river sand matrix contact parameters.

Experimental parameter screening and preliminary design

A screening test design was performed using Minitab software, where the nine parameters to be calibrated were set to two levels, 1 and − 1, representing the high and low levels of each parameter. One center point was selected, totaling 25 trials. The experimental program and results are shown in Table 3.

Table 3 Screening test design and results.
Full size table
Steepest ascent experiment and optimization parameter determination

The hill-climbing test is capable of quickly identifying the region where the best response value is located with minimal trials. According to the screen test results (P-BD), only the significant parameters were selected, and their values were gradually increased according to the selected step size, with other parameters set to intermediate levels. The hill-climbing test was conducted afterward, and the relative error between the simulated stacking angle and the actual stacking angle was calculated. The test program and results are shown in Table 4, and the formula for the relative error (N, %) is shown in Eq. (12).

$$N=\frac{{\left| {\sigma - \left. \theta \right|} \right.}}{\theta } \times 100\%$$
(12)
Table 4 Significance analysis of experimental parameters for screening test design.
Full size table
RSM experimental design and parameter optimization

Based on the hill-climbing test results, a response surface experimental design (B-BD) was conducted, setting two levels for each of the three significant factors. Three center points were selected for error estimation, and a total of 15 trials were performed. The experimental program and results are shown in Table 5.

Table 5 Climbing test design and results.
Full size table

Field experiment and simulation test design

Field trenching experiment design and implementation

The field experiment was conducted strictly following the guidelines outlined in the “Field Trenching Machinery Work Quality” (NY/T 740–2003) standard42. The aim of the experiment was to investigate the response of the river sand substrate to trenching depth, trench width, and other parameters under different operation speeds. Key data collected included trench depth, trench shape, surface width, and bottom width, along with other critical parameters, as shown in Table 6. The experiment was conducted at the experimental area of Aksu Naida Agricultural Company for facility agriculture (Fig. 14) to verify the accuracy of the river sand substrate parameter calibration. The company’s self-developed trenching and mulching integrated machine was used for trenching operations at speeds of 0.4 m/s, 0.5 m/s, and 0.6 m/s over a distance of 50 m. These speeds were selected to represent the typical operational range encountered in actual agricultural work, as well as to analyze the effect of different speeds on soil and equipment interaction. Each test at each speed was repeated five times to ensure the reliability and accuracy of the data.

Table 6 Response surface experimental design optimization model ANOVA.
Full size table

The measurement method for trench depth was as follows: Prior to measurement, the river sand at the trench bottom and its surroundings were cleared to ensure accuracy. Subsequently, five equidistant measurement points were selected along two work paths (each at least 50 m in length), totaling ten measurement points. At each measurement point, a ruler was placed at the intersection of the original surface and the trench walls, with the trench depth defined as the vertical distance from the center of the trench bottom to the ruler.

Fig. 14
figure 14

Trenching test conducted under river sand substrate.

Full size image

DEM-based simulation trenching experiment

Using EDEM software, DEM simulations were conducted for trenching experiments. As illustrated in Fig. 15, a simulated soil bin with dimensions of 6 m × 2.5 m × 1 m (length × width × height) was created in EDEM software. During the simulation, the parameters of the river sand within the soil bin were based on the optimal combination of parameters obtained from the previous procedures.

Fig. 15
figure 15

Simulation of trenching test 3D modeling (a) 3D discrete element simulation of river sand matrix particles. (b) Simulation of trenching device in granular bed operation.

Full size image

Results and discussion

Analysis and evaluation of Plackett-Burman experiment simulation results

The results from the Plackett-Burman experiment (Table 3) and the ranking of the significant factors influencing the bulk angle (Table 4) indicate that the static friction coefficient between river sand, the rolling friction coefficient between river sand and steel, and the restitution coefficient between river sand are the key parameters affecting the bulk angle. Particularly, these three parameters significantly impacted the bulk angle (P < 0.05) and are positively correlated with it, suggesting that an increase in these parameters leads to a higher bulk angle.

Further analysis reveals that an increase in the river sand static friction coefficient significantly enhances the sliding resistance between particles, promoting interlocking effects and improving the inherent stability of the pile. This finding aligns with Zhu et al.43, who observed similar effects in their three-dimensional root-soil contact model, where increased contact at the root-soil interface enhances overturning resistance. Similarly, an increase in the rolling friction coefficient between river sand and steel results in higher rolling resistance of particles on the steel surface, reducing particle mobility and further raising the bulk angle. This aligns with the findings of Yim et al.44 regarding the rolling behavior of particles on different contact surfaces.

The river sand coefficient of restitution reflects the retention of kinetic energy during collisions. A higher coefficient of restitution facilitates energy transfer, strengthens the pile’s internal structure, reduces particle sliding, and prevents local collapse. This is closely related to the role of the coefficient of restitution in particle collisions, as discussed by Zou et al.45, suggesting that the coefficient’s influence on the bulk angle is closely linked to particle morphology and interactions.

In summary, increases in both the static friction coefficient and the coefficient of restitution between river sand lead to an increase in the bulk angle. This observation is consistent with the findings of Yan et al.18 and Liu et al.46. However, the optimal coefficient of restitution found in this study is significantly lower than those reported in the other literature, likely due to the angular morphology of river sand particles, which causes higher collision energy dissipation. This further highlights the key impact of particle morphology on the calibration of discrete element parameters. By enhancing interlocking effects between particles, reducing particle mobility, and increasing the retention of energy during collisions, these parameters collectively contribute to the stability of the pile, resulting in an increased bulk angle.

Analysis and optimization of steepest ascent experiment results

The results from the steepest ascent experiment (Table 5) demonstrated that as the static friction coefficient between river sand, rolling friction coefficient between river sand and still, and coefficient of restitution between river sand increase, the simulated bulk angle gradually rises from 21.89° to 53.78°. This clear trend emphasizes the significant impact of these parameters on the bulk angle. Zhou et al.47 similarly observed that the friction and coefficients of restitution influenced the bulk angle of soil in a comparable manner, reinforcing the importance of these parameters in particle packing behavior. However, when examining relative error trends, a distinct pattern emerges. In Experiment 2, the simulated bulk angle of 32.44° had a relative error of just 1.65%, the closest match to the actual value. This result suggests that this parameter combination accurately replicates the actual packing behavior. Yan et al.18 also found that optimized parameter combinations produced good alignment between the simulated and actual packing behaviors in DEM, ensuring the simulation’s reliability. However, when parameters were further increased, the simulated bulk angle in Experiments 4 and 5 rose to 38.94° and 53.78°, respectively, but the relative errors grew significantly to 22.02% and 68.53%, deviating from actual results. This phenomenon aligns with the findings of Li et al.48, who noted that excessively high friction and coefficients of restriction in DEM models may result in increasing error, leading to nonlinear errors.

Comprehensive analysis reveals that the optimal parameter combination lies near Experiment 2, where the simulation model most accurately represents the actual behavior. The values from Experiment 2 were selected as the center point, with those from Experiments 1 and 3 serving as the low and high levels for the subsequent response surface design.

Analysis of response surface experiment results and multi-factor optimization

The response surface test design and its results are shown in Table 7. A second-order regression model of the river sand matrix accumulation angle, based on three significant parameters, was developed using Design Expert 10 as shown in Eq. (13).

$$\begin{aligned} \theta & = 32.15 + 1.34A + 0.9737B + 2.37C - 0.555AB \\ & \;\;\; - 0.0975AC + 0.2575BC + 0.2967A^{2} \\ & \;\;\; + 0.5317B^{2} + 0.2342C^{2} \\ \end{aligned}$$
(13)
Table 7 Results of response surface experimental design.
Full size table

Where A is the river sand-river sand static friction coefficient, B represents the river sand-steel rolling friction coefficient, and C denotes the river sand-river sand recovery coefficient. The ANOVA results for this regression model are presented in Table 8, showing that all three factors, the static friction coefficient between river sand, the rolling friction coefficient between river sand and steel, and the recovery coefficient between river sand, have significant effects on the stacking angle of the river sand substrate. With a p-value of the model of P < 0.0001 and the lack-of-fit term (P = 0.2012), the model’s fit is robust. The coefficient of determination (R² = 0.9947) and the adjusted R² (R²adj = 0.9852) both confirmed the excellent reliability of the regression equation. The model’s precision of 32.71 further indicates its accuracy. After confirming the model’s significance and eliminating non-significant terms, the revised regression equation was shown as Eq. (14).

$$\begin{aligned} \theta & = 32.15 + 1.34A + 0.9737B + 2.37C \\ & \;\;\; - 0.555AB + 0.2575BC + 0.2967A^{2} \\ & \;\;\; + 0.5317B^{2} + 0.2342C^{2} \\ \end{aligned}$$
(14)
Table 8 Response surface experimental design quadratic regression model ANOVA.
Full size table

The ANOVA results for the optimized regression model are shown in Table 6. The coefficient of variation for the optimized model decreased to 0.79%, further enhancing its reliability; the coefficient of determination R² is 0.9942, and the adjusted coefficient of determination R²adj is 0.9864, both approaching 1, indicating an excellent model fit. Additionally, the precision was improved to 32.71, surpassing the performance of the pre-optimization model. This demonstrated that the optimized model is well-suited for accurately predicting the particle accumulation angle.

Determination of optimal parameter combination and application of regression model

The quadratic multiple regression was fitted to the model data using Design-Expert software, and the obtained response surface plots and contour distributions illustrating the interactions between the parameters affecting the stacking angle of the objective function are shown in Fig. 16.

Fig. 16
figure 16

Three-dimensional interaction analysis of the effect of river sand friction and coefficient of restitution parameters on the angle of accretion. (a) A and B interactions. (b) A and C interactions. (c) B and C interactions.

Full size image

The regression equation was solved and optimized with the actual stacking angle of the river sand matrix as the objective. This process obtained the optimal combinations for three significant parameters: the static friction coefficient between river sand (0.533), the rolling friction coefficient between river sand and steel (0.209), and the recovery coefficient between river sand (0.213). The remaining non-significant parameters were set to their intermediate values: river sand Poisson’s ratio (0.3), river sand shear modulus (10.5 MPa), river sand density (1300 kg/m³), rolling friction coefficient between river sand (0.25), collision recovery coefficient between river sand (0.5), and static friction coefficient between river sand (0.6).

Comparison and analysis of field experiment and simulation validation results

The comparison between the field and simulation experiments (Figs. 17 and 18) is summarized in Table 9. The analysis shows that at different operational speeds, the errors in trench depth, surface width, and bottom width for the river sand matrix were 8.8%, 4.8%, 7.9%, and 1.7%, respectively, all within an acceptable range. These results are consistent with the validation errors (approximately 10%) reported by Yan et al.18 for the sandy loam trenching model, further validating the reliability of the calibrated parameters in this study and demonstrating their alignment with industry standards. Further analysis reveals that the errors between the field and simulation tests (all under 9%) indicate a high degree of consistency between the simulation parameters and the field test data, validating the accuracy and reliability of the discrete element simulation parameter calibration method for the river sand matrix employed in this study.

Table 9 Measurement indexes of river sand substrate field and simulation tests at different operating speeds.
Full size table
Fig. 17
figure 17

Simulation operation process under different working conditions (a), (b) and (c) represent the furrow patterns at 0.4 m/s when the furrow cutter just entered the river sand substrate, reached the intermediate position, and fully opened, respectively; (d), (e), and (f) represent the same process at 0.5 m/s; and (g), (h), and (i) represent the same process at 0.6 m/s.

Full size image
Fig. 18
figure 18

Effect of the open furrow in river sand substrate. (a) Side throwing effect. (b) Floating soil at the bottom of the ditch, ditch type.

Full size image

Conclusion

This study presents a novel discrete element model for the river sand substrate used in facility agriculture in the Gobi desert, integrating the Hertz-Mindlin with the JKR contact model utilizing EDEM software. The study focuses on calibrating simulation parameters for the river sand matrix and its interaction with trenching devices. A combined approach using Plackett-Burman and BBD was employed to identify key contact parameters affecting the bulk angle and to optimize the model parameters. This innovative approach not only provides theoretical support for discrete element modeling of river sand matrices in Gobi desert agriculture but also offers scientific evidence for optimizing trenching device design.

The study results show that the optimal parameters combination derived from the regression model are the static friction coefficient between river sand (0.533), the rolling friction coefficient between river sand and steel (0.209), and the restitution coefficient between river sand (0.213). The remaining non-significant parameters were set to their intermediate values, including the Poisson’s ratio of river sand (0.3), shear modulus (10.5 MPa), density (1300 kg/m³), rolling friction coefficient between river sand (0.25), restitution coefficient (0.5), and static friction coefficient (0.6). Additionally, the BBD experiments revealed that the quadratic terms of these have a notable impact on the bulk angle, with considerable interactions between parameters. Optimization through steepest ascent experiments and regression models provided the fittest parameter combination, establishing clear parameter ranges for engineering applications in the Gobi region. Compared to other studies, this study stands out by integrating practical working conditions and using discrete element modeling to simulate interactions between river sand matrices and trenching devices. The model was further validated through field trials. The results show minimal error between the simulation and field tests (with errors in trench depth, surface width, and bottom width of 8.8%, 4.8%, and 7.9%, respectively), thus confirming the model’s accuracy and applicability. Unlike traditional methods, this study offers a more accurate representation of the river sand matrix’s behavior in facility agriculture and provides more reliable technical parameters for optimizing mechanized equipment.

Despite the successful outcomes, some limitations in this study should be emphasized. First, the model is based on a homogeneous river sand substrate, whereas the actual Gobi matrix often contains mineral heterogeneities, which could impact interface dynamics. Second, the study does not address changes in the matrix over long-term use or its dynamic interactions with mechanical equipment. Future research should focus on enhancing the compatibility of sand-based substrates with mechanical equipment, particularly in optimizing performance across varying operational environments and conditions. Furthermore, the development of a multiphase DEM model incorporating organic additives to reflect the complex composition of actual sand-based systems, coupled with a parameter adaptation algorithm that accounts for real-time changes in tool wear and surface roughness, would provide stronger technical support for the sustainable development of non-cultivated agricultural systems.