Introduction

The ongoing COVID-19 pandemic has demonstrated a swift global spread, posing a serious threat to human health and life1,2,3. The exponential proliferation of COVID-19 has exerted significant strain on the healthcare infrastructure, underscoring the critical importance of prompt diagnosis for effective treatment and containment4. It is imperative to develop efficacious diagnostic modalities for COVID-19 to enable clinicians to swiftly and accurately identify affected patients, thereby facilitating the implementation of necessary isolation and therapeutic interventions. Despite being deemed the “gold standard” for diagnosing COVID-19, the reverse transcription-polymerase chain reaction (RT-PCR) method of nucleic acid detection yields occasional false negatives, and its sensitivity remains limited5,6,7. In real-world scenarios, it is common to miss COVID-19 patients, thus RT-PCR fails to fully satisfy the diagnostic requirements for the disease. A range of medical imaging techniques can serve as alternative methods to RT-PCR for COVID-19 detection, such as computed tomography (CT), chest X-ray (CXR)8 and magnetic resonance imaging (MRI)9. Researchers have found that chest CT scans can non-invasively provide comprehensive information on the lung structure of patients, offering high accuracy in the early diagnosis of COVID-1910,11. In addition, the convenience of CT imaging enables real-time monitoring of the patient’s condition, providing strong support for timely treatment and effective disease control. As a result, computed tomography (CT) imaging and RT-PCR have been adopted as an ancillary diagnostic tool and have proven its utility and efficacy12,13. While CT exhibits superior sensitivity, its operational efficiency remains suboptimal. The evaluation of each case takes a long time, even for experienced radiologists14. Consequently, the development and enhancement of computer-aided diagnosis (CAD) systems is crucial15,16. This progression will facilitate faster and more efficient COVID-19 diagnosis, thereby alleviating the burden on healthcare systems.

Amidst the swift advancements in artificial intelligence (AI) technology, deep learning methodologies have demonstrated significant potential in the evolution of computer-aided diagnosis (CAD) systems17,18. Deep learning methodologies are capable of comprehensively and automatically extracting feature information from data, efficiently processing and analyzing large-scale datasets, significantly reducing human errors. Through continuous self-optimization, deep learning improves prediction and analytics accuracy19. In the field of medical imaging, deep learning excels in image classification and segmentation, automatically identifying different types of lesions, which enhances treatment effectiveness and precision20. Among deep learning methods, deep bidirectional long short-term memory (BiLSTM) is widely applied in the classification and diagnosis of medical images21. The BiLSTM architecture, comprising numerous forward and backward LSTM layers, mitigates the limitations inherent in the individual LSTM units22, its two-way learning mechanism enables it to efficiently capture both forward and backward information in sequence data, thereby comprehensively understanding the relationships between image features. BiLSTM not only reduces network variance but also accelerates the computation of network weights and biases, thus enhancing the model stability. In addition, the BiLSTM network has better classification and generalization performance. Currently, BiLSTM have been extensively applied in the field of medical imaging diagnosis, thereby providing robust support for the advancement of personalized medicine. Yang et al.23 established a whale optimization algorithm-bidirectional long short-term memory model, which demonstrates high accuracy in predicting the number of COVID-19 infections. This model is beneficial in helping epidemic control authorities in formulating effective containment measures. Alkhodari et al.24 appiled a deep learning model based on smartphone breathing sounds to differentiate between COVID-19 infected individuals (including asymptomatic cases) and healthy individuals, which was experimentally demonstrated to have high accuracy. Aslan et al.25 proposed two deep learning models for the automatic detection of COVID-19 positive cases using chest CT X-ray images, the experiments demonstrated that both models achieved satisfactory results. Although the BiLSTM network model has many advantages, it contains a large number of hyperparameters26. These parameters have an important impact on the efficiency of the BiLSTM architecture. Manually adjusting these parameters is cumbersome and time-consuming, In order to solve the above problems, we integrated an optimization algorithm into the construction of the BiLSTM model to perform multi-objective optimization of its hyperparameters in this paper, thereby reducing errors associated with suboptimal hyperparameter settings.

The Arithmetic Optimization Algorithm (AOA) proposed by Abdullah et al.27 in 2021, is a novel optimization algorithm inspired by basic arithmetic operations. By simulating the characteristics of these operations, AOA performs the search process and optimizes complex problems.Compared with other methods, the AOA has the advantages of high computational efficiency, low resource consumption, strong global search capability and dynamic adjustment. Currently, AOA has been widely applied in fields such as machine learning, image processing, engineering optimization, medical diagnosis, and financial analysis28,29,30,31. Additionally, AOA can be combined with existing methods to address various complex problems, such as hybrid AOA, adaptive AOA, and multi-objective AOA. A novel multi-objective arithmetic optimization algorithm (MOAOA) is initially proposed, and a sophisticated deep BiLSTM model is developed to facilitate the automatic recognition of COVID-19 from CT images in this paper. The MOAOA is employed to optimize the hyperparameters of the deep BiLSTM network. This approach autonomously extracts salient features from patient lung CT images and conducts classification diagnosis. The core innovation of this study is the introduction of the MOAOA algorithm to tune the hyperparameters of the deep Bi-LSTM model. This initiative effectively avoids the problem of misdiagnosis caused by improper parameter settings. The dynamic tuning mechanism of MOAOA algorithm can effectively prevent the model from falling into local optimal solutions. It occupies low medical resources while meeting the high accuracy requirements of COVID-19 for CT image diagnosis. The MOAOA optimization technique meticulously adjusts the network’s hyperparameters and optimizes diagnostic metrics to achieve optimal accuracy, sensitivity, specificity, and F1 score.

The main contributions of this work are summarized as follows.

  • We propose a improved multi-objective arithmetic optimization method and verify its optimization performance by four benchmark functions.

  • An effective MOAOA-BiLSTM model for autonomous diagnosis of COVID-19 CT images is proposed.

  • The performance of BiLSTM networks largely depends on the selection of hyperparameters. Improper selection of hyperparameters in BiLSTM networks may lead to more false negatives. Effectively utilize MOAOA to optimize the BiLSTM network with hyperparameters.

  • We conduct a number of experiments using a COVID-19 dataset of chest CT images to compare the performance of our proposed model with existing methods for classifying COVID-19 patients. Our study provides a viable solution for early diagnosis and surveillance of COVID-19 and has potential clinical applications.

This study primarily concentrates on the development and testing of the proposed MOAOA-BiLSTM for automatic diagnostics. The paper is structured as follows. Section “Related work” provides an overview of the existing research. Section “Methodology” introduces the COVID-19 automatic diagnosis model and its calculation process based on the MOAOA algorithm optimized BiLSTM. Section “Multi-objective arithmetic optimization algorithm” evaluates and analyzes the performance of multi-objective algorithm optimization algorithm. Section “Experimental examples of COVID-19 CT classification” presents a comprehensive comparison between the proposed method and existing approaches, followed by a detailed discussion of the experimental results. Finally, Section “Conclusion” describes the key conclusions and prospects.

Related work

The integration of deep learning methodologies in detecting and identifying COVID-19 has exhibited exceptional efficiency and resilience32. This section comprehensively reviews current deep learning-based methodologies employed in the classification and diagnosis of pulmonary diseases using CXR (chest X-ray) and CT imaging modalities.

Zhao et al.33 established a publicly available COVID-CT dataset, which includes 275 confirmed positive CT scan samples for COVID-19, with the intent of advancing research and development in deep learning methodologies. Kaur extit et al.34 proposed a COVID-19 diagnosis methodology predicated on transfer learning techniques, utilizing architectures such as ResNet50 and MobileNetv2. Loey et al.35 utilized a conditional generative adversarial network built upon a deep transfer learning model to enhance the precision of COVID-19 classification. Soares et al.36 established a publicly available CT scan data set for the type 2 SARS coronavirus and achieved good results using deep learning methods to analyze whether a person was infected with SARS-CoV-2. Abbas et al.37. utilized a deep Cellular Neural Network (CNN), built on the principles of decomposition, transmission, and synthesis, to categorize COVID-19 chest radiographs. Lins et al.38 presented a deep learning-based approach to assess the presence of COVID-19-related findings on CT images, as a supportive diagnostic mechanism.

Conventional deep learning techniques, when applied to chest CT scan analysis, exhibit overfitting due to the use of an extensive array of features for categorization39. Consequently, the scalability of these approaches to larger datasets remains questionable40. Another problem with traditional deep learning solutions is that when considering supervised learning and using backpropagation to update the connection weights of neural networks, gradient disappearance and explosions are serious obstacles to successfully training recurrent neural networks41. The popular LSTM provides forgetting gates and memory gates to prevent or reduce gradient disappearance or explosion, effectively overcoming gradient vanishing problems in long-term sequences of recurrent neural networks in traditional deep learning.

Hochreiter et al.42 used the recurrent neural networks (RNNs) of LSTM memory units to solve the problem that backpropagation learning takes a long time to store information at long intervals. Persio et al. emphasized the significance of carefully selecting and preprocessing input features for learning algorithms in their proposal of a method to predict stock market indices using Artificial Neural Networks43. Felder et al.44 appiled LSTM to predict the time probability distribution of the power output, successfully performed a 48-hour power forecast using historical data from wind farms and compared it with multi-layer perceptrons and baseline predictors. Edward et al.45 developed an artificial intelligence doctor called “Doctor AI”, which used LSTM time models to cover observed medical conditions and drug use. Maknickienė et al.46 demonstrated through statistical analysis that the improved algorithm significantly improves the reliability of prediction results based on evolutionary recurrent neural networks for LSTM. LSTM is a one-way recurrent network that only uses the content in the previous text and cannot consider the information of the “following text”47. It has disadvantages in parallel processing, long running time, and low efficiency48.

In response to the above issues and the long-term co-existence and continuous mutation of the COVID-19 virus with humans, we choose BiLSTM as the autonomous diagnostic model for COVID-19 CT images. BiLSTM is a bidirectional LSTM that combines information from input sequences in both forward and backward directions, effectively utilizing hardware resources and improving work efficiency49,50. The BiLSTM network model encompasses an extensive array of hyperparameters, the selection of which significantly impacts the accuracy and efficiency of COVID-19 CT image autonomous diagnosis. The examination of relevant literatures reveals the development of numerous strategies and techniques dedicated to the automatic generation of neural network structures. The use of optimization and evolution techniques to optimize connections and topology has been proven to have significant advantages51,52,53, among which the most commonly used is based on optimization algorithms54. Some famous algorithms include Particle Swarm Optimizer (PSO)55, Genetic Algorithm (GA)56, Artificial Be Colony Algorithm (ABC)57, Cultural Algorithm (CA)58, Fire Algorithm (FA)59, etc., which have been successfully applied to COVID-19 CT image classification and diagnosis. In order to improve the accuracy and computational efficiency, several improved optimization algorithms and hybrid optimization algorithms have also proved the progressiveness of this field. For example, Accelerated Gravitational Search (AGS)60, Improved Grey Wolf Optimizer (IGWO)61, Particle Swarm Optimization and Cultural Hybrid Algorithm (CA-PSO)62 Electromagnetic Firefly Algorithm (EFA)63, and so on. Although the improved optimization algorithm mentioned above can effectively improve the accuracy of classical algorithms, its accuracy and effectiveness are still relatively low, and the complexity of the algorithm also increases accordingly.

A recently developed metaheuristic algorithm, known as the arithmetic optimization algorithm (AOA), leverages the distribution characteristics of principal arithmetic operators in mathematics. It displays commendable performance in solving optimization issues, a claim proven in diverse fields such as mathematics, physics, and medicine as cited in references64,65,66,67. Due to the simple structure and high optimization efficiency of AOA, various modified AOA have been developed68. Dieu et al.66, integrate Differential Evolution (DE) with AOA to enhance the precision of the truss optimization design. Stankovic et al.69 demonstrated that the proposed hybrid algorithm optimization algorithm had superior performance compared to standard AOA, and the optimized structure could assist medical personnel in early diagnosis. In addition, Ewees et al.70 combined genetic algorithm (GA) operators with traditional AOA and proposed an improved AOA optimization method called AOAGA feature selection method. The findings suggest that this approach has identified novel optimal solutions for numerous test cases, yielding results that are superior to those of alternative methods. The above work shows that AOA and improved AOA optimization algorithms have been applied in various fields and achieved outstanding results. However, it is worth noting that research on multi-objective arithmetic optimization methods in automatic disease diagnosis has not yet been involved. This paper presents a Multi-Objective Arithmetic Optimization Algorithm (MOAOA) to optimize the BiLSTM architecture with the goal of boosting computational efficiency, improving accuracy, and enhancing generalization capabilities.

Methodology

LSTM principle

The Long Short-Term Memory (LSTM) network42, a highly sophisticated development beyond traditional Recurrent Neural Networks (RNNs), integrates an internal cell state mechanism within its structure to control the circulation of extensive information. And it greatly alleviates the long-term dependency problem of traditional RNN models, reduces the loss of long-distance historical information, and produces more accurate prediction results. Figure 1 illustrates the structure of the LSTM network.

Fig. 1
figure 1

LSTM network cell structure..

Full size image

Formally, the operations executed inside an LSTM cell can be depicted by the subsequent mathematical formulas71.

$$\begin{aligned}&{f_t} = \sigma ({w_f}[{h_{(t - 1)}},{x_t}] + {b_f}) \end{aligned}$$
(1a)
$$\begin{aligned}&{I_t} = \sigma ({w_i}[{h_{(t - 1)}},{x_t}] + {b_i})\end{aligned}$$
(1b)
$$\begin{aligned}&\widetilde{{C_t}} = \textrm{tanh}({w_c} * [{h_{(t - 1)}},{x_t}] + {b_c})\end{aligned}$$
(1c)
$$\begin{aligned}&{C_t} = {f_t}{C_{(t - 1)}} + {I_t} * \widetilde{{C_t}}\end{aligned}$$
(1d)
$$\begin{aligned}&{O_t} = \sigma ({w_o} * [{h_{(t - 1)}},{x_t}] + {b_o})\end{aligned}$$
(1e)
$$\begin{aligned}&{h_t} = {O_t} * {\textrm{tanh}}({C_t}) \end{aligned}$$
(1f)

where w and b are the matrices for weight coefficients and biases respectively. The sigmoid activation function is denoted as \(\sigma\)72. Additionally, \(\textrm{tanh}\) represents the hyperbolic tangent activation function. \({C_t}\) is the current state value of the unit, whereas \({h_t}\) is its output value. Furthermore, \({i_t}\), \({O_t}\), and \({f_t}\) signify the activation functions for the input gate, the output gate, and the forget gate, respectively.

BiLSTM principle

To address the limitation that LSTM units can process previous content but cannot use future content, BiLSTM incorporates a combined feature extraction method using forward and reverse sequences73. The two LSTM networks–one operating in the forward direction, the other in reverse–process the input sequence to distill features. The output vectors (i.e., extracted feature vectors) produced by the two LSTM networks are conflated into a single word vector, which stands as the ultimate representation of the word’s distinct features. Compared to a single LSTM structure, the BiLSTM demonstrates higher efficiency and performance in extracting local features, as shown in Fig. 2.

Fig. 2
figure 2

BiLSTM structure diagram.

Full size image

The calculation method of the reverse layer LSTM is similar to that of the forward layer LSTM, where the direction is reversed to obtain subsequent information, i.e.,

$$\begin{aligned} {h_f}= & f({w_{f1}}{x_t} + {w_{f2}}{h_{t - 1}}) \end{aligned}$$
(2)
$$\begin{aligned} {h_b}= & f({w_{b1}}{x_t} + {w_{b2}}{h_{t + 1}}) \end{aligned}$$
(3)

where \({h_f}\) denotes the output value of the forward LSTM network, \({h_b}\) symbolizes the output value from the backward LSTM network. The final output result of the hidden layer is calculated by

$$\begin{aligned} {y_i} = g({w_{o1}}{h_f} + {w_{o2}}{h_b}) \end{aligned}$$
(4)

BiLSTM is employed to deal with the problem of high variance in deep neural network training in this paper. The parallel training of numerous neural networks for classification or diagnostic functions not only decreases network variance but also bolsters the generalization competence of the neural network. The implementation of BiLSTM necessitates the calibration of the network’s weights and biases. Critical hyperparameters, including batch size, learning rate, momentum, number of epochs, and regularization coefficients, exert a significant influence on the efficacy of gradient descent optimization. Therefore, the fine-tuning of these hyperparameters is imperative to enhance the performance of BiLSTM neural networks.

Multi-objective arithmetic optimization algorithm

Multi-objective optimization problems

Multi-objective optimization (MOP) refers to an optimization challenge where multiple objective functions are evaluated concurrently in the decision-making process. The general formulation of MOP is expressed as

$$\begin{aligned} \text {Minimize/Maximize} \quad&\textbf{F}(\textbf{x}) = (f_1(\textbf{x}), f_2(\textbf{x}), \ldots , f_k(\textbf{x})) \end{aligned}$$
(5)
$$\begin{aligned} \text {Subject to} \quad&g_i(\textbf{x}) \le 0, \quad i = 1, 2, \ldots , m \end{aligned}$$
(6)
$$\begin{aligned}&h_j(\textbf{x}) = 0, \quad j = 1, 2, \ldots , p \end{aligned}$$
(7)

where \(\textbf{x}\) stands for the vector of decision variables, \(g_i(\textbf{x})\) and \(h_j(\textbf{x})\) represent the inequality and equality constraints respectively. In contrast to single-objective optimization issues, multi-objective problems yield a series of outcomes. These are known as Pareto optimal solutions, and the compendium of all objective space vectors corresponding to this set is labeled as the Pareto front74.

To rigorously assess the efficacy of optimization algorithms within the context of multi-objective optimization problems (MOP), four widely recognized evaluation metrics were employed75,76. The metrics used in this study to evaluate the performance of the optimization algorithm are the Inverted Generational Distance (IGD), Spacing (SP), Hypervolume (HV), and the Diversity Metric (\(\Delta\)). Each of these metrics is defined as follows.

$$\begin{aligned} I G D=\frac{\sqrt{\sum _{i=1}^{n_{p f}} ( d_{i} )^{2}}}{n_{p f}} \end{aligned}$$
(8)

where \(d_i\) represents the Euclidean distance between the ith acquired candidate solution and the closest solution among the actual Pareto solutions, \(n_{pf}\) signifies the total count of actual Pareto solutions.

$$\begin{aligned} S P=\sqrt{\frac{1}{n_{o}-1} \sum _{i=1}^{n_{o}} \left( d_{i}-\overline{{{{d}}}} \right) ^{2}} \end{aligned}$$
(9)

where \(d_i\) denotes the minimum distance from the ith solution to the other solutions, and d is the mean of \(d_i\).

$$\begin{aligned} H V=\delta \left( \cup _{i=1}^{| n_{o} |} \theta _{i} \right) \end{aligned}$$
(10)

where \(\delta\) represents Lebesgue measure of hypercube volume, \(\theta _{i}\) denotes hypercube volume constituted by the corresponding reference point and the ith solution.

$$\begin{aligned} \Delta =\frac{d_{f}+d_{e}+\sum _{p=1}^{n_{o}-1} \left| d_{p}-\overline{{{{d}}}} \right| }{d_{f}+d_{e}+( n_{o}-1 ) \overline{{{{d}}}}} \end{aligned}$$
(11)

where \(d_p\) denotes the Euclidean distance among the acquired candidate solutions, d represents the average value of \(d_p\), \(n_o\) indicates the count of candidate solutions within the obtained Pareto solutions. The variables \(d_f\) and \(d_e\) correspond to the Euclidean distances between the obtained extreme solutions and the boundary solutions, respectively.

Arithmetic optimization algorithm

The arithmetic optimization algorithm (AOA) is a novel metaheuristic optimization algorithm that draws inspiration from the mixed quadratic operations in arithmetic, as proposed by scholars Abualigah et al.64. To determine the most effective optimization framework within a feasible temporal constraint, AOA integrates a mathematical function accelerator to delineate the optimal approach. This paradigm segregates the entire procedure into the exploration and exploitation phases, employing multiplicative and divisive operations to foster comprehensive exploration, while harnessing additive and subtractive operations to augment local exploitation. These two phases are systematically selected based on models that correlate with the current iteration number t as

$$\begin{aligned} \rho _t= T_{\min }+ t \times \frac{ T_{\max }-T_{\min }}{T} \end{aligned}$$
(12)

where \(\rho _t\) is the interpretation threshold for the \(t^{\text {th}}\) iteration \(M\_Iter\). \(T_{\max }\) and \(T_{\min }\) are the maximum and minimum values of the acceleration function, respectively. T is maximum number of iterations. In cases where stochastic variable \(r_1\) is found to be less than \(\rho _t\), AOA transitions to the global exploration phase. Conversely, if \(r_1\) is greater than or equal to \(\rho _t\), the algorithm advances to the local exploitation phase.

In the exploration phase, the AOA operator randomly explores the search area in multiple regions and searches for better solutions based on the two main division operators (\(\mathcal {D}\)) and multiplication operators (\(\mathcal {M}\)). The next position \(x_{t+1}\) is given as

$$\begin{aligned} x_{t+1}=\left\{ \begin{array}{ll} x_{\text {best}} \div (\mathbb {M O P}(t)+\varepsilon ) \times ((x_u-x_l) \times \mu +x_l), & \quad r_{2}<0.5, \\ x_{\text {best}}\times \mathbb {M O P}(t) \times ((x_u-x_l) \times \mu +x_l), & \quad \text{otherwise } \end{array}\right. \end{aligned}$$
(13)

where \(x_{\text {best}}\) represents the j-th best solution so far, \(\mu =0.5\) is the search process control coefficient77. and \(x_u\) and \(x_l\) are the upper and lower bound of the variable respectively. \(r_2\) is a random number between 0 and 1. The mathematical optimization probability \(\mathbb {M O P}\) is

$$\begin{aligned} \mathbb {M O P}(t)=1- \left( \frac{t}{T}\right) ^ {1/{\alpha }} \end{aligned}$$
(14)

where \(\alpha\) stands for a sensitive parameter77.

During the exploitation phase, AOA is subject to local refinement through additive (\(\mathcal {A}\)) and subtractive (\(\mathcal {S}\)) mechanisms. These approaches are characterized by negligible dispersion and facilitate prompt convergence to the target, thus expediting the identification of the optimal solution. The formula is given as

$$\begin{aligned} x_{t+1}=\left\{ \begin{array}{ll} x_{\text {best}} - \mathbb {M O P}(t) \times ((x_u-x_l) \times \mu +x_l), & \quad r_{3}<0.5, \\ x_{\text {best}} + \mathbb {M O P}(t) \times ((x_u-x_l) \times \mu +x_l). & \quad \text{otherwise } \end{array}\right. \end{aligned}$$
(15)

where \(r_3\) stands for a random number between 0 and 1.

Multi-objective arithmetic optimization algorithm

The grid method represents a prevalently utilized multi-objective optimization technique for deriving Pareto solutions within multi-objective optimization frameworks. This methodology entails the establishment of a regular grid within the objective space to rigorously search for and assess potential solutions, thereby attaining equilibrium among diverse objectives75. The selection of the leader \(x_{leader}\) from the non-dominated Pareto set in the context of the grid method should be executed as

$$\begin{aligned} \triangle f_{i}^n=\dfrac{\textrm{max}f_{i}^n-\textrm{min}f{i}^n}{M} \end{aligned}$$
(16)

where M is the number of grids, and \(F_i\) denotes object space value for the i-th object. To expand the range of the Pareto Front (PF), the procedure should select a non-dominated solution in the sparsest region of corresponding objective space. This algorithm commences by partitioning the objective space of the Pareto non-dominated set into several equal regions. Subsequently, the procedure identifies one solution as the leader on the likelihood that inversely correlates with the density of the solution set within the restricted unit interval. The selection of leader in division of objective space is shown in Fig. 3, The probability of selected solution in current area is

$$\begin{aligned} P_k=\text {e}^{-\dfrac{\beta \cdot m_k}{m_{set}}} \end{aligned}$$
(17)

where k is the corner mark of current area. \(\beta\) is a parameter controlling the pressure of probability. \(m_k\) represents number of solutions in current area and \(m_{set}\) denotes total number of solutions in Pareto non-dominated set.

In the MOAOA algorithm, the \(x_{\text {leader}}\) is chosen from the external archive through the roulette wheel selection method, as explained in Eq. (16). Afterward, the particle’s position is updated by Eqs. (13)–(15), while the non-inferior solutions from the population are incorporated into the external archive.

Fig. 3
figure 3

The division of objective space and selection of leader in MOAOA. represent non-dominated solutions, represent the selected leader.

Full size image

To update the Pareto no-dominated set, the program calculates the objective function expressed in the current iteration. If \(\textbf{F}(\textbf{x})\) is dominated by any objective value in the current set, the iteration value will be abandoned. Otherwise, the iteration value of the solution will be added into the Pareto no-dominated set and the program will wipe out all the solutions dominated by the current solution immediately. For controlling the size of no-dominated set, the program will delete the solutions randomly while the element number exceeds the pre-set size of set. The deleting process preferentially selects the high-density solutions in the objective space to enhance the homogeneity of Pareto set. The deleting process preferentially selects the high-density solutions in the objective space to enhance the homogeneity of Pareto set. Based on the above content, Algorithm 1 provides a pseudocode flowchart for the proposed MOAOA.

Algorithm 1
figure c

The proposed Multi-objective arithmetic optimization algorithm.

Full size image

Optimization of BiLSTM based on MOAOA for COVID-19 automatic diagnosis model

Model evaluation indicators

In our research, we implement a variety of evaluation criteria to assess the proficiency of each predictive model constructed using diverse supervised deep learning algorithms78. These evaluation criteria employ a confusion matrix to distinguish between accurate and erroneous outcomes, utilizing various classification metrics such as true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN).

The accuracy of algorithm performance, an important indicator for techniques utilized both pre-processing and post-processing, can be evaluated through a scale composed of TP and TN. The accuracy follow as

$$\begin{aligned} \textrm{Accuracy} = \frac{{(\textrm{TP} + \textrm{TN})}}{{(\textrm{TP} + \textrm{TN} + \textrm{FP} + \textrm{FN})}} \end{aligned}$$
(18)

Specificity quantifies the proportion of individuals who tested negative for COVID-19 out of the total population of uninfected individuals, and it is given as

$$\begin{aligned} \textrm{Specificity} = \frac{{\textrm{TN}}}{{(\textrm{TN} + \textrm{FP})}} \end{aligned}$$
(19)

Precision represents a key measure for assessing the merit of technical performance methods executed prior to and following algorithmic processing. The precision scale and error rate comprises TP and TN. The precision can be obtained as

$$\begin{aligned} \textrm{Precision} = \frac{\textrm{TP}}{{(\textrm{TP} +{ \mathrm FP})}} \end{aligned}$$
(20)

Recall is a measure computed by the ratio of TP to the sum of TP and FN, serving as a critical indicator for quantifying correct predictions and assessing the impact of data imbalance on outcomes. Recall can be solved by

$$\begin{aligned} \textrm{Recall} = \frac{\textrm{TP}}{{(\textrm{TP} + \textrm{FN})}} \end{aligned}$$
(21)

F1 Score is considered one of the important indicators sensitive to mismatched data and affecting efficiency results, which is calculate computed as

$$\begin{aligned} \begin{array}{*{20}{c}} \mathrm{{F1 \ Score} = 2 \times \frac{{\textrm{Precision} \times \textrm{Recall}}}{{\textrm{Precision} + \textrm{Recall}}}} \end{array} \end{aligned}$$
(22)

Model process

This manuscript proposes a BiLSTM COVID-19 autonomous diagnostic model based on MOAOA, which automatically classifies CT images as Non-COVID-19, COVID-19, and pneumonia patients. The convolutional neural network (CNN) is used to extract 128 features from the dataset, which served as input to the BiLSTM model. Moreover, Cross-validation partitioned the dataset and validated it in multiple cycles, confirming the model’s generalization ability. The performance of the model training is significantly dependent on the appropriately chosen hyperparameters. The proposed MOAOA method is employed to optimize these hyperparameters. In addition, before model training, we perform duplicate data removal, missing value processing, and data normalization operations. Subsequently, we use random oversampling and undersampling to balance the dataset and apply data enhancement techniques such as rotation, flipping, cropping, and brightness adjustment to improve the diversity of the data. The flow diagram of our proposed COVID-19 diagnostic model is illustrated in Fig. 4.

Fig. 4
figure 4

The flowchart of MOAOA-BiLSTM model for COVID-19 diagnosis.

Full size image

Performance testing of multi-objective arithmetic optimization algorithms

Table 1 The ZDT functions of multi-objective optimization79.
Full size table

We used a series of Zitzler-Deb-Thiele (ZDT)80 functions to validate the proposed MOAOA and compared it with NSGA-II81 (deb2002fast) and the original MOPSO82, the ZDT functions are shown in Table 1. The parameters for these algorithms are set as follows: \(k_{\max }\)=500, \(N=100\), the maximum size of the archive is set to 200, and 30 independent runs are performed.

Fig. 5
figure 5

Comparison of pareto fronts of different algorithms on ZDT test problems. ‘PF’ denote the theoretical optimal solution for the ZDT series problems.

Full size image
Table 2 Performance comparison of different algorithms on ZDT functions, the indicators’ values are the means and the variance in brackets.
Full size table

Figure 5 presents the Pareto frontiers generated by various algorithms, figures a, b, c, and d correspond to the ZD1, ZD2, ZD3, and ZD4 test problems, respectively. The MOAOA accurately captures the true Pareto Frontier (PF) compared to NSGA-II and MOPSO. Table 2 summarizes the statistical data for various performance metrics across different multi-objective optimization algorithms, the bold values are the best values for the indicator. The numerical experiments demonstrate that the optimization performance of MOAOA surpasses those of NSGA-II and MOPSO.

Experimental examples of COVID-19 CT classification

In this section, the correctness of the MOAOA-BiLSTM model is demonstrated through two sets of real-world datasets. The proposed MOAOA-BiLSTM model is utilized for automatic diagnosis in two image datasets, with its performance evaluated based on accuracy, recall, precision, and F1 score metrics. The proposed method is compared and analyzed through experiments using various diagnostic and optimization algorithms to demonstrate its effectiveness and accuracy. The selected parameters of MOAOA are presented in Table 4, including the learning rate, number of epochs, L2 regularization factor, and the number of hidden nodes. To ensure fairness among the algorithms, this study tested all the algorithms in the same environment. The device information is shown in Table 3.

Table 3 The device information for the model in this paper.
Full size table

Dataset 1

This study utilize publicly available CXR images of patients with Non-Covid-19 and Covid-19. The dataset consists of 3000 images with a resolution of 224 \(\times\) 224 pixels, half of which are labeled as Non-Covid-19. The dataset 1 is available on Mendeley Data via the link https://data.mendeley.com/datasets/db4wdy7cdf/1. Before training the model, the dataset should be provided for pre-processing, with 70% allocated for training and 30% for testing.

ROC and CM

The classification performance of the MOAOA-BiLSTM model is evaluated using ROC and CM. The proposed MOAOA-BiLSTM model produces better accuracy in the COVID-19 (\(95.6\%\)) and Non-COVID-19 (\(95.1\%\)) categories. Therefore, this MOAOA-BiLSTM model can be used for automatic screening of COVID-19. ROC (Receiver Operating Characteristic) and CM (Confusion Matrix) generated from the analysis are depicted in Fig. 6. The ROC curve is a performance measurement tool for classification problems that takes into account various thresholds. The proximity of the curve to the upper left boundary of the ROC space is directly proportional to the robustness and accuracy of the proposed model’s outcomes. Figure 6a illustrates the ROC curve of the proposed MOAOA-BiLSTM diagnostic model, demonstrating the successful performance of the automatic screening model presented in this study. The confusion matrix analysis of the proposed COVID-19 disease model is shown in Fig. 6b. The findings demonstrate that the MOAOA-BiLSTM-based diagnostic model proposed in this article consistently outperforms in terms of true positive and true negative values. Additionally, the model exhibits lower false negative and false positive rates.

Fig. 6
figure 6

(a) The ROC of MOAOA; (b) The confusion matrix of MOAOA.

Full size image
Table 4 Parameters of MOAOA.
Full size table

Performance comparison of different optimizers

This section presents a performance comparison of various optimization algorithms in the BiLSTM model. PSO55, GWO83, AOA74, NSGA-II84, MOPSO85, MOGWO86, and the proposed MOAOA are applied to optimize the BiLSTM neural network. Table 5 shows the performance analysis of different optimizations, and the results show that the AOA optimization method has the most stable performance among the single-objective optimization (SOP) neural networks. Compared to MOP, the generalization of SOP results is better. The MOAOA-optimized BiLSTM network outperforms other optimization algorithms, delivering the superior performance indicators for accuracy, precision, specificity, recall, and F1 score.

Table 5 The performance comparison of different optimizers.
Full size table

The performance comparison of different optimization algorithms in CM and ROC is shown in Figs.  7 and  8, figures a, b, c, d, e, and f correspond to the results obtained using the AOA, GWO, MOGWO, PSO, MOPSO, and NSGA algorithms, respectively.

Fig. 7
figure 7

Confusion matrix of different optimizers with BiLSTM.

Full size image

Through analyzing and comparing Figs. 6b and 7, it is obvious that The proposed MOAOA optimized BiLSTM model exhibits excellent performance, achieving a maximum accuracy of 95.32%, an accuracy of 95.13%, a recall of 95.56%, and an F1 score of 95.34%. Compared to other optimization algorithm models, the BiLSTM model optimized by MOAOA demonstrates superior accuracy and performance.

Fig. 8
figure 8

ROC of different optimizers with BiLSTM.

Full size image

Figure 8 compares the ROC curve of existing optimization models. The efficiency of the MOAOA optimization model is demonstrated by displaying nearest ROC curve in the upper left corner. By analyzing and comparing all the curves in Figs. 6a, 8, the MOAOA optimization model demonstrates superior accuracy and generalization compared to others.

Performance analysis with different neural networks

In this section, we utilize six established deep neural networks for the purpose of image classification and diagnostic analysis: Extreme Learning Machines (ELM)87, Radial Basis Function Neural Network (RBFNN)88, CNN89, Random Forest (RF)90, LSTM91, and BiLSTM of the proposed MOAOA optimization algorithm. The performance comparison indicators of these networks include accuracy, specificity, sensitivity, precision, and F1 score, as shown in Table 6. The statistical results show the comparison between this study and recent studies. In terms of accuracy, the RBFNN network performs the worst with a result of 0.9031, while the BiLSTM method achieves the highest accuracy at 0.9532. Regarding Recall, the Random Forest method is the best, with a Recall value of 0.9778, followed by the BiLSTM method at 0.9556. In terms of Precision and Specificity, the BiLSTM method outperforms all others, with corresponding values of 0.9513 and 0.9509, respectively. These comparisons indicate that the optimized BiLSTM model demonstrates superior accuracy, specificity, sensitivity, and F1 score compared to other deep learning networks, highlighting its high efficiency and generalization capabilities.

Table 6 Performance comparison of different neural networks with MOAOA.
Full size table

Dataset 2

To further validate the accuracy and efficiency of the model constructed, we apply another dataset. The dataset 2 is available on Mendeley Data via the link https://www.kaggle.com/datasets/francismon/curated-covid19-chest-xray-dataset/data. The accuracy and loss of the optimized BiLSTM model for high-dimensional datasets are evaluated, as shown in Figs. 10 and 11. These figures compare the performance of the BiLSTM neural network optimized using MOAOA and AOA in terms of accuracy and loss. Figure 10 illustrates that the accuracy of training and validation increases linearly and remains stable for an extended period after a certain point, indicating that the model is well fit (without underfitting or overfitting. Figure 11 presents the loss curve, which shows that there are slight variations in training and validation losses. The MOAOA optimization model achieves the highest accuracy with minimal loss compared to the AOA model. Furthermore, the optimization model remains stable during long-term iterations. In Figs. 10 and 11, subfigures (a) and (b) represent the AOA and MOAOA, respectively.

Fig. 9
figure 9

(a) The ROC of MOAOA; (b) The confusion matrix of MOAOA.

Full size image
Fig. 10
figure 10

The graphical illustration of accuracy.

Full size image
Fig. 11
figure 11

The graphical illustration of loss.

Full size image
Fig. 12
figure 12

Confusion matrix of different optimizers with BiLSTM.

Full size image

Figures 9b, 12 present the confusion matrices for the COVID-19 dataset (Class 3) alongside the three classes (Class 1: normal, Class 2: pneumonia, and Class 3: COVID-19) under different optimization algorithms, which are employed to assess the model’s sensitivity. As shown in Figs. 9b and 12, the MOAOA optimization algorithm achieved correct prediction rates of 90.7% for normal images, 90.7% for pneumonia images, and 98% for COVID-19 images, all surpassing 90% accuracy, demonstrating the algorithm’s high accuracy. In comparison, the MOGWO optimization method predicted pneumonia with an accuracy of 99%, but its COVID-19 prediction accuracy was only 85.7%. Meanwhile, the MOPSO optimization method achieved a COVID-19 prediction accuracy of 99.7%, but its pneumonia prediction accuracy was only 76.7%, significantly below 90%. Among the three types of predictions-normal, pneumonia, and COVID-19-the MOAOA optimization algorithm proved to be the most stable and accurate. The ROC curves for the three classes of the BiLSTM model under different optimization methods are shown in Figs. 9a and 13. In Figs. 12 and 13, subfigures (a) to (f) represent the AOA, GWO, MOGWO, PSO, MOPSO, and NSGA, respectively.

Fig. 13
figure 13

ROC of different optimizers with BiLSTM.

Full size image

The curves in Figs. 9a, 13 illustrate the trade-off between sensitivity and specificity for various optimization model solutions. The graphs indicate that the MOAOA-optimized model delivers superior results, demonstrating that the network model optimized by MOAOA can be reliably utilized for real-time COVID-19 diagnosis.

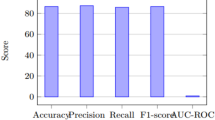
To further examine the results, this study compares the performance indicators of the proposed MOAOA optimized BiLSTM network with other state-of-the-art optimization methods. Performance indicators obtained using the proposed method exhibit superiority over other methods, as depicted in Fig. 14. It demonstrates that the performance indicators calculated by the MOAOA optimization method maintain the highest stability, outperform other methods. Specifically, the model achieved an Accuracy of 95.22%, a Precision of 95.42%, a Recall of 95.22%, and an F1 Score of 95.32%, all of which significantly surpass the results obtained by other optimization algorithms.

Fig. 14
figure 14

The performance of various optimizers with BiLSTM.

Full size image

Conclusion

In this study, we propose a novel COVID-19 automatic diagnosis model, the MOAOA-BiLSTM deep network. The proposed enhanced MOAOA algorithm can automatically optimize the hyperparameters of BiLSTM deep neural network, solving the problem of irrationality in the setting of BiLSTM hyperparameters, improving the accuracy of COVID-19 diagnosis. By testing the MOAOA optimization algorithm on multiple benchmark functions, its strong optimization performance and robustness are demonstrated. The proposed automatic diagnosis model is applied to two publicly available CT image datasets and evaluated using various metrics in comparison with existing optimization algorithms and deep learning models. Compared to other diagnostic methods, this approach can autonomously diagnose the etiology of the patient’s disease while achieving highly accurate diagnostic results. This enables rapid diagnosis in the face of a large number of patients, which is important for the prevention and control of epidemics and the treatment of patients. In addition, the dynamic adjustment mechanism of the MOAOA algorithm increases the flexibility of the solution process and avoids falling into the local optimal solution, which ensures the consistency and reliability of the diagnosis.

It is worth noting that the model only serves as an auxiliary tool for physicians and is intended to provide valuable reference opinions for medical professionals, rather than replacing the professional judgment of physicians. The model still has some limitations in relevant aspects, such as The model has certain requirements on the quality of CT images, otherwise it will affect the diagnostic accuracy of the clinical data. Furthermore, real-time diagnosis continues to pose significant challenges, especially in emergency situations or large-scale screening efforts.The ability to quickly process large numbers of CT images and provide accurate diagnostic results remains a key issue.

In the future, the MOAOA-BiLSTM model can be deployed in internet of things and cloud-based diagnostic tools to assist remote patients, it can be further extended into a multimodal model that combines different data sources such as breathing sounds, blood monitoring data, etc. In addition, the MOAOA-BiLSTM model can be applied to radiological image analysis, detecting complex abnormalities, diagnosing other image-related diseases. Combined with XAI technologies such as SHAP and Grad-CAM, it attains more intuitive visualization while providing accurate diagnostic recommendations. With the growing prevalence of wearable devices and smart health monitoring systems, this model can be integrated into daily health monitoring tools, enabling real-time monitoring and analysis of patient health data. This integration will facilitate the prevention of disease progression and ensure patient safety by providing timely medical interventions.