Wave driven cross shore and alongshore transport reveal more extreme projections of shoreline change in island environments

Abstract

Coastal erosion, intensified by sea level rise, poses significant threats to coastal communities in Hawaiʻi and similar island communities. This study projects long-term shoreline change on the Hawaiian Island of O‘ahu using the data-assimilated CoSMoS-COAST shoreline change model. CoSMoS-COAST models four key shoreline processes: (1) Alongshore transport, (2) Recession due to sea level rise, (3) Cross-shore transport due to waves, and (4) Residual processes represented by a linear trend term. This study marks the first application of CoSMoS-COAST for an oceanic equatorial island with narrow beaches and a dynamic wave climate. The model is informed with a novel combination of shoreline data derived from high-resolution imagery from Planet, Sentinel-2, and Landsat satellites, wave-climate hindcasts specific to Hawai‘i, and regional beach-slope surveys. On a dynamic northern Oʻahu beach, the model achieved a root mean square error of 9.4 m between observations and model output. CoSMoS-COAST predicts that 81% of O‘ahu’s sandy beach coastline could experience beach loss by 2100; with 39.8% of this loss happening by 2030. This represents an increase, 43.3%, in net landward shoreline change compared to previous erosion forecasts, for 0.3 m of sea level rise (2050). Additionally, dynamic processes such as cross-shore equilibrium processes and alongshore sediment transport, play a large contribution to gross shoreline change within the next decade, particularly on O ‘ahu’s north and west shores. In the long term, we find that recession due to sea level rise and residual processes dominate, but dynamic, wave-driven processes (longshore and cross-shore transport) still account for 34% of shoreline change between present and 2100. We assert dynamic, wave-driven processes are a crucial addition for accurate modeling of island sandy beach environments. These findings have implications for O‘ahu’s coastal planning and development, suggesting updates to shoreline policies that rely upon erosion forecasting, and highlights the importance of incorporating wave and alongshore transport in erosion models for other Pacific islands.

Introduction

Sea level rise is a recognized phenomenon for coastal communities around the world¹. Increased rates of sea level rise will exacerbate hazards such as coastal erosion, flooding, storm surges, salt-water intrusion, and habitat loss^1,2. These hazards disproportionately affect equatorial island communities, and decrease the already limited availability of land and natural resources¹. The shores of the main Hawaiian islands are no exception to the effects of sea level rise, including overland and groundwater flooding³, wave inundation⁴, and coastal erosion⁵. According to the Hawaiʻi Sea Level Rise Vulnerability and Adaptation Report, climate change could affect approximately 6500 structures under 3.2 feet of sea level rise (SLR), resulting in the displacement of 19,800 residents and more than $19 billion of land and structure loss statewide⁶. As of 2012, 70% of the beaches on the islands of Kauaʻi, Oʻahu and Maui are undergoing long-term erosion⁷. Coastal erosion, in particular, can directly undermine critical infrastructure, render historic cultural sites inaccessible, and cause populations to lose their homes.

In response to historic coastal erosion, island communities such as Hawaiʻi have used science-informed coastal policies, such as setback laws for coastal development, and coastal zone special management areas, aimed at preserving, protecting, and restoring the coastal zone⁸. Several studies in Hawai‘i investigate the feasibility of alternate adaptation strategies such as “managed retreat” or “living shoreline” solutions and their appropriate implementations^9,10. Coastal armoring, such as seawalls, revetments, and temporary “sand burritos” are common where erosion is already impacting private property^7,11. Understanding the timing, locations, and severity of erosion is critical for identifying adaptation mechanisms and producing scientific findings that can support policies for coastal resilience^12,13,14.

With recent advances in both shoreline process models and the ability to monitor coastlines with satellite imagery, researchers now aim to predict shoreline change across multiple time and spatial scales, in nearly any region in the world^{15,16,17,18,19}. A number of numerical shoreline models have been created and some compared against each other for accuracy and reproducibility of known shoreline responses¹⁶. Some of these are classified as “hybrid”, named for the combination of physics-based and data-driven modeling approaches. Hybrid models often assume that a beach system has a dynamic equilibrium position of its shoreline that moves in response to waves and sea level^{20,21,22,23,24,25,26}. The models also require extensive observations to calibrate their many parameters. One such hybrid model, CoSMoS-COAST (Coastal Storm Modeling System—Coastal One-line Assimilated Simulation Tool)²⁷, aims to model both short-term (< month) and long term (> decade) shoreline change patterns. CoSMoS-COAST debuted in 2017 to project shoreline change for the California coastline²⁸ as part of the CoSMoS²⁹ project, and has been updated in subsequent years^30,31. In a blind study, this model forecasted more accurate results than other similar hybrid models¹⁶ and has shown skill in predicting shoreline positions on many wide, sandy beaches on the continental United States³².

This study aims to validate CoSMoS-COAST’s ability to predict shoreline change for oceanic equatorial island beaches, which are relatively narrow and typically have more dynamic wave climates compared with continental beaches. To do this, we implement CoSMoS-COAST along all sandy and mixed sediment beaches of the most populated and urbanized Hawaiian island of O‘ahu. O‘ahu has faced significant challenges with coastal erosion for many decades as development collides with rising tides. In this study, we first provide a case study of a high-energy beach, namely Paumalū Beach, to confirm that the model captures known beach behavior. Model performance is assessed along the entire island using three statistical measures (i.e., root mean square error (RMSE), index of agreement, and confidence-interval comparisons). We then forecast coastal erosion hazard zones for the entire island, assuming the intermediate sea-level rise scenario of 1.19 m (3.90 ft) by 2100 presented in the 2022 U.S. Sea Level Rise Interagency Task Force Report³³, and compare the CoSMoS-COAST findings directly with a previous coastal erosion model⁵ (Anderson et al. 2018) used administratively for O‘ahu through the department of Land and Natural Resources (Fig. 1). By evaluating the model outputs, this study explores the importance of alongshore sediment transport and short-term cross-shore transport for high stand, Pacific beaches. We anticipate that using CoSMoS-COAST and the new shoreline data sets used therein will provide a more comprehensive representation of shoreline change in Hawai‘i, therefore better informing erosion hazard zones for planning and policy administration and serving as an example for using this model in other island settings.

Fig. 1

Flowchart overview showing the inputs, parameters, uncertainty methods, and outputs for the CoSMoS-COAST^28,30 (light blue, left boxes) and Anderson et al. model⁵ (light pink, right boxes), used in previous erosion projects in Hawaiʻi. Anderson et al. model uses input from Fletcher et al.⁷. Equations are colored to match the process descriptions, (e.g. Green terms are described as a linear type component in both models). CoSMoS-COAST uses input from Li et al.³⁴; as well as theory from: Pelnard-Considere et al.³⁵, and Vitousek et al.³¹. Anderson et al. uses theory from Davidson-Arnott³⁶. See Methods for a description of equation symbols and see Supplement for a description of beach slope inputs.

Results

We first assess CoSMoS-COAST through a case-study of Paumalū Beach (Section “Paumalū Beach (north O‘ahu) case study”). Then we present CoSMoS-COAST’s island-wide model performance statistics and forecasted erosion hazards for Oʻahu, Hawai‘i (Section “Island-wide modeling using CoSMoS-COAST” and Section “Shoreline change model comparison”); and compare the CoSMoS-COAST forecasts to the previous erosion modeling for Hawai‘i (Sect. 2.4).

Paumalū Beach (north O ‘ahu) case study

Paumalū is situated on the world-famous north shore of Oʻahu, renowned for its surf breaks (Fig. 2A, B), between Rocky Point and Sunset Point. In general, the coastline of northern Oʻahu contains isolated outcrops of beach rock and coarse sand beaches. The Paumalū area experiences large swell events from the northwest during winter months, and smaller tradewind waves which occur year-round, but are slightly intensified during the summer months. These seasonal wave oscillations, combined with complex reef morphology, result in pockets of beach erosion and accretion along Paumalū that vary over time. This all occurs alongside private property and public infrastructure built on ancient sand dunes and paleo-beach deposits, already impacted by high-wave flooding, and berm destruction³⁷. Erosion hotspots have threatened homes and have been a subject of state media^38,39. Kamehameha Highway, a key route around much of O‘ahu, lies just meters from the active beach in places like Sunset Beach Park. As a highly threatened yet understudied area, Paumalū serves as a case study for shoreline change on complex island beaches.

Fig. 2

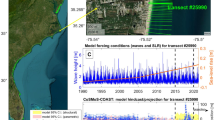
(A) Displays the island of Oʻahu, along with all transect locations where modeling was performed (green), and the 50-m contour isobath where wave hindcasts were extracted and later used for model forcing (blue dots). The Paumalū case study region (pink box) is also shown, with the particular wave hindcast location (red dot) used in modeling shoreline change at Transect #1323 (highlighted bold red and labeled in B). (B) Shows the Paumalū study region with model transects overlaid in orange. Transects #1295 and #1345 are labeled to show the end points of the case study region. Shoreline modeling at Transect #1323 (bold red) is presented in C. (C) Displays wave height hindcast data (C1), and shoreline modeling components (C2–C6) between 1990 and 2023 for Transect #1323. Daily significant wave height (C1) shows strong seasonality, with smaller waves in the summer (May–October; pink background shading) and larger wave heights during winter months (white background). (C2) represents the simulated total shoreline position (YY) with a 95% confidence interval (shaded maroon bands), along with satellite observations (blue circles with uncertainty bars) and a few historical aerial photo observations (pink circles with uncertainty bars). Also displayed are the modeled individual shoreline change components due to: (C3) short-term cross-shore wave-driven processes, STW; (C4), sea level rise, or the Bruunian response, BRU; (C5) long-term linear residual processes, LTR; and (C6) alongshore transport, ALST. Negative (positive) shoreline change indicates shoreline recession (advance). Model parameters are allowed to assimilate according to data during the hindcast (calibration) period (1990–2020), while no assimilation takes place during the hindcast (validation) period (2020–2023). Panel A: Satellite imagery hosted by ESRI through the “geobasemap” function, Matlab (R2023b). Panel B: Satellite imagery map of area of interest with transects overlaid, Google Earth (2024), accessed September 2024.

In Fig. 2C, an example of model component evolution at one location (transect #1323, Fig. 2B) is shown. The hindcast time series of significant wave height (C1) illustrates the strong seasonality, showing winter wave heights that peak around 4 m in the winter months, and reduce to roughly 1–1.5 m during summer months. This seasonality is reflected in the shoreline position at transect #1323, where shoreline data (C2, blue and pink circles with error bars) indicate shoreline recession during winter months when wave heights are largest (in plots, negative shoreline movement indicates retreat), followed by shoreline advance or recovery during summer months with smaller wave heights. The modeled total shoreline change (C2, maroon line with 95% confidence interval band) captures the short-term wave oscillations well, especially toward the end of the Hindcast (calibration) period. The individual modeled components (C3–C6), whose sum equals the total shoreline change, indicate that the wave-driven short-term component dominates the total shoreline change signal during the hindcast period, shown by its large cyclical magnitude signal. Note that the y-axis scale differs across C3–C6. The effects of data assimilation can also be seen, especially in the shoreline change due to alongshore transport (C6), where the initial model conditions lead to an immediate rise in value (indicating sediment accumulation) from 1990 to 1992; at this time, the model assimilates a few data points (shown in C2) which correct the alongshore component back down. The model marches through time until it encounters many data points to assimilate near year 2000; at which time, there is a noticeable reduction in model error as indicated by the narrowed shaded error bands. Between the 2020–2023 validation period, the model does not assimilate data, and the differences between modeled and measured shoreline positions are used to assess model performance. Our results are consistent with other studies that have investigated the drivers of erosion events and volume change in the Paumalū region⁴⁰. Notably, subpanel C3 shows an example of greater than normal erosion due to waves in winter 2016, which is known to have been an erosive winter season for the area, and was reported in the local news³⁹. Every modeled transect contains information about hindcasting similar to Transect #1323 and can be examined for patterns based on individual modeled components.

To place our model’s performance as compared to other shoreline models, we follow Vitousek et al.³⁰, and calculate three performance metrics for Paumalū: root mean square error (RMSE), percentage of time within the hindcast (validation) period (2020–2023) in which the model is within the satellite confidence intervals (called, “Within C.I”), and index of agreement⁴¹, d. A model with low RMSE, high percentage within C.I, and a high index of agreement is considered to have good performance.

The mean RMSE between the model predictions and the satellite imagery for Paumalū during the validation period was 10.9 m. This is more than reported RMSE values for models that were tested at Tairua Beach, including CoSMoS-COAST, which achieved an RMSE of 5.04 m; although it should be noted that Tairua beach has a less extreme wave climate (~ 2 m maximum Hs during the study’s hindcast period)¹⁶ with more mild seasonal erosion cycles and a lower foreshore slope (0.02) than Paumalū (2–4 m Hs, 0.147 foreshore slope). In Vitousek et al.³⁰ and³², their mean RMSE for the whole of California and the South Atlantic is 12.4 m and 12.4 m, respectively, suggesting that this RMSE is consistent with both the performance of CoSMoS-COAST in other regions as well as with the accuracy of the underlying satellite observations themselves.

The index of agreement for Paumalū is 0.36, suggesting the model predictions have weak agreement with the observations. This is lower than CoSMoS-COAST performance in California³⁰ (d = 0.56), in the south Atlantic³² (d = 0.44), and in Tairua Beach¹⁶ (d = 0.54). This may be due to the large variability in shoreline positions from the satellite shorelines that have an average standard deviation of 10.5 m across the beach cell, which is consistent with satellite error metrics across many sites⁴². The modeled shoreline positions during the validation period are within the confidence interval (C.I.) 95% of the time for Paumalū, indicating that the model has sufficiently assimilated its model parameters to the given observations.

Paumalū forecasting

Below we analyze CoSMoS-COAST’s ability to forecast shoreline positions using future sea level rise conditions. The calibrated model is used to forecast shoreline change at Paumalū for up to 1.2 m of SLR (Fig. 3). Each colored vector represents a predicted vegetation line (landward edge of the beach) under 0.3 m increments of SLR, with a baseline vegetation line digitized from 2022 Natural Resources Conservation Service (NRCS) satellite imagery⁴³ (Fig. 3, black vector).

Fig. 3

On the left are examples of time series of forecasted shoreline positions (A–E), relative to a 2022 present-day baseline position, for five sample transects in the Paumalū area. Negative values indicate landward direction, and positive values indicate seaward direction. In each plot, the forecast for the labeled transect location is shown in dark red, with gray lines as forecasts of the other labeled transects. Black-purple-yellow vertical lines represent the timing of every 0.3 m increment of SLR. For example, 0.9 m of SLR is predicted to occur in ~ 2090 (orange vertical line). On the right, the map of Paumalū Beach shows shoreline vectors (lines along shore) colored in a black-purple-yellow coloring, representing the amount of SLR associated with the shoreline vector. The black line closest to the ocean represents the vegetation line in 2022, with successive lines representing 0.3 m (1 ft) increments of SLR up to 1.5 m of SLR (yellow). The yellow–red gradient colored dots represent the absolute distance from the 2022 baseline and are shown in the rightmost colorbar. The redder the color, the greater the distance landward, cropped at -50 m. Right Panel: Satellite imagery hosted by ESRI through the “geobasemap” function, Matlab (R2023b).

Paumalū is forecasted to recede landward between 20 and 100 m by 2100 (1.2 m of SLR) depending on the location within the cell. For example, between transects 1295 and 1320 (Fig. 3, locations A and C, respectively), there is a strong consistent signal of recession up to 50 m by 2100. Yet, moving north, to transect 1332 (Fig. 3, location D), the shoreline is forecasted to recede landward by about 25 m. At transect 1345 (location E) recession is forecasted in excess of 100 m. This indicates small-scale (< ~ 250 m) spatial variability between transects along shore of the beach cell. It is likely heavily constrained by the specific reef morphology surrounding this beach. Note that the shoreline results in Fig. 3 represent a snapshot of forecasted positions during summer wave conditions (July). It has been observed that in the summer, the relatively small northern swells move sand away from Kammie’s and Sunset Point, and this allows more sediment to collect near Sunset Beach Park.

To investigate the relative contribution of each model component to the total shoreline position, we approximate both the gross and net shoreline change for each of the components (Fig. 4). Gross shoreline change represents how much the shoreline moved around over a span of time, including back and forth fluctuations. Relative gross contribution is quantified as the variance of shoreline change due to each model component, relative to the variance of the total shoreline change (YY). Figure 4 pie charts show the mean over all transects at Paumalū. For example, the relative gross contribution over all transects in Paumalū from short-term wave influence (STW) between 2023 and 2050, becomes mean(var(STW_2023–2050)/var(YY_2023–2050)).

Fig. 4

Gross relative contribution (pie charts, top row) and net relative contribution (bar charts, bottom row) of model components at Paumalū Beach for the validation period (left, 2019–2023), and forecast periods ending in 2050 (middle) and 2100 (right). Colors represent the different model components: long-term linear change (LTR, green), Recession due to SLR (BRU, maroon)^36,44,45,46, alongshore transport (LST, pink)³⁵, and cross-shore, short term wave change (STW, blue)^31,47. In the bar plots, bar heights represent the median net shoreline change contribution over all transects during a set ten-year time period centered around 2023, 2050, and 2100 respectively, and whiskers represent the 20th and 80th percentiles, within which 60% of the transect values are found. Figure created in Matlab (R2023b).

Net shoreline change represents the shift in the median shoreline position over a time period due to each model component. We take only the median of shoreline positions during the 10-year period centered on a target date, then find the median over all transects. For example, the relative net contribution from short-term wave influence (STW) forecasted around 2050 over all transects in Paumalū is median(median(STW_2045–2055)) And similarly, the relative net contribution from short-term wave influence (STW) between forecasted around 2100 over all transects in Paumalū is median(median(STW_2095–2105)). We focus on the 10-year period centered on the target date, in order to illustrate the contribution of the components to net change, and not the cumulative change (shown in the pie charts).

During the hindcast (Validation) period (2019–2023), short-term shoreline change due to waves (STW) dominates the signal, accounting for nearly 90% of the total variance (representing gross change, Fig. 4, pie chart at top left); by contrast, the median shoreline change (net change, Fig. 4, bar plot at bottom left) due to short-term wave influence during this period hovers around zero. This indicates that although the seasonally oscillating wave signal causes the largest short-term changes in shoreline position over time, those changes fluctuate about an equilibrium shoreline position, and do not necessarily contribute to chronic, long-term erosion.

For the short-term forecast between 2019 and 2050, we see that waves (STW) and alongshore transport (ALST) play a large contribution to the shoreline position (Fig. 4). In the longer term, up to 2100, the Bruunian recession⁴⁵ (BRU) and processes captured by the linear long term rate (LTR) contribute more. This is consistent with the theory that waves (STW) impact shoreline change in the short term, whilst shoreline change due to sea level rise (BRU) is more impactful in the long term. According to the previous modeling that accounted for long-term erosion rates and Bruunian recession, long term erosion rates are up to − 1.01 m/year for this area by 2100⁴⁴, supported by Fig. 4’s 2023–2100 pie chart, in which 72% of the shoreline change comes from these terms (LTR and BRU).

When we investigate the magnitude and direction that each component contributes to recession or advancement of the overall shoreline position (YY), there are different patterns. The median magnitude of contribution to the shoreline position from ALST is positive with a relatively large spread of values. This may indicate that sand accumulates in one area, shifting the median towards transects in which there is an anomalous/high amount of sand from ALST. We expect the average contribution of STW to be centered around zero, since its contribution is short-term and sand moved from waves fluctuates seasonally around an equilibrium point. It is expected that the long-term (LTR) and Bruunian (BRU) processes compound over time, increasing in both magnitude of contribution and percentage as time goes on. Paumalū Beach is an example in which high-energy swells can cause substantial change, which is meant to be captured in the ALST and STW terms of the model– where they play large gross contributions in the short-term, but overall move the net shoreline position much less than LTR and BRU over many decades.

In this case study, CoSMoS-COAST identifies the general patterns of beach change, even for the highly dynamic beach with seasonally variable wave climate, of Paumalū. The model is able to parse short-term seasonal shoreline change from the longer-term general recession along the beach, and provides the first analysis of shoreline recession of the area in which individual shoreline change processes are identified.

Island-wide modeling using CoSMoS-COAST

Shoreline change modeling was performed on all beaches around the island of O‘ahu to explore large-scale spatial patterns and assess if the model can effectively forecast change for varying geological and wave conditions. We first report model performance using the metrics introduced in the case study above. Then, we present some examples of erosion hazard forecasting using CoSMoS-COAST, patterns in the island-wide forecast, and an analysis of the gross and net contributions from individual model components.

Island-wide model performance statistics

We extend performance metrics between predicted and observed shoreline positions over the validation period (2019–2023), to include the whole island of Oʻahu. We find that model performance around O‘ahu varies (Fig. 5). Most variation in performance occurs along northwest-facing coastlines (which includes Paumalū), which is likely due to the nature of the coastline in these areas—highly dynamic, often steep, embayed beaches with significant north-swell exposure that are positioned next to rocky headlands or outcrops, causing satellite observations to be less accurate.

Fig. 5

Model performance metrics around the O‘ahu coastline show (a) Root Mean Square Error (meters), (b) percentage of time model is within the confidence interval of the satellite observations, and (c) index of agreement values for each transect. Note that the scales for all metrics vary, but blue colors indicate better model performance in all images, while red colors indicate poorer performance. A low RMSE (m), a high % within confidence interval, and a high index of agreement (range is 0–1.0), indicates better model performance. Figure generated using the “scatter” function, Matlab (R2023b). Outline of Oahu coastline provided through the Hawaii Statewide GIS Program, from the 1983 1:24,000 USGS Digital Line Graphs.

The mean RMSE over all model transects is 9.0 m, in which 98% of transects have a < 15 m RMSE, and 69% of transects have an RMSE in the range of 5–10 m. This performs better than the CoSMoS-COAST model for California that reports a mean RMSE of 12.4 m, in which 77% of the transects have a < 15 m RMSE^28,30. The model predictions are again “within C.I.” 95% of the time, indicating that modeled shorelines regardless of region on the island are reasonable as compared to observations. The island-wide average index of agreement is $\overline{d} = 0.3$. Generally, this may be a function of the overall variability of the satellite shorelines, which have a standard deviation of 9.2 m on average for all of Oʻahu. Given all metrics together, CoSMoS-COAST performs reasonably well on Hawaiian beaches, as it did on previous implementations on continental beaches.

Island-wide erosion hazard forecasting

In Fig. 6, we present a sample of the forecasted coastal erosion hazard lines for the island of O‘ahu assuming the intermediate sea-level rise scenario of 1.2 m (3.9 ft) by 2100³³, at the 50th percentile (median) probability, meaning that anything seaward of this line has a 50% chance of being affected by erosion. Each colored vector represents a predicted vegetation line (landward edge of the beach) under 0.3 m increments of SLR, with a baseline vegetation line digitized from 2022 Natural Resources Conservation Service (NRCS) satellite imagery. Full results of the forecasted shorelines for the intermediate and intermediate high SLR scenarios can be found at www.soest.hawaii.edu/crc/slr-viewer/.

Fig. 6

Six example sites around Oʻahu with forecasted vegetation line positions for the month of July, under 0.3–1.2 m (1 ft (black)—4 ft (yellow)) of SLR. Locations are labeled by number and common beach name, and oriented with North pointing upwards in every photo except for Kūʻau. Inset of Oʻahu has labels of approximate locations of the example sites. All basemap imagery is from Google Earth (2024), ‘Satellite Imagery’ layer, accessed September 2024. Outline of Oahu coastline in the inset is provided through the Hawaii Statewide GIS Program, from the 1983 1:24,000 USGS Digital Line Graphs.

We observe general trends of erosion on an island-wide basis. By 2050 (0.3 m (1 ft) SLR, dark purple line, Fig. 6), we see beaches such as Waikīkī and Mākaha will experience shoreline recession that will significantly affect buildings and roads directly adjacent to the beach. Kū‘au is an example of a beach that the model predicts accretion from the baseline in 2050, but erosion for all other years. By 2100 (1.2 m SLR, Fig. 6), all example sites, including Kū‘au, forecast interference with critical infrastructure such as highways and beach parks. Although the model does not explicitly account for future nourishment plans for areas such as Waikīkī or the direct effects of sea wall fortification, it is known that these two methods are only temporary solutions, unlikely to be effective against increased storm surge and potentially up to 60 m of recession. Given that this is the median projection, the exact future erosion hazard zone could be located either landward or seaward of this line, but is most likely near it.

Out of the 112 beaches as part of this study on Oʻahu, 61.3% of them are projected to experience recession by 2050. Out of the sandy and mixed sediment coastline modeled around Oʻahu, 46.9% of the coastline will experience beach recession greater than its current beach width (defined here as the distance between the beach toe in 2022 and the landward vegetation line or the first hard-structure) by 2050 (0.3 m SLR). This is especially important for areas in which there are seawalls or hardening where the beach cannot recede backward naturally to maintain its current width, ultimately leading to complete loss of the beach fronting the hard structures. Projected erosion in excess of current beach width, in the presence of hard structures, will result in total beach loss. 71.7% of the 112 beaches modeled will be affected by shoreline recession by 2100. For 2100 (1.2 m SLR), 81.0% of the coastline will experience beach recession greater than their current beach widths. Most of this recession will be seen within the next ten years—where 39.8% of the coastline could recede more than their current beach width by 2030 (0.14 m SLR).

Recent studies have investigated the uncertainty related to shoreline model components and their contributions^48,49,50. These studies suggest that: SLR is a dominant factor in long-term shoreline recession predictions, especially when larger SLR projections are used. As SLR projections increase, the shoreline recession term (BRU) becomes more influential. Long-term shoreline change is affected by sediment supply, such as river discharge and beach nourishments. Over time, long-term processes lead to increasing variance, while wave-driven cross-shore transport (STW) remains stable, causing the contributions of each factor to shift over time. Figure 7 shows that for Oʻahu as a whole, its patterns are consistent with these findings. Waves (STW) and alongshore transport (ALST) dominate shoreline change contributions on shorter time scales, although they are smaller in median contribution overall. As the forecast continues to 2100, the BRU component, that is, shoreline recession due to SLR, dominates in gross and net contribution. The long-term linear erosion rate (LTR) component plays a less pivotal role for all of Oʻahu than for the Paumalū case study, most likely due to the fact that many LTR rates are small (a median of − 0.04 m/year) compared to Paumalū’s median rate of − 0.33 m/year.

Fig. 7

Gross relative contribution (pie charts, top row) and net relative contribution (bar charts, bottom row) of model components O‘ahu, including Paumalū Beach for the validation period (left, 2019–2023), and forecast periods ending in 2050 (middle) and 2100 (right). Colors represent the different model components: long-term linear change (LTR, green), Recession due to SLR according to the Bruun rule (BRU, maroon)⁴⁵, alongshore transport (LST, pink), and cross-shore, short term wave change (ST, blue). In the bar plots, bar heights represent the median net shoreline change contribution over all transects during a set ten-year time period centered around 2023, 2050, and 2100 respectively, and whiskers represent the 20th and 80th percentiles, within which 60% of the transect values are found. Figure created in Matlab (R2023b).

Shoreline change model comparison

In this section, we compare the CoSMoS-COAST results with shoreline change modeling done for Oʻahu from Anderson et al.⁵. Unlike the section above, we use the 80th percentile projection, indicating that there is a “80% chance that erosion will occur seaward of the given erosion vector.” Planners in Hawai‘i often opt for the 80th percentile, which is a more conservative forecast of erosion from a planning perspective, in that it identifies more land exposed to coastal erosion but at a lesser probability, compared to using the 50^th percentile (median). Note also that since beach slope is an important input in the BRU term of both models, we interpolate our beach slope values for CoSMoS-COAST from the Anderson et al. beach slopes, in most cases, taking the maximum value of the interpolated slopes and therefore the most conservative forecast of BRU impact (Supplementary Figures S1.1, and S3.1).

By overlaying 80th-percentile Anderson et al.⁵ and CoSMoS-COAST shoreline vectors onto the CoSMoS-COAST transects, we make a direct comparison using the projected amount of shoreline change, relative to the 2022 baseline. For both models, the direction of shoreline displacement is consistent: a positive displacement represents advancement/accretion of the shoreline seaward from the 2022 vegetation line. A negative displacement represents projected recession/erosion from the 2022 vegetation line. We then obtain the difference between model projections by taking the CoSMoS-COAST shoreline position minus the Anderson et al. shoreline position, at each model transect. A zero difference indicates that both models forecast the same amount of recession/advancement. Positive difference values indicate that the Anderson model forecasts are landward of the CoSMoS-COAST forecasts, while negative values indicate that CoSMoS-COAST forecasts are landward of the Anderson model forecasts. Anderson et al. did not include all areas modeled by CoSMoS-COAST, due to limited available data; so model comparisons here are constrained to areas in which both models were run.

In Fig. 8, the differences between models are displayed for 0.3 m (1 ft) and 1.2 m (4 ft) of SLR. At 0.3 m, approximately 2050, the northwestern coastline of the island, and near Waikīkī/Honolulu in southeast Oʻahu show a large difference, where CoSMoS-COAST projects much more erosion (red areas, Fig. 8). On the east side of Oʻahu, near Lāʻie, CoSMoS-COAST is typically seaward of the Anderson model (blue areas). The distribution of values for the 0.3 m scenario is centered around − 5 to − 20 m, but flattens for 1.2 m SLR (Fig. 8, Histograms). The extreme magnitudes of the differences in projections between the models increases with SLR and time, as shown by the darker colors in the 1.2 m map, in areas such as ‘Ewa Beach and Kailua.

Fig. 8

A detailed version of the 0.3 m and 1.2 m of SLR projections, expected to occur around 2050 and 2100, respectively, under the intermediate SLR scenario. A general outline of the O‘ahu shoreline is shown in black. Areas that do not have color along the shoreline are areas where either model did not produce any output. Color bar is cropped to the ± 2 standard deviations from the mean (− 47–33 m), and more red (more blue) represents that the CoSMoS-COAST model (Anderson et al. model⁵) forecasts a more landward position. Inset histograms show the distribution of difference values for each scenario, with color shading corresponding to the colorbar gradient, but showing the full range of values (− 120–60 m). Figure generated using the “scatter” function, Matlab (R2023b). Outline of Oahu coastline provided through the Hawaii Statewide GIS Program, from the 1983 1:24,000 USGS Digital Line Graphs.

Net shoreline change statistics are presented in Table 1. By using CoSMoS-COAST as compared to Anderson et al.⁵, the forecasted results for coastal erosion on Oʻahu increases by 43.3% for the 2050 forecast and 4.3% for the 2100 forecast, respectively, generally predicting more extreme values of erosion than previously predicted. If we account for only BRU + LTR averages in CoSMoS-COAST as compared to the Anderson et al. model, CoSMoS-COAST predicts less change in shoreline position than Anderson et al., although these still fall within the standard deviations of the models. Note that these results are for each model’s respective “full-model” transects, which is approximately ~ 5,000 transects for both models. The median and average shoreline change values for both models are well within the standard deviation of each other in 2100, suggesting that CoSMoS-COAST’s contributions are most valuable in the short term, when its dynamic processes are more significant.

Table 1 Average net shoreline change for CoSMoS-COAST and Anderson et al.⁵ models for 0.3 m and 1.2 m of SLR using the 80th percentile projections.

Discussion

Despite Hawai‘i’s complex beach configurations, the CoSMoS-COAST model displays consistent performance metrics in comparison to the continental United States (US), and is able to replicate broad sediment change patterns known around O‘ahu. In the short-term (< 10 years), sediment transport from waves dominates contribution, whereas recession driven by sea level rise dominates in the long-term. The model’s ability to show long-term shoreline response independently from seasonal variability, sediment transport from one part of a beach cell to another part, and longer-term, more stable changes from rising sea levels is highly beneficial for areas such as the north shore of Oʻahu, shown in the case study of Paumalū Beach.

The forecast for Oʻahu is slightly more extreme in the CoSMoS-COAST model as compared to the Anderson et al.⁵ model, especially for west and north-facing shorelines, which are affected by winter swells. For areas that see significantly less erosion predicted by CoSMoS-COAST as compared to the Anderson et al., we conjecture that this is a product of the way that the long-term rate (LTR) is calculated for these areas. For the Anderson et al. model, only shorelines that were observed before any seawall hardening are used in calculating the long-term rate. These shorelines often interpolate to a negative LTR, indicating that the general trend for the area is recession, as if the seawalls were never built. In the CoSMoS-COAST implementation, LTR is assimilated using a different dataset, which includes many recent observations in which there are seawalls or other factors that constrain shoreline migration. Since seawalls do not move even when the beach retreats landward and is lost, the LTR rate calculated from these observations is much less extreme, as the model “thinks” that the shoreline is stable (adjacent to the seawall) and is not expected to retreat anymore. As the models forecast into the future, this LTR term’s contribution scales linearly, so CoSMoS-COAST is probably under—predicting erosion for this component. Future work could use more nuanced ways to account for sea walls or beach nourishments within the LTR component. You can see this in the result for the dark blue area directly south of Kailua in Fig. 8, in which the wide sandy beaches that existed before the 1970s have been lost to seawall construction, yet the median LTR for this area is + 0.02 m/year in CoSMoS-COAST, and − 0.06 m/year for Anderson et al.

As with all shoreline-change models, there are limitations that could be improved with future iterations, or could be addressed within our uncertainty and error calculations. Below, we briefly discuss each of these limitations and their implications for erosion hazard forecasting on equatorial island settings. First, uncertainty exists from the model-forcing methodology. This implementation of CoSMoS-COAST uses a temporally and spatially dense wave hindcast at a 50-m isobath contour around the island (between 200 and 4 km offshore). This 50-m isobath means that wave parameters likely do not account for transformation across reefs as waves impact beaches. Additionally, for lack of available forecasting data, instead of inputting a new wave forecast to 2100, we use this hindcast to assume future wave climate. We statistically pick values from the wave hindcast data as a forecast (see methods), and assume that a given month in the hindcast will correspond to the similar wave conditions in the future (following Davidson et al., 2017)⁵¹. In the north Pacific, studies have shown that there may be a slight decrease in projected median significant annual wave heights and a decrease in wave variability^52,53,54. Annual mean wave direction is projected to also change up to 10 degrees in the anticlockwise direction⁵². All studies point to an increase in wave height and period in the Southern Ocean and tropical eastern Pacific due to sea level pressure⁵⁵ and wind waves⁵². These forecasted changes are not directly accounted for in the wave forecast used here. A separate wave forecast, including a way to use an ensemble of potential wave climates is highly desired. We recognize that there is an intrinsic uncertainty due to unknown forcing conditions that is generally not irreducible, and therefore, even if we had a separate high resolution wave forecast, this would not eliminate the uncertainty entirely.

Secondly, it can be argued that the components of the CoSMoS-COAST model were not formulated for complex beach morphologies, specifically those with reefs in the nearshore. A very recent study found that reef-protected beaches experience 97% less erosion than unprotected beaches in response to storm events and that reef degradation and sea level rise are likely correlated with increased long-term erosion rates⁵⁶. The effect of reef channels on sediment exchange is unclear. Several studies criticize the validity of assuming a time-constant depth of closure for reef-fringed beaches^25,57, which this implementation uses (See Supplementary S.3). It has been long debated on whether the Bruun rule and its modified counterparts are appropriate for forecasting coastal change given the assumptions of a constant wave climate and reliance on often sparse or unknown active beach slope profiles (Supplementary S.1). We argue that in order to best compare this implementation of CoSMoS-COAST to previous modeling in Hawai’i, the use of the modified Bruun rule (using the D-A slope)³⁶ used in Anderson et al.⁵ is an appropriate first step. It will be worthwhile in future studies to model high-resolution wave attenuation and dynamic closure-depths, over specific reef environments to see if this improves results for beaches with complex nearshore morphology. Some recent studies reinterpret the Bruun rule’s role in the context of equilibrium shoreline models^58,59.

Lastly, the use of satellite-derived shorelines in this study introduces inherent uncertainties related to measuring the instantaneous waterline. Tidal fluctuations, wave setup, runup, and seasonal water-level variability cause changes in the waterline, while image misalignment, cloud, haze, and misclassification contribute to potential erroneous detection. Although Hawai‘i’s microtidal and steep beach environments typically minimize water level differences along the beach profile, the relatively low natural variability in shoreline position can result in lower signal-to-noise ratios for SDS measurements, complicating the detection of true shoreline change⁴². To address water level variability, tidal corrections were applied using a global tide model combined with a generalized foreshore slope. However, these corrections cannot fully account for the transient dynamics of the waterline, also influenced by waves setup and swash, and seasonal variability in water level^30,60,61,62. Wave set-up was also not accounted for due to lack of high-resolution wave data and the complex bathymetry, which lead to alongshore variations in wave run-up. Additionally, studies conducted in similar environments have shown minimal to no improvements when wave set-up is corrected for^63,64. Discrepancies among satellite sensors (PlanetScope, Sentinel-2, Landsat) in spatial resolution and georeferencing can further contribute to positional uncertainties that may be misinterpreted as genuine shoreline change. Past studies indicate minimal differences between shorelines derived from Landsat compared with shorelines derived from Sentinel-2⁴², while shorelines derived from PlanetScope generally produced shorelines with lower error⁶³. We observed different biases in shoreline position between the satellites and frameworks. Within the CoastSat framework, Sentinel-2 shorelines were on average 3.6 m further inland compared to Landsat-derived shorelines, although not statistically significant (p = 0.99, Mann–Whitney). CoastSat-derived shorelines were on average 4.2 m further inland compared to PlanetScope shorelines, derived with CoastVision (p << 0.01, Mann–Whitney). We removed the bias in shoreline position between CoastVision and CoastSat over an overlapping time period (2017–2022). For each transect, the standard deviation was on average 7.2, 8.9, and 8.1 m for PlanetScope, Sentinel-2, and Landsat, respectively. The absence of site-specific in situ shoreline measurements prevented localized vertical correction and error assessments (discussed in Methods), requiring us to rely on uncertainty values obtained from a single beach, Waikīkī, as representative of Oʻahu’s beaches. While the increased number of shoreline data points (278–1761 per transect) significantly improves data availability compared to traditional methods, these limitations must be considered when interpreting model outcomes.

We propose a few additions to the model that would improve it for tropical islands and their specific geologies. First, any image segmentation model used for shoreline detection should be calibrated to the island environment. Since island beaches are narrow (< 100 s of meters), beaches can be completely obscured by clouds, images can be too low resolution to detect significant change, or the shoreline detection framework can mistake small in-land water features for the sand/water interface. Limitations specific to remote atolls include: less image availability, georeferencing challenges that cause more extreme offsets between images, and differences in shoreline morphology that would warrant additional considerations for adapting CoSMoS-COAST to atolls in areas such as the southern Pacific or northwestern Hawaiian Islands. We plan to continue to constrain the machine-learning (ML) shoreline-detection algorithms to improve its detection accuracy in tropical islands with narrow, steep beaches through the continued collection and comparison of ground-truth survey data (e.g., from drones and GPS surveys). Additional ground-truth data would allow for site specific water-level corrections such as wave-set up corrections. Creating improved pixel classification models that more precisely identify wet sandy pixels versus white-washed water for Hawai‘i beaches would also be a helpful future addition. Although there are challenges in georeferencing, automation, and site-verification, we anticipate that satellite imagery and machine learning algorithms will allow a further expansion of study areas such as remote low-lying atolls, a more complete record of complex historic shoreline change, and timely forecasts of future scenarios⁶⁵.

Secondly, Hawai‘i’s dynamic geology lends itself to varying coastal environments, headland features, and submerged paleo-channels within a much smaller geographic area than is typical on continental coastlines. This not only makes satellite detection more difficult, but also means that typical continental beach sediment transport may not apply in the same way. For example, coastlines on active volcanoes can change within a matter of months because of recent lava flows⁶⁶. These can override sandy areas or change the way waves interact with nearshore features. Some island coastlines are tall alluvial or basaltic sea cliffs, with ephemeral coarse sand beaches. An important addition to the model would be to add a cliff recession component. Cliff erosion rate could be related to wave height⁶⁷, or could follow the probabilistic methodology outlined in the Department for Environment Food and Rural Affairs (DEFRA) Flood Management Division’s technical report on soft rock cliffs⁶⁸.

Lastly, a very pressing issue in Hawai‘i, is the presence of shoreline hardening such as sea walls, and how they affect surrounding sediment transport. It is known that sea walls exacerbate erosion in adjacent non-hardened beaches by flanking and contribute to complete beach loss^10,11. Adding a process that accounts for these occurrences would greatly improve the spatial forecasting for the eastern side of Oʻahu, as well as other highly developed and armored coastal neighborhoods in Hawai‘i. Previous projects have attempted to survey all seawalls and publicly accessible beaches around the state⁶⁹, but an update to this survey would be greatly beneficial to modeling high-resolution shoreline change on a property or neighborhood scale.

We anticipate that CoSMoS-COAST will serve as an update to modeling-based policies. The counties of Maui, Kaua‘i, and the City and County of Honolulu (Oʻahu) have set-back laws informed by previous erosion modeling rates. Specifically, the setback law for the City and County of Honolulu is “70 times the historical erosion rate plus 60 feet (18.28 m)”⁸. Where 70 represents the average lifetime of a wooden framed house in years, and the historical erosion rate is calculated based on a least-squares linear regression of the historical shoreline change for that place, not accounting for sea level rise. Coastal Setback Ordinance 23–3 and Special Management Area (SMA) Ordinance 23–4 have updated these requirements⁷⁰. Beginning on July 1, 2024, for lots within urban Honolulu, the shoreline setback line will be 60 feet from the certified shoreline⁷⁰. Lots outside of Urban Honolulu will be subject to a shoreline setback line ranging from 60 to 130 feet based on the annual coastal erosion rate associated with the lot. Kaua‘i County has a lot-based setback rule that takes effect when it is greater than the rate-based setback specified above⁷¹. Lastly, Maui County’s shoreline setback uses Anderson et al. (2018)’s coastal erosion forecast at 0.97 m (3.2 ft) of sea level rise^5,70. Anderson et al.’s r coastal erosion hazard forecast is displayed on the online atlas: Hawaiʻi Sea Level Rise Viewer⁷² using the upper-end projection of SLR from the 2013 Intergovernmental Panel on Climate Change (IPCC) Fifth Assessment Report of 0.97 m (3.2 ft) of global mean SLR by 2100⁷³. The viewer and its accompanying Hawaiʻi SLR Vulnerability and Adaptation Report^6,74 was mandated by Act 83, Session Laws of Hawaiʻi (SLH) 2014 and Act 32, SLH 2017^6,74. The report and viewer was last updated in 2022 with more current SLR projections, and has been an important resource for planners, developers, and legislators throughout the three counties⁷⁴.

Overall, these results provide an update to sea level rise information that may inform development and permitting policies in Hawai‘i. In terms of methodology, CoSMoS-COAST is efficient in providing new forecasting results as new satellite imagery is acquired with comparatively low computational power needed²⁹. The model incorporates previous drone and historical aerial imagery, while leveraging the quickly developing field of satellite imagery. Once configured for an area, updated results can be published rapidly. For some places in Hawai‘i, such as Moloka‘i and Hawai‘i islands, this would be the first presentation of coastal erosion forecasting. Implementing this model in places that have no previous erosion modeling both inside and out of the main Hawaiian islands is an important next step. The main Hawaiian islands are classified as high volcanic islands⁶⁰, the most common classification in the Pacific basin aside from coral islands, noted to have calcareous sandy beaches and fringing reefs protecting those beaches. This study shows that CoSMoS-COAST can investigate coastal erosion for tropical island settings, expanding its scope from continental beaches to island geology. Islands similar to Hawai‘i in geology around the Pacific, like the Galapagos, Marquesas, Solomon, and Fijian islands, could use this model to obtain coastal erosion rates for their local wave and SLR projections and be more empowered to develop sea level rise resilient policies.

Conclusion

We applied the data-assimilated CoSMoS-COAST shoreline change model to Oʻahu, marking its first use on an oceanic equatorial island with narrow beaches and a dynamic wave climate. This study integrates high-resolution shoreline data from satellite imagery, a Hawai‘i-specific wave climate hindcast, and regional sea level rise projections to inform long-term shoreline change projections. The model projects that 81% of O‘ahu’s sandy beach coastline could experience beach loss by 2100. Most of this beach recession will be seen within the next 10 years—where 39.8% of the coastline could recede greater than their current beach width by 2030. Compared to previous modeling approaches, incorporating dynamic processes—such as cross-shore equilibrium responses and alongshore sediment transport—reveals a 43.3% increase in net landward shoreline change for 0.3 m of sea level rise (2050).

Our findings emphasize the importance of dynamic, wave-driven processes in shaping short-term and long-term shoreline change, particularly on O‘ahu’s north and west shores, where seasonal wave variability is pronounced. While recession due to sea level rise and residual processes dominate long-term projections, wave-driven transport still accounts for 34% of total shoreline change by 2100. This study underscores the value of integrating high-resolution satellite imagery and dynamic shoreline processes into erosion models for other Pacific islands facing similar SLR-related coastal hazards.

Methods

This section details study site, error and performance metrics, and the methodology of the two models compared, including the inputs necessary for each model.

Study area

We focus on the island of O‘ahu, Hawai‘i, as a representative of equatorial oceanic islands with dynamic wave climates and large coastal communities. Oʻahu’s approximately 110 km of sandy beaches are mainly composed of calcareous sediments from microorganisms, coral fragments and shells⁷⁵. Beaches are often fringed by a carbonate reef platform composed of fossil Pleistocene reefs from interglacial high sea-level stands of the past several hundred thousand years^7,76. In many places on the island, beaches are simply the eroded edge of the sand-rich low-lying coastal plain⁷. They are often narrow⁷ and can range between reflective and dissipative seasonally. Oʻahu experiences a wave cycle in terms of four swell regimes: the north Pacific swell, northeast trade-wind waves, Kona storm waves, and southern swell⁷⁵. In the winter months (November–April), north Pacific swells dominate and can create annually recurring maximum significant wave heights of up to 7.7 m (25.3 feet)⁷⁷. In the summer months (May–October), southern swells and trade-wind waves increase. Several case studies of Hawaiian beaches found that sediment movement was predominantly controlled by alongshore transport⁷⁸, highlighting the importance of seasonal wave influence on island shoreline dynamics⁷⁹.

Shoreline change model comparison

This section explains the terminology used in this manuscript to compare the two shoreline change models (Fig. 1). The CoSMoS-COAST model is able to forecast a total shoreline position, $YY$, as the sum of four independent coastal processes or components, each of which is based on popular, individual shoreline change models. See Vitousek et al., 2023³⁰, and Methods section “Cosmos-coast shoreline model” for details.

The four independent model components are:

• 1. Shoreline change due to long-term residual processes, modeled as a linear term: LTR

• 2. Shoreline change due to SLR, also called Bruunian Change: BRU

• 3. Shoreline change due to short-term cross-shore wave-driven processes: STW

• 4. Shoreline change due to alongshore transport: ALST

The conceptual equation for CoSMoS-COAST is the sum of (time-varying) contributions from individual model components, which is simply:

$$YY = \overbrace {{\underbrace {LTR + SLR}_{{{\text{Anderson et}}\,{\text{al}}{., 2018}}} + STW + ALST}}^{{\text{CosMoS - COAST}}}$$

(1)

in which any of these terms can be negative to indicate recession landward (erosion), or positive to indicate advancement seaward (accretion), or zero for no change from a 2022 baseline. In a few isolated locations, specific geologic morphology or sediment composition warrant omitting certain processes from the full model suite³⁰. For example, mixed sediment beaches (or with cobble-grain size) include only LTR and BRU processes; where the processes driven by waves are omitted, since higher mass and size grains are less susceptible to shoreline change than sand⁸⁰. Small, highly-embayed “pocket” beaches include only BRU, LST, and STW. These pocket beaches may have a wave climate within the embayment that refracts in complex ways due to embayed beaches’ restricted, small, and concave geometries. Therefore, we assume these sites do not follow the one-line model assumption of along-shore profile uniformity and unlimited sand, and the ALST term is omitted. Models such as COVE⁸¹ use a local coordinate system to address cells with complex geometries, in which an implementation of this into future CoSMoS-COAST models may allow pocket beaches to include an alongshore transport term.

Historically, the majority of Hawai‘i’s shoreline regulations (e.g., setbacks) used results based on either a simple linear long-term erosion rate⁷, or a long-term erosion rate plus recession due to sea level rise from Anderson et al.⁵. The Anderson et al. model contains the most comprehensive analysis of coastal erosion for Hawai‘i thus far⁵. It combines the long-term historical shoreline change rates derived from historical air photos⁷ and, a geometric Bruunnian recession-type model from Davidson-Arnott³⁶ to adjust for future SLR, representing the first two terms in Eq. (1). In Fig. 1, $r$, is the rate given by the historical shorelines, average nearshore slope, tan(β), is estimated from profile surveys⁸², S(t_f)–S_hist(t_f) is the difference between predicted sea level and extrapolated historical sea level at future time ${t}_{f}$.

The Anderson et al. model does not explicitly account for short-term (< 10 years) shoreline changes from wave climate, storms, or alongshore transport (i.e., the last two terms in Eq. 1), but it served as an inspiration for CoSMoS-COAST in how to combine shoreline-change components that had previously been treated separately. It assumes constant sediment transport rates, with any time-varying wave-driven transport assumed to exist within modeled error, despite evidence that some Oʻahu beaches respond strongly to seasonal changes^40,79,83, and that some beaches have been observed to be driven by alongshore transport⁷⁸. Another key assumption in this model is that sand along one model transect does not interact with adjacent transects. For this study, the Anderson et al. model was reconfigured with the intermediate SLR scenario from the 2022 U.S. Sea Level Rise and Coastal Flood Hazard Scenarios and Tools Interagency Task Force Report^1,33, and baseline shoreline was changed to a vegetation line from 2022 that aligns with the CoSMoS-COAST baseline. The governing equation from Anderson et al. remains the same.

There are several differences between the two model approaches: (1) Historical shoreline data for Anderson et al.⁵ is derived from ~ 100 years of aerial imagery, approximately one data point per decade. CoSMoS-COAST relies on satellite-derived shoreline observations, providing a shorter time span (~ 1990-present) but a significant increase in available data points (~ 100 s of data points per transect). (2) These two additions improve shoreline response patterns for areas dominated by alongshore sediment transport⁷⁸ and with strong seasonal variability in wave climate. (3) CoSMoS-COAST is forced with a time series of parametric wave conditions from Li et al.³⁴, while Anderson et al. does not take this input, but accounts for variability due to waves through its uncertainty and error calculations (Fig. 8).

Both models are forced with the same SLR projection from Sweet et al.³³ and give a probabilistic position of the shoreline at a specified amount of SLR. Depending on the end user’s preference, the shoreline position can be reported to a certain probability; for example, the 75th percentile, meaning that anything seaward of this line has a 75% chance of being affected by erosion. In this case, we report either the 50-th or 80-th percentile shoreline position. Note that Anderson et al. smooths shoreline outputs across transects within the same littoral cells, but transects do not generally interact aside from that. CoSMoS-COAST transects are assimilated and localized across the entire littoral cell.

CoSMoS-COAST shoreline model

For the most updated information about the CoSMoS-COAST model as applied to the coast of California, see Vitousek et al.^30,32. Below we provide a more detailed overview of the model methodology and state any differences between our implementation and Vitousek et al. (2023)³⁰.

CoSMoS-COAST is a data-assimilated one-line shoreline change model forced with wave and SLR inputs, and assimilated with any local vectorized shoreline observations, such as survey, aerial, and ML-detected satellite imagery. The model first starts with an initial shoreline position, usually taken from one of the observations, as well as approximate parameters that form a state vector for each transect across a beach/littoral cell. Those parameters are sequentially attuned to fit the observations, using a 200-member Kalman Filter ensemble (EnKF)⁸⁴. A localization filter is applied so that transects within the same littoral cell will be calibrated to all local observations at a given time. With enough (~ monthly observations or more) data, the model parameters will generally converge to an appropriate value before forecasting. During forecasting, the model statistically outputs the shoreline position, defined as the start of the subaerial beach, at each transect given the following governing equation, which was initially developed in Vitousek²⁸:

$$\begin{aligned} \frac{{\partial Y}}{{\partial t}} & = \underbrace {{ - \frac{1}{{d_{c} }}\frac{{\partial Q}}{{\partial X}}}}_{{[1]{\text{longshore}}\,{\text{transport}}}}\underbrace {{ - \frac{c}{{\tan \beta }}\frac{{\partial S}}{{\partial t}}}}_{{[2]{\text{shoreline}}\,{\text{migrationdue}}\,{\text{to}}\,{\text{SLR}}}}\underbrace {{ + \upsilon _{{lt}} }}_{{[3]{\text{long}} - {\text{term}}\,{\text{residual}}\,{\text{shoreline}}\,{\text{trend}}}} \\ & \underbrace {{ + \frac{1}{\tau }(Y_{{eq}} - Y)}}_{{[4]{\text{cross}} - {\text{shore}} '{\text{equilibrium}}'\,{\text{transport}}}}\underbrace {{ + \varepsilon }}_{{[5]{\text{additive}}\,{\text{noise}}}} \\ \end{aligned}$$

(2)

Equation 2: CoSMoS-COAST Governing Equation, where $Y$ is the total shoreline position along a given cross-shore transect, $t$ is time, where the time-step is one day. Y_eq, υ_lt, Q, c, τ variables represent driving functions and parameters assimilated in the model. d_c and β are user-defined values representing the depth of closure (10 m, see Supplementary S.1 and S.3), and the slope angle (varies by transect), respectively.

This equation is described in Vitousek³⁰, and encompasses several process models including: (1) a “one-line” model for longshore transport³⁵ (ALST); (2) a cross-shore beach profile change model due to SLR^36,44,45,46 (BRU); (3) a long-term residual shoreline trend v_lt that represents long-term processes like sources and sinks of sediment (LTR); (4) a modified wave-driven cross-shore equilibrium shoreline change model^31,47 (STW); and⁵ a noise term, ϵ that represents random, short-term, unresolved processes that cause fluctuations in shoreline position with zero mean and user-prescribed standard deviation $\sigma$ (in this case, 0.01 m). This noise term addresses the epistemic uncertainty of the model parameters. It also includes an ensemble Kalman filter (EnKF) data-assimilation method based on “littoral cells” that adjusts the model parameters to best match local observations at each time step where data is available. For our study, sandy, carbonate beaches are best represented by the “Full-Model” regime, and so the majority of our model grid uses all 5 terms in Eq. 1.

In Vitousek et al., the 50th percentile (median) is used as the forecasted shoreline position of the beach toe. Performance is evaluated by comparing model output to known satellite and survey observations within a four-year validation period, 2019 to 2023. In this study, we present the 50th-percentile (median) forecasted shoreline from the vegetation line for Results Sections “Paumalū Beach (north O‘ahu) case study” and “Island-wide modeling using CoSMoS-COAST”. For Results Section “Shoreline change model comparison”, we present the 80th percentile, as in previous coastal erosion studies for Hawaiʻi⁶. As noted in the results, the CoSMoS-COAST modeled shoreline can vary by up to 20 m depending on the season, and so all forecasted shoreline positions in the publication are reported for the month of July (summer).

We briefly describe the methodologies of the “dynamic” sediment transport terms, STW and ALST, and how they address complex beach morphologies. The STW term follows a modified methodology of Yates et al.⁴⁷, that simulates episodic beach erosion and recovery with respect to wave energy. If the shoreline change rate coefficient, $C$, and the calibration parameters $a$ and $b$, are constant, in relation to shoreline change in the short-term, ${Y}_{st}$, one can assert that changes in wave climate will result in changes in shoreline position^47,85. In Eq. 2, ${Y}_{eq}$ is equilibrium shoreline position; τ is the background equilibrium time scale parameter, proportionally related to background wave height³¹.

The ALST term is a one-line model that simulates the evolution of longshore sediment transport across a littoral cell⁸⁶. In Eq. 2, $Q$ is the longshore sediment-transport rate, $X$ represents the alongshore coordinate, and ${d}_{c}$ is the depth of closure. This component is greatly influenced by wave angle, but does not account for high-wave angle instability or the appearance of local sediment features. For highly-embayed beaches, the assumptions of the one-line model that sediment travels linearly alongshore is not accurate. We also recognize that the ALST term does not explicitly account for headland bypassing or interactions with reef morphology. However, such processes and their influence on the shoreline position may appear with the assimilated residual trend term ${v}_{lt}$.

Transect system & littoral cells

We use a 20-m spaced transect grid that is approximately orthogonal to the shoreline and encompasses the whole island of Oʻahu, excluding Pearl Harbor. This region was omitted given the large amount of anthropomorphic modifications and the lack of wave climate hindcasting within the harbor. Permanent river mouths and small harbor openings with large changes in coastline aspect are also omitted. Transects are classified into “littoral cells”, which we define as consecutive regions of coastline that generally share sediment, geology type, and/or experience a similar wave climate. Littoral cells are often separated by rocky headlands or hard structures that are classified as “no prediction”. Each littoral cell is then assigned a model regime (full model; cross-shore only (excludes¹ in Eq. 2); or “rate-only” (excludes¹ and⁴ in Eq. 2). Sandy beaches are considered “Full Model” (51%). Embayed Pocket beaches with clearly defined headlands that are approximately less than 1 km in length are considered “cross-shore only” (2%), and along-shore transport (ALST) is considered negligible. Mixed, non-sandy, or large sediment beaches are considered “rate only” (6%); and all other shorelines, including rocky volcanic, mangrove, and historic fishpond structures, are considered “no prediction” (41%). For our study, sandy, carbonate beaches are best represented by the “Full-Model” regime, and so the majority of our model grid uses all 5 terms in Eq. 2. All transects and their specific model designations have their own defined modeled parameters and variables, except variable “longshore transport rate” $Q$, which is defined at the mid-point between transects. Areas historically known as sandy beaches but have been armored with seawalls are designated “full model”, to show the potential for erosion if/when these hard structures fail. This is in line with previous erosion modeling in Hawaiʻi.

Preliminary investigations show that littoral cell size does not affect the forecasted shoreline position, but, littoral cell boundaries can show artificial and abrupt changes in the forecasted shoreline at the cell boundaries due to alongshore transport, in which $Q = 0$ at cell boundaries. If an area can share sand at any time throughout the year, those transects are designated within the same littoral cell. This can create cells up to ~ 300 transects long (~ 6000 m in length). Boundaries were kept in places with clear alongshore sediment disruption, such as headlands, large changes in shoreline angle, and stretches of man-made sea walls. Model results can also be affected by the transect angle; if the transect angles are normal to the predicted wave angle, the long-shore transport term may be overestimated. Although Kāneʻohe Bay in East Oʻahu has transects, due to its lack of wave information sufficiently close to shore, and nearly no sandy beaches, most cells in that region are classified as “no prediction”. Although not modeled everywhere, this is the first implementation of a full transect grid around Oʻahu with preliminary classifications based on geology and anecdotal beach behavior. This grid may be useful for other studies adjacent to shoreline change, that require a classification of the Oʻahu coastline.

Anderson et al.⁵, also uses a 20 m spaced transect system, but only spans sandy beaches, and have different transect angles that are less variable. Although not explicitly called littoral cells, Anderson et al. also categorize transects into regions that share historical aerial or drone imagery. Alongshore smoothing is applied within each cell for a coherent forecasted shoreline. For sake of comparison in Results 2.3, we calculate the distance of Anderson et al.’s shoreline vectors when projected onto CoSMoS-COAST transects.

Model performance metrics

Below are brief descriptions of model performance metrics. Root-mean-square error (RMSE) is given by:

$$\varepsilon_{{{\text{RMSE}}}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {((Y_{{{\text{obs}}}} )_{i} - (Y_{\bmod } )_{i} )^{2} } }$$

(3)

where ${Y}_{mod}$ and ${Y}_{obs}$ are the modeled and observed shoreline positions, respectively, for $N$ observation points. RMSE is sensitive to the scale of the data, meaning it will be larger for datasets with higher variability or magnitudes. Observed and modeled $Y$ values in our case are within the ~ 10-m magnitude range.

The index of agreement⁴¹, d, which is given by:

$$d = 1 - \frac{{\sum\nolimits_{i = 1}^{N} {((Y_{\bmod } )_{i} - (Y_{{{\text{obs}}}} )_{i} )^{2} } }}{{\sum\nolimits_{i = 1}^{N} {\left( {\left| {(Y_{\bmod } )_{i} - \overline{Y}_{{{\text{obs}}}} } \right| + \left| {(Y_{{{\text{obs}}}} )_{i} - \overline{Y}_{{{\text{obs}}}} } \right|} \right)^{2} } }}$$

(4)

where the overbar indicates the mean. The index of agreement ranges from 0 to 1, with values close to zero (one) indicating poor (good) performance. The best performing shoreline models in a blind-test competition¹⁶ reported a d =  ~ 0.5–0.7. The index of agreement is sensitive to the magnitude of errors and penalizes under and overestimations. It can detect additive and proportional differences in the observed and modeled means and variances. However, it is also overly sensitive to extreme values due to the squared differences.

The final model performance metric simply reports the percentage of modeled shoreline positions that fall within the satellite confidence intervals, named here and in Vitousek et al.²⁸ as “Within C.I”. We validate the model over a 3-year time period (2020–2023) with nearly daily observations, and calculate the percentage of time that the modeled shoreline position is within the confidence intervals of the satellite observations, that is, if ${Y}_{mod}$ falls within ± 10 m of ${Y}_{obs}$. High percentage means that the model was often predicting reasonable, realistic values within observational range.

Model inputs

Waves forcing input

Waves dominate shoreline response and uncertainty at short time scales⁸⁷. For the north shore of Oʻahu near Paumalū Beach specifically, it has been shown that the direction of alongshore transport of sediment is controlled by the seasonal wave direction and the tradewinds⁸⁸. Therefore, a comprehensive wave climate input is needed to access cross-shore and alongshore transport accurately.

The main Hawaiian islands have four primary wave climate regimes: The north Pacific swell, northeast trade wind waves, southwestern Kona storm waves, and southern swells; in which the maximum significant wave height annually is 7.7 ± 0.28 m from the north Pacific Swell^75,77. Tides on Oʻahu are macrotidal (tide range ≤ 1 m)⁷. Given this complex wave climate, we use a high-resolution 30-year hindcast time series (1979–2021)³⁴ developed using a nested WaveWatchIII and unstructured SWAN (Simulating WAves Nearshore) models for all of the Hawaiian islands, with a resolution of 100 m at the coastlines and 300 m at 30 km offshore⁸⁹. We obtained significant wave height (Hs), peak period (Tp), and peak direction (Dp) from the 50 m isobath contour of the hindcast database at 3-h intervals. For every 10th model transect (~ 200–300 m intervals, at a distance of 200 m offshore) we chose the nearest 50 m isobath grid point and its time series was used for that group of ten transects. These data were then downsampled to obtain daily median significant wave height, daily median period, and daily median directions. We decided to downsample to daily values in order to decrease processing time and match the model time-step of one day. As shown in Fig. 9, the largest wave heights come from the northeastern Pacific.

Fig. 9

A wave rose showing percentage of mean significant wave height ranges and wave origin direction in degrees, for the model hindcast period from Li et al.³⁴, from the 50-m isobath contour around O ‘ahu for all model transects. Figure created in Matlab (R2023b).

To project future wave conditions beyond the available hindcast data (January 2021 and onwards), we statistically shuffle the hindcast years. This methodology assigns every forecasted month a wave parameter from the same month from a random hindcast wave year. For example, the first month (January 1–31, 2022) of the forecast will use data from a uniformly distributed random selection in the hindcast, e.g.: January 1–31, 2005.

Sea level rise projections

Sea level rise (SLR) is an important factor in shoreline change in Hawai‘i⁹⁰. This study uses local SLR projections from the 2022 U.S. Sea Level Rise Interagency Task Force Report Scenarios³³, focusing on the Intermediate scenario (3.9 ft; 1.2 m by 2100) since current SLR rates exceed the Low and Intermediate-Low scenarios⁹¹. The projections are based on the Honolulu tide gauge, adjusted by 0.04 m to match the mean sea level for the median tidal epoch in Honolulu, with a baseline year of 1992^1,33. These projections are interpolated annually from 1992 to 2150 using a Piecewise Cubic Hermite Interpolating Polynomial (pchip)^92,93 and applied to all modeled regions on Oʻahu (Fig. 10). Although the original Anderson et al.⁵ results were based on an upper-end projection in the 2013 Intergovernmental Panel on Climate Change (IPCC) Fifth Assessment Report⁷³ of 3.2 feet of global mean sea level rise by 2100; it was implemented again with the same sea level rise scenarios for the purposes of comparison within this manuscript.

Fig. 10

Blue line represents the “Permanent Service for Mean Sea Level” (PSMSL) tidal observations³³. Shaded areas of increasing opacity show the approximate timing of 1-foot increments (1–7 ft) of relative SLR for the Honolulu tide gauge. Yellow circles represent the values provided by the 2022 U.S. Sea Level Rise Interagency Task Force Report³³ between 1992 and 2150, and the dark orange represents the interpolation between those points. Points for 2050, 2100, and 2150 are marked in blue, and their relative SLR values are listed above. Figure created in Matlab (R2023b).

Satellite imagery observations

We use satellite imagery from Landsat, Sentinel-2, and PlanetScope to obtain 30 + years of shoreline positions for each littoral cell on O‘ahu. Below, we outline two methods for obtaining satellite-derived waterlines (SDW), and subsequent water-level corrections to convert them into Satellite-Derived Shorelines (SDS) used in CoSMoS-COAST data assimilation. This study includes the use of PlanetScope imagery (3 m resolution with near-daily revisit time) in addition to open-source satellite archives from Landsat and Sentinel-2 missions.

CoastSat

Following Vitousek et al.³⁰, the open source toolkit CoastSat is used to obtain shoreline positions from satellite imagery⁹⁴. CoastSat was developed to work with Landsat 5, 7, 8, and 9 and Sentinel-2 imagery. CoastSat downloads and processes imagery for any coastal region of interest. Shorelines are automatically detected using the following steps: (1) Each image pixel is classified into one of four classes (water, white-wash, land, or sand) using a pixel classification model, (2) the Modified Normalized Difference Water Index (MNDWI) feature is calculated for every pixel. This feature is effective at separating open water and land, with values close to 1 signifying water, and values between − 1 and 0 signifying non-water. (3) A threshold value on the MNDWI is determined by Otsu thresholding⁹⁵, which maximizes intra-class variability of ‘sand’ and ‘water’. (4) The marching squares algorithm is applied to achieve a sub-pixel shoreline contour along the pixels with the determined MNDWI threshold value. This shoreline represents the instantaneous land–water interface. Once the shorelines are contoured, they are intersected with the model transect grid and applied to the Kalman filter with an assumed confidence interval of ± 10 m. This application uses Landsat Collection 2 imagery and CoastSat version 2.2⁹⁴.

To improve shoreline detections in this study, a new pixel classification model for CoastSat was trained on 121,932 pixels from 58 images of eight different sites across O ‘ahu with a variety of light and ocean conditions. We used the same multilayer perceptron (neural network classifier) model architecture as provided in the default classification model in CoastSat. Additionally, a reference shoreline was drawn for each littoral cell representing a general shoreline position, and a buffer of approximately 80 m was applied to ignore any shorelines that were falsely detected outside of this buffer. For some small embayments or shorelines with rapid changes in aspect, we found that the integrated intersect function in CoastSat sometimes created erroneous intersections, such as reaching across the bay or smoothing over rugged areas. For these sites, shoreline positions were determined by directly intersecting the shoreline vector with each transect, rather than using an alongshore median over a fixed distance (typically 50 m) as in the CoastSat intersection function, which smooths localized water level variations in the swash zone. Following the CoastSat 2.2. workflow, Landsat and Sentinel-2 images were not co-registered.

CoastVision

The additional use of PlanetScope satellite imagery and processing it via the CoastVision framework⁹⁶. (https://github.com/Coastal-Research-Collaborative/CoastVision) is one of the most notable differences between our methodology and Vitousek et al.³⁰. Some beaches in Hawaiʻi are smaller than the original pixel size of Landsat (30 m) and Sentinel-2 (10 m) images. To increase accuracy, in addition to using CoastSat, we developed a methodology to detect shoreline positions from PlanetScope imagery. It should be noted that an extension of CoastSat was developed specifically to process PlanetScope imagery⁶³ after this project started, called CoastSat.PlanetScope. The primary difference between this and CoastVision (developed here), is that CoastSat.PlanetScope uses a threshold on a water index (NIR-Blue); while CoastVision contours the shoreline directly on the classified image. We found that direct contouring was more effective for Hawai‘i’s beaches, while using a threshold on PlanetScope’s “NIR minus Blue” band sometimes produced errors around reefs, headlands, and wet sand.

The PlanetScope satellite constellation, operated by Planet Inc., comprises over 180 cube satellites that possess the capacity to image the entire land surface of Earth on a near daily basis since 2014⁹⁷. These images have an average resolution of 3.7 m at nadir, which is resampled to a finer-resolution of 3 m and includes red, green, blue, and near-infrared bands⁹⁷. Positional accuracy is reported to be below 10 m RMSE and verified to be between 3.4 and 5.2 RMSE by independent studies^98,99. To remove image offset and improve georeferencing between all images, we use Arosics¹⁰⁰ to co-register each image to a selected reference image for each littoral cell. A logistic regression was trained to classify pixels based on 18 features into two classes; water and land. The model was trained on 1.2 million pixels from 23 PlanetScope images of 10 Hawaiian beaches. To refine the binary land/water image, a series of morphological operations were applied. Binary erosion and dilation were used to smooth land water interfaces and small patches of water and land were removed. With the improved resolution of the imagery, we directly contour the shoreline between the water and land pixel classes using the marching square algorithm without relying on water indices such as the MNWDI. With the addition of CoastVision, we doubled the available assimilated data for all littoral cells around Oʻahu. On average, each litoral cell had 354 shorelines derived from Landsat & Sentinel, and 693 shorelines derived from PlanetScope.

Satellite observation corrections & uncertainty

Many factors influence the instantaneous waterline derived from satellite imagery, including water level variability from tides, wave set-up and run-up, and errors from e.g., image offset, image mis-classification, haze, and clouds. Below, we describe how we account for these variabilities and remaining uncertainties.

After obtaining the the instantaneous waterlines (or the SDW), we translate them into Satellite-Derived Shorelines (SDS); a datum based shoreline at the Local Mean Sea Level (LMSL) for the Honolulu Tide Gauge (PSMSL ID: 155)¹⁰¹. This is achieved by correcting for water level variability caused by tides. Tidal elevations at the time of each image are recorded using the Finite Element Solution (FES) 2014 global tide model¹⁰² from the nearest offshore grid, approximately 1 mile offshore. By approximating a beach slope, as described in detail below, the vertical difference in water level is translated to a horizontal correction, as ${x}_{corrected} = x - \frac{\Delta z }{\beta }$, where $x$ is the shoreline position along each transect from the on-shore point, $\Delta z$ is the difference in water level between the time of image and a standard datum (here LMSL), and $\beta$ is the foreshore slope. Tidal corrections reduce error in SDS when compared to ground-truth^42,61,62,63. We did not perform wave set-up correction as it primarily shifts the shoreline bias seaward, and has been shown to make little difference to overall accuracy in similar environments^63,66. Secondly, to account for the differences in methodology between CoastSat and CoastVision, we ensure their biases are aligned by adjusting the PlanetScope-derived shorelines to match the bias observed in CoastSat-derived shorelines over an overlapping period from 2017 to 2023. On average PlanetScope shorelines were 4.2 m more seaward compared with CoastSat-derived shorelines. These biases arise from differences in methodology between CoastSat and CoastVision, the satellite sensors, and difference in annotated training data used to train pixel segmentation models for each framework. Third, to reduce outliers in satellite imagery caused by factors like clouds, shallow reefs, or inland water bodies, we excluded observation points outside the median ± 40 m for each transect. This threshold was empirically determined based on shoreline variability around O‘ahu. Additionally, all shoreline vectors were overlaid on satellite imagery for each littoral cell and manually inspected for outliers, particularly near headlands, small embayments, and shallow reefs. If necessary, the littoral cell was reprocessed using a different classification model and intersection function to improve accuracy.

The foreshore slope for tidal corrections was obtained from a series of repeat surveys between 1994 and 1999 at 35 transects around O‘ahu⁸². The foreshore slope was generalized using an average slope across all repeat surveys for each side of the island (n = 20 surveys for each side). For each GPS survey, we calculated the linear slope from the berm crest, wet-dry line, or the high swash line to the beach toe or the step crest. The specific points used were dependent on which features were recorded during each survey. A constant slope was used for tidal corrections regardless of time of year, and average foreshore slopes are presented in Figure S2.1. Theoretically, a site and season specific slope should be used to translate instantaneous waterlines to datum based shorelines. We recognize that generalized slopes may under- or overestimate shoreline translations, particularly in seasonally fluctuating coastlines, however not all modeled sites on O‘ahu had surveyed slopes, and given that Oʻahu’s wave climate is aspect dependent, we group beach slopes by side of the island. Previous studies investigating the sensitivity of foreshore slope variability for water-level corrections found no significant improvement when using time-variant slopes compared to time-averaged slopes as used here^61,63,103. Water-level corrections improve the overall accuracy of SDS, however slope and water level data are highly variable, and uncertainty remains in SDS despite corrections.

To investigate SDS uncertainty specific to Hawai‘i, we evaluate cross-shore positions between SDS and in-situ shoreline observations obtained from a single beach in Waikīkī. Unfortunately no other consistent ground truth data exist that overlap with our satellite-derived shorelines. Therefore SDS uncertainty estimation relies on comparison with 128 in situ surveys for Waikīkī beach. These surveys were conducted using small Uncrewed Aerial Systems (sUAS) and Total station surveys over 3.5 years (2018–2021)¹⁰⁴. Each survey produced near-weekly 0.5 m resolution DEMs. The mean sea level contours from these surveys were compared to satellite-derived shorelines along the same transect grids, using the framework of Vos et al.⁴². RMSE of SDS ranged from 4.2 m (PlanetScope) to 7.8 m (Sentinel-2) when applying tidal correction to shorelines. Past studies found RMSE values for Landsat/Sentinel-2 ranging from 24.8 m in Truc Vert, France, to 8.1 m in Duck Beach, United States⁴². Specifically, for sites in microtidal environments our uncertainty values resemble those from Duck Beach, United States, and Narrabeen, Australia (8.1–10.6 m). For PlanetScope, CoastSat.PlanetScope obtained RMSE values of 3.5–5.1 m for these same beaches⁶³.