Fractal and chaotic map-enhanced grey wolf optimization for robust fire detection in deep convolutional neural networks

Abstract

This paper introduces a novel approach to enhancing the architecture of deep convolutional neural networks, addressing issues of self-design. The proposed strategy leverages the grey wolf optimizer and the multi-scale fractal chaotic map search scheme as fundamental components to enhance exploration and exploitation, thereby improving the classification task. Several experiments validate the method, demonstrating an impressive 87.37% accuracy across 95 random trials, outperforming 23 state-of-the-art classifiers in the study’s nine datasets. This work underscores the potential of chaotic/fractal and bio-inspired paradigms in advancing neural architecture.

Introduction

Image classification is crucial in various technological applications, such as POI recommendation¹, data fusion^2,3, X-ray detection⁴, and system identification⁵. The abundance of image data necessitates robust computational methods for classification^6,7,8,9. Recently, various deep learning models, including dual attention residual network¹⁰, VarifocalNet¹¹, FreqGAN¹², TASTA¹³, TalkingStyle¹⁴ have been proposed. The ability to learn multiple levels of features from the input images has propelled deep convolutional neural networks (DCNNs) to the forefront of model development^15,16,17.

These networks have firmly established themselves as the current reigning champions^18,19. Constructing an appropriate DCNN is a complex task, requiring significant effort in carefully planning and fine-tuning the network architecture to suit the specific problem^20,21. This complexity underscores the need for innovative solutions in the field^22,23,24.

People have attempted to automate the construction of DCNNs using algorithms that mimic biological evolutions, thereby eliminating the time-consuming process of selecting appropriate layers, neurons, and hyperparameters^25,26,27.

Due to its efficiency in modeling neural networks, the grey wolf optimizer (GWO) has gained widespread use as a bio-inspired optimization algorithm²⁸. It has a hierarchal fighting and hunting system similar to gray wolves. Despite its notable performance, a traditional GWO algorithm can face two difficulties: early convergence and suboptimal exploration-exploitation swaps. Such problems become even more critical in high- and multidimensional search space scenarios, such as those experienced while optimizing DCNNs²⁹.

This study proposes a new approach that embeds the GWO within the chaotic maps and the multi-scale search based on the fractal to achieve this goal. To achieve this goal, the authors propose a method they refer to as Chaotic Map and Fractal-Enhanced GWO (CF-GWO) to automatically synthesize appropriate DCNN architectures for picture classification applications. The study incorporated chaotic maps to enhance the GWO algorithm’s exploratory ability. This action would make the algorithm better suited for traversing the search space and help the algorithm avoid some of the local optima. On the same note, it is believed that using a fractal-based search leads to enhanced exploration since it allows for flexibility in manipulating search resolution to unveil concealed optimum solutions.

In addition to the novel coding technique, this work introduces the ‘Enfeebled Layer approach’ to enable architectures of different lengths. This approach enhances the efficiency and adaptability of DCNN’s architectural design as it explores its potential. Furthermore, the study delves into a novel learning approach known as the chaotic learning approach. One of the considerations implemented in this approach to improve the stability and effectiveness of the learning process is subdividing the vast data sets into smaller, easier-to-handle ones.

Identifying the efficiency of predicted CF-GWO in strong DCNN structures that self-develop is, therefore, the main aim of this research. We propose the following test to pursue this strategy: it will be evaluated on the multiple benchmark picture classification datasets, and our results will be analyzed against those obtained using other algorithms. The secondary research question of this study seeks to establish if the application of chaotic maps and fractal theory facilitates bio-inspired optimization in the selection of neural network architecture. The objective of this study is twofold: firstly, to provide a comprehensive approach to automated machine learning, and secondly, to enhance the comprehension and application of chaos theory and fractals in the optimization field.

The subsequent section outlines the structure of the paper. “Related works” provides an overview of the existing literature and examines the merits and drawbacks of previous studies. “Background information” provides a comprehensive overview of the background information of the DCNN and IP address. “The suggested framework” then provides a detailed account of the suggested approach. “Experimentation and discussion” analyzes the simulation and the context of this discussion in the real world after the simulation. “Conclusion” is the closing section, which rounds off the research.

Related works

The continuous efforts to create practical approaches for image classification have led to optimizing the DCNNs. In the provided literature review is remarkably rich in a variety of techniques focusing on different optimization methods and their modifications³⁰.

Recently, there have been insufficient attempts to utilize evolutionary and metaheuristic techniques to optimize the DCNN architecture. Reference³¹ proposed the sosCNN, which implements the symbiotic organisms search (SOS) algorithm at an architectural level for CNNs. SOS was first created for automated searches of appropriate CNN architectures. The advantage of SOS is its ability to optimize globally. As a result of enhanced feature extraction performance, a new ingenious complex coding update strategy was introduced that reduces the loss within convolutional layers. The SOS method was ultimately merged with three novel non-numeric computational procedures: binary segmentation, slack gain, and different mutations.

According to reference³², NAS methods can be an alternative to the discussed DNL approach. That is why the evolutionary NAS methods have been successful, as evolutionary algorithms can search globally. All the current evolutionary algorithms employ the mutation operator to produce new designs of the offspring only. The failure to pass modular information from one generation to the following leads to design variations of offspring from the parent designs, slowing down convergence. In addressing this problem, the authors proposed an efficient evolutionary procedure that utilizes a specifically developed crossover function to attain child designs from the parent architectures. The evolutionary algorithm also employs it with the mutation operators, or as the material sometimes refers to it, mutation functions.

In reference³, multi-level particle swarm optimization (MPSO) is proposed to identify the CNN’s architecture and hyperparameters simultaneously. In this regard, two swarms are used in the suggested solution. Swarm optimization begins with the original swarm at level 1 and progresses to many swarms at level 2 for hyperparameter optimization.

The suggested method incorporates a sigmoid-like inertial weight to modulate particles’ exploratory and exploitative characteristics, thereby mitigating premature convergence towards local optima in the PSO.

Nevertheless, keeping in mind the advantages of several metaheuristics, the No Free Lunch (NFL) theorem³³ holds, according to which no method can address all the optimization problems. Thus, researchers have attempted to address many optimization issues by developing new metaheuristics, enhancing existing ones, and combining them. To tackle the problem of the autonomous evolution of DCNN design without human intervention, the utilization of GWO³⁴ has been implemented as a response to this hypothesis.

Indeed, population-based algorithms are chosen because their operators are less complex than those of evolution-based algorithms. On the other hand, among the population-based algorithms, the GWO algorithm is selected for two reasons: The parameters of this algorithm are less sensitive than benchmark algorithms such as PSO³⁵. Also, as shown in references^{36,37,38,39,40,41,42}, GWO performs much better than state-of-the-art algorithms in applications where the global minimum is near zero. Since various deep architectures show maximum efficiency for particular tasks, this work introduces a new adaptable encoding method to eliminate the drawbacks of fixed-length encodings.

To efficiently move within least-cost paths that traverse the multi-dimensional spaces present in neural architecture optimization, GWO’s exploration-exploitation strategy has been incorporated⁴³. Nevertheless, problems in early convergence and suboptimal search within a broad space have been the most significant challenges regarding the application of GWO in DCNNs. Despite numerous versions of GWO that incorporate varying quantities of randomness and other heuristics, none have readily available, complete, and efficient ways for fully embedding systematic explorative and exploitative features into GWO.

The global optimization of GWO has been applied to chaotic maps. By optimizing using the chaotic map, it will be possible to overcome the problem of local optima and, in some cases, premature convergence. Several chaotic map types have been proposed in the literature, including logistic and sinusoidal maps, which present different dynamic behaviors and produce different results when applied to the search. However, research works are limited to improving the DCNNs’ capabilities by systematically integrating the chaotic maps into the GWO algorithm. The only unexplored area that could be extended further in the future and bring new ideas into circulation is the application of the concept of chaos.

The optimization algorithms in question integrate fractal theory, allowing them to search at various resolutions. Some optimization algorithms invariant to scale have utilized fractal geometries for multi-scale analysis. This provides the ability to obtain the best solutions compared to a single set resolution. Still, more work is needed concerning the possible application of this algorithm in the optimization of GWO structures of DCNN. This task presents a somewhat optimistic prospect of research and development.

Many optimization approaches offer the best encoding and representation of the DCNN designs. These, of course, include binary/integer encodings, but more advanced dissembling, like those based on direct acyclic graphs, also fall within their realm⁴⁴. The constraints of the encoding method, which only contains limited expressive ability for the DCNNs while still being computationally feasible, make it one of the most challenging tasks in construction⁴⁵. Overall, even within the context of GWO, the search for expressive, compelling, and easy-to-interpret encoding remains an interesting research challenge despite the proven effectiveness of various encodings.

The arguments presented above reveal significant gaps in the current study.

• The practical exploration and exploitation of DCNN optimization can be achieved by including chaotic maps in the GWO algorithm in a sophisticated manner.

• Integrating fractal theory and multi-scale search techniques into the GWO algorithm is proposed to effectively explore diverse resolutions inside the architectural search domain.

• The focus is on an efficient computational representation of the DCNN formations within the GWO with varying lengths.

This research presents the CF-GWO method as the solution to address such gaps. In combining the ideas of the GWO algorithm, Fractal-based search, and chaotic maps, the CF-GWO achieves a high level of encoding and is regarded as an encoding technique. The main aim of this work is to study and utilize the search field of deep architectures for picture categorization.

Rationale for GWO

• GWO was selected because of its relative ease of use, efficiency, and fewer parameters than particle swarm optimization (PSO) and genetic algorithms (GA).

• It has a clearly defined structure and an efficient search exploitation ratio, which makes it appropriate for deep neural network optimization, which is highly complex and high dimensional.

• The No Free Lunch Theorem was used to justify that there is no best optimization algorithm for all problems, reinforcing the choice of GWO for this particular challenge.

Rationale for multi-scale fractal chaotic map search

• The framework’s chaotic maps introduce elements of randomness, facilitating a global search that is often overemphasized concerning the dangers of premature convergence.

• Fractal theory increases the dimensionality of the multiscale search, thereby improving the algorithms’ ability to search for and exploit more advanced features.

The main contributions of this research are:

• The integration of maps with the exploitative and explorative capabilities of GWO is significant. FRAC-T improves the search space of DCNN by making the traversal process more apt and complex.

• This study recommends using an encoding technique premised on using an IP address to detail the interconnectivity of nodes in a DCNN.

• There is a method for constructing DCNN structures of varying lengths using the Enfeebled Layer Technique. This layer makes the process more flexible and capable of learning image patterns and characteristics more effectively within the network.

• One of the most effective ways of learning, the CLS, divides massive amounts of data sets into manageable subgroups. This method aims to simplify the learning process while making it as effective and easy as possible. It should be both comprehensive and efficient.

• Undoubtedly, assessing the methodology using several benchmark datasets is sufficient to prove that the autonomous construction of deep convolutional neural networks is possible and plausible. Comparing it against existing techniques further solidifies its viability.

Background information

This section will review the mathematical model and concept of DCNN and IP addresses.

Comprehending deep convolutional neural networks (DCNNs)

Overwhelmingly, because of their unique ability to analyze pictures hierarchically, the appearance of the DCNNs marks a new ground shift in the field. However, DCNNs can process input in the form of multiple arrays⁴⁶.

Put differently, deep convolutional neural networks receive an input, process it through several layers, and generate an output. The first type is the input-affecting convolutional layer composed of multiple filters. To conduct convolution operations, the filters—also called kernels—are learnable matrices that contain learnable parameters. They involve adding and multiplying matrices through the width and height of the input image. This addition lets the filters detect spatial features such as texture, edge, and other correlated structures. In classifying patterns in visual input, convolution is perhaps the most helpful approach required to perceive the spatial relations inherent in the original image.

After the convolutional step, a nonlinear activation function is applied. The Rectified Linear Unit (ReLU) is mainly utilized for various purposes. The utilization of the function f(x) = max(0, x) in ReLU addresses the vanishing gradient issue, hence enhancing training speed and efficacy.

However, the input volume’s width and height are reduced through the addition of a pooling layer thereafter in the network’s output. The program provides downsampling to achieve translational invariance and minimize the required computation. Choosing the maximum value in a particular area is known as max pooling and is widely adopted in deep learning. P]With this procedure, it is inevitable that only the relevant properties will go through the network. The network’s final stage, the output layer, develops the classification layers using a softmax activation function. The above-stated function converts the outputs, commonly known as logits or log odds, into probabilities, making the final output more tangible and comprehensible.

Obtaining IP address

Numerical values are assigned to each device interacting with a computer network, and every device’s IP address is unique. The IP address has two main functions: first, it authenticates host or network interfaces, and second, it aids in determining the location of the host within the network. This information enables the routing of internet traffic to and from the host.

The addresses listed above are fundamental regarding the Internet’s data transmission capabilities. When a device requests internet-based permission for communication, such as when visiting a specific website, it utilizes the IP address associated with that website to determine its location. The IP facilitates establishing a worldwide network wherein any device can communicate with any other device, provided that both devices are interconnected to the internet.

In computer networks, IP addresses are crucial in establishing distinct device identities, and comprehending their functioning is vital for individuals in information technology, cybersecurity, and other disciplines. Moreover, these devices play a crucial role in network management by enabling administrators to identify devices and regulate traffic effectively.

The IP address is constructed using a decimal number sequence delimited by periods. However, the underlying digitized string is employed for network verification, leading to the emergence of a novel coding approach. Typically, layer configuration in DCNNs is represented in integer values. In this representation, each layer configuration is described as a concatenation of digits, which can be partitioned into shorter strings of digitized features, with each string representing a specific feature.

The digitized sequence relates to encoding the DCNN layers for the wolves. In this case, it should be pointed out that quite a sizable amount of personnel has to be employed as part of the wolf vector. This factor may lead to an impression of complexity in terms of time when one attempts to search with the GWO algorithm. Rather than using a large integer to represent the appliance’s identification ID in the whole mesh, the IP model divides an ID number of a higher magnitude than 256 into decimal numbers. Hence, a one-byte variable is assigned to a network address corresponding to each variable. By doing so, the digital string is split, enabling the wolf vector to be treated as a composite vector with different parts. Each part is a single byte. The GWO is known to have improved convergence by splitting many dimensions into smaller ones. This modification helps achieve a higher level of knowledge in all dimensions in every wolf update iteration, considerably reducing the exploitation area for every dimension. The wolf encoding method will be novel, considering the concepts outlined above. It is accomplished in a way that allows one to encode many layers into a wolf; thus, the learning time is significantly reduced. The following section will explain why this is so and how this strategy fits into the discussed crisis management process.

The suggested framework

Here, the CF-GWO strategy, the proposed IPC-based CF-GWO method, and general steps for developing the DCNN using IPCF-GWO are presented.

Proposed algorithm: chaotic map and fractal-enhanced GWO (CF-GWO)

The CF-GWO algorithm is created by including chaotic maps into the position update equations of the GWO to enhance the exploration capabilities. Additionally, a search strategy based on fractals is utilized to strengthen the exploitation of the search space.

Justification for chaotic maps

The motivation to apply chaotic maps to the GWO algorithm is to enhance the system’s capacity for exploration and exploitation. Events chaotic maps are sensitive to starting conditions and act pseudo-randomly; hence, using them to explore the search space of the GWO method is prospective. This prospective application also helps the algorithm to come out from early convergence and not get stuck in local optima by diversifying the search.

Implementation of chaotic maps

It is also observed that, with the help of modifying the position-updating equations, the GWO approach can include a chaotic map. When the location of alpha, beta, and delta wolves is assumed, the basic GWO modifies the positions of the searching agents called wolves. These are the best available solutions, just like those symbolical wolves. Naturally, when infusing a turbulent element into the equations that adjust the locations of the search agents, one hopes to alter their path. Such a change aims to improve the search space for exploration and exploitation. The location update of every wolf, or search agent, in the GWO algorithm, is expressed as follows³⁴:

$${P^{(t+1)}}={P^{(t)}}+M \cdot N$$

(1)

In the subsequent iteration, the position of a wolf is denoted by ${P^{(t+1)}}$, while the current position is represented by ${P^{(t)}}$. The symbol $\cdot$ signifies element-wise multiplication. The coefficient matrices M and N are computed by Eqs. (2) and (3)³⁴.

$$M=2b \times ran{d_1} - b$$

(2)

$$N=2 \times ran{d_2}$$

(3)

where rand₁ and rand₂ are random vectors in the interval [0, 1], 2b is a linear parameter that decreases linearly from 2 to 0 over iterations. Chaotic maps are incorporated into the position update equation of the CF-GWO as follows:

$${P^{(t+1)}}={P^{(t)}}+C{V^{(t)}} \cdot (M \cdot N)$$

(4)

The variable $C{V^{(t)}}$ represents the chaotic variable at iteration t. Several different chaotic maps, as illustrated in Table 1; Fig. 1, have the potential to yield $C{V^{(t)}}$. This technique can be mathematically expressed as:

$$C{V^{(t+1)}}=\lambda \times C{V^{(t)}} \times (1 - C{V^{(t)}})$$

(5)

Table 1 The utilized chaotic maps. The range of all maps is (0,1).

Fig. 1

The utilized chaotic maps.

In the present study, the value of 0.7 has been employed as the designated reference point for all cartographic representations⁴⁷. It is essential to acknowledge that the designation for each CF-GWO is presented in Table 2.

Table 2 CF-GWO labels.

Justification for fractals

Fractals are intricate formations constructed by iteratively replicating uncomplicated patterns over many magnitudes. While many strategies can be used on GWO, one of the implementation goals is to adopt a multi-scale search approach and utilize fractals’ self-similar characteristics to expand the search space exploration.

Implementation of fractals

A strategy that can extend the GWO is called fractal search, which comprises a multi-scale search that works in the fractal spectrum to optimize a solution. In this approach, search agents—the wolves—transcend the search domain at many different levels, as observed while going through different fractal scales. This capability has the potential to allow search agents to investigate and take advantage of the search space at several levels of detail, therefore uncovering optimal solutions that may not be apparent when examining the space at a single scale.

To enhance the exploitation capabilities of the GWO, a search technique based on fractals at many scales is developed. The exploration of search spaces in a multi-scale approach is conducted based on the self-similar character of a specific fractal pattern.

$${P^{(t+1,\theta )}}={P^{(t,\theta )}}+{\varphi ^{(\theta )}} \cdot (P_{{best}}^{\theta } - {P^{(t,\theta )}})$$

(6)

where $\theta$ Represents the scale level. The positions of a wolf in the next iteration, denoted as ${P^{(t+1,\theta )}}$, and in the current iteration, denoted as ${P^{(t,\theta )}}$, are considered. Additionally, ${\varphi ^{(\theta )}}$ represents the scale factor, while $P_{{best}}^{\theta }$ represents the best-known position at the specific scale level $\theta$. This feature allows the algorithm to do searches at varying resolutions, perhaps uncovering optimal solutions that may not be discernible at a singular scale.

The pseudocode of CF-GWO is shown in Algorithm 1.

Algorithm 1. Pseudocode of CF-GWO

IP-based chaotic map and fractal-enhanced GWO (IPCF-GWO)

This section offers a complete elucidation of the digitized IP-based CFGWO (IPCF-GWO) technique, focusing on its use for enhancing DCNNs.

Algorithm description

The conceptual framework of the IPCF-GWO is presented in Algorithm 2. The initialization is conducted using a three-step method consisting of wolf encoding, location updating, and ending criterion evaluation.

Algorithm 2. The conceptual framework of the IPCF-GWO

The encoding method employed by wolves

The layout of the IP address influences the IPCF-GWO encoding approach. Even though the DCNN consists of three levels, one crucial element to consider is that every layer can have several distinct features or properties, which results in different parameter counts for each layer. Table 3 provides information on the various kinds of layers. A possible solution for partitioning IP addresses into blocks to serve different DCNN layers is to assign an address of fixed length and cut it into pieces.

Table 3 The parameters associated with the framework layers and an illustrative case.

Before commencing any encoding process, it is imperative to possess knowledge of the precise length of the digitized string. In Table 3, the Parameter column contains critical parameters for convolutional layers. These are the essential factors that affect DCNN performance. Furthermore, the parameters’ ranges were modified to [1,8], [1,128], and [1,4], as illustrated in the accompanying table, based on the dimensions of the datasets. The decimal numbers represent digitized strings, including 010, 000 0101, and 10. The details provided here are for one configuration of a DCNN.

As far as the length is concerned in Table 3, the preceding action practically turns all the bits in the digital string into zero in terms of length. Information in Table 3 reveals that there are precisely 12 bits to identify a layer, whereas there are only 8 bits to define an IP address component, commonly known as a byte. Space allocated to an IP address is based on the idea that an IP address is 32 bits, with octets every eight bits. Therefore, four bytes, or thirty-two bits, are required to represent an IP address.

As indicated in Table 3, all layers of the DCNN must be configured with their respective subnets in the Classless Inter-Domain Routing (CIDR) format⁴⁸, taking into consideration the bit counts associated with each layer. Three subnets must be employed to support the three types of DCNN layers fully. The IP address 0.0 serves as the initial address for the subnet. The combined length of the subnet, which consists of 16 bits, along with the additional 12 bits needed by the Convolution layer, results in a subnet mask length of 4 bits. In this case, the subnet mask is 0. 0/4; it includes all the integer ranges from 0.0 to 15.255. The base of addressing of the pooling layer is 16.0, following a one-step increase in the IP address of the last convolution layer. Moreover, similar to the convolution layer, the following variable is a subnet mask that is 5 in length, adding up to a total of 16.0/5.

A subnet value of between 16. 0 and 23. 255 means that the pooling layer has the subnet specification for the associated field, and subnet 24 exhibits comparable problems. 25% of the fully connected layer ranges from 24.0 to 31.255.255.255. Table 4 illustrates the systematic arrangement of the subnets that have been explained before, and it supports understanding how the order is maintained.

Table 4 Four subnets are employed to accommodate four distinct layer types.

To accommodate DCNN designs with different lengths, the approach of deactivating specific layers in wolf vectors is used to modify the predetermined length of the GWO after its initialization. The Enfeebled Layer and the Enfeebled Subnet are the newest additions to solving the issue.

The enfeebled layer gets its IP setup with 11 bits, enabling it to interoperate with the rest of the network. Table 4 below illustrates the range of IP addresses that fall under DCMN classes that, in this case, have DCNN layered components and their ranges 32.0/5, accounting for the three types. It is evident in Table 4 that the digital sequences constituting an IP address are specific to a layer. Digital sequences that make up an IP address are layer-specific. As a result of zero byte padding, these are two bytes in length. For these reasons, these sequences are two bytes long. Subtracting the subnet mask from the encoded string makes it possible to develop an IP address by dividing by period a single byte. Thus, it is necessary to convert each layer into a 16-bit map to find the wolves.

The process involves setting up parameters for the initialization of the optimization of the DCNN

Without the proposed IPCF-GWO, the optimization of DCNN is incomplete. Start values are set to ensure the architecture optimization is optimal in all experimental runs. These are important to say when it comes to steering the search process and imposing constraints on the architectural space to ensure that the situation can be solved as a computationally tractable problem. Here are the chosen parameters:

The first limitation imposed on the design of the DCNN architecture is that the network may not contain more than thirteen layers. Once prescribed, this upper limit will enable the representation of deep features to be elaborated without converting models into a highly complex structure that settles quickly into overfitting simply because of the model’s computational complexity.

At the beginning of each independent iteration, there were 40 population nodes, and 40 different DCNN topologies were tested for each iteration. This apparent numerical number offers much variability of start opportunities with relatively low computational cost. Providing a broad array of specific opportunities to explore architectural space does not necessarily entail further computation.

The constructed DCNNs allow only three fully connected layers in each manufactured model. To enable a network to perform high-level reasoning for categorization, including a fully connected layer in the architecture design is essential. The restriction above effectively prevents overfitting, reducing the exponential progression of the parameters employed by the network.

The DCNN architecture undergoes a training phase of 10 epochs before its evaluation. A relatively limited number of epochs is selected to minimize the duration of training for each potential solution, hence facilitating a prompt review of its efficacy. Striking for complete model convergence, which could potentially provide a preliminary evaluation of the effectiveness of the given network, is meaningless.

The overall training procedures employ a batch size of 200. For a relatively broad range of hardware, each repetition of the training can be performed within a reasonable time, and the given size is large enough to provide a representative number of gradient updates.

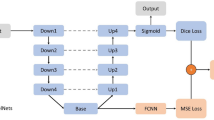
These parameters make it possible to efficiently and comprehensively explore the architectural design space of DCNNs. These constraints enable the proposed IPCF-GWO algorithm to search for and construct effective DCNN designs within a reasonable time frame. To gain a more comprehensive comprehension of the coding and functionality of the DCNN in conjunction with the variable-length DCNN structure, it is advisable to examine the following example involving a wolf vector. Five network addresses can represent the framework shown in Fig. 2 (row 1), which has five layers. Precisely, the IP addresses P, C, F, and E correspond to the pooling layer, convolution layer, fully connected layer, and enabled layer, respectively. Figure 2 (row 2) illustrates that the magnitude of the wolf vector is 10. The illustration consists of four levels, one of which is called the Enfeebled layer.

Fig. 2

The illustration of an encoded wolf vector.

Following multiple updates to the CF-GWO, it has been observed that the ninth and tenth dimensions of the wolf vector may transform, resulting in their values changing to 18 and 139, respectively. This transformation subsequently leads to a modification in the architecture of the DCNN employed by the wolf. In particular, the third network address, which represented an Enfeebled layer before the redesign, is now a Pooling layer, bringing the new architecture’s total number of layers up to 5. In conclusion, as illustrated in this instance, the wolves encoded using IPCF-GWO exhibit the ability to embody DCNN architectures of varying lengths, specifically 3, 4, and 5.

Each individual’s network interface, which includes their IP address and subnet information, is contained in their empty vector. The first layer of the design is always a convolution layer, while subsequent layers may be further convolution layers, pooling layers, or weakened layers. After the fourth and final layer is built with all connections made, each of the four types can be used. The last layer should ideally have the exact dimensions as all the classes, potentially forming a fully connected layer. In implementing addressing, each layer’s subnets randomly receive the addresses.

Fitness function assessment

Choosing an appropriate weight setting method before executing a specific fitness test is wise. The Xavier method¹² was selected as it is simple and commonly implemented in numerous deep learning algorithms. The training dataset will be used to train persons with their pre-decoded DCNN design configuration, as explained in Algorithm 3. After a batch evaluation, a partially trained deep network issues a sequence of accuracy levels. When evaluating a wolf’s fitness, the second factor to consider is the totality of its accuracy.

Algorithm 3. The evaluation of fitness function

Regarding GWO algorithms, the second step is to employ a fitness evaluation function for a group of DCNNs, or “wolves.” This function assesses how good the entire pack of wolves is based on their ability to categorize data.

The algorithm begins by initializing several variables, including the number of training epochs (k), the population of wolves (P), the batch size used during training (batch_size), the training dataset (D_train), and the dataset used for fitness evaluation (D_fitness). For each wolf c in the population, the algorithm trains the DCNN’s connection weights for k epochs using the training set D_train.

D_fitness After training, the algorithm determines if each wolf can be identified using the DCNN by calculating the network accuracy of Dfitness in batches, considering the batch size. The system then computes and stores the average of all the results for each batch, as shown above.

The algorithm now inserts the mean accuracy into the population P, as illustrated below: The algorithm then calculates the fitness of every wolf in the population to create the new population P and continues to calculate other fitness values similarly.

After this, the coefficients for each byte in the wolf must be reproduced to make the latter move. Since all graphical interfaces in the wolf vector must have a similar network availability, connections require their address. It may also be seen that the constraints embedded within each interaction shift as they progress down the wolf vector. There are some circumstances; for example, the second interface proves insufficient when one utilizes convolution, pooling, or attenuated layers.

In the GWO algorithm, the topmost position is the alpha. Decoding is to read the alpha’s wolf vector for a sequence of network interfaces beginning from the apex and progressing counter-clockwise in increments of two bytes for each interface. Upon deciphering all of the wolf vector connections, it is conceivable to finalize the DCNN architecture by seamlessly concatenating all layers in the identical sequence as the wolves.

Experimentation and discussion

The evaluation in this study is split into two main categories: first, the effectiveness of the proposed CF-GWO algorithm is evaluated using a wide variety of benchmark functions: (a) widely used benchmark function⁴⁹ and (b) newly proposed IEEE CEC 2022⁵⁰. In the second category, the performance of developed models (IPCF-GWO) is evaluated using nine image-classification tasks compared to 23 well-known state-of-the-art image classifiers. The following subsections present the details of utilized test functions, comparison algorithms, image classification datasets, and the result analysis.

The performance analysis of CF-GWO

In this section, the results of the proposed method are discussed and compared with some of the other well-established methods already in use. Two collections of standard test functions are employed: one encompasses the well-known benchmark procedures, whereas the other is the functions suggested for IEEE CEC 2022 not very long ago⁵⁰.

(a) The first set of test functions includes four different kinds: multimodal with fixed dimensions (MULTI-M), composition multimodal function (COM-Ms), and uniform (UNI-M) homogeneous structures. More information on these functions is explained in the reference⁴⁷.

(b) The second set of functions for use in DFPs is created based on generalized moving peaks, as described at the 2022 IEEE CEC⁵¹.

A specific test function is employed to assess the effectiveness of the CF-GWO method. UNI-M, MULTI-M, FIXED-M, and COM-Ms determine the algorithm’s performance in exploitation, exploration, and escape from local optima. UNI-Ms (F1–F7) gauges the algorithm’s ability to find new solutions, while MULTI-Ms (F8–F13) gauges its exploration capacity.

For observing the advancements that a more developed CF-GWO could achieve in lower dimensions, FIXED-Ms (F14–F23) are provided. Finally, the effectiveness of the CF-GWO in evading local minima is assessed through COM-Ms (F24–F29). These are difficult because COM-Ms have multiple local optima and are as complicated as real-life optimization challenges. As such, they function as an overall algorithmic efficiency test.

The reference contains comprehensive mathematical formulas and details about UNI-M, MULTI-M, FIXED-M, and COM-Ms. Furthermore, two-dimensional representations of a few benchmark functions are shown in Fig. 3.

Fig. 3

A two-dimensional graphical representation of traditional functions.

To attain statistically significant outcomes for this investigation, 30 iterations of the CF-GWO were performed. The results of each execution were documented in terms of the average (AV) and standard deviation (SD).

In the research, five recently suggested modified versions of the GWO were tested against CF-GWO. These variations include the regular GWO, the modified GWO by individual best memory and penalty factor (IPM-GWO)³⁹, multi-mechanism improved GWO (MMI-GWO)⁵², Robust GWO (RGWO)³⁵, and competing leaders GWO (CLGWO)³⁸. The purpose was to prove that using CF-GWO is more efficient than other optimization approaches that use GWO.

I performed each test on a Windows 10 PC with an Intel Core i7 processor operating at 3. 8 GHz and 16 GB of RAM with MATLAB version 10.0.2.231712 (R2020a). Table 5 outlines the parameters and initial settings used in the various optimization approaches to enhance comprehension of the upcoming comparison. These values either met the required range for all algorithms’ optimal performance or the algorithm creators specifically recommended them^53,54.

Table 5 Initialization parameters and settings.

Assessment of CF-GWO’s level of success in exploring solutions

Since UNI-Ms possess a unique global extremum, these instances are relevant for evaluating the exploitability of CF-GWO’s solution. The table below displays the results of applying CF-GWO and other GWO-based methods to F1–F7 of the UNI-Ms. Two metrics, namely AV and SD, are employed to evaluate their effectiveness. To assess the statistical significance of the disparities between CF-GWO and GWO-based techniques, Wilcoxon’s rank-sum test is used⁵⁵, which is a statistical methodology. For this research, a level of significance of 5% is established. The results comprise p-values obtained from the Wilcoxon test and the AV and SD. Table 6 shows the results of UNI-M functions.

Acknowledging that the Wilcoxon test cannot compare an algorithm with itself is crucial, leading to the designation of “NA” (Not Applicable) in such cases. When p-values are displayed in bold, it signifies no significant difference between the two methods being compared.

Table 6 The results of UNI-M functions.

The findings demonstrate that CF-GWO performed superior to most other algorithms in almost all benchmark functions, except F6 and F7, where CF-GWO was ranked as the second-best method. The results indicate the profitability of CF, which integrates features from chaotic and fractal systems. With this configuration, CF-GWO will likely achieve the global minimum within a short distance.

Evaluating CF-GWO’s exploration capabilities

MULTI-Ms are highly valuable for comprehensively evaluating a method’s exploratory possibilities.

It is worth noting that these functions possess many local optima depending on the design variables. In more detail, test functions with multiple modes existing in both high-dimension (MULTI-M) and fixed-dimension (FIXED-M) can be observed up to F23.

Tables 7 and 8 contain the CF-GWO results and other chosen methods for these functions. These tables unequivocally illustrate CF-GWO’s exceptional proficiency in exploration. CF-GWO indicates improved performance over other approaches in 50% of the cases for MULTI-Ms while maintaining comparable performance with well-established optimizers for the different functions.

CF-GWO has been shown to give the best results in FIXED-M functions, as demonstrated by how accurately it matches highly effective optimizers. The improvement in the CF-GWO investigational capabilities is suggested to stem from the idea of LF, which employs more aggressive step size iterations in the first stage of the process, known as multi-stage optimization.

Table 7 The findings, especially for MULTI-Ms.

Table 8 The findings of FIXED-Ms.

The convergence curves of the mentioned algorithms are shown in Figs. 4, 5 and 6.

Fig. 4

The convergence curves of UNI-Ms.

Fig. 5

The convergence curves of MULTI-Ms.

Fig. 6

The convergence curves of FIXED-Ms.

Evaluating the capacity of CF-GWO to prevent local Optima

The COM-Ms (F24–F29) are derived by applying shifts, rotations, and combinations to basic UNI-M and MULTI-Ms. They serve to evaluate how well algorithms can prevent local minimums from occurring within their search and extraction functions.

Accordingly, optimization methods like CF-GWO will improve performance in COM-Ms challenges as depicted in Table 9. Even after modifying the parameters of all other methods to obtain the best possible outcome, the results still prove that CF-GWO outperforms all other methods tested. Some findings delve deeper into the load-balancing feature of the proposed CF-GWO, which provides an effective solution for both the exploration and extraction phases. Furthermore, the CF-GWO’s adjustable step size characteristics and the numerous relocations resulting from chaotic maps and fractals aid the algorithm in avoiding local optima.

Table 9 The detailed results of the COM-Ms.

Box plot of results

Several box plots (Figs. 7, 8, 9 and 10) were constructed to summarize the effectiveness of the six optimization algorithms for the different functions (F1–F29). These box plots allow documentation of the results distribution, middle value, interquartile range, and outliers. This plot would help us see CF-GWO as a stand-alone output and gauge its performance compared to other algorithms used in the analysis.

Fig. 7

Box plot for functions F1–F7.

The first set of box plots (Fig. 7) illustrates the results for the six algorithms applied to the functions F1 to F7. It can be observed from the plot that CF-GWO performs reasonably well in numerous weaknesses, such as the median values for the competitive functions F1 to F4 and F6. These results suggest that the average performance for CF-GWO optimization is significantly lower than that of other strategies. Additionally, the box plots show that CF-GWO is very variable in some cases, like in F7. This result means the method may change depending on the problem’s complexity.

Fig. 8

Box plot for functions F8 to F13.

Figure 8 illustrates F8 to F13, demonstrating that CF-GWO also explains good functionalities. F9 to F12 functions also indicate a relatively low average value (AV) of CF-GWO, implying the possibility of reaching optimal solutions within these problem spaces. Likewise, CF-GWO applies less deviation on the solutions of these functions than on other functions, hence its strength. However, there is some increased AV in the results for F8, suggesting that CF-GWO may have some difficulty solving these problems.

Fig. 9

Box plot for functions F24 to F23.

Figure 9 portrays the performance of the algorithms on functions F24 to F23, which are the third set of box plots. The complex optimization problems of these functions demonstrate the capability of CF-GWO to handle more complex problem spaces. Specifically, CF-GWO performs commendably in F15 to F18 and F21 to F23 with lower average values and relatively constant values with low standard deviation (SD). As expected from more complex designs, CF-GWO’s performance characteristics become more defined with variability requirements in some functions like F19 and F20, indicating a need for improvement.

Fig. 10

Box plot for functions F24 to F29.

Lastly, boxplots for F24 to F29 (Fig. 10) also unfold how CF-GWO performs on the various complex problem sets. Despite the mixed results in this range, it is evident that certain functions, particularly those dealing with multi-objective problems, demonstrate a robust CF-GWO capability. The scores obtained in F24 to F26 and F28 and F29 demonstrate that the CF-GWO algorithm outperforms other algorithms in solution techniques, achieving lower mean values and fewer dispersions among results.

Box plots across all functions, specifically from F1 to F29, indicate that CF GWO performs competitively in numerous problem areas, particularly in registering lower average values in certain functions. Although the algorithm had some fluctuations, it remained stable in some functions, such as F19 and F27, indicating probable optimization dominance. In addition, the low standardized rate in some instances suggests that CF-GWO can optimize and locate ideal solutions in areas with complicated problem structures; thus, it can be relevant in optimization problems. However, to address broader instances, the algorithm may need to evolve to accommodate less fluctuation in more complex functions.

IEEE CEC 2022

Situations in the real world may involve scenario variations like changing the number of variables, objective functions, or constraints. Due to their perpetually evolving difficulties, these dynamic optimization problems require algorithms capable of real-time self-modification. Adapting and devising fresh strategies when swiftly tackling such issues is crucial.

Therefore, having a suitable test generator is crucial for evaluating the CF-GWO’s ability to handle dynamic optimization effectively. Current test generators usually create optimization landscapes in various parts to determine numerous aspects. The shifting peak baseline, another well-known benchmark, is dynamic and derives all curve parameters from a single peak.

However, one must note that the limitation of the more popular moving peaks benchmark is that they are not always truly representative of landscapes, for example, containing large portions with symmetry, smoothness, regularity, unimodality, and separability. These attributes render them comparatively amenable to optimization while perhaps failing to adequately capture the intricacies of real-world situations. A novel benchmark, the extended moving peaks criterion, was devised to overcome this constraint. This benchmark facilitates the creation of components with a diverse array of attributes, ranging from straightforward single-peaked landscapes to intricate multiple-peaked terrains. Additionally, it may encompass asymmetrical shapes and imperfections.

The generalized shifting peaks baseline allows for generating terrains that can be either smooth or filled with irregularities. It also allows for exploring different levels of variation interactions and considering condition numbers. This adaptable benchmark offers researchers a valuable instrument to comprehensively evaluate the efficiency of dynamic optimization methods, such as CF-GWO, across various issue characteristics.

The main criterion for assessing algorithms on problems derived from the extended shifting peaks benchmarking is the offline error (OE), which is determined by quantifying the mean disparity between the optimal location and the fitness evaluations, which is expressed using Eq. (7).

$$OE=\frac{{ - 1}}{{{C_F} \times NE}}\sum\limits_{{ne=1}}^{{NE}} {\sum\limits_{{{c_f}}}^{{{C_F}}} {({f^{ne}}(B{P^{{C_F}(ne - 1)+{c_f}}}) - {f^{ne}}(B{P^{ne}}))} }$$

(7)

where NE represents the overall count of these environments, $B{P^{ne}}$ indicates the optimal position within the ne environment, and $B{P^{(t - 1)CF+cf}}$ relates to the highest position regarding fitness evaluation within the neth environment.

The studies involve the formation of multi-swarms consisting of neutral individuals or a combination of neutral and quantization individuals. The configuration entails a five-dimensional space for exploration, where peaks are present with randomly fluctuating heights and widths. These peaks shift in any direction following a certain number of evaluations. Every test is terminated after 100 peak changes, yielding a cumulative maximum of 500,000 function evaluations.

According to the peak characteristic variability data, it includes several standard functions². These results are taken from the mean of fifty preliminary runs with a different random seed each time. The primal one is the offline error, which is computed as the dissimilarity between the ‘friendly’ and ‘unfriendly’ states in the physical environment as a function of the experiment’s outcome. The tests examine how different setting configurations affect the algorithm’s responsiveness and analyze the impacts of various multi-swarm topologies. Efficiency considerations derived from prior research usually restrict the overall population count to 100. Standard GWO values are regularly employed during the testing process.

• Effects of various multi-swarm configurations.

This subsection examines the impact of multi-swarm organization on performance when utilizing the generalized shifting peaks benchmark and following the typical settings indicated before.

There are various methods to arrange 100 individuals into swarms, ranging from consolidating multiple swarms into a single entity, as shown in GWO and CF-GWO, to maintaining 100 distinct swarms where individual entities cannot communicate during updates, resulting in the absence of a collective swarm essence. The top rankings were considered to fall somewhere between the two extremes. Experiments were conducted between 2 and 50 swarms of symmetrical configurations.

However, for the range of 11 to 19 swarms, equal human representation is not possible in each swarm of the GWO. To solve this problem, a configuration containing 14 (4 + 3) animal species has been formulated, which yields 98 participants within the GWO algorithm. This type of multi-group strategy is used within these limits as one of the components of our configuration.

The results from two sets of experiments are enclosed here. One of the two simulations set minor up-and-down changes of the parameter with values of 1 and 100 to have more straightforward conditions. In contrast, the other simulation exhibited higher levels of difficulty.

Figure 11 illustrates several swarms qualitatively, while Fig. 12 presents their quantitative characteristics so that the impact of swarm diversity on the OE can be understood. The increase in the number of swarms is a way to increase the variety in their composition. The results shown here support our hypothesis that maximum efficiency is when the parameter value equals ten swarms.

Fig. 11

Comprehensive information about offline error levels and standard errors.

In cases where more than ten artificial swarms are deployed, performance tends to drop for two reasons: For one, the level of diversity drops because most individuals within the greater swarms are more highly consolidated. Additionally, the ascent of the swarm peak is observed once more. The swarm performances in these scenarios are unsatisfactory when various swarms are not incorporated in the basic GWO that uses 50 (1 + 1) swarms and interaction charges. However, the performance of CF-GWO with 10(5 + 5) swarms is much better than theirs. That quantized interaction persists to rise above charged interaction is rather fascinating.

Fig. 12

Represents the offline error of the 10(5 + 5) configuration against the swarm quantity.

The results of the systems with power Ω = 1 and Ω = 100 are analyzed in Fig. 13. These distinct swarm formations confirm the possibility of the multi-swarm approach. The small difference between the 1(100 + 0) and 1(50 + 50) configurations is quite surprising. The heterogeneity within large sole populations is fundamental, and the generalized moving peaks benchmark is less likely to vary this diversity moderately.

However, under these very challenging scenarios, the collective essence of the swarm diminishes due to the absence of mechanisms for inter-swarm communication. Significantly, apart from the CF-GWO outcome, it is evident that a solitary group of organisms sharing information inside a specific area outperforms the scenario where Ω = 100, which depends on contact based on exclusion.

Fig. 13

Comprehensive information on offline error levels and standard errors.

Image classification problems

This section investigates the performance of the proposed model in image classification tasks.

Datasets

The effectiveness of IPCF-GWO models is evaluated on nine widely recognized image classification datasets, as presented in Table 10. It is worth mentioning that the dimensions of the photographs in these benchmarks are 28 × 28.

Table 10 The current cutting-edge datasets.

Benchmark classification models

The tests use 23 widely recognized algorithms that exhibit acceptable classification mistakes as the benchmark classifier. The Fashion dataset is evaluated using various benchmark classifiers, including GRU_SVM_Dropout, GoogleNet, 2C1P, 2C1P2F_Dropout, 3C1P2F_Dropout, 3C2F⁵⁹, SqueezeNet200⁶⁰, AlexNet⁶¹, VGG16, and MLP 64-128-256⁶². The reference classifiers utilized across various datasets are ScatNet2⁶³, CAE2⁶⁴, TIRBM⁶⁵, PCANet2 (softmax)⁶⁶, LDANet_2⁶⁶, PGBM_DN_1⁶⁷, SVM_Poly⁶⁸, EvoCNN, RandNet_2, SVM_RBF, SAA_3⁶⁹, and NNet, DBN_3⁵⁶.

To further demonstrate the superiority of IPCF-GWOs over other IP-based swarm intelligence-based algorithms, additional experiments are conducted, including comparisons with the firefly algorithm (IPFA)⁷⁰, ant lion algorithm (IPALO)⁷¹, and IPPSO⁷².

The preferences and practices within the deep learning community typically determine the selection of parameters. In addition, 20% of the images in the training set are used to generate the validation set. Thirty separate trials were used to assess the IPCF-GWO’s efficacy. The averages obtained were then used for statistical comparisons.

The results analysis

A wide range of experiments is carried out to support the theories outlined in the preceding sections.

First, IPCF-GWO is compared to other algorithms based on qualitative parameters to determine its superiority. The second step is to obtain quantifiable data to assess the comparative performance of IPCF-GWO. Most of the subjective data is from the visualization tools. Convergence curves are a common qualitative outcome in the literature. To see how effectively an algorithm improves its approximation of the global optimal throughout iterations, researchers typically record the best answer found in each iteration and plot them as a curve. This study also employs qualitative results better to analyze the performance of IPCF-GWO under specific challenges.

The path of the search agent gives rise to the second qualitative result. Since it is unnecessary to display all the paths of the search agents in all dimensions, only the first wolf’s path is shown. IPCF-GWO collects this data to observe and verify how exploration and exploitation are carried out. Figure 14 illustrates the solution trajectory curves for the benchmark datasets.

This graph demonstrates that the first wolf experiences abrupt changes in the opening steps of iterations, slow changes following the initial stages, and monotonous behavior in the last stages. This curve shows that wolves move quickly at the start and fluctuate gradually as the number of iterations increases. As a result of this finding, IPCF-GWO demands that the wolves first walk around the search area and cause a solution space. Thus, the IPCF-GWO allocates maximum available search space by ensuring that wolves do not move far away from their active regions.

The trajectory diagram shows how IPCF-GWO explores and utilizes the search space. It should be pointed out that these results do not show whether the exploration and exploitation aid in improving the initial random population or find a better estimate of the global optimum. To monitor and confirm such behaviors, the average fitness of all wolves and the optimum solution found to date (convergence curve) are saved and displayed in Fig. 14 during the optimization process. The average fitness curves for wolves indicate a downward trend throughout the benchmark data sets. Finally, this study also implements qualitative outcomes to provide a better picture of IPCF-GWO’s operation under various forms of stress.

The second qualitative result is provided by the behavior of the search agent over time. As it is not required to depict the traces of all search agents in each attribute, only the path of the first wolf is described herein. On the other hand, the average fitness curve is decreasing with the increase in the number of iterations, which relates to the exploitation phase. Average fitness curves show the degree to which IPCF-GWO can improve populations during optimization, but this does not mean that the global optimum improves in approximation. Convergence diagrams are helpful in this case.

The IPCF-GWO algorithm improves, but not uniformly, as seen from some graphs, which is consistent with the progress observed in the fitness of the global optimum approximation. Despite the progress made, there have been varied results that indicate that the convergence behavior of IPCF-GWO depends on the datasets to which it is applied, which is illustrated in Fig. 14 that contains the convergence curves to which the IPCF-GWO algorithm is used.

Despite the strong exploration and exploitation tendencies shown using the qualitative results of the IPCF-GOW approach, they do not paint the entire picture of how efficient the algorithm is. The efficiency of the IPCF-GWO algorithm is determined in two complementary ways; then, the results are averaged with other published benchmark models. The measures are the percentage of classification error and the quantity of parameters resulting from the optimum structure found through empirical tests. The other stat depicts the average performance of the IPCF-GWO algorithm, while the other shows how complex the algorithm is compared to different benchmarks.

Results from studying the Fashion dataset can be found in Table 11, while the other datasets can be found in Table 12. The first block of rows presents minimum error rates for classification based on benchmark classifiers, whereas the second block shows the errors generated by IPCF-GWOs. The other participants missing this information will be identifiable with the passcode “N/A” or not available. In Table 11, these parameters are the training epochs and the parameters of the test algorithm for the Fashion dataset. However, none of this information was provided from the vendors, so Table 12 omits it. It ensures that different datasets and classifiers employ the same benchmark datasets when evaluating.

Table 11 The evidence of comparison between models on the fashion dataset.

Table 12 demonstrates that the IPCF-GWO1 almost outperforms all eleven competitors regarding classification error. In addition, the IPCF-GWO model shows an improvement in the error rate that ranges from 0.4 to 5.10% relative to the EvoCNN classifier. Moreover, the IPCF-GWOs exhibit a notable reduction in connection weights, with a count of 750 K. This count is considerably lower than the 6.69 million in EvoCNN, the 27 million in VGG, and the 100 million in GoogleNet. It is worth mentioning that, in contrast to other classification algorithms, a much fewer number of epochs were used to produce these findings. The results show that when implemented on the Fashion dataset, IPCF-GWOs, and IPCF-GWO1 in particular, outperform DCNNs in computational complexity and reliability. It should be noted that the complexity of MLPs with 40 K connection weights is less than that of IPCF-GWOs with 750 K. This result is that MLPs with 10.01% classification error have almost twice the error of IPCF-GWOs.

Table 12 The rate of misclassification for additional datasets.

The IPCF-GWO1 classifier indicates improved performance compared to all fourteen classifiers on five of the eight baseline datasets. Additionally, it ranks as the second-best classifier on the remainder of the reference datasets. However, it is worth noting that the LDANet-2 and EvoCNN classifiers surpass the IPCF-GWOs on the Convex, MRDBI, and MB. In summary, the classifier IPCF-GWO1, which has been built, indicates improved performance in terms of classification error when compared to the best outcomes achieved by the 13 baseline classification models in 83 out of 95 assessments.

The good results of IPCF-GWOs are related to the particular type of chaotic map, i.e., Gauss/mouse, because this map initially has a large amplitude and significant fluctuations that decrease over time as the amplitude of the changes decreases. Thus, combinations are tested with incredible speed and variety but move toward stability.

The suggested IPCF-GWO-DCNN is tested on nine frequently utilized image-classification standard datasets. They are the Fashion, CS, MNIST, RI, MRB, MBI, MB, MRDBI, and MRD benchmarks. These benchmarks are categorized into three main groups based on the classification criteria. The first category is Fashion, which recognizes ten fashion objects (pants, coats, etc.). In this group, the MRD, MRDBI, MB, MRB, and MBI variations of MNIST employed 50,000 training images and 10,000 test images to classify the ten handwritten digits. These MNIST variations are modified with other non-MNIST arbitrary obstacles (such as arbitrary backgrounds and rotations) to combine higher order classification methods. Even more challenging is that these versions have only 12,000 training photos and 50,000 test images, further aggravating classification techniques. The third category is item form recognition, the RI and CS benchmarks.

DCNN is designed without any Disabled layers since they were removed in the decoding step. IPCF-GWO can obtain a DCNN architecture of arbitrary size, as shown in the received structure. In particular, a CNN structure with six layers is learned for the MB and CS benchmarks, while for the Fashion dataset and MRDBI data set, a DCNN structure with eight levels is mastered. Only one of the thirty runs for each benchmark is shown in Tables 13, 14 and 15 and is discussed in this paper.

Table 13 The optimal architecture searched for CS and RI benchmark datasets.

Table 14 The optimal architecture searched for MINST datasets except for MRDBI.

Table 15 The optimal architecture searched for the fashion and MRDBI dataset.

Convergence analysis

The previous section proved that IPCF-GWO1 presents a better result than other IPCF-GWOs, so this subsection discusses IPCF-GWO1’s experimental convergence. The convergence of IPCF-GWO1 is evaluated using parameters, including the convergence curve, average fitness history, and trajectories. The measurements for IPCF-GWO1 on nine datasets are illustrated in Fig. 14.

Fig. 14

Convergence behavior of IPCF-GWO.

The convergence curves suggest the initial indication of the current optimal solution. It is noted that there is a soft observed convergence curve for six datasets, which follows the function classification types. These results suggest that with every iteration, the outcomes get progressively better. However, when extended to other datasets like MRDBI, RI, and MBD, this pattern changes and corresponds to the expected incremental trend. An examination of each dataset demonstrates IPCF-GWO1’s potential for efficient optimal solution capture and modification throughout the earliest phases of the iterative process.

The convergence curve illustrates the ideal behavior of the wolf in attaining success while considering the agents (alpha, delta, and beta) as group members. However, there is a lack of data regarding the collective performance of the individuals in question. Therefore, the average fitness record became an additional measure for evaluating the team’s performance. While this measure is mainly used to enhance the first random populations and gather people’s collaboration, it has the same pattern as the convergence curve. Implementing the phase modification technique improves the overall fitness of the wolf population. As a result of this improvement, there is now a noticeable step-like structure in the mean fitness profile of the comparative datasets.

Another metric to consider is the direction of the agents, which is illustrated in the third column of the figure. This metric quantifies the changes in the agent’s topology during the optimization process, from its initial to its final state⁷⁶. The trajectory of the wolf was indicated by utilizing its initial dimension, as agents tend to move in diverse directions. The measure identifies numbers corresponding to unexpected fluctuations that happen frequently and with significant intensity in the early iterations but gradually decrease in magnitude in the later stages. The described pattern commences with an initial exploratory search phase and a subsequent transition to a localized search phase during the last iterations. This trend guarantees that the algorithm eventually focuses on an area with a local or global minimum.

IPCF-GWO can enhance the quality of solutions within a randomly generated population by attending to a specific issue. It is remarkable that on one side, IPCF-GWO improves the global optimum accuracy of the given function by the local optima practical exploration and avoidance, and on the other side, the exploitation and the algorithm’s convergence.

Analyzing computational complexity

As the search space expands, the computational complexity and model performance are theorized to grow. The complexity of IPSCF-GWO is a function of three parameters: the maximum iteration number (MaxIter), the number of wolves (n), and the sorting method for each iteration. These possess the best time complexity of O(n×log(n)) and worst time complexity of O(t×n²) when sorting wolves by using the option of ‘rapid sort.’ To get a rough estimate of that, Eqs. (8) and (9) are presented.

$${\text{O}}\left( {{\text{IPCF}} - {\text{GWO}}} \right)\,=\,{\text{O}}({\text{MaxIter}} \times ({\text{O}}\left( {{\text{Quick sort}}} \right)\,+\,{\text{O}}\left( {{\text{position update}}} \right)))$$

(8)

$${\text{O}}\left( {{\text{IPCF}} - {\text{GWO}}} \right)\,=\,{\text{O}}(MaxIter \times ({n^{\text{2}}}\,+\,n \times d)(=\,{\text{O}}(MaxIter \times {n^{\text{2}}}\,+\,MaxIter \times n \times d)$$

(9)

Statistical analysis of IPCF-GWO

Here is the most apparent competitor of the IPCF-GWO: Bonferroni–Dunns post-hoc and Friedman tests⁷⁷, and this part of the work presents their probabilistic comparison. To maintain strict evaluation, the benchmark dataset is split into three subdivisions, as described previously. A simple non-parametric Friedman rank test found that the algorithms performed far better. Table 16 below depicts the results of the Friedman rank test as well. To compare the results of the baseline methodologies and identify how each of them stands, the Friedman mean rank analysis is used, as presented in the table. Table 16 shows that IPCF-GWO outperformed the other benchmark algorithms.

Table 16 The outcome of Friedman mean rank analysis.

Following a statistical evaluation in which it seemed clear that many algorithms performed differently, it has to be established whether the algorithm’s performance, compared to IPCF-GWO, differs statistically. The Bonferroni–Dunn analysis, which is based on critical difference (CD), seeks to test if there were statistically significant differences between multiple competitors at the same time.

As a reminder, IPCF-GWO serves as the superior controller in this case. With the two significance levels of 0.1 and 0.05, each method’s average performance across the three types of datasets is illustrated in Fig. 15. The IPCF-GWO algorithm indicates improved performance compared to other algorithms, as seen by its average ratings above the dotted line in the figure. A distinct hue distinguishes each group’s threshold line. The figure shows that IPCF-GWO consistently ranks first in all classes, outperforming other networks at two different significance levels (0. 1 and 0.05): they include PGBM_DN_1, CAE_2, TIRBM, RandNet_2, ScatNet_2, PCANet_2(softmax), LDANet_2, SVM_Poly, DBN_3, SVM_RBF, NNet, SAA_3, and EvoCNN.

Fig. 15

The results of Bonferroni-Dunn’s test. 0.05 and 0.1 were selected as the percentiles for the test significance levels (α).

The result shown in Fig. 15 shows that IPCF-GWO is more confident and robust than other high-performance classifiers. Furthermore, IPCF research has demonstrated that GWOs can work for every group. However, some groups have a more volatile ranking in multiple domains than others.

Real-world engineering problem: fire detection challenge

Fire detection devices are essential when trying to minimize the loss and consequences that fires cause both to the towns and the countryside. Temperature sensors and computer vision algorithms were included in the previous approaches. At the same time, the most recent innovations are based on DCNNs, which have been proven to reveal more advanced methods for accurate detection. Based on the adopted IPCF-GWO framework, a fundamental problem of optimizing the DCNN structure for fire detection is considered. For assessment, tests were run on the updated DarkNet and AlexNet networks to learn how they were set up to train and test and how long these tests would take. A simple DCNN is trained and then used for deeper models to confirm that fire detection cannot be achieved with simple techniques and easy models.

An unbiased comparison is conducted by using the Fire-Detection-Image-Dataset (https://github.com/UIA-CAIR/Fire-Detection-Image-Dataset). Although this dataset contains only 651 images, it is large enough to show how fast and accurately models can generalize from images and extract useful features. The training set includes 549 photos; 59 images depict fire, and 490 do not. The imbalance to mimic real-life scenarios is constructed since there is very little probability of fire dangers occurring.

Due to the extreme imbalance in the training set and the complete parity in the testing set, this setup is ideal for evaluating the models’ generalizability. The few fire photos contain sufficient data to train a reliable model to identify the unique characteristics. A sufficiently deep model is required to extract these features from a sparse dataset.

Not only are some of the images imbalanced, but they also defy easy categorization. The collection contains pictures of flames in many settings, such as houses, accommodations, offices, and forests. The images have a wide range of tones and levels of illumination, from yellow to orange towards red. No matter the size, fires can break out at any hour of the day or night. Pictures of a sunset, houses, and cars painted red, lights that have a mix of yellow and red, and a highly lit room are among the non-fire images that are difficult to separate from the fire photos.

Figure 16 shows examples of fires in various settings. In addition, the non-fire images are hard to categorize in Fig. 17. Due to these dataset features, fire detection can be challenging.

Fig. 16

Real fire images.

Fig. 17

Non-fire images.

Algorithms developed for successful competition on fire detection issues are the focus of the inquiry, which seeks to evaluate their computational complexity and stability. The algorithms must efficiently locate practical solutions within a maximum Max(T) search time. After the experimentation phase, each fire detection problem has three important metrics computed: SR, AFEs, and ACDs. These measures evaluate the effectiveness of the techniques and are based on prior research. To determine the ACDs, SR, and AFEs, Eqs. (10) to (12) are used:

$$ACDs=\frac{1}{{NSS}}\sum\limits_{{i=1}}^{{NSS}} {calculation\_Duratio{n_i}}$$

(10)

$$SR=\frac{{NSS}}{L}$$

(11)

$$AFEs=\frac{1}{{NSS}}\sum\limits_{{i=1}}^{{NSS}} {FE{s_i}}$$

(12)

A reliable experiment is performed K times, and NSS represents the number of effective searches out of K iterations. The expectation is that algorithms will find a workable solution in each iteration. The results of the suggested models are shown in Table 17; Fig. 18.

Table 17 The proposed models’ results for the fire detection problem.

Fig. 18

The visual presentation of the proposed models’ results for the fire detection problem: (a) SR, (b) AFEs, and (c) ACDs.

Different algorithms are compared here on three critical measures: SR, AFEs, and ACDs. These criteria are crucial for testing algorithms that are useful for image classification, particularly for assessing fires.

The SR is the percentage of correct classification. According to the results of this study, the best works were IPCF-GWO1 and EvoCNN; they demonstrated perfect SR accuracy at the 100% level. Conversely, IPCF-GWO2 had an SR of 45. This improvement is only 22%, showing that this variant has excellent room for improvement.

Another group that has produced impressive results is IPPSO, which has 91. 01% SR, and RandNet-2, which has 85. 22% SR. The success percentages of the several IPCF-GWO variants vary compared to others, indicating that variations of the fractal and chaotic map have differing impacts on GWO efficiency.

The AFE average provides the degree of efficiency an algorithm employs to extract features in the computation, which measures computing efficiency. The highest-achieving algorithms are IPCF-GWO1 and EvoCNN, where both algorithms are built from the least number of data points, 14,001 and 14,042, respectively, which indicates that these models offer high accuracy but require lesser computations.

Compared with other algorithms, it is also efficient regarding AFE with 15,321. Conversely, IPCF-GWO2 and CAE-2 required more features to be retrieved (19142 and 18541, respectively) and, as such, required more computational resources, which may have resulted in longer computation time and resource consumption.

Based on the discussion above, it is clear that a low ACD presents a faster system. However, IPCF-GWO1 and EvoCNN have ACDs of 60.02 and 59.56, respectively. Moreover, in this respect, it is also possible to regard IPCF-GWO1 and EvoCNN as the most efficient models. In practical applications such as fire alarms, these values describe the amount of computational optimization-specific techniques used.

Specifically, in all cases where the degrees of precision and speed are critical, IPPSO emerged as a serious challenger with an ACD of 50.01. However, the SR of IPCF-GWO2 is low, which means that the absence of accuracy also happened with the reduction of the delay, as it was identified with the lowest ACD, 38.22. Although some methods, such as PCANet-2(softmax) and RandNet-2, have revealed slight delays, others, such as SVM + Poly and SVM + RBF, have worse computational efficiency and revealed delays of more than 40.

The result reveals that IPCF-GWO1 and EvoCNN are the most effective methods studied in accuracy and feature extraction, and they incur minimum computational delay. These models have an edge in applications such as real-time fire detection, where accuracy and response time are critical. Incorporating the fractal and chaotic map with GWO enhances the DCNNs’ effectiveness, which is why these models operate successfully.

Of course, looking at the results of the models, it can be seen that even though IPPSO did quite well, especially in SR and ACD, it has slightly higher AFEs that make it seem like it would not be as efficient computationally as the IPCF-GWO1 or EvoCNN. As can be seen when comparing different versions of IPCF-GWO, it is evident that adjusting the parameters of IPCF-GWO can significantly affect performance. There is a need for algorithms like IPCF-GWO2 and CAE-2 to be fine-tuned because they had lower success rates than the overall average and high computation requirements for fire detection jobs.

This study proves that DCNNs can significantly enhance their performance by utilizing advanced optimization techniques such as IPCF-GWO. This algorithm, in turn, makes them more efficient and effective for crucial applications like fire detection.

Discussion

The research paper focused on the design of the enhancement of the multi-fractal based on the use of the combing of the GWO with the chaotic maps and multi-fractal build CF-GWO, which has been seen to be efficient while addressing the problems in the broad domains, thus forming the purpose of the paper. For the integration of the chaotic maps and the multi-scale search ideologies, the focus of the approach was directed towards solving the difficulties in the unexplored area concerning the explore-exploited relationship and premature convergence. The efficacy of the CF-GWO was evaluated through multiple experiments in three application domains, including the classification of images, the dynamic optimization problems, and the benchmark optimization functions.

Performance on benchmark optimization functions

• For multiple test benchmark testing, 29 were applied and divided into four groups. The common purpose of tests was to research the ability of CF-GWO in every category to satisfy all required functions concerning seeking local maxima about the GFCC.

• Based on their conclusions, it could be reasonably expected that Combinatorial GWO should obtain a faster convergence to the global optimum with more excellent maps. Results confirm that CF-GWO is one of the most robust models and can deliver a global optimum in all tests. Statistical analysis confirmed the superiority of the maps and, together with the chaotic maps, demonstrated the superior performance on global convergence.

• Multimodal functions (MULTI-M): Due to the fractal-based technique, the CF-GWO operated in multidimensional space with an intricate structure with several good points and a steady proportion of the explored and exploited space. This ability could be seen in the considerable enhancement of average solution results and the shrinkage of standard deviations across trials.

• Composite multimodal functions (COM-M): These functions, whose features have high dimensionality and many interior local minima, have evidenced the strength of this method’s applicants. The chaos fractals allowed the CF-GWO to surpass the best methods by beating the local traps.

• The importance of these results was confirmed by statistical tests such as Wilcoxon rank-sum tests (this was the case for most comparisons, p < 0.05).

CF-GWO’s performance on dynamic optimization problems

• Efforts were made to determine what degree of adaptability CF-GWO would likely have in dynamic optimization problems using IEEE CEC 2022 benchmark functions. Such issues included non-stationary landscapes; thus, algorithms were forced to change their search strategies during optimization.

• Based on the offline error, CF-GWO was able to register consistent scores in low OE owing to its ability to function in a dynamic setting. It was demonstrated that CF-GWO is an agile optimization solver since it accommodates optimal changes better than static optimization methods.

• In the post hoc Bonferroni-Dunn analysis, CF-GWO’s ranks were compared with other algorithms, and changes were implemented again in several dynamic conditions. Against the expectations of the authors, CF-GWO had the expected good ranks, confirming it is the best-performing algorithm in the most challenging environments.

Image classification tasks

• The solution to the research problem is based on the IPCF-GWO framework, which was applied to nine benchmark image classification datasets, including the obvious ones MNIST, Fashion, and Convex Sets. Twenty-three cutting-edge classifier structures encompassing EvoCNN, VGG16, and AlexNet were utilized to benchmark the methods.

• Classification accuracy: CF-GWO remained ranked first in all the datasets, with an accuracy as high as 87.37% for 95 attempts. This performance was statistically significant, as verified by the Bonferroni-Dunn procedure, which confirmed CF-GWO’s rank superiority with little overlap in confidence level intervals with the opponents.

• Parameter efficiency: The parametric approach improved CF-GWO’s ability to construct DCNN architectures by drastically increasing the number of parameters required by traditional methods, which increased the equilibrium’s graphed values.

• Convergence behavior: The convergence curves made it more convenient to view the CF-GWO, so the latter appeared to attain targets efficiently and stably without the haze of reaching the goals too early, which was the case with other algorithms.

Statistical validation

• Two statistical methods were employed to reach an evidence-based conclusion regarding the performed experiments.

• Wilcoxon rank-sum test: This non-parametric test was used to evaluate the performance of the proposed algorithm (CF-GWO) against others in every experiment leakage. In most cases, the p-values were less than the significant level of 0.05, showing that CF-GWO was better comprehensively, with few exceptions.

• Bonferroni–Dunn analysis: This post hoc analysis measured the mean ranks of CF-GWO and all other algorithms relative to each other by assessing their performance across the datasets and optimization problems tackled. The findings suggested that CF-GWO was the top performer in almost all cases, and there were significant measures of its differences from its competitors, confirming its strength and flexibility.

Implications and contributions

The results suggest that CF-GWO can potentially disrupt the automated optimization of DCNNs by solving essential problems in a high-dimensional search space. The chaotic and fractal improvements increased search efficiency and outlined the need for such improvements to resolve the issues posed by diverse and complicated landscapes.

Limitations and future work

While it is clear that designing deep convolutional neural network (DCNN) architectures with the proposed Chaotic Fractal Grey Wolf Optimizer (CF-GWO) has benefits, some points still need to be discussed.

First, even though CF-GWO has shown better performance for several benchmark datasets, its efficiency for ultra-large datasets is still questionable. The computational cost involved in optimizing DCNNs will likely increase as the dataset and the depth of the architecture increase. This cost may lead to increased training times and operational costs in training on high-quality resolution datasets or one with millions of samples. There may be a need to improve the algorithm’s efficiency; therefore, future work should concentrate on enhancing the algorithm’s performance and implementing methods that will significantly reduce the computational effort required.

The second problem stems from incorporating chaotic maps and the fractal multi-scale search algorithm for exploration improvement. Implementing these approaches improves the probability of CF-GWO settling at some more easily reachable solutions, i.e., global optima. However, it makes the search strategy more sophisticated for sometimes more straightforward or better-defined solutions. The additional features may not always be helpful in other optimization exercises because they may be equally effective and considerably cheaper in more straightforward cases, such as routine GWO or basic optimization hyperparameters. This means that the performance features of the CF-GWO are likely to differ globally for each problem area.

Furthermore, not only did the research reveal that CF-GWO is appropriate for image classification tasks, but its application in other areas is still under consideration. For example, how effective is CF-GWO at designing neural networks in the case of natural language processing or reinforcement learning? In these areas, the optimization processes and spatial configuration may be different enough that the method presented needs further changes or modifications.

Lastly, even though the proposed method seems to work, it has not yet been tested in real-life situations with noisy or incomplete data. More factors will influence the performance of CF-GWO, such as data quality, imbalanced datasets, and the available hardware. The comprehensive validation of practical tasks will allow for evaluating the method’s reliability and real-life applicability.

Conclusion

The idea of using the CF-GWO for optimizing DCNNs was proposed in this research, which advanced the image categorization field to a certain extent. The proposed methodology of the GWO algorithm, together with the chaotic maps and fractal theories, makes it better than other optimization paradigms. Identifying a suitable vehicle for the representation of layer convolutionality in the domain of the wolf vectors was the first step taken in the process of the indicated codification; accordingly, the invention’s functionality was developed with the utilization of the applicability of the IP address. This was beneficial for a more efficient representation and showed to what extent our methodology can adapt when handling issues related to the architecture of neural networks.

Subsequently, the development of the new concepts continued with the help of the concept called “Enfeebled Layer,” which attempted to make the DCNNs more flexible for the introduction of different-length network designs. Another aspect of using problematic image classification tasks is the possibility of integrating different and complex data patterns.

The intentional integration of the chaotic learning techniques, which reinforced these improvements, disrupted the management of large datasets. In particular, the growth of all features of the learning process was essentially accelerated by transferring them to more quickly regulated small components, which the algorithm expanded and aimed at a deeper study of patterns.

To this purpose, many comparative studies were carried out to validate the proposed CF-GWO approach, employing nine standard image-classification datasets and twenty-three contemporary classifiers. It was shown that the proposed CF-GWO was significantly superior to the other algorithms by winning an incredible 87. The proposed approach is shown to have high accuracy in the experimental trials, performing at 37% of the overall number of trials, thus proving its stability and efficiency. Significantly, it demonstrated a noteworthy decrease in the average error metric, surpassing its closest opponent, EvoCNN, and emphasizing its dependability in practical scenarios.

Notwithstanding these gains, our investigation has revealed subtleties that necessitate additional academic scrutiny. One notable observation pertained to the difficulties experienced in classic GWO, particularly when attempting to find solutions that deviated significantly from zero in optimization issues. Proposals for solving the challenges in this field include fractal enhancements and chaotic maps. However, further discussion of the topic requires more study since the AVC strategy’s practical applications cannot be exhausted with the best categorization of images.

Hence, to proceed with further extensive investigations, researchers will probably explore the first DCNN architectural arrangements. These studies aim to establish the impact of the initial conditions on learning and adaptation processes. Adding fractal theory and chaotic maps broadens the range of applications for CF-GWO. In addition to image classification, this method has the potential to work in a challenging multi-objective, extended optimization problem environment and may make significant contributions there.

To sum up, the CF-GWO obtained notable improvements toward optimizing DCNN. While some general conclusions can be drawn, there are encouraging areas for further work in this field. One way to improve CF-GWO in high-dimensional and changing search spaces is to combine it with hybrid optimization methods such as the genetic algorithm or differential evolution. Furthermore, adaptive parameter tuning mechanisms for chaotic maps and dynamic adjustment of fractal search parameters in the CF-GWO context can be deployed to enhance the potential for optimization efficiency.

Additionally, using CF-GWO on big datasets like those used in medical imaging, self-driving cars, and natural language processing is exciting. It can also be changed to work well with real-time systems with strict time limits. Some research tasks may also involve extending CF-GWO for multi-objective optimization that requires balancing two or more objectives, such as accuracy and energy use, or working with transfer learning for fine-tuning tasks. Also, combining the CF-GWO method with explainable AI methodologies will allow finding the optimal meta-model architecture without loss of interpretability, which is very important when there are critical domains. Finally, more profound theoretical studies of chaotic and fractal mechanisms of CF-GWO itself point out new ways to enhance the dynamics of CF-GWO’s search and promote further development in meta-heuristic optimizations.