Introduction

Today, electrical energy is indispensable due to its ease of conversion to other forms of energy, efficient transmission, ease of control, and environmental considerations. The distribution system plays a crucial role by receiving electricity at a specific voltage from the generation or transmission stage and delivering it to consumers through distribution networks. However, distribution system losses pose significant challenges, mainly caused by high current values, low voltage levels, radial structure, and reactive power flow1,2,3. Reactive power compensation is a well-known method for minimizing grid losses and offers additional benefits such as power factor correction and voltage profile enhancement. Parallel capacitors strategically placed in the system can effectively compensate for reactive power and reduce losses4.

The placement and sizing of capacitor banks in distribution feeders is an important consideration for improving power factor, reducing losses, and enhancing voltage profiles. Several methods are commonly used for capacitor bank placement and sizing5,6,7. Capacitor banks can be placed at locations where there is a high concentration of inductive loads causing low power factor8. By analyzing the load characteristics and power factor measurements, the appropriate size and number of capacitor banks can be determined to achieve power factor correction. Also, capacitor banks can be strategically placed to mitigate voltage drop issues in distribution feeders. Voltage drop analysis helps identify sections of the feeder where capacitors can be installed to boost voltage levels, especially towards the end of long feeders or in areas with high load demand9,10. On the other hand, capacitor banks can help reduce losses in distribution feeders. Various optimization techniques, such as iterative load flow analysis or sensitivity analysis, can be employed to determine the optimal placement and size of capacitor banks that minimize losses in the system11,12,13. Finally, advanced optimization algorithms, such as genetic algorithms or particle swarm optimization, can be utilized to determine the optimal placement and sizing of capacitor banks. These algorithms consider multiple factors, including load characteristics, system constraints, and cost considerations, to find the most effective solution.

In13, the utilization of graph theory is employed to address the issue of reactive power compensation in radial distribution networks through the installation of capacitor banks. The primary objective of optimizing and compensating reactive power is to achieve voltage balance and enhance power quality within the network. The compensation of unbalanced networks stands as a critical goal in distribution feeders. Simulation results demonstrate that network modifications and voltage balancing lead to a reduction in losses. In14, the particle swarm optimization algorithm is utilized to tackle the problem of capacitor bank placement in distribution networks. This article employs the particle swarm algorithm to simultaneously minimize feeder losses, voltage deviations in buses, and compensate for reactive power. The study is conducted on the IEEE 33-bus standard feeder. Reference15 investigates novel approaches to the location and sizing of capacitor banks in radial distribution feeders. The objective of positioning and determining the capacity of parallel capacitors is to diminish ohmic losses in feeders and enhance the network’s voltage profile. Simulation results indicate that the extensive and individual placement of parallel capacitors yields improvements in the research objectives compared to a centralized and complex capacitor configuration. Reference16 evaluates the impact of employing parallel capacitors with varying permeability levels on the economic and technical parameters of distribution networks. The utilization of parallel capacitors enhances the power factor and reduces reactive power flow through the lines, resulting in decreased ohmic losses, improved voltage profiles, and enhanced power quality indicators. However, this reference highlights that improper placement and suboptimal capacity of capacitors can lead to increased losses or network instability. Reference17 focuses on reactive power compensation in distribution feeders with the aim of minimizing electrical energy losses. The installation of parallel capacitors in radial distribution networks is proven to balance the network, reduce ohmic losses, and improve the loading capacity of distribution lines. Reference18 mixed integer linear programming (MILP) to determine the optimal installation locations for parallel capacitors in distribution networks. The optimization objective in this study is to minimize ohmic feeder losses, with voltage deviation considered as a constraint in the simulations. The research is conducted on two standard radial distribution feeders, one with 33 buses and the other with 69 buses. Simulation results demonstrate that compensating reactive power through parallel capacitors leads to minimal losses in the distribution system.

Reference19 studies hybrid algorithms for reactive power compensation in renewable-integrated distribution networks. Therefore, the authors suggest combining the advantages of metaheuristic algorithms like Genetic Algorithms and Particle Swarm Optimization in a hybrid way and consider it for reactive power management in renewable energy integrated grids. The proposed scheme is particularly adaptable to high penetration networks containing intermittent renewable energy sources to mitigate power loss and enhance voltage stability. Results show that this two-part approach considerably improves performance under diverse operational scenarios, minimizing energy losses and improving voltage profiles.

Reference20 focuses on the modeling of dynamic loads effect on smart grid voltage stability. The authors consider dynamic loads in real time and assess the influence on voltage stability in the grid. They discovered that voltages stutter when the loads are dynamic—a phenomenon that may play a role in grid instability. A potential solution is more adaptive reactive power compensation strategies alone or based on data-driven load condition prediction, as indicated by the results from the study. It also highlights that in such volatile environment, application of appropriate capacitors location strategies are critical for the provision of stable and reliable voltage support.

Reference21 provides a method to optimize reactive power management for handling renewable energy variability. The authors proposed a multi-objective optimization method of minimizing energy losses and operation costs along with voltage stability in the system. The study targets the problem of the reactors of this technology: Agend of renewable energy like wind turbines and solar panels, wind an explosion voltages. For this approach, the IEEE 33-bus system is used as a test system that exhibits remarkable reduction of Total Energy loss (TEL), along with improvement of a voltage profile when compared with previous classical algorithms.

In22, a multi-objective particle swarm optimization (MOPSO) method was introduced to determine the optimal placement of capacitor banks in distribution networks. The results revealed that the MOPSO approach achieved a substantial reduction in energy losses and significantly enhanced voltage profiles when compared to conventional techniques. Similarly, in23, a hybrid approach combining genetic algorithms and particle swarm optimization (PSO) was proposed for capacitor placement, which led to a noticeable decrease in power losses. The study in24 also utilized a genetic algorithm for determining the optimal location of capacitor banks in radial distribution networks, demonstrating a considerable reduction in operational costs and improved voltage stability.

Moreover, the research conducted in25 combined two different optimization algorithms to enhance the accuracy and efficiency of capacitor placement in distribution networks. In26, the application of PSO for capacitor bank sizing and placement showed promising results in reducing power losses and improving voltage profiles. Additionally, a modified version of the PSO algorithm was introduced in27 to improve optimization accuracy and avoid premature convergence, resulting in a more efficient power distribution system.

In28, a hybrid optimization approach integrating PSO and simulated annealing was proposed for capacitor bank placement, yielding better performance in minimizing energy losses and stabilizing voltage levels. Another study in29 applied a genetic algorithm for optimizing capacitor placement and sizing, which effectively reduced operating costs and improved power factor correction. Furthermore, a comprehensive review presented in30 explored various capacitor placement strategies, emphasizing the effectiveness of different optimization algorithms in reducing power losses and enhancing voltage profiles. In31, a multi-objective PSO method was introduced to optimize capacitor bank placement, showing significant improvements in voltage stability and energy efficiency. The proposed approach demonstrated superior performance in minimizing power losses and promoting sustainable power distribution.

The study in32 introduced a Many-Objective Marine Predators Algorithm (MaMPA) for solving single-objective, multi-objective, and many-objective optimal power flow (OPF) problems. The algorithm incorporated advanced techniques such as non-dominated sorting and crowding mechanisms to enhance optimization performance. Simulation results on IEEE 30- and 118-bus systems confirmed that MaMPA outperformed existing methods by reducing operational costs by up to $1000 per hour and achieving up to 85.23% superiority in Pareto front improvement. Similarly, in33, a Two-Archive Harris Hawk Optimization (TwoArchHHO) algorithm was proposed to solve many-objective optimal power flow (MaOOPF) problems. By introducing a two-archive mechanism in the Harris Hawk Optimization (HHO) approach, the authors significantly improved search efficiency. Experiments conducted on IEEE 30-, 57-, and 118-bus systems demonstrated the superior performance of TwoArchHHO in achieving high-quality Pareto fronts and providing optimal trade-off solutions, with hypervolume improvements ranging from 33.96 to 99.59%.

Another relevant study34 introduced the Crayfish Optimization Algorithm (COA) for optimizing the placement and capacity of multiple battery energy storage systems (BESSs) in distribution networks with high penetration of distributed generation (DG). The primary goal was to minimize total system costs, enhance voltage stability, reduce peak demand, and decrease power losses. The simulation results on IEEE 33- and 69-bus systems confirmed that deploying multiple BESS units, although costly, resulted in higher performance compared to single-unit deployment. The COA approach showed superior results compared to PSO and SSA, achieving up to 43.43% reduction in voltage deviation, 50.00% reduction in peak demand, and 12.21% reduction in power losses in the IEEE 33-bus system.

Increasing electrification and integration of advanced technologies in modern smart grids cause load to change frequently and unpredictably. These dynamic conditions present challenges to traditional capacitor bank placement methodologies which, by and large, are developed for static or quasi-static operation. Renewable energy sources like solar and wind can create variability and intermittency on the grid, leading to voltage fluctuations and power quality concerns. In fact, the placement of capacitor banks must take into consideration these factors so that there is voltage stability and reactive power compensation. Second, the dynamic loads and renewable integration further complicate the multi-objective optimization problem for the placement of the capacitor bank—the conflicting objectives of loss reduction, cost savings, and improvement in the voltage profile must be satisfied.

In previous studies, various optimization methods have been proposed for multi-objective problems in power distribution systems. Although three methods have achieved success in certain applications, there are limitations. Two meta-heuristic algorithms can be compared in this way, for example, NSGA-II suffers from slow convergence and high computational costs, particularly in large-scale and dynamic problem settings, while MO-GWO is a local optima trapping algorithm, which requires manual tuning of parameters, and thus it is not as adaptable to complex tasks such as placement of capacitor banks.

Among the various optimization algorithms, this study selects MOPSO as the appropriate algorithm for optimally determining the placement and sizing of capacitor banks. The major benefit of MOPSO is that it provides a good balance between exploration and exploitation, improving convergence speed and accuracy toward the best solutions while optimizing various objectives such as the reduction of loss, the enhancement of the voltage profile, and the reduction of cost at the same time.

Moreover, the MOPSO algorithm has the ability to adapt to dynamic system conditions such as load changes and renewable energy sources, which suits modern distribution networks with novel characteristics. The algorithm itself is highly efficient in solving complex, multi-objective optimization problems where the objectives have conflicting goals, especially in applications within power distribution systems.

In recent years, Battery Energy Storage Systems (BESSs) have gained significant attention for their role in improving energy efficiency and reducing costs when integrated with renewable energy sources. However, in this study, we focus on the use of capacitor banks due to their specific advantages in distribution networks, particularly for reactive power compensation and voltage regulation. Capacitor banks are more cost-effective, easier to maintain, and have a longer operational life compared to BESSs. While BESSs provide the flexibility of both active and reactive power support, their higher costs, complexity, and shorter lifespan make them less attractive in scenarios where the primary goal is to enhance energy efficiency through reactive power management. Furthermore, BESSs require more advanced control systems and greater investment, making them less suitable for applications where only reactive power compensation is needed. In this context, capacitor banks provide a simpler and more efficient solution, especially in the scope of our study.

The positioning and sizing of capacitor banks can be approached with various objectives that may either align or contradict one another. While single-objective algorithms are suitable for pursuing a singular objective, multi-objective algorithms are necessary to address multiple objectives simultaneously. This study presents an adapted variant of the multi-objective particle swarm algorithm to optimize the selection of capacitor bank locations and capacities within the distribution feeder. The proposed approach aims to achieve diverse objectives, including loss reduction, operating cost reduction, and voltage profile enhancement.

Based on the explanations provided in the previous papers and the innovations presented in the current paper, the Table 1 compares various approaches for the location and sizing of capacitor banks in distribution networks. Table 1 analyzes the strengths and weaknesses of each method and evaluates how the performance is improved in comparison to existing approaches.

Table 1 Comparative analysis of capacitor bank placement techniques in distribution networks.
Full size table

The proposed research introduces a novel approach to the optimal placement and sizing of capacitor banks in distribution networks, leveraging the Multi-Objective Particle Swarm Optimization (MOPSO) algorithm. The key innovations of this study are outlined as follows:

  • Enhanced Optimization Efficiency: Unlike traditional optimization techniques such as Genetic Algorithm (GA) and conventional Particle Swarm Optimization (PSO), the proposed MOPSO-based method improves the balance between exploration and exploitation, leading to faster convergence and more accurate solutions.

  • Multi-Objective Optimization Framework: Unlike previous studies that focus primarily on single-objective optimization, this research simultaneously optimizes multiple conflicting objectives, including power loss reduction, voltage stability improvement, and cost minimization, ensuring a more comprehensive and effective solution for distribution network enhancement.

  • Dynamic Adaptability to Smart Grid Conditions: The proposed approach is designed to operate effectively under dynamic network conditions, considering load variations and the integration of renewable energy sources. This adaptability makes it particularly suitable for modern smart grid applications.

  • Scenario-Based Validation and Benchmarking: The effectiveness of the method is evaluated under various operational scenarios on standard IEEE test systems. The comparative analysis demonstrates that the proposed algorithm outperforms existing methods in terms of solution quality and computational efficiency.

These innovations collectively distinguish this research from previous works and establish its significance in advancing the field of capacitor bank optimization in smart distribution networks.

Section “Principal of distribution reactive power compensation” briefly discusses the principal of distribution feeders reactive power compensation. Section “The objective function and the constraints” expresses the problem’s objective functions and constraints as a problem formulation. Section “Multi-objective particle swarm optimization (MOPSO)” introduces the proposed algorithm for optimizing the objective function. Section “Simulation and results analysis” implements the proposed strategy on IEEE 33-bus and IEEE 69-bus distribution feeders in two scenarios. Finally, conclusions and suggestions for future studies are made in section “Conclusion”.

Principal of distribution reactive power compensation

For decades, distribution networks have been built and utilized based on experience. Historically, specialists have placed a premium on the generation and transmission sectors. Thus, while generation and transmission system problems have been addressed to some extent, due to a lack of attention paid to distribution networks, this segment of the power system has remained unchanged in terms of form and function throughout the years. The structure of a radial distribution network is depicted in Fig. 1.

The process of identifying ideal locations and sizes for capacitor installations within a radial distribution network is known as strategic capacitor deployment (SCD). The primary objective of SCD is to enhance economic efficiency by curbing power and energy losses while also factoring in the initial expenses associated with capacitor installation. Successful implementation of SCD necessitates adherence to various physical, engineering, and operational limitations, thus rendering it a meticulously constrained optimization endeavor.

Fig. 1
figure 1

Structure of a radial network.

Full size image

The equilibrium prerequisites demand that the distribution network maintains adequate provision for active and reactive power to meet load demands and compensate for feeder segment power losses. These requisites are articulated through active and reactive power flow equations governing each network node. Furthermore, limitations on voltage levels throughout the feeder impose stringent constraints. Capacitor placement and sizing are subject to financial and physical considerations, including the requisite minimum number of installations at bus locations to fulfill system requirements effectively.

Efficient management of reactive load components is facilitated by strategically placing shunt capacitors, which counteract lagging currents with leading counterparts. Optimal placement, ideally positioned at the core of reactive loads, effectively relieves the system of KVAR, thereby freeing up generator capacity for active power loads. Poorly positioned capacitors, whether excessively distant or proximate to inductive load centers, may still offer reactive power support but fail to maximize voltage improvements and loss reductions. Given the significant capital outlay associated with shunt capacitor installations, the selection of installation sites is crucial to minimize capital expenses, maximize power loss savings, and ensure optimal node voltage profiles. This study endeavors to address the challenge of strategic capacitor deployment by determining the minimum requisite number of installations and identifying optimal locations and sizes within radial distribution networks. For this purpose, the objective functions and constraints should be provided.

Shunt capacitors represent one of the most efficient and economical way of reactive power compensation in distribution networks, and this is the subject of this study. Nevertheless, we cannot ignore some recent technological developments like Energy Storage Systems (ESS) and Active Network Management (ANM) for network performance optimization, particularly for dynamic applications with renewable energy integration. Future studies should be carried out even to compare these emerging technologies with shunt capacitors as alternatives.

The objective function and the constraints

It is vital to choose a proper objective function to locate capacitor banks optimally utilizing optimization techniques. The capacitors employed in this investigation are fixed. This assumption facilitates the optimization process and closely corresponds to practice in distribution networks, where fixed capacitor banks are typically deployed due to lower cost and operational simplicity. In this paper, the objective function is defined as a function of line losses and the voltage across the bus. The objective is to minimize this function35.

$${f}_{1}=\sum _{i=1}^{{N}_{branch}}{R}_{i}{I}_{i}^{2}$$
(1)
$${f}_{2}= \sum _{i=1}^{n}\left|{v}_{i}-{v}_{nom}\right|$$
(2)
$${f}_{3}={C}_{Loss}+{C}_{Cap}$$
(3)

In Eq. (1), f1 is a loss function, where R is the resistance of each branch and i denote the active and reactive current flowing through that branch. The voltage profile function is also the second objective function (total voltage deviation). \({v}_{i}\) is the voltage of the ith bus in p.u., and Vnom is the nominal voltage in p.u. (which is assumed to be 1), i is the bus number and n is the number of buses. Voltage constraints are intrinsic to the optimization-based framework and explicitly represented in the model’s mathematical descriptions. To keep the system stable and reliable, these limits guarantee that the voltage at all buses stays within bounds, which is ultimately defined as [0.95 pu, 1.05 pu]. In Eq. (3), CLoss is the cost per kilowatt of energy lost in the line, and CCap is the cost of each megawatt of capacitor installed in the system. The objective functions exhibit conflicting characteristics. As an example, the inclusion of capacitor banks in the distribution feeder can lead to loss reduction, albeit with an associated rise in costs.

Capacitor banks must be connected to the existing network in a way that does not compromise the network’s normal operation. This means that the network is up and running properly and that the demand is being responded to properly. There is a limit to the amount of power that lines can transmit. As a result, the amount of current (or power) flowing through the network’s lines must not be greater than the lines’ capacity36.

$$\left|{I}_{ij}\right|\le \left|{I}_{ij}^{max}\right|$$
(4)

For Eq. (4), \({{\rm I}}_{ij}^{max}\) is the maximum allowed the current to pass through the line between uses i and j. Also, capacitor banks should generate a reactive power in the following range.

$${Q}_{\text{C}\text{a}\text{p}\text{i}}^{\text{m}\text{i}\text{n}}\le {Q}_{\text{C}\text{a}\text{p}\text{i}}\le {\text{Q}}_{\text{C}\text{a}\text{p}\text{i}}^{\text{m}\text{a}\text{x}}$$
(5)

In Eq. (5), \({Q}_{Capi}\) is the reactive power generated by the ith capacitor bank. If there is a limit for the number of installed capacitor banks, this limit is introduced in the objective function.

$${N}_{Cap}\le {N}_{Cap}^{Max}$$
(6)

Multi-objective particle swarm optimization (MOPSO)

Due to the PSO method’s exceptional effectiveness in addressing single-objective optimization issues, scientists and researchers have attempted to utilize it to solve multi-objective problems, and multiple variations of the PSO algorithm for solving multi-objective problems have been reported. Professor Coello and colleagues’ work is one of the most well-known algorithms introduced in this field. They have named their algorithm MOPSO, a term that is used only for this method37.

This algorithm uses a mutation operator that selects a member of the population and changes one of its dimension values to a value between allowed values. In addition, an elitism policy is defined to keep the superior and dominant results in the algorithm iterations. The dominant responses are stored in the external archive of the grid structure. Proper management of the archive results in a diverse population and proper distribution of the solutions.

Pbest and Gbest are selected based on a particular mechanism. The multi-objective algorithm cannot select a particular Pbest and Gbest as the best solution, because all dominant responses are of the same superiority. Pbest is updated only when a new particle dominates its previous value. Gbest is also selected among the dominant solutions of the archive38.

Because many objective functions must be maximized simultaneously in multi-objective problems, the problem will typically have more than one optimum solution, dubbed Pareto optimal solutions. The Pareto optimal concept can be summarized as follows:

$$\overline{{x}_{0}}=({x}_{1},{x}_{2},\ldots ,{x}_{n})$$
(7)

An optimum is Pareto if there is an acceptable domain member for every other x and i = 1, 2…, k (for a minimization problem):

$${\forall }_{\text{i} \in 1} ({f}_{i}\left({\overline{x}}_{*}\right)\le f\left({\overline{x}}_{i}\right))$$
(8)

In which n is the number of variables of the decision space and k is the number of the objective functions. In other words, \({\overline{x}}_{*}\) is Pareto optimal if there are no other \({\overline{x}}_{i}\)that worsen an objective function for improving some objective functions. The Pareto optimal solutions are known as NON-POST solutions.

The value of the congestion distance for each solution is an estimate of the density of the surrounding solutions. To calculate the congestion distance, we first sort the solutions in descending order according to one of the objective functions. To calculate the congestion distance attributed to each point on a front, the previous and subsequent points regarding the objective functions are selected, and a rectangle, as shown in Fig. 2 is formed. If the number of objective functions is more than 2, the desired points will form a cube. As shown in this figure, the numbers on the Pareto front are shown in solid form, and the other solutions are represented by hollow circles38.

Fig. 2
figure 2

The dominant and the dominated particles of the MOPSO algorithm38.

Full size image

To calculate the congestion distance of the ith solution in this figure, a rectangle is drawn in which the next and previous solutions to the two objective functions are in the corners. The congestion distance for this point is equal to the mean of the sides of this rectangle. The shorter the congestion distance, the greater the density of the solutions. It should be noted that where the problem has more than two objective functions, the points i-1 and i + 1 will not be the same for all objective functions.

Appropriate selection of optimal universal solutions is critical in a multi-objective particle swarm algorithm, as it affects the algorithm’s convergence and capacity to achieve a wide variety of non-post solutions in the decision space. The restricted external archive in the MOPSO algorithm stores non-post solutions. To identify optimal solutions, the particle swarm must not condense at specified spots to completely cover the search space. To do this, non-post solutions with a longer congestion distance are prioritized in this technique. Non-post solutions are sorted in the external archive by the level of congestion. Then, in each phase, one of the few solutions at the top of the archive is randomly selected (for example, 10% at the bottom of the archive). This descending order in the external archive also assists us in another situation, namely when the archive is full. In such instances, one of the non-post solutions at the bottom of the archive is randomly chosen and substituted with a new non-post solution discovered in the most recent iteration39,40,41,42,43.

The performance of optimization algorithms relies on the accurate determination of their parameters. If these parameters are not selected correctly, there is a risk of encountering issues such as getting stuck in local optima or experiencing non-convergence of the algorithm. In the modified version of the MOPSO algorithm, the coefficient C1, C2 and ω are dynamic and variable in each iteration. Using the dynamic coefficients have increased the accuracy of the algorithm. In the modified version of the MOPSO algorithm, the coefficients are dynamic and variable in each iteration. Using the dynamic coefficients have increased the accuracy of the algorithm. The parameters are updated as follow:

$$\text{C}1=2.04-\left(\frac{\text{I}\text{t}\text{e}}{{\text{M}\text{a}\text{x}}_{\text{I}\text{t}\text{e}}}\right) * 1.95$$
(9)
$$\text{C}2=2.04-\left(\frac{\text{I}\text{t}\text{e}}{{\text{M}\text{a}\text{x}}_{\text{I}\text{t}\text{e}}}\right) * 1.95$$
(10)
$${\upomega }=0.94-\left(\frac{\text{I}\text{t}\text{e}}{{\text{M}\text{a}\text{x}}_{\text{I}\text{t}\text{e}}}\right) * 0.75$$
(11)

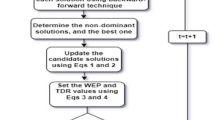
Where, Ite is iteration number and MaxIte is maximum number of iterations. The steps for determining the location and capacity of the reactive power resources in the unbalanced distribution system using the MOPSO algorithm are as follows:

Step 1. Enter the parameters of the MOPSO algorithm (number of particles, iteration, Rep, C1, C2 …).

Step 2. Enter the information of the study network (network configuration, active and reactive load power in each bus, line parameters).

Step 3. Initialize the parameters randomly. Each particle describes the location and capacity of the reactive power resources, which are selected randomly in the allowed range.

Step 4. Execute power flow and calculate the objective functions.

Step 5. Check the limits; if the limits are not observed, apply the penalty factor.

Step 6. Determine the best personal experience, and best swarm experience and determine the dominant particles based on these values.

Step 8. Substitute the new particles in the objective functions and calculate the objective functions again.

Step 9. Update algorithm parameters.

Step 10. If the termination condition is not met (number of iterations), go to Step 6 and continue.

Step 11. The end.

The proposed modified version of the multi-objective particle swarm algorithm exhibits superior accuracy in tackling optimization challenges, with its Pareto front particles demonstrating a uniform distribution. Additionally, the pre-initial algorithm boasts exceptional precision and resilience against local optima entrapment as distinctive attributes. In this paper, the MOPSO algorithm was chosen for its fast convergence, lower computational complexity, and ability to avoid local optima. These features make MOPSO an ideal choice for large and complex optimization problems, particularly in the context of power distribution network optimization44,45,46,47,48.

Multi-Objective Particle Swarm Optimization (MOPSO) has been widely applied in solving complex optimization problems due to its ability to efficiently explore the search space and maintain a well-distributed Pareto front. However, in recent years, novel metaheuristic algorithms such as Grey Wolf Optimizer (GWO), Whale Optimization Algorithm (WOA), Multi-Verse Optimizer (MVO), and Hybrid Evolutionary Algorithms have been introduced, offering improved convergence rates, reduced computational costs, and enhanced exploitation mechanisms.

One key advantage of MOPSO is its ability to efficiently handle multi-objective trade-offs while maintaining solution diversity. However, traditional MOPSO can suffer from premature convergence and local optima stagnation, particularly in high-dimensional search spaces. Additionally, its computational complexity may increase due to the need for external archives to store Pareto-optimal solutions. In contrast, newer algorithms often integrate adaptive mechanisms and hybridization strategies to enhance performance49,50,51,52,53.

To overcome MOPSO’s inherent limitations, this study proposes an improved dynamic-parameter MOPSO that incorporates adaptive inertia weight control and leader selection mechanisms. These enhancements help prevent premature convergence, improve computational efficiency, and refine the optimization process, making it highly suitable for capacitor bank placement in power distribution networks. The comparative results further confirm the superiority of the modified MOPSO in terms of solution accuracy, convergence behavior, and computational efficiency.

Simulation and results analysis

The simulations are done for IEEE 33-bus and IEEE-69-bus distribution feeders in two scenarios. The optimization results achieved by the proposed modified MOPSO algorithm are compared with the non-dominated sorting genetic algorithm (NSGAII). Multi objective differential evolution algorithm (MODE) and multi objective gray wolf optimization algorithm (MOGWO). The algorithms parameters are included in Table 2.

Table 2 The optimization algorithm parameters.
Full size table

First scenario simulation results analysis (IEEE 33-bus)

The IEEE 33-bus power system single lie diagram is depicted in Fig. 3. This is a radial network connected to the upstream system via a step-down transformer.

Fig. 3
figure 3

A single-line diagram of the IEEE 33-bus feeder.

Full size image

The IEEE 33-bs feeder’s rated active and reactive load are 3.72 MW and 2.3 MVar respectively. Figure 4 illustrates the power system load profile.

Fig. 4
figure 4

IEEE 33-bus load profile.

Full size image

The minimum power requirement of the load is below 0.58 p.u, while the peak load is assumed to be 1 p.u. Figure 5 illustrates the active losses of the lines based on variations in the feeder load. The total ohmic loss in this feeder is estimated to be 1618 KW for 24 h.

Fig. 5
figure 5

IEEE 33-bus active power losses.

Full size image

The IEEE 33-bus voltage profile is shown in Fig. 6. The minimum voltage amplitude is 0.86 p.u.

Fig. 6
figure 6

IEEE 33-bus voltage profile.

Full size image

This study shows these Pareto fronts for the multi-objective optimization process with the MOPSO algorithm, and indicates the best size and placement of capacitor banks in the IEEE 33-bus and IEEE 69-bus distribution feeders. These Pareto fronts represent favorable trade-offs among diverse objectives that were taken into account while optimizing. The main objectives to optimize in this work are energy losses, operation costs and voltage profile. After solving the optimization problem using multi-objective optimization algorithms and estimating the optimal capacity and installation location of the capacitor banks in the IEEE 33-bus feeder, the Pareto front is obtained as depicted in Fig. 7.

Fig. 7
figure 7

Pareto fronts in the first part of optimization.

Full size image

In Fig. 7, the Pareto fronts attained in the case of the IEEE 33-bus system are presented. These fronts represent the best compromise between reducing losses and reducing the cost to operate the system, whilst also maintaining or improving the voltage profile. The results illustrated in the figure present the Pareto fronts that depict a series of optimum solutions for determining the optimal size and location of capacitor banks in the power distribution network. From the results obtained in the Pareto front, the final optimal solution has been selected, and its corresponding values are presented in Table 3.

Table 3 Optimization results for the IEEE 33-bus feeder.
Full size table

Based on the findings, bus 9, which has a power capacity of 1435 KVar, and bus 15, with a capacity of 785 KVar, were chosen by the NSGAII algorithm. As a result, the ohmic feeder losses decreased by 30% to 1132 kW. The cost of operation decreased to 2137$, and the total voltage deviation decreased to 7.78 p.u. The MODE algorithm is chosen bus 14 with a capacity of 1280 KVar and bus 27 with a capacity of 785 KVar. In this scenario, the losses of the resistive feeder have been decreased by 25.96% to 1198 kW. The operational cost has been reduced to 2198$, and the voltage variation has been mitigated to 6.18 p.u.

In the given scenario, buses 17 and 31 are chosen by the MOGWO algorithm with capacities of 1385 KVar and 970 KVar respectively. The ohmic feeder have experienced a significant reduction of 31.81%, resulting in a decrease to 1103 kW. Moreover, the operating cost has been effectively lowered to 2089$, and the total voltage deviation has been successfully minimized to 5.63 p.u. Finally, the proposed MOPSO algorithm selected buses 15 and 30 for capacitor banks with capacities of 1405 KVar and 935 KVar respectively. As a result, the loss has a reduction of 25.96%, resulting in a decrease to 1031 kW. Furthermore, the operational expenses have been effectively decreased to 2063$, and the deviation in voltage has been mitigated to 5.14 p.u. The power system losses after installing capacitor banks are shown in Fig. 8.

Fig. 8
figure 8

IEEE 33-bus loss after reactive power compensation.

Full size image

As shown in Fig. 8, after the installation of capacitor banks in feeder 33 buses, losses in most lines have decreased. Next, in Fig. 9, the voltage profile is shown after reactive power compensation by installing capacitor banks.

Fig. 9
figure 9

IEEE 33-bus voltage profile after reactive power compensation.

Full size image

As illustrated in Fig. 9, after the installation the capacitor banks, the network voltage profile has been improved. The minimum voltage amplitude in the power system has reached more than 0.96 p.u.

Second scenario simulation results analysis (IEEE 69-bus)

The second scenario of the simulations involved conducting investigations on a standard IEEE 69-bus distribution system. A visual representation of this feeder can be observed in Fig. 10, illustrating the linear diagram. The figure provides clear visibility of the bus and line numbers. As part of the analysis, the slack bus has been designated as bus number one.

Fig. 10
figure 10

A single-line diagram of the IEEE 69-bus feeder.

Full size image

The feeder has a rated load of 3.8 MW and 2.69 MW. The per-unit profile of the feeder load for 24 h has been graphically presented in Fig. 11.

Fig. 11
figure 11

IEEE 69-bus load profile.

Full size image

It can be observed that the network experiences a lower load during the early hours of the day, which gradually increases over time. The minimum load requirement is below 0.58 p.u, while the peak load is assumed to be 1 p.u. To assess the impact on the ohmic feeder, Fig. 12 showcases the variations in feeder losses corresponding to the changes in load throughout the 24-h study period. The total ohmic loss in this feeder is estimated to be 1226.7 kW.

Fig. 12
figure 12

IEEE 69-bus active power losses.

Full size image

The IEEE 69-bus voltage profile is illustrated in Fig. 13. The total voltage deviation of the feeder in 24 h is equal to 13.18 p.u.

Fig. 13
figure 13

IEEE 69-bus voltage profile.

Full size image

Following the optimization algorithms’ utilization in determining the positions and size of the capacitor banks within the 69-bus feeder, the Pareto fronts are obtained, resembling the visual representation illustrated in Fig. 14.

Fig. 14
figure 14

Pareto fronts in the first part of optimization.

Full size image

Similarly, Fig. 14 displays the Pareto fronts for the IEEE 69-bus system, which were obtained using the same multi-objective optimization approach (MOPSO) to determine the optimal placement and sizing of capacitor banks. These fronts, like those in Fig. 7, represent the optimal solutions for the three primary objectives. Notably, compared to Fig. 7 (IEEE 33-bus), the number and variety of optimal solutions are greater, which is due to the higher complexity and the need for more precise adjustments in a system with more buses. The final optimal solution has been determined based on the outcomes obtained from the Pareto front analysis. The corresponding values of the selected solution have been compiled and presented in Table 4.

Table 4 Optimization results for the IEEE 69-bus feeder.
Full size table

The NSGAII algorithm identified bus 19 and bus 59 as the optimal choices, with power capacities of 1350 KVar and 470 KVar respectively. Consequently, the losses in the resistive feeder dropped by 24.02% to 932 kW. The operational cost decreased to 1673$, and the total voltage deviation reduced to 10.45 p.u. Similarly, the MODE algorithm selected bus 17 with a capacity of 1365 KVar and bus 57 with a capacity of 540 KVar. This led to a reduction in losses by 25.17% to 918 kW. The operational cost decreased to 1673$, and the total voltage deviation was mitigated to 10.83 p.u. In another case, the MOGWO algorithm selected buses 14 and 54 with capacities of 1270 KVar and 635 KVar respectively. The losses in the ohmic feeder experienced a significant reduction of 23.78%, resulting in a decrease to 935 kW. Additionally, the operating cost was effectively lowered to 1714$, and the total voltage deviation was successfully minimized to 9.79 p.u. Finally, the proposed MOPSO algorithm chose buses 12 and 60 for the capacitor banks, with capacities of 1385 KVar and 430 KVar respectively. This led to a loss reduction of 26.06%, resulting in a decrease to 907 kW. Furthermore, the operating expenses were effectively decreased to 1507$, and the total voltage deviation was mitigated to 9.32 p.u. The power system losses following the installation of capacitor banks are visually represented in Fig. 15.

Fig. 15
figure 15

IEEE 69-bus loss after reactive power compensation in.

Full size image

Figure 15 demonstrates the noticeable reduction in losses across multiple lines following the successful implementation of capacitor banks in feeder 33 buses. Furthermore, Fig. 16 displays the voltage profile subsequent to the compensatory measures taken through the installation of capacitor banks to regulate reactive power.

Fig. 16
figure 16

IEEE 69-bus voltage profile after reactive power compensation.

Full size image

Comparative simulation analysis

Figures 17 and 18 provide a comparative visualization of the optimization results for both IEEE 33-bus and IEEE 69-bus networks. These figures clearly illustrate the enhancement in system performance due to capacitor bank placement, demonstrating reductions in power loss and voltage deviation while optimizing the overall cost. The base case, representing the system before capacitor installation, is compared with results obtained using four optimization algorithms: NSGAII, MODE, MOGWO, and MOPSO. As shown in the figures, the optimized scenarios exhibit significant improvements, particularly in loss reduction and voltage profile enhancement, validating the effectiveness of the proposed optimization approach.

In multi-objective optimization problems, evaluating the quality of Pareto-optimal solutions is essential. One of the most reliable metrics for this purpose is the hypervolume (HV) indicator, which assesses both convergence and diversity of the Pareto front. A higher hypervolume value indicates a better spread of solutions, implying superior optimization performance. Table 5 presents the computed hypervolume values for four optimization algorithms applied to the IEEE 33-bus and IEEE 69-bus feeders.

MOPSO achieves the highest hypervolume values (0.821 and 0.779) for both test systems, demonstrating superior performance in maintaining a well-spread and high-quality Pareto front.

MOGWO (0.793 and 0.751) also performs well, producing competitive Pareto-optimal solutions.

MODE and NSGAII exhibit lower hypervolume values, indicating that their solutions are less diverse and not as well-distributed in the objective space.

Fig. 17
figure 17

Comparison of key performance metrics before and after capacitor bank installation for the IEEE 33-bus feeder (a) loss reduction percentage, (b) total cost ($), (c) total power loss (kW), and (d) total voltage deviation (pu).

Full size image
Fig. 18
figure 18

Comparison of key performance metrics before and after capacitor bank installation for the IEEE 69-bus feeder (a) loss reduction percentage, (b) total cost ($), (c) total power loss (kW), and (d) total voltage deviation (pu).

Full size image

These findings confirm that MOPSO provides an optimal trade-off between loss reduction, cost minimization, and voltage deviation, making it the most effective approach for capacitor bank placement in distribution networks.

Table 5 Performance comparison of optimization algorithms using hypervolume indicator.
Full size table

Conclusion

The use of capacitor banks in distribution feeders is an efficient approach to minimizing losses, decreasing the expense of operation, and optimizing the voltage profile of the electrical network. In the feeder capacitor banks placed to compensate for reactive power and improve power factor. Even so, a proper sizing and placement of capacitor banks will yield better results. This study proposes a multi-opened particle swarm optimization (MOPSO) method with dynamic parameters for optimum setting of two capacitor banks in the standard IEEE 33-bus and IEEE 69-bus distribution feeders, and then the optimization problem is solved. This will aim to minimize losses and operational costs while enhancing the voltage profile at the same time. The simulation results prove that the loss of electrical energy can be reduced by more than 25% through proper placement and compensation with optimum capacitor banks in different distribution feeders for a better voltage profile. This in turn can help the organisation to save around 20% in their operating costs. Plus, many of these enhancements also have the side effect of reducing carbon emissions. It accentuates all proposed MOPSO algorithm denouements covered in greater depth and outperformed all application establishing prior optimization methods to fathers (MOPSO) denouements. Future studies may focus on implementing the application of the D-STATCOM instead of capacitor banks placed in distribution feeders. These approaches would help researchers see how D-STATCOM compares to the results from this paper, based on cost, loss and voltage deviation values.