Introduction

Bovine milk is an important source of nutrients in human nutrition and fat is one of the main components in bovine milk. Milk fat contains a large number of individual fatty acids (FA) which can be identified based on their number of carbons, the saturation of their carbon chain, and the conformation of double bonds. Milk fat consists of around 70% of saturated FA (SFA), 25% monosaturated FA (MUFA), and 5% polyunsaturated FA (PUFA)1. Milk FA composition is one of the most important aspects of milk nutritional quality and has gained the interest of manufacturers and consumers as it influences nutritional, physical and flavor properties of dairy products2. The increasing consumer interest on the nutritional quality of dairy product pushes toward the inclusion of fine milk composition traits among breeding goals of dairy cattle. In particular, milk PUFA like isomers of C18:2n9c11t and C18:2n10t12c (Conjugated linoleic acid), C20:4n6 (Arachidonic acid), C20:5n3 (Eicosapentanoic acid) and C22:5n3 (Docosapentaenoic acid) have known positive associations with a range of human health conditions like cardiovascular diseases, anticancer effects, antiadipogenic, antiatherogenic, antidiabetogenic and anti-inflammatory3,4. For these reasons, dairy producers are looking for ways to optimize milk beneficial components. Genetic variability of FA indicates the possibility of using genomic selection to improve milk traits5.

Studies in dairy production system were carried out looking for efficient strategies to optimize milk beneficial components such as milk fatty acids. They indicated that the milk FA composition can be modified by altering dietary or feeding supplementation in the dairy production system6,7,8; however, genetic improvement for milk fatty acids through genomic selection can provide better permanent alterations compared with the dietary changes in the milk fatty acid profile. The studies on FA indicated that FA composition in bovine milk could vary among dairy breeds, herds and cows9,10,11 and be affected by environmental factors, especially dairy cows’ ration12,13,14 and genetic factors6,10,15. The genetic variability for FA is an important characteristic to modify the FA composition in bovine milk through breeding methods. Heritability is a well-known genetic parameter indicating the proportion of the genetic variation to the total variation. Genomic selection programs require to obtain the estimates of genetic parameters (heritability and genetic correlation) of traits and the accuracy of breeding values of animals from the models used in genomic selection.

Therefore, recent studies have focused on estimating genetic parameters of major milk FA by using pedigree-based BLUP models for Korean Holstein cattle16, for New Zealand dairy cattle17, for Italian Brown Swiss cows18, genome-based BLUP model for Danish Holstein cattle19 and for North American Holstein cattle20 and have indicated the existence of genetic variability among cows with respect to milk fatty acids.

The accuracy of breeding values is key to the successful application of genomic selection in animal breeding. The aims of this study were (1) to investigate the genetic relationship between FA within MUFA, PUFA and SFA groups by estimating of genetic correlations from the Bayesian bivariate Genomic Best Linear Unbiased Prediction (GBLUP) and (2) to compare the predictive ability and accuracy of the Bayesian univariate GBLUP and Bayesian alphabet models by estimating heritability for milk FA within MUFA, PUFA and SFA groups from Canadian Holstein cows randomly allocated to the training and cross-validation datasets. Results from this endeavor will positively impact the genomic selection approach in livestock and improve accuracies for selecting animals that will produce more nutritious milk for human consumption.

Results

Descriptive statistics of fatty acids

Descriptive statistics of the total and individual FA traits in MUFA, PUFA and SFA (% total FA) are given in (Table 1). Total SFA made up 71.20% (on average 68.568 with the range of 56.215 to 77.283% total FA) of total FA, while total MUFA and PUFA represented 25.30% (on average 24.513 with the range of 16.894 to 33.740% total FA) and 3.50% (on average 3.370 with the range of 2.002 to 5.375% total FA) of total FA in Canadian Holstein cows, respectively.

Table 1 Descriptive statistics of minimum (Min), maximum (Max), mean, standard deviation (Sd) and percentages of fatty acids (% total fatty acids).
Full size table

As seen in (Table 1), the most abundant individual FA (on average) in SFA were C16:0 (34.589), C14:0 (12.643) and C18:0 (9.371% total FA), respectively and they consisted of 36.07% (50.67%), 13.17% (18.49%) and 9.70% (13.63%) of total FA (total SFA). In addition, the means of C12:0, C10:0, C15:0 and C6:0 were 3.599, 2.703, 1.147 and 1.008% total FA, and they represented 3.75% (5.27%), 2.81% (3.95%), 1.20% (1.68%) and 1.05% (1.48%) of the total FA (total SFA). However, C4:0, C8:0, C11:0, C13:0, C17:0, C20:0, C22:0, C23:0 and C24:0 in SFA with the mean of lower than 1.000 g/100 g total FA represented relatively low proportion (< 1% each) of the total FA.

In MUFA, Oleic acid with mean of 19.787% total FA had 20.55% of the total FA which was the most prominent in MUFA with 81.19% of the total MUFA. In addition, C16:1t, C14:1t and C18:1n11t with the means of 1.807, 1.058 and 0.987% total FA made up 1.87% (7.39%), 1.08% (4.28%) and 1.01% (4.00%) of the total FA (total MUFA). However, C14:1, C16:1 and C18:1n9t in MUFA represented less than 1% of the total FA.

In PUFA, C18:2n6cc with the mean of 1.831% total FA was the most abundant individual PUFA which made up 1.91% of the total FA and 54.65% of the total PUFA. However, C18:2n6tt, C18:2n9c11t, C18:2n10t12c, C18:3n3, C183tcc, C20:3n6, C20:4n6, C20:5n3 and C22:5n3 in PUFA with the mean of lower than 1.000% total FA represented relatively low proportion (< 1% each) of the total FA.

Estimates of phenotypic and genetic correlations

A total of 630 phenotypic and genetic correlations with standard errors between the total and individual MUFA, PUFA and SFA for Canadian Holstein cows were presented in Table S1 in the supplemental file and those for FA within MUFA, PUFA and SFA groups presented by using blue and red colors indicating correlations from 1 to −1 were given in Figs. 1, 2 and 3, respectively.

Fig. 1
figure 1

Phenotypic and genetic correlations between monounsaturated fatty acids (MUFA).

Full size image
Fig. 2
figure 2

Phenotypic and genetic correlations between polysaturated fatty acids (PUFA).

Full size image
Fig. 3
figure 3

Phenotypic and genetic correlations between saturated fatty acids (SFA).

Full size image

As seen in Fig. 1, most of the phenotypic and genetic correlations for MUFA were positive. The very strong positive phenotypic (0.97) and genetic (0.97) correlations were obtained between total MUFA and Oleic acid which was expressed in 81.19% in total MUFA. There were moderate positive phenotypic (0.52) and genetic (0.48) correlations between total MUFA and C16:1t within MUFA. For individual MUFA, the phenotypic and genetic correlations were moderate positive between C14:1 and C16:1 (0.46 and 0.41, respectively), between C16:1t and C18:1n9c (0.46 and 0.41, respectively), C14:1t and C18:1n9t (0.43 and 0.46, respectively) and between C18:1n9t and C18:1n11t (0.59 and 0.56, respectively). However, moderate negative genetic correlations were observed between C16:1 and C18:1n9t (−0.42) and C18:1n11t (−0.43) acids and low negative phenotypic and genetic correlations between C14:1 and C18:1n9t (−0.14, −0.20, respectively), C18:1n11t (−0.25, −0.34, respectively), and between C16:1 and C14:1t (−0.27, −0.26, respectively).

For PUFA, as seen in Fig. 2, the phenotypic and genetic correlations between total and individual PUFA were mostly positive. Total PUFA resulted in positive phenotypic and genetic correlations ranging from 0.12 to 0.92 with individual FA in PUFA.

The very strong positive phenotypic (0.91) and genetic (0.92) correlations were obtained between total PUFA and C18:2n6cc which was represented with high percentage (54.65%) in total PUFA. There were moderate positive correlations (0.40 and 0.70, respectively) between total PUFA and C18:3n3, C22:5n3, C20:3n6 and C18:3tcc within PUFA. For individual PUFA, the phenotypic and genetic correlations were moderate positive between C18:2n6cc and C18:3n3 (0.46, 0.45, respectively), C20:3n6 (0.40, 0.46, respectively), C20:4n6 (0.47, 0.41, respectively), C22:5n3 (0.38, 0.46, respectively); between C18:2n9c11t and C18:3tcc (0.54, 0.55, respectively), between C18:2n10t12c and C20:5n3 (0.38, 0.42, respectively); between C18:3n3 and C20:5n3 (0.38, 0.64, respectively) and C22:5n3 (0.45, 0.45, respectively); between C20:3n6 and C20:4n6 (0.55, 0.62, respectively).

For SFA, there were negative correlations between total SFA and individual FA in SFA and between individual FA in SFA. The strong positive phenotypic (0.75) and genetic (0.72) correlations were obtained between total SFA and C16:0 which was represented with high percentage (50.67%) in total SFA. There were moderate positive correlations (0.40 and 0.70, respectively) between total SFA and C6:0 (0.39, 0.43, respectively), C8:0 (0.52, 0.54, respectively), C10:0 (0.57, 0.66, respectively), C12:0 (0.53, 0.60, respectively) and C14:0 (0.51, 0.56, respectively); however, negative low correlations with C17:0 (−0.01, −0.16, respectively), C18:0 (−0.25, −0.22, respectively) and C20:0 (−0.11, −0.05, respectively) within SFA.

For individual FA in SFA, in contrast to the phenotypic and genetic correlations between individual FA in MUFA and PUFA, strong/moderate positive phenotypic and genetic correlations were obtained for seven even-numbered SFA, 0.93 and 0.92 for C10:0 and C12:0, respectively, 0.88 and 0.90 for C6:0 and C8:0, respectively, 0.87 and 0.89 for C8:0 and C10:0, respectively, 0.66 and 0.83 for C20:0 and C22:0, respectively, 0.77 and 0.68 for C12:0 and C14:0 (Myristic), respectively, 0.66 and 0.70 for C8:0 and C12:0, respectively, 0.69 and 0.69 for C4:0 and C6:0, respectively and for two odd-numbered SFA, 0.63 and 0.59 for C15:0 and C17:0, respectively, and 0.64 and 0.55 for C13:0 and C15:0 acids, respectively. However, moderate negative phenotypic and genetic correlations were obtained between C4:0 and C13:0 (−0.42, −0.29, respectively) and C15:0 (−0.43, −0.40, respectively) acids, between C18:0 and C11:0 (-0.48, -0.54, respectively), and C15:0 (−0.45, −0.39, respectively), and C14:0 (−0.35, −0.40, respectively), and C16:0 (−0.59, −0.58, respectively) acids, C20:0 and C11:0 (−0.32, −0.48, respectively) acids. Phenotypic and genetic correlations between other individual FA in SFA were found generally low positive or negative.

The fatty acids in dairy milk are generally classified based on their chain lengths between 4 and 24 carbons. The even-numbered FA being 4–16 carbons in chain length arise from de novo synthesis in the mammary gland and the other FA, which include approximately half of the 16 carbon and all those 18 carbons or greater in length, are taken up preformed from the blood21. The phenotypic and genetic correlations between MUFA, PUFA and SFA given in Table S1 in the supplementary file could be evaluated by similarities in the origin of FA. Positive phenotypic and genetic correlations were generally obtained between C6:0, C8:0, C10:0, C12:0, C14:0 and C16:0 acids in SFA which were synthesized de novo in the mammary gland and between C18:1n9c, C18:1n9t and C18:1n11t in MUFA and between C18:2n6cc, C18:2n6tt, C18:2n10t12c, C18:3n3 and C18:3tcc acids in PUFA which were extracted from blood. However, as seen in Table S1 in the supplementary file, negative moderate/low phenotypic and genetic correlations were obtained for C6:0, C8:0, C10:0, C11:0, C12:0, C13:0, C14:0, C15:0 and C16:0 acids in SFA (de novo synthesis in the mammary gland) with C18:1n9t, C18:1n9t and C18:1n11t acids in MUFA and with C18:2n6cc, C18:2n9c11t and C18:3tcc acids in PUFA (the mammary uptake of preformed FA).

The estimates of genetic correlations (Table S1 in the supplementary file) indicated the existence of the strong positive and negative genetic relationships between total and individual FA within MUFA, PUFA and SFA groups in bovine milk and the importance of using genetic relationships in the selection programs for fatty acids to improve the nutritional quality of bovine milk and milk products.

Heritability estimates from Bayesian GBLUP and Bayesian alphabet models in random training data sets

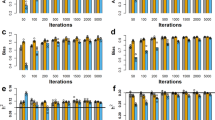
Heritability estimates of total and individual FA within MUFA, PUFA and SFA groups from 10-fold random cluster training data sets were obtained from Bayesian GBLUP and Bayesian alphabet models and presented in Fig. 4. As seen in Fig. 4, heritability estimates from Bayesian GBLUP model were higher than those from Bayesian alphabet models for total and individual FA within MUFA, PUFA and SFA groups. In Bayesian alphabet models, BayesB model produced generally higher heritability estimates than BayesA and BayesC models and BayesC model resulted in the lowest heritability estimates for total and individual FA within MUFA, PUFA and SFA groups.

Fig. 4
figure 4

Heritability estimates for total and individual MUFA, PUFA and SFA from 10-fold cross-validation data sets using Bayesian GBLUP, and Bayesian alphabet (BayesA, BayesB, BayesC) models.

Full size image

For total MUFA, PUFA and SFA, as seen in Fig. 4A, heritability estimates with standard error of 0.01 indicated that Bayesian GBLUP (0.67, 0.49, 0.60, respectively) yielded higher heritability estimates than BayesA (0.63, 0.41, 0.55, respectively), BayesB (0.63, 0.45, 0.56, respectively) and BayesC (0.61, 0.35, 0.51, respectively) models and heritability estimates from BayesA and BayesB models for total MUFA, PUFA and SFA were found similar and higher than those from BayesC model.

For individual FA in MUFA, as seen in Fig. 4B, Bayesian GBLUP model produced higher heritability estimates than Bayesian alphabet models. The lowest heritability estimates were obtained for C14:1 ranged from 0.27 of BayesC to 0.45 of GBLUP and the highest heritability estimates for C14:1t ranged from 0.63 of BayesC to 0.69 of GBLUP. Heritability estimates from Bayesian GBLUP, BayesA and BayesB models were generally equal to or higher than 0.50 for C14:1t, C16:1, C16:1t, C18:1n9c, C18:1n9t and C18:1n11t.

For individual FA in PUFA, as seen in Fig. 4C, the lowest heritability estimates were obtained for C18:3tcc ranged from 0.27 of BayesC to 0.45 of GBLUP and C18:2n6tt ranged from 0.27 of BayesC to 0.44 of GBLUP, and the highest heritability estimates for C18:2n6cc ranged from 0.63 of BayesA and BayesC to 0.68 of GBLUP. Although Bayesian GBLUP model yielded higher heritability estimates for individual PUFA, Bayesian GBLUP and BayesB models resulted in similar heritability estimates for C20:4n6 (0.57 and 0.56) and C22:5n3 (0.47 and 0.46) acids. Heritability estimates from Bayesian GBLUP and Bayesian alphabet models were higher than 0.50 for C18:2n6cc, C18:2n10t12c, C18:3n3 and C20:3n6.

For individual FA in SFA, as seen in Fig. 4D, Bayesian GBLUP model resulted in considerably higher heritability estimates than Bayesian alphabet models. Heritability estimates for individual SFA ranged from 0.35 of BayesC to 0.69 of GBLUP. The lowest heritability estimates ranged from 0.35 to 0.49 were obtained from Bayesian GBLUP and Bayesian alphabet models for C24:0 and the highest heritability estimates ranged from 0.64 to 0.69 for C18:0. Heritability estimates from Bayesian GBLUP and Bayesian alphabet models were higher than 0.50 for C4:0, C6:0, C8:0, C10:0, C11:0, C12:0, C13:0, C14:0, C15:0, C16:0, C17:0, and C18:0.

Predictive ability and accuracy of Bayesian GBLUP and Bayesian alphabet models

Predictive abilities of Bayesian GBLUP and Bayesian alphabet models were explored by using the Pearson’s correlation coefficient (\(\:{r}_{y,GEBV}\)) between the observed phenotypic values (\(\:y)\) and GEBV from 10-fold random cluster cross-validation data sets and mean values and standard errors of correlations for predictive ability of models were given in Fig. 5A for total MUFA, PUFA and SFA, in Fig. 5B–D for individual MUFA, PUFA and SFA, respectively. The mean values and standard errors of correlations from 10-fold cross-validation data sets for total MUFA, PUFA and SFA in Fig. 5A indicated that the predictive abilities of Bayesian GBLUP and Bayesian alphabet models ranged from 0.46±0.01 to 0.47±0.01 for total MUFA, from 0.37±0.01 to 0.40±0.01 for PUFA and from 0.43±0.01 to 0.45±0.01 for SFA. As seen in Fig. 5A and from the range of predictive abilities of models, Bayesian GBLUP and BayesA models resulted in similar predictive ability for total MUFA, PUFA and SFA and BayesB model yielded the lowest predictive ability for total MUFA, PUFA and SFA.

Fig. 5
figure 5

Mean of Pearson’s correlation coefficient (\(\:{r}_{y,GEBV}\)) between the observed phenotypic values (\(\:y)\) and GEBV for individual and total MUFA, PUFA and SFA from 10-fold cross-validation data sets using Bayesian GBLUP, and Bayesian alphabet (BayesA, BayesB, BayesC) models.

Full size image

The predictive ability of Bayesian GBLUP and Bayesian alphabet models for individual FA within MUFA, PUFA and SFA groups indicated that Bayesian GBLUP and BayesA models resulted in similar predictive ability and BayesB model generally yielded the lowest predictive ability in each individual FA within MUFA, PUFA and SFA groups.

For individual FA in MUFA, as seen in Fig. 5B, the lowest predictive ability from Bayesian GBLUP and Bayesian alphabet models was obtained for C14:1 ranging from 0.36±0.02 to 0.38±0.02 and the highest predictive ability for C14:1t ranging from 0.47±0.01 to 0.49±0.01. Bayesian GBLUP and Bayesian alphabet models also showed similar predictive ability (0.42±0.01 to 0.47±0.01) for C18:1n9c, C16:1, C16:1t and C18:1n11t acids. For individual FA in PUFA, as seen in Fig. 5C, the lowest predictive ability from Bayesian GBLUP and Bayesian alphabet models was obtained for C18:3tcc ranging from 0.25±0.01 to 0.27±0.01 and C22:5n3 ranging from 0.29±0.02 to 0.31±0.02. Besides, the highest predictive ability from Bayesian GBLUP and Bayesian alphabet models was obtained for C18:2n6cc, C18:3n3 and C20:3n6 ranging from 0.43±0.01 to 0.47±0.01. For individual FA in SFA, as seen in Fig. 5D, Bayesian GBLUP and Bayesian alphabet models resulted in similar predictive ability ranging from 0.38±0.02 to 0.48±0.01. The lowest predictive ability from Bayesian GBLUP and Bayesian alphabet models was obtained for C24:0 ranging from 0.38±0.02 to 0.41±0.02 and the highest predictive ability for C11:0 ranging from 0.46±0.01 to 0.48±0.01. Fatty acids in total and individual MUFA, PUFA and SFA having higher heritability resulted in higher predictive ability regardless of Bayesian GBLUP and Bayesian alphabet models.

After removing the effect of heritability on the predictive ability of Bayesian GBLUP and Bayesian alphabet models (Eq. 9), mean values and standard errors of accuracies of Bayesian GBLUP and Bayesian alphabet models for total and individual MUFA, PUFA and SFA were calculated and presented in Fig. 6 for total (Fig. 6A) and individual MUFA, PUFA and SFA (Fig. 6B–D). As seen in Fig. 6, BayesC and BayesA models resulted in slightly higher accuracy than Bayesian GBLUP and BayesB models. As seen in Fig. 6A, the accuracy of Bayesian GBLUP and Bayesian alphabet models for total MUFA, PUFA and SFA ranged from 0.56±0.02 to 0.65±0.02 and BayesC and BayesA models resulted in higher accuracy than Bayesian GBLUP and BayesB models. Accuracies in Fig. 6B, C indicated that accuracies ranged from 0.55±0.02 to 0.70±0.03 for individual MUFA and from 0.41±0.02 to 0.65±0.03 for individual PUFA. Figure 6B, C also showed that BayesC model generally produced higher accuracy than Bayesian GBLUP, BayesA and BayesB models for individual MUFA and PUFA. Higher accuracies from BayesC model were obtained for C14:1 (0.70±0.03), C16:1 (0.63±0.02), C18:1n9t (0.66±0.03) and C18:1n11t (0.65±0.02) in individual MUFA and for C18:2n6tt (0.65±0.03), C18:2n9c11t (0.62±0.02), C20:4n6 (0.62±0.02), C20:5n3 (0.62±0.02), C22:5n3 (0.54±0.03) and C18:3tcc (0.50±0.03) in individual PUFA. As seen in Fig. 6D, the accuracies from Bayesian GBLUP and Bayesian alphabet models ranged from 0.52±0.02 to 0.65±0.03 and BayesA model resulted in higher accuracies for individual SFA. The lowest accuracy was obtained for C18:0 ranging from 0.52±0.02 to 0.54±0.02 and the highest accuracies for C24:0 and C22:0 ranging from 0.60±0.02 to 0.65±0.03. Accuracies for total and individual MUFA, PUFA and SFA in Fig. 6 indicated that Bayesian alphabet models yielded more reliable prediction than Bayesian GBLUP model for FA traits.

Fig. 6
figure 6

Accuracies from Bayesian GBLUP, and Bayesian alphabet (BayesA, BayesB, BayesC) models for total and individual MUFA, PUFA and SFA.

Full size image

In addition to accuracy of Bayesian GBLUP and Bayesian alphabet models for reliable prediction, MSE was calculated to determine the better fit of Bayesian GBLUP and Bayesian alphabet models for total and individual MUFA, PUFA and SFA and presented in Table 2. As seen in Table 2, although Bayesian GBLUP and Bayesian alphabet models yielded same or similar MSE for C14:1 (0.11), C16:1 (0.09 and 0.10, respectively) and C18:1n9t (0.06) in MUFA, C18:1n11t (0.03), C18:2n9c11t (0.16 and 0.17, respectively), C18:2n10t12c (0.0002 and 0.0003, respectively), C18:3n3 (0.18 and 0.19, respectively), C18:3tcc (0.01), C20:3n6 (0.01), C20:4n6 (0.02), C20:5n3 (0.0011) and C22:5n3 (0.06 and 0.07, respectively) acids in PUFA, C11:0 (0.05 and 0.06, respectively), C13:0 (0.20 and 0.21, respectively), C20:0 (0.01 and 0.02, respectively) and C23:0 (0.0004 and 0.0005, respectively) in SFA, MSE values indicated that Bayesian alphabet models generally outperformed Bayesian GBLUP model and in Bayesian alphabet models, BayesA model outperformed BayesB and BayesC models for total and individual MUFA, PUFA and SFA.

Table 2 Mean squared errors from Bayesian GBLUP, and Bayesian alphabet (BayesA, BayesB, BayesC) models for total and individual MUFA, PUFA and SFA.
Full size table

Discussion

Descriptive statistics of fatty acids

The percentages of total SFA (71.20%), MUFA (25.30%) and PUFA (3.50%) found in this study were similar to the percentages of SFA (71.09%), UFA (28.95%) and PUFA (4.10%) from New Zealand dairy (Holstein-Friesian × Jersey) cows reported by Lopez-Villalobos et al.17 and the percentages of SFA (70.3%), MUFA (26.6%) and PUFA (3.1%) from Danish Holstein cattle reported by Krag et al.19. However, these percentages were slightly different than the percentages of SFA (68.9%), MUFA (28.2%) and PUFA (2.9%) from Norwegian Red cows reported by Olsen et al.22 and the percentages of SFA (73.6%) and MUFA (26.4%) from the dairy cattle in the Walloon region of Belgium reported by Soyeurt et al.23. These differences observed in the concentration of FA across studies could be attributed to the effects of diet, stage of lactation, parity, breed and genetic variation between cows6,10,17.

Bovine milk fat includes fatty acyls, triglycerides, glycerophospholipids, sphingolipids and saccharolipids; however, 98% of milk fat is made up of triglycerides which are synthesized from more than 400 different FA. Many of the FA are about trace quantities and only a few FA are at the 1% level or higher24. Lopez-Villalobos et al.17 indicated that C14:0 10.53%, C16:0 23.92% and C18:0 12.20% of the total FA in SFA and C18:1n9c 16.95% of the total FA in MUFA were the most abundant FA in New Zealand dairy cows, respectively. Krag et al.19 also reported that while the most abundant FA was C16:0 comprising 28.95% of the fat, the combination of C14:0, C16:0 and C18:0 in SFA, and C18:1n9c in MUFA accounted for 70.56% of the total fat content in Danish Holstein cattle. Olsen et al.22 also studied the FA in Norwegian Red cow population and found that C14:0, C16:0 and C18:0 acids in SFA, and C18:1n9c in MUFA were the most abundant FA by comprising 12.03, 27.11, 12.12 and 22.98% of the total fat, respectively. As seen in Table 1, the most abundant FA were C18:1n9c (20.55%) in MUFA and C14:0 (Myristic) (13.17%), C16:0 (36.07%) and C18:0 (9.70) in SFA and accounted for 79.49% of the total fat content in Canadian Holstein cows which were in a similar range to the percentages reported in the literature.

About 50–60% of the total SFA in bovine milk fat is C14:0, C16:0 and C18:025. Astrup et al.26 indicated that C14:0, C16:0 and C18:0 are associated with increased levels of cholesterol and an increased risk of cardiovascular diseases. Desirable changes in milk FA in regard to human health are to increase the amounts of MUFA and PUFA, particularly C18:2n9c11t and n-3 FA, and to decrease in the amounts of SFA, particularly C14:0 and C16:0. FAO27 also recommended to consumers to reduce SFA intake and consume more UFA.

Estimates of phenotypic and genetic correlations

Estimates of phenotypic and genetic correlations among 36 total and individual FA in MUFA, PUFA and SFA groups from Canadian Holstein cows are presented in Table S1 (the supplementary file) and correlations only for MUFA, PUFA and SFA are also showed in Figs. 1, 2 and 3. As seen in Figs. 1, 2 and 3 and Table S1, overall, the estimates of phenotypic correlations had the same direction of variation (negative or positive) as the corresponding estimates of genetic correlations. As seen in Fig. 1, phenotypic (−0.27 to 0.97) and genetic (-0.43 to 0.97) correlations for total and individual MUFA from Canadian Holstein cows were consistent with those reported for Italian Holstein-Friesian cows by Mele et al., for Italian Brown Swiss cows by Pegolo et al.18 and for New Zealand crossbred Holstein-Friesian×Jersey cows by Lopez-Villalobos et al.17.

For individual FA in PUFA, higher correlations between C18:3n3 and C18:2n9c11t acids for Danish Holstein cows19 and strong positive genetic correlations for C18:2n6cc with C18:3n3 (0.92) and C18:2n9c11t (0.63) for Canadian Holstein cattle28 compared with those from this study were reported. However, genetic correlations among C20:3n6, C20:4n6, C20:5n3 and C22:5n3 reported by Bilal et al.28 were found to be similar with those from this study.

As seen in Fig. 1 and Table S1, C14:1, C16:1 and C18:1n9c in MUFA were positively genetically correlated with each other (0.11 to 0.41) and with C18:2n9c11t (0.40) in PUFA which was consistent with those reported for Canadian Holstein cattle by Bilal et al.28. Moreover, Bilal et al.28 indicated that the possible explanation of positive genetic correlations among C14:1, C16:1 and C18:1n9c in MUFA and between MUFA and C18:2n9c11t lies in their common mode of synthesis. C18:1n9c which is expressed in 81.19% in total MUFA and constitutes about 20.55% of the total milk fat, is predominantly synthesized by mammary uptake of C18:0 and its conversion to C18:1n9c acid by the enzymatic activity of the stearoyl-CoA desaturase enzyme (SCD)29.

Correlation estimates between total and individual MUFA and PUFA ranged from − 0.31 to 0.49 for phenotypic correlations and from −0.34 to 0.50 for genetic correlations, which were similar with those reported by Krag et al.19 for Danish Holstein cows. Correlation estimates between total and individual SFA and MUFA (PUFA) ranged from −0.97 to 0.69 (from −0.51 to 0.74) for phenotypic correlations and from −0.97 to 0.57 (from −0.53 to 0.81) for genetic correlations. There were also very strong phenotypic and genetic correlations for total SFA and MUFA (−0.97 and −0.97, respectively), for total SFA and C18:1n9c (−0.93 and −0.93, respectively) which was expressed in 81.19% in total MUFA. The very strong negative phenotypic and genetic correlations between total SFA and total MUFA and C18:1n9c in MUFA were also reported for Danish Holstein cows by Krag et al.19; for Danish Holstein and Danish Jersey cattle by Buitenhuis et al.30 and Hein et al.31; for Italian Brown Swiss cows by Pegolo et al.18 and for New Zealand crossbred Holstein-Friesian×Jersey cows by Lopez-Villalobos et al.17 and indicated that dairy cows with a reduced the stearoyl-CoA desaturase enzyme (SCD) activity in the mammary gland tended to produce dairy milk with lower MUFA content and with greater preformed FA32. Moderate negative phenotypic and genetic correlations among total MUFA (C18:1n9c in MUFA) and the individual SFA were consistent with the negative genetic correlation pattern among the total MUFA and the individual SFA reported by Stoop et al.10, Mele et al.15, Lopez-Villalobos et al.17 and Soyeurt et al.23.

The fatty acids in dairy milk are generally classified based on their chain lengths between 4 and 24 carbons. The even-numbered fatty acids being 4–16 carbons in chain length arise from de novo synthesis in the mammary gland and the other fatty acids, which include approximately half of the 16 carbon and all those 18 carbons or greater in length, are taken up preformed from the blood21. The phenotypic and genetic correlations between MUFA, PUFA and SFA given in Table S1 in the supplementary file could be evaluated by similarities in the origin of fatty acids. Positive phenotypic and genetic correlations were generally obtained between C4:0, C6:0, C8:0, C10:0, C12:0, C14:0 and C16:0 in SFA which were synthesized de novo in the mammary gland and between C18:1n9c, C18:1n9t and C18:1n11t in MUFA and between C18:2n6cc, C18:2n6tt, C18:2n9c11t, C18:2n10t12c, C18:3n3 and C18:3tcc in PUFA which were extracted from blood. However, as seen in Table S1 in the supplementary file, negative phenotypic and genetic correlations were obtained for C4:0, C6:0, C8:0, C10:0, C12:0, C14:0 and C16:0 in SFA (de novo synthesis in the mammary gland) with C18:1n9c, C18:1n9t and C18:1n11t in MUFA and with C18:2n6cc, C18:2n6tt, C18:2n9c11t, C18:2n10t12c, C18:3n3 and C18:3tcc in PUFA (the mammary uptake of preformed fatty acids).

The estimates of genetic correlations (Table S1 in the supplementary file) indicated the existence of the strong positive and negative genetic relationships between total and individual FA in MUFA, PUFA and SFA in bovine milk and the importance of using genetic relationships in the selection programs for FA to improve the nutritional quality of bovine milk and milk products.

Heritability estimates from Bayesian GBLUP and Bayesian alphabet models in random training data sets

In the literature, heritability estimates for SFA, MUFA and PUFA in bovine milk differ across studies based on the combination of individual FA, sample size, breed, statistical method and FA analytical methods. Heritability estimates for SFA, MUFA and PUFA in this study were generally higher than those reported for American Holstein cows by Bobe et al.33, for Italian Holstein cows by Mele et al.15, for mixed-breed population of the Walloon region of Belgium by Soyeurt et al.23, for Danish Holstein cows by Krag et al.19, for Italian Brown Swiss cows by Pegolo et al.18, for Norwegian Red cattle by Olsen et al.22 and for New Zealand crossbred Holstein-Friesian × Jersey cows by Lopez-Villalobos et al.17, but agree well with the heritability estimates of PUFA reported for Korean Holstein cows by Park et al.16. Olsen et al.22 also indicated that heritability estimates for FA obtained from Fourier transform infrared spectroscopy analyses in Norwegian Red cattle were usually lower than those from FA studies based on mid-infrared spectroscopy, but in the same range as in the FA studies based on gas chromatography. However, our heritability estimates for FA were found higher than those from Fourier transform infrared spectroscopy, mid-infrared spectroscopy or gas chromatography analyses reported in the literature15,16,17,18,19,22,23,33. Lopez-Villalobos et al.17 indicated that comparisons of heritability estimates among the various studies were difficult because of differences in the analytical methods (GC or spectroscopy), the method of expressing FA contents (g/100 g of milk, g of FA/100 g of fat, or g of FA/100 g of total FA), sample size, breed, parity number, stage of lactation, and the statistical methods (e.g., sire, animal model and random regression).

As seen in Fig. 4, heritability estimates changed across the total and individual MUFA, PUFA and SFA and for individual SFA heritability estimates were also found higher than those for individual MUFA and PUFA in Canadian Holstein cows, which agreed with the results from Stoop et al.10, Lopez-Villalobos et al.17, Pegolo et al.18, Krag et al.19 and Bilal et al.28. Bovine milk FA were synthesized de novo in the mammary gland of cows or derived from the diet of cows which leads to the possible physiological explanation of the heritability estimates of individual FA13. As seen in Fig. 4, the heritability estimates for individual SFA, MUFA and PUFA were generally moderate, and indicated that de novo synthesized FA (such as \(\:{h}_{\text{C}4:0}^{2}=[0.58,\:0.66]\), \(\:{h}_{\text{C}8:0}^{2}=\left[\text{0.58,0.66}\right]\), \(\:{h}_{\text{C}10:0}^{2}=\left[\text{0.55,0.63}\right]\), \(\:{h}_{\text{C}12:0}^{2}=\left[\text{0.57,0.65}\right]\), \(\:{h}_{\text{C}14:0}^{2}=\left[\text{0.59,0.65}\right]\), \(\:{h}_{\text{C}16:0}^{2}=\left[\text{0.57,0.63}\right]\) in SFA) were under genetic control and genetic selection could be effectively applied to alter the FA composition of bovine milk for human and animal health16,17.

Predictive ability and accuracy of Bayesian GBLUP and Bayesian alphabet models

Predictive abilities of Bayesian GBLUP and Bayesian alphabet models were presented in Fig. 5 for total and individual MUFA, PUFA and SFA. As seen in Fig. 5, predictive ability of Bayesian GBLUP was higher than or similar with those of Bayesian alphabet models for total and individual MUFA, PUFA and SFA. The differences and similarities among the predictive abilities of Bayesian GBLUP and Bayesian alphabet models for total and individual MUFA, PUFA and SFA could result from the model assumptions, heritability and genetic architecture of total and individual MUFA, PUFA and SFA traits.

Bayesian GBLUP model is considered as a direct estimation approach for genetic effects and variances. The estimation of the genetic effects in GBLUP model is based on the genomic relationship matrix (G) computed from SNP markers34. The relatively few causative SNP markers hardly affect the genomic relationship matrix because of the equally contribution of each SNP marker to the genomic relationship34,35. However, Bayesian alphabet models are considered as a SNP-based estimation approach for genetic effects and variances. The estimation of the genetic effects in Bayesian alphabet models is based on the \(\:\pi\:\) proportion of SNP markers having non-null effects, which are assumed to follow a univariate Student’s t, multivariate Student’s t distribution depending on the Bayesian models36,37.

Heritability estimates and predictive ability results for total and individual MUFA, PUFA and SFA traits were based on the direct additive gene effect and variances; however, could depend on the number of loci affecting the FA traits, distribution of their effects, underlying relationship between FA traits and dominance and epistatic gene effects38,39,40.

Freitas et al.20 studied the estimation of genetic parameters and determination of genomic regions for the short-chain, medium-chain, long-chain, saturated, and unsaturated FA from North American Holstein cattle and indicated that various genomic regions are associated with the short-chain, medium-chain, long-chain, saturated, and unsaturated FA, but many regions across the genome have small individual effects on the total genetic variation of each trait. Wang et al.41 compared the genomic selection models (RR–BLUP, GBLUP, BayesA, BayesB, BayesCp and Bayesian LASSO, ) for breeding value prediction in a simulation study and found that the predictive ability of BayesB model decreased markedly for the trait determined by many genes and were much better than GBLUP for the trait determined by 20 QTL. However, as the number of QTL determined the trait increased, the predictive ability of BayesB decreased gradually to a plateau even lower than that of GBLUP.

Mean accuracy values with standard errors of Bayesian GBLUP and Bayesian alphabet models were given for total and individual MUFA, PUFA and SFA from Canadian Holstein cows in Fig. 6 after removing the effect of heritability of FA traits on the predictive ability of the models. As seen in Fig. 6, error-bar intervals of mean accuracy values of Bayesian GBLUP and Bayesian alphabet models indicated that mean accuracy values of Bayesian GBLUP and Bayesian alphabet models were similar for large number of individual MUFA, PUFA and SFA. However, BayesC model resulted in slightly higher accuracy than Bayesian GBLUP for C14:1, C18:2n6tt, C18:3tcc, C20:4n6, C20:5n3, C22:5n3, C24:0. When the number of SNP markers increases the computational time for Bayesian alphabet models take longer time to obtain the estimates of parameters. Therefore, Bayesian GBLUP is an effective method in providing the best compromise between computational time and prediction ability if there are no major gene effects for FA traits.

Conclusions

The heritability estimates ranged between 0.61±0.01 and 0.67±0.01 for total MUFA, between 0.35±0.01 and 0.49±0.01 for PUFA and between 0.51±0.01 and 0.60±0.01 for SFA, respectively and for individual FA, ranged between 0.27±0.01 and 0.69±0.01 for MUFA, between 0.27±0.01 and 0.68±0.01 for PUFA and between 0.35±0.01 and 0.69±0.01 for SFA. The heritability estimates indicated that total and individual MUFA, PUFA and SFA traits were under moderate genetic control in Canadian Holstein cattle and can be improved through genomic selection. Moderate and high genetic correlations among total and individual MUFA, PUFA and SFA traits were also determined and these underlying genetic linear relationships among individual MUFA, PUFA and SFA traits need to be taken into consideration for successful genomic selection for FA traits. Comparison of mean accuracy values of Bayesian GBLUP and Bayesian alphabet models based on their standard errors indicated that Bayesian GBLUP and Bayesian alphabet models resulted in similar accuracies for large number of individual MUFA, PUFA and SFA. However, BayesC model yielded better accuracies than Bayesian GBLUP for C14:1, C18:2n6tt, C18:3tcc, C20:4n6, C20:5n3, C22:5n3, C24:0, indicating that these individual FA traits might be determined by many genes having non-null effects, which are assumed to follow a univariate or multivariate Student’s t distribution. Overall comparison and evaluation of Bayesian GBLUP and Bayesian alphabet models based on heritability estimates of FA traits, predictive ability and accuracies of models indicated that when the number of SNP markers increases the computational time for Bayesian alphabet models take longer time to obtain the estimates of parameters. Therefore, Bayesian GBLUP is an effective method to estimate heritabilities of FA traits and to provide the best compromise between computational time and prediction ability and accuracy if there are no major gene effects for FA traits41.

Methods

Ethical statement

Animal use procedures and protocols were according to the national codes of practice for the care and handling of farm animals (http://www.nfacc.ca/codes-of-practice) and the milk samples were collected by the technicians of the Valacta laboratory.

Animals and milk sampling

Milk samples from 1246 Canadian Holstein cows from 16 herds in the province of Quebec, Canada, were collected during the morning milking by Valacta (www.valacta.com) (now Lactanet, https://lactanet.ca/) as part of its routine monthly milk collection for Dairy Herd Improvement services. The dairy farms in Quebec are managed following standard procedures instituted by the Dairy Farmers of Quebec and Canada (https://lait.org/; https://dairyfarmersofcanada.ca/). Milk samples were delivered to our laboratory on the same day of collection and processed immediately. Detailed procedures for milk processing, fatty acid analysis, DNA isolation and SNP genotyping by the method of genotyping-by-sequencing (GBS) have been reported in our previous work42.

Phenotypes

Out of the 1246 cows, the phenotypic data of individual FA within MUFA, PUFA and SFA groups from 695 individuals in mid-lactation and with lactation number ranging from one to five were further analyzed. Data manipulation for the phenotypic data of individual FA traits was carried out to identify outliers and provide normally distributed data before the genomic analysis. Then, the number of observations ranging from 636 to 695 were used for the genomic analysis of the FA traits.

Forty mL of milk sample from each cow was used to extract the milk fat followed by FA analysis as reported previously by Ibeagha-Awemu et al.42. Briefly, FA in the extracted milk fat were re-esterified to their methyl esters. Then, FA methyl esters were determined by gas chromatography (GC) method using Varian CP-3900 GC based on O’Fallon et al.43. After determining the individual FA methyl ester peaks, FA proportion is specified by counting peak area proportion to the total peak area of all determined fatty acids and weight% fatty acid data (% total FA) were calculated from the area data. A total of 33 individual FA, C14:1 (Myristoleic), C14:1t (Myristelaidic), C16:1 (Palmitoleic), C16:1t (Palmitelaidic), C18:1n9c (Oleic), C18:1n9t (Elaidic), C18:1n11t (Trans vaccenic) acids in MUFA; C18:2n6cc (Linoleic), C18:2n6tt (Trans-linoleic), C18:2n9c11t (Cis-9 trans-11 CLA), C18:2n10t12c (Trans-10 cis-12 CLA), C18:3n3 (Alpha linolenic), C18:3tcc (Gamma linolenic), C20:3n6 (Dihomogamma linolenic), C20:4n6 (Arachidonic), C20:5n3 (Eicosapentanoic), C22:5n3 (Docosapentaenoic) acids in PUFA; and C4:0 (Butyric), C6:0 (Caproic), C8:0 (Caprylic), C10:0 (Capric), C11:0 (Undecanoic), C12:0 (Lauric), C13:0 (Tridecylic), C14:0 (Myristic), C15:0 (Pentadecylic), C16:0 (Palmitic), C17:0 (Margaric), C18:0 (Stearic), C20:0 (Arachidic), C22:0 (Behenic), C23:0 (Tricosanoic), C24:0 (Lignoceric) acids in SFA were identified by the GC method. Total MUFA, PUFA and SFA values were calculated by summing the individual FA values within MUFA, PUFA and SFA groups, respectively.

Genotyping-by-sequencing SNP marker genotypes

The genomic DNA for genotyping-by-sequencing was isolated from milk somatic cells obtained from the 40 mL of milk sample taken from each cow followed by GBS analysis as reported previously by Ibeagha-Awemu et al.42. Briefly, after preparing GBS libraries, they were multiplexed and subjected to single end 100 bp sequencing on an Illumina HiSeq 2000 system (Illumina Inc., San Diego, CA, USA). The Tassel software package was utilized to process raw Illumina DNA sequence data and to call SNP markers. Further details on the GBS analysis and bioinformatics for GBS SNP marker calling have been given by Ibeagha-Awemu et al.42. In this study, a total of 76,299 SNPs out of 515,787 with call rates > 85%, accuracy of imputation score > 50% and MAF ≥ 1.5% were used. After quality control of GBS SNP marker data, considerable amounts of GBS SNP markers were removed from the genotype data set since GBS SNP markers had the capacity to deliver a large number of markers, but with considerable amounts of missing values and unknown marker positions44. The findings from Elbasyoni et al.44, Gouesnard et al.45 and Negro et al.46 also indicated that GBS SNP markers had low coverage leading to a high (65%) missing data rate and had low call rate compared to the findings from array SNP markers.

Estimates of phenotypic and genetic correlations between fatty acids

Genetic correlations among 36 total and individual MUFA, PUFA and SFA were calculated based on the (co)variance components obtained from a total of 630 Bayesian bivariate GBLUP models.

A Bayesian bivariate GBLUP model for any two fatty acids is given in Eq. (1) as follows:

$$\:\left[\begin{array}{c}{\varvec{y}}_{1}\\\:{\varvec{y}}_{2}\end{array}\right]=\left[\begin{array}{cc}{\varvec{X}}_{1}&\:0\\\:0&\:{\varvec{X}}_{2}\end{array}\right]\left[\begin{array}{c}{\varvec{b}}_{1}\\\:{\varvec{b}}_{2}\end{array}\right]+\left[\begin{array}{cc}{\varvec{Z}}_{1}&\:0\\\:0&\:{\varvec{Z}}_{2}\end{array}\right]\left[\begin{array}{c}{\varvec{g}}_{1}\\\:{\varvec{g}}_{2}\end{array}\right]+\left[\begin{array}{c}{\varvec{e}}_{1}\\\:{\varvec{e}}_{2}\end{array}\right]$$
(1)

where \(\:{\varvec{y}}_{1}\) and \(\:{\varvec{y}}_{2}\) were the vector of observations from any two fatty acids among 36 total and individual MUFA, PUFA and SFA; \(\:{\varvec{X}}_{1}\), \(\:{\varvec{X}}_{2}\), \(\:{\varvec{Z}}_{1}\) and \(\:{\varvec{Z}}_{2}\) were the design matrices relating the fixed (overall mean, lactation number, herd) and random (direct additive genetic) effects for two fatty acids; \(\:{\varvec{b}}_{1}\) and \(\:{\varvec{b}}_{2}\) were the vectors of fixed effects (overall mean, lactation number and herd) for two fatty acids; and \(\:{\varvec{g}}_{1}\) and \(\:{\varvec{g}}_{2}\) were the vectors of random direct additive genetic effects following a bivariate Normal distribution \(\left[ {\begin{array}{*{20}c} {\user2{g}_{1} } \\ {\user2{g}_{2} } \\ \end{array} } \right]\sim N\left( {0,~\user2{G} \otimes \user2{\Sigma }} \right)\) with the mean zero and (co)variance \(\user2{G} \otimes \user2{\Sigma }\) where \(\:\varvec{G}\) is the genomic relationship matrix and \(\:\varvec{\varSigma\:}=\left[\begin{array}{cc}{\sigma\:}_{{g}_{1}}^{2}&\:{\sigma\:}_{{g}_{1}{g}_{2}}\\\:{\sigma\:}_{{g}_{1}{g}_{2}}&\:{\sigma\:}_{{g}_{2}}^{2}\end{array}\right]\) is the direct additive genetic (co)variance matrix with the direct additive genetic (co)variance components of \(\:{\sigma\:}_{{g}_{1}}^{2}\), \(\:{\sigma\:}_{{g}_{2}}^{2}\) and \(\:{\sigma\:}_{{g}_{1}{g}_{2}}\) for two fatty acids; and \(\:{\varvec{e}}_{1}\) and \(\:{\varvec{e}}_{2}\) were the vectors of random residuals following a bivariate Normal distribution \(\left[ {\begin{array}{*{20}c} {\user2{e}_{1} } \\ {\user2{e}_{2} } \\ \end{array} } \right]\sim N\left( {0,~\user2{I} \otimes \user2{R}} \right)\) with the mean zero and the residual (co)variance matrix \(\:\varvec{R}=\left[\begin{array}{cc}{\sigma\:}_{{e}_{1}}^{2}&\:{\sigma\:}_{{e}_{1}{e}_{2}}\\\:{\sigma\:}_{{e}_{1}{e}_{2}}&\:{\sigma\:}_{{e}_{2}}^{2}\end{array}\right]\) where \(\:{\sigma\:}_{{e}_{1}}^{2}\), \(\:{\sigma\:}_{{e}_{2}}^{2}\) and \(\:{\sigma\:}_{{e}_{1}{e}_{2}}\) were the residual (co)variance components for two fatty acids. The vectors of fixed effects are assigned flat prior (a Gaussian prior with null mean and very large variance) and the covariance matrices of direct additive genetic and residual random effects are assigned Inverse Wishart priors.

The genomic relationship matrix (\(\:\varvec{G}\)) was computed as in Eq. (2)

$$\:\varvec{G}=\frac{(\varvec{M}-\varvec{P}){(\varvec{M}-\varvec{P})}^{\varvec{T}}}{2{\sum\:}_{i=1}^{k}{p}_{i}(1-{p}_{i})}$$
(2)

where the matrix of \(\:\varvec{M}\) included the values of 0, 1 or 2 for SNP markers; the matrix of \(\:\varvec{P}\) included the allele frequencies of SNP markers multiplied by 2; \(\:{p}_{i}\) was the allele frequency of SNP marker \(\:i\); and the \(\:k\) was the number of SNP markers34,47.

The Bayesian bivariate GBLUP models were applied using the Multitrait function in the statistical package BGLR (https://cran.r-project.org/web/packages/BGLR/index.html (accessed on 15 May 2023)) in the R program37,48.

A total of 630 genetic (\(\:{r}_{G}\)) and phenotypic (\(\:{r}_{P}\)) correlations among 36 total and individual MUFA, PUFA and SFA were calculated as in Eq. (3)

$$\:{r}_{G}=\frac{{\sigma\:}_{{g}_{1}{g}_{2}}}{\sqrt{{\sigma\:}_{{g}_{1}}^{2}{\sigma\:}_{{g}_{2}}^{2}}}\:\text{a}\text{n}\text{d}\:{r}_{P}=\frac{{\sigma\:}_{{p}_{1}{p}_{2}}}{\sqrt{{\sigma\:}_{{p}_{1}}^{2}{\sigma\:}_{{p}_{2}}^{2}}}$$
(3)

where \(\:{\sigma\:}_{{p}_{1}}^{2}\), \(\:{\sigma\:}_{{p}_{2}}^{2}\) and \(\:{\sigma\:}_{{p}_{1}{p}_{2}}\) were the phenotypic (co)variance components for two fatty acid traits. The standard error (\(\:{r}_{se}\)) of \(\:{r}_{G}\) or \(\:{r}_{P}\) was calculated as \(\:{r}_{se}=\sqrt{(1-{r}^{2})/(n-2)}\) where \(\:r\) was the \(\:{r}_{G}\) or \(\:{r}_{P}\) and \(\:n\) was the sample size49.

Genomic selection

Analyses of 36 total and individual FA traits in MUFA, PUFA and SFA groups for genomic selection were carried out by applying the univariate Bayesian (GBLUP) and the Bayesian alphabet models36,37.

The phenotypes from a FA were modeled by using the statistical model in Eq. (4):

$$\:\varvec{y}=\varvec{X}\varvec{b}+\varvec{Z}\varvec{g}+\varvec{e}$$
(4)

where \(\:\varvec{y}\) was the vector of observations from a FA trait in MUFA, PUFA or SFA; \(\:\varvec{X}\) was the design matrix allocating a FA trait in MUFA, PUFA or SFA to the fixed effects of overall mean, lactation number and herd. \(\:\varvec{b}\) was the vector of fixed effects (overall mean, lactation number and herd) and flat (un-informative) priors were assigned. \(\:\varvec{e}\) was the vector of random residuals and assigned a priori multivariate Normal distribution \(\user2{e}\sim N\left( {0,~\user2{I}\sigma _{e}^{2} } \right)\) with the mean zero and variance \(\:\varvec{I}{\sigma\:}_{e}^{2}\) where \(\:\varvec{I}\) is the identity matrix. \(\:{\sigma\:}_{e}^{2}\) is the residual variance with prior density \(\:{\chi\:}^{-2}({\nu\:}_{e},{S}_{e})\) with degrees of freedom \(\:{\nu\:}_{e}=5\) and scale \(\:{S}_{e}\) parameters which is derived using the following equation \(\:0.5\times\:var\left(y\right)\times\:({\nu\:}_{e}+2)\)37.

The term of \(\:\varvec{Z}\varvec{g}\) in Eq. (4) was explained based on the Bayesian GBLUP and the Bayesian alphabet models.

Bayesian GBLUP model

For GBLUP, \(\:\varvec{Z}\) was the design matrix allocating a FA trait in MUFA, PUFA or SFA to additive genomic breeding values of animals and \(\:\varvec{g}\) was the vector of additive genomic breeding values for animals following a priori multivariate Normal distribution \(\user2{g}\sim N\left( {0,~\user2{G}\sigma _{g}^{2} } \right)\) with mean zero and variance \(\:\varvec{G}{\sigma\:}_{g}^{2}\) where \(\:\varvec{G}\) is the genomic relationship matrix and \(\:{\sigma\:}_{g}^{2}\) is the direct additive genetic variance with prior density \(\:{\chi\:}^{-2}({\nu\:}_{g},{S}_{g})\) with degrees of freedom \(\:{\nu\:}_{g}=5\) and scale \(\:{S}_{g}\) parameters.

The Bayesian alphabet models

The phenotypes from a FA were modeled as a function of the SNP marker effects in the Bayesian alphabet models. Thus, for Bayesian alphabet models, \(\:\varvec{Z}\:\)was the matrix of SNP marker values (0, 1 or 2) from animals and \(\:\varvec{g}\) was the vector of SNP marker effects. The prior distribution for individual SNP marker effect (\(\:{g}_{i}\)) depends on the SNP marker-specific variance \(\:{\sigma\:}_{{g}_{i}}^{2}\) and the parameter \(\:0\le\:\pi\:\le\:1\) which represents the prior proportion of non-zero SNP marker effects. In BayesA, every SNP marker is assumed to have an effect on the phenotypes of FA. Hence, \(\:\pi\:=1\) and the prior distribution of \(\:{g}_{i}\) is assumed to be Normal \(g_{i} |\sigma _{{g_{i} }}^{2} ,~\sim N\left( {0,\sigma _{{g_{i} }}^{2} } \right)\) with prior density \(\:{\chi\:}^{-2}(\nu\:,S)\) for \(\:{\sigma\:}_{{g}_{i}}^{2}\). Thus, the marginal distribution of \(\:{g}_{i}\) will be the univariate scaled-Student’s t distribution \(\:t(0,\nu\:,S)\) with parameters \(\:\nu\:\) and \(\:S\). In BayesB, only a small proportion (\(\:\pi\:)\) of SNP markers have non-zero effect and the majority \(\:\left(1-\pi\:\right)\) of the SNP markers have exactly zero effect on the phenotypes of FA. The Gaussian Mixture prior distribution of \(\:{g}_{i}\) is defined as in Eq. (5)

$$g_{i} |\pi ,\sigma _{{g_{i} }}^{2} \left\{ {\begin{array}{*{20}l} { = 0} \hfill & {with~\left( {1 - \pi } \right)} \hfill \\ {\sim N\left( {0,\sigma _{{g_{i} }}^{2} } \right)} \hfill & {with~\pi } \hfill \\ \end{array} } \right.$$
(5)

with prior density \(\:{\chi\:}^{-2}(\nu\:,S)\) for \(\:{\sigma\:}_{{g}_{i}}^{2}\). Thus, the marginal distribution of \(\:{g}_{i}\) with the \(\:\pi\:\) will be the univariate scaled-Student’s t distribution \(\:t(0,\nu\:,S)\) with parameters \(\:\nu\:\) and \(\:S\). In BayesC, the prior distribution for \(\:{g}_{i}\) depends on the SNP marker-common variance \(\:{\sigma\:}_{g}^{2}\) and a small proportion (\(\:\pi\:\)) of SNP markers have non-zero effect. Hence, The Gaussian Mixture prior distribution of \(\:{g}_{i}\) is defined as in Eq. (6)

$$g_{i} |\pi ,\sigma _{g}^{2} \left\{ {\begin{array}{*{20}l} { = 0} \hfill & {with~\left( {1 - \pi } \right)} \hfill \\ {\sim N\left( {0,\sigma _{g}^{2} } \right)} \hfill & {with~\pi } \hfill \\ \end{array} } \right.$$
(6)

with SNP marker-common variance \(\:{\sigma\:}_{g}^{2}\) which is distributed \(\:{\chi\:}^{-2}(\nu\:,S)\). Thus, the marginal distribution of \(\:{g}_{i}\) with the \(\:\pi\:\) will be the mixture of multivariate Student’s t distributions \(\:t(\varvec{0},\nu\:,\varvec{I}S)\) with parameters \(\:\nu\:\) and \(\:S\)[36,37. In BayesB and BayesC, \(\:{\uppi\:}\) is treated as known with the value of 0.05.

The GEBV of animal \(\:j\) for a FA in Bayesian alphabet models was calculated as in Eq. (7)

$$\:{GEBV}_{j}=\sum\:_{i=1}^{k}{m}_{ji}{\widehat{g}}_{i}$$
(7)

where \(\:{m}_{ji}\) is the SNP marker score (0, 1 or 2) for animal \(\:j\) at SNP \(\:i\) and \(\:{\widehat{g}}_{i}\) is the estimated effect of \(\:{i}^{th}\) SNP marker36. Then, the estimates of heritability for a FA from Bayesian alphabet (BayesA, BayesB, BayesC) models was computed as \(\:{\widehat{h}}^{2}=\frac{{\widehat{\sigma\:}}_{g}^{2}}{{\widehat{\sigma\:}}_{g}^{2}+{\widehat{\sigma\:}}_{e}^{2}}\) where \(\:{\widehat{\sigma\:}}_{g}^{2}\) and \(\:{\widehat{\sigma\:}}_{e}^{2}\) are the estimates of direct additive genetic and residual variances. The BGLR package (https://cran.r-project.org/web/packages/BGLR/index.html (accessed on 15 May 2023)) in the R program37,48 was utilized to get the estimates (\(\:\widehat{\varvec{b}}\), \(\:\widehat{\varvec{g}}\), \(\:{\widehat{\sigma\:}}_{g}^{2}\) and \(\:{\widehat{\sigma\:}}_{e}^{2}\)) of \(\:\varvec{b}\), \(\:\varvec{g}\), \(\:{\sigma\:}_{g}^{2}\) and \(\:{\sigma\:}_{e}^{2}\). Fixed and random direct additive genetic effects and variance components in Bayesian GBLUP and Bayesian alphabet models were estimated using the Markov chain Monte Carlo sampling algorithm. Markov chains were run for 25,000 cycles of Gibbs sampling. The first 5,000 cycles were discarded as burn-in and then every fifth sample in the cycle was saved for estimating model parameters.

10-fold cross-validation and predictive ability of the models

The cross-validation (CV) is a robust and nonparametric technique to test the predictive ability of the model by splitting the data set into the training and the validation data sets to train and evaluate the model. In this study, after the FA data set based on the CV strategy was randomly split into 10-fold CV data sets, all the observations from the nine CV data sets were used to train the Bayesian GBLUP and the Bayesian alphabet models. Then, all the observations from the leave-one-out CV data set were used to validate the models. This procedure based on the 10-fold CV was replicated five times.

The predictive abilities of the Bayesian GBLUP and the Bayesian alphabet models were determined in the 10-fold CV data sets using Pearson’s correlation coefficient (\(\:{r}_{\varvec{y},\varvec{GEBV}}\)) between the observed phenotypic values (\(\:\varvec{y})\) and GEBV for each FA trait in MUFA, PUFA or SFA (Eq. 8):

$$\:{r}_{\varvec{y},\varvec{G}\varvec{E}\varvec{B}\varvec{V},}=\frac{Cov(\varvec{y},\varvec{G}\varvec{E}\varvec{B}\varvec{V})}{\sqrt{Var\left(\varvec{y}\right)Var\left(\varvec{G}\varvec{E}\varvec{B}\varvec{V}\right)}}$$
(8)

where \(\:Cov(\varvec{y},\varvec{G}\varvec{E}\varvec{B}\varvec{V})\) was the covariance between the observed phenotypic values (\(\:\varvec{y})\) and GEBV for the FA trait in MUFA, PUFA or SFA; \(\:Var\left(\varvec{y}\right)\) and \(\:Var\left(\varvec{G}\varvec{E}\varvec{B}\varvec{V}\right)\) were the variances for the observed phenotypic values (\(\:\varvec{y})\) and GEBV for the FA trait in MUFA, PUFA or SFA, respectively.

Accuracy of the Bayesian GBLUP and the Bayesian alphabet models was defined as the correlation of \(\:r(\varvec{g},\widehat{\varvec{g}})\) between genomic breeding values (\(\:\varvec{g}\)) and genomic estimated breeding values (\(\:\widehat{\varvec{g}}\)) for animals and approximately estimated from the predictive ability of the models as shown by Legarra et al.50 (Eq. (9)):

$$\:{r}_{\varvec{g},\widehat{\varvec{g}}}=\frac{r(\varvec{y},\varvec{G}\varvec{E}\varvec{B}\varvec{V})}{\sqrt{{\widehat{h}}^{2}}}$$
(9)

where \(\:{\widehat{h}}^{2}\) was the heritability estimate from the Bayesian GBLUP or the Bayesian alphabet models for FA.

The mean squared error (MSE) of prediction in the CV data sets was used to measure the overall fit of model, and the computation equation (Eq. 10) was

$$\:MSE=\frac{1}{N}\sum\:_{i=1}^{N}{\left({y}_{i}-{GEBV}_{i}\right)}^{2}$$
(10)

where N is the number of individuals. A large estimated value of accuracy is indicative of reliable prediction, and a low MSE value means a better overall fit51.