Ensemble learning with explainable AI for improved heart disease prediction based on multiple datasets

Abstract

Heart disease is one of the leading causes of death worldwide. Predicting and detecting heart disease early is crucial, as it allows medical professionals to take appropriate and necessary actions at earlier stages. Healthcare professionals can diagnose cardiac conditions more accurately by applying machine learning technology. This study aimed to enhance heart disease prediction using stacking and voting ensemble methods. Fifteen base models were trained on two different heart disease datasets. After evaluating various combinations, six base models were pipelined to develop ensemble models employing a meta-model (stacking) and a majority vote (voting). The performance of the stacking and voting models was compared to that of the individual base models. To ensure the robustness of the performance evaluation, we conducted a statistical analysis using the Friedman aligned ranks test and Holm post-hoc pairwise comparisons. The results indicated that the developed ensemble models, particularly stacking, consistently outperformed the other models, achieving higher accuracy and improved predictive outcomes. This rigorous statistical validation emphasised the reliability of the proposed methods. Furthermore, we incorporated explainable AI (XAI) through SHAP analysis to interpret the model predictions, providing transparency and insight into how individual features influence heart disease prediction. These findings suggest that combining the predictions of multiple models through stacking or voting may enhance the performance of heart disease prediction and serve as a valuable tool in clinical decision-making.

Introduction

Cardiovascular diseases, particularly heart disease, remain the leading cause of death globally. According to data from international healthcare organisations, 17.9 million people (32% of all global deaths) died from cardiovascular diseases in 2019, and this number is projected to rise to 23 million by 2030¹. Heart disease and stroke account for 85% of all cardiovascular disease fatalities. The incidence of heart disease was expected to quadruple by the year 2020, and it is estimated that by 2050, one person will develop the disease every 30 s². Research has indicated that heart disease is responsible for 80% of deaths and 85% of disabilities in low-income countries¹.

The best way to reduce these deaths is to predict the likelihood of heart disease or detect it as early as possible, allowing for precautionary measures to be taken in advance. Several factors, including age, dietary habits, and a sedentary lifestyle, influence heart-related disorders^3,4,5. Furthermore, other health issues, such as high blood pressure, elevated glucose levels, increased blood lipids, obesity, and being overweight, are often considered contributing factors to heart disease.

Early and accurate diagnosis is crucial for reducing morbidity and mortality rates. Machine learning has emerged as a promising tool for predicting and detecting various diseases in their early stages. Several studies have explored the application of machine learning in predicting and diagnosing heart disease, utilising diverse data sources such as medical records and electrocardiograms (ECGs)^6,7.

Although individual machine learning models have shown promise in predicting heart disease, their limitations often result in suboptimal performance⁸. Complex data patterns and biases frequently challenge conventional machine learning techniques, leading to overfitting and sensitivity to data noise. Factors such as data quality, feature selection, and model parameters can significantly influence the performance of these algorithms.

In medical diagnosis, ensemble learning is widely regarded as one of the most effective machine learning algorithms. Ensemble methods aggregate numerous base learners to create a single, more robust model⁹. This approach has the potential to enhance prediction accuracy and generalisability compared to individual models. Relative to traditional machine learning, ensemble learning presents numerous advantages that render it a powerful technique for improving prediction accuracy across various tasks. Owing to these benefits, ensemble learning techniques are increasingly favoured for more precise disease prediction^{10,11,12,13,14}.

This study aims to demonstrate the efficacy of ensemble learning, particularly stacking and voting ensembles, in advancing heart disease prediction. Given the critical nature of this application, our objective is to develop a model that showcases enhanced accuracy, additional performance metrics, and robustness in heart disease prediction. We believe that this approach can improve the accuracy, robustness, and interpretability of heart disease prediction models, ultimately leading to better healthcare outcomes for patients worldwide.

The main contributions of this research are as follows:

• Designing stacking and voting models for heart disease prediction: We present a comprehensive framework that combines diverse machine learning algorithms to enhance predictive performance.

• Addressing the selection of diverse base models: We consider a range of machine learning algorithms that allow our models to capture the strengths of different approaches and mitigate their weaknesses.

• Conducting experiments on multiple datasets: Our rigorous experimentation was conducted on two distinct heart disease datasets.

• Comprehensive assessment of the models: The proposed ensemble models are rigorously evaluated using various metrics, showcasing their superiority over individual base models and state-of-the-art models.

• Application of rigorous statistical analysis: To ensure the statistical significance of performance improvements, a robust statistical framework—including the Friedman Aligned Ranks test and Holm post-hoc analysis—is implemented.

• Incorporation of Explainable AI (XAI) through SHAP: Our study integrates XAI techniques, specifically SHAP (Shapley Additive Explanations), to interpret the predictions made by the stacking and voting models. This enables us to provide transparency in model predictions and better understand how various features influence the final decision, thereby addressing the interpretability challenges often associated with complex ensemble models.

The remainder of the paper is organised as follows: Section 2 reviews related work, providing an overview of existing studies in heart disease prediction and highlighting the necessity for ensemble methods. Section 3 outlines the research methodology adopted in this study, detailing the framework and key processes involved. Section 4 offers extensive information about the datasets used, including their sources, features, and preprocessing steps. Section 5 explains the experimental setup and presents the results of the model evaluations. Section 6 provides a thorough analysis of the experimental outcomes, featuring a critical discussion of the findings and a comparison of the stacking and voting models with other comparable works. Section 7 concludes the study, summarising the key contributions and indicating potential areas for future research.

Related work

The proliferation of machine learning has resulted in its implementation in numerous domains, such as disease diagnosis and prediction^15,16. Ensemble learning has been proven to be successful in the prediction, detection, diagnosis, and prognosis of different diseases^{17,18,19,20,21}. For heart disease prediction, ensemble learning methods such as bagging^22,23,24 and boosting^25,26,27 have also been popularly used. Some researchers have considered multiple ensemble learning methods, including bagging, boosting, stacking and voting, for heart disease prediction^28,29,30. The following highlights the studies that primarily focused on stacking and voting for heart disease prediction.

Chandrasekhar and Peddakrishna³¹ demonstrated the effectiveness of combining multiple algorithms with hyperparameter optimisation and ensemble techniques in heart disease prediction. The study employed GridSearchCV and five-fold cross-validation to optimise model accuracy, achieving notable results: logistic regression achieved 90.16% accuracy on the Cleveland heart disease dataset (HDDC), AdaBoost achieved 90% accuracy on the IEEE Dataport dataset (IDD), and a soft voting ensemble classifier combining all six algorithms further enhanced accuracy to 93.44% and 95% for the HDDC and IDD, respectively. Tiwari et al.³² presented and discussed the critical need for early and accurate diagnosis of heart disease to prevent further injury and save lives. The publicly available IDD dataset was used for this research. The study evaluated the model’s efficacy using performance measures such as the ROC-AUC curve, specificity, F1-score, sensitivity, MCC, and accuracy. A stacked ensemble classifier framework incorporating multiple machine learning algorithms is proposed, achieving an accuracy of 92.34%, surpassing previous results found in the literature. Raza³³ experimented with heart disease detection using ensemble learning and majority voting rules based on clinical reports. The results indicate that the voting classifier achieved an accuracy rate of 89% over single classification models, suggesting potential integration into U-healthcare monitoring systems for improved diagnosis and decision-making in cardiac care. Mienye et al.³⁴ focused on developing and applying an improved ensemble learning method for predicting heart disease risk. This approach involves partitioning the dataset into smaller subsets using a mean-based splitting method and modelling these partitions with classification and regression tree (CART) algorithms. The model outperformed existing works, achieving 93% and 91% classification accuracies using the HDDC and Framingham Heart Study Datasets (FHSD), respectively. Ambrews et al.³⁵ utilised stacking and voting architectures for heart disease prediction across multiple datasets. This study aims to provide a straightforward analysis of the effectiveness of ensemble learning in enhancing the prediction accuracy for heart disease diagnosis. Among all classifiers, voting showed notable results on the UCI heart disease dataset (UHDD), achieving an accuracy, F1-score, recall, precision, and specificity of 91.96%, 91.69%, 91.72%, 92.40%, and 90.77%, respectively. Ashfaq³⁶ proposed a multimodel ensemble-based approach for heart disease diagnosis using the HDDC. This study evaluated ensemble methods such as stacking, bagging, voting, and boosting to enhance prediction accuracy. Notably, the bagging method with extreme gradient boosting (XGB) achieved the highest accuracy of 88%. This study demonstrated the efficacy of ensemble techniques in predicting heart disease, suggesting that these methods can significantly improve diagnostic processes compared to traditional single-model approaches. Habib and Tasnim³⁷ presented an ensemble machine learning approach using a voting classifier to predict cardiovascular disease (CVD). The hard voting classifier integrates logistic regression, random forest, multilayer perceptron, and Gaussian naïve Bayes classifiers, achieving a test accuracy of 88.42% on the FHSD. This study emphasises the effectiveness of ensemble methods and hard voting in improving prediction accuracy for heart disease diagnosis. Mohapatra et al.³⁸ proposed a predictive model for heart disease based on a two-level stacking of classifiers that combines various machine learning algorithms to enhance prediction accuracy. Focusing on the UHDD, this study employed preprocessing techniques, including outlier detection and normalisation, to improve model performance. The stacking model, incorporating diverse base learners and a meta-learner, achieved an accuracy of 92%, demonstrating the effectiveness of ensemble methods in medical diagnostics. Saboor et al.³⁹ presented a comprehensive study on enhancing heart disease prediction accuracy through various machine learning classifiers. The heart disease dataset was used to evaluate the performance of nine classifiers, both before and after hyperparameter tuning. This study employs a k-fold cross-validation technique for training and validating the algorithms. Among all classifiers, the support vector machine achieved an accuracy of 96.72% through data standardisation and hyperparameter tuning, demonstrating the potential of machine learning in heart disease diagnosis. Aldossary et al.⁴⁰ examined the efficacy of tree-based models (random forest, decision tree, extra trees, and gradient boosting) and the impact of ensemble techniques (voting and stacking) on predicting heart disease using the HDDC. The study revealed that the extra tree model achieved the highest accuracy at 92%, while ensemble methods, particularly stacking, matched this performance, demonstrating the potential of these approaches for improving diagnostic accuracy for heart disease. Duraisamy et al.⁴¹ explored various voting ensemble models for predicting heart disease. The models employed in this study include light gradient boosting machine (LGBM), stack ensemble, XGB, random forest (RF), and logistic regression (LR) with the Kaggle dataset. The voting ensemble method achieved over 80% accuracy, demonstrating its potential for identifying systolic blood pressure as a primary factor in heart disease.

This study builds on prior research that employed stacking and voting to predict heart disease. However, it sets itself apart through the following aspects:

• We extensively explored various base models with differing characteristics for developing stacking and voting frameworks.

• We designed unique pipelines to enhance the efficacy, generalisability, and robustness of these stacking and voting frameworks.

• We examined the role of stacking and voting in providing valuable insights into the underlying features and models that influence the final prediction, thereby fostering a better understanding of the disease.

• We employed the Friedman Aligned Ranks test along with Holm’s post-hoc analysis to confirm the statistical significance of the designed model’s performance.

• Unlike many previous studies that regard ensemble models as “black boxes,” our work integrates XAI to provide transparency in model predictions. This sets our study apart by offering interpretable insights into how individual features impact the final prediction, addressing the frequently overlooked issue of model explainability in heart disease prediction.

Research methodology

This section provides a comprehensive overview of the research procedures undertaken and the ensemble learning methods utilised during the experiment.

Research workflow

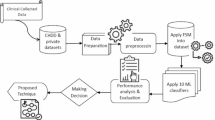
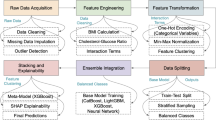
The flow of the proposed work is illustrated in Fig. 1. We considered two different heart disease datasets for this study. Initially, we conducted exploratory data analysis to assess and enhance the quality of the datasets. We searched for missing values and outliers, but found no such instances. Following this, the data were normalised and standardised according to established procedures. The training data were then used for model building. We first evaluated fifteen base models. After experimenting with various combinations of these base models, we selected six to create the stacking and voting models. The proposed models were trained on 80% of the dataset, while the remaining 20% was reserved for testing and validating their effectiveness. Hyperparameter tuning and feature ranking were applied to enhance the models. We validated the designed stacking and voting models using several performance metrics. The results were evaluated through various performance metrics.

Fig. 1

Proposed methodology for the research.

Stacking and voting

The fundamental concept behind ensemble learning is that several traditional machine learning models are combined to mitigate the shortcomings of any single model. The newly ensembled model integrates the strengths of various models, resulting in enhanced performance. The literature describes several ensemble learning approaches, such as stacking, voting, boosting, and bagging^42,43, all of which aim to enhance the predictive performance of machine learning models by amalgamating the strengths of multiple base models. Each of these methods has its advantages and disadvantages, and the choice of method depends on the specifics of the dataset and the prediction problem at hand. Generally, stacking and voting offer versatility and resilience by leveraging the attributes of different models, whereas boosting and bagging focus on reducing variation and sequentially correcting errors. In this study, we opted for stacking and voting methods due to their merits (as illustrated in Figs. 2 and 3, respectively) in comparison to boosting and bagging. Both stacking and voting are effective techniques for harnessing the diversity of multiple models to enhance prediction accuracy and robustness in machine learning tasks. The following is a brief overview of the stacking and voting methods.

Stacking

Stacking (stacked generalisation) involves training multiple individual models and then combining their predictions using another model, often referred to as a meta-model. During the training phase of stacking, the first step involves training a set of diverse base models with the available training data. These base models can be selected based on various algorithms or parameters, allowing for different predictions. Once these base models have been trained, they are used to generate predictions for the same training data on which they were trained. This step results in a new set of predictions, which are then combined with the original features to create a new dataset. This new dataset comprises the original features and the predictions made by the base models. In the final step of the training phase, a meta-model is trained using this new dataset, with the target variable being the true outcome or label. This meta-model learns to make predictions based on the combined information from the base models and original features, thus improving the model’s overall performance. During the stacking prediction phase, the first step is to generate predictions for the test data by employing the trained base models. This is achieved by applying each of the trained base models to the test data, leading to a set of predictions from each model. The next step is to combine these predictions to create a new dataset. This new dataset consists solely of the predictions made by the base models on the test data. In the final step of the prediction phase, the trained meta-model is used to arrive at the final prediction based on this new dataset. The meta-model utilises the information from the base model predictions to make a final, more accurate prediction for the test data. Using a trained meta-model to derive a final prediction based on the predictions of multiple base models makes stacking a powerful technique for enhancing the performance of machine learning models.

Voting

Voting involves combining the predictions of multiple models by taking a majority vote or averaging their outputs. It can be conducted in two main ways: hard and soft voting. In hard voting, each model in the ensemble produces a prediction, and the final prediction is determined by selecting the class that receives the majority of votes from the models. In the case of regression, the final prediction can be the average of the predictions made by the models. This approach is simple and effective, as it allows for the strengths of each model to be leveraged, resulting in a more accurate prediction. Conversely, soft voting involves each model in the ensemble producing a probability distribution over the classes. The predicted probabilities from each model are then averaged or combined in some manner, and the final prediction is made by selecting the class with the highest combined probability. Voting can be performed with equal voting weights for each model, or weights can be assigned based on the performance or confidence of the models.

Fig. 2

Advantages of stacking.

Fig. 3

Advantages of voting.

Constituent models

This ensemble learning method enhances prediction results by creating new features for training sets through the combination of predictions from the base learners. This approach generates the meta-features necessary for the final prediction by integrating both traditional and advanced classifiers. This section offers a brief discussion of the constituent base learners utilised to construct the stacking and voting models. The base learners are selected to ensure diversity within the study. The models possess different characteristics and learning mechanisms.

Weak models

Weak learners are generally simple models that perform just slightly better than random chance on a particular task. While they may not be especially accurate on their own, they act as a basis for more complex models. The following traditional machine learning algorithms are regarded as weak models.

LR is a classification algorithm approximating the relationship between input features and the likelihood of belonging to a specific class. It maps input values to [0, 1] using a logistic function (sigmoid)⁴⁴. It is a practical method for comprehending the influence of individual features on the classification outcome due to its straightforwardness and interpretability.

K-nearest neighbors (KNNs) are nonparametric algorithms that use the feature space to classify new instances according to their similarity to the k-nearest training instances. Understanding and implementing KNN is simple. It supports multiclass categorization and complex decision boundaries. It works well for regression and classification applications and is resilient to noisy data.

A multilayer perceptron (MLP) is a feedforward neural network comprising several layers of interconnected nodes (neurons). It employs activation functions and weights to represent complex nonlinear relationships between input features and target variables. It is a robust and adaptable model capable of approximating a wide range of functions. It works well for regression and classification problems and can handle complicated patterns.

Linear discriminant analysis (LDA) is a linear classification algorithm that identifies a linear combination of features to maximize class separation. It maps the input data to a lower-dimensional space while maintaining class discrimination. It is a dimensionality reduction technique that reduces the number of input features while retaining class-discriminatory information. It works best with well-separated classes and Gaussian feature distributions.

NB is a Bayesian theorem-based probabilistic algorithm that assumes that features related to the class label are conditionally independent. It calculates the probability of each class for a set of features and chooses the most likely class. NB is computationally efficient and performs well on high-dimensional datasets. It can handle both binary and multiclass classification problems with a small amount of training data. It excels at text categorization and spam filtering.

The support vector classifier (SVC) is a supervised learning algorithm that determines the best hyperplane to divide the classes with the greatest margin⁴⁵. After mapping the input data into a higher-dimensional feature space, support vectors are used to construct a decision boundary. SVC is capable of handling high-dimensional feature spaces and is efficient at capturing complex correlations in the data. It handles linear and nonlinear data effectively and resists overfitting. It can also handle binary and multiclass classification tasks.

A decision tree (DT) is a hierarchical structure that divides the input data according to feature values in a recursive manner⁴⁶. Making a choice or assigning a class label poses a sequence of yes/no questions. DTs are simple to comprehend and interpret. They can handle both categorical and numerical data and can detect nonlinear patterns. Decision trees can also deal with missing values and outliers in the data.

Ensemble models

To make stacking and voting more efficient and robust, we also considered several ensemble models to build the pipelines. This study uses the following ensemble algorithms based on their popularity and capability.

RF uses multiple decision trees for ensemble learning. Each tree trains on a random subset of the data, and the final prediction is the average of all trees. To mitigate overfitting, RF aggregates predictions from numerous trees. It is resilient to missing values and outliers and can handle high-dimensional data. It estimates feature importance and performs well without hyperparameter adjustment.

Extra trees (ET) is another RF-like ensemble learning method. It builds several decision trees using arbitrary subsets of the data and then averages the outcomes to generate predictions. In contrast to RF, ET uses a more aggressive randomization algorithm to choose features. ET lowers computing costs and overfitting by employing more randomness in the feature selection method. It can manage noisy and missing data and performs well with high-dimensional data.

GB is a general ensemble learning technique that combines weak models sequentially. It optimizes a loss function by iteratively adding models to the ensemble and concentrating on the residual errors of the preceding models. GB is a powerful technique that can capture complex nonlinear relationships in data. It can handle both regression and classification problems effectively. In addition to offering feature importance measures, gradient boosting allows the customization of hyperparameters.

LGBM is a GB framework that relies on tree-based learning methods. It constructs a strong model by training numerous weak models successively, with each succeeding model correcting the errors committed by the prior models. LGBM provides rapid and efficient training and prediction, making it ideal for large datasets and time-constrained applications. It generates accurate and powerful models, efficiently handles categorical features, and supports feature importance analysis and hyperparameter customization.

Categorical boosting (CB) is a GB method that works well with categorical features. It employs a variation of gradient boosting known as “ordered boosting” and unique techniques to cope with categorical data without requiring human preprocessing. CatBoost does not require one-hot or label encoding because it can handle category features directly. It performs well with the default hyperparameters and includes built-in support for missing values. CatBoost also supports GPU acceleration to expedite training and inference.

XGB, another GB technique, is well known for its scalability and efficiency. It builds a potent ensemble model by combining GB methods with tree-based models. XGB efficiently handles large datasets with high-dimensional features. It supports various loss functions and evaluation measures and offers regularization techniques to prevent overfitting. Additionally, XGBoost provides versatility in terms of parallel processing and customization options.

Adaptive boosting (ADB) uses ensemble learning to produce a strong classifier from weaker classifiers. It gives greater weights to misclassified instances in each iteration to handle challenging samples and modifies the weights of weak classifiers based on their performance. ADB is effective in handling complex classification problems and achieves high accuracy. Even with weak base classifiers, it performs well and is less prone to overfitting. ADB is capable of classifying both binary and multiclass instances.

Stochastic gradient descent (SGD) is a popular optimization technique for machine learning models. Each iteration changes the model’s parameters using a random mini-batch of training data, making it computationally efficient. SGD is ideal for large-scale datasets and online learning scenarios in which data arrives in a steady stream. It handles high-dimensional data effectively and supports a variety of loss functions. Additionally, SGD is also parallelizable and memory-efficient.

Dataset for experiment

We used two datasets comprising information about heart disease patients. The first dataset (D1), HDDC, and the second dataset (D2), UHDD, were collected from Kaggle. The distribution of target variables in both datasets is shown in Fig. 4. D1 contains records for a total of 1,190 individuals, with 629 having heart disease, while the remaining 561 did not. In contrast, 526 out of 1,025 individuals in D2 had heart disease, leaving 499 free of heart ailments. D1 consists of twelve attributes for each record, where the first eleven attributes are independent (or predicate), and the final attribute is dependent (or target). In addition to the twelve attributes of D1, D2 includes two extra attributes. The specifics of all the attributes in both datasets are detailed in Table 1.

Fig. 4

Distribution of target variables in both datasets.

Table 1 Attribute information of both datasets.

IQRs and imputation methods were used to identify any outliers and missing values in the datasets. However, no such occurrences were found in either D1 or D2. To quantify and manage multicollinearity, we employed the variance inflation factor (VIF), a statistical measure that helps in identifying and addressing potential multicollinearity issues, thus enhancing the interpretability and reliability of the model. Multicollinearity among features can distort the coefficients of the predictive model, leading to unstable predictions. Features with high VIF values indicate significant multicollinearity, and in such cases, they may need to be excluded or transformed.

In our analysis, several features exhibited elevated VIF values (e.g., AG: 34.318 in D1; RBP: 57.953 in D2), as shown in Table 2. While a VIF greater than 10 is often deemed indicative of significant multicollinearity⁴⁷, these features were retained due to their critical predictive importance, as validated by feature importance rankings and SHAP analysis. For instance, SHAP values demonstrated that high-VIF attributes such as AG and RBP contributed substantially to the prediction of heart disease. The domain-specific relevance and model performance justified their inclusion, aligning with recommendations to prioritise theoretical and empirical utility over rigid thresholds in applied contexts^48,49.

Table 2 VIF values for both datasets.

Furthermore, we employed the CCA (correlation coefficient analysis) method to ascertain and visualise the associations among the dataset’s features. It detects the strength and direction of the linear relationship between two variables and is used for feature selection, identifying redundant features, or assessing the relevance of features to the target variable. CCA helps identify variables that are strongly correlated with the disease outcome and eliminates redundant features that are highly correlated with each other, which could complicate the model without adding value. It directly influences the model-building process by enhancing the quality of the data supplied to the models, ensuring that the ensemble methods are trained on a more effective set of features. By mitigating feature redundancy and multicollinearity, CCA primarily reduces the risk of overfitting, which in turn improves the model’s generalisation capability^50,51. However, it is important to note that CCA does not directly address underfitting, as underfitting typically arises from insufficient feature representation or model complexity rather than multicollinearity⁵². Although CCA itself does not inherently improve the interpretability of the model, it provides a foundation for identifying meaningful relationships between feature sets, which can be further explored using explainability techniques such as SHAP or LIME^53,54. These techniques can then be applied to enhance the interpretability of predictive models, making them more reliable and actionable. The CCAs for the attributes D1 and D2 are presented in Figs. 5 and 6, respectively. There was no significant correlation between any two features in the dataset concerning heart disease.

Both datasets comprise a mix of heterogeneous variables, including categorical, decimal, and numeric features. Normalising the data was essential to ensure that all features contributed equally to the model’s performance, as some features with larger numeric ranges could dominate the learning process. To normalise the feature values in both datasets, we employed Eq. 1 which scales the feature values from 0 to 1. Min-max scaling was specifically chosen because it is a widely used normalisation technique that transforms all features to a common scale (typically between 0 and 1), which is particularly effective for datasets with varied feature types and scales, as is the case here. We observed that applying min-max scaling improved the stability and convergence of the models, as it prevented certain features from disproportionately influencing the base learners.

$$\:{x}_{scaled}=\frac{x-{x}_{min}}{{x}_{max}-{x}_{min}}$$

(1)

where x is the feature value and x_min and x_max denote the minimum and maximum values of x, respectively.

Fig. 5

Correlation coefficient analysis for D1.

Fig. 6

Correlation coefficient analysis for D2.

Experiment and results

The following section presents the experimental details of predicting heart disease using ensemble learning algorithms. Table 3 contains the specifics of the experimental setup and the configuration of the computer on which the experiment was conducted.

Table 3 Hardware and software used to conduct the experiment.

Evaluation metrics

Evaluation metrics assess how effectively a model performs in relation to a problem statement. Various evaluation metrics are applied depending on the nature of the data and the type of problem being analysed. Table 4 summarises the performance metrics used to evaluate the experimental findings of the models presented in this study. These metrics utilise the following base measures:

• A true positive (TP) signifies that the patient has heart disease, and the model correctly predicts this.

• A true negative (TN) means that the patient does not have heart disease, and the model accurately predicts it.

• False positives (FPs) indicate that the patient does not have heart disease, yet the model incorrectly predicts a positive result for heart disease.

• A false negative (FN) represents a situation where the patient has heart disease, but the model incorrectly predicts a negative result.

Table 4 Performance evaluation metrics.

Prediction results of the base models

This section presents the prediction results of the base learners, as discussed in Sect. 3.3. The models are assessed based on six metrics: accuracy, precision, recall, specificity, F1-score, and ROC. Figures 7 and 8 show the prediction results for D1 and D2, respectively. ET attained the highest accuracy in both cases, while KNN had the lowest accuracy in D1, and MLP had the lowest accuracy in D2. On average, RF, ET, LGBM, CB, and XGB exhibited better results on both datasets.

Fig. 7

Performance of the base models with D1.

Fig. 8

Performance of the base models with D2.

Pipeline design for stacking and voting

To construct an efficient ensemble model, we aimed to identify the optimal combination of base models. Initially, we experimented with fifteen base models, as discussed in the previous section. We tried various permutations and combinations, as shown in Fig. 9. In the first combination, we utilised the top ten models, primarily based on their accuracy. In the second combination, ten models randomly selected by the program were employed. Six models common to both combinations were considered for the final set. These six models performed best in both combinations.

Using the six selected models (LR, ET, RF, CB, XGB, and LGBM), we built a pipeline for both stacking and voting, as depicted in Fig. 10. The pipeline-building processes for stacking and voting are presented in Algorithm 1 and Algorithm 2, respectively.

As detailed in Algorithm 1, LR was utilised as the meta-model in our study for stacking. The choice of LR as the meta-classifier was grounded in both foundational literature and empirical validation. Wolpert⁵⁵, who pioneered stacking, advocated for linear meta-learners like LR due to their robustness in combining base model outputs while mitigating overfitting⁵⁶. Subsequent studies, such as Ting and Witten⁵⁷, empirically demonstrated LR’s superiority over complex alternatives in maintaining interpretability and generalizability⁵⁸. In healthcare contexts, Zhou⁵⁹ further validated LR’s suitability for meta-learning, emphasizing its stability with heterogeneous base classifiers. Our prior experiences with ensemble frameworks⁶⁰ align with these findings, as LR consistently delivered strong performance as a meta-model. Its simplicity, computational efficiency, and interpretability make it ideal for biomedical applications^61,62, where transparency is critical.

In this study, we also experimented with alternative meta-classifiers such as KNN and LDA. However, as anticipated, these models did not yield competitive performance in comparison to LR, both in terms of accuracy and stability. The comparative performance of LR, KNN, and LDA as meta-learners is shown in Fig. 11. LR exhibited superior generalisation ability when aggregating the predictions from diverse base learners, which is why it was retained as the meta-classifier in our stacking model.

Fig. 9

Model selection.

Fig. 10

Pipeline building for stacking and voting.

Fig. 11

Comparative performance of LR, KNN, and LDA as meta-learners.

Algorithm 1

Stacking procedure.

Algorithm 2

Voting procedure.

Cross-validation

K-fold cross-validation is commonly employed to minimise the bias present in the dataset. In this technique, the dataset is divided into k subsets of roughly equal size, known as “folds.” In this experiment, the initial k-fold cross-validation was utilised on the training dataset for the base models. We tried various values of k for cross-validation to evaluate its influence on model performance. After assessing different options, we concluded that 10-fold cross-validation produced the most consistent and reliable results regarding accuracy and stability. The same k value was applied for combinations 1 and 2 (Fig. 9). The final combination was also validated using 10-fold cross-validation. The k-fold cross-validation process is visualised in Fig. 12.

Fig. 12

The k-fold cross-validation process.

Assessing feature importance

The predictor variables (input attributes) are ranked in the feature significance procedure according to the extent to which they contribute to predicting the target variable (output feature). This stage is essential for machine learning and ensemble learning models to yield more accurate predictions. We utilised the feature significance score (F score), a metric that indicates how often an attribute is employed for splitting during the training process which is defined by Eq. 2⁶³.

$$\:{F}_{i}\:=\frac{{({\stackrel{-}{X}}_{i}^{\left(+\right)}\:-\:{\stackrel{-}{X}}_{i})}^{2}+\:{({\stackrel{-}{X}}_{i}^{\left(-\right)}\:-\:{\stackrel{-}{X}}_{i})}^{2}}{\frac{1}{{n}^{+}-1}\sum\:_{k=1}^{{n}^{+}}{{(X}_{k,i}^{(+)}-\:{\stackrel{-}{X}}_{i}^{\left(+\right)})}^{2}+\:\frac{1}{{n}^{-}-1}\sum\:_{k=1}^{{n}^{-}}{{(X}_{k,i}^{(-)}-\:{\stackrel{-}{X}}_{i}^{\left(-\right)})}^{2}\:}$$

(2)

Where $\:{\stackrel{-}{X}}_{i}$, $\:{\stackrel{-}{X}}_{i}^{\left(+\right)}$, and $\:{\stackrel{-}{X}}_{i}^{\left(-\right)}$ represent the average of the i^th feature across the entire dataset, positive dataset, and negative dataset, respectively; $\:{X}_{k,i}^{(+)}$denotes the i^th feature of the k^th positive instance, while $\:{X}_{k,i}^{(-)}$ denotes the ith feature of the kth negative instance. The numerator indicates the discrimination between positive and negative samples, whereas the denominator defines the discrimination within each of the two samples. A larger F-score suggests that this feature is more discriminative⁶⁴.

The contributions of each predicate parameter employed in this study to heart disease incidence are illustrated in Fig. 13. When stacking was applied to D1, STS and FBS contributed the most and least, respectively. In the context of voting with D1, GD and RBP contributed the most and least, respectively. Likewise, CP and FBS showed the greatest and least contributions, respectively, with D2 using both stacking and voting.

Fig. 13

Feature importance of (a) stacking with D1, (b) voting with D1, (c) stacking with D2 and (d) voting with D2.

Hyperparameter tuning

Hyperparameter tuning is an extremely important process, as it controls the behaviour of the training algorithm and significantly influences the evaluation of the model’s performance. We employed PyCaret (https://pycaret.org/), a popular tool for automating machine learning workflows, to tune the hyperparameters and achieve optimal performance in the proposed model. The details of the hyperparameters for each model are presented in Table 5. Our experiment determined that the specified values for each parameter in the relevant model are the optimal values.

Table 5 Hyperparameters for the pipelined models used in stacking and voting.

Prediction results of the stacking and voting models

The classification performances of the algorithms are evaluated using a confusion matrix. The confusion matrices from the stacking and voting experiments on both datasets are displayed in Fig. 14. Figure 14c indicates that the designed stacking model performed best with D2. Among the 308 instances in D2, all instances were classified correctly, while two instances were misclassified. In contrast, from the 357 instances in D1, as depicted in Fig. 14b, the designed voting model correctly classified 330 instances while misclassifying 27 instances.

The accuracies of the stacking and voting models for D1 and D2 are illustrated in Fig. 15. The figure presents the accuracies for each fold of both designed models as well as the mean of the 10 folds. Both stacking and voting exhibited a mean accuracy of 91% with D1 and 98% with D2. Figure 16 displays the results for other performance metrics of both designed models, such as precision, recall, F1-score, Kappa, and MCC. The stacking model performed slightly better across all metrics except for recall for both datasets. The recall values of the voting approach are marginally higher for both datasets.

The performance deviations of the stacking and voting models with both datasets across ten folds for each metric are presented in Fig. 17. Stacking with D1 demonstrated the most consistency for each metric except for recall. Voting with D1 was the most inconsistent across all metrics except for recall, where stacking with D1 exhibited greater deviation.

According to the ROC-AUC scores, as displayed in Fig. 18, stacking and voting performed similarly (0.97 for both classes) for D2, while for D1, stacking (0.92 for both classes) was marginally ahead of voting (0.91 for both classes). Conversely, there is significant variation in the performance of stacking and voting regarding AUPRC. As illustrated in Fig. 19, the best AUPRC was achieved by stacking with D2 (0.98), whereas voting with D2 produced the lowest AUPRC (0.91). Figure 20 suggested that the MCR of stacking with D2 was the lowest at 1.67, while voting with D1 had the highest MCR of 9.12.

We also recorded the running time for the four combinations of the models and datasets. As shown in Fig. 21, stacking was slightly quicker than voting, and as anticipated, the models required less time with D1 compared to D2 due to D1 being smaller in size than D2.

Fig. 14

Confusion matrices of (a) stacking with D1, (b) voting with D1, (c) stacking with D2 and (d) voting with D2.

Fig. 15

Accuracy of 10-fold stacking and voting on both datasets.

Fig. 16

Other performance metrics for stacking and voting on both datasets.

Fig. 17

Standard deviation of folds for different metrics for stacking and voting with both datasets.

Fig. 18

ROC-AUC of (a) stacking with D1, (b) voting with D1, (c) stacking with D2 and (d) voting with D2.

Fig. 19

The AUPRC of (a) stacking with D1, (b) voting with D1, (c) stacking with D2 and (d) voting with D2.

Fig. 20

MCR and for stacking and voting with both datasets.

Fig. 21

Execution time (seconds) for stacking and voting on both datasets.

Analysis and discussion

This section thoroughly analyses and discusses the predictive performance of the proposed stacking and voting models from various angles, comparing them with the individual base models and the empirical research that has utilised stacking or voting for heart disease prediction.

Stacking and voting models in comparison with the base models

The performances of the designed stacking and voting models were compared with those of the constituent models considered. The comparison was based on accuracy, precision, recall, F1-score, and ROC metrics for both datasets. The top performances among the 15 models for each metric were contrasted with those of the stacking and voting models, as shown in Fig. 22. For example, as discussed in Sect. 5.2, ET demonstrated the best accuracy across both datasets. Figure 22a illustrates that both the stacking and voting models achieve higher accuracy than ET. Similarly, CB exhibited the best recall among the 15 models. As depicted in Fig. 22c, the stacking and voting models attained higher recall than CB. Therefore, the proposed stacking and voting models outperform all the best-performing constituent models across both datasets, with the exception of precision on D1, where SGD surpasses the stacking and voting models.

Fig. 22

Comparing stacking and voting models with the top performer base models in terms of (a) accuracy, (b) precision, (c) recall, (d) F1-score, and (e) ROC with both datasets.

Statistical analysis of the stacking and voting models

To assess the statistical significance of the performance differences among the models, we conducted a non-parametric Friedman-aligned ranks test⁶⁵, followed by post-hoc pairwise comparisons using the Holm method⁶⁶, with a significance level of 0.05. The statistical tests were performed using the STAC (statistical tests for algorithms comparison) web platform (https://tec.citius.usc.es/stac/index.html).

Friedman-aligned ranks test

To holistically compare models across datasets and metrics while accounting for dataset variability, the Friedman-aligned ranks test was employed⁶⁷. This non-parametric test treats datasets as blocks and aligns ranks globally across metrics, making it suitable for multi-dataset evaluations with limited groups⁶⁸. The rank test assesses whether there are statistically significant differences in performance among the models. Table 6 presents the average rank assigned to models based on their performance for the respective metric. For both datasets, the stacking model received a rank of 3.5, indicating relatively higher performance compared to the voting model, which received a rank of 1.5. However, the test statistic was 1.6 with a p-value of 0.2059, which is above the significance threshold (p > 0.05). Consequently, the null hypothesis (H0) was accepted for all the metrics, stating that no significant differences exist between the models.

Post-hoc analysis

The post-hoc comparisons employing the Holm method⁶⁸, as illustrated in Table 7, precisely examined the pairwise performance of the stacking model against the voting model across all metrics. The test statistic was 1.54919 for both datasets, with corresponding adjusted p-values of 0.12134. As these p-values surpassed the 0.05 threshold, the pairwise comparisons did not reveal any statistically significant differences.

Table 6 Friedman aligned ranks test of the stacking and voting models.

Table 7 Post-hoc test of stacking vs. voting for both datasets.

Explainability of the stacking and voting models using SHAP

XAI aims to enhance the transparency and interpretability of machine learning models, allowing users to comprehend the reasoning behind predictions. This is particularly crucial in high-stakes domains like healthcare, where trust and accountability are essential⁶⁹. Among XAI techniques, SHAP has risen to prominence for its capacity to provide consistent, fair, and detailed explanations of feature importance in predictive models. Grounded in cooperative game theory, SHAP assigns each feature an importance value, clarifying its contribution to a specific prediction⁷⁰. This capability renders SHAP an indispensable tool for unveiling the decision-making processes of complex models, fostering better understanding and actionable insights, particularly in critical healthcare and clinical applications.

In the context of heart disease prediction, SHAP proves invaluable. It assists clinicians and researchers in identifying which attributes play the most significant roles in diagnosing heart disease. By illuminating the relative importance of these features, SHAP not only enhances the interpretability of models but also bolsters confidence in their clinical application, ensuring that predictions are both accurate and actionable.

Global explanation

A global explanation aids in interpreting how an AI model performs across an entire dataset by revealing general trends and relationships between variables (e.g., age, genetic markers, lab results) and the model’s outcomes. It identifies the most influential features affecting predictions, enabling verification against domain-specific knowledge, such as medical guidelines. This assists in validating model performance and identifying areas that require optimisation.

Furthermore, global explanations are crucial in detecting biases, promoting fairness across diverse demographic groups, and ensuring compliance with ethical and regulatory standards like GDPR, HIPAA, and FDA requirements. Such transparency builds trustworthiness in healthcare systems.

In our analysis, we employed the mean absolute SHAP feature importance values to rank features according to their overall influence on predictions, irrespective of whether their impact was positive or negative. The global analyses of stacking and voting models across D1 and D2 are illustrated in Figs. 23 and 24, respectively. Features are organised by significance on the y-axis, with their mean SHAP values displayed on the x-axis for an unbiased view of their relative importance.

In the stacking model applied to D1, the slope of the peak exercise ST segment (STS) emerges as the most significant feature, reflecting its strong correlation with heart disease. Similarly, chest pain type (CP) is a critical factor, consistent with its established diagnostic relevance. Other influential features include serum cholesterol (CL) and gender (GD), which contribute moderately to the model’s predictive power. By contrast, features like fasting blood sugar (FBS), resting electrocardiographic results (REC), and maximum heart rate achieved (MHR) show limited impact, possibly due to weaker associations with heart disease in this dataset.

For D2, the stacking model highlights number of major vessels colored by fluoroscopy (CF) as a dominant predictor, suggesting its importance in distinguishing heart disease within this population. Interestingly, CP retains a high SHAP value, emphasizing its common relevance across datasets. Features such as thallium heart rate (TH) and oldpeak (OP) also gain prominence in D2, reflecting their increased significance in this dataset’s patient demographics. These differences suggest the influence of dataset-specific attributes on model behavior.

The voting model presents a more distributed influence of features, with smoother variations in SHAP values. In D1, STS and CP remain the top predictors, but their dominance is slightly reduced compared to the stacking model. Features like CL and gender maintain moderate importance, reflecting a consistent trend. Meanwhile, lower-impact attributes such as resting blood pressure (RBP) and exercise-induced angina (EA) show minimal contribution.

In D2, the voting model again highlights CP and CF as key predictors. However, the impact of TH and GD is slightly less pronounced than in the stacking model, suggesting a more balanced reliance on features. The voting model’s even distribution of feature importance might make it more robust in diverse datasets.

Overall, CP consistently emerges as a top predictor across all models and datasets, underscoring its universal diagnostic value. D2 emphasizes the significance of CF and TH , which are less prominent in D1. The stacking model appears better suited for datasets with distinct, dominant features, while the voting model is advantageous for datasets requiring a broader feature representation. These findings highlight the need to tailor model selection and feature emphasis to the characteristics of the dataset for optimal prediction accuracy.

Fig. 23

Absolute mean SHAP for (a) stacking and (b) voting on D1.

Fig. 24

Absolute mean SHAP for (a) stacking and (b) voting on D2.

Local explanation

A local explanation focuses on understanding the reasons behind a specific prediction made by an AI model for an individual instance, such as diagnosing a particular patient. This approach is particularly valuable in healthcare, where personalized treatment is crucial. Local explanations shed light on the unique factors, such as biomarkers or medical history, that influenced the model’s decision for a specific patient, aiding in the creation of tailored treatment strategies. By providing this case-specific insight, these explanations also foster trust in AI-assisted decisions, especially in critical medical scenarios.

Local explanations further assist in identifying errors by revealing features that contributed to incorrect outcomes, enabling model refinement and improved reliability. They also allow medical professionals to evaluate whether the model’s predictions align with established medical research, thus enhancing transparency in AI diagnostics.

In this research, SHAP’s waterfall and force plots were utilized to deliver localized explanations for predictions made by the stacking model in detecting heart disease. The waterfall plot breaks down how individual features influence the prediction step-by-step, starting from the model’s baseline output. On the other hand, the force plot visually represents how specific features increase or decrease the prediction, clearly illustrating the factors that impact the result.

Waterfall plot

The SHAP waterfall plot is an effective visualization tool for understanding how individual features contribute to a model’s prediction in a systematic, step-by-step manner. This plot breaks down the prediction into contributions from specific features, clearly distinguishing between positive and negative impacts on the target variable. The x-axis represents the predicted value, while the y-axis lists the features influencing the outcome. Features contributing positively to the prediction are shown in red. Features contributing negatively to the prediction are shown in blue. The size of each bar represents the magnitude of impact on the model’s output.

This visualization is particularly valuable in predicting heart disease. It highlights how factors such as health conditions or demographic attributes significantly shape the prediction for each individual, enhancing the interpretability of the model by identifying the most critical features in a patient-specific context. Figures 25 and 26 showcase the SHAP waterfall plots for D1 using stacking and voting, respectively. The SHAP waterfall plots for D2, using stacking and voting are shown in Figs. 27 and 28, respectively. For each case, the data of patient no. 5 have been used for the SHAP waterfall plot analysis.

In the stacking model, on D1 (Fig. 25), the overall predicted value (f(x)) for heart disease risk is + 5.79. The expected value of the target variable, E[f(x)] = + 0.042, represents the mean prediction across all observations. The STS feature has the most significant positive impact at + 2.09, indicating a strong correlation with a higher risk of heart disease. In this instance, STS has an actual value of + 0.616. Other notable positive contributors include CP and OP, with values of + 1.19 and + 1.02, respectively. MHR stands at + 0.69, EA at + 0.59, GD at + 0.42, and RBP at + 0.31, all of which also contribute positively to some extent. This suggests that increases in these values are associated with an elevated risk of heart disease. Conversely, features such as FBS (− 0.11) and REC (− 0.11) show negative contributions, implying that normal blood sugar levels and more typical ECG results can reduce the risk of heart disease. CL (-0.37) also contributes negatively, indicating that higher cholesterol in this context slightly reduces the risk, potentially due to data interactions or specific patterns learned by the model. Finally, AG at + 0.02 plays a minor role, with a small positive contribution, suggesting that while age is a factor, it is less impactful in this specific case. The combined contributions result in a final adjusted prediction of + 5.79, suggesting the patient is at risk of heart disease.

Fig. 25

Waterfall plot for stacking on D1.

For the same patient, the voting model yields a predicted value of 3.686 for heart disease risk on D1 (Fig. 26). Here, STS (+ 1.74) remains the strongest positive contributor, while AG (1.18), OP (+ 0.98), and GD (+ 0.73) exhibit crucial positive impacts, suggesting their heightened relevance in this context. Interestingly, CP (− 0.249) presents the highest negative contribution, differing from its role in the stacking model. The contribution of MHR (-0.29) has also been changed from the stacking model.

Fig. 26

Waterfall plot for voting on D1.

In contrast, on D2, in the stacking model, the feature GD emerges as the most significant positive contributor with a value of + 2.86 (Fig. 27), indicating that the female patient is strongly associated with an increased risk of heart disease. Following GD, CF (− 1.8) and CP (− 1.21) have notable negative contributions, suggesting that higher values of these features might correlate with a reduced risk of heart disease. Other features contributing positively include TH (+ 0.99), STS (+ 0.71), EA (+ 0.55) and RBP (+ 0.61) indicating that these factors also increase the risk. Conversely, features like AG (− 0.46) and REC (− 0.45), have slightly lower negative impacts on the prediction. The overall predicted value for heart disease risk is 2.87, indicating that the patient is at moderate risk.

Fig. 27

Waterfall plot for stacking on D2.

The voting model yields a higher predicted value of 5.455 for heart disease risk on D2 (Fig. 28). Here, GD remains a critical positive contributor, with a value of + 2.6, reinforcing its importance in heart disease prediction. The feature OP (+ 1.43) also contributes significantly, indicating that higher OP values are associated with increased risk. Following these, STS (+ 0.81), CP (+ 0.76), TH (+ 0.68) and AG (+ 0.64) have substantial positive contributions. MHR (-0.55) has a negative impact, indicating that higher heart rates may not correlate positively with heart disease risk in this model. Other features like EA (− 0.41) and REC (− 0.41) also present negative contributions, suggesting that their higher values may relate to lower heart disease risk. FBS (− 0.03) has a minimal contribution to the overall prediction.

Fig. 28

Waterfall plot for voting on D2.

Force plot

While the waterfall plot offers a sequential breakdown of feature contributions, the SHAP force plot highlights the overall impact of features in relation to a baseline value. These plots visually convey the factors influencing the stacking model’s predictions by demonstrating how specific features either support or oppose a given classification. The effect of each feature is represented with arrows indicating its direction (positive or negative) and magnitude, providing a clear and interpretable view of the model’s decisions. By offering an interactive and user-friendly method to analyse predictions, the force plot facilitates a comprehensive understanding of how individual features contribute to the final outcomes. Figures 29 and 30 present the SHAP force plots for the stacking and voting models on D1 and D2, respectively, for a specific instance.

Fig. 29

Force plot for (a) stacking and (b) voting on D1.

The SHAP force plot for the stacking model on D1 (Fig. 29a) demonstrates a predominantly negative contribution from the features, resulting in a low prediction score (f(x) = -4.46). This indicates that the model predicts a lower likelihood of heart disease for this instance. Among the features, AG has the most significant positive contribution, strongly indicating its association with heart disease. Similarly, FBS moderately increases the prediction score, reinforcing its role as a risk factor. Conversely, STS has the strongest negative contribution, while CP and GD present moderate negative contributions, diminishing the overall likelihood of heart disease. These negative contributions correspond with their protective roles in certain instances.

For the voting model (Fig. 29b) on the same dataset (D1), the prediction is markedly different, with a high positive prediction score (f(x) = 6.97) indicating a strong likelihood of heart disease. In this instance, CL has the most substantial positive contribution. FBS, CP, and STS also demonstrate moderate positive contributions. AG contributes negatively, although its impact is relatively minor compared to other positively influential features.

Fig. 30

Force plot for (a) stacking and (b) voting on D2.

The stacking and voting models on D2 (Fig. 30) present moderately positive prediction scores (f(x) = 5.45 and 4.54, respectively), indicating an increased likelihood of heart disease for this patient. In both instances, GD has the strongest positive contributions. Additionally, OP, STS, CP, TH, and RBP exhibit a positive influence on heart disease in both models. In both cases, CF reveals a moderate negative contribution. However, we also observe a distinct differentiation between the two models. In stacking, AG has a positive contribution, whereas in voting, it exhibits the strongest negative contribution.

Critical analysis

The SHAP waterfall and force plots reveal significant variations between the stacking and voting models in predicting heart disease across two datasets. The waterfall plot highlights differing risk assessments: on D1, the stacking model assigns a higher risk score (5.79) (Fig. 25) than the voting model (3.686) (Fig. 26), whereas on D2, the voting model produces a higher score (5.455) (Fig. 27) than stacking (2.87) (Fig. 28). These differences suggest that the stacking model is more sensitive to nuanced feature interactions, while the voting model reacts more strongly to dominant risk indicators. Key features such as CP, MHR, and REC on D1, and OP, CP, and MHR on D2 exhibit substantial variations in interpretation, emphasising how different ensemble learning strategies influence feature importance. However, STS and GD consistently emerge as dominant positive contributors, while FBS remains a consistently weak negative contributor, reinforcing its relatively minor role in the model’s decision-making. These variations underscore the necessity of considering both dataset characteristics and model selection when making clinical predictions.

The force plot analysis further emphasises these distinctions. On D1, the stacking model predicts a low likelihood of heart disease, considering STS, CP, and GD as protective factors, while age and FBS contribute positively to the risk (Fig. 29(a)). In contrast, the voting model predicts a high likelihood of heart disease, primarily driven by CL, FBS, CP, and STS, with age playing only a minor negative role (Fig. 29(b)). On D2, both models predict a moderate risk, with GD, OP, STS, CP, TH, and RBP emerging as consistent risk factors (Fig. 30). However, the interpretation of AG differs significantly—it contributes positively in the stacking model (Fig. 30(a)) but is the strongest negative contributor in voting (Fig. 30(b)), suggesting that the two models assess age differently in their predictions.

The key distinction between the stacking and voting models arises from their differing ensemble learning strategies. Stacking employs multiple base models in a hierarchical manner, capturing complex feature interactions and dependencies, whereas voting combines predictions in a parallel way, emphasising strong individual predictors over subtle interactions.

One major reason for their differing predictions is that stacking refines its final decision through a meta-model, making it more adaptable to varying feature influences. This explains why, on D1, stacking assigns both risk-enhancing and protective roles to different features, resulting in a lower prediction score (Fig. 29(a)). In contrast, voting, which relies on a simple majority decision, tends to overemphasise dominant risk factors, such as cholesterol, leading to a higher prediction score (Fig. 29(b)).

Another crucial distinction is how the models manage feature correlations. Stacking identifies compensatory effects, such as the protective influence of STS and CP in certain cases (Fig. 29(a)), which prevents an overestimation of heart disease risk. Voting, however, treats each feature independently, rendering it more susceptible to overemphasising high-risk indicators like CL and FBS (Fig. 29(b)).

The treatment of age further illustrates this difference. On D2, stacking acknowledges age as a risk factor (Fig. 30(a)), likely in conjunction with other medical variables, while voting assigns it a significant negative contribution (Fig. 30(b)), possibly due to a threshold effect where other risk factors diminish its importance. This indicates that voting relies more on absolute feature strength, whereas stacking adjusts predictions based on interdependent relationships between features.

Ultimately, stacking delivers a more context-aware and balanced assessment by integrating multiple feature interactions, whereas voting provides a more direct and high-sensitivity approach by prioritising dominant predictors. Stacking is beneficial in complex cases where nuanced interactions are important, while voting may be preferred when strong individual risk factors require emphasis.

Despite the generally expected predictions, certain unexpected observations arise in both models. For instance, in the waterfall plot, CP (in voting on D1 (Fig. 26) and stacking on D2 (Fig. 27)) and CL (in stacking on D1 (Fig. 28)) act as negative contributors, contradicting established medical knowledge. Similarly, in the force plot for voting on D1 (Fig. 29(b)), cholesterol is the strongest positive contributor, despite the patient having a negative cholesterol value.

These anomalies may be attributed to various factors. One possible explanation is the non-linear nature of the model, where the relationship between cholesterol and heart disease does not strictly increase or decrease. The model may have determined that moderate cholesterol levels present a lower risk than extremely low or very high levels, as very low cholesterol can sometimes indicate underlying health issues, such as liver disease or malnutrition.

Another factor is the interactions between features in the model. SHAP values represent the combined effect of multiple features, indicating that the influence of cholesterol may depend on other variables such as RBP, REC, or FBS. For instance, if a patient has moderately high cholesterol but otherwise normal vital signs, the model might conclude that cholesterol does not significantly increase risk. Furthermore, preprocessing techniques like feature scaling and transformations may have affected these interpretations.

Lastly, dataset biases and unforeseen correlations may have influenced these findings. If the training dataset consisted of a significant number of patients with low cholesterol who already had cardiovascular conditions (potentially due to cholesterol-lowering treatments), the model could have unintentionally learned a link between lower cholesterol and heightened heart disease risk. This underscores the necessity of thoroughly analysing data distributions and feature dependencies when interpreting SHAP values.

Comparing the stacking and voting models with state-of-the-art

The performance of our model was established by comparing it to several similar research papers using various metrics, as demonstrated in Table 8. In our experiment, the stacking methodology exhibited the best overall performance in predicting heart disease; thus, we focused solely on the results obtained with stacking. The improved performance of our model with stacking can be ascribed to the implemented methodologies, which include the selection of base models, the choice of the meta-learner, efficient cross-validation, and proper tuning of the hyperparameters.

Table 8 Comparison of the proposed work with recent literature.

Conclusions, limitations, and future directions

This paper explores the application of ensemble learning techniques, specifically stacking and voting, to enhance the accuracy of heart disease prediction. Researchers have conducted experiments using multiple datasets related to heart disease prediction and compared the performances of stacking and voting models against those of individual models. The results demonstrated that both the stacking and voting models outperformed the individual base models, as well as existing models, in predicting heart disease, with the stacking model exhibiting higher accuracy than the voting model. The statistical analysis further confirms the superiority of the stacking model. The improved performance of the stacking and voting models can be attributed to the employed methodologies, including the selection of base models, the choice of the meta-learner, efficient cross-validation, and proper tuning of hyperparameters. Specifically, the combination of predictions from multiple models allowed for the strengths of each individual model to be harnessed. These findings suggest that stacking and voting can be valuable in clinical decision-making for heart disease prediction.

However, the comparison of stacking and voting models in SHAP analysis demonstrates their distinct approaches to risk prediction. Stacking accounts for feature interdependencies and compensatory effects, leading to more context-sensitive predictions, while voting emphasizes strong individual predictors, often resulting in higher risk assessments. These differences highlight the importance of selecting an appropriate ensemble technique based on the specific clinical or predictive requirements. Furthermore, unexpected feature impacts underline the need for careful data analysis, feature engineering, and validation, ensuring that the model’s learned relationships align with medical knowledge and real-world patterns.

This research holds significant potential. Enhanced accuracy and precision in heart disease prediction can lead to early diagnosis, customised treatment regimens, and ultimately improved patient outcomes. Furthermore, better model interpretability assists doctors in making informed decisions and devising tailored therapies. To broaden the applicability of this study, the proposed method may be extended to include additional healthcare datasets with similar characteristics.

While this study demonstrates the effectiveness of stacking and voting ensembles in heart disease prediction, several limitations must be acknowledged. Firstly, the generalisability of the findings is constrained by the use of publicly available datasets, which may not fully reflect the diversity of real-world patients. Validating these results on larger and more diverse datasets is crucial to ensuring their broader applicability. Secondly, although SHAP analysis enhances interpretability, certain unexpected feature contributions suggest the presence of biases or data anomalies that require further investigation. Future research should explore avenues to refine feature selection and address potential biases. Thirdly, the computational complexity of stacking—particularly regarding hyperparameter tuning and cross-validation—may pose challenges for implementation in resource-constrained healthcare environments. Efficient optimisation techniques and lightweight ensemble architectures should be investigated to alleviate this issue. Finally, this study did not examine the challenges of real-time deployment, such as model drift or integration with electronic health records (EHRs), which are critical for practical adoption in clinical settings. Future work should focus on confronting these challenges to enhance the real-world usability of ensemble learning in healthcare applications.

To address the limitations of this study and extend its applicability, future research should explore several key directions. One promising avenue is the development of multi-tier stacked ensembles (MTSE), where hierarchical stacking architectures with multiple meta-learning layers can model deeper feature interactions. By integrating diverse data sources, MTSE enhances adaptability across populations and improves explainability through hierarchical SHAP analysis, thereby making AI-driven insights more reliable for clinical use. Techniques such as dynamic model weighting and adaptive ensemble selection may further increase the models’ adaptability across varied patient populations. Additionally, incorporating ensemble models into live clinical workflows alongside interactive explainability dashboards would enable clinicians to validate AI-driven predictions and dynamically refine treatment plans. Another significant area is the comparison of stacking-based ensembles with advanced AI techniques, including deep learning architectures like transformers and Bayesian probabilistic ensembles, to uncover strategies for enhancing both predictive accuracy and uncertainty quantification. Furthermore, integrating longitudinal patient data and causal inference methods can assist ensemble models in distinguishing between correlation and causation, leading to more clinically meaningful predictions. These advancements will propel the next phase of AI-driven heart disease prediction, rendering models more robust, interpretable, and practically viable for deployment within real-world healthcare environments.