Introduction

Primary liver cancer (PLC) is one of the most common malignancies worldwide, ranking sixth in morbidity and third in mortality1. PLC is also listed as the fourth most common malignant tumor and the second most cancer-related cause of death in China2. hepatocellular carcinoma (HCC) is the most common subtype of PLC, and its incidence is closely related to hepatitis virus infection3,4. Despite the tremendous progress of targeted therapy and immunotherapy in the treatment of HCC in recent years, surgical resection is still the first choice for patients with resectable HCC. However, Post-hepatectomy liver failure (PHLF), as a severe postoperative complication, greatly affects the prognosis of patients. PHLF has become the main cause of short-term death after surgery5.

Due to the high risk and incidence of PHLF, effective perioperative evaluation and postoperative management are critical. At present, there are a variety of liver function assessment methods, such as Child–Pugh grade, the model for end-stage liver disease (MELD) score, albumin-bilirubin (ALBI) score, and indocyanine green retention rate at 15 min (ICG-R15). While these models offer some predictive value for PHLF, they have limitations and do not comprehensively reflect the prognosis of liver cancer patients. The Child–Pugh grade is less effective for non-cirrhotic patients and does not comprehensively indicate liver cancer outcomes6,7,8. Although the ALBI score removes the subjective variables in the Child–Pugh grade, it still does not cover all aspects of liver function8,9. The MELD score was widely used in liver transplantation, cirrhosis, and other prognostic situations, and it assigned different weights to variables based on their impact on prognosis, leading to complex calculations and difficulty in categorizing the results of the assessment6,10,11. Although the indocyanine green (ICG) clearance test is a dynamic and quantitative liver function test, ICG-R15 has been proven to be an independent risk factor for predicting PHLF4,12. The reliability of ICG-R15 in assessing liver function may be affected by factors such as hepatic blood flow and biliary obstruction13.

Cirrhotic patients typically exhibit reduced liver function compared to non-cirrhotic individuals with similar volumes. Although imaging can show the presence of liver fibrosis in cases of cirrhosis, noninvasive biomarkers can be used to determine the degree of cirrhosis. The World Health Organization has recently validated various non-invasive scores based on biological parameters14,15, including aspartate aminotransferase to platelet ratio index (APRI)16, fibrosis-4(FIB-4) index17, γ glutamyl transpeptidase to platelet ratio (GPR)18, and aspartate aminotransferase to alanine aminotransferase ratio (AAR)19.

In oncology, systemic inflammation is commonly linked to alterations in blood markers. Specific immune and inflammatory biomarkers—including the lymphocyte to monocyte ratio (LMR), neutrophil to lymphocyte ratio (NLR), platelet to lymphocyte ratio (PLR), and γ glutamyl transpeptidase to lymphocyte ratio (GLR) have predictive value for post-resection outcomes in hepatocellular carcinoma patients20,21,22.

Traditional liver function assessment models are widely used to predict the risk of developing PHLF, but their predictive accuracy is relatively low. By analyzing the data of 13,783 patients, one researcher found that the AUC of ALBI score and MELD in predicting PHLF was respectively 0.67 and 0.6023. In recent years, with the development of artificial intelligence technology, more and more advanced algorithms incorporating more comprehensive risk factors have been applied in the field of PHLF prediction. Machine learning (ML) algorithms analyze a large amount of data to identify patterns, trends, and associations automatically, and they have been widely used in many different sciences. ML algorithms can find non-linear and seemingly unrelated factors that are difficult to find by traditional methods24,25. Previous studies have used ML methods to construct a model to predict PHLF. The AUC value of the model reached 0.944 in the training cohort. However, the AUCs of ALBI, FIB-4, APRI, MELD and Child-Turcotte-Pugh scores were 0.570, 0.595, 0.568, 0.512 and 0.512, respectively26. ML algorithms construct models that are praised for their excellent predictive performance. But at the same time, due to the opacity and complexity of their internal decision-making processes, these models are often referred to as “black box” models. To date, lack of interpretability has been a major barrier to implementing ML models in medicine27. To interpret the results of ML models, we combined ML algorithms with the SHapley Additive exPlanations (SHAP) to gain insight into the complex relationship between variables and PHLF28.

Given the limitations of existing assessment methods, this study focused on applying ML algorithms to construct a more comprehensive and accurate risk prediction model for PHLF, in order to facilitate postoperative recovery and reduce mortality rates.

Methods

Patients population

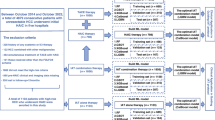
A retrospective cohort study enrolled 704 patients hospitalized in Liaoning Cancer Hospital from October 2016 to May 2020. Following rigorous screening, 392 patients were excluded for not meeting the predefined inclusion and exclusion criteria, resulting in a final cohort of 312 patients for subsequent analysis. A predictive model was developed based on the entire cohort, with 30% of the sample randomly selected for internal validation. From February 2023 to February 2024, a prospective cohort of 62 patients was recruited for our model accuracy assessment through prospective validation. Patients were categorized into PHLF and non-PHLF groups according to the International Study Group of Liver Surgery (ISGLS) criteria. In this investigation, HCC patients deemed suitable for surgical intervention were selected based on China liver cancer staging (CNLC) criteria. All participants provided written informed consent. Schematic of the study workflow was detailed in Fig. 1.

Fig. 1
figure 1

Schematic of the study workflow.

Full size image

Inclusion and exclusion criteria

The inclusion criteria were as follows: (1) Patients underwent hepatectomy for liver cancer; (2) Preoperative ICG clearance test and ICG-R15 < 30; (3) Primary liver cancer surgery; (4) Preoperative Child–Pugh grade was A or B; (5) Eastern Cooperative Oncology Group (ECOG) performance score ≤ 2.

The exclusion criteria were as follows: (1) Patients with severe comorbidities involving critical organs such as the heart, brain, lungs, and kidneys; (2) Patients had received transcatheter arterial chemotherapy and/or embolization before the operation; (3) Hepatitis virus replication was active before surgery; (4) Previous history of liver surgery; (5) Patients whose pathological assessments did not confirm; (6) Patients with Child–Pugh grade C who were unlikely to improve to Child–Pugh grade A or B even with short-term liver-protective therapy; (7) Incomplete clinical data.

Data collection

65 clinical characteristics and predictors associated with PHLF were collected. These included patient demographics, complications, imaging data, preoperative laboratory tests, inflammatory and immune function indicators, traditional models, tumor markers, postoperative pathology, ICG clearance test data, and operative data. Detailed variables were presented in Table S1.

In this study, the majority of patients (n = 252) in the training cohort chose to undergo conventional open surgery through a right subcostal incision, while a minority (n = 60) underwent laparoscopic surgery. All procedures were performed by physicians with over 10 years of expertise in hepatobiliary surgery. The Pringle maneuver was employed to temporarily occlude blood flow to the liver to minimize hepatic bleeding and ensure a clear surgical field during the procedure. The duration of hepatic blood flow occlusion should not exceed 15 min per session, followed by prompt restoration of hepatic blood supply for 5 min after each occlusion period. The extent of resection was categorized as major hepatectomy (≥ 3 segments) or minor hepatectomy (< 3 segments)29. Liver resection was performed using the clamp-crushing technique. Drainage tubes were routinely placed on the liver wound before the end of the operation to promote postoperative recovery.

The Child–Pugh grade is calculated based on five items: serum albumin (ALB), serum total bilirubin (TBIL), prothrombin time, hepatic encephalopathy, and ascites. Child–Pugh grade is defined as follows: grade A (5–6 points), grade B (7–9 points) and grade C (10–15 points). There were no patients with Child–Pugh grade C in this study. MELD score = 11.2 × ln [international normalized ratio(INR)] + 9.6 × ln (Creatinine [mg/dL]) + 3.8 × ln (TBIL [mg/dL]) + 6.410. ALBI score = -0.085 × ALB [g/L] + 0.66 × log10 (TBIL [μmol/L])9. A lower ALBI score indicates better liver function. APRI score = (AST/ upper limit of normal)/platelet (PLT)[109/L]) × 10030, the upper limit of normal is 40. FIB-4 index = aspartate aminotransferase (AST)[U/L] × age [years]/PLT [109/L] × alanine aminotransferase (ALT) [U/L])1/231. A higher score on this scale reflects a higher level of liver fibrosis. PNI = lymphocyte × 5 + ALB. Diagnosis of portal hypertension: clinically significant portal hypertension (CSPH) is diagnosed by endoscopy with the presence of oesophageal varices or a low PLT count (< 100 × 109/L) with splenomegaly (greater than 12 cm in diameter on ultrasound, CT, or MRI images)17.

Definition of PHLF

In most hepatectomy patients, TBIL and INR levels return to normal within 5 days after surgery. According to the criteria proposed by the International Study Group of Liver Surgery (ISGLS), patients with an increased INR and increased serum bilirubin level on or after postoperative day 5 were diagnosed with PHLF32. Combined with the reference values of the clinical laboratory in our hospital, INR > 1.2 and TBIL > 20.5 μmol/L on the 5th or after the 5th day after surgery were used as diagnostic criteria in this study.

Indocyanine green clearance test

Before the ICG clearance test, we checked for iodine allergy and biliary obstruction and ensured the patient fasted for 4–6 h. We then drew blood to check hemoglobin and recorded the patient’s height and weight. The DDG-5301K+ analyzer used these data to calculate ICG dose. A nurse prepared a 5 mg/ml ICG solution in sterile water. The patient had a quick venipuncture through the median cubital vein for ICG injection and waited 6 min for the ICG test using the Pulse Dye Density (PDD) method. This process provided key indicators: ICG clearance rate, ICG-R15, effective hepatic blood flow, and circulating blood volume.

Statistical analysis

The data of patients with missing values were excluded. Patient data were categorized as continuous or categorical variables, and the Kolmogorov–Smirnov test assessed whether the data followed a normal distribution. Normally distributed continuous variables were expressed as means ± standard deviations and compared between groups using t test. Continuous variables that were not normally distributed were reported as medians (interquartile ranges) using the Mann–Whitney U test. Categorical variables were presented as numbers and frequencies and compared using χ2 or Fisher’s exact test. Delong test was used to determine whether there were statistical differences between the receiver operating characteristic (ROC) curves, all statistical tests were two-sided, and P < 0.05 was considered statistically significant. Statistical analyses were performed with R, version 4.0.3.

We developed and compared 12 ML models to predict the risk of PHLF, including Logistic Regression (LR), K-Nearest Neighbor (KNN), XGBoost, Random Forest (RF), Naive Bayes (NB), ADAboost classifier (ADA), Support Vector Machine (SVM), Neural Network (NN), Gaussian Processes (GP), Gradient Boosting Machine (GBM), C5.0, Multi-Layer Perception (MLP).

The model construction and evaluation steps were as follows: (1) 65 clinical variables and predictors associated with PHLF were collected. After excluding near-zero variance and highly correlated variables, the remaining variables were screened using random forest and recursive feature elimination (RF-RFE) algorithm combined with the least absolute shrinkage and selection operator (LASSO) regression; (2) 5-repeated tenfold cross-validation method combined with a random search method were used to control and adjust hyperparameters33, and the optimal combination of hyperparameters was selected to construct the model; (3) 12 different ML algorithms were selected to construct 12 models. The area under the curve (AUC), accuracy (ACC), sensitivity (SEN), specificity (SPE), F1 score and learning curve were used to compare the performance of each models, and the best prediction model was finally determined; (4) The ROC curve, Calibration curve, and decision curve analysis (DCA) curve were performed on the training, validation, and prospective cohorts to evaluate the discrimination, calibration, and clinical utility of the model; (5) The constructed model was compared with the conventional models; (6) The “black box” model was interpreted using SHAP. SHAP revealed how each variable affected the results of the XGBoost model; (7) The construction of an online web page allowed further visualization and practicality of the XGBoost model.

Results

Patient characteristics

In this study, we initially identified a total of 704 hospitalized patients, of which 392 patients who failed to meet the inclusion criteria were excluded. Eventually, 312 patients were incorporated for analysis. PHLF occurred in 25.64% of the patients (n = 80). Table 1 summarized the baseline clinical characteristics of the training cohort (n = 312), validation cohort (n = 93), and prospective cohort (n = 62). The training cohort consisted of 312 patients who were used to construct a predictive model for PHLF. The validation and prospective cohorts were employed to assess the accuracy and generalizability of the XGBoost model.

Table 1 Baseline characteristics of the patients.
Full size table

Variables selection

A total of 65 variables were included in this study. Direct bilirubin, carbohydrate antigen 199, white blood cells, prothrombin time before surgery, fibrinogen to albumin ratio, ALBI, and APRI/ALBI—seven variables with the variance of 0 or collinearity—were excluded using the “finCorrelation” and “nearZeroVar” function from the “caret” package and the “vif” function from the “car” package of R. The remaining 58 variables were further screened by RF-RFE algorithm and LASSO regression. LASSO regression compressed the regression coefficients by increasing the penalty term. We found the best model fit by adjusting the λ (lambda) value. When the model included 21 variables, it achieved the best-fitting effect (Fig. 2A,B). RFE enhanced the generalization ability and effectiveness by initially considering all variables, then sequentially removing irrelevant or redundant ones based on a specific ranking criterion, ultimately retaining the most important variables34. RFE can be combined with different ML models. RF-RFE was used in this study. In the RF-RFE process, when the number of variables was reduced to 20, the model’s accuracy reached 0.772 (Fig. 2C). Variable importance was then ranked using the RF-RFE algorithm (Fig. 2D). Further, we selected the intersection of variables selected by LASSO regression and the RF-RFE algorithm to determine the key variables of the model (Fig. 2E). Finally, we determined the 12 best variables for the model’s construction, which included TBIL, MELD, ICG-R15, PLT, tumor size, hepatic portal occlusion time, operation time, LMR, GLR, intraoperative blood transfusion, Child–Pugh grade, and Major hepatectomy.

Fig. 2
figure 2

The LASSO regression and RFE-RF algorithms were used to screen the variables. (A) Path plot of LASSO regression coefficients for 58 risk variables. The vertical axis showed the value of the coefficients, the lower horizontal axis showed the log(λ) of the regularization parameter, and the upper horizontal axis indicated the number of nonzero coefficients retained in the model at each point. (B) Cross-validation curve. The vertical axis represented the log value of the penalty coefficient, denoted as log(λ). The lower horizontal axis represented the likelihood bias, while the upper horizontal axis indicated the number of variables selected. Smaller values on the vertical axis indicated a better fit of the model. (C) Variable ranking change curve. The horizontal axis represented the number of variables, and the vertical axis represented the accuracy of the curve after fivefold cross-validation. Among them, the accuracy for 20 variables was 0.772. The closer this value was to 1, the higher the accuracy. (D) The 20 variables after RF-RFE screening were ranked by importance, and only the top 13 variables were shown in this figure. (E) Venn diagram. Visually presented the commonalities and differences in variable selection between LASSO and RF-RFE.

Full size image

Model construction

In this study, the “trainControl” function of “caret” package in R software was used to set the training control parameters for model tuning. reduce the influence of randomness on model evaluation. During the training process, hyperparameter tuning was performed by adopting a random search method. The tolerance method was used to select the optimal combination of hyperparameters to build the machine learning model. Then the “train” function of the “caret” package in R software was used to build 12 different ML models through different machine learning algorithms. The evaluation results of the 12 ML models were summarized in the ROC curve (Fig. 3) and the performance evaluation Table (Table 2).

Fig. 3
figure 3

The Receiver operating characteristic (ROC) curves of the twelve models. (A) Training cohort. (B) Validation cohort. (C) Prospective cohort. Note SVM, support vector machine; KNN, K-nearest neighbor; XGB, eXtreme gradient boosting; MLP, multi-layer perception.

Full size image
Table 2 Performance evaluation of twelve prediction models.
Full size table

To observe whether the model was overfitting or underfitting, we drew learning curves (Figure S5) to observe the generalization ability of the model and the trend of model performance as the number of internal training sets changes. When the number of internal training was small, the accuracy of GBM, ADA, and RF models was 1, and there was no significant change in accuracy as the proportion of internal training sets increased. The accuracy of the internal validation set fluctuated greatly, and the overall level was lower than the accuracy of the internal training set. This may indicate an overfitting problem in the model. When analyzing the learning curves of XGBoost, SVM and KNN models, the accuracy of XGBoost model decreasesd with the increase of the proportion of internal training set, and the accuracy of internal validation set increased, indicating that XGBoost algorithm was more suitable for building our expected machine learning model than SVM and KNN algorithms. Therefore, we chose the XGBoost algorithm to build the model.

The XGBoost model not only performed well in avoiding overfitting but also showed excellent performance in multiple evaluation indicators such as AUC, ACC, SEN, SPE, and F1 score, which made it an ideal choice for our prediction task. Finally, we used a confusion matrix to show the prediction results of the prediction model and the actual results in detail (Figure S1).

Model evaluation and comparison

We analyzed the ROC curves to validate the XGBoost model: the AUC was 0.983 in the training cohort, 0.981 in the validation cohort, and 0.942 in the prospective cohort (Fig. 3A–C). Our model showed high accuracy in predicting PHLF. The calibration curves of the training, validation, and prospective cohorts for predicting PHLF demonstrated a strong correlation between the predictions of the model and the actual observations (Fig. 4A–C). To confirm the clinical utility of the XGBoost model, we used DCA to plot the curves on the training, validation, and prospective cohorts. The XGBoost model showed high net clinical benefit within a certain threshold probability range (Fig. 4D–F).

Fig. 4
figure 4

The calibration curve and decision curve analysis curve were used to evaluate the accuracy and clinical application value of the XGBoost model. (A) Calibration curve for the training cohort. (B) Calibration curve for the validation cohort. (C) Calibration curve of the test cohort. (D) DCA curve for the training cohort. (E) DCA curve for the validation cohort. (F) DCA curve for the prospective cohort. Note The all curve illustrated the benefit rates for all cases that received the intervention, while the none curve depicted the benefit rates for all cases that did not received any intervention. The pred curves represented the XGBoost model. DCA, decision curve analysis.

Full size image

When comparing the constructed XGBoost model with the conventional model, we observed that the XGBoost model showed excellent performance. Specifically, the AUC of the XGBoost model reached 0.983, which was significantly better than the traditional models such as the MELD score (AUC = 0.664), APRI score (AUC = 0.646), FIB-4 index (AUC = 0.694), ALBI score (AUC = 0.577) and Child–Pugh grade (AUC = 0.663) (P < 0.05) (Fig. 5). These data powerfully demonstrated the significant advantage of the XGBoost model in prediction accuracy and its high AUC value, meaning that the model has high accuracy and reliability in its ability to distinguish PHLF.

Fig. 5
figure 5

The prediction accuracy of the XGBoost model and conventional models for post-hepatectomy liver failure was compared. Note MELD, the model for end-stage liver disease; ALBI, albumin-bilirubin score; ICG R15, indocyanine green retention rate at 15 min; APRI, aspartate aminotransferase to platelet ratio index; FIB-4, fibrosis-4 index; XGB, eXtreme Gradient Boosting.

Full size image

Model interpretation

In this study, We ranked each variable in the XGBoost model in order of importance (Fig. 6A). Figure 6A showed that TBIL had the greatest impact on the model prediction results, followed by the MELD, ICG-R15, PLT, and other factors. Figure 6B illustrated the specific contributions of each variable to the prediction of PHLF using SHAP analysis. Points were colored based on individual patient eigenvalues and accumulated vertically to represent density. SHAP values indicated the degree to which each variable contributes to model predictions. Positive values indicated an increased likelihood of the predicted outcome, while negative values indicated a decreased likelihood. We found that the increase of TBIL, MELD, ICG-R15, tumor size, hepatic portal occlusion time, operation time, GLR, intraoperative blood transfusion, Child–Pugh grade, and major hepatectomy improved the predictive risk of PHLF. The increase of PLT and LMR reduced this risk. In addition, we provided two typical examples, one predicting the occurrence of PHLF (Fig. 6C) and the other predicting the absence of PHLF (Fig. 6D), to demonstrate the interpretability of the model. The Waterfall plots not only illustrated the influence of key variables on the model output but also helped us understand the specific role of each variable by means of visualization. SHAP force plot was used to visually display the SHAP values of a single sample and its impact on the model’s prediction results (Fig. 6E). In order to improve the clinical practicability, we constructed an online PHLF prediction network calculator based on the “shiny” package of the R software, which was easy to display the data analysis and visualization (http://124.221.189.227/webapp/) (Figure S4).

Fig. 6
figure 6

SHAP explained the XGBoost model. (A) Global bar graph. The average SHAP absolute value for each variable was on the X-axis. The Y-axis was sorted by variable importance, with the most critical variable appearing at the top of the graph. (B) SHAP summary plot. Yellow indicates high SHAP values, while red indicates low SHAP values. The farther a point was from the baseline SHAP value of 0, the greater its effect on the output. (C) and (D) Waterfall plot. (C) represented a sample with PHLF, and (D) represented a sample without PHLF. The X-axis showed the SHAP values. The Y-axis was sorted by variable importance, with the most essential variables appearing at the top of the graph. Variables with positive contributions were colored yellow, and those with negative contributions were red. The length of the bars represents the contribution magnitude of the variables. (E) SHAP predictions for sample without PHLF. Yellow arrows signified an increased risk of PHLF, while red arrows denoted a decreased risk of PHLF. The length of the arrows served to illustrate the predicted degree of influence, with longer arrows representing more substantial effects.

Full size image

Discussion

In this study, we successfully developed a personalized prediction model utilizing the ML algorithm to assess the risk of PHLF in HCC patients. Firstly, we applied LASSO and RF-RFE to screen out 12 critical variables, including TBIL, MELD, ICG-R15, PLT, tumor size, hepatic portal occlusion time, operation time, LMR, GLR, intraoperative blood transfusion, Child–Pugh grade, Major hepatectomy. After a comprehensive evaluation, the XGBoost model was selected as the final model for its excellent predictive performance, significantly superior to traditional clinical models such as Child–Pugh grade, MELD, FIB-4, ALBI, APRI, and ICG-R15. The XGBoost model showed excellent AUC values on training, validation, and independent prospective cohort, which verified its good predictive performance and robustness. To enhance the transparency and interpretability of the model, we used SHAP analysis to reveal the specific contribution of each variable to the predicted outcome, which helped to enhance the trust of clinicians in the model.

Previous research has extensively employed traditional logistic regression to construct clinical models for predicting PHLF, showing that these models outperform conventional models in terms of predictive accuracy4,12,35. Although there were relatively few studies about ML methods to construct predictive PHLF, studies that have utilized artificial neural network algorithms36,37,38, LightGBM37 and XGBoost algorithms39 have indicated superior predictive performance than traditional logistic regression. Therefore, it was essential to develop an individualized prediction model for PHLF, tailored specifically for HCC patients, using ML algorithm. The XGBoost algorithm built a strong prediction algorithm by integrating multiple weak prediction models. The XGBoost algorithm excelled at managing complex nonlinear relationships between variables and was particularly favored in medical data analysis for its strong generalization capabilities, low risk of overfitting, and high interpretability40. After comparing 12 ML algorithms, we adopted XGBoost algorithm to build the model.

Among the variables we included, ICG-R15 mainly aimed at PHLF in patients with cirrhosis4,41. For non-cirrhotic ones, the predictive accuracy of it was relatively low and had certain limitations 42. Studies have shown that the preoperative ICG clearance test alone was not necessarily a reliable method for predicting liver failure after hepatectomy43. However, it played an important role in predicting PHLF in a multivariate model combining clinical and imaging data4.Although rarely adapted in Western countries, ICG-R15 was widely used to assess liver reserve before hepatectomy in Asia44. In our hospital, ICG test was an important basis for us to evaluate liver function reserve. The specific value of ICG-R15 as a prerequisite for surgical resection varied in different studies45. In China, ICG-R15 < 30 was considered to be a necessary condition for surgical resection. Tumor size and resection range had a significant impact on postoperative liver function. Studies have shown that patients with large tumors and a wide resection range had a significantly increased risk of PHLF12,46. Therefore, tumor size and resection range should be comprehensively evaluated in surgical planning. Hepatic ischemia–reperfusion injury was aggravated, and the risk of PHLF was increased by the repeated process of blocking and restoring hepatic blood flow during surgery47. Therefore, it was recommended to use individualized hepatic blood flow control techniques to reduce the duration and frequency of hepatic portal occlusion and balance the reduction of bleeding and liver injury. Intraoperative blood transfusion affected the immune function of patients, leading to a decrease in the immune ability of the body, increased the risk of postoperative systemic infection, and then affected the liver function48. There was a certain association between intraoperative blood transfusion and PHLF, and more studies were needed to further explore this relationship. In the context of hepatectomy, precise assessment of intraoperative blood loss was vital for evaluating patient prognosis and implementing appropriate therapeutic interventions. An inaccurate estimation of blood loss could have resulted in a misinterpretation of the patient’s condition, potentially impacting treatment decisions. In this study, blood loss and blood transfusion were included as categorical variables to reduce error due to numerical estimation. This method could help to reduce the inaccuracies caused by subjective estimation of blood loss and improve the reliability of the study results. Current studies mainly focused on the relationship between LMR, GLR, and the prognosis of HCC after resection rather than directly linking LMR, GLR, and PHLF49,50. This study found that LMR and GLR were risk variables that led to PHLF. To gain a deeper understanding of the relationship between LMR, GLR and PHLF, further clinical research might have been required to explore this connection and determine the effectiveness of LMR and GLR in predicting the risk of PHLF.

A significant strength of our study was constructing a risk assessment model that can efficiently and accurately predict PHLF. The XGBoost model showed an AUC of 0.983 in the training cohort and 0.981 in the validation cohort. Further analysis found that the XGBoost model performed best in overall prediction performance, surpassing several clinical models, including Child–Pugh grade, MELD, FIB-4, ALBI, APRI, and ICG-R15. Secondly, our model was also prospectively tested, and an AUC of 0.942 was found in the prospective cohort, indicating good generalization ability. We employed SHAP analysis to address ML models’ “black box” nature and enhance interpretability. This method visualized model outcomes, offering medical staff clearer insights into the model’s predictive mechanisms. By leveraging SHAP’s game-theoretic approach to fairness, we could attribute each variable’s contribution to the model’s output, thus demystifying the decision process and fostering greater trust in the model’s predictions.

To facilitate the clinical use of this model, a free web calculator was developed to predict the risk of PHLF (http://124.221.189.227/webapp/).

There are several limitations to this study that deserve attention in future studies. Firstly, the lack of 3D reconstruction techniques to assess the preoperative liver volume and anticipated resection volume limits our ability to thoroughly investigate the impact of liver volume on PHLF. Second, the predominance of hepatocellular carcinoma linked to hepatitis B virus infection in our cohort resulted in an incomplete evaluation of other potential causes of HCC, which may limit the applicability of our findings. Third, MELD score and Child–Pugh grade both include TBIL. During the data cleaning process, this study found that the correlation coefficients between TBIL, MELD score, and Child–Pugh grade were all less than 0.5. A correlation coefficient greater than 0.7 was usually considered to indicate potential collinearity51 (Figure S3A). In addition, the variance inflation factors for these three variables were all less than 2, far below the threshold of 10, which was commonly regarded as indicative of multicollinearity51 (Figure S3B). This suggested that the collinearity among these three variables was weak, and including them together in the model was unlikely to cause collinearity issues. This study used RF-RFE and LASSO for variable selection and found that all three variables made significant contributions to the model, which also supported their inclusion. The SHAP analysis of the XGBoost model also showed that these 3 variables were the ones with a higher degree of influence. Therefore, 3 variables were finally included in the model. Both the MELD score and Child–Pugh grade include TBIL, but they also integrate a variety of other factors. These factors may complement the information reflected by TBIL, thus helping to improve the predictive efficacy of the model for patient prognosis. Fourth, this investigation is being conducted at a single center, making further validation through external multi-center studies necessary to confirm the model’s effectiveness and practicality. Lastly, the relatively small sample size may introduce variability in results. Consequently, while this study provides valuable insights, additional research efforts are essential for validating and refining these conclusions.

Conclusion

We successfully developed the XGBoost model to predict the risk of PHLF in HCC patients after hepatectomy. This predictive model can help identify patients with PHLF and can provide patients with early and personalized treatment to further improve outcomes and quality of life.