Introduction

Drought is one of the spatially most complex Earth hazards, persisting for years and profoundly affecting socio-economic sectors. Despite its significant impacts, drought remains less understood among natural hazards due to its diverse triggering mechanisms and influencing factors at different temporal and spatial scales1. Drought phenomenon occurs in every climate and geographical location, inflicting substantial damage to various sectors. For instance, the East African drought of 2010–2011, the Texas drought in 2011, the Central Great Plains drought in the United States in 2012, and the California drought during 2012–2015 caused significant agricultural, societal, and ecosystem damages, directly affecting crop production and water supply2,3,4.

Monitoring drought using indices can play a crucial role in improved understanding of this natural hazard. Considering the role of temperature and its increasing influence on drought frequency, it is necessary to consider this variable as it affects evapotranspiration rates, which are influential in decrease of agricultural production. Indices that incorporate both precipitation and evapotranspiration are more relevant for drought prediction5. The main advantage of this type of index over other drought monitoring indices is its ability to detect the impact of changes in evapotranspiration and temperature on global warming. One of the significant challenges in drought prediction is the use of local and regional data from local meteorological stations and rain gauges. These data either have limited time extension or may suffer from inadequate quality, necessitating data reconstruction6. Naturally, under such circumstances, the reliability of the predictions decreases, increasing uncertainty. To address such challenges, researchers have turned to the use of large-scale climate signals6. Climate signals often have long temporal extension, high adequacy and reliability, and can be used to predict worldwide droughts, floods, minimum or maximum river flows, and the onset of warm or cold seasons7. Large-scale climate signals are represented by standardized numerical indices such as the North Atlantic Oscillation (NAO), the Arctic Oscillation (AO), the Pacific Decadal Oscillation (PDO), and the Southern Oscillation Index (SOI). These indices, when combined with meteorological parameters, can improve the quality of drought prediction8,9,10,11.

To predict these indices, various machine learning methods for short-term and long-term prediction can be used. Such models have also been used in hydrology and hydrogeology when there is limited information about a system. The advantages of machine learning models for simulation include the absence of fundamental data, low cost, and less modeling time12. Consequently, in recent years, the use of models of this kind has been employed in various research problems for predicting hydrological and hydrogeological parameters13,14,15,16. The models can identify hidden or nonlinear patterns in historical data and then use these patterns to better predict future scenarios. The assessment of machine learning applications in hydrology indicates that these methods can provide more accurate performance compared to other models17,18,19,20. The ANFIS combines the advantages of artificial neural networks (ANN) and fuzzy inference system (FIS) in a unified framework. This model provides fast learning capabilities and adaptive interpretation for modeling complex patterns and understanding nonlinear relationships. Despite such advantages, according to various researchers, traditional algorithms within the ANFIS structure sometimes fail to improve the ANFIS model, and therefore, meta-heuristic algorithms capable of escaping local optima are used for this purpose21,22,23.

In recent years, the development of hybrid ANFIS models has been further enhanced by meta-heuristic algorithms. However, evaluations of new and powerful algorithms like the Harris Hawks Optimization (HHO) algorithm are rarely performed. The development of the HHO-ANFIS hybrid model in the past two years by various researchers has shown very positive performance in predictions22,24. The Whale Optimization Algorithm (WOA) is another of the newest meta-heuristic algorithms that has been used to improve the accuracy of ANFIS simulation. So far, limited research has, however, been done on combining WOA with individual algorithms for prediction purposes25,26,27. Rezaei et al.28 used the Marine Predator’s Algorithm (MPA) in combination with ANFIS, ANN, and support vector regression (SVR) algorithms to predict drought indices in warm and arid climates. Malik et al.29 utilized two meta-heuristic algorithms, Particle Swarm Optimization (PSO) and HHO, in combination with the SVR model to predict meteorological drought indices. Their results indicated that the meta-heuristic algorithm HHO, in combination with SVR, had a higher prediction accuracy. Banadkooki et al.30 used three meta-heuristic algorithms, the Slap Swarm Algorithm (SSA), PSO, and Genetic Algorithm (GA) in combination with ANN. Hybrid models have been used not only for predicting drought indices but also in other environmental and hydrological issues31,32,33.

In addition to the algorithms mentioned earlier, such as ANFIS + Water Cycle Optimization Algorithm + Moth Flame Optimization Algorithm (WCANFO) proposed by Adnan et al.34 and ANFIS + MPA proposed by Adnan et al.35, which have demonstrated promising prediction accuracy in predicting reference evapotranspiration and biochemical oxygen demand, respectively, there is a lack of research in using algorithms like Reptile Search Algorithm (RSA) in combination with ANFIS for predicting drought indices. RSA, introduced by Abualigah et al.36, is a relatively new meta-heuristic algorithm that has shown promising performance in optimization problems. However, it has not been extensively applied to hydroclimatic time series prediction tasks.

Iran, due to its location in the arid and semi-arid belt of the world, possesses vast expanses and a wide variety of climates. Therefore, this country serves as an excellent example for evaluating and predicting meteorological droughts in these climatic regions. Various studies have utilized machine learning models to predict various drought indice37,38,39,40, yet they are still rare in large-scale climate and meteorological signals to be considered in simulating the SPEI index in different climates. Therefore, in this study, the novel meta-heuristic RSA algorithm, combined with ANFIS, was employed to enhance the prediction of SPEI. Additionally, the hybrid models, ANFIS + WOA and ANFIS + GWO, were employed for comparison. The developed hybrid model was subject to evaluation in three distinct climatic conditions prevalent in Iran. Initially, the SPEI index for each climate was calculated using precipitation, evaporation, and temperature variables. Subsequently, input patterns for the models were developed using meteorological data and large-scale climate signals. The performance of machine learning models under three input patterns in predicting SPEI was evaluated using statistical and visual criteria to identify the best predictive model and the most effective input variables.

Study area and data used

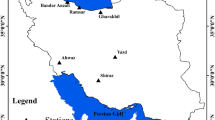
Iran, situated in the arid and semi-arid region of the world, has faced numerous challenges due to drought and reduced rainfall in recent decades. These challenges have severely impacted water supply. Analyzing the SEPI index and accurately predicting it can be a crucial step in effectively managing water resources in Iran. Iran, covering an area of over 1.6 million square kilometers (with about 50% of its territory consisting of mountains), is the sixteenth largest country globally, located in the eastern part of the Northern Hemisphere in southwestern Asia.

Physiographically, Iran is divided into four regions: the Caspian Sea region, the Central Plateau, the Zagros region, and the southern coastal plain41. Positioned in the arid belt, roughly 30% of the land (located in the Central Plateau) receives low annual precipitation (50–250 mm/year), while the Caspian Sea plain in the north receives over 1000 mm/year. The annual potential evaporation in the central part of Iran exceeds 4000 mm/year42. (Qadir et al., 2008). Temperatures vary from − 30 to + 50 °C, and annual precipitation from about 25 mm in the Central Plateau to over 2000 mm in the Caspian coastal plain.

The altitude of Iran varies from less than − 28 m amsl in the Caspian Sea to 5610 m amsl at Mount Damavand of the Alborz Mountain range. Mount Alborz in the north and Mount Zagros in the west play a significant role in dividing the country into different climate zones. These mountainous areas prevent moisture from reaching the central part of the country, which receives little rain and hosts one of the hottest deserts in the world, the Lut Desert. Approximately 88% of Iran is located in arid and semi-arid areas. The average annual rainfall in the studied period (1966–2014) for the whole country was 253 mm, which ranged from 144 to 342 mm per year. The northern part of Iran has a good average rainfall, but still, Iran receives less than a third of the world’s average rainfall.

The present study was conducted in homogeneous arid and semi-arid climatic regions of Iran. Therefore, using the modified Dumarten method, the climate was determined in 39 synoptic stations with 48 years of statistics (577 months). According to the above method, arid and semi-arid regions of Iran are divided into 8 homogeneous climates. Therefore, in this research, each sample station of a climatic region was selected and analyses were carried out on these regions. The results of the SPEI index surveys during the period 2010–2017 prepared by the Iranian Meteorological Organization show that the north and northwest of Iran, which have a more suitable climate, experienced less drought, while the center of Iran and especially the southwest experienced more severe conditions.

Data used

Two sets of meteorological data and large-scale climate signals were used to estimate the SPEI index, and from their combination, input patterns are presented in Table 1. Therefore, the models were implemented for all three developed patterns. Subsequently, three input scenarios were developed for the machine learning by combining meteorological variables and large-scale climate signals. In the first scenario (S1), the southern oscillation Index (SOI), and the North Atlantic oscillation (NAO), and SPEI(n − 1) were considered. The second scenario (S2) included meteorological variables maximum temperature (Tmax), minimum temperature (Tmin), average temperature (Tmean), precipitation (Pr), potential evapotranspiration (PEVs) and SPEI(n − 1). The third scenario (S3) included meteorological variables, large-scale climate signals, and SPEI(n − 1).

Table 1 Developed scenarios to estimate SPEI using input and output variables.
Full size table

Meteorological data

Figures 1, 2 and 3 shows the input and target variables that were prepared for three climates in Iran. In the semi-arid and cold climate, the variation resembles a sinusoidal pattern, and from monthly step 350 to the end of the period, this index turned negative. In the arid and super-cold climate (Fig. 2), from step 1 to 300, the SPEI was mostly above zero, and from 350 step onwards, it was mainly negative, indicating the onset of a drought period for this climate. However, in the arid and moderate climate (Fig. 3), for step 300, 400, 500, and 570, the SPEI reached its lowest values, indicating more severe drought in these months.

Fig. 1
figure 1

Trends in input and output variables in the semi-arid and cold climate.

Full size image
Fig. 2
figure 2

Trends in input and output variables in the arid and super-cold climate.

Full size image
Fig. 3
figure 3

Trends in input and output variables in the semi-arid and moderate climate.

Full size image

According to Figs. 1, 2 and 3, the changes in average temperature in the arid and super-cold, and semi-arid and cold climates have been similar, sometimes dropping to 9 °C. While the temperature rarely dropped below zero in the semi-arid and moderate climate, it has been higher compared to the other two climates. In the arid and super-cold, semi-arid and cold, and semi-arid and moderate climates, the average monthly mean temperature was 11.2, 13.7, and 17.6 °C, respectively, while the average monthly precipitation was 11.5, 27.1, and 20.0 mm in these climates, respectively.

The semi-arid and moderate climate had the highest maximum potential evapotranspiration among the three investigated climates (Fig. 3). Changes in precipitation during the study period (Fig. 3) show that the amount of precipitation in the semi-arid and cold climate has been less than the other two climates. Additionally, the semi-arid and moderate climate had more precipitation. Therefore, as shown in Fig. 3, the evapotranspiration was also higher in this climate.

Large-scale climate signals

Large-scale climate signals have a relative impact on Iran’s climate such as the Arctic Oscillation, the Pacific Decadal Oscillation, the Southern Oscillation Index, and the North Atlantic Oscillation. A brief description of these climate signal is presented in Table 2. Monthly time series of climate signals were taken from the Climate Prediction Center and National Climatic Data Center, National Oceanic and Atmospheric Administration (http://www.cpc.ncep.noaa.gov, https://www.ncdc.noaa. gov) for the period 1966–2014.

Table 2 Description of investigated large-scale climate signals.
Full size table

The variation range of AO, NAO, PDO, and SOI indices are (− 4.266: 3.495), (− 3.14, 3.06), (− 2.33, 3.51) and (− 6: 4.8), respectively. During the studied period, two indices AO and NAO were in the range of negative and the other two indices were in the range of positive values.

Research outline

Methods

In the current study, three different climates of Iran, including arid and super-cold, semi-arid and cold, and semi-arid moderate, were selected. Based on this, climate determination using the modified Thornthwaite Method was used for 13 synoptic stations with 48 years of data (577 months). The data ranged from 1966 to 2014. Each station represented a climatic region, and further analyses were conducted for these regions. Subsequently, the SPEI 12-month index was calculated using available data for each of the three climates. To simulate SPEI, variables affecting this index that depend on time were selected. These variables included meteorology (Tmax, Tmin, Tmean, Pr, and PEVs) at a monthly time step. Along these variables, large-scale climate signals including NAO, AO, PDO, and SOI were used to determine the effect of these signals on the SPEI index. Subsequently, three input scenarios were developed for the machine learning models by combining meteorological variables and large-scale climate signals. The SPEI index, considering three input scenarios, was estimated using ANFIS + RSA, ANFIS + WOA, ANFIS + GWO, and ANFIS models, and the results were evaluated using statistical criteria and graphical representations (Taylor diagram, time series plot, scatter plot, and violin plot) to select the most effective variables on the SPEI index for each climate (Fig. 4).

Fig. 4
figure 4

Schematic of the methodology in the present study.

Full size image

Standardized precipitation evapotranspiration index

The standardized precipitation evapotranspiration index, introduced by Vicente-Serrano in 2010, serves as a suitable index for drought assessment43. This index considers three variables: precipitation, temperature, and potential evapotranspiration (PEVs). SPEI combines the sensitivity of the palmer drought severity index (PDSI) to evapotranspiration changes with the simple calculations and multiscale nature of the standardized precipitation index (SPI). Hence, it can possess characteristics of both SPI and PDSI indices. To calculate the SPE index, in the first step, the evapotranspiration value for each month needs to be estimated. Then, using a simple water balance model, the difference between the precipitation (Pr) and PEVs for month ‘i’ is calculated as:

$${D}_{i}={Pr}_{i}-PEVs$$
(1)

where Pr and PEVs represent precipitation and potential evapotranspiration, respectively. Calculation of this index, similar to the method presented for calculation of the SPI index, requires estimating the cumulative probability values of Di through i by fitting a probability density function. Since the values of D converge to negative values at the lower bound, two-parameter probability functions cannot be selected for this purpose. Vicente-Serrano and colleagues identified the three-parameter log-logistic probability density function as having the best fit for the values of D after examining various functions. The general form of the probability density function for this function is given by:

$$f(x) = \frac{\beta }{\alpha }\left( {\frac{{n - \gamma }}{\alpha }} \right)^{{\beta - 1}} \left[ {1 + \left( {\frac{{n - \gamma }}{\alpha }} \right)^{2} } \right]$$
(2)

where the parameters α, β, and γ represent the scale, shape, and major parameters, respectively, for the values of Di in the domain ∞ < D > γ. The cumulative probability function form of the three-parameter log-logistic function is also according to:

$$F(x) = \left[ {1 + \left( {\frac{\alpha }{X - \gamma }} \right)^{\beta } } \right]^{ - 1}$$
(3)

The classic Aramovich-Wistigian function (Eqs. 4 and 5) estimates the SPEI value using the estimated values of the function F(X):

$${\text{SPEI}} = W - \frac{{C_{0} + C_{1} W + C_{2} W^{2} }}{{1 + d_{1} W + d_{2} W^{2} + d_{3} W^{3} }}$$
(4)
$$W = \sqrt { - 2\ln (p)} \;\;\;\;\;\;for\;\;p \le 0.5$$
(5)

where p represents the probability of the specified D values being exceeded. The values of C0, C1, and C2, as well as d1, d2, and d3, are constants. The SPEI index is a standardized variable, enabling spatial and temporal comparisons with other SPEI values. A SPEI value equal to zero corresponds to cumulative probabilities of D equal to 0.5. According to Table 3, the range of the SPEI index categories is between − 2 and 2. Values greater than zero indicate a wet period, with values above 2 indicating a severe wet period. Conversely, values less than zero indicate a drought, with values below − 2 indicating a severe drought. Additional categories can be found in Table 3.

Table 3 SPEI classification of dry and wet conditions.
Full size table

Adaptive neuro-fuzzy inference system

The ANFIS is a hybrid model that combines artificial neural network and fuzzy inference system. This model was developed to enhance simulation accuracy by leveraging the performance of both artificial neural networks and fuzzy inference systems44. Like a neural network, this model consists of different layers, and similar to a fuzzy inference system, it utilizes formulation of rules. Similar to a fuzzy inference system, two types of fuzzy inference, namely Mamdani and Sugeno, can be employed in ANFIS to determine the output, with the Sugeno method being preferred. The structure of ANFIS can be described as follows for two input parameters such as x1, x2, with fuzzy If–then rules, and an output y):

$$Rule \, 1. \, \;If \, ( x_{1} \;is\;A_{1} ) \, and \, ( x_{2} \;is\;B_{1} ) \, than\;f_{1} = p_{1} x_{1} + q_{1} x_{2} + r_{1}$$
(6)
$$Rule \, 2. \, \;If \, ( x_{1} \;is\;A_{2} ) \, and \, ( x_{2} \;is\;B_{2} ) \, than\;f_{2} = p_{2} x_{1} + q_{2} x_{2} + r_{2}$$
(7)

where B and A are fuzzy sets, q, p, and r are subsequent parameters of the model evaluated during the training phase.

The ANFIS structure employs five different layers. In the first layer, inputs pass through various membership functions, and the membership degree of input nodes to different fuzzy intervals is determined. Triangular, trapezoidal, Gaussian, and sigmoid functions are examples of membership functions commonly used in various studies. In the second layer, or rule nodes, the inputs to each node are multiplied together, resulting in the weights of the rules. In this layer, “AND” or “OR” operators can be used; in this study, the “AND” operator is utilized. The third layer normalizes the weights of the rules. The result nodes, called the rule layer, obtain the rules in this layer. Finally, the fifth layer consists of a single node that calculates the overall system output by summing all input values to it. This layer transforms the results of each fuzzy rule into non-fuzzy outputs through a defuzzification process.

Reptile search algorithm

The reptile search algorithm is a meta-heuristic algorithm inspired by the predatory strategy of crocodiles to search for food. Crocodile behavior was divided into two categories including high walking and belly walking in terms of exploration strategy. The total number of repetitions was divided into four parts based on these methods. In the exploration strategy, two conditions for high walking (\(t\le \frac{T}{4}\)) and belly walking (\(t>\frac{T}{4} and t\le \frac{2T}{4}\)) must be met (Fig. 5a, b). The step-by-step method of RSA algorithm can be summarized as follows:

Fig. 5
figure 5

Encircling the prey; (a) when (\(t\le \frac{T}{2})\), (b) when (\(t>\frac{T}{2})\).

Full size image

The RSA algorithm is implemented by starting with solutions chosen at random and generating them as:

$${y}_{(i,j)}=rand\times \left(UB-LB\right)+LB, j=\text{1,2},\dots ,n$$
(8)
$$\begin{aligned} y_{{\left( {i,j} \right)}} (t + 1) = & \left\{ {Best_{{j1}} \left( t \right) \times h_{1} \left( t \right) \times \beta _{1} - R_{{1\left( {i,j} \right)}} \times rand,\;t} \right. \\ \le & \frac{T}{4}\;Best_{{j1}} \left( t \right) \times x_{{(r,j)}} \times ES_{1} \left( t \right) - R_{{1\left( {i,j} \right)}} \times rand,\;t \\ < & \frac{T}{4}\;and\;t \le \frac{{2T}}{4} \\ \end{aligned}$$
(9)

\({Best}_{j1}\left(t\right)\) is the best previous solution, rand is a random number between 0 and 1. In addition, b1 is a critical parameter that affects the heuristic performance, while t and T reflect the current and total number of iterations. ES(t) is the random value between − 2 and 2 in all iterations evaluated, and x(r1,j) is the arbitrary position of solution i. R1(i,j) is a diminished search, r1 is the random choice lying in [1N], It defines the hunting operator to the jth position of ith solution. However, the positions are updated until the hunt is completed correctly. For more details, see36.

Whale optimization algorithm

The WOA was proposed by Mirjalili and Lewis45 that operates based on the bubble-net hunting strategy of Humpback Whales. However, because the search space’s optimal position is unclear, it assumes that the best current answer is the adjacent prey. After determining this point, the search for other optimal points and position updates continues as:

$$D=\left|\overrightarrow{c.} \overrightarrow{{X}_{t}^{*}}-\overrightarrow{{X}_{t}}\right|$$
(10)
$${\overrightarrow{X}}_{t+1}={\overrightarrow{X}}_{t}^{*}-\overrightarrow{A}.\overrightarrow{D}$$
(11)

where t is the current iterator, C and A are the coefficient vectors, X* is the best position vector so far, and X is the position vector. The vectors A and C are calculated as:

$$\overrightarrow{A}=2\overrightarrow{a}.\overrightarrow{r}-\overrightarrow{a}$$
(12)
$$\overrightarrow{C}=2.\overrightarrow{r}$$
(13)

The vectors are in both exploration and exploitation phases and reduced from 2 to 0 per repetition and in the range [0 and 1] (Fig. 6).

Fig. 6
figure 6

Flowchart of the WOA algorithm.

Full size image

Grey wolf optimizer

This algorithm is population-based and has a simple process to achieve the optimal solution. In implementing this algorithm, four types of gray wolves, i.e., alpha, beta, delta, and omega, are used to simulate the leadership hierarchy46. Searching for prey, besieging the prey, and attacking the prey are the three main steps of hunting. Alpha wolves, the highest-ranking wolves, are responsible for leading the herd and making decisions about rest and hunting. Beta wolves help the alpha group in the decision-making process and are also prone to be chosen as an alpha wolf. Delta wolves include older wolves, hunters, and baby care wolves. Omega wolves are located at the lowest position in the hierarchy, have the least rights over the rest of the wolves, and are not involved in the decision-making process. The mathematical model of the position of prey and wolves is expressed by46:

$$\vec{D} = \left| {\vec{C}.\overrightarrow {{X_{p} }} \left( t \right) - \vec{X}t} \right|$$
(14)
$$\overrightarrow{X}\left(t+1\right)=\overrightarrow{{X}_{p}}\left(t\right)-\overrightarrow{A}.\overrightarrow{D}$$
(15)

where A and C are the coefficient vectors, Xp is the location vector of the prey, and X is the location vector of each wolf, and t is the iteration number. The two vectors A and C are calculated using46:

$$\overrightarrow{A}=2\overrightarrow{a}.\overrightarrow{{r}_{1}}-\overrightarrow{a}$$
(16)
$$\overrightarrow{C}=2\overrightarrow{{r}_{2}}$$
(17)

where a components decrease linearly from 2 to 0 during successive iterations, and r1 and r2 are random vectors in the range of [0,1]. When the prey is cornered by wolves and ceases movement, the alpha wolf initiates the attack. The algorithm evaluates all solutions and selects the top three as alpha, beta, and delta wolves until the end of the process. This iterative approach updates the superior position of each wolf and then the positions of the other wolves in each iteration. After all iterations, the alpha wolf’s position is presented as the optimal solution.

Each model utilized necessitates fine-tuning certain parameters. These adjustments essentially refine the model’s structure, resulting in improved predictive performance. The ANFIS model’s optimal structure and parameter values were discerned through rigorous model training, as detailed in Table 4. Notably, the Gaussian membership function emerged as the best-fitting fuzzy function according to the table. Given ANFIS’s utilization of the Sugeno fuzzy type and its output being function-based, the optimal output function, first-order linear, was selected. The remaining optimal parameters are likewise delineated in Table 4. Within the RSA algorithm, achieving appropriate parameter values entails iterative model runs with varying parameters until suitable values are identified for the specific problem at hand. A population size of approximately 30 individuals was employed for RSA, with a maximum of 1000 iterations. The β was fixed at 0.10 and α was 0.15. Similarly, within the WOA and GWO model, 1000 iterations were executed, as beyond this threshold, no discernible improvement in prediction accuracy was noted. A population size of 30 individuals was utilized for the WOA. Additional suitable parameter values for each algorithm are outlined in Table 4.

Table 4 Optimized parameters of ANFIS, RSA, GWO, and WOA models.
Full size table

To evaluate patterns and utilized models, several error evaluation criteria have been used including root mean square error (RMSE) (Eq. 18), mean absolute error (MAE) (Eq. 19), Nash–Sutcliffe efficiency coefficient (NASH) (Eq. 20), normalized RMSE (NRMSE) (Eq. 21), and combined accuracy (CA) (Eq. 22)47,48.

$$RMSE = \sqrt {\frac{{\sum _{{i = 1}}^{{number\;of\;samples}} \left( {SPEI_{i}^{{actual}} - SPEI_{i}^{{prediction}} } \right)^{2} }}{{number\;of\;samples}}}$$
(18)
$$MAE=\frac{{\sum }_{i=1}^{number\; of\; samples}|{SPEI}_{i}^{prediction}-{SPEI}_{i}^{actual}|}{number \;of \;samples}$$
(19)
$$NASH=1-\frac{{\sum }_{i=1}^{number \;of \;samples}{({SPEI}_{i}^{prediction}-{SPEI}_{i}^{actual})}^{2}}{{\sum }_{i=1}^{number \;of \;samples}{({SPEI}_{i}^{actual}-\overline{SPE{I }^{actual}})}^{2}}$$
(20)
$$NRMSE=\frac{RMSE}{\sqrt{\frac{\sum_{i=1}^{number \;of \;samples}{\left({SPEI}_{i}^{actual}\right)}^{2}}{number \;of \;samples}}}$$
(21)
$$CA=0.33 \times (RMSE+MAE+(1-{R}^{2})$$
(22)

where SPEI actual represents the observed values, SPEI prediction denotes the predicted values, and \(\overline{SPE{I }^{actual}}\) denotes the average observed values. Lower RMSE, NRMSE, CA, and MAE, along with higher NASH, indicate better model performance.

Results and discussion

Machine learning models development for the SPEI index prediction

In this section, the prediction results of the SPEI drought index are analyzed separately for each climate using statistical and graphical criteria.

Semi-arid and moderate climate results

In the semi-arid moderate climate, the highest accuracy among models in estimating training data was observed in scenario S3 with the ANFIS model, achieving error metrics RMSE = 0.17, MAE = 0.12, NASH = 0.97, NRMSE = 0.17, and CA = 0.11 (Table 5). However, in this scenario, the ANFIS model demonstrated the lowest accuracy in estimating test data, with error metrics RMSE = 0.90, MAE = 0.40, NASH = 0.08, NRMSE = 0.82, and CA = 0.73. Although the ANFIS model has estimated the training data in S2 with almost the same error as S1, it has improved its accuracy in predicting the test data with (RMSE = 0.41, MAE = 0.24, NRMSE = 0.37, CA = 0.28, NASH = 0.81) criteria. As a result, the disparity in error between the two segments of the training and test data is evident in ANFIS for each scenario.

Table 5 Error evaluation criteria for SPEI prediction models in semi-arid and moderate climate (Appropriate values are marked in bold and underlined).
Full size table

According to the results of the test and training data, in the S1 scenario, the ANFIS + GWO (RMSE = 0.34, MAE = 0.24, NRMSE = 0.31, CA = 0.23, and NASH = 0.87) and ANFIS + RSA (RMSE = 0.34, MAE = 0.23, NRMSE = 0.30, CA = 0.23, and NASH = 0.87) models performed better. In S2, ANFIS + WOA performed best with the error evaluation criteria RMSE = 0.28, MAE = 0.19, NRMSE = 0.25, CA = 0.18, and NASH = 0.91). In this scenario, ANFOS + RSA also performed similarly (RMSE = 0.28, MAE = 0.20, NRMSE = 0.26, CA = 0.19, and NASH = 0.91. In the third scenario (S3), the ANFIS + WOA model continued to excel, achieving the lowest error metrics (RMSE = 0.30, MAE = 0.21, NRMSE = 0.27, CA = 0.20, and NASH = 0.90 on the test data).

The scatterplots of the test data for the selected scenarios of each model around the regression line for semi-arid and moderate are presented in Fig. 7. The results of R2 in the figures show that there is a high correlation between the simulation and observational data. The highest value of R2 is in scenario S2 for the ANFIS + RSA model (R2 = 0. 96), in scenario S3 for the ANFIS + GWO model (R2 = 0. 96) and the lowest value is in scenario S3 for the ANFIS model (R2 = 0.75). The results presented in Fig. 8 demonstrate that the correlation coefficient for the hybrid models exceeded 0.90, which signifies the satisfactory performance of the meta-heuristic algorithms employed.

Fig. 7
figure 7

Scatter plot of observed and simulated data in the semi-arid and moderate climate– test datasets.

Full size image
Fig. 8
figure 8

Comparing models in semi-arid and moderate climates using violin diagrams.

Full size image

The violin chart and a box plot were employed to compare the outcomes of the chosen models and scenarios presented in Table 5, as well as the data distribution (Fig. 8). Based on Fig. 8, the minimum values ​​in the two models (ANFIS + WOA (S2) and ANFIS + GWO (S3) are largely similar to the observational data. On the contrary, the maximum values ​​of the data in the ANFIS + RSA (S1) model are more extended. On the other hand, the median values in the box plot of the ANFIS + RSA (S1) model are consistent with the median observational data. In the ANFIS + WOA (S2) model, these values ​​are lower and in the ANFIS + GWO (S1) model ​​are slightly higher than the average of the observational data. Therefore, this graph shows that the performance of the hybrid models in this climate is better than ANFIS.

Semi-arid and cold climate results

The result of evaluation criteria for machine learning models in semi-arid and cold climate is presented in Table 6. According to the table, the ANFIS model has performed similarly in estimating training data, yet performed differently in simulating test data. This model has the best performance (RMSE = 0.42, MAE = 0.26, NMRSE = 0.42, CA = 0.30, and NASH = 0.76) for test data using S2 parameters. The ANFIS + RSA model performed best in simulating the training and test data in scenario 1 ((RMSE = 0.41, MAE = 0.29, NMRSE = 0.40, CA = 0.30, and NASH = 0.76 for test dataset).

Table 6 Results of error evaluation criteria for SPEI prediction models in semi-arid and cold climate (Appropriate values are marked in bold and underlined).
Full size table

In the third scenario, ANFIS + RSA demonstrated the most promising performance among the hybrid models. In these scenarios, which included all input parameters, it was able to estimate the test data with RMSE = 0.33, MAE = 0.23, NMRSE = 0.32, CA = 0.23, and NASH = 0.85. The performance of this model in the second scenario was also good, but it had less accuracy than ANFIS + WOA. ANFIS + WOA was able to predict the SPEI value with RMSE = 0.34, MAE = 0.23, NMRSE = 0.33, CA = 0.24, and NASH = 0.85 better than other hybrid models. However, in these scenarios, the accuracy of the hybrid models was notable. On the other hand, the ANFIS + RSA algorithm has performed a better prediction than the ANFIS model in all three scenarios, which shows that the RSA algorithm has covered the weaknesses of the ANFIS model. The model errors in all three scenarios reveal that the prediction accuracy in the second and third scenarios was superior to the first scenario. This difference is somewhat substantial, suggesting that meteorological variables play a more significant role in predicting SPEI.

The correlation coefficients between the observed and predicted values in each scenario, calculated from the test data, indicate that the models’ performance has consistently been between 0.81 and 0.92. The second and third scenarios had the highest correlation values (All hybrid models in S2, and ANFIS + RSA in S3), while the first scenario (S1) had the lowest, at 0.81. Notably, the overall correlation value in the S1 scenario was below 0.90, and the data exhibited greater dispersion around the y = x line compared to the other scenarios (Fig. 9).

Fig. 9
figure 9

Scatter plot of observed and simulated data in the semi-arid and cold climate.

Full size image

In Fig. 10, the results of the violin diagram for the chosen models in each scenario reveal that their performance exhibited some similarity. In the initial scenario, ANFIS + RSA (S1) underestimated values exceeding the median, which is not statistically significant. Consequently, it can be concluded that the performance of the selected hybrid models in the semi-arid and cold climates was remarkably consistent and suitable. According to the results obtained, it is evident that the majority of the SPEI values fall within the range of less than 0.5.

Fig. 10
figure 10

Comparison of models in semi-arid and cold climate using a violin diagram.

Full size image

Arid and super-cold climate results

In arid and super-cold climate, the ANFIS model has the weakest performance in simulating testing data of scenario S1 (RMSE = 0.39, MAE = 0.29, NRMSE = 0.31, CA = 0.37, and NASH = 0.58). The ANFIS + RSA model has proven to be the most accurate in the S1 scenario. This is attributed to the error evaluation criteria used in the training and test data. The RMSE is 0.28, MAE is 0.21, NRMSE is 0.29, CA is 0.20, NASH is 0.89, and RMSE is 0.30, MAE is 0.22, NRMSE is 0.24, CA is 0.25, and NASH is 0.75, respectively (Table 7).

Table 7 Results of error evaluation criteria for SPEI prediction models in arid and super-cold climate (Appropriate values are marked in bold and underlined).
Full size table

The ANFIS + RSA model estimated training and test data in two scenarios S2 and S3 with the same error values. In the third scenario (S3), the performance of ANFIS + GWO was remarkably similar to that of ANFIS + RSA with evaluation criteria of RMSE = 0.24, MAE = 0.18, NRMSE = 0.19, CA = 0.19, and NASH = 0.84 for the test dataset. As it is clear, the models used in this research had the least accuracy in the S1 scenario where large scales climate signals parameters were involved. Among the models, the ANFIS + RSA model with scenario S2 data has the best performance in predicting SPEI (Table 7).

The scatter plot of observational and simulation data in Fig. 11 shows that the simulations have a high correlation with the observational data. The highest correlation of model data with observation data is obtained in S2, where R2 values are almost equal to 0.92. In the S3 scenario, the ANFIS model data have a large scatter around the regression line. The data of this model have the lowest correlation with the observational data (R2 = 0.80). However, the results indicate that, similar to the climates examined, scenarios S2 and S3 exhibited superior performance in estimating SPEI, exhibiting the highest correlation and the lowest RMSE.

Fig. 11
figure 11

Scatter plot of observed and simulated data in the arid and super cold climate.

Full size image

In the arid and super-cold climate (Fig. 12), for minimum values, the shape of the violin diagram of the two hybrid algorithms (ANFIS + RSA and ANFIS + WOA) is closer to the shape of the observational data. The data in the depths in the ANFIS + RSA model have a closer distribution to the observational data than the ANFIS + WOA model. On the other hand, the shape of ANFIS + RSA (S1) model data is elongated at the tops. Since the observational data in the peaks are a bit more elongated, the data of the models are almost similar to each other and different from the observational data. According to the box plot, the median data in the ANFIS chart is at a far point from the median of the observational data, but the median of the combined data is largely consistent with the observational data.

Fig. 12
figure 12

Comparison of models in arid and super-cold climate; (a) Taylor diagram, (b) Violin diagram.

Full size image

Our evaluation of the Taylor diagram results, conducted using three indicators: RMSE, CC, and STD, in terms of location, reveals that the RSA algorithm provides a satisfactory estimate of SPEI. The algorithm’s location in all three climates closely aligns with the observational data. The RMSE error rate in the hybrid models consistently falls below half, while the correlation coefficient ranges from 0.90 to 0.92, indicating an accurate prediction (Fig. 13). Moreover, both WOA and GWO algorithms outperform ANFIS. As a result, the drought index SPEI has exhibited significance, displaying variation across different regions of Iran characterized by diverse climates. The outcomes underscore the promising performance of the employed models. Notably, among these, the ANFIS results showed potential for enhancement through the utilization of meta-heuristic algorithms.

Fig. 13
figure 13

Taylor diagram illustrating the spatial distribution of model-predicted and observed data across various climate regions.

Full size image

Figure 14 displays the estimated values of the drought index in all three different climates, along with the uncertainty band (the range marked in light green) estimated by ANFIS + RSA. Due to the successful results of the ANFIS + RSA model in estimating SPEI in various patterns and climates, it was selected as the representative model to analyze uncertainty. As shown in Fig. 14, the predicted values consistently fall within the specified uncertainty band. Additionally, in certain instances, such as extreme index values, the estimated values align closely with the upper and lower uncertainty bands. These findings are further illustrated in Fig. 14. While the results in Fig. 14 demonstrate that the predicted values consistently fall within an acceptable uncertainty range, there are instances, particularly when the index reaches maximum or minimum values, where uncertainty increases, necessitating further investigation and attention. Therefore, despite the accurate estimation provided by the ANFIS + RSA model in SPEI estimation, the results remain within an acceptable uncertainty range.

Fig. 14
figure 14

Estimated and observed SPEI values ​​along with 95% confidence interval of the best SPEI for semi–arid and cold, arid and super–cold, and semi-arid and moderate by ANFIS + RSA– using entire datasets.

Full size image

In addition to examining the uncertainty in the output results, a Q–Q plot was also used to further examine the normality of the results. The output results from ANFIS + RSA were analyzed in three different climates for this purpose. In this chart, the vertical values represent the quantile values estimated by ANFIS + RSA, while the horizontal axis represents the empirical distribution of the data with a mean and variance different from the standard normal distribution. Figure 15 shows that the chart in all three figures forms an almost straight line (without dispersion) passing through the center of the coordinates, indicating normality of the estimated values in all three climates. In Fig. 15 and semi-arid and cold, some poorly estimated points cause a slight deviation in the chart, but overall, the results indicate that the values estimated by ANFIS + RSA still follow a normal distribution.

Fig. 15
figure 15

Q-Q ANFIS + RSA predictions for entire data sets.

Full size image

The convergence of the RMSE for each algorithm varied based on its structure. Figure 16 illustrates that across all scenarios and climates, the algorithm consistently found the initial values with the lowest error. Notably, the WOA algorithm always commenced with a higher error but rapidly converged. For instance, in numerous cases, WOA began with an error exceeding ten but swiftly reduced it to less than one within the initial iterations. The convergence patterns of the GWA and the RSA are somewhat similar. They typically started with an error of less than two and converged swiftly. All algorithms eventually reached the optimal values within less than 500 iterations.

Fig. 16
figure 16

Convergence rates of RMSE in various iterations for GWO, WOA, and RSA algorithms.

Full size image

Discussion

This study focused on estimating the SPEI drought index across three distinct climates in Iran: arid and super-cold, semi-arid and cold, and semi-arid and moderate climates. We employed meteorological variables and large-scale climate signals in conjunction with ANFIS + RSA, ANFIS + WOA, and ANFIS models. The findings underscore the enhanced prediction accuracy achieved through the simultaneous utilization of meteorological data and climate signals. Comparisons between two sets of meteorological data and climate signals revealed that the incorporation of meteorological data yielded relatively higher accuracy in predicting the SPEI index. Moreover, the performance of the machine learning models across the three climates exhibited consistency. In contrast to similar studies that employed hybrid models, the utilization of hybrid models, specifically SVR + PSO and SVR + HHO, for drought forecasting by Malik et al.29 can be noted. This approach aligns with the findings of this study. Furthermore, the research conducted by Kikon et al.49 demonstrated the superior performance of hybrid models. They employed ANFIS + PSO to predict the impact of drought, highlighting the efficacy of hybrid models. The results of this study also concur with the research conducted by Mirboluki et al.50, which utilized ANFIS + GWO for drought forecasting. In this study, hybrid models exhibited a more pronounced role.

Research within the fields of hydrology and environmental science further corroborates the accuracy of these models in predicting target parameters, as exemplified by studies such as the prediction of longitudinal dispersion coefficient by Ohadi et al.51, evaporation prediction by Arya Azar et al.15, runoff simulation by Han et al.52, and groundwater level investigation by Pham et al.53. Additionally, these models accurately simulated various drought indices, as demonstrated by Piri et al.54, who utilized machine learning models including ANN, SVR, response surface method (RSM) combined by the SVR to simulate standardized precipitation index, percentage of normal precipitation, effective drought index, and modified China-Z index with high precision.

This study also revealed that individual models such as the ANFIS model occasionally exhibits lower prediction accuracy, consistent with findings from previous studies15,55. Therefore, employing meta-heuristic algorithms or optimization algorithms emerges as a viable strategy to address such weaknesses. In our investigation, this notion was substantiated by the efficacy of RSA and WOA algorithms. These findings are aligned with the research conducted by Kayhomayoon et al.56, where optimization algorithms like PSO, an Ant Colony Optimization (ACOR), GA, and Differential Evolution (DE) augmented the accuracy of ANFIS, and by Yaseen et al.57, where the Firefly Algorithm (FFA) bolstered the accuracy of ANFIS in river flow prediction. Another notable outcome of this study is the acceptable performance of machine learning models when provided with large-scale climate parameters, suggesting their utility even in data-scarce conditions.

The application of the large-scale climate signals indices in the three investigated climates demonstrated their limitations in standalone prediction of SPEI. However, their integration with meteorological parameters substantially enhanced the prediction accuracy. Consequently, the utilization of meteorological data in conjunction with the large-scale climate signals indices is recommended. Denoising and preprocessing of input data were not considered in this study, which is a suggestion for future research. This could improve the prediction accuracy. The results of evolutionary algorithms indicated that all three algorithms performed similarly, with RSA having slightly higher accuracy. RSA had a more complex structure compared to WOA and GWO. Despite the numerous advancements made in the field of metaheuristic algorithms, it is always recommended to utilize the latest algorithms and compare their results with those obtained from this research to achieve the most accurate predictive model. Finally, the integration of deep learning models and metaheuristic algorithms, as well as the combination of machine learning models and satellite measurements of the direction and impact of SPEI drought on other drought indices, are suggested as potential avenues for future research.

Conclusions

This study aimed to forecast the SPEI index across three distinct cli-mates in Iran: arid and super-cold, semi-arid and cold, and semi-arid and moderate climates. Analysis based on the SPEI index revealed variations in drought severity across these climates, with the most severe occurrences observed in the arid and super-cold climate. Subsequently, leveraging meteorological variables and large-scale climate signals, the SPEI index was simulated under three input scenarios using machine learning models, namely ANFIS, ANFIS + WOA, ANFIS + GWO, and ANFIS + RSA. The research findings underscored the acceptable performance of machine learning models in estimating SPEI across the investigated climates. Among these models, the hybrid ANFIS + RSA model showcased superior prediction accuracy compared to ANFIS and ANFIS + WOA across all three climates. The integration of large-scale climate signals alongside meteorological parameters in predicting the target index proved to be effective. While predictions solely based on large-scale climate signals exhibited relatively lower accuracy compared to those derived from local meteorological data, their utility as dependable input parameters can be advantageous in scenarios where meteorological data are scarce or incomplete. Moreover, the utilization of evolutionary optimization algorithms holds promise in augmenting the accuracy of individual models, particularly in addressing challenges related to rapid convergence or algorithm convergence issues in simulation tasks. Looking ahead, machine learning models offer promising avenues for predicting various drought indices while accounting for the complexities of climate change phenomena. Such endeavors can significantly contribute to enhancing our understanding of drought dynamics and improving preparedness and mitigation measures in the face of evolving climatic conditions.