Introduction

Optical materials known as photonic crystals (PCs) stand out from the crowd due to the unique structure of their dielectric constants, which allows for precise control over the propagation of light1,2. Photonic band gaps (PBGs), or ranges of wavelengths that cannot pass through crystal, are the consequence of this periodic structure3,4,5,6,7,8. For devices that require precise control over light, such as optical filters, waveguides, and lasers, PCs are essential9,10. One-dimensional PCs (1D-PCs) are structures that explore PBG11,12,13,14,15. They consist of alternating layers of materials with varying RIs arranged in a linear configuration. 1D-PCs are widely studied and utilized in various practical applications such as thin-film coatings and Bragg mirrors. Theoretical models and simulations of 1D-PCs are much easier to understand than those of structures with higher dimensions, which makes it easier to understand how light works in these crystals16,17. The presence of these defects in 1D-PCs results in the formation of localized states within the PBG. This enables the defect to transmit specific frequencies of light. Defective PCs are used to create high-quality resonators, waveguides, and filters with limited frequency selectivity. Defected 1D-PCs play a crucial role in sensors, adapting to environmental variations such as temperature or chemical composition by selectively transmitting or reflecting a specific range of wavelengths.

In symmetrical 1D-PC, topological edge states (TES) can emerge within the PBGs due to the nontrivial topological properties of the system. These edge states arise from topological phase transitions, which are characterized by changes in bulk topological invariants, such as the Zak phase. A PC with inversion symmetry can exhibit a quantized Zak phase of 0 or π, leading to distinct topological phases. When two regions with different topological phases form an interface, a localized edge state appears within the PBG, enabling robust light confinement at the boundary18. Unlike conventional defect-induced modes, these topological edge states are protected by bulk-boundary correspondence and remain robust against structural perturbations and imperfections19. Such states have attracted significant interest for applications in optical waveguiding, topological photonic devices, and quantum optics20.

Gamma radiation detectors (GRDs) are devices designed to detect and measure gamma rays that are a form of high-energy electromagnetic radiation21,22,23,24,25,26. Gamma rays demonstrate considerable penetrative abilities, requiring specialized materials for effective detection. Commonly utilized GRDs encompass scintillation detectors, semiconductor detectors, and gas ionization detectors. Each possesses distinct qualities that render it advantageous for various applications in medical imaging, environmental monitoring, and nuclear industry safety27,28. One of the most common types of GRDs is the scintillation detector. Sodium iodide crystals can be utilized, which engage with gamma radiation to emit visible light. Photomultiplier tubes subsequently detect and amplify this light, facilitating the measurement of gamma radiation. Radiation detection instruments extensively utilize scintillation detectors for environmental monitoring and medical imaging due to their heightened sensitivity27,29.

Porous materials are defined as substances that possess a network of interconnected spaces or pores within their structure, facilitating the entrapment of gases, liquids, or smaller molecules. Due to their high surface area, tunable porosity, and unique physicochemical properties, the materials in question have garnered significant interest in various fields, such as catalysis, energy storage, and environmental remediation. Porous silicon (PSi), a subset of silicone-based compounds, is characterized by its interconnected pores and sponge-like architecture. The porosity of these materials results in a substantial surface area, making them suitable for applications necessitating flexibility, breathability, and controlled permeability. PSi is utilized in medical implants and filtering systems due to its biocompatibility, chemical stability, and adjustable porosity30,31.

Recently, many polymers such as polyurethane, polyethylene, polyacetal, polytetrafluoroethylene, polyethylene terepthalate, polymethylmethacrylate, polysulfone, silicone rubber, poly(lactic acid), polyetheretherketone, and poly(glycolic acid) are employed in a variety of biological and industrial applications. This is primarily because these polymer materials come in a wide range of compositions, characteristics, and forms (solids, films, fibers, textiles, and gels) and may be easily produced into complicated shapes and structures32. Furthermore, sterilizing techniques such as autoclaving, ethylene oxide, and \({}^{60}\text{Co}\) irradiation may have a strong effect on polymer characteristics. So, polymer nanocomposites (PNCs) have attracted more interest as an active material for GRDs33, as well as other applications34,35,36,37,38.

Recently, the coupling between different resonances recorded very high performance39. The integration of PC technology with GRDs offers novel approaches to enhance sensitivity and minimize detector dimensions. Photomultiplier tubes improve the signal-to-noise ratio and make it easier to control the light path, which makes scintillation light more effective at being collected in GRDs. PCs, particularly defective 1D-structures, significantly enhance scintillation detectors by selectively transmitting scintillation wavelengths while blocking others. This design minimizes background noise and improves detection accuracy16. Defective 1D-PCs are very good at finding gamma radiation because they are designed to limit and boost the wavelengths of light produced by scintillating materials used in the detection process.

In this study, we explore the coupling between TES and defect resonance to achieve enhanced gamma radiation detection. GRD composed of defected symmetrical 1D-PC (SPC) of \(\text{PSi}\) containing PNC (polymer of Poly Vinyl Alcohol, carbol fuchsin, and crystal violet) inside pores is proposed to detect gamma doses (γD). To the best of our knowledge, this is the first implementation of a symmetrical 1D-SPC sensor incorporating PNC materials that leverages the interplay between a defect mode and a topological edge state for GRD. This unique design architecture enables ultra-high sensitivity and resolution, with a record-high quality factor of 447,747 and a sensitivity of 0.2267 nm/RIU. The introduction of topological photonic principles into gamma radiation sensing represents a significant advancement over conventional photonic sensors, providing enhanced stability and precision, particularly for detecting minute radiation dosage changes. This novel approach opens new avenues for the development of highly accurate, scalable, and cost-effective sensors in critical domains such as environmental monitoring, medical diagnostics, and nuclear safety.

Theoretical model and equations

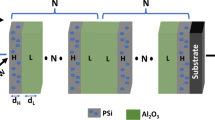
As clear in \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) construction in Fig. 1, the proposed GRD is composed of N unit cells of \({PSi}_{1}\text{ and }{PSi}_{2}\) containing PNC inside pores. Initially, the ratio of the pores (\(P\)) in the first and second layers \({PSi}_{1}\text{ and }{PSi}_{2}\) are 20% and 80%, respectively. The thickness of the first and second layers \({PSi}_{1}\text{and }{PSi}_{2}\) are 100 nm and 170 nm, respectively.

Fig. 1
figure 1

Geometrical representation of defected-SPC with unit cells of PSi containing PNC as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\).

Full size image

Using Bruggeman’s effective equation, the dispersion relations or RIs of PSi layers in each unit cell of the proposed \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) containing PNC are simulated as follows40:

$$\begin{aligned} {\text{n}}_{{{\text{PSi}}}} = & 0.5\sqrt {{\uppsi } + \sqrt {{\uppsi }^{2} + 8 \times 3.7^{2} {\text{ n}}_{{{\text{PNC}}}}^{2} } } , \\ {\uppsi } = & 3{\text{ P }}\left( {{\text{n}}_{{{\text{PNC}}}}^{2} - 3.7^{2} } \right) + \left( {2 \times 3.7^{2} - {\text{n}}_{{{\text{PNC}}}}^{2} } \right), \\ \end{aligned}$$
(1)

where \(P\) is the PNC ratio in the cavities of PSi layers of each unit cell. Bruggeman’s effective medium theory showed strong agreement with the experimental results for the porous material41. In the wavelength and gamma doses ranges of concern, the impact of gamma dose on \(Si\) can be ignored. The following dispersion relations of PNC as a function of wavelength and different irradiation doses using \({}^{60}\text{Co}\)-source (from 0 to 70 Gy) can be as follows (\(390\text{ nm}\le \lambda \ge 550\text{ nm}\))33,42:

At 0 Gy:

$${n}_{PNC}=-3.5482\times {10}^{-11} {\lambda }^{5}+8.5122\times {10}^{-8} {\lambda }^{4}-8.1190\times {10}^{-5} {\lambda }^{3}+0.0385 {\lambda }^{2}-9.0595 \lambda +850.5266,$$
(2)

At 10 Gy:

$${n}_{PNC}=-1.7847\times {10}^{-11} {\lambda }^{5}+4.4209\times {10}^{-8} {\lambda }^{4}-4.3404\times {10}^{-5} {\lambda }^{3}+0.0211 {\lambda }^{2}-5.0877 \lambda +488.8556,$$
(3)

At 20 Gy:

$${n}_{PNC}=-1.5042\times {10}^{-11} {\lambda }^{5}+3.7253\times {10}^{-8} {\lambda }^{4}-3.6566\times {10}^{-5} {\lambda }^{3}+0.0178 {\lambda }^{2}-4.2831 \lambda +411.7151,$$
(4)

At 30 Gy:

$${n}_{PNC}=-1.5212\times {10}^{-11} {\lambda }^{5}+3.7537\times {10}^{-8} {\lambda }^{4}-3.6723\times {10}^{-5} {\lambda }^{3}+0.0178 {\lambda }^{2}-4.2769 \lambda +410.0556,$$
(5)

At 40 Gy:

$${n}_{PNC}=-1.0031\times {10}^{-11} {\lambda }^{5}+2.4969\times {10}^{-8}{\lambda }^{4}-2.4613\times {10}^{-5} {\lambda }^{3}+0.0120 {\lambda }^{2}-2.9006 \lambda +280.1490,$$
(6)

At 50 Gy:

$${n}_{PNC}=-1.0059\times {10}^{-11} {\lambda }^{5}+2.5123\times {10}^{-8} {\lambda }^{4}-2.4838\times {10}^{-5} {\lambda }^{3}+0.0122 {\lambda }^{2}-2.9420 \lambda +284.7669,$$
(7)

At 60 Gy:

$${n}_{PNC}=-7.0564\times {10}^{-12} {\lambda }^{5}+1.7922\times {10}^{-8} {\lambda }^{4}-1.7963\times {10}^{-5} {\lambda }^{3}+0.0089 {\lambda }^{2}-2.1701 \lambda +212.1611,$$
(8)

At 70 Gy:

$${n}_{PNC}=-5.4184\times {10}^{-12} {\lambda }^{5}+1.3961\times {10}^{-8} {\lambda }^{4}-1.4156\times {10}^{-5} {\lambda }^{3}+0.0071 {\lambda }^{2}-1.7394 \lambda +171.5838,$$
(9)

where \(\lambda\) is in nm. The transmittance spectra (T) of photons with wavelengths in the range of concern through defected SPC with unit cells of PSi containing PNC as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) are simulated by the TMM as follows2:

$$T\left( \% \right) = 100 \times \frac{{p_{s} }}{{p_{0} }}t^{2} ,$$
(10)

where,

$$t=\frac{2{p}_{0}}{\left({A}_{11}+{A}_{12}{p}_{s}\right){p}_{0}+\left({A}_{21}+{A}_{22}{p}_{s}\right)},$$
(11)
$$\left|\begin{array}{cc}{A}_{11}& {A}_{12}\\ {A}_{21}& {A}_{22}\end{array}\right|={\left({a}_{PSi1}{a}_{PSi2}\right)}^{N}*{a}_{D}*{\left({a}_{PSi2}{a}_{PSi1}\right)}^{N},$$
(12)
$${p}_{i}={n}_{i} cos\left({\theta }_{i}\right), i={PSi}_{1},{PSi}_{21},\text{ and} \, \text{ defect} \, \text{ layer},$$
(13)

where \({p}_{s}={n}_{substrate} cos\left({\theta }_{substrate}\right)\), \({p}_{0}={n}_{Air} cos\left({\theta }_{Air}\right)\), \({n}_{Air}=1\), and \({n}_{substrate}=1.52\). This analytical method was commonly employed for building a variety of studies, filters43, and sensors39. The results of many simulations using the TMM analytical method coincided with different experimental research44,45. The experimental results may suffer from intensity reduction due to the absorption.

Results and discussions

The dispersion relation (RIs) of PNC, \({PSi}_{1}\), and \({PSi}_{2}\) at different γDs according to the experimental42 and fitted data in Eqs. (2)–(8)33 are cleared in supplementary material (S1). As clear in S1, by irradiating the PNC inside PSi pores, the RI of PNC increases may be due to atomic displacements, ionization, or changing the internal structure in the PNC42. As a result, the RI of \({PSi}_{1}\), and \({PSi}_{2}\) changes depending on the ratio of PNC in both of them. The contrast between refractive indices of PNC, \({PSi}_{1}\), and \({PSi}_{2}\) at different γDs increases at higher wavelengths in the range of concern. At λ = 500 nm, the RI of PNC changes from 2.3484 to 2.3723, 2.3953, 2.4068, 2.4160, 2.4324, 2.4419, and 2.4591 with irradiating from 0 to 70 Gy. Besides, the RI of \({PSi}_{1}\) changes from 3.4213 to 3.4262, 3.4310, 3.4334, 3.4353, 3.4387, 3.4407, and 3.4442 with irradiating from 0 to 70 Gy. Also, the RI of \({PSi}_{2}\) changes from 2.5944 to 2.6146, 2.6341, 2.6438, 2.6515, 2.6654, 2.6733, and 2.6878 with irradiating from 0 to 70 Gy.

Topological edge states (TES)

In Fig. 2, the transmittance spectra of SPC without defect as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) using unirradiated (black line) and irradiated PNC (other spectra) with γDs from 0 to 70 Gy are cleared at normal incident angle (\({\theta }_{i}\)). For unirradiated SPC structure, a PBG extended from wavelength range 505 nm to 531 nm as a consequence of the periodicity of the SPC structure and the multiple Bragg scattering. At the wavelength of 523.3 nm inside the PBG, a TES is excited as a consequence of the localization of photons of this wavelength at the interface between \({({PSi}_{1}*{PSi}_{2})}^{N}\) and \({({PSi}_{2}*{PSi}_{1})}^{N}\) PCs46. As a result of the increasing of the RIs of PNC, \({PSi}_{1}\) and \({PSi}_{2}\) with increasing γDs, both PBG and TES are shifted to higher wavelengths. The TES is shifted from 523.297 to 524.945, 527.680, 543.859, 530.873, 532.312, 533.740, and 535.879 nm.

Fig. 2
figure 2

Transmittance of SPC-GRD without defect as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) using unirradiated (black line) and irradiated PNC (other spectra) with γD from 0 to 70 Gy.

Full size image

The proposed SPC-GRD with unit cells of PSi containing PNC will perform effectively by possessing high S, narrow bandwidth (FWHM), high figure of merit (FoM), low detection limit (LoD), and high quality-factor (Q). S, FoM, Q, and LoD can be calculated as follows:

$$S =\frac{\Delta {\lambda }_{d}}{\Delta \gamma D},$$
(14)
$$FoM=\frac{S}{FWHM},$$
(15)
$$\begin{array}{l}Q=\frac{{\lambda }_{d}}{FWHM}\end{array},$$
(16)
$${\text{LoD}} = \frac{{\lambda_{d} }}{20 S Q}$$
(17)

where \({\lambda }_{d}\) refers to resonant peak position. As clear in Fig. 3(A-C), the suggested SPC-GRD has average transmitances of 96.8%, FWHM between 0.24 and 0.48 nm, S between 0.14 and 0.27 nm/Gy, FoM between 0.33 and 0.91 \({\text{Gy}}^{-1}\), Q between 2177.68 and 1115.02, and LoD between 0.055 and 0.150 Gy.

Fig. 3
figure 3

A T/FWHM, B S/FoM, and C Q/LoD of the SPC-GRD as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) at \({d}_{1}=100\,{\text{nm}}\), \({d}_{2}=170\,{\text{nm}}\), \({P}_{1}=20 \%\), \({P}_{2}=80 \%\) ,and \({d}_{D}=0\,{\text{nm}}\).

Full size image

Coupling between defect mode and TES

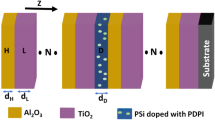
In Fig. 4, the transmittance spectra of defected SPC as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) using unirradiated (black line) and irradiated PNC (other spectra) with γD from 0 to 70 Gy are cleared at normal incident angle (\({\theta }_{i}=0\) degrees) using a defect layer \({d}_{D}=100\,{\text{nm}}\). As a consequence of the coupling between TES and defect resonances (coupled mode), the TES is blue shifted from 523.30 to 520.25 nm. As a result of the increasing of γDs, both PBG and coupled mode are shifted to higher wavelengths. The coupled mode is shifted from 520.249 to 522.077, 524.919, 526.425, 528.215, 529.739, 532.208, and 533.449 nm.

Fig. 4
figure 4

Transmittance of defected SPC as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) using unirradiated (black line) and irradiated PNC (other spectra) with γD from 0 to 70 Gy at \({d}_{1}=100\,{\text{nm}}\), \({d}_{2}=170\,{\text{nm}}\), \({P}_{1}=20 \%\), \({P}_{2}=80 \%\) ,and \({d}_{D}=100\,{\text{nm}}\).

Full size image

As clear in Fig. 5A–C, the suggested defected SPC-GRD has average transmitances of 96.4%, FWHM between 0.16 nm and 0.35 nm, S between 0.15 and 0.21 nm/Gy, FoM between 0.48 and 1.36 \({\text{Gy}}^{-1}\), Q between 1523.71 and 3197.59, and LoD between 0.037 and 0.105 Gy. By comparing between the performance of the GRD using TES and coupled mode, the performance is inhanced by the coupling between TES and defect modes. Consequently, in the following simulations, we will focous on the coupled mode.

Fig. 5
figure 5

A T/FWHM, B S/FoM, and C Q/LoD of the defected SPC-GRD as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) at \({d}_{1}=100 \, \text{nm}\), \({d}_{2}=170 \, \text{nm}\), \({P}_{1}=20 \%\), \({P}_{2}=80 \%\) ,and \({d}_{D}=100 \, \text{nm}\).

Full size image

In Fig. 6A–C, T, FWHM, S, FoM, Q, and LoD of the defective SPC-GRD as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) versus the thickness of defect at \({d}_{1}=100\,{\text{nm}}\), \({d}_{2}=170\,{\text{nm}}\), \({P}_{1}=20 \%\), and \({P}_{2}=80 \%\) are investigated. The FWHMs are calculated for the peak of 0 Gy. T of all peaks slightly changes around 96%. The FWHM has the maximum value at \({d}_{D}=800\,{\text{nm}}\), and minimum value at \({d}_{D}=900\,{\text{nm}}\). The reason behind the unexpected change for FWHM at 900 nm is that the peak’s position is near the center of the PBG. By increasing \({d}_{D}\) 300 nm to 800 nm, the resonant peak intensely red-shifted, and a new peak came from the left side. The new position of the new peak approaches to the left edge of the PBG with increasing \({d}_{D}\). At \({d}_{D}=900\,{\text{nm}}\), a suitable peak exists at the center of the PBG. The FWHM decreases at the center of the PBG and increases at the edges. For the same reason, the S has the highest value at \({d}_{D}=900\,{\text{nm}}\) because the peak shift and photons confinement are strong at the center of the PBG47,48. The behaviors of FoM, Q, and LoD strongly depends on S and FWHM according to Eqs. (14)–(17). For \({d}_{D}\) higher than 900 nm, the shift increases longer than the width of the PBG and the peaks begin to overlap. So, \({d}_{D}=900\,{\text{nm}}\) will be the best choice.

Fig. 6
figure 6

A T/FWHM, B S/FoM, and C Q/LoD of the defected SPC-GRD as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) versus the thickness of defect at \({d}_{1}=100\,{\text{nm}}\), \({d}_{2}=170\,{\text{nm}}\), \({P}_{1}=20 \%\), and \({P}_{2}=80 \%\). The FWHMs are calculated for the peak of 0 Gy.

Full size image

As clear in Fig. 7, the FWHM of the coupled mode of the defected SPC-GRD as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) at 0 Gy intensively depends on N. The sharpness of peaks increases because the reflectivity increases at the edges of the PBG because of the enhancement of the interference behavior. As the absorption increases with N, the T decreases for N higher than 20 unit cells.

Fig. 7
figure 7

Transmittance of the 0 Gy peak of the defected SPC-GRD as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) versus the number of periods at \({d}_{1}=100 \, \text{nm}\), \({d}_{2}=170 \, \text{nm}\), \({P}_{1}=20 \%\), \({P}_{2}=80 \%\), and \({d}_{D}=900 \%\) for different numbers of unit cells.

Full size image

In Fig. 8(A-C), the T of the coupled mode of the defected SPC-GRD as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) at 0 Gy intensively decreases with increasing N from 20 to 25 cells. On the other hand, the FWHM of the coupled mode of the defected SPC-GRD as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) at 0 Gy achieved the lowest value at N = 25 cells. For S, N doesn’t affect it because the peak position doesn’t change. The behaviors of FoM, Q, and LoD strongly depend on S and FWHM according to Eqs. (14)–(17). As N of 25 unit cells has very low T, N of 20 unit cells is the best choice.

Fig. 8
figure 8

A T/FWHM, B S/FoM, and C Q/LoD of the defected SPC-GRD as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) versus the number of periods at \({d}_{1}=100 \, \text{nm}\), \({d}_{2}=170 \, \text{nm}\), \({P}_{1}=20 \%\), \({P}_{2}=80 \%\), and \({d}_{D}=900 \%\). The FWHMs are calculated for the peak of 0 Gy.

Full size image

As clear in Fig. 9A, each γD corresponds to a narrow and clear transmittance coupled modes at a specific wavelength. The distinct separations between coupled modes mean a high sensitivity of the GRD. The progressively shifting of the coupled modes to longer wavelengths (redshift) as the γD increases indicates that the sensor’s optical response varies systematically with radiation exposure. The transmittance values are consistently high (about 96%), highlighting the efficiency of the GRS for detecting these dose ranges. Besides, the non-overlapping and sharpness nature of the coupled modes clear the sensor’s capability to differentiate between very close γD.

Fig. 9
figure 9

A T of the peaks of the defected SPC-GRD as \(\left[\text{Air}*{({PSi}_{1}*{PSi}_{2})}^{N}*\text{PNC }*{({PSi}_{2}*{PSi}_{1})}^{N}*\text{Substrate}\right]\) versus the γD at \({d}_{1}=100 \, \text{nm}\), \({d}_{2}=170 \, \text{nm}\), \({P}_{1}=20 \%\), \({P}_{2}=80 \%\), \({d}_{D}=900 \%\), and \(N=20\), and B the linear relation between coupled mode position and gamma doses.

Full size image

Figure 9B represents the relationship between γD and the coupled mode position (wavelength), showing both the analytical data points and a linear fit. The position of the coupled mode increases linearly with γD, as indicated by the strong alignment of the analytical data points with the linear fit (\({R}^{2}=99 \%\)). This suggests a predictable and stable response of the sensor to γD. The analytical data points are closely aligned with the linear fit, with minimal deviation. This implies a high level of accuracy and repeatability in the sensor’s performance. Table 1 clear an outstanding performance of our proposed design as GRD. Finally, by knowing the position of the coupling mode, we can investigate the value of γD using the following equation:

$$\upgamma D \left( {Gy} \right) = 4.504 \lambda_{d} - 2350.450.$$
(18)
Table 1 Comparison with other detectors.
Full size table

In future work, we aim to expand the range of gamma doses studied to better understand the system’s response across a broader spectrum of radiation exposure. Additionally, we will focus on enhancing the sensitivity of the proposed system to enable more precise detection of higher radiation levels. Improving sensitivity will require optimizing material properties, refining structural designs, and exploring advanced fabrication techniques to minimize losses and enhance performance. Furthermore, addressing the scalability and practical implementation challenges, such as environmental stability, reproducibility, and temperature will be essential for transitioning this research toward real-world applications. The long-term stability of polyvinyl alcohol (PVA)-based sensors under extended gamma radiation exposure is a critical factor in their practical implementation. Previous studies have shown that while PVA-based films doped with dyes such as crystal violet and carbol fuchsin exhibit reliable dosimetric properties at moderate doses, prolonged exposure to high radiation levels can induce structural and optical changes49. These effects may include chain scission, crosslinking, and oxidation, which can alter the sensor’s absorption characteristics and overall performance42.

The minimum gamma radiation dose required to cause swelling or oxidative changes in polymers and nanocomposite materials depends on their specific composition and environmental conditions. Poly(ethylene oxide) hydrogels exhibited swelling at radiation levels as low as 5 kGy. At this dosage, an increase in the gel fraction was observed, indicating the onset of crosslinking or structural modifications that influence swelling behavior50. Oxidative degradation induced by gamma radiation has been reported at doses starting from 20 kGy, leading to chemical changes such as chain scission and enhanced crystallinity in poly(ethylene oxide)/silica nanocomposites51. Oxidative modifications in various polymer systems have been detected at lower radiation doses (4–8 kGy), influenced by factors such as filler type and irradiation conditions52. Consequently, the threshold dose for noticeable effects ranges from 5 to 20 kGy, depending on the material’s composition and environmental factors such as oxygen exposure.

Ahmed et al.53 examined the effects of gamma radiation on Si–PC devices using Monte Carlo simulations. Their findings indicated that key optical parameters, including the dispersion, thermo-optic coefficient, characteristic group index, temperature sensitivity, peak width, and peak center, remained stable for cumulative doses up to 1 MGy. Similarly, even at 46 kGy, no significant changes were observed in the optical properties of Al₂O₃54.

Conclusion

A symmetrical 1D-SPC sensor utilizing PNC materials has been demonstrated as an innovative and efficient platform for GRD. By exploiting the coupling between a defect mode and topological edge state, the sensor achieves unparalleled optical characteristics, including a Q of 447,747.5 and an exceptional sensitivity of 0.2267 nm/RIU. The linear dependence of the resonance wavelength shift on γD is reflected in its high FoM of 188.91 Gy⁻1, enabling reliable and precise dose measurements. Additionally, the GRS’s remarkable LoD of 0.000265 Gy demonstrates its capacity to monitor extremely low radiation levels. The proposed design is scalable and cost-effective, making it a promising candidate for commercial applications in fields such as medical imaging, nuclear safety, and space exploration.