Introduction

Primarily, the core metal of ferromagnetic alloys is iron, followed by nickel. These alloys are widely used in electromagnet engineering applications1,2. Many studies mentioned that under the changes in the magnetic field, the magnetic domain walls of ferromagnetic materials will vibrate or have the ability to leap small in their hysteresis loop3,4. The Barkhausen effect is a famous phenomenon that explains the relationship between the applied magnetic field on the ferromagnetic material and the generated noise from this field. This phenomenon is always associated with changes.

in the elastic energy of these materials, (ferromagnetic material)5,6selected a group of ferromagnetic materials such as pure nickel (Ni200), pure Iron, and many Fe–Ni alloys. Then, they studied these alloys’ Magnetomechanical acoustic emission (MAE) because this group represents the broad spectrum of magnetic crystal anisotropy among all the solid materials7. concentrated on the relationship between the microstructure of A508-Class (II) forged steel and the magnetic anisotropy of this alloy8. Focused on the relationship between the angle of tensile and magnetic response for martensitic stainless steel. All these studies confirmed that the acoustic wave passing through the microstructure of ferromagnetic alloys suffers from different conditions from those waves passing through non-ferromagnetic alloys. Therefore, this study treated ferromagnetics as a special material compared to other materials in ultrasonic tests.

On the other hand, acoustic tests are regarded as one of the important methods to find the mechanical properties of non-ferromagnetic alloys9,10,11,12. The main mechanical properties are the modulus of elasticity (E), yield strength (YS), ultimate strength (US), and Poisson’s ratio (υ)12,13. The longitudinal velocity (CL) to calculate the dynamic modulus of elasticity (ED) by using \(\left({E}_{D}=\frac{{C}_{L}^{2}\rho (1+\nu )(1-2\nu )}{(1-\nu )}\right)\). Studies14,15,16,17,18,19,20,21 focused on the difference between the dynamic modulus of elasticity ED and static modulus of elasticity Escalculated from tensile tests for many materials22,23 highlighted the differences between ED and Es for refractory materials, where they found the body forces (such as magnetic forces and piezoelectric forces) were canceled from the mother equation of ED. Therefore, all materials with body force, such as refractory and magnetic materials, give different results between ED and Es.

As a matter of fact22,came up with a new method to find E by using the pressure transmission coefficient (PTC), without going through the ED equation, where they got an excellent matching, for about 27 metals, between E calculated from the proposed method and standard values of EASTM according to ASTM (American Society for Testing and Materials).

In addition, the other important properties are YS and US. A small punch test was employed to measure YS and US for steel alloys24,25. To find the toughness of steel pipelines23, utilized non-destructive evaluation. Using genetic algorithms26, predicted the values of YS and US for cold-rolled steel. All these studies are limited to specific materials and not general tests for all the materials except reference27, where they proposed a set of equations to link values of YS and US from the side and PTC for all pure metals and alloys. Despite this success (matching between the proposed method and ASTM Values for YS and US), this success is just for pure metals and pure alloys.

First, this study chose the method followed by reference22. Then, this study checked if this method is correct for all solid alloys. In the same way27, highlighted only the pure materials (not in general for all alloys) and classified these pure materials according to their crystal structure (FCC, BCC, or HCP).

As a matter of fact, most factories and corporations use general alloys (not pure alloys or metals), so this study proposed a method for finding the mechanical properties of solid materials by using PTC, but only for general alloys. In other words, this study began when references22,27 were stopped. To achieve that, this study classified the solid materials as ferromagnetic and non-ferromagnetic. Then, the ferromagnetic alloys were classified into sub-classifications of steel alloys. At last, regular relationships were derived between PTC from the side and each stage or classification of these classifications.

Methodology

PTC denotes the pressure amplitude of the transmitted wave between two materials. Theuse of PTC is nothing new in mechanical tests25,26, but the use of pure magnesium metal as a constant metal in each test is a different matter from other tests. The proposed method in this study selected magnesium metal (Mg) because it has minimal acoustic impedance among solid materials. Equation (1) explains how to calculate PTC22.

$$PTC= \frac{4{Z}_{SP}\times {Z}_{Mg}}{\left({Z}_{W}+{Z}_{SP}\right)\left({Z}_{SP}+{Z}_{Mg}\right)}=\frac{\left(39.9{Z}_{SP}\right)}{\left(1.5+{Z}_{SP}\right)\left({Z}_{SP}+9.97612\right)}$$
(1)

In fact, there are three steps to produce Eq. 1, First, calculate PTC1 between the acoustic impedance of water (ZWa) and the acoustic impedance of the specimen (ZSp) \(P{TC}_{1}=2{Z}_{SP}/\left({Z}_{Wa}+{Z}_{SP}\right).\) The second step was the calculation of the PTC2 between the ZSp and the acoustic impedance of Mg (ZMg) \({PTC}_{2}=2{Z}_{Mg}/\left({Z}_{SP}+{Z}_{Mg}\right)\). The last step was \(PTC=P{TC}_{1}\times {PTC}_{2}\). Where \({Z}_{Mg}=\rho {c}_{L}=9.9761\times {10}^{6}\frac{\text{Kg}}{{\text{m}}^{2}\text{s}}\), where ρ is the density of Mg and CL is the longitudinal velocity of the ultrasonic wave passing through Mg. Also, ZWa is \({Z}_{Wa}=1.49\times {10}^{6}\frac{\text{Kg}}{{\text{m}}^{2}\text{s}}\). To verify the validity of the PTC method’s choice as a coefficient sensitive to mechanical properties, this study started to test the set of Eq-8 in reference22 to find the E values for around 56 metals and alloys. Figure 1confirms the matching of the values of these alloys and metals with the curve. In addition to that, the matching between E calculated from reference22 and EASTM was around (90 ~ 96) %, as shown in Fig. 2.

Fig. 1
figure 1

The relationship between PTC and E * density.

Full size image
Fig. 2
figure 2

Comparison between calculated Ecalculated and E according to ASTM.

Full size image

Figure 1 proves that the value of E for any solid material depends on the value of its acoustic impedance (Z), where \(Z={C}_{L}\times \rho\), CL is the longitudinal velocity of the acoustic wave, and ρ is the density of this material.

After the values of E were calculated, the values of Possion’s ratio (υ) for all these alloys and metals were calculated too from Eq. 222. This study compared υ calculated from Eq. 2 and values of υ according to ASTM, as shown in Fig. 3.

Fig. 3
figure 3

A comparison between calculated υ from Eq. 2 and the values of υ according to ASTM.

Full size image
$$\nu =\frac{\left(E-K\right)+\sqrt{{(E-K)}^{2}+8k(k-E)}}{4K}$$
(2)

The comparisons shown in Fig. 2 and 3 proved that the use of PTC in finding mechanical properties is very accurate for all solid materials (metal and alloys), therefore, this study took this PTC as a common denominator in all tests of this research. According to ASTM, all data (YS, US, CL, and ρ) were collected from significant references such as28,29,30,31,32,33.

Here, the general alloys were classified into ferromagnetic materials and non-ferromagnetic materials. This classification was because the ferromagnetic alloys have different responses to acoustic waves (Barkhausen effect) from the non-ferromagnetic alloy.

Then, the ferromagnetic alloys were classified into steel alloys and nickel alloys. Then, the steel alloys were divided into a group of plain carbon steel and low-alloy steels and another group of stainless-steel alloys. Finally, stainless steel alloy was classified into austenitic (annealed) alloys and another group. This group was composed of the alloys of martensitic, duplex, and ferritic alloys. At last, regular relationships were found between PTC from the side and each stage or classification of these classifications.

This study followed the algorithm shown in Fig. 4 to achieve the aims of this study in finding the values of yield strength and ultimate strength of the general alloys.

Fig. 4
figure 4

Algorithm of calculation of yield of strength and ultimate strength for general alloys.

Full size image

The first step in Fig. 4 is for non-ferromagnetic. Figure 5 indicates a regular relationship between PTC, calculated from Eq. 1, from the side and values of yield strength (YS) and ultimate strength (US) for around 12 materials of non-ferromagnetic materials. By using the curve fitting method, Eq. 3 and Eq. 4 were derived.

Fig. 5
figure 5

The relationship between PTC values of non-ferromagnetic materials and their YS and US.

Full size image
$${YS}_{other}=821.681-420.481*\left(PTC\right)-453.234*\left({PTC}^{2}\right)+748.257*\left({PTC}^{3}\right)-253.854*\left({PTC}^{4}\right)$$
(3)
$$\begin{aligned}{US}_{other}&= 2468.6-14270.9*\left(PTC\right)+48760.9*\left({PTC}^{2}\right)-81776.7*\left({PTC}^{3}\right)\\&+69186.1*\left({PTC}^{4}\right)-28462.3*\left({PTC}^{5}\right)+4531.2*\left({PTC}^{6}\right)\end{aligned}$$
(4)

From Fig. 5 and Table 1, the accuracy of these two Eqs. (3 and 4) is around (80 ~ 9.99)%, except the tensile strength of TiC (9-TiC inside the figure) was 71%. The reduction in accuracy for TiC is because Ti, one of this alloy’s components, changes its phase (phase transformation) from HCP to BCC during the tensile test27. In addition34, mentioned that they discovered three stages of phase transformation in Ti alloys (β decomposition, layered α to β, and equiaxed α to β) according to temperature levels, and it is well known that the level of temperature increases during the tensile tests. Both things that were likely mentioned about the phase transition of TiC alloy are behind the inaccuracy in the measurement.

Table 1 indicates the standard value of all the alloys used in this study28,29,30,31.
Full size table

Magnetomechanical acoustic emission (MAE) is one of the important phenomena in ferromagnetic materials8. declared that there is a difference between MAE levels of Nickel alloys and iron alloys, where the level of MAE of iron alloys is the highest5. According to that, this study sorted the ferromagnetic alloys into nickel alloys on one side and steel alloys on the other side to find the regular relationship between YS and US on the one side and the values of PTC of these two groups. This study could collect the required data for only eight types of nickel alloys as shown in Fig. 6. The behavior of these two curves was translated into two equations as shown in Eq. 5 and Eq. 6. According to Table 1, the accuracy of Eq. 5 and Eq. 6 is around (81 ~ 99) %.

Fig. 6
figure 6

The regular relationship between nickel alloys and their values of PTC.

Full size image
$${YS}_{Ni}= 66034.8-341570*\left(PTC\right)+702861*\left({PTC}^{2}\right)-715450*\left({PTC}^{3}\right)+359930*\left({PTC}^{4}\right)-71627.2*\left({PTC}^{5}\right)$$
(5)
$${US}_{Ni}= 70313.1-333420*\left(PTC\right)+624558*\left({PTC}^{2}\right)-573156*\left({PTC}^{3}\right)+257345*\left({PTC}^{4}\right)-45171.2*\left({PTC}^{5}\right)$$
(6)

There is a common denominator for all behaviors YS and US with PTC, where these two properties (YS and US) decrease with an increase in the values of PTCs.

The third step of the algorithm in Fig. 4is distinguishing between plain carbon steel and low-alloy from the one side and stainless steel alloys on the other. Stainless steel alloy consists of 10.5% chromium and less than 1.2% carbon, while the ratio of carbon in plain carbon steel is about 0.20 to 0.25%, and most of them are in the annealed condition. The annealed process is a heat treatment that alters physical properties and sometimes chemical properties. This change in mechanical properties due to annealed treatment leads to a change in elastic wave propagation inside the material35. In addition to this difference in the composition of these alloys, this study also found a difference in the behavior of PTC values between these two groups.

Figure 7 indicates that the behavior of YS and US decreases with the increase in the values of PTC for plain carbon steel and low-alloy in annealed conditions.

Fig. 7
figure 7

The relationship between YS and US with PTC values for plain carbon and low-alloy steel alloy in the annealed condition.

Full size image
$${YS}_{Low carb}= = 10333900-55416300*(PTC)+111307000*({PTC}^{2})-99238400*({PTC}^{3})+33137200*({PTC}^{4})$$
(7)
$${US}_{Low carbon }=3928070-20141900*(PTC)+38613400*({PTC}^{2})-32788000*({PTC}^{3})+10402200*({PTC}^{4})$$
(8)

According to Fig. 7 and Table 1, the accuracy of the results of the two Eqs shown in (Eq. 7 and Eq. 8), for plain carbon and low-alloy steel alloys (for alloys from 1 ~ 13 in Fig. 7), is between (82 ~ 96)% except for the two alloys steel 1018, and steel 4330. These two alloys (steel 1018 and steel 4330) were represented in Fig. 7 by a triangle symbol. The result’s accuracy for the values of YS, for these alloys, was from (52 ~ 62)%, while for the US were about (7.8 and 79.7)%, respectively. This difference in results for these two alloys is due to the fact that they are alloys with high or medium carbon content. As a matter of fact, the increase in carbon percentage raises or enhances tensile strength. These differences in the accuracy of the results between groups of plain carbon and low-alloy steel alloys from one side and medium and high carbon steel from another side prove that this proposed method, in this study, is sensitive to changes in carbon percentage for steel alloys.

On the other hand, it can be distinguished, through the color, between stainless steel and any other steel alloys, where the stainless steel is silver and shiny. Also, the magnetic properties can distinguish it from austenitic stainless steel and different types of stainless steel such as martensitic, ferritic, and duplex stainless steel, where austenitic stainless steel has no magnetic attraction.

Figure 8-a indicates the behavior of YS and US for Martensitic, duplex, and ferritic stainless steel, while Fig. 8-b represents the regular changing of austenitic stainless steel of YS and US with PTC values. It’s worth mentioning that if all data of austenitic, martensitic, duplex, and ferritic stainless steel were collected together, it couldn’t be obtained any regular relationship with the PTC values of these alloys. Equation 9 and Eq. 10 represent the mathematical expressions of YS and US in Fig. 8-a.

Fig. 8
figure 8

(a) Behaviour of YS and US of Martensitic, duplex, and ferritic alloys with their PTCs value (b) explains the difference in values of YS and US of austenitic than the rest of the stainless steel alloys.

Full size image
$${YS}_{mart+Ferr}= 203907-564347*\left(PTC\right)+390741*\left({PTC}^{2}\right)$$
(9)
$${US}_{mart+Ferr}=172075-472818*(PTC)+325457*({PTC}^{2})$$
(10)

Figure 8-b confirmed another distinction where austenitic stainless steel alloys differentiated through their behavior with PTC, where the range of PTC in austenitic alloys is wider than the other types of stainless steel.

Equation 11 and Eq. 12 represent the YS and US of the austenitic stainless steel curves shown in Fig. 8-b

$${YS}_{Austen}=393930-3247210*(PTC)+10701500*({PTC}^{2})-17535800*({PTC}^{3})+14256400*({PTC}^{4})-4596810*({PTC}^{5})$$
(11)
$${US}_{Austen}= 864411-7326320*\left(PTC\right)+24729300*\left({PTC}^{2}\right)-41406800*\left({PTC}^{3}\right)+34354800*\left({PTC}^{4}\right)-11298000*\left({PTC}^{5}\right)$$
(12)

This study compared (plain carbon steel and low-alloy), and stainless steel alloy groups (martensitic, duplex, ferritic, and austenitic) through their behavior with their PTCs value as shown in Fig. 9.

Fig. 9
figure 9

A comparison of values of YS and US for (plain carbon steel and low-alloy), austenitic, and martensitic stainless steel according to their PTC values.

Full size image

The comparison proved that the range of PTC and acoustic impedance was (42 ~ 57.6), and \(42\times {10}^{6}\sim 57.4\times {10}^{6})\frac{kg}{{m}^{3}s}\), respectively for austenitic stainless steel alloys, and they are wider than the range of PTC, and acoustic impedance for groups of martensite, duplex, and ferritic stainless steel alloys, where they were (0.659 ~ 0.71) and \((44.38\times {10}^{6}\sim 48.75\times {10}^{6})\frac{kg}{{m}^{3}s}\) respectively for this group. Also, that means the common area between the two groups is within the range of acoustic impedance \((44.38\times {10}^{6}\sim 48.75\times {10}^{6})\frac{kg}{{m}^{3}}\) as shown in Fig. 9. In addition, it can be said that any stainless steel alloy outside this common area is not within the group of martensitic, duplex, and ferritic stainless steel alloys but within austenitic alloys. It is also noticeable from Fig. 9, that within the range of \((44.38\times {10}^{6}\sim 48.75\times {10}^{6})\frac{kg}{{m}^{3}s}\) the values of YS and UT of the two groups of (martensitic, duplex, and ferritic stainless steel alloys) and the group of (plain carbon steel and low-alloy steels) are so close to each other.

It can be said from Fig. 9, that even though stainless steel austenitic alloys and a group of (plain carbon steel and low-alloy steels) are in the annealed condition, their behavior with PTC is different. That means the effect of the annealing condition is not an effective factor on PTC, where PTC is one of the aspects of expressing the behavior of sound waves inside metal or alloy. It is worth mentioning that36,37found that the intermetallic precipitates greatly affect ultrasonic waves’ longitudinal velocity more than grain boundary carbides. The change from martensite to austenite in steel alloys is also an important factor in changing the longitudinal wave velocity38. It is known that austenite alloys contain these intermetallic precipitates39. The comparison in Fig. 9 confirms the suggestion of these references that the intermetallic precipitates and the change from martensite to austenite in steel alloys are the reasons behind the difference in PTC values between the austenitic alloy and a group of (plain carbon steel and low-alloy steels), even though both are in an annealing condition. It is worth mentioning that all data needed (YS, US, CL, and ρ) to draw all figures from Fig. 5 to Fig. 9were collected from significant references such as28,29,30,31,32,33.

The results obtained from Eqs. 3–12 were compared with the standard values of the ASTM using Eq. 13 and Eq. 14. Equation 13 tests the rapprochement between the calculated values for yield stress and ASTM yield stress values. Equation 14 does the same comparison but for the ultimate stress.

$${APP}_{YS}=100-\sqrt{{[(({YS}_{ASTM}-{YS}_{cal})/{YS}_{ASTM})\times 100]}^{2}}$$
(13)
$${APP}_{UT}=100-\sqrt{{[(({US}_{ASTM}-{US}_{cal})/{US}_{ASTM})\times 100]}^{2}}$$
(14)

Table 1 clarifies the results of these rapprochements through the two columns APPYS% and APPUT%. Also, for more accuracy, R-squared (R2) was used as an accuracy metric to strengthen the validity of this study’s results, as shown in Eq. 15 and Eq. 16.

\({({YS}_{ASTM}-{YS}_{cal})}^{2}\) ……\({SS}_{totYS}=Sum{({YS}_{ASTM}-{YS}_{avg})}^{2}\)

$${R}_{YS}^{2}=1-\frac{{SS}_{resYS}}{{SS}_{totYS}}$$
(15)

\({SS}_{resUT}=Sum{({US}_{ASTM}-{US}_{cal})}^{2}\) ……\({SS}_{totUS}=Sum{({UT}_{ASTM}-{UT}_{avg})}^{2}\)

$${R}_{US}^{2}=1-\frac{{SS}_{resUS}}{{SS}_{totUS}}$$
(16)

The results of these two Eqs. (15 and 16) were clarified in the first column of Table 0.1.

It is worth noting that the samples in Table 1 of (A ~ H) are samples that have been tested practically, as shown in the next part (experimental part).

Experimental part

Practically and according to the algorithm in Fig. 4, the first step is distinguishing between ferromagnetic and non-ferromagnetic materials using any magnet. If the metal or alloy isn’t attracted to the magnet, this material is non-ferromagnetic and can be used in Eqs. 3 and 4 to find YS and US, respectively.

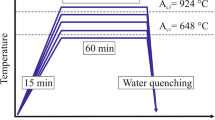
Before going to these equations, the value of the PTC from Eq. 1 must be calculated. The alloy’s longitudinal velocity of the ultrasonic wave (CL) must be measured to calculate PTC. The echo pulse technique was utilized to measure CL. First, the 2.5 MHz probe was connected with Ultrasonic Pulse UP200 (OSUN), from the side to generate the ultrasonic waves. In contrast, the other side of this probe was connected to a DSEX1102 A (100 MHz) oscilloscope. To calibrate the oscilloscope, the default setup button was selected to start a new test. Then, a High-resolution option from the Acquire mode list was selected. The High-resolution option works as a filter for the noise associated with the required signal. On the other hand, the Ultrasonic Pulse UP200 (OSUN) was calibrated at 208 V, the frequency at 1000 Hz, and the duration of the excitation signal was 0.1 s. In the same context, the probe of the Ultrasonic Pulse UP200 was calibrated to calculate the wedge delay of this probe, and it was found to equal 4.5µsec.

Test specimens were prepared before the experimental test started. First, the surface of the samples is smoothed to avoid reflection and scattering of the signal falling from the probe on the specimen. The dimensions of the specimen test are flexible matter in ultrasonic tests. In fact, two conditions should be taken care of in the thickness of the specimens. First, the thickness should preferably be longer than 1 cm to reduce the effect of human error during the test. The second is that the thickness shouldn’t be so long to avoid the attenuation of the signal through passing in the specimen body. All the specimens achieve these two conditions.

The first stage of the experimental part was to test three non-ferromagnetic alloys. The goal of putting ultrasonic gel between this probe and the surface of three types of non-ferromagnetic alloys was to prevent the dispersal of these ultrasonic waves. The time of flight of the waves (go and back), through the nonferromagnetic samples, directly appeared at the top of the used DSEX1102 A (100 MHz) oscilloscope. This oscilloscope is highly accurate because its sample rate is 2G sample/sec.

Figure 10 illustrates the time of flight (tTOF) of the ultrasonic waves through the non-ferromagnetic specimens A, B, and C, as shown in the red circle in Fig. 10. The longitudinal velocity was calculated through the two equations Eq. 1740 and Eq. 18.

Fig. 10
figure 10

Test of longitudinal velocity through a measure of the time of flight of the ultrasonic waves for non-ferromagnetic specimens (A), (B), and (C).

Full size image
$${t}_{TOF}=\frac{2L}{{C}_{L}}+2{t}_{o}$$
(17)
$$\therefore {C}_{L}=\frac{2L}{({t}_{TOF}-2{t}_{o})}$$
(18)

Each used probe in ultrasonic tests, especially in the echo pulse technique, has a wedge delay (to)40. The wedge delay of 2.5 MHz used probe was 4.5µsec. L is the length of the test specimen. The specimen’s length is an elastic issue, which is one of the advantages of non-destructive tests over tensile tests. To prove the flexibility of this method, sample C was tested in a diagonal direction (placing the probe parallel to diameter D) and not in a longitudinal direction L. Therefore, D was used instead of L in Table 2 to calculate the longitudinal velocity of the wave.

Table 2 indicates the chemical composition and the method of calculation of YS and US for the test samples.
Full size table

After finishing the first stage of the algorithm in Fig. 4 (testing whether the material is a ferromagnetic alloy), the next stage confirmed whether this alloy was a nickel alloy. It does this by using XRD or chemical analysis.

Unfortunately, only two of the samples tested, which were selected at random, were from nickel alloys. Figure 11 and Fig. 12 indicate the duration of flight of the ultrasonic wave that passed through samples D (tTOF = 28μsec), E (tTOF = 79μsec), F (tTOF = 53μsec), and G (tTOF = 26.8μsec), respectively, as shown in the red circle in this figure above.

Fig. 11
figure 11

The Longitudinal velocity test is done by measuring the time of flight of the ultrasonic waves for the (D) and (E) samples test.

Full size image
Fig. 12
figure 12

Longitudinal velocity test through a measure of the time of flight of the ultrasonic waves for steel alloys (F), and (G) samples tests.

Full size image

CL was calculated using Eqs. 15 and 16. Then, using Eqs. 5 and 6, YS and US for nickel alloys were calculated.

Table 2 indicates the chemical composition and the method of calculation of YS and US for the test samples. It is worth mentioning that the number of samples is different for each alloy, but it is around two to four samples for each alloy, according to the available samples during the tests. However, the number of the test processes (ultrasonic tests) was repeated at least ten times for each sample.

In the introduction of this study, it was mentioned that this study started at the point at which the two references22,27 were stopped. The Chart in Fig. 13tries to complete the whole picture of the importance of using the PTC in finding some of the mechanical properties (E, v, YS, and US) for all metals and alloys. The reference22proposed using PTC to calculate E and v, while the reference27 proposed using PTC in calculating YS and US for pure metals and pure alloys only. The plotted part in green color of the figure represents the more important part of the view represented by using PTC to find YS and US for general alloys, which are more important and more commonly used in manufacturing corporations.

Fig. 13
figure 13

Chart represents the role of PTC in finding some of the mechanical properties of general alloys.

Full size image

Conclusions

This study is considered the last and most important step in completing the use of PTC to find the most important mechanical properties (YS and US) of alloys in general, and this is what distinguishes it from other previous studies. Two studies preceded this study. The first was presented to find the values of E and ν, and the second was presented to find YS and US, and the latter was limited only to pure metals and is of little use compared to the use of the alloys in engineering applications. Several conclusions were reached, in addition to its success in providing a distinctive method for calculating YS and US for alloys in general. This study did not succeed in finding a systematic or regular relationship between the PTC and the values of YS and US until the alloys were classified into ferromagnetic and non-ferromagnetic as the first stage of classification. The accuracy of the proposed equations for non-ferromagnetic alloys, as a first stage, was around 80 ~ 99%, except for TiC alloy, where it was 70%. After focusing on this alloy, this study found that the reason behind the inaccuracy, especially for this alloy, is the phase transformation, where Ti suffers from phase transformation from the HCP to the BCC during the tensile tests, and the TiC alloy itself has three stages of phase transformation according to its temperature. That means any alloy that has a phase transformation will fail, not only in this proposed study but in all ultrasonic tests to calculate YS and US because it has not had regular behavior during tensile tests. Then, the second stage of classification was classified ferromagnetic into nickel alloys and steel alloys because of the difference in the level of magnetomechanical acoustic emission (MAE) where the MAE for steel alloys, according to the previous studies, is the highest. Eight nickel alloys were tested using this proposed method, and the accuracy was also around 80 ~ 99%. This indicates that the results of this study are consistent with the previous studies. The third stage of classification was classifying the steel alloys into stainless alloys and groups of plain carbon steel and low-alloy steel. This study distinguished between stainless steel, which has 12% chromium, and low-alloy steel, which contains a maximum of 5% of other materials, during the classification because of the difference in components between these two groups and the change in their behavior with the values of PTC. The accuracy of the proposed equations to calculate YS and US for plain carbon steel and low-alloy steel was about 82 ~ 99%. This study tried to apply these equations to medium-carbon steel, such as carbon steel 4330, and high-carbon, such as carbon steel 1018, but its match with ASTM values was very weak. A higher carbon content, such as carbon steel 1018 alloy and carbon steel 4330 alloy, affects the steel’s density and elasticity, which in turn impacts its acoustic impedance. This can change how waves reflect at boundaries. Additionally, increased carbon results in larger or less uniform grains, which increases wave dispersion and reduces signal clarity. Fine-grained, low-carbon steel alloys, shown in Fig. 7, provide better wave transmission. That means the proposed method is sensitive or affected by the percentage of carbon in steel alloys. In the final stage of classification, it was found that the behavior of PTC, which is one of the expression forms of the acoustic wave, is different in austenitic alloys than in other types of stainless steel alloys. Therefore, the last classification was the classification of the stainless steel alloys into austenitic stainless alloys and another group of stainless steel alloys, such as martensitic, duplex, and ferritic. In comparison with the ASTM values, the accuracy of these last proposed equations for these two groups was also around 80 ~ 99%. The comparison was done among stainless steel alloys (austenitic, martensitic, duplex, and ferritic), and a group of (plain carbon steel and low-alloy steel). The comparison proved the range of austenitic alloys is wider than a group of martensite, duplex, and ferritic, and the common scope of acoustic impedance was (44.38 × 106 ~ 48.75 × 106) kg/(m3 s). Also, it was proven that any stainless steel alloys outside this common area are austenitic alloys. In addition, it was noticeable that within the range of (44.38 × 106 ~ 48.75 × 106)kg/(m3 s), the values of YS and UT of the two groups of (martensitic, duplex, and ferritic stainless steel alloys) and the group of (plain carbon steel and low-alloy steels) are so close to each other, while austenitic alloys have different behavior. The explanation that this study tends toward regarding what the results confirmed is that austenitic alloys have different behavior along the PTC values line from the rest of the groups, because these alloys (austenitic alloys) contain intermetallic precipitates. Some sources mentioned that these intermetallic precipitates affect the velocity of ultrasonic wave transmission.