A new family of alpha power-G using cosine function with applications and regression modeling

Abstract

This paper discusses a novel technique to creating distribution families by combining the transformation of alpha power and the cosine function. The proposed technique have been named the cosine alpha power-generated family. The Weibull distribution is employed to produce a distinctive model for the cosine alpha power generated family, the specific model is called the cosine alpha power-Weibull (CAP-W). The distribution statistical characteristics are investigated, involving quantiles, Rényi entropies, and order statistics. The CAP-W has a density function that is right-skewed, symmetrical, and decreases continuously, along with J-shape, upside down bathtub, increasing and decreasing hazard rate function. Various methods of estimation–maximum likelihood, ordinary least-squares, weighted least-squares, and cramér–von mises were utilized to estimate the distribution parameters, and a simulation study is carried out to examine their performance. Furthermore, the efficiency of the provided distribution is demonstrated by four real data sets. Ultimately, the log cosine alpha power Weibull regression model is constructed and examined with a real dataset.

Introduction

Statistical models are commonly utilized in real-life situations to analyze and explain datasets. Classical distributions such as Weibull, Lomax, and exponential are widely employed for this purpose. However, these distributions cannot always fit complicated datasets well. Therefore, in order to make the classical distribution more flexible and adaptable to fit data from different fields of study, several researchers have attempted to extend it by producing new families of distributions. Various techniques for generalizing distributions are proposed in literature. Some of these techniques include the exponentiated family by ¹, the T-X generalized family by ², and the alpha power (AP) transformation family by ³. The cumulative distribution function (CDF) of the AP is described as follows:

$$\begin{aligned} F_{AP}(w) = \left\{ \begin{array}{rcl} \frac{\alpha ^{F(w)}-1}{\alpha -1} & \qquad \text{ for } & \alpha >0 ,\alpha \ne 1,\\ F(w) & \qquad \text{ for } & \alpha =1, \end{array}\right. \end{aligned}$$

(1)

and the corresponding probability density function (PDF) is

$$\begin{aligned} f_{AP}(w) = \left\{ \begin{array}{rcl} \frac{log\alpha }{\alpha -1} f(w)\alpha ^{F(w)} & \qquad \text{ for } & \alpha >0,\alpha \ne 1, \\ f(w) & \qquad \text{ for } & \alpha =1, \end{array}\right. \end{aligned}$$

(2)

where F(w) represents the CDF and f(w) denotes the PDF of any continuous distribution.

Many distributions have been produced by the AP family, like the AP exponential distribution by ³, the AP Weibull distribution by ⁴, the AP Fréchet distribution by ⁵ , the AP inverted Topp–Leone by ⁶ , the AP generalized Pareto distribution ⁷, and the AP Lindley distribution by ⁸.

Recently, the trigonometric transformation of conventional distributions has attracted a lot of interest since of its variety of appealing features, such as the capacity to improve the properties of existing distributions while including no extra parameters to those in the baseline model. Also, the trigonometric function is adaptable and flexible because the parameter(s) fluctuate as the values alter, and the periodic function determines how the distribution curve behaves.

Numerous studies have introduced new families and distributions using the trigonometric transformation. For example, the sin-G ^10,11, the tan-G ^11,12, the sec-G ^11,13, the sine unit exponentiated half-logistic distribution ¹⁴, the new weighted sine-G family ¹⁵, the weighted sine very flexible Weibull distribution ¹⁶, the tangent exponential-G family ¹⁷, the new logarithmic tangent-U family ¹⁸, the new cotangent-G family ¹⁹, the tan Weibull loss distribution ²⁰ ,the exponentiated arctan-X family ²¹, and the sine alpha power-G family ²², among others.

Souza ^11,23 introduced a new approach of the trigonometric transformation to producing a unique family of distributions known as the cosine-G (CG) family by applying a cosine transformation to the CDF of a baseline distribution. The CDF of the CG family is stated as

$$\begin{aligned} G(w)=1-\cos \left[ \frac{\pi }{2}F(w)\right] ,~~~ w\in \mathbb {R}, \end{aligned}$$

(3)

and its PDF is presented by

$$\begin{aligned} g(w)=\frac{\pi }{2} f(w)\sin \left[ \frac{\pi }{2}F(w)\right] , ~~~ w\in \mathbb {R}. \end{aligned}$$

(4)

Several studies have extended cosine-G framework to develop new families with varying shapes that are flexible in modelling data. For example, the novel arc cosine-$\Psi$ class of distribution ²⁴, the extended cosine generalized family ²⁵, the cosine Topp–Leone family ²⁶, the cosine pie-power odd-G family ²⁷, the cosine inverse Lomax?G family ²⁸, the cosine Weibull family ²⁹, the new cosine trigonometric-G family  ³⁰,the new class of cos-G family ³¹, and the cosine Kumaraswamy -G family ³²

In this paper, our main goal is to produce a novel family of the CG using the AP family as the baseline distribution in the CG. This new family is known as the cosine alpha power generated (CAP-G) family of distributions. The primary features for creating this novel family are as follows:

• The CAP-G family distinctive feature is the lack of extra parameters with flexibility in fitting various datasets.

• The CAP-G family is formulated within a trigonometric framework, yielding a novel trigonometric distribution that has the ability to capture different levels of shapes versatility and tail behaviors. In particular, the periodic nature of the trigonometric family is used to shape the forms of the density and hazard rate functions, as well as providing versatility to the family’s special models, which produces novel and flexible models.

• Incorporating the alpha?power transformation within the proposed family provides additional flexibility to control both the degree of skewness and the heaviness of the tails.

• The CAP-G family is expected to supply better fit and forecasting precision for datasets displaying patterns that are complex to explain using classical distributions.

• When F(w) is a baseline CDF, transformations such as $\sin (\frac{\pi }{2}F(w))$ or $1-\cos (\frac{\pi }{2}F(w))$ map the unit interval [0,1] into itself, remain continuous and monotone over the relevant range, and therefore their compositions is a valid CDF, where $w \in R$.

This paper expands its objectives of studies by selecting the Weibull distribution as the baseline distribution, yielding the CAP-W distribution. The choice of this distribution is motivated by the widely recognized versatility of the Weibull distribution for modeling lifetime and reliability data, with its capability to accommodate increasing, decreasing, and constant hazard rate patterns. Therefore, the resulting CAP-W distribution has the advantages of illustrating various curve shapes for both the PDF and the hazard rate function, indicating its adaptability and performance for displaying actual-life data in a variety of application fields. Moreover, the Weibull distribution encompasses the exponential and Rayleigh distributions as special cases, which further reinforces its appropriateness as a baseline model. Additionally, the CAP-W displays a better fit against four rival models across three real-life scenarios. Moreover, a novel log location-scale regression model has been constructed.

The following sections are arranged as: Section "The cosine AP-generated family" describes the CAP-G family along with their characteristics. Section "Properties of cosine AP- Weibull distribution" explains the CAP-W and analyzes the important statistical features. The four various approaches are employed to produce the estimators of the distribution parameters in Section "Estimation methods". In section "Simulation study", the Monte Carlo simulation has been carried out to assessing the accuracy of the estimations. Section "Applications" discusses four real-world data sets that are examined to explain the CAP-W’s efficiency. The log CAP-W (LCAP-W) regression model is discussed in Section "The log CAP-W regression model". Ultimately, the result of this study is given in Section "Conclusions".

The cosine AP-generated family

Let W be a random variable (RV) that follows the CAP-G with CDF $G_{CAP-G}(w)$. Thus, $G_{CAP-G}(w)$ of the CAP-G family is simple to produced via replacing F(w) in Eq. (3) with Eq. (1) in the following form:

$$\begin{aligned} G_{CAP-G}(w)=1-\cos \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{F(w)}}{1-\alpha }\right) \right] ,~w\in \mathbb {R}; \alpha >0, \alpha \ne 1, \end{aligned}$$

(5)

and the related PDF is

$$\begin{aligned} g_{CAP-G}(w)=\frac{\pi }{2}\frac{\log \alpha }{(\alpha -1)} \alpha ^{F(w)} f(w)\sin \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{F(w)}}{1-\alpha }\right) \right] , w\in \mathbb {R}; \alpha >0, \alpha \ne 1, \end{aligned}$$

(6)

where $\alpha$ is the transformation parameter, F(w) and f(w) refer to the CDF and PDF of baseline distribution, respectively.

The CAP-G family’s hazard rate function, $h_{CAP-G}(w)$, is shown as

$$\begin{aligned} h_{CAP-G}(w)=\frac{\pi }{2}\frac{log\alpha }{(\alpha -1)}\alpha ^{F(w)} f(w)\frac{\sin \left[ \frac{\pi }{2} \left( \frac{1-\alpha ^{F(w)}}{1-\alpha }\right) \right] }{\cos \left[ \frac{\pi }{2} \left( \frac{1-\alpha ^{F(w)}}{1-\alpha }\right) \right] }, \end{aligned}$$

(7)

and the CAP-G family’s survival function, $s_{CAP-G}(w)$, can be stated by

$$\begin{aligned} s_{CAP-G}(w)=\cos \left[ \frac{\pi }{2} \left( \frac{1-\alpha ^{F(w)}}{1-\alpha }\right) \right] . \end{aligned}$$

(8)

To produce the quantile function for the CAP-W, the CDF is inverted in Eq. (5) according to the following:

$$\begin{aligned} Q_{CAP-G}(p)= F^{-1} \left[ \frac{\log \left( 1-\frac{2(1-\alpha )\arccos (1-p)}{\pi } \right) }{\log \alpha }\right] ,~ 0<p<1. \end{aligned}$$

(9)

The related median, lower quartile, and higher quartile are determined by replacing $p = 0.5, 0.25$, and 0.75, respectively, in Eq. (9).

Special models of the CAP-G family

Cosine AP Weibull distribution

The CAP-W distribution is classified as a part to the CAP-G family. We let F(w) in Eq. (5) represents the Weibull distribution’s CDF ³³, thus the CDF of CAP-W distribution will be

$$\begin{aligned} G_{CAP-W}(w)=1-\cos \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\eta w^{\theta })}}{1-\alpha }\right) \right] ,\quad w>0; \alpha , {\eta ,\theta }>0,\alpha \ne 1. \end{aligned}$$

(10)

The associated PDF can be written as follows:

$$\begin{aligned} g_{CAP-W}(w)=\frac{\pi }{2}~\frac{\eta ~\theta ~(\log \alpha )}{(\alpha -1)}~{ (w^{\theta -1})}\exp (-\eta w^{\theta })~{\left( \alpha ^{1-\exp (-\eta w^{\theta })}\right) }\sin \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\eta w^{\theta })}}{1-\alpha }\right) \right] . \end{aligned}$$

(11)

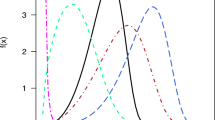
The PDF of the CAP-W distribution in Fig. 1 indicates a variety of symmetrical, decreasing, and right-skewed shapes that illustrate the flexibility of the distribution using various combinations of the parameters $\alpha$, $\eta$ and $\theta$. The transformation parameter $\alpha$ is used as a shape-controlling parameter that controls the degree of skewness and tail heaviness. While, the scale and shape parameters $\eta$ and $\theta$ of the baseline Weibull distribution modulate the expansion and the peak, respectively.

Fig. 1

PDF plots for various CAP-W parameter values.

Cosine AP exponential distribution

Applying the exponential distribution ³⁴ as the baseline distribution, the CDF and PDF of the cosine AP exponential (CAP-E) distribution are provided by

$$\begin{aligned} G_{CAP-E}(w)=1-\cos \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\lambda w)}}{1-\alpha }\right) \right] ,~ w>0; \alpha ,\lambda >0,~\alpha \ne 1, \end{aligned}$$

$$\begin{aligned} g_{CAP-E}(w)=\frac{\pi }{2}~\frac{\lambda ~(\log \alpha )}{(\alpha -1)}~ \exp (-\lambda w)~{\left( \alpha ^{1-\exp (-\lambda w)}\right) }\sin \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\lambda w)}}{1-\alpha }\right) \right] , \end{aligned}$$

where $\lambda$ is the scale parameter of the exponential distribution. Figure 2 illustrates the PDF plots of the CAP-E distribution, showing its right-skewed and nearly symmetrical forms.

Fig. 2

PDF plots for different values of the CAP-E parameters.

Cosine AP Rayleigh distribution

The cosine AP Rayleigh (CAP-R) distribution is obtained by inserting the CDF of Rayleigh distribution ³⁵ in Eq. (5). Therefore, the CDF of the CAP-R distribution is displayed as

$$\begin{aligned} G_{CAP-R}(w)=1-\cos \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\lambda w^{2})}}{1-\alpha }\right) \right] , ~ w>0; \alpha ,\lambda >0,~\alpha \ne 1, \end{aligned}$$

and the CAP-R distribution’s PDF is provided as

$$\begin{aligned} g_{CAP-R}(w)=\frac{\pi \lambda ~(\log \alpha )}{(\alpha -1)}~ w~ \exp (-\lambda w^{2})~{\left( \alpha ^{1-\exp (-\lambda w^{2})}\right) }\sin \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\lambda w^{2})}}{1-\alpha }\right) \right] . \end{aligned}$$

Figure 3 illustrates the PDF plots of the CAP-R distribution, which shows right-skewed, nearly symmetric, and symmetric.

Fig. 3

PDF plots representing a variety of CAP-R parameter values.

Cosine AP Lomax distribution

The cosine AP Lomax (CAP-L) distribution is determined by replacing the CDF of Lomax distribution ³⁶ in Eq. (5). Hence, the CAP-L distribution’s CDF is supplied by:

$$\begin{aligned} G_{CAP-L}(w)=1-\cos \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-(1+\frac{w}{\lambda })^{-\theta }}}{1-\alpha }\right) \right] , ~ w>0; \alpha ,\lambda , \theta >0,~\alpha \ne 1, \end{aligned}$$

and the PDF will be

$$\begin{aligned} g_{CAP-L}(w)=\frac{\pi }{2}~\frac{\theta ~(\log \alpha )}{\lambda ~(\alpha -1)}~ \left( 1+\frac{w}{\lambda }\right) ^{-(\theta +1)}~ {\left( \alpha ^{1-(1+\frac{w}{\lambda })^{-\theta }} \right) }\sin \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-(1+\frac{w}{\lambda })^{-\theta }}}{1-\alpha }\right) \right] . \end{aligned}$$

The CAP-L density is represented to be right-skewed shapes as observed in Fig. 4.

Fig. 4

PDF plots for various values of the CAP-L parameters.

Cosine AP Lindley distribution

By applying the CDF and PDF of Lindley distribution ³⁷ in Eq. (5) and Eq.(6), the CDF and PDF of the cosine AP Lindley (CAP-Li) distribution are provided , respectively, as

$$\begin{aligned} G_{CAP-Li}(w)=1-\cos \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\left( \frac{1+\theta +\theta w}{\theta +1}\right) ~\exp (-\theta w)}}{1-\alpha }\right) \right] , ~ w>0; \alpha , \theta >0,~\alpha \ne 1, \end{aligned}$$

and

$$\begin{aligned} g_{{CAP - Li}} (w) = & \frac{\pi }{2}~\frac{{\theta ^{2} ~(\log \alpha )}}{{(\alpha - 1)(\theta + 1)}}~\left( {1 + w} \right)~\exp ( - \theta w)~~\left( {\alpha ^{{1 - \left( {\frac{{1 + \theta + \theta w}}{{\theta + 1}}} \right)~\exp ( - \theta w)}} } \right) \\ & \sin \left[ {\frac{\pi }{2}~\left( {\frac{{1 - \alpha ^{{1 - \left( {\frac{{1 + \theta + \theta w}}{{\theta + 1}}} \right)~\exp ( - \theta w)}} }}{{1 - \alpha }}} \right)} \right], \\ \end{aligned}$$

where $\theta$ is the shape parameter of Lindley distribution. Figure 5 shows PDF graphs for CAP-Li with its right-skewed and nearly symmetric shapes.

Fig. 5

PDF plots of various CAP-Li parameter values.

Properties of cosine AP- Weibull distribution

This section focuses on producing and discussing the various features of CAP-W distribution.

Hazard rate and survival functions

The CAP-W distribution’s hazard rate and survival functions are provided by

$$\begin{aligned} h_{CAP-W}(w)=\frac{\pi }{2}~\frac{\eta ~\theta ~(log\alpha )}{(\alpha -1)}{\left( w^{\theta -1}\right) }\exp (-\eta w^{\theta })~{\left( \alpha ^{1-\exp (-\eta w^{\theta })}\right) }~{\tan \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\eta w^{\theta })}}{1-\alpha }\right) \right] }, \end{aligned}$$

(12)

and

$$\begin{aligned} s_{CAP-W}(w)=\cos \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\eta w^{\theta })}}{1-\alpha }\right) \right] , ~ w>0; \alpha , \eta ,\theta >0,\alpha \ne 1, \end{aligned}$$

(13)

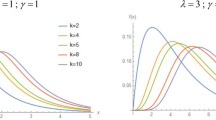
respectively. Figure 6 illustrates several shapes of the CAP-W hazard function using different values of the parameters $\alpha$, $\eta$ and $\theta$, which appear to be upside down bathtub, J shape, decreasing, and increasing, indicating the flexibility of the distribution to model different real-world datasets.

Fig. 6

Hazard function plots of the CAP-W distribution.

Expansion for the cosine AP-Weibull density

Consider the following series for the sine function

$$\begin{aligned} { \sin (w)}=\sum _{s_{1}=0}^{\infty }\frac{(-1)^{s_{1}}}{(2s_{1}+1)!}w^{2s_{1}+1}, \end{aligned}$$

into Eq. (11), we get the CAP-W distribution’s PDF by the following:

$$\begin{aligned} g_{{CAP - W}} (w) = & ~\eta ~\theta ~(\log \alpha )~\left( {w^{{\theta - 1}} } \right)\exp ( - \eta w^{\theta } )~\left( {\alpha ^{{1 - \exp ( - \eta w^{\theta } )}} } \right) \\ & \sum\limits_{{s_{1} = 0}}^{\infty } {\frac{{( - 1)^{{s_{1} + 1}} }}{{(2s_{1} + 1)!}}} \left( {\frac{\pi }{{2(1 - \alpha )}}} \right)^{{2s_{1} + 2}} \left( {1 - \alpha ^{{1 - \exp ( - \eta w^{\theta } )}} } \right)^{{2s_{1} + 1}} . \\ \end{aligned}$$

Then, utilizing the following binomial series expansion

$$\begin{aligned} (1-w)^{2s_{1}}=\sum _{{s_{2}}=0}^{\infty }(-1)^{s_{2}} \left( \begin{array}{c} 2s_{1} \\ s_{2} \end{array} \right) w^{s_{2}};{\quad |w|<1}, \end{aligned}$$

(14)

we obtain:

$$\begin{aligned} g_{{CAP - W}} (w) = ~ & \eta ~\theta ~(\log \alpha )~\left( {w^{{\theta - 1}} } \right)\exp ( - \eta w^{\theta } )\sum\limits_{{s_{1} = 0}}^{\infty } {\sum\limits_{{s_{2} = 0}}^{\infty } {\frac{{( - 1)^{{s_{1} + s_{2} + 1}} }}{{(2s_{1} + 1)!}}} } \\ & \left( {\begin{array}{*{20}c} {2s_{1} + 1} \\ {s_{2} } \\ \end{array} } \right)\left( {\frac{\pi }{{2(1 - \alpha )}}} \right)^{{2s_{1} + 2}} \left( {\alpha ^{{1 - \exp ( - \eta w^{\theta } )}} } \right)^{{s_{2} + 1}} . \\ \end{aligned}$$

Furthermore, by employing the following series representation:

$$\begin{aligned} \alpha ^{-z}=\sum _{s_{3}=0}^{\infty }\frac{(-\log \alpha )^{s_{3}}}{s_{3}!}(z)^{s_{3}}, \end{aligned}$$

(15)

the CAP-W’s PDF will be written as

$$\begin{aligned} g_{CAP-W}(w)=\eta \theta \sum _{s_{3}=0}^{\infty } \varphi _{s_{3}} {\left( w^{\theta -1}\right) }\exp (-(s_{3}+1)\eta w^{\theta }), ~~w>0;\alpha , \eta , \theta >0, \alpha \ne 1, \end{aligned}$$

(16)

where

$$\begin{aligned} \varphi _{s_{3}}=\sum _{s_{1}=0}^{\infty }\sum _{s_{2}=0}^{\infty }\frac{(-1)^{s_{1}+s_{2}+s_{3}+1}}{(2s_{1}+1)! s_{3}!} \left( \begin{array}{c} 2s_{1}+1 \\ s_{2} \end{array} \right) \left( \frac{\pi }{2(1-\alpha )}\right) ^{2s_{1}+2} (\log \alpha )^{s_{3}+1}(s_{2}+1)^{s_{3}} \alpha ^{s_{2}+1}. \end{aligned}$$

(17)

Quantile function and median

The CAP-W quantile function is derived from Eq. (10) as the following:

$$\begin{aligned} Q_{CAP-W}(p)=\left\{ \frac{-\log \left[ \log \left[ \pi \alpha /(a)\right] /(\log \alpha )\right] }{\eta }\right\} ^{\frac{1}{\theta }},~~ 0<p<1, \end{aligned}$$

(18)

where $a(p)=\pi +2(\alpha -1)arccos(1-p)$. The median can be acquired as

$$\begin{aligned} Median=\left\{ \frac{-\log \left[ \log \left[ \pi \alpha /(b)\right] /(\log \alpha )\right] }{\eta }\right\} ^{\frac{1}{\theta }}, \end{aligned}$$

where $b=\pi +2(\alpha -1)arccos(1-0.5)$.

Skewness and kurtosis

The Moors kurtosis ³⁸ and Galton skewness ³⁹ of the CAP-W distribution can be derived by applying Eq. (18) into the following measures:

$$\begin{aligned} Kurtosis= \frac{Q\left( \frac{7}{8}\right) -Q\left( \frac{5}{8}\right) -Q\left( \frac{1}{8}\right) +Q\left( \frac{3}{8}\right) }{Q\left( \frac{3}{4}\right) -Q\left( \frac{1}{4}\right) }. \end{aligned}$$

$$\begin{aligned} Skewness= \frac{Q\left( \frac{3}{4} \right) -2Q\left( \frac{1}{2} \right) +Q\left( \frac{1}{4}\right) }{Q\left( \frac{3}{4}\right) -Q\left( \frac{1}{4}\right) }. \end{aligned}$$

Fig. 7

Plots for skewness and kurtosis of the CAP-W distribution.

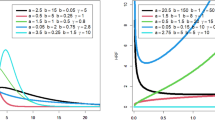
Figure 7 shows the behavior of the skewness and kurtosis of the CAP-W model, with the transforming parameter $\alpha$ varying approximately from 0.05 to 0.40 and shape parameter $\theta$ from 1.0 to 4.0. It is clear that when $\alpha$ increases, the skewness decreases while being modulated by $\theta$. This indicates that the cosine-AP family, specifically the parameter $\alpha$ , has the regulation over the distributional skewness. Regarding the behavior of the kurtosis, we can observe that small value of $\alpha$ leads to larger kurtosis (high peaked distribution), whereas increasing $\alpha$ creates distribution with lower kurtosis, which gives us the same conclusion of the Galton-skewness.

Moments

If W has a CAP-W distribution, then the rth moment of W can be acquired via

$$\begin{aligned} \mu _r=E(W^{r})=\int _{0}^{\infty }w^{r}g(w) dw. \end{aligned}$$

(19)

Substituting Eq. (16) into Eq. (19), we have

$$\begin{aligned} \mu _r=\eta \theta \sum _{s_{3}=0}^{\infty }\varphi _{s_{3}} \int _{0}^{\infty }{\left( w^{r+\theta -1}\right) }\exp (-(s_{3}+1)\eta w^{\theta }) dw. \end{aligned}$$

Let $u=(s_{3}+1)\eta w^{\theta }$, we get

$$\begin{aligned} \mu _r=\sum _{s_{3}=0}^{\infty } \frac{\varphi _{s_{3}}}{\eta ^{\frac{r}{\theta }}(1+s_{3})^{\frac{r}{\theta }+1}}\int _{0}^{\infty }u^{\frac{r}{\theta }}\exp (-u) du. \end{aligned}$$

Then, we obtain the formula for the rth moment of CAP-W as

$$\begin{aligned} \mu _r=\sum _{s_{3}=0}^{\infty }\frac{\varphi _{s_{3}}\Gamma (\frac{r}{\theta }+1)}{\eta ^{\frac{r}{\theta }}(s_{3}+1)^{\frac{r}{\theta }+1}}, \end{aligned}$$

(20)

where $\varphi _{s_{3}}$ is given by Eq. (17).

Table 1 The mean and variance of CAP-W for various parameter values.

Table 1 shows that when theta increases, the mean and variance of the CAP-W decrease for fixed alpha and eta.

Moment generating function

The moment generating function, $M_W(t)$, for the CAP-W distribution is indicated by

$$\begin{aligned} M_W(t)=E(e^{tw})=\sum _{r=0}^{\infty }\frac{t^{r}}{r!}\mu _r~~ . \end{aligned}$$

(21)

Setting Eq. (20) into Eq. (21), we get the following:

$$\begin{aligned} M_W(t)=\sum _{r=0}^{\infty }\sum _{s_{3}=0}^{\infty }\frac{t^{r}}{r!}\frac{\varphi _{s_{3}}\Gamma (\frac{r}{\theta }+1)}{\eta ^{\frac{r}{\theta }}(s_{3}+1)^{\frac{r}{\theta }+1}}. \end{aligned}$$

where $\varphi _{s_{3}}$ is given by Eq. (17).

Characteristic function

The CAP-W characteristic function, $\phi _W(t)$, is derived as

$$\begin{aligned} \phi _W(t)=E(e^{itw})=\sum _{r=0}^{\infty }\frac{(it)^{r}}{r!}\mu _r. \end{aligned}$$

(22)

Using Eq. (20) in Eq. (22), we get the following:

$$\begin{aligned} \phi _W(t)=\sum _{r=0}^{\infty }\sum _{s_{3}=0}^{\infty }\frac{(it)^{r}}{r!}\frac{\varphi _{s_{3}}\Gamma (\frac{r}{\theta }+1)}{\eta ^{\frac{r}{\theta }}(s_{3}+1)^{\frac{r}{\theta }+1}}. \end{aligned}$$

where $\varphi _{s_{3}}$ is provided in Eq. (17).

Rényi entropies

The Rényi entropy quantifies the degree of uncertainty or variability in the RV W. It is supplied by

$$\begin{aligned} RE_{W}(v)=\frac{1}{1-v} \log \left( \int _{0}^{\infty } g^{v}_{CAP-W}(w)dw \right) ,~~~v>0, v\ne 1, \end{aligned}$$

(23)

where

$$\begin{aligned} g^{v}_{CAP-W}(w)=\left( \frac{\pi \eta ~\theta ~\alpha ~(\log \alpha )}{2( \alpha -1)}\right) ^{v} w^{v (\theta -1)}\exp (-v\eta w^{\theta })~\alpha ^{-v\exp (-\eta w^{\theta })} \sin ^{v}\left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\eta w^{\theta })}}{1-\alpha }\right) \right] . \end{aligned}$$

By substituting g(w) indicated in Eq. (11) into Eq. (23), we obtain

$$\begin{aligned} RE_{W}(v)=\frac{1}{1-v} \log \left[ \left( \frac{\pi \eta ~\theta ~\alpha ~(\log \alpha )}{2( \alpha -1)}\right) ^{v}\psi \right] ,~~w, \alpha , \eta , \theta >0, \alpha \ne 1, \end{aligned}$$

and $\psi =\int _{0}^{\infty } {\left( w^{v (\theta -1)}\right) }\exp (-v\eta w^{\theta })~{\left( \alpha ^{-v\exp (-\eta w^{\theta })}\right) } \sin ^{v}\left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\eta w^{\theta })}}{1-\alpha }\right) \right] dw.$

According to ¹¹, the Taylor series formula of $T(s)=\sin ^{v}[\frac{\pi }{2}s]$ can be expressed as

$$\begin{aligned} \sin ^{v}[\frac{\pi }{2}s]=\sum _{k=0}^{\infty }\sum _{r=0}^{k}(-1)^{r}b_{k}\left( \begin{array}{c} k \\ r \end{array} \right) s^r, \end{aligned}$$

where $b_{k}=\frac{(-1)^{k}T^{(k)}(1)}{k!}$, and $T^{(k)}(1)$ denotes the $k^{th}$ derivative of T(.) calculated at the value 1.

Thus, by expanding the $\sin ^{v}\left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\eta w^{\theta })}}{1-\alpha }\right) \right]$ component, we get

$$\begin{aligned} \sin ^{v}\left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp (-\eta w^{\theta })}}{1-\alpha }\right) \right] =\sum _{k=0}^{\infty }\sum _{r=0}^{k}(-1)^{r}b_{k}\left( \begin{array}{c} k \\ r \end{array} \right) \left( \frac{1-\alpha ^{1-\exp (-\eta w^{\theta })}}{1-\alpha }\right) ^{r}. \end{aligned}$$

By employing expansions in Eq. (14) and Eq. (15) yields

$$\begin{aligned} g^{v}_{CAP-W}(w)=\left( \frac{\pi \eta \theta \alpha \log \alpha }{2(\alpha -1)}\right) ^{v}\sum _{k=0}^{\infty }\sum _{r=0}^{k}\sum _{s_{2}=0}^{\infty }\sum _{s_{3}=0}^{\infty } \frac{(-1)^{r+s_{2}} b_{k}\alpha ^{s_{2}} (-\log \alpha )^{s_{3}} (v+s_{2})^{s_{3}}}{(1-\alpha )^{r} s_{3}!}~ \rho , \end{aligned}$$

(24)

where $\rho =\left( \begin{array}{c} k \\ r \end{array} \right) \left( \begin{array}{c} r \\ s_{2} \end{array}\right) w^{v(\theta -1)}\exp (-(v+s_{3})\eta w^{\theta })$.

substituting $g^{v}(w)$ in Eq. (24) into Eq. (23), and computing the integral. Then, the Rényi entropy of the CAP-W distribution can be obtained as

$$\begin{aligned} RE_{X}(v)=\frac{v}{1-v}\left( \log (\frac{\pi }{2})+\log (\alpha \log \alpha )\right) -\log \theta -\frac{log~\eta }{\theta } +\frac{1}{1-v}\log \left( \frac{\zeta \Gamma \left( \frac{v\theta -v+1}{\theta }\right) }{(v+s_{3})^{\frac{v\theta -v+1}{\theta }}}\right) , \end{aligned}$$

and

$$\begin{aligned} \zeta =\sum _{k=0}^{\infty }\sum _{r=0}^{k}\sum _{s_{2}=0}^{\infty }\sum _{s_{3}=0}^{\infty }(-1)^{(v+r+s_{2})}\left( \begin{array}{c} k \\ r \end{array} \right) \left( \begin{array}{c} r \\ s_{2} \end{array} \right) \frac{b_{k}\alpha ^{s_{2}}(-\log \alpha )^{s_{3}}(v+s_{2})^{s_{3}}}{(1-\alpha )^{r+v}s_{3}!}. \end{aligned}$$

Order statistics

Let $W_{1}, W_{2},....., W_{m}$ be a random sample from CAP-W distribution. The PDF of the kth order statistics $W_{k:m}$, denoted by $g_{k:m}(x)$, can be expressed as

$$\begin{aligned} g_{k:m}(w)=\frac{m!}{(k-1)!(m-k)!}g(w)[G(w)]^{k-1}[1-G(w)]^{m-k}. \end{aligned}$$

(25)

Employing the binomial expansion in Eq. (14) onto Eq. (25), we get

$$\begin{aligned} g_{k:m}(w)=\sum _{j=0}^{\infty }\frac{m!~(-1)^{j}}{(k-1)!(m-k)!}\left( \begin{array}{c} m-j \\ j \end{array} \right) g(w)[G(w)]^{k+j-1}. \end{aligned}$$

(26)

By putting Eq. (10) and Eq. (11) into Eq. (26), we obtain

$$\begin{aligned} g_{{k:m}} (w) = & \frac{{\pi \eta ~\theta ~(\log \alpha )}}{{2(\alpha - 1)}}\sum\limits_{{j = 0}}^{\infty } {\frac{{m!~( - 1)^{j} }}{{(k - 1)!(m - k)!}}} \left( {\begin{array}{*{20}c} {m - j} \\ j \\ \end{array} } \right)\left( {w^{{\theta - 1}} } \right)\exp ( - \eta w^{\theta } )~\left( {\alpha ^{{1 - \exp ( - \eta w^{\theta } )}} } \right) \\ & \times \sin \left[ {\frac{\pi }{2}~\left( {\frac{{1 - \alpha ^{{1 - \exp ( - \eta w^{\theta } )}} }}{{1 - \alpha }}} \right)} \right]\left\{ {1 - \cos \left[ {\frac{\pi }{2}~\left( {\frac{{1 - \alpha ^{{1 - \exp ( - \eta w^{\theta } )}} }}{{1 - \alpha }}} \right)} \right]} \right\}^{{k + j - 1}} . \\ \end{aligned}$$

Estimation methods

In this section, the parameters of the CAP-W distribution are estimated using the following methods: the maximum likelihood estimation method, the ordinary least squares method , the weighted least squares method, and the Cramér–von Mises method. These four estimation procedures are well established and are usually applied in reliability and lifetime analyses. The MLE serves as the official likelihood based method, while LS and WLS yield regression type estimates by minimizing squared deviations between empirical and theoretical distribution functions. The CVM estimator, is a minimum distance approach that depend on the integrated squared difference between the empirical and the model CDFs.

Maximum likelihood estimation method

Suppose $w_1,w_2,...,w_n$ be a random sample from CAP-W distribution. Then, the log-likelihood $(\ell )$ for the vector of the parameters $\Omega = (\alpha , \eta ,\theta )$ is:

$$\begin{aligned} \ell (\Omega ;w) = & n\log \left( {\frac{\pi }{2}} \right) + n\log \left( {\frac{{\log \alpha }}{{\alpha - 1}}} \right) + n\log (\alpha \eta \theta ) + (\theta - 1)\sum\limits_{{j = 1}}^{n} {\log } w_{j} \\ & - \left( {\log \alpha } \right)\sum\limits_{{j = 1}}^{n} {\exp } ( - \eta w_{j}^{\theta } ) - \eta \sum\limits_{{j = 1}}^{n} {w_{j}^{\theta } } + \sum\limits_{{j = 1}}^{n} {\log } \left\{ {\sin \left[ {\frac{\pi }{2}\left( {\frac{{1 - \alpha ^{{1 - \exp ( - \eta w_{j}^{\theta } )}} }}{{1 - \alpha }}} \right)} \right]} \right\}. \\ \end{aligned}$$

(27)

The first partial derivatives of Eq. (27) with respect to $\eta , \alpha ,$ and,$\theta$ are as follows:

$$\begin{aligned} \frac{{\partial \ell }}{{\partial \eta }} = & \frac{n}{\eta } - \sum\limits_{{j = 1}}^{n} {w_{j}^{\theta } } + \log \alpha \sum\limits_{{j = 1}}^{n} {(w_{j}^{\theta } )} \exp ( - \eta w_{j}^{\theta } ) - \frac{{\pi \log \alpha }}{{2(1 - \alpha )}} \\ & \times \sum\limits_{{j = 1}}^{n} {w_{j}^{\theta } } \left( {\alpha ^{{1 - \exp ( - \eta w_{j}^{\theta } )}} } \right)\exp ( - \eta w_{j}^{\theta } )\left\{ {\cot \left[ {\frac{\pi }{2}\left( {\frac{{1 - \alpha ^{{1 - \exp ( - \eta w_{j}^{\theta } )}} }}{{1 - \alpha }}} \right)} \right]} \right\}, \\ \end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial \ell }{\partial \alpha }=&\frac{n}{\alpha }-\frac{\sum _{j=1}^{n}\exp (-\eta w_{j}^{\theta })}{\alpha }+\frac{n(\alpha -1-\alpha \log \alpha )}{\alpha (\alpha -1)\log \alpha }+ \sum _{j=1}^{n}\left\{ \cot \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{1-\exp (-\eta w_{j}^{\theta })}}{1-\alpha }\right) \right] \right\} \\ &\times \nonumber \left[ \frac{\pi (1-\alpha ^{1-\exp (-\eta w_{j}^{\theta })})}{2(1-\alpha )^{2}}-\frac{\pi ~{\left( \alpha ^{-\exp (-\eta w_{j}^{\theta })}\right) }\left( 1-\exp (-\eta w_{j}^{\theta })\right) }{2(1-\alpha )}\right] , \end{aligned}$$

(29)

$$\begin{aligned} \frac{\partial \ell }{\partial \theta }=&\frac{n}{\theta }+\eta \log \alpha \sum _{j=1}^{n} w_{j}^{\theta }\exp (-\eta w_{j}^{\theta }){(\log w_{j})}-\eta \sum _{j=1}^{n} w_{j}^{\theta }\log w_{j} +\sum _{j=1}^{n}\log w_{j}\\ &\nonumber - \frac{\pi \eta \log \alpha }{2(1-\alpha )} \sum _{j=1}^{n}w_{j}^{\theta }{\left( \alpha ^{1-\exp (-\eta w_{j}^{\theta })}\right) }\left( \exp (-\eta w_{j}^{\theta })\right) { (\log w_{j})}\left\{ \cot \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{1-\exp (-\eta w_{j}^{\theta })}}{1-\alpha }\right) \right] \right\} . \end{aligned}$$

(30)

It is obvious that Eqs. (28)-(30) are challenging to solve traditionally. As a result, a numerical optimization technique can be applied to estimate the parameters.

Ordinary and weighted least-squares methods

The ordinary least squares (LS) estimation and the weighted least squares (WLS) estimation were suggested by ⁴⁰. The LS estimates may be obtained via minimizing the following function:

$$\begin{aligned} LS =\sum _{j=1}^{n}\left[ G_{CAP-W}(w_{(j)})-\frac{j}{n+1}\right] ^{2}, \end{aligned}$$

with respect to the unknown parameters. Thus, the LS estimation of vector of parameters $\Omega$ are calculated via minimizing

$$\begin{aligned} LS =\sum _{j=1}^{n}\left[ 1-\cos \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp ({-\eta w^{\theta }_{(j)}})}}{1-\alpha }\right) \right] -\frac{j}{n+1}\right] ^{2}. \end{aligned}$$

The WLS estimators for the CAP-W parameters can be determined by minimizing the following objective function:

$$\begin{aligned} WLS=\sum _{j=1}^{n}\frac{(n+1)^{2}(n+2)}{j(n-j+1)}\left[ G_{CAP-W}(w_{(j)})-\frac{j}{n+1}\right] ^{2}, \end{aligned}$$

or

$$\begin{aligned} WLS=\sum _{j=1}^{n}\frac{(n+1)^{2}(n+2)}{j(n-j+1)}\left[ 1-\cos \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp ({-\eta w^{\theta }_{(j)}})}}{1-\alpha }\right) \right] -\frac{j}{n+1}\right] ^{2}, \end{aligned}$$

with respect to $\Omega$.

Cramér–von Mises method

The Cramér–Von Mises (CVM) technique, commonly known as the minimal distance estimator, were produced via ⁴¹ to estimate unknown parameter by minimizing the following function:

$$\begin{aligned} CVM=\frac{1}{12n}+\sum _{j=1}^{n}\left[ 1-\cos \left[ \frac{\pi }{2}~\left( \frac{1-\alpha ^{1-\exp ({-\eta w^{\theta }_{(j)}})}}{1-\alpha }\right) \right] -\frac{2j-1}{2n}\right] ^{2}, \end{aligned}$$

with respect to $\alpha , \eta ,$ and, $\theta$.

Simulation study

In this part, Monte Carlo simulation will be used to assess the performance of the four methods of estimation based on sample size (n). We use the CAP-W quantile function to generate 1000 random samples with $n =165, 200, 300,500,$ and 700 to investigate the following parameter sets:

$$\begin{aligned} Set I: \alpha =0.085, \eta =3.500, \theta =3.100 , \end{aligned}$$

$$\begin{aligned} Set II: \alpha =0.050, \eta =1.200, \theta =2.900 , \end{aligned}$$

$$\begin{aligned} Set III: \alpha =0.100, \eta =1.500, \theta =1.500 , \end{aligned}$$

$$\begin{aligned} {Set IV: \alpha =0.080, \eta =1.900, \theta =0.70}. \end{aligned}$$

For every sample size, parameter estimates were computed, and the mean square error (MSE) was obtained and calculated using

$$\begin{aligned} {MSE}_{\Phi }=\frac{1}{1000}\sum _{i=1}^{1000} (\hat{\Phi }_i-\Phi )^2 , \end{aligned}$$

where $\Phi = (\alpha , \eta ,\theta )$. Estimates, absolute bias and MSE values of $\alpha , \eta ,$ and $\theta$ produced by applying the MLE, LS, WLS, and CVM methods are shown in Tables 2, 3, 4 and 5. All the estimation techniques studied achieved consistency, according to Tables 2, 3, 4 and 5. When the sample size becomes larger, the MSE and absolute bias in most of cases decreases, and the parameter estimates approach the actual values. Moreover, Tables 6, 7 and 8 demonstrate the coverage probability with the length for the estimates of the parameters using a nominal coverage of $1-\alpha =0.95$. By looking at the tables, it can be observed that converge probability is increasing while the length is decreasing in almost all cases to reach 95% nominal coverage. Furthermore, Figures 8, 9, 10 and 11 illustrate the MSE of the estimates for different sample sizes. It is observed that the LS technique is considered more efficient in estimating the parameter $\alpha$, while the MLE is more accurate than other techniques in estimating $\eta$ and $\theta$ of the CAP-W distribution.

Table 2 Estimates and MSE of $\alpha , \eta$, and $\theta$ for set I.

Table 3 Estimates and MSE of $\alpha , \eta$, and $\theta$ for set II.

Table 4 Estimates and MSE of $\alpha , \eta$, and $\theta$ for set III.

Table 5 Estimates and MSE of $\alpha , \eta$, and $\theta$ for set IV.

Table 6 The coverage probability and coverage length of $\alpha , \eta$, and $\theta$ for set I.

Table 7 The coverage probability and coverage length of $\alpha , \eta$, and $\theta$ for set II.

Table 8 The coverage probability and coverage length of $\alpha , \eta$, and $\theta$ for set III.

Fig. 8

MSE for parameters $\alpha ,\eta$ and $\theta$ applying the MLE, LSE, WLS, and CVM approaches for set I.

Fig. 9

MSE for parameters $\alpha ,\eta$ and $\theta$ applying the MLE, LSE, WLS, and CVM approaches for setII.

Fig. 10

MSE for parameters $\alpha ,\eta$ and $\theta$ applying the MLE, LSE, WLS, and CVM approaches for setIII.

Fig. 11

MSE for parameters $\alpha ,\eta$ and $\theta$ applying the MLE, LSE, WLS, and CVM approaches for setIV.

Applications

This section examines the flexibility and efficiency of the CAP-W distribution using four real-life data sets in different fields. The datasets have been given below.

First data set

The set of data shows the wait times (in minutes) for one hundred customers in bank to get serviced, as expressed by ⁴². The data are presented below:

0.8, 0.8, 1.3, 1.5, 1.8, 1.9, 1.9, 2.1, 2.6, 2.7, 2.9, 3.1, 3.2, 3.3, 3.5, 3.6, 4.0, 4.1, 4.2, 4.2, 4.3, 4.3, 4.4, 4.4, 4.6, 4.7, 4.7, 4.8, 4.9, 4.9, 5.0, 5.3, 5.5, 5.7, 5.7, 6.1, 6.2, 6.2, 6.2, 6.3, 6.7, 6.9, 7.1, 7.1, 7.1, 7.1, 7.4, 7.6, 7.7, 8.0, 8.2, 8.6, 8.6, 8.6, 8.8, 8.8, 8.9, 8.9, 9.5, 9.6, 9.7, 9.8, 10.7, 10.9, 11.0, 11.0, 11.1, 11.2, 11.2, 11.5, 11.9, 12.4, 12.5, 12.9, 13.0, 13.1, 13.3, 13.6, 13.7, 13.9, 14.1, 15.4, 15.4, 17.3, 17.3, 18.1, 18.2, 18.4, 18.9, 19.0, 19.9, 20.6, 21.3, 21.4, 21.9, 23.0, 27.0, 31.6, 33.1, 38.5.

Second data set

The second dataset shows the active repair times (in hours) for a transceive used for aerial communication. These data were obtained from ^19,43, and are available below:

0.50, 0.60, 0.60, 0.70, 0.70, 0.70, 0.80, 0.80, 1.00, 1.00, 1.00, 1.00, 1.10, 1.30, 1.50, 1.50, 1.50, 1.50, 2.00, 2.00, 2.20, 2.50, 2.70, 3.00, 3.00, 3.30, 4.00, 4.00, 4.50, 4.70, 5.00, 5.40, 5.40, 7.00, 7.50, 8.80, 9.00, 10.20, 22.00, 24.50.

Third data set

The third dataset includes the survival times for a group of patients with head and neck cancer who obtained treatment utilizing both radiation and chemotherapy (RT+CT). The dataset derived from ⁴⁴ is presented as follows: 12.20, 23.56, 23.74 ,25.87, 31.98, 37, 41.35, 47.38, 55.46, 58.36, 63.47, 68.46, 78.26, 74.47, 81.43, 84, 92, 94, 110, 112, 119, 127, 130, 133 ,140, 146, 155, 159, 173, 179 ,194, 195 ,209, 249, 281, 319 , 339, 432, 469, 519, 633, 725, 817, 1776.

Fourth data set

The dataset illustrates the number of failures in the air conditioning systems of jet aircraft. This data were examined by  ^45,46. The data are 194, 413, 90, 74, 55, 23, 97, 50, 359, 50, 130, 487, 57, 102, 15, 14, 10, 57, 320, 261, 51, 44, 9, 254, 493, 33, 18, 209, 41, 58, 60, 48, 56, 87, 11, 102, 12, 5, 14, 14, 29, 37, 186, 29, 104, 7, 4, 72, 270, 283, 7, 61, 100, 61, 502, 220, 120, 141, 22, 603, 35, 98, 54, 100, 11, 181, 65, 49, 12, 239, 14, 18, 39, 3, 12, 5, 32, 9, 438, 43, 134, 184, 20, 386, 182, 71, 80, 188, 230, 152, 5, 36, 79, 59, 33, 246, 1, 79, 3, 27, 201, 84, 27, 156, 21, 16, 88, 130, 14, 118, 44, 15, 42, 106, 46, 230, 26, 59, 153, 104, 20, 206, 5, 66, 34, 29, 26, 35, 5, 82, 31, 118, 326, 12, 54, 36, 34, 18, 25, 120, 31, 22, 18, 216, 139, 67, 310, 3, 46, 210, 57, 76, 14, 111, 97, 62, 39, 30, 7, 44, 11, 63, 23, 22, 23, 14, 18, 13, 34, 16, 18, 130, 90, 163, 208, 1, 24, 70, 16, 101, 52, 208, 95, 62, 11, 191, 14, 71.

 Table 9 displays a variety of statistical measures for the three datasets, which provide an overview of the initial information, such as sizes, measures of central tendency, and variability to illustrate the appropriateness of the CAP-W distribution for these datasets.

Table 9 Summary information for all three sets of data.

The CAP-W distribution is contrasted to four various rival distributions, using the CDF as follows:

• Gull AP Weibull (GAPW) distribution in ⁴⁷:

  $$\begin{aligned} F_{GAPW}(x)=\frac{\alpha (1-\exp (-\theta x^{\gamma }))}{\alpha ^{1-\exp (-\theta x^{\gamma })}},~x>0,~~\alpha ,\gamma ,\theta >0. \end{aligned}$$

• AP Weibull (APW) distribution in ⁴:

  $$\begin{aligned} F_{APW}(w) =\left\{ \begin{array}{rcl} \frac{1}{1-\alpha }(1-\alpha ^{1-\exp (-\lambda w^{\beta })}) & \text{ if } & \alpha >0 ,\alpha \ne 1,\\ 1-\exp (-\lambda w^{\beta }) & \text{ if } & \alpha =1, \end{array}\right. \end{aligned}$$

  where $w>0, ~~ \lambda ,\beta >0$.

• New cosine Weibull (NCW) distribution in ⁴⁸:

  $$\begin{aligned} F_{NCW}(w)=1-\cos \left[ \frac{\pi (2-2^{\exp (-\alpha w^{\beta })})}{2}\right] ,~w>0,~~\alpha ,\beta >0. \end{aligned}$$

• Sine exponential (SX) distribution in ¹⁰:

  $$\begin{aligned} G_{SX}(w)=\cos \left[ \frac{\pi }{2} \exp (-\theta w)\right] , ~w>0,~~\theta >0. \end{aligned}$$

The selected distributions were chosen because they are widely used for reliability and lifetime data and collectively demonstrate a variety of shapes and tail behaviors. These distributions share structural features with the proposed distribution, having Weibull and exponential distribution, which permits a fair and informative comparison in terms of flexibility and goodness of fit, with varying non-monotonic failure patterns.

The efficiency of CAP-W distribution will be examined applying the goodness of fit criteria (GoF), including the negative log-likelihood ($-\hat{\ell }$), Akaike information criterion ($A_{1}$), Bayesian information criterion ($A_{2}$), consistent Akaike information criterion ($A_{3}$), and non-parametric statistical tests such as Kolmogorov Smirnov ($A_{4}$) with its p-value ($A_{5}$).

The MLEs along with their standard error (SE) of the CAP-W, GAPW, APW, NCW, and SX distributions for the three data sets are provided in Table 10. Based on the outcomes in Tables 11, 12, 13 and 14, the CAP-W distribution has minimal values for $-\hat{\ell }$,$A_{1}$, $A_{2}$, $A_{3}$, and $A_{4}$ with a high $A_{5}$. This indicates that for the three real data sets, the CAP-W distribution gives the perfect fit when compared to others rival distributions. Figures 12, 13, 14 and 15 display the estimated PDF and CDF of the CAP-W distribution and competing distributions, which assert its superiority in fitting different datasets. Figures 16, 17, 18 and 19 demonstrate the P-P plots for the CAP-W distribution with the other competing distributions using the empirical and theoretical CDF of the three datasets. It can be seen that the plotted points for the CAP-W distribution fall very close to the diagonal line, indicating that its theoretical CDF closely matches the empirical CDF compared to the other models. This provides further evidence of the better performance of the proposed model.

Table 10 MLEs, SE (in parentheses) for the four data sets.

Table 11 The values of GoF for first data.

Table 12 The values of GoF for second data.

Table 13 The values of GoF for third data.

Table 14 The values of GoF for fourth data.

Fig. 12

The theoretical and empirical CDF (a) and PDF (b) of distributions for Data 1.

Fig. 13

The theoretical and empirical CDF (a) and PDF (b) of distributions for Data 2.

Fig. 14

The theoretical and empirical CDF (a) and PDF (b) of distributions for Data 3.

Fig. 15

The theoretical and empirical CDF (a) and PDF (b) of distributions for Data 4.

Fig. 16

P-P plot for First data.

Fig. 17

P-P plot for Second data.

Fig. 18

P-P plot for Third data..

Fig. 19

P-P plot for Fourth data..

The log CAP-W regression model

In this section, we present the LCAP-W regression model. Using the transformation $Y = \log (W)$ in Eq. (11) and re-parameterization $\theta =\frac{1}{\sigma }$, $\eta =e^{\frac{-\mu }{\sigma }}$ yields the LCAP-W. Thus, the LCAP-W PDF will be displayed by

$$\begin{aligned} g(y)=\frac{\pi }{2}\frac{\log \alpha }{(\alpha -1)\sigma } ~e^{\frac{y-\mu }{\sigma }}~e^{{-e}^{\frac{y-\mu }{\sigma }}} \alpha ^{1-e^{{-e}^{\frac{y-\mu }{\sigma }}}} \sin \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{1-e^{{-e}^{\frac{y-\mu }{\sigma }}}}}{1-\alpha }\right) \right] , \end{aligned}$$

(31)

where $\mu \in \mathbb {R}$ is the location paramater, $\sigma >0$ is the scale paramater, and $\alpha >0,\alpha \ne 1.$ The associated CDF is shown as

$$\begin{aligned} G(y)= 1- \cos \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{1-e^{{-e}^{\frac{y-\mu }{\sigma }}}}}{1-\alpha }\right) \right] . \end{aligned}$$

(32)

The survival function will be supplied by

$$\begin{aligned} s(y)=\cos \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{1-e^{{-e}^{\frac{y-\mu }{\sigma }}}}}{1-\alpha }\right) \right] , \end{aligned}$$

(33)

and hazard function is

$$\begin{aligned} h(y)=\frac{\pi }{2}\frac{\log \alpha }{(\alpha -1)\sigma }~e^{\frac{y-\mu }{\sigma }}~e^{{-e}^{\frac{y-\mu }{\sigma }}}\alpha ^{1-e^{{-e}^{\frac{y-\mu }{\sigma }}}}~{\tan \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{1-e^{{-e}^{\frac{y-\mu }{\sigma }}}}}{1-\alpha }\right) \right] }. \end{aligned}$$

Also, the quantile function is given by

$$\begin{aligned} Q(p)=\sigma \log \left[ \log \left( \frac{\log \alpha }{\log \left( (\pi \alpha )/(\pi +2(\alpha -1)\arccos (1-p))\right) }\right) \right] +\mu . \end{aligned}$$

The standardized RV, $z =\frac{y-\mu }{\sigma }$, produces the following PDF:

$$\begin{aligned} g(z)=\frac{\pi }{2}\frac{\log \alpha }{(\alpha -1)\sigma }~e^{z}~e^{{-e^{z}}}\alpha ^{1-e^{{-e^{z}}}} \sin \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{1-e^{{-e^{z}}}}}{1-\alpha }\right) \right] , \end{aligned}$$

(34)

with the survival function stated as

$$\begin{aligned} s(z)=\cos \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{1-e^{{-e^{z}}}}}{1-\alpha }\right) \right] . \end{aligned}$$

(35)

In numerous real-world situations, factors such as cholesterol, blood pressure and weight affect life expectancy. Several regression models are utilized in survival analysis, and one widely used model is the log-location-scale regression, which statisticians apply to estimate univariate survival functions for censored data ³⁴. A number of studies have recommended the log-location-scale regression model, based on continuous distributions, for use in multiple disciplines like ^26,49,50,51. Thus, we provide a novel linear location-scale regression model based on LCAP-W:

$$\begin{aligned} y_{j}=\nu w^{T}_{j}+\sigma z_{j},~~~j=1,2,..,n, \end{aligned}$$

(36)

where $\nu =(\nu _{1},..,\nu _{p})^{T}, \alpha ,\sigma >0$, and $z_{j}$ is the random error with PDF in Eq. (34). The explanatory vector is $w^{T}_{j}=(w_{i1},...,w_{jp})^{T}$. The parameter $\mu _{j}=\nu w^{T}_{j}$ represents the location of $y_{j}$, and the location parameter vector $\mu =(\mu _{1},...,\mu _{n})^T$ can be stated as a linear model $\mu =\nu w$, where $w=(w_{1},...,w_{n})^T$ is the known matrix.

Estimation of the LCAP-W regression model

The LCAP-W regression model’s parameters are estimated using the maximum likelihood technique. Assume that $(y_{1},w_{1}),...,(y_{n},w_{n})$ be a random sample of n observations from a right-censored lifetime dataset, where $y_{j} =$min$[\log (t_{j}),\log (c_{j})]$. Let $t_j$ be the lifetime and $c_{j}$ be the censoring time, then the likelihood function for parameter $\Omega =(\alpha ,\sigma ,\nu )$ is provided by

$$\begin{aligned} L(\Omega )=\prod _{j=1}^{n} \left[ g(y_{j})^{\tau _{i}}~s(y_{j})^{1-\tau _{j}}\right] , \end{aligned}$$

(37)

where $\tau _j=\left\{ \begin{array}{rcl} 1 & \text{ if } & y_j=\log (t_j) \\ 0& \text{ if } & y_j=\log (c_j)\end{array} \right.$ is the censoring indicates. The log-likelihood function for $\Omega$ reduces to

$$\begin{aligned} \log L(\Omega ) = & d\log (\pi \log (\alpha )) - d\log (2(\alpha - 1)) - d\log (\sigma ) \\ & + \sum\limits_{{j = 1}}^{n} {\tau _{j} } \left[ {z_{j} - e^{{z_{j} }} } \right] + \sum\limits_{{j = 1}}^{n} {\tau _{j} } \left[ {1 - e^{{ - e^{{z_{j} }} }} } \right]\log (\alpha ) \\ & + \sum\limits_{{j = 1}}^{n} {\tau _{j} } \log \left[ {\sin \left[ {\frac{\pi }{2}\left( {\frac{{1 - \alpha ^{{1 - e^{{ - e^{{z_{j} }} }} }} }}{{1 - \alpha }}} \right)} \right]} \right] + \sum\limits_{{j = 1}}^{n} {(1 - \tau _{j} )} \log \left[ {\cos \left[ {\frac{\pi }{2}\left( {\frac{{1 - \alpha ^{{1 - e^{{ - e^{{z_{j} }} }} }} }}{{1 - \alpha }}} \right)} \right]} \right], \\ \end{aligned}$$

(38)

where d is the number of uncensored observations and $z_{j}=(y_{j}-\nu w^{T}_{j})/\sigma$. The MLEs of the parameters may be obtained via maximizing the log-likelihood function in Eq. (38). The “optim” function in R package may be employed to get the MLEs.

Applications for the LCAP-W regression model

The effectiveness of the LCAP-W regression model is studied through use of an actual dataset and comparing it with a variety of contrasting models. The dataset is referred to the Leukemia Data (LD) and was provided by Lawless in ³⁴. The data are presented below:

y: 65, 140, 100, 134, 16, 106, 121, 4, 39, 121, 56, 26, 22, 1, 1, 5, 65, 56, 65, 17, 7, 16, 22, 3, 4, 2, 3, 8, 4, 3, 30, 4, 43.

AG: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.

WBC: 2.3, 0.75, 4.3, 2.6, 6, 10.5, 10, 17, 5.4, 7, 9.4, 32, 35, 100, 100, 52, 100, 4.4, 3,4, 1.5, 9, 5.3, 10, 19, 27, 28, 31, 26, 21, 79, 100, 100.

status: 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1.

The study includes the following variables: $t_{j}$: survival time, $y_{j}$: log survival time, status_j: censoring indication (0=censoring, 1 =lifetime), $w_{j1}$: white blood cell characteristics (AG) test (0 =negative, 1 =positive), $w_{j2}$: white blood cell count (WBC).

Thus, the fitted model may be stated like the following:

$$\begin{aligned} y_{j}=\nu _{0}+\nu _{1}w_{j1}+\nu _{2}w_{j2}+\sigma z_{j},~~j=1,2,...,33. \end{aligned}$$

(39)

The MLEs and their SEs are shown in Table 15. The criteria $A_{1}$, $A_{2}$ , $A_{3}$, and Hannan-Quinn information criterion ($A_{6}$) are displayed in Table 16. The LCAP-W regression model is compared with log cosine Topp–Leon Weibull (LCTLWe) in ²⁶, log tangent Topp-Leone Weibull (LTTLWe) in ⁴⁹, log sine alpha power Weibull (LSAPWe) in ²², and the log Marshall-Olkin odd log-logistic Weibull (LMOOLLWe) in ⁵¹. Table 13 illustrates that, when compared with the others competing model, the LCAP-W has the lowest values of all criteria, demonstrating that it best fits the leukemia data. The coefficients for the variables AG and WBC are consistently positive and negative, respectively, in each of the fitted models.

Table 15 MLEs, SE in () for LD.

Table 16 The value of GoF for LD.

Residual analysis

Residual analysis is used to assess the adequate accuracy of the fitted model and determine outlier observations. This study involved residual analysis using martingale residuals and deviance residuals.

Martingale residual

The martingale residual is described by ⁵² as follows:

$$\begin{aligned} r_{Mj}=\delta _{j}+\log (s(y_{j};\hat{\Omega })) \end{aligned}$$

where $\delta _{j}$ indicates the censor indicator; $\delta _{j}=0$, if the jth observation is censored , and $\delta _{j}=1$, if the jth observation is uncensored , and $s(y_{j},\hat{\Omega })$ is the survival function of LCAP-W .

The LCAP-W regression model’s martingale residual is

$$\begin{aligned} r_{M_j}=\left\{ \begin{array}{rcl} 1+\log \left\{ \cos \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{1-e^{{-e^{\hat{z_{j}}}}}}}{1-\alpha }\right) \right] \right\} ~~~~~~~ \text {if}~~~ j\in \text {lifetime},\\ \log \left\{ \cos \left[ \frac{\pi }{2}\left( \frac{1-\alpha ^{1-e^{{-e^{\hat{z_{j}}}}}}}{1-\alpha }\right) \right] \right\} ~~~~~~~ \text {if}~~~ j\in \text {censored}, \end{array}\right\} \end{aligned}$$

(40)

where $\hat{z_{j}}=(y_{j}-\hat{\nu }w^{T}_{j})/\hat{\sigma }$. The value of $r_{M_j}$ ranges from $-\infty$ to $+1$ and is skewed.

Deviance residual

This is a modification of the martingale residual, which reduces skewness and provides it more symmetrical around zero. It can be stated as

$$\begin{aligned} r_{D_{j}}=\text {sign}(r_{M_{j}})\sqrt{-2[r_{M_{j}}+\delta _{j}\log (\delta _{j}-r_{M_{j}})]}, \end{aligned}$$

where $r_{M_j}$ is given in 40. The LCAP-W regression model’s deviance residual is

$$r_{{M_{j} }} = \left\{ {\begin{array}{*{20}c} \begin{aligned} & {\text{sign}}\left( {1 + \log \left\{ {\cos \left[ {\frac{\pi }{2}\left( {\frac{{1 - \alpha ^{{1 - e^{{ - e^{{\widehat{{z_{j} }}}} }} }} }}{{1 - \alpha }}} \right)} \right]} \right\}} \right) \\ & \quad \times \left\{ { - 2[1 + \log \left\{ {\cos \left[ {\frac{\pi }{2}\left( {\frac{{1 - \alpha ^{{1 - e^{{ - e^{{\widehat{{z_{j} }}}} }} }} }}{{1 - \alpha }}} \right)} \right]} \right\}] + \log \left[ { - \log \left\{ {\cos \left[ {\frac{\pi }{2}\left( {\frac{{1 - \alpha ^{{1 - e^{{ - e^{{\widehat{{z_{j} }}}} }} }} }}{{1 - \alpha }}} \right)} \right]} \right\}} \right]} \right\}^{{\frac{1}{2}}} \\ \end{aligned} & {{\text{if}}\;j \in {\text{lifetime}},} \\ {{\text{sign}}\left( {\log \left\{ {\cos \left[ {\frac{\pi }{2}\left( {\frac{{1 - \alpha ^{{1 - e^{{ - e^{{\widehat{{z_{j} }}}} }} }} }}{{1 - \alpha }}} \right)} \right]} \right\}} \right) \times \left\{ { - 2\left[ {\log \left\{ {\cos \left[ {\frac{\pi }{2}\left( {\frac{{1 - \alpha ^{{1 - e^{{ - e^{{\widehat{{z_{j} }}}} }} }} }}{{1 - \alpha }}} \right)} \right]} \right\}} \right]} \right\}^{{\frac{1}{2}}} } & {{\text{if}}\;j \in {\text{censored}}.} \\ \end{array} } \right\}$$

Fig. 20

Plot of the deviance residual for the LCAP-W regression model for the LD.

Figure 20 illustrates the deviance residuals compared with the observation index for the dataset. All observations are contained inside the interval $(-3,3)$. We conclude that no observed values show to be outliers. As a result, the fitted model is well suited to this data.

Simulation study for the LCAP-W regression model

We perform simulation studies to examine the performance of the MLE in the LCAP-W regression model for a variety of sample size (n), value of parameter, and censoring percentage values. The lifetimes represented by $w_1,..., w_n$ were obtained from the CAP-W defined in 11, with the reparameterization $\theta =\frac{1}{\sigma }, \eta =e^{-\frac{\mu }{\sigma }}$, and by assuming $\mu _j = \nu _0 + \nu _1 w_j$, where $w_j$ generated from uniform distribution (0, 1). The censoring times $c_1,c_2,..., c_n$ are generated from a uniform distribution $(0,\tau )$, where $\tau$ was changed until $0.1, 0.2, \text {and}~ 0.5$ censoring percentages were obtained. The lifetimes considered for each fit are computed as $y_{j}=\text {min}[\log (w_j),\log (c_j)]$. The simulation was repeated $N=1000$ times with various sample sizes: n = 60, 120, 250, 350, and 500. The values of the parameters were:

• Set I $\nu _{0}=0.70,\nu _{1}=1.09,\sigma =3.20,\alpha =2.70.$

• Set II $\nu _{0}=1.30,\nu _{1}=0.07,\sigma =4.10,\alpha =4.5.$

For every parameter, the estimate and MSE are computed, and the outcomes are shown in Tables 17, 18 and 19. Tables 17, 18 and 19 demonstrate that as sample sizes rise, estimates tend approach the true values of the parameters and the MSE of estimates decreases. The outcomes show that the maximum likelihood approach consistently estimates for the LCAP-W regression model’s parameters.

Table 17 The simulation study for the two sets when censoring percentage equal 0.1.

Table 18 The simulation study for the two sets when censoring percentage equal 0.2.

Table 19 The simulation study for the two sets when censoring percentage equal 0.5.

Conclusions

In this study, we proposed a new technique for creating a new family of distributions with extra flexibility for modeling real-life data in a variety of fields without adding additional parameters. This new technique combines two famous methods: cosine-G and alpha power transformation. The proposed approach is known as the cosine alpha power-G family. To explain the CAP-G family, a specific model called the cosine alpha power-Weibull was created. The density function graphs reveal that the CAP-W distribution is symmetrical, skewed to the right, and decreasing, whereas the hazard rate function indicates increasing, decreasing, upside down bathtub, and J shapes. Various mathematical features of the CAP-W are obtained, including the quantile function, moments, Rényi entropies, and order statistics. The CAP-W parameters are estimated using four methods: MLE, LS, WLS and CVM, and Monte Carlo simulations are used to examine the performance of parameters. The simulation results indicate that the MLE and LS techniques shown superior efficiency and accuracy in estimating parameters. We analyze four real-world data applications and indicate that the CAP-W distribution is the best model against its rivals. Furthermore, We introduced a novel location-scale regression model known as the LCAP-W. We anticipate that the suggested approach and family will have a lot of applications for use in several domains. One of the many guides this study provides for future research is the generation of new distribution families using the proposed approach. Furthermore, the best estimate approach can be examined by estimating the parameters with Bayesian and classical estimation methods.