Introduction

Land resource supply, as a fundamental social and economic endeavor, involves the government allocating land resources to various entities based on specific regulations. This process encompasses two primary facets: land acquisition and land distribution, with the latter exerting a series of influences on the regional economy and society. Of course, land tenure and management systems vary from country to country. In Egypt, the Egyptian government influences land tenure, delivery and supply systems, and land prices through urban land policies (El Araby, 2003). The Israeli government engages in the real estate market by regulating the supply of land resources through land bidding. (Rubin and Felsenstein, 2017). The land resource supply planning system in the UK imposes significant constraints on urban space, directly influencing the escalation and fluctuation of housing prices (Cheshire, 2004). In China, in 2016, the National People’s Congress issued the “Outline of the Thirteenth Five-Year Plan for National Economic and Social Development of the People’s Republic of China.” The document emphasized prioritizing the provision of land resources for major projects outlined in this plan. In mid-December 2016, the Central Economic Work Conference first proposed the concept that ‘housing is for living in, not for speculation.’ This assertion clarified the residential nature of housing, influenced the formulation of land supply policies, and fostered a path toward sustainable development for real estate enterprises (Li et al., 2021). In 2021, the State Council issued the “Notice on Issuing the Tourism Development Plan for the 14th Five-Year Plan”, stipulating that the supply of land resources for tourism public service facilities must be ensured in compliance with the law. The Land Management Law of the People’s Republic of China underwent revisions and enhancements in 1998, 2004, and 2019. This document mandates that governments at all levels organize the formulation of land resource utilization plans in accordance with national economic and social development plans.Footnote 1 Indeed, around 2003, the Chinese government implemented a series of significant measures to regulate the supply of land resources. A notable aspect among them is the spatial distribution of land resource supply. In pursuit of balanced regional development, the nation commenced implementing land resource supply policies that favored the central and western regions. (Liang et al., 2016). There is evidence indicating that after 2003, the proportion of land resource supply in the central and western regions of the country experienced a significant upward trend (Yang et al., 2022). From this perspective, the government engages in macro-control through land control policies to achieve the purpose of rational distribution of land resources in space and time, and thereby promote the development of the national economy and society (Li et al., 2020).

However, the supply of land resources profoundly influences housing prices. Numerous scholars have investigated the intrinsic relationship between land resource supply policies and regional housing prices. It is widely acknowledged that shifts in regional land resource supply have had a substantial impact on fluctuations in regional housing prices. In China, the supply of regional land resources is primarily influenced by macro land control policies (Fan et al., 2021). The issue of high housing prices has gradually become a focal point of social concern, drawing the attention and research of many scholars regarding its impact on innovation (Yu and Cai, 2021). Current research shows that the rapid increase in housing prices leads to higher costs of labor, land, and other factors. Consequently, this triggers an over-concentration of resource factors within the real estate industry, resulting in a crowding-out effect on innovative human resources, R&D investment, and other areas. This phenomenon represents the inhibitory impact of high housing prices on innovation (Miao and Wang, 2014). China has entered a new phase of high-quality development, where innovation, serving as the primary driver, is increasingly becoming the decisive factor propelling such development. The competitive landscape among local governments has shifted from the initial “race for growth” to a focus on “competition for innovation” (He et al., 2018). As outlined in China’s 14th Five-Year Plan, there exists a disparity between China’s innovation capabilities and the requirements for high-quality development. Numerous obstacles hinder the advancement of the innovation-driven development strategy, such as an unfavorable innovation environment, dispersed innovation resources, and insufficient vitality among innovation entities (Niu, Zhang, et al., 2023). So, will the land resource supply policy that favors the central and western regions influence housing prices and innovation (Zhang et al., 2024)? Additionally, is this influence spatially heterogeneous? To answer this question, based on the existing literature (Liang et al., 2016) on the relationship between “land supply and housing prices” (Fan et al., 2021) and “housing prices and innovation” (Yu and Cai, 2021), this paper further integrates the analysis of land resource supply, housing prices, and innovation within the same framework.

The innovative aspects of this paper are as follows: (1) While most studies typically focus solely on either the impact of land supply on housing prices (Yii et al. 2022) or the influence of housing prices on regional innovation (Li et al., 2023), this paper distinguishes itself by constructing a theoretical analysis model and utilizing instrumental variables to integrate land resource supply, housing prices, and innovation within a unified framework (Li and Li, 2024). (2) This paper temporally and spatially presents current land supply, housing prices, and regional innovation, while also measuring and analyzing regional innovation efficiency. (3) Furthermore, this paper conducts a double robustness test by substituting the explained variables and employing the fixed effects model (Li et al., 2022). In conclusion, the research presented in this paper offers insights that can inform the development of government land supply policies worldwide.

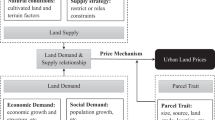
The research framework of this paper unfolds as follows: Initially, a theoretical model is formulated, and corresponding hypotheses are posited. Leveraging the regional land resource supply status as an instrumental variable addresses the endogeneity concern. Subsequently, the dynamics of land supply, housing prices, and regional innovation are examined across both temporal and spatial dimensions. Concurrently, regional innovation efficiency is assessed and analyzed. Finally, TSLS regression is employed to delve into the impact of land resource supply on housing prices and the reciprocal influence of housing prices on innovation efficiency. Additionally, the paper furnishes recommendations and insights for refining national land resource supply policies. The research results of this paper: China’s land resource supply policy, which favors the central and western regions, has exacerbated the surge in housing prices in the eastern region. Consequently, the escalating housing costs are impeding the region’s innovation efficiency. The research framework of this paper is outlined below (Fig. 1).

Fig. 1
figure 1

Research framework diagram.

Full size image

Literature review

Pathways of land resource supply policy impacting housing prices

Currently, many countries or regions are enhancing regional land resource supply preparations through intensified land expropriation (Xu et al., 2022), which constitutes a pivotal aspect of land resource provision (Magliocca et al., 2020). Obviously, unscientific forced land acquisition will result in more negative impacts (Larbi et al., 2004). Of course, land distribution, as the second step in the supply of land resources, has a more significant impact on the economy and society of the entire region (Monk et al., 1996). China’s distinctive foundational land conditions and systems determine that land resource supply policies have a significant impact on the housing market (He, 2022). The land resource supply policy encompasses various aspects, including land supply quantity, structure, method, and pricing. Among these, there exists ample research on the impacts of land supply quantity (Huang et al., 2015). The impact of land supply quantity on housing prices can be summarized into four pathways. The first is the production function channel, which influences the quantity of housing supply through the amount of land supplied, thereby affecting housing prices (Tian and Ma, 2009). In general, an increase in land supply can effectively facilitate real estate destocking, although disparities exist between land supply and housing stock across various regions or periods (Shen et al., 2018). The second is the anticipatory channel. The modification of land resource supply policy impacts the supply and demand dynamics of the housing market by influencing market participants’ expectations for future real estate trends, ultimately influencing housing prices (Hu and Qian, 2017). The third aspect is supply scale. Disparities in supply scale will impact housing prices by influencing the elasticity of housing supply (El Araby, 2003). The fourth factor is the structure of land resource supply. Various land supply structures yield distinct effects on housing prices. Owing to historical and geographical factors, notable differences exist in the impact of government’s existing land planning policies on housing prices (Meen and Nygaard, 2011). For instance, the advancement of high-speed railways directly catalyzes shifts in land use structure, subsequently exerting varying impacts on housing prices across different regions (Chen et al., 2021). Land use planning varies significantly among different countries. The United Kingdom, for example, grapples with considerable uncertainty in land planning, coupled with a lack of control in the housing land market, resulting in heightened speculative risk-taking. House prices in France are subject to tighter controls, with speculation being more limited. Sweden, on the other hand, is utilizing its land resource reserves to mitigate the increase in housing prices (Barlow, 1993).

Researching the link between land resource supply and housing prices

In the case of China, since around 2003, the Chinese government has essentially regulated the supply of urban residential land. This has led to a decrease in residential land supply and supply elasticity, consequently placing downward pressure on new housing availability (Yan et al., 2014). Based on the average land prices of residential, industrial, and commercial plots, they were respectively 57%, 24%, and 41% higher in 2012 compared to 2007 (Qin et al., 2016). It’s evident from this that in recent decades, escalating housing prices have gained widespread acknowledgment. The majority of scholars hold the view that augmenting the supply of land resources can effectively curb the surge in housing prices. Particularly, China has adopted a policy addressing the spatial and structural mismatch in land resource supply. Specifically, the supply of land resources increases in the central and western regions, while decreasing in the eastern region. This imbalance causes land prices in the eastern region to rise (Grimes and Aitken, 2010), subsequently leading to a rapid increase in housing prices (Fan et al., 2021). Correspondingly, as housing prices rise, wages in the area also rise (Liang et al., 2016). Furthermore, local governments can assume a more significant role in land supply. By increasing the supply of residential land, they can mitigate housing prices, and employ dynamic procyclical land resource supply policies to dampen macroeconomic fluctuations (He, 2023). For this reason, some scholars suggest that policymakers should prioritize increasing the supply of land to mitigate the rise in housing prices (Yii et al., 2022). On the contrary, some scholars hold differing views, suggesting that the influence of land supply on housing prices is minimal or that there is no direct causal relationship between land resource availability and housing price fluctuations (Tse, 1998). Research conducted by scholars on Melbourne’s urban growth boundary has found no conclusive evidence indicating that the escalation in land prices is solely attributable to land resource supply policies (Buxton and Taylor, 2011). Likewise, certain scholars posit a positive correlation between land supply and housing prices, particularly evident in regions characterized by higher housing costs (Wang et al., 2023).

Exploring the relationship between housing prices and regional innovation

In academic discourse, there’s a prevailing notion that the escalation of housing prices tends to stifle the advancement of regional innovation. Mechanistically, this inhibition of regional innovation stems from three primary channels. The first factor involves the crowding-out effect of rising housing prices on innovative funding. The second pertains to the crowding-out effect of rising housing prices on innovative talent. Lastly, there’s the blocking effect of rising housing prices on the spirit of innovation, entrepreneurship, and vitality. Naturally, the influence of housing prices on innovation varies over time. Generally, housing prices exhibit a U-shaped relationship with innovation. Beyond a certain point, the continued increase in housing prices diminishes regional innovative vigor. This study primarily focuses on the national context of China, where it is evident that in many regions, housing prices have surpassed this critical juncture (Yu and Cai, 2021), thereby stifling regional innovation.

Crowding-out effect: investigating the impact of rising housing prices on innovative funding

When it comes to innovation funding, particularly for enterprises engaged in any form of innovation activities, sustained long-term investment from their internal financing channels is crucial for maintenance (Brown et al., 2012). Hence, the rapid surge in housing prices has spurred greater investment in real estate. This inevitably entails a notable crowding-out impact on the long-term investment funds essential for enterprises to pursue innovative R&D activities, consequently discouraging further innovation efforts. While there’s no direct evidence linking housing prices to the high savings rate of Chinese households, it’s undeniable that a high savings rate translates to reduced investment in innovation (Wang and Wen, 2012). Drawing from theoretical models, scholars have further substantiated the crowding-out impact of rapid growth in real estate investment on long-term investment in other sectors (Bleck and Liu, 2018). In first-tier urban agglomerations, housing prices exert significant spillover effects on urban innovation, influencing the innovative spirit of surrounding cities as well (Wang and Hu, 2023). The adverse effects of high housing prices on regional innovation manifest across various aspects including innovation input, output, and the transformation of innovation achievements (Li et al., 2023).

Crowding out effect: examining how rising housing prices impact innovative talent

In terms of the impact on innovative talents, as China’s housing prices continue to rise, entrepreneurial activities among urban adults are generally hindered (Li and Wu, 2014). Excessively high housing prices draw funds into the real estate market, thereby constraining residents’ consumption levels and impeding the entry of innovative talent to some extent (Ding et al., 2023). Hence, in the current urban development context, it is crucial to prioritize examining how housing costs influence the employment and residential choices of talents (Ling et al., 2023). Of course, the impact of rising housing prices on talent attraction should be considered at different stages. In the initial phase of urban housing price increases, there is indeed a certain level of attraction for talent. However, in recent years, the escalation of housing prices has transformed into a bubble. During this period, high housing prices exert a significant crowding-out effect on innovative talent and talent attraction (Lin et al., 2021).

Blocking effects: researching how rising housing prices impact innovation and entrepreneurship

In regard to the impact on the vitality of entrepreneurial spirit, when housing prices surpass a certain threshold, it inevitably hampers the innovative endeavors of businesses, particularly those with limited enthusiasm for innovation (Chu et al., 2023). According to labor force dynamics data, scholars have demonstrated that exorbitant housing prices have a substantial adverse effect on the inclination of urban individuals to pursue demand-driven entrepreneurship (Hu and Qian, 2022). Elevated housing prices significantly impede innovation within manufacturing companies. As housing prices appreciate, companies divert funds toward real estate investments, thereby diminishing their innovation drive (Rong et al., 2016). In pursuit of this goal, scholars have suggested that decreasing housing price fluctuations and increasing liquidity in the real estate market can encourage families to embrace entrepreneurial pursuits (Oh et al., 2021). Conversely, other scholars have put forth differing perspectives on this matter. They argue that there exists a positive correlation between regional innovation quality and housing price appreciation. Specifically, the enhancement of innovation quality can stimulate housing price escalation (Beracha et al., 2022). Some studies have also indicated that housing prices can bolster the innovation and entrepreneurial vitality of both local cities and their neighboring counterparts (Fan et al., 2023). From this observation, it’s evident that the impact of increasing housing prices on regional innovation varies significantly across different periods (Hu et al. 2019). Certainly, the rise in housing prices will also yield other ancillary effects (Fang and Lv, 2023), such as enhancing the quality of green innovation within enterprises (Yan et al., 2024). Nonetheless, the current surge in housing prices across China has outpaced both public and business expectations, potentially exerting a detrimental effect on regional innovation. Consequently, it is imperative for the government to prioritize the impact of housing macro-prudential policies (Chen et al., 2023).

A review of the existing literature reveals that although academic research findings on land resource supply, housing prices, and innovation are relatively abundant. However, most of the literature primarily delves into the relationship between two of these factors, with few studies examining the interplay among all three. In light of this gap, this paper endeavors to integrate land resource supply, housing prices, and innovation within a unified analytical framework, drawing upon existing research findings. It seeks to investigate how land supply influences housing prices and subsequently impacts innovation. Employing panel data comprising 31 provinces and regions in China, this paper empirically examines the relationship between land resource supply, housing prices, and innovation. Specifically, it focuses on analyzing whether biases in land resource supply policies exert a spatially heterogeneous impact on both regional housing prices and innovation efficiency in China.

Research design

Theoretical model construction and hypothesis proposing

Before delving into empirical analysis, this paper references the paradigms of Helpman (Helpman, 1995) and Ottaviano (Ottaviano et al., 2011) to explore spatial agglomeration efficiency within the framework of the new economic geography model. Simultaneously, Krugman’s new economic geography theory holds significant reference value (Krugman, 1991). Building upon these paradigms and theories, this paper examines how land resource supply policies across various regions influence housing prices, thereby impacting innovation.

Assume that the central and western region a and the eastern region b (Table 1), the labor force in the two regions can flow freely. Consumers optimize their utility by efficiently allocating their income towards the consumption of both tradable industrial products and non-tradable housing. The consumer utility function for region \(q(q=a,b)\) is then:

$$\begin{array}{c}{U}_{\!q}={C}_{{qm}}^{\mu }{C}_{{qh}}^{1-\mu }\\ s.t.\,{P}_{{\!qm}}{C}_{{qm}}+{P}_{{\!qh}}{C}_{{qh}}={W}_{\!q}\end{array}$$
(1)
Table 1 Model variable explanation.
Full size table

In formula (1), \({C}_{{qm}}\) and \({C}_{{qh}}\) respectively represent the quantity of industrial products and the quantity of housing consumed by consumers in region q. \({P}_{{qm}}\) and \({P}_{{qh}}\) denote the prices of industrial products and housing, respectively. \({W}_{q}\) represents the income of consumers in region q. μ denotes the proportion of consumer expenditure allocated to industrial product consumption, 0 < μ < 1.

After optimization, the consumer’s indirect utility function can be derived:

$${V}_{\!q}={\mu }^{\mu }{\left(1-\mu \right)}^{\left(1-\mu \right)}{W}_{\!q}/{P}_{{qm}}^{\mu }{P}_{{qh}}^{1-\mu }$$
(2)

Take the logarithm of Eq. (2) and perform monotonic transformation to obtain:

$${v}_{q}={w}_{q}-\theta {p}_{{qh}}$$
(3)

In formula (3), \({v}_{q}\) represents the monotonic transformation of the indirect utility function \({V}_{q}\) after taking the logarithm. \({w}_{q}\) signifies the logarithmic income. \(\theta =1-\mu\) denotes the share of housing consumption in consumption expenditure, and \({p}_{{qh}}\) stands for the logarithmic housing price. This paper normalizes the price of tradable industrial goods to 1 and does not consider the investment function of housing. Therefore, house prices are relative to tradable industrial goods.

To begin with, to analyze the distribution of labor across various regions, we adopt Moretti & Perloff’s methodology and incorporate labor’s individual preferences for regions (Moretti and Perloff, 2002), denoted as \({e}_{{qj}}\), using Eq. (3) as a basis.

$${v}_{q}={w}_{q}-\theta {p}_{{qh}}+{e}_{{qj}}$$
(4)

In Eq. (4), \({e}_{{qj}}\) represents labor force j's personal preference for region q, \({e}_{{qj}} \sim U\left(-r,r\right)\). The greater the value of r, the more significant personal preference becomes in the choice of residence.

Given the free flow of labor, equilibrium dictates that utility levels attained in different regions are equal, implying \({v}_{a}={v}_{b}\), as derived from Eq. (4).

$${e}_{{aj}}-{e}_{{bj}}={(w}_{b}-\theta {p}_{{bh}})-({w}_{a}-\theta {p}_{{ah}})$$
(5)

Furthermore, it can be observed that the distribution of labor force population in regions a and b at equilibrium is.

$$\frac{{l}_{a}}{l}=\frac{r-\left[{(w}_{b}-\theta {p}_{{bh}})-({w}_{a}-\theta {p}_{{ah}})\right]}{2r}$$
(6)
$$\frac{{l}_{b}}{l}=\frac{r+\left[{(w}_{b}-\theta {p}_{{bh}})-({w}_{a}-\theta {p}_{{ah}})\right]}{2r}$$
(7)

In the above formulas (6) and (7), \({l}_{q}\) represents the logarithm of the labor force population in area \(q(q=a,b)\), \(l={l}_{a}+{l}_{b}\).

Secondly, from the perspective of producers, following Kline & Moretti (Kline and Moretti, 2014) analysis based on the constant returns to scale production function model. Under the assumption of unrestricted capital mobility, when solving the first-order conditions to maximize corporate profits, the ensuing relationship can be derived.

$${l}_{q}=-\frac{{w}_{q}\left(1-\beta \right)}{1-\alpha -\beta }+C$$
(8)

In formula (8), α represents the elastic coefficient of labor output, β denotes the elastic coefficient of capital output, where \(\alpha +\beta < 1\), and C is a constant.

Thirdly, from the perspective of the housing market, if each labor force consumes 1 unit of housing, and \({\rho }_{q}\) represents the housing supply elasticity of region q (Saiz, 2010), then the following relationship holds.

$${l}_{q}={p}_{{qh}}/{\rho }_{q}$$
(9)

Among these, the larger \({\rho }_{q}\) is, the smaller the housing supply elasticity is.

Combining Eqs. (6) to (9), the following equilibrium solution can be obtained:

$${p}_{{qh}}={\rho }_{q}\left(1-\frac{{\varphi }_{q}}{{\varphi }_{b}+{\varphi }_{a}}\right)l$$
(10)

In Eq. (10), \({\varphi }_{q}=l\theta {\rho }_{q}\left(1-\beta \right)+l\left(1-\alpha -\beta \right)+r(1-\beta )\).

In order to analyze the impact of biased land supply policies on housing prices in the eastern, central, and western regions, Eq. (10) is further employed to derive \({\rho }_{b}\), yielding the following results:

$$\frac{\partial {p}_{{bh}}}{\partial {\rho }_{b}}=\frac{{\varphi }_{a}}{{\left. ({\varphi }_{b}+{\varphi }_{a}\right)}^{2}}l[{\varphi }_{a}+l\left(1-\alpha -\beta \right)+{\rm{r}}\left(1-{\rm{\beta }}\right)] > 0$$
(11)
$$\frac{\partial {p}_{{ah}}}{\partial {\rho }_{b}}=\frac{{\varphi }_{a}}{{\left. ({\varphi }_{b}+{\varphi }_{a}\right)}^{2}}{\rho }_{a}\theta {l}^{2}(1-\beta ) > 0$$
(12)
$$\begin{array}{ll}\displaystyle\frac{\partial {p}_{{bh}}}{\partial {\rho }_{b}}-\frac{\partial {p}_{{ah}}}{\partial {\rho }_{b}}=\frac{{\varphi }_{a}}{{\left({\varphi }_{b}+{\varphi }_{a}\right)}^{2}}l\left[2l\left(1-\alpha -\beta \right)+2r\left(1-\beta \right)\right]\\ > 0\end{array}$$
(13)

From Eqs. (11) to (13), it’s evident that the land resource supply policy favoring the central and western regions results in a decrease in the elasticity of housing supply in the eastern region (\({\rho }_{b}\) becomes larger) (Fan et al., 2021). On the one hand, the house price \({p}_{{bh}}\) in the eastern region and the house price \({p}_{{ah}}\) in the central and western regions both rise with the increase of \({\rho }_{b}\). On the other hand, it also accelerates the increase in housing prices, \({p}_{{bh}}\), in the eastern region compared to housing prices, \({p}_{{ah}}\), in the central and western regions. Based on this, the research hypothesis 1 of this paper is put forward:

Research Hypothesis 1: The land resource supply policy favoring the central-western regions has caused housing prices to rise in both the eastern and central and western regions, with the eastern region experiencing a faster rate of increase compared to the central-western regions.

From the preceding mechanism analysis, it’s evident that increasing housing prices will impede regional innovation through three channels: the crowding out effect of innovation funds, the crowding out effect of innovative talents, and the blocking effect of innovation and entrepreneurship spirit and vitality. Building on this, the research hypothesis 2 of this paper is formulated, based on the research hypothesis 1:

Research Hypothesis 2: Faster housing price growth in the eastern region will lead to a stronger inhibitory effect on innovation than in the central and western regions.

Regional innovation efficiency measurement model setting

Based on the Stochastic Frontier Analysis (SFA) model of Battese & Coelli (Battese and Coelli, 1995). Primarily, this model serves as a tool for assessing the efficiency of the production process (Sartori et al., 2024). It proficiently estimates the technical efficiency, as well as the influence of random errors that may arise during the production process (Danelon and Kumbhakar, 2023). Therefore, this paper opts for the Stochastic Frontier Analysis model (Zhan et al., 2022), which surpasses the traditional logarithmic production function form, to accurately assess regional innovation efficiency. The specific model settings are as follows:

$$\begin{array}{ll}{\mathrm{ln}}\,{{In}{n}_{{product}}}_{{it}}={\mathrm{ln}}\,f\left({x}_{{it}},t\right)+{v}_{{it}}-{u}_{{it}}={\beta }_{0}+{\beta}_{1}{\mathrm{ln}}\,{{Inn}{{\_}}{labor}}_{{it}}\\ \qquad\qquad\qquad\qquad+\,{\beta }_{2}{\mathrm{ln}}{Inn}{{\_}}{{capital}}_{{it}}+{\beta }_{3}{\mathrm{ln}}^{2}{{In}{n}_{{labor}}}_{{it}}+{\beta }_{4}{\mathrm{ln}}^{2}{In}{n}_{{{capital}}_{{it}}}\\\qquad\qquad\qquad\qquad +\,{\beta }_{5}{\mathrm{ln}}^{2}{{Inn}{{\_}}{labor}}_{{it}}{Inn}{{\_}}{{capital}}_{{it}}+{v}_{{it}}-{\mu }_{{it}}\end{array}$$
(14)

In the above equation, i and t respectively represent provincial regions and years. \({Inn\_product}\) represents actual innovation output. f() represents frontier innovation output. \({x}_{{it}}\) denotes the set of variables influencing regional innovation output, including innovative labor input \({Inn\_labor}\) and innovative capital input \({Inn\_capital}\). \({v}_{{it}}-{\mu }_{{it}}\) represents the composite error term. Among them, the random error term \({v}_{{it}}\) obeys \(N(0,{\sigma }_{v}^{2})\) and is independent of the technical inefficiency term \({\mu }_{{it}}\). \({\mu }_{{it}}\) obeys \({N}^{+}(\mu ,{\sigma }_{v}^{2})\). \({\mu }_{{it}}={\mu }_{i}\exp \left[-\eta (t-T)\right]\), η represents the time-varying parameter.

Regional innovation efficiency is defined as the ratio of actual innovation output to frontier innovation output, expressed as:

$${In}{n}_{{{efficiency}}_{{it}}}=\frac{E\left[f\left({x}_{{it}},t\right)\exp \left({v}_{{it}}-{\mu }_{{it}}\right)\right]}{E\left[f\left({x}_{{it}},t\right)\exp \left({v}_{{it}}\right)\right]}=\exp (-{\mu }_{{it}})$$
(15)

The range of values for \({Inn\_}{{efficiency}}_{{it}}\) is [0, 1]. If \({Inn\_}{{efficiency}}_{{it}}=1\), it indicates full technological effectiveness. If \({Inn\_}{{efficiency}}_{{it}} < 1\), it suggests technological inefficiency.

Basic econometric model settings

The empirical model in this paper primarily examines how the elasticity of land supply, influenced by biased land resource supply policies, impacts housing prices and consequently influences innovation. The fundamental econometric model here is the equation depicting the influence of housing prices on innovation:

$${In}{n}_{{{efficiency}}_{{it}}}={\alpha }_{0}+{\alpha }_{1}{{Ho}{u}_{{price}}}_{{it}}+{\alpha }_{2}{Z}_{{it}-1}+{\delta }_{i}+{\omega }_{t}+{\varepsilon }_{{it}}$$
(16)

In this equation, i and t respectively represent provincial regions and years. \(I{nn}{\_efficiency}\) is the dependent variable measuring regional innovation efficiency. The core explanatory variable \({Hou\_price}\) represents housing prices across provincial regions. Z denotes the control variable. \({\delta }_{i}\) and \({\omega }_{t}\) respectively stand for dummy variables representing provincial regions and year fixed effects. \({\alpha }_{0}\), \({\alpha }_{1}\), and \({\alpha }_{2}\) are the parameters to be estimated, and ε represents the random error term. To clarify the representation of variables in the models discussed in the preceding three sections, Table 1 is utilized to explain these variables.

Endogeneity and instrumental variables

There may be specific endogeneity issues between housing prices and innovation within a region. Primarily, there is an endogeneity problem caused by the connection between housing prices and innovation. The higher the level of innovation in a region, the stronger its ability to sustain economic development. The demand for real estate increases due to the expansion effect of enterprise production and rising residents’ income, thereby driving up housing prices. (Beracha et al., 2022). Secondly, the influence of housing prices on innovation also faces endogeneity challenges due to omitted variables (Hu et al., 2019). For instance, each province and region will implement a range of distinct innovation encouragement policies tailored to their specific resource endowments and economic development stages. These policies not only influence innovation endeavors but may also impact the investment choices of local residents and businesses, consequently affecting local housing prices. In addressing the issue of omitted variables, this paper has made efforts to control for a range of provincial-level characteristic variables associated with the level of innovation and for which information is accessible. However, theoretically, there may still be omitted variables that cannot be effectively controlled for.

A viable approach to address the aforementioned endogeneity issue is through the instrumental variable method, which involves identifying a suitable instrumental variable for housing prices (Han and Kung, 2015). Prior studies have extensively explored potential instrumental variables for housing prices, with regional land supply status being among the most commonly utilized (He, 2022). Following the fundamental principle of the instrumental variable method, it’s imperative to identify an exogenous variable that affects the endogenous variable (house price) but does not directly affect the explained variable (innovation) as the corresponding instrumental variable (Shen et al., 2024). This paper opts for the state-owned construction land transfer area variable from the previous year in each province and region as the instrumental variable for housing prices.

The rationale for variable selection is as follows: (1) Regional land resource supply conditions have a direct impact on housing prices. Existing research suggests four primary pathways through which land supply influences housing prices. The first pathway is through its effect on the quantity of housing supply via the quantity of land resource supply, subsequently impacting housing prices (Tian and Ma, 2009). The second pathway is that modifications to land resource supply policies will influence market entities’ expectations of future housing prices, consequently impacting the supply and demand dynamics of the real estate market (He, 2023). The third pathway involves variations in the scale of land resource supply, which alter the elasticity of housing supply, consequently impacting housing prices (El Araby, 2003). The fourth pathway suggests that varying structures of land resource supply result in different impacts on housing prices (Barlow, 1993). (2) Regional land supply conditions solely impact housing prices without directly affecting innovation. China enforces a rigorous land use control system and farmland protection regulations under public land ownership. Consequently, land supply in a region is tightly regulated by both the central and provincial governments. In 1999, the Ministry of Land and Resources of China introduced the “Annual Land Use Plan Management Measures,” subsequently revised in 2004, 2006, and 2016. These regulations stipulate that the Ministry of Natural Resources will draft a national land use annual plan based on two recommendations. On one hand, there are proposals for overall control indicators in the national annual land use plan. On the other hand, provinces, autonomous regions, and municipalities directly under the Central Government put forward planning indicator suggestions. Following deliberation and approval by the State Council and the National People’s Congress, the draft national economic and social development plan becomes officially implemented. Within this institutional framework, the land supply status of each province and region must align with the annual land use plan. Primarily determined by the central government, the annual land use plan ensures that the land resource supply situation in each province solely influences housing prices and does not directly impact innovation. (3) Utilizing the state-owned construction land transfer area variable from the previous year can mitigate the potential channel mechanism by which changes in housing prices impact the state-owned construction land transfer area.

Variable selection

Explained variables

Regional innovation efficiency (\({Inn\_efficiency}\)) is calculated using stochastic frontier analysis, as parameters \({\sigma }^{2}\) and γ are significantly positive, and the one-sided LR test values have also passed significant testing. This demonstrates the appropriateness of the stochastic frontier model. Innovation output \(({Inn\_product}\)): is quantified by the number of invention patent authorizations. Innovation investment encompasses innovation labor input (\({Inn\_labor}\)) and innovation capital investment (\({Inn\_capital}\)). Specifically, innovation labor input is gauged by the full-time equivalent of R&D personnel, and innovation capital investment is measured by internal expenditure of R&D funds.

Explanatory variable

House price (\({Hou\_price}\)) is determined by the average sales price of commercial housing in each province and region.

Instrumental variable

Land supply (\({Land\_supply}\)) is quantified by the state-owned construction land transfer area in each province and region from the preceding year.

Control variables

①The level of regional economic development is gauged by GDP per capita (\({Per\_gdp}\)). ②Human capital level (\({Hum\_capital}\)) is assessed by the density of universities in each province and region. ③Industrial structure level (\({Ind}{\_structure}\)) is determined by the ratio of the output value of the secondary industry and the output value of the tertiary industry in each province and region. ④The degree of openness to the outside world is measured by the import volume (\({Imp\_}{volume}\)) and export volume (\(Ex{p\_}{volume}\)) of each province and region. ⑤Tax level is evaluated based on the tax revenue (\({Tax\_revenue}\)) of each province and region.

Moreover, recognizing the potential reverse causality of specific control factors in the econometric equation on innovation, this study employs lagged control variables to mitigate it. Acknowledging that the correlation between housing prices and innovation could be influenced by unobservable factors, this paper incorporates dummy variables for province, region, and year fixed effects in the econometric equation.

Data sources and spatial analysis

Owing to data availability constraints, this study compiles panel data from 31 provinces and regions across the nation (excluding Hong Kong, Macao, and Taiwan) spanning a 16-year period from 2003 to 2018. These 31 provinces and regions are categorized into two primary regions: the eastern and western regions (Table 2). The regional classification follows the delineation established in the “Seventh Five-Year Plan” ratified by the Fourth Session of the Sixth National People’s Congress in 1986. Broadly speaking, the eastern region comprises coastal areas with relatively advanced economic development, while the central and western regions encompass inland territories with comparatively lower economic development levels.

Table 2 Division of provinces and cities in the east and west regions.
Full size table

Among these, data on the number of invention patents granted, full-time equivalent of R&D personnel, and internal expenditure on R&D funds are sourced from the “China Science and Technology Statistical Yearbook” over the years. The average sales price data of commercial housing is sourced from the “China Real Estate Statistical Yearbook” over the years. Data on the transfer area of state-owned construction land is obtained from the “China Land and Resources Yearbook” over the years. The remaining data is derived from the “China Statistical Yearbook”, the statistical yearbooks of various provinces and regions, and the National Economic and Social Development Statistical Bulletin over the years. The descriptive statistics of relevant variables are presented below (Table 3).

Table 3 Descriptive statistics of variables.
Full size table

After completing the descriptive statistics of the variables, to illustrate the strength and direction of the linear relationship between different variables, this paper generated a Pearson correlation coefficient matrix for the relevant variables (Fig. 2). Specifically, the value of the correlation coefficient ranges between −1 and 1, where 0 indicating no linear relationship, 1 indicating a perfect positive correlation, and −1 indicating a perfect negative correlation. The correlation coefficient between land supply and housing prices is −0.0527, indicating a negative correlation. This suggests that a decrease in land supply has resulted in an uptick in housing prices. This observation underscores the skewness of the land supply policy toward the western region, diminishing land availability in the eastern region and consequently impacting housing prices there.

Fig. 2
figure 2

Pearson correlation coefficient matrix plot.

Full size image

To distinctly illustrate the spatial and temporal distribution characteristics of land supply, housing prices, and innovation, this paper focuses on three variables for analysis: construction land transfer area, average sales price of commercial housing, and the comprehensive utility value of regional innovation capabilities. Additionally, the comparison years are set as 2003, 2008, 2013, and 2018. Specifically, Beijing and Shanghai are selected from the eastern region, while Hubei and Chongqing represent the central and western regions.

Judging from the area of construction land transfer in China (Fig. 3). It’s evident that around 2013, the government boosted land supply to central and western provinces. The quantity of land supplied in these regions notably exceeds that in the eastern provinces, indicating a clear bias in China’s land supply policy.

Fig. 3
figure 3

Regional distribution of construction land transfer area in China.

Full size image

Based on the average sales price of commercial housing in China (Fig. 4), it’s apparent that housing prices in the eastern, central, and western regions are generally on the rise. However, due to the implementation of biased land supply policies, prices in the eastern region have experienced a faster increase compared to the slower rise observed in central and western provinces.

Fig. 4
figure 4

Regional distribution of average sales price of commercial housing in China.

Full size image

Analyzing the data on the comprehensive utility values of China’s regional innovation capabilities (Fig. 5), it is evident that the regional innovation capabilities of most provinces in the eastern region are experiencing a downward trend. Conversely, the regional innovation capabilities of most provinces in the central and western regions have shown a slight increase. This trend can be attributed to the land supply policy favoring the central and western regions, which has, to some extent, impeded the regional innovation capabilities of the eastern region. To better verify the relationship between land supply, housing prices, and regional innovation, further discussion and verification will be provided below.

Fig. 5
figure 5

Distribution of comprehensive utility value of China’s regional innovation capabilities.

Full size image

Analysis of empirical results

Analysis of regional innovation efficiency measurement results

This paper utilizes Frontier4.1 to estimate the parameters of the Stochastic Frontier Analysis model of innovation efficiency in each province and region (Table 4). The parameters \({\sigma }^{2}\) and γ are both significantly positive, and the one-sided LR test value also passed the significance test. These results indicate the suitability of employing the Stochastic Frontier Analysis method to gauge China’s regional innovation efficiency. Through further calculation, the value of generalized likelihood statistic \({L}_{R}=-2\left\{\mathrm{ln}\left[L({H}_{0})/L({H}_{1})\right]\right\}\) is 35.3615, passing the 1% significance level test. This indicates excellent fit between the model and the data, affirming that the Translog stochastic frontier model is suitable and exhibits strong adequacy for interpreting the studied data.

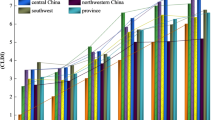
Table 4 The estimation results of SFA model.
Full size table

After estimating the parameters of the Stochastic Frontier Analysis model for innovation efficiency in each province and region, the innovation efficiency across the eastern, central, and western regions, as well as nationally, was calculated for different years (Fig. 6).

Fig. 6
figure 6

Evolution process of regional innovation efficiency in China.

Full size image

From a national level, regional innovation efficiency shows an upward trend year by year, but the overall level is still low. From a regional perspective, both the eastern and central and western regions show an upward trend year by year, but the pronounced regional imbalance remains evident. The innovation efficiency of the eastern region holds an absolute advantage over the central and western regions, with the gap likely to widen further. The eastern region benefits from clear geographical advantages, a greater concentration of innovation factors, and a superior innovation and entrepreneurship environment. These factors likely contribute significantly to the spatial heterogeneity observed in regional innovation efficiency.

Benchmark regression results analysis

TSLS regression first stage results

In the initial stage results of the Two-Stage Least Squares (TSLS) regression, column 1 illustrates the regression outcomes utilizing panel data from 31 provinces and regions nationwide. Columns 2 and 3 depict the regression outcomes utilizing panel data from 9 provinces and regions in the east, and 22 provinces and regions in the central and western areas, respectively (Table 5). In the instrumental variable estimation process of TSLS, the F values estimated in the first stage are 772.74, 391.20 and 320.00 respectively. All exceed the critical value of 16.38 for the F value at the 10% bias level as considered by Stock & Yogo (Stock and Yogo, 2002), affirming the appropriateness of the instrumental variables set in this paper. This robust fit enhances the reliability of our subsequent analyses regarding the impact of regional land resource supply on housing prices. Hence, there is no weak instrumental variable problem, affirming the appropriateness of the instrumental variables set in this paper.

Table 5 House prices and innovation: first-stage regression results of instrumental variables.
Full size table

Analyzing the impact of regional land resource supply on housing prices, the regression results in column 1 reveal that various relevant influencing factors are controlled at the national level. The transfer area of state-owned construction land in the previous year exhibits a notably negative effect on current housing prices, with an impact coefficient of −0.1300. In particular, smaller areas of state-owned construction land transferred in the previous year correlate with higher current housing prices. This finding suggests that the nationwide bias in land supply toward the central and western regions has exerted a certain negative impact on housing prices while also contributing to their escalation. To delve deeper into the spatial heterogeneity of the influence of land resource supply on housing prices, the regression outcomes in columns 2 and 3 are presented. The transfer area of state-owned construction land in both the eastern and central-western regions during the previous year also exhibits a notable negative effect on current housing prices. Moreover, the coefficient of influence in the eastern region (−0.1476) is lower than that in the central-western regions (−0.0792). This indicates that the bias in land supply toward the central and western regions adversely impacts housing prices not only in those areas but also in the eastern region. Furthermore, the adverse effect on housing prices in the eastern region surpasses that in the central and western regions, resulting in a swifter rise in housing prices in the eastern region compared to the central and western regions. These empirical findings substantiate the first research hypothesis of this paper: The land resource supply policy favoring the central-western regions has caused housing prices to rise in both the eastern and central and western regions, with the eastern region experiencing a faster rate of increase compared to the central-western regions.

TSLS regression second stage results

In the second-stage findings of the TSLS regression, the analysis delves into the influence of housing prices on innovation efficiency (Table 6). The regression outcomes in column 1 reveal that a range of pertinent influencing factors are controlled at the national level. The effect of housing prices on innovation efficiency is notably negative, evidenced by a coefficient of −0.0757. The negative coefficients estimated for housing prices on innovation efficiency across all regions underscore a consistent trend nationwide. This robust pattern is indicative of a strong fit of the model to the data, suggesting that the selected instrumental variables effectively capture the variation in housing prices and innovation efficiency. This underscores that across the nation, the swift escalation of housing prices has significantly impeded the enhancement of innovation levels.

Table 6 Housing prices and innovation: the results of the second stage regression of instrumental variables.
Full size table

Further, investigate the spatial heterogeneity in how housing prices influence innovation. The regression outcomes in columns 2 and 3 reveal that, even after accounting for various influencing factors, the effect of housing prices on innovation efficiency remains notably negative across the eastern, central, and western regions. The regression coefficient in the eastern region is −0.0924, smaller than the coefficient in the central and western regions, which is −0.0160. This indicates that the considerable increase in housing prices across the eastern, central, and western regions has notably hindered the enhancement of regional innovation efficiency, with the inhibitory effect being more pronounced in the eastern region compared to the central and western regions. The inhibitory impact of housing prices on innovation efficiency is predominantly fueled by the eastern region, characterized by constrained land supply and rapid housing price escalation. The empirical test results above substantiate the second research hypothesis of this paper: Faster housing price growth in the eastern region will lead to a stronger inhibitory effect on innovation than in the central and western regions.

Robustness test with replacement of the explained variable

To ensure the reliability of the above research conclusions, this paper employs a robustness test method by substituting the explained variables (Zhan et al., 2022). This approach offers a more lucid comprehension of how various variables influence outcomes, facilitating a more precise assessment of both the direction and magnitude of causal relationships (Xie et al., 2023). Utilize data from the “China Regional Innovation and Entrepreneurship Index,” as released by the Peking University Open Research Data Platform, to reconstruct the measurement index for regional innovation efficiencyFootnote 2 (Table 7).

Table 7 Housing prices and innovation: the results of the second stage regression of instrumental variables after replacing the explained variables.
Full size table

Derived from the second-stage results of Two-Stage Least Squares (TSLS) regression following the substitution of explained variables, the robustness test conducted by substituting the explained variables offers additional insight into the reliability of our findings. Despite the replacement of the explained variables, the consistently negative coefficients estimated for housing prices on innovation efficiency across all regions suggest a robust fit of the model to the data. This indicates that the observed inhibitory effect of housing prices on innovation remains stable and significant even under alternative specifications of the regression model. Thus, the strong alignment between the benchmark regression outcomes and the results of the robustness test underscores the reliability and robustness of our conclusions. The coefficients are −0.2622, −0.3290 and −0.2563, respectively. The inhibitory effect of housing prices on innovation efficiency in the eastern region is stronger than that in the central and western regions. It is evident that the primary source of the inhibitory effect of housing prices on innovation stems from the eastern region, characterized by tighter land supply and faster rising housing prices. The robustness test results above align entirely with the benchmark regression outcomes, affirming the reliability of the benchmark regression results.

Fixed effects model robustness test

After conducting parameter estimation using the Stochastic Frontier Analysis model and analyzing benchmark regression results for regional innovation efficiency, this paper will proceed to further analyze the fixed effects model. The introduction of the fixed effects model will provide a more comprehensive understanding of the impact of relevant factors on regional innovation efficiency and further validate the robustness of the previous conclusions. The 31 provinces are categorized into two regions: the eastern region and the central and western regions. The fixed effects model incorporates province fixed effects to account for the heterogeneity among different provinces (Fig. 7).

Fig. 7
figure 7

Fixed effects model results.

Full size image

It’s evident that the coefficient of house price (\({Hou\_price}\)) is −0.0002424, displaying statistical significanc (P < 0.05), suggesting that regional innovation efficiency slightly decreases with rising house prices. This implies that high housing prices might exert a certain negative influence on regional innovation efficiency. The rationale behind this is that elevated housing prices translate to heightened housing expenses, consequently raising costs for companies in terms of recruitment and employee welfare. Furthermore, high housing prices hinder population mobility, making it challenging for skilled individuals to relocate to regions with vibrant innovation scenes, thereby diminishing innovation efficiency in those areas. The coefficient for land supply (\({Land\_supply}\)) is 0.0000707, despite having weak statistical significance (P = 0.048), it indicates that land resource supply has a positive impact on regional innovation efficiency. This stems from the fact that an expansion in land resource supply can stimulate enterprise production and investment, consequently enhancing innovation efficiency. Moreover, the heightened land resource supply can also draw more businesses or talent to the region, thereby further fostering the region’s economic development and innovation capabilities. As a direct consequence, land resource supply policies favoring the central and western regions have resulted in increased land supply in those areas, while reducing land supply in the eastern region. The outcome has been the inhibition of regional innovation efficiency improvement in the eastern region.

Conclusions and recommendations

Research conclusions

After conducting theoretical analysis and empirical testing, this paper delves into the impact of biased land resource supply policies on housing prices and their subsequent influence on innovation, with a particular focus on the spatial heterogeneity of this effect. The findings of this study can be summarized as follows: (1) Policies favoring land resource supply in the central and western regions have contributed to the increase in housing prices across the eastern, central, and western regions. Notably,l the eastern region has experienced a more rapid escalation compared to the central and western regions. Specifically, the impact of the transfer of state-owned construction land area on housing prices is significantly negative at both national and regional levels. The influence coefficients stand at −0.1300 nationally, −0.1476 in the eastern region, and −0.0792 in the central and western regions, with the coefficient in the eastern region being lower than that in the central and western regions. (2) The accelerated growth of housing prices in the eastern region is poised to exert a more pronounced inhibitory impact on innovation compared to the central and western regions. Specifically, the focus is on the influence of housing prices on innovation efficiency, which registers a notably negative effect nationwide, in the eastern region, and in the central and western regions. The respective influence coefficients stand at −0.0757, −0.0924, and −0.0160, with the coefficient in the eastern region significantly lower than that in the central and western regions. In the context of the innovation-driven development strategy, these research findings provide policy guidance for the stability of the real estate market and the optimization of land policies.

Based on the above results analysis, after 2003, the rapid rise in housing prices in the eastern region significantly hindered regional innovation. The underlying reason lies in the central government’s implementation of land resource supply policies favoring the central and western regions. While the policy was intended to support the development of underdeveloped areas, it resulted in a rapid increase in housing prices in the eastern region, ultimately significantly stifling innovation in the region. Indeed, this policy facilitated economic growth in underdeveloped regions for a certain period. However, it also led to efficiency deterioration and local debt issues, posing significant risks to the sustainable development of the local economy. Relying solely on administrative measures for land resource allocation, while neglecting market forces and geographic factors, resulted in spatial misallocation of resources and adverse effects on high-quality economic development. At its core, the phenomenon of spatial misallocation resulting from the administrative allocation of resources stems from a divergence between government-led resource allocation and market-driven population movements. During this period, the eastern region continued to attract population inflows. The influx of people led to soaring housing demand, yet local government land fiscal policies resulted in insufficient land supply, exacerbating the already tense land supply-demand contradiction. Therefore, the inadequate land supply has led to a crowding-out effect on human capital for innovation and R&D investment, driving up costs for factors such as labor and capital, ultimately significantly stifling regional innovation.

Certainly, this study has its limitations, but it serves as a foundation for further exploration. Firstly, it focuses on the relationship between land supply, housing prices, and innovation in the eastern and midwestern regions. However, it overlooks the interconnections among land supply, housing prices, and innovation across different provinces. This aspect warrants further investigation in the future. Furthermore, although this study discusses how biased land supply policies affect regional housing prices and innovation, it does not delve into the specific reasons behind these differences. In the future, a more in-depth comparative analysis could be conducted to explore the impact of factors such as economic development and policy disparities across different regions on housing prices and innovation. Finally, in addition to utilizing instrumental variable methods for data analysis, comparing different cases could be employed to investigate how biased land supply policies influence regional housing prices and subsequently affect regional innovation.

Research recommendations

Research on the factors influencing regional housing prices and innovation is not only relevant to the implementation of innovation-driven development strategies and the construction of an innovative nation, but also crucial for the high-quality development of the national economy and the realization of the great “Chinese Dream”. Therefore, based on the findings of this study, the following recommendations are proposed:

  1. (1)

    Enhance land resource supply policies. The government can implement tailored land supply policies, finely adjusting regulations based on factors like regional economic development (Niu, Chen, et al., 2023) and land resource utilization (Shen et al., 2023). This ensures stability and innovation vitality in real estate markets across different areas. The “people, land, and money” linkage policy proposed during the 2016 Two Sessions stated that urban construction land indicators are linked to the number of agricultural population resettlement.

  2. (2)

    Strengthen land use planning and management. The government can adjust land supply structures and strategically allocate various land types through scientifically sound land use planning to meet the development needs of different regions (Feng et al., 2023). China’s 14th Five-Year Plan emphasizes aligning the allocation of construction land indicators with population migration trends and maximizing the market’s decisive role in resource allocation.

  3. (3)

    Foster policy coordination and interagency collaboration. The government enhances communication and coordination among departments to establish a cohesive framework for land resource supply policies (Liu et al., 2024). Local governments prioritize regional coordination and comprehensive planning in the formulation and execution of land supply policies, fostering a collaborative effort to promote balanced regional economic development effectively (Feng et al., 2024).