Introduction

The various problems caused by climate warming, such as rising sea levels, melting glaciers, ecosystem degradation, frequent extreme weather, and insufficient food supply, have caused increasingly serious negative impacts on the lives of global residents. Climate change is caused primarily by carbon emissions. According to “The State of the Global Climate 2023”, a report released by the World Meteorological Organization (WMO), in 2023, the global carbon dioxide concentration reached 419.3 ppm, which is 150% of the preindustrial level. The rapid increase in carbon emissions has attracted considerable attention from scholars and governments (Rahman and Ahmad 2019), and a global consensus has formed around limiting carbon emissions and addressing climate change (Wang et al. 2022a; Zhao et al. 2022). Recently, governments worldwide have taken various proactive measures, developed various carbon peaking and carbon neutrality action plans, and introduced strict regulatory policies through legislation and other means to curb excessive carbon emissions (Karim et al. 2021). China is in the midst of rapid development, and most cities have experienced the development model of “development first, governance later”. China, beset with severe environmental pollution, has ascended to the position of the world’s foremost carbon emitter, thereby imposing significant pressure to mitigate its emissions. Consequently, the implementation of stringent environmental regulations has emerged as a pressing concern (Shen et al. 2017; Li and Xu 2020). In 2018, an ecological civilization and “beautiful China” were written into the constitution. In 2020, China officially proposed the “dual carbon” goal, which aims to achieve a “carbon peak” by 2030 and “carbon neutrality” by 2060. With respect to carbon emission governance, China has gradually formed a governance mechanism that takes the carbon emissions trading system as the main means, improves the carbon emission statistics and accounting system, and enhances the regional carbon sink stock. Environmental regulation means that both ecological and economic development are increasingly improved.

Environmental regulation is a policy measure taken by a government to reduce environmental externalities, and its goal is to achieve environmental protection and sustainable economic development (Liu et al. 2023). However, there are disparate views among scholars regarding the effect of environmental regulation on carbon emission efficiency (CEE).

The first view is suppression theory. This theory argues that strict environmental regulation can increase the expected costs of enterprises, and when there is policy rigidity, unreasonable carbon taxes will not lead enterprises to reduce their fossil energy consumption and, instead, will cause enterprises to confront and accelerate current energy consumption, thus causing more serious carbon emissions. That is, environmental regulation has a “green paradox” effect (Sinn 2008). Especially in regions with low external costs and high resource endowments, environmental regulation is more likely to accelerate current resource overconsumption and worsen the impact of the regional “resource curse”. In addition, owing to the scarcity of fossil fuels, the early announcement of environmental regulations may lead to a tendency in which firms accelerate fossil fuel extraction to avoid losses, resulting in increased energy consumption and carbon emissions (Smulders et al. 2012; Ritter and Schopf 2014; Liang et al. 2022a). Therefore, the implementation of environmental policies may actually exacerbate carbon emissions and reduce carbon efficiency (Yuan et al. 2022).

The second view is facilitation theory. According to the Porter hypothesis, under an environmental policy of appropriate intensity, firms can improve their CEE and ultimately achieve low-carbon development by retrofitting and upgrading their equipment (Wang et al. 2018). The costs associated with environmental regulation can be compensated for by technological advancement and innovation, thus generating a certain “push-back effect” that improves CEE (Pei et al. 2019; Liu et al. 2021). In addition, by limiting fossil energy usage, strict environmental regulatory policies can promote a low-carbon transition of the energy mix to improve energy use efficiency to achieve carbon emission reduction targets (Wang et al. 2022b). Porter’s hypothesis has also been validated at the firm level, such as environmental regulation policies that promote synergistic emission reductions in pollutants and greenhouse gases from firms (Du and Li 2020). In addition to the indirect evidence provided above, environmental regulation can directly affect carbon productivity in a positive way. For example, the Action Plan for Air Pollution Prevention and Control (APAPPC) was found to significantly contribute to improving carbon productivity in pollution-intensive industries, and this contribution has steadily increased over time (Zhou and Tang 2021). Thus, an effective environmental regulation system plays a critical role in driving regional carbon efficiency. However, this does not imply that the role of environmental regulation is unlimited. Its effect is limited by the type of environmental regulation instrument, the degree of regional economic development, and differences in resource endowments; thus, there is some heterogeneity in the effect (Wang and Zhang, 2022). For example, some scholars argue that carbon emission trading systems are more effective at reducing emissions than low-carbon pilots are and that carbon emission trading performs better in Eastern China while low-carbon pilots perform better in Central China and Western China (Huang and Yi 2023). Carbon productivity is negatively affected by command-and-control environmental regulation, whereas it is positively affected by market-based environmental regulation (Song and Han 2022).

Third, environmental regulation may also have a nonlinear effect on carbon efficiency, i.e., the two have an inverted U-shaped relationship (Zhang et al. 2020, 2021). Environmental regulation changes the speculative psychology and expectations of firms, and when the cost of fines is greater than the cost of governance, firms shift away from long-term gains to the innovative use of green production technologies, thereby increasing productivity. With increasing environmental regulation intensity, the “green paradox” effect changes into an “anti-coercive reduction” effect, which can effectively reduce carbon emissions (Guo and Chen 2018). Other scholars argue that the relationship between environmental regulations and carbon emissions has a more complex N-shaped relationship. That is, before the first inflection point, there is a “green paradox” effect; before the second inflection point, there is an “emission reduction effect”; and after the second inflection point, there is a “green paradox” effect again (Lu et al. 2022). There exists a threshold level in the influence of environmental regulations on carbon productivity. Initially, as the intensity of these regulations shifts from lax to stringent, their effect on carbon productivity transitions from being detrimental to being beneficial, but China has yet to reach this threshold in terms of environmental regulation intensity (Hu and Wang 2020). In different industries, such as the marine industry and the construction industry, there is a nonlinear relationship between environmental regulation and carbon efficiency (Zhang et al. 2018; Wang et al. 2023a).

The social network analysis (SNA) approach is applied to explore the structure of socioeconomic systems from a relational perspective. Recently, this approach has been widely used in the fields of international trade, international business, the tourism economy, green information and communication technology, healthcare, the digital economy, green infrastructure and green innovation (Kurt and Kurt 2020; Fan and Xiao 2021; Gan et al. 2021; Li et al. 2022; Liu et al. 2022; Liang et al. 2022b). Similarly, SNA has been applied to the environmental energy domain to reveal spatially linked network features of environmental change or energy consumption. For example, Liu et al. (2020) selected electricity consumption and economic growth data from eight industries in China from 2007 to 2017 and constructed an overall relationship network (ORN) and an economic growth relationship network (GRN). Dong and Li (2022) introduced regional economic differences and revised the distance in the gravity model to explore the spatial correlation network characteristics of carbon emissions in seven urban agglomerations in China. Wang et al. (2023b) considered the effects of variables such as regional carbon emissions, population size, regional GDP, and economic distance when constructing a spatial correlation network for carbon emissions in the United States and made corresponding modifications to the traditional gravity model. Similarly, Wang and Ge (2023) used the entropy-TOPSIS method to measure the economic elasticity of 31 provinces in mainland China and used the modified gravity model to construct a spatial correlation network of economic elasticity. Wang and Liu (2023) also used a modified gravity model to explore the spatial correlation network of energy consumption in China from 2004 to 2017. Despite the widespread use of SNA in various areas of society, in general, SNA is still used relatively infrequently for environmental regulation.

In summary, there is no unified view in academia regarding how environmental regulation affects CEE. Owing to increasing carbon emissions, to achieve the expected “dual carbon” goals smoothly, the Chinese government has invested considerable energy and funds in environmental regulation. The interaction of environmental regulation behaviors between different cities has become increasingly frequent and in depth, thus forming an environmental regulation network (ERN) throughout China. The ERN may promote CEE by enhancing the location of central cities, reducing energy intensity, and fostering technological innovation and FDI. However, in existing research, relatively few studies have explored the relationship between the ERN and CEE. Therefore, by employing SNA, this paper delves into the ERN of China’s 254 cities, examining its structure and the subsequent influence on CEE. The contributions of this study include the following:

(1) According to the relational data, a modified gravity model is applied to build the ERN, revealing the structural form of the ERN in more detail from a city viewpoint, which enriches the current quantitative analyses of the ERN. Compared with the provincial level, the city level can be used to explore the characteristics of the ERN and its relationship with CEE in more detail, which is helpful for achieving regional synergistic reductions in CO2 emissions.

(2) The position and role of Chinese cities in the ERN are revealed by degree centrality, and the effect of the central characteristics of the ERN on CEE is examined using this indicator as an explanatory variable. The heterogeneity of the effect of degree centrality on CEE is discussed on the basis of differences in geographical location, resource endowment and urban size. This provides a new research dimension for understanding the complex relationship between environmental regulation and CEE.

(3) This paper investigates the mediating effect of energy intensity on the relationship between degree centrality and CEE, as well as the moderating effect of green innovation and foreign direct investment (FDI) on the relationship between degree centrality and CEE. Additionally, it examines the effect of degree centrality on CEE from a spatial perspective using a spatial econometric model. This reveals the key mechanism by which the ERN affects CEE.

The paper is organized as follows: Section “Methods and materials” systematically introduces the research methods, covering gravity models, network feature indicators, econometric model construction, and the basis for variable selection, while clarifying the data sources. Section “Results and discussion” specifically analyzes the overall and individual characteristics of the ERN and explores the impact of degree centrality on CEE from an econometric perspective. Section “Conclusions and policy implications” presents the significance of the research findings, proposes policy recommendations, and discusses the limitations of this study.

Methods and materials

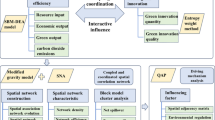
Gravity model

In SNA, gravity models are commonly used to construct association networks (Liu et al. 2020; Wang and Ge 2023). Compared with vector autoregressive models and Granger tests, gravity models are more widely used because several factors can be considered, including the economy, population, distance and environmental regulation between regions. Therefore, the association relationship of the ERN among cities is determined via a modified gravity model. The formula is as follows:

$$\begin{array}{c}{Y}_{{\rm{ij}}}={k}_{ij}\frac{\root3\of{{P}_{i}{T}_{i}{G}_{i}}\root3\of{{P}_{j}{T}_{j}{G}_{j}}}{{{M}_{ij}}^{2}}\\ {k}_{ij}=\frac{{T}_{i}}{{T}_{i}+{T}_{j}}\\ {M}_{ij}=\frac{{D}_{ij}}{pgd{p}_{i}-pgd{p}_{j}}\end{array}$$
(1)

where \({Y}_{{\rm{ij}}}\) represents the environmental regulation gravity, \({P}_{i}\) and \({P}_{j}\) represent the populations, \({G}_{i}\) and \({G}_{j}\) represent the GDP, \({T}_{i}\) and \({T}_{j}\) represent the environmental regulation indicators, \({D}_{ij}\) represents the distance between two cities, and \(pgd{p}_{i}\) and \(pgd{p}_{j}\) represent the per capita GDP.

The association matrix of environmental regulation among cities is calculated on the basis of the modified gravity matrix. To facilitate the description, the matrix is binarized. The focus of this paper is not on the specific strength of the relationship but on the existence or nonexistence of the relationship. Therefore, when the average is used as a threshold, the data are divided into two groups, above average and below average, thereby transforming the correlation relationship into a matrix with only two states (0 and 1) and simplifying the data structure. This method focuses on the presence or absence of relationships by ignoring their specific strength, making the connections between individuals in the network clearer and facilitating the identification of key nodes and group structures in the network. The average value of each row in the matrix is set as a threshold (\({A}_{ij}\)), and if the value exceeds the threshold, it is recorded as 1, indicating that these two cities are spatially associated. If the value is below the threshold, it is recorded as 0, which indicates that the two cities do not have a spatial association, as shown in below equation:

$$I=({i}_{ij})=\left\{\begin{array}{c}\begin{array}{cc}1 & {y}_{ij}\ge {A}_{ij}\end{array}\\ \begin{array}{cc}0 & {y}_{ij}\, < \,{A}_{ij}\end{array}\end{array}\right.$$
(2)

Network characteristic indicators

Overall network characteristic indicators

Network density is an indicator of the tightness of connections between nodes in a network. In the ERN, nodes can be regulatory agencies, enterprises, communities, or other relevant organizations, whereas edges represent their cooperative relationships, information exchange, or regulatory relationships. A higher network density means that there are more connections between nodes in the ERN, which helps to facilitate the rapid dissemination and sharing of information and improve supervision efficiency. Network density also reflects the degree of collaboration in the ERN, and a high density may indicate the existence of effective multiparty collaboration, which helps to form unified regulatory standards and strategies. However, excessive network density may also lead to information overload and increased management complexity, requiring appropriate information management and coordination mechanisms. Therefore, we employ the metric of network density to characterize the overarching features of ERN, and the greater this number is, the closer the relationships between cities in terms of environmental regulation. The formula for calculating the density is as follows:

$$D=\frac{{\sum }_{i=1}^{n}{\sum }_{j=1}^{n}d({k}_{i},{k}_{j})}{n(n-1)}$$
(3)

where n denotes the number of nodes and a node’s relationship to another node is denoted by \(d({k}_{i},{k}_{j})\).

Individual network characteristic indicators

In the SNA method, the individual network characteristics of each node can be characterized by degree centrality. Degree centrality refers to the number of nodes directly connected to other nodes in a network and is an indicator of node importance. Highly centralized nodes play a crucial role in the network, as they may be the hubs of information or the cores of regulatory decision-making. Nodes with high degree centrality have a significant effect on the stability and influence of the network, and their behavior and decisions may have a significant effect on the entire network. In the ERN, identifying and utilizing nodes with high centrality can help quickly promote best practices, policies, and regulations and improve regulatory efficiency and effectiveness. By utilizing the number of connections, the degree centrality can measure the degree to which each node is at the center of the ERN.

$$De{g}_{i}=\frac{n}{N-1}$$
(4)

Where n represents the total number of nodes that are directly interconnected with node i, whereas N signifies the overall count of nodes within the network.

Econometric model

To explore the effect of degree centrality on CEE, this paper first constructs a panel fixed-effects model, as shown in below equation:

$$CE{E}_{it}={\alpha }_{0}+{\alpha }_{1}De{g}_{it}+{\alpha }_{2}Con{t}_{it}+{\mu }_{i}+{\nu }_{t}+{\varepsilon }_{it}$$
(5)

where i represents the city, t represents time, \(CE{E}_{it}\) represents carbon emission efficiency, \(De{g}_{it}\) represents degree centrality, \(Co{n}_{it}\) represents the control variables.

In addition to the overall impact stated in Eq. (5), the degree centrality of the ERN may have an indirect effect on CEE through some mediating mechanisms. In accordance with the literature, energy consumption may act as a mediating agent, so we develop the following mediating model:

$$E{C}_{it}={\beta }_{0}+{\beta }_{1}De{g}_{it}+{\beta }_{2}Con{t}_{it}+{\mu }_{i}+{\nu }_{t}+{\varepsilon }_{it}$$
(6)
$$CE{E}_{it}={\gamma }_{0}+{\gamma }_{1}De{g}_{it}+{\gamma }_{2}E{C}_{it}+{\gamma }_{3}Con{t}_{it}+{\mu }_{i}+{\nu }_{t}+{\varepsilon }_{it}$$
(7)

where \(E{C}_{it}\) is the energy intensity, and the meanings of the other variables are as shown in Eq. (5). To ascertain the presence of a mediating effect, we evaluate the statistical significance of parameters \({\beta }_{1}\), \({\gamma }_{1}\) and \({\gamma }_{2}\). Specifically, we sequentially test the significance of\({\beta }_{1}\) and \({\gamma }_{2}\). If both \({\beta }_{1}\) and \({\gamma }_{2}\) are found to be significant, the model is deemed to exhibit a mediating effect. Conversely, if either \({\beta }_{1}\) and \({\gamma }_{2}\) fails to reach significance, we resort to the bootstrap method to directly assess whether the product of coefficients \({\beta }_{1}\) and \({\gamma }_{2}\) is significantly non-zero, thereby confirming or refuting the mediating effect.

In addition to considering the mediating effect, this paper introduces two variables, green innovation and FDI, to examine their moderating role in the relationship between the degree centrality of the ERN and CEE with the following model setup:

$$\begin{array}{l}CE{E}_{it}={\delta }_{0}+{\delta }_{1}De{g}_{it}\times G{I}_{it}+{\delta }_{2}De{g}_{it}+{\delta }_{3}G{I}_{it}+{\delta }_{4}Con{t}_{it}\\\qquad\qquad+\,{\mu }_{i}+{\nu }_{t}+{\varepsilon }_{it}\end{array}$$
(8)
$$\begin{array}{l}CE{E}_{it}={\delta }_{0}+{\delta }_{1}De{g}_{it}\times FD{I}_{it}+{\delta }_{2}De{g}_{it}+{\delta }_{3}FD{I}_{it}+{\delta }_{4}Con{t}_{it}\\\qquad\qquad+\,{\mu }_{i}+{\nu }_{t}+{\varepsilon }_{it}\end{array}$$
(9)

where \(G{I}_{it}\) denotes green innovation, \(FD{I}_{it}\) denotes foreign direct investment, and \({\delta }_{1}\) is the coefficient of the interaction term between degree centrality and the moderating variables, which reflects the effect of degree centrality on CEE under the effect of the moderating variables. If \({\delta }_{1}\) is significant, it indicates that there is a moderating effect, and vice versa.

To mitigate the potential for spatial correlation bias, this paper incorporates spatial variables into the equation. The spatial Durbin model (SDM) is constructed to explore the spatial spillover effect of degree centrality on CEE, as shown in below equation:

$$\begin{array}{l}CE{E}_{it}={\eta }_{0}+{\eta }_{1}\mathop{\sum }\limits_{i=1}^{n}{w}_{ij}CE{E}_{jt}+{\eta }_{2}De{g}_{it}+{\eta }_{3}\mathop{\sum }\limits_{i=1}^{n}w{}_{ij}De{g}_{jt}\\\qquad\qquad+\,{\eta }_{4}\sum Con{t}_{it}+{\eta }_{5}\mathop{\sum }\limits_{i=1}^{n}{w}_{ij}Con{t}_{it}+{\nu }_{t}+{\varepsilon }_{it}\end{array}$$
(10)

where \({w}_{ij}\) is the spatial weight matrix, geographical distance is chosen to represent it, and the meanings of the remaining variables are the same as those above. \({\eta }_{1}\) is the spatial autoregressive coefficient, which represents the spatial spillover effect of CEE. The estimated coefficient with \({\eta }_{2}\) as the core independent variable is used to measure the impact of degree centrality on local CEE. \({\eta }_{3}\) is used to measure the spatial spillover effect of degree centrality on CEE in other regions.

Moran’s I index

The Moran I index is widely used in existing research to observe whether variables have spatial clustering. The equation is presented:

$$I=\frac{{\sum }_{i=1}^{n}{\sum }_{j=1}^{n}{w}_{ij}({x}_{i}-\bar{x})({x}_{j}-\bar{x})}{{s}^{2}{\sum }_{i=1}^{n}{\sum }_{j=1}^{n}{w}_{ij}}$$
(11)

where \({s}^{2}=\tfrac{{\sum }_{i=1}^{n}{({x}_{i}-\bar{x})}^{2}}{n},\bar{x}=\tfrac{{\sum }_{i=1}^{n}{x}_{i}}{n},\) the observation value for the i-th city is \({x}_{i}\), the number of samples is n, and the spatial weight matrix is \({w}_{ij}\).

Variable selection

Environmental regulation: Since it is difficult to directly measure the strength of environmental regulation, most of the previous literature has used the number of environmental protection personnel, environmental pollution control inputs, and pollution control costs as proxy indicators of environmental regulation. However, these indicators are largely endogenous to the stage of economic development, which can easily lead to endogeneity problems. In addition, environmental regulation has a rich connotation, including both economic instruments such as carbon tax and carbon emissions trading systems and legal instruments such as environmental protection regulations. Therefore, most existing indicators focus on reflecting a specific area of environmental regulation, and it is difficult to portray the whole picture of environmental regulation. For this reason, we refer to Chen and Chen (2018) and select the frequency of environment-related terms in each city’s government work report to measure the strength of environmental regulation. This type of report summarizes the government’s policy priorities and public commitments, and the frequent mention of environmental terminology directly reflects the government’s emphasis on environmental protection. In addition, the frequent use of terminology helps enhance public awareness of environmental issues and promotes social support for environmental policies. Moreover, the openness of government work reports provides easily accessible and quantifiable data for research, making term frequency an intuitive and reliable measurement tool. Therefore, by monitoring the use of these terms in government work reports, the strength and policy direction of environmental regulation can be effectively evaluated.

Carbon emission efficiency (CEE): We chose the super-slack-based measure (SBM) super-efficiency model with undesired outputs from data envelopment analysis for measurement, including capital input with regional per capita capital as the indicator, energy input with regional energy consumption as the indicator and labor input with the number of urban employed residents at the end of the year as the indicator. The regional GDP is the desired output, and CO2 emissions are the undesired output.

To reduce the error in the empirical results and with reference to existing studies, we select the economic development (RGDP), urbanization rate (Urban), industrial structure (IS), government intervention (Gov), and educational level (Edu) as control variables. In addition, this paper uses energy consumption (EC) as a mediator variable and green innovation (GI) and foreign direct investment (FDI) as moderating variables. The specific indicators are described as follows:

RGDP: With economic growth, energy efficiency can be improved, thereby reducing carbon emissions per unit of output and enhancing CEE. Moreover, economic development promotes the optimization of the industrial structure, with resources tilted toward efficient and low-emission industries, further reducing carbon emissions. In addition, economic development has led to an increase in environmental demand, and governments and enterprises are paying more attention to environmental protection, promoting the research and application of clean energy and energy-saving technologies and thereby improving CEE (Sun and Huang, 2020). RGDP is defined as the logarithm of GDP per capita in each city.

Urban: On the one hand, the process of urbanization promotes economic growth, technological progress, and energy efficiency improvement, which helps reduce carbon emissions per unit of output and thus improves CEE (Xiao et al. 2023). On the other hand, urbanization has also brought about population concentration and increased energy consumption, which can have a negative impact on CEE (Sun and Huang 2020). Urban is defined as the percentage of residents who live in urban areas.

IS: Upgrading industries to cleaner production methods can optimize the allocation of production factors. When production factors shift from resource-intensive industries to industries that rely more on technology and capital, energy efficiency improves, which reduces overall energy consumption and helps lower carbon emissions related to energy use (Wu et al. 2020; Zhang and Liu, 2022). IS is expressed as the share of the value added to the tertiary industry in GDP.

Gov: The government plays a crucial role in addressing energy consumption and environmental issues. Ensuring the implementation of environmental policies, investing in pollution control, and controlling emissions all urgently require active government intervention and effective management (Huang and Yi 2023). Gov is determined by the proportion of general public budget expenditures to the GDP.

Edu: Education not only enhances the public’s understanding of environmental issues and raises environmental awareness but also generally makes individuals with higher levels of education more inclined to adopt low-carbon lifestyles, choose environmentally friendly products and services, and promote resource conservation and carbon emission reduction from lifestyle to consumption choices (Song and Han 2022). Edu is expressed as the logarithm of the number of college students per 10,000 people.

EC: Electricity plays a crucial role in energy consumption in cities. However, coal-fired power generation still accounts for a significant share of China’s electricity industry (Yi et al. 2020). In the process of electricity consumption, we also consider the corresponding carbon emissions caused by coal-fired power generation. Therefore, EC is expressed as the proportion of total electricity consumption to GDP.

GI: By promoting energy efficiency improvement, clean energy substitution, and the research and application of technologies such as carbon capture, utilization, and storage, green innovation can significantly reduce energy consumption and carbon emissions. In addition, green innovation promotes the industrial structure upgrading, promotes the development of low-carbon and environmental protection industries, and further enhances CEE (Wu et al. 2020). GI is expressed as the logarithm of the number of green patent applications.

FDI: On the one hand, FDI promotes the technological progress and industrial upgrading of host country enterprises by introducing advanced production technology and management experience, thereby improving energy utilization efficiency, reducing carbon emission intensity, and positively affecting CEE. On the other hand, FDI may also lead to high energy consumption and high-emissions production activities, especially in some developing countries or regions. Without effective environmental regulations and supervision, FDI may exacerbate carbon emission problems (Fan et al. 2022). FDI is measured by the proportion of actual FDI utilized in GDP.

Data sources

We took 254 cities in China as network nodes to empirically examine the ERN and its impact on carbon emissions, and the sample period spanned from 2007 to 2019. The data for the selected indicators in the paper are obtained mainly from the China Urban Statistical Yearbook. GDP is deflated on the basis of 2007 data to eliminate the impact of price factors on GDP. The distance between cities is measured geographically. In terms of data processing, we first filled in a small number of missing values through interpolation, identified outliers using box plots, and then removed these outliers. Second, to adapt to subsequent analysis, we standardized certain variables to eliminate the influence of dimensionality.

Results and discussion

Characteristics of the ERN

Overall characteristics

Since the study sample consists of 254 cities, this network can have up to 64,262 possible connections. Figure. 1 shows the results of calculating the network density. We can see that the number of associations in all years, except for 2013, is greater than 8000, and a fluctuation of 0.14–0.16 is generally observed in network density. One possible reason is that in 2013, a new environmental protection law was revised, which stipulated measures such as daily penalties and administrative detention, significantly increasing the cost of violating the law. The revision of the Environmental Protection Law may have changed the incentive mechanism for intercity cooperation, leading some cities to adopt more conservative or independent strategies in environmental regulation, reducing intercity cooperation and information exchange. In addition, the newly revised laws may increase the standards and requirements for environmental regulation and increase compliance costs, and some cities may focus their resources and attention on meeting new legal requirements, which may reduce cooperation with other cities in environmental regulation. Therefore, during the transitional period between new and old laws, the enforcement efforts in different regions have varied, resulting in a weakening of the relevance of environmental regulation. However, in the same year, ecological civilization construction was written into the Chinese Communist Party Constitution, the first ruling party in the world to increase the importance of environmental regulation to the level of the ruling party’s constitution. This event represents the Chinese government’s determination to govern the environment. In 2018, the network density reached its highest value of 0.1505 after it steadily increased from 2014 to 2019. Compared with those of mature networks, the association relationships of the ERN are relatively few, and the network structure is not particularly tight.

Fig. 1: Network density of the ERN.
figure 1

The number of associations in all years, except for 2013, is higher than 8000, and a fluctuation of 0.14–0.16 is generally observed in network density.

Full size image

In this work, the time series correlation coefficients of the ERN obtained via quadratic assignment procedure (QAP) correlation analysis are measured and plotted as a heatmap, as shown in Fig. 2. The color of the graph changes from blue to white to red, indicating that the correlation between matrices changes from a negative correlation to an uncorrelated or positive correlation. There is a high degree of similarity and self-stability in the structure of the ERN from 2007 to 2019, and the network structure does not show a large degree of “variation” in a short period. Notably, the correlation coefficients of the associated networks in adjacent years are approximately 0.8, and the correlation coefficient between 2007 and 2019 is the smallest at 0.47, i.e., the correlation coefficients of each year’s ERN and the remaining years are between 0.47 and 0.9, which means that it is meaningful to study the ERN in China using the 2007–2019 sample data.

Fig. 2: Time series correlation coefficients of the ERN from 2007 to 2019.
figure 2

There is a high degree of similarity and self-stability in the structure of the ERN from 2007 to 2019, and the network structure does not show a large degree of "variation" in a short period.

Full size image

Individual characteristics

The degree centrality of the ERN is obtained via Eq. (4), and the kernel density estimates of degree centrality are presented in Fig. 3. We can see that a tight-sided distribution is evident in the kernel density. This result indicates that there are mainly a few cities involved in environmental regulation linkages, while most cities have fewer partners to contact. The distribution of the kernel density did not change significantly from 2007–2019, and all of the values first tended to increase but then decreased.

Fig. 3: Kernel density of degree centrality.
figure 3

The distribution of the kernel density does not change significantly during the period 2007–2019, and all values show a trend of first increasing and then decreasing.

Full size image

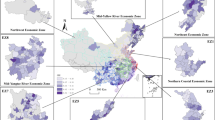
Table 1 reports the top ten cities in terms of degree centrality in 2007, 2012, 2014 and 2019. The cities ranked in the top ten from 2007 to 2019 changed little, with Suzhou being in first place for all four years and Wuxi, Dongying, and Shanghai appearing more frequently in the top five. In terms of geographical location, a total of 70% of the top ten cities came from the east in the four years, while only Ordos and Baotou appeared a total of 4 times in the western region, and only Daqing appeared once in the northeast region. Central cities, with their policy-making power and resource aggregation advantages, not only play a key role in formulating and promoting effective environmental regulatory policies but also have a positive effect on neighboring cities. As centers of information exchange, they quickly disseminate advanced knowledge and best practices in environmental regulation, promoting knowledge sharing and technology transfer. Central cities utilize their abundant resources and funds to provide technical and financial support to other cities, helping them enhance their environmental regulatory capabilities. In the handling of cross-regional environmental issues, central cities play the role of coordinators, promoting cooperation between cities and jointly addressing regional environmental challenges. At the same time, the environmental supervision capability of central cities radiates to other cities through their network relationships, enhancing the overall environmental supervision efficiency of the network.

Table 1 Top 10 cities by degree centrality.
Full size table

This study also plotted the spatial distribution characteristics of degree centrality in 2019, as shown in Fig. 4. Green is the lowest level of degree centrality, followed by yellow, orange, and red. The Yangtze River Delta urban agglomeration is a concentrated area of red and orange, and it is the area with the highest degree centrality. From east to west, the overall color of the picture gradually changes from red to green, indicating that degree centrality successively decreases. The inland area is represented by Wuhan, Changsha and Hefei, which are red and show higher degree centrality. The mean value of the 254 cities is 56.87, with 55 cities having above average values. Among the 254 cities selected in this paper, 85, 72, 65, and 32 cities are in the east, central, west, and northeast regions, respectively. The numbers of cities with values above the average in the eastern, central, western and northeast regions are 33, 13, 8 and 1, accounting for 38.82%, 18.06%, 12.31% and 3.13%, respectively. Only Dalian exceeds the average in Northeast China, and nearly 97% of northeast cities are smaller than the average, indicating that northeast cities occupy fewer seats in the ERN and that the number of active relationships issued is lower. Moreover, among the 26 cities in the bottom 90% of the degree centrality rankings, the east, central, and west regions have 16, 8 and 2 cities, respectively, accounting for 18.82%, 11.11% and 3.08% of each region’s overall number of cities, respectively, and there are no cities in Northeast China. These results indicate that cities in the eastern region exhibit serious bifurcation in their status in the network, with both core cities in the network and cities at the edge of the network. They also indicate that the ERN among cities needs to strengthen communication and cooperation, and the connections among cities have further deepened.

Fig. 4: Spatial distribution of degree centrality in 2019.
figure 4

The Yangtze River Delta urban agglomeration is the area with the highest degree centrality. From east to west, the overall color of the picture gradually changes from red to green, indicating that degree centrality successively decreases.

Full size image

The impact of the ERN on CEE

Scatter plot

To explore the relationship between the degree centrality of the ERN and CEE, a correlation trend analysis is conducted, and Fig. 5 shows the scatter plots and fitted curves. There is a significant positive correlation between degree centrality and CEE, indicating that as the degree centrality of each city increases, the overall CEE tends to increase.

Fig. 5: Scatter plot of degree centrality and CEE.
figure 5

There is a significant positive correlation between degree centrality and CEE.

Full size image

Baseline regression results

The effect of the central characteristics of the ERN on CEE is examined using degree centrality as an explanatory variable, and Table 2 presents the results. After controlling for a series of factors affecting CEE, the coefficients of Deg are all significantly positive, indicating that the elevated location of each city center increased CEE. Specifically, when no control variables are added, each 1% increase in degree centrality increased CEE by 0.103%. However, by gradually adding control variables, the coefficients of Deg first increased, then decreased, and finally rebounded close to the original level. After all control variables are added, each 1% increase in degree centrality increase CEE by 0.097%. Therefore, the control variables selected in this paper, which are credible, do not affect the estimation results. These results indicate that the CEE of a city can be improved if it increases its level of environmental regulation, establishes more links with other cities in environmental regulation, and occupies a more important position in the ERN. This may be because the government puts pressure on enterprises to use less fossil energy by setting strict emission standards, imposing relevant taxes and fees or improving energy efficiency by using new technologies and equipment, thus reducing carbon emissions and improving CEE.

Table 2 Baseline regression results.
Full size table

For the control variables, the coefficient of Urban is negative at the 1% level, indicating that the urbanization rate has a suppressive effect on CEE. This is consistent with the viewpoint of Fang et al. (2022), which may be due to the expansion of urbanization, accompanied by large-scale infrastructure construction and housing demand, which will inevitably drive the growth of energy consumption. With the widespread use of high-energy-consuming products, the elasticity of energy demand gradually weakens. Moreover, large-scale population migration significantly contributes to a surge in energy consumption, which in turn intensifies carbon emissions and subsequently results in a decline in CEE. At the 1% level, the coefficient of RGDP is significantly positive, indicating that economic growth promotes CEE, which is consistent with the findings of Sun and Huang (2020). A possible reason is that economic development has brought about an increase in technological innovation, the development of low-carbon products, a sound carbon emission governance system, and improved environmental supervision, which helps improve CEE. The coefficient of IS is negative at the 10% significance level, suggesting that industrial structure exerts a restraining influence on CEE, aligning with the findings presented by Gao et al. (2023). The high proportion of the tertiary industry does not directly inhibit CEE, but certain sectors, such as transportation, may reduce overall CEE due to high emissions. Specifically, although the transportation sector belongs to the tertiary industry, it generates a large amount of carbon emissions during its operation, and its CEE is relatively low compared with the value it creates. The coefficient of Gov is significantly negative at the 1% level, meaning that government intervention inhibits CEE, aligning with the findings presented by Fan et al. (2022). If the government intervenes excessively, it may aggravate market dysfunction and lead to problems such as intensified competition, rent-seeking and corruption among local governments. All of these negative effects lead to the relaxation of environmental regulatory standards and a decline in environmental quality and CEE (Deng et al. 2019). The coefficient of Edu is significantly negative at the 10% level, and since the measure here is the number of college students per 10,000 people, college students do not engage in productive work while in school and cannot directly generate output for society; i.e., they cannot be considered the social labor force. Therefore, in the short term, the greater the number of laborers in a society who do not perform activities with economic output, the more carbon emissions are created by basic living; therefore, the CEE is negatively affected. Moreover, owing to the lagging nature of education, students who receive environmental education in schools today may not realize the impact of their educational outcomes on CEE until years or decades later, when they enter the workforce and become decision-makers.

Robustness tests

Robustness tests are conducted in four ways. First, we refer to the approach of Wang and Zhang (2022) and select five indicators to measure the intensity of environmental regulation: industrial SO2 removal, industrial smoke (powder) dust removal, industrial wastewater treatment, general industrial solid waste comprehensive utilization, and domestic waste harmless treatment. Degree centrality is recalculated via Eqs. (1)–(4), and an empirical regression is then conducted, as presented in column 2 of Table 3. The coefficient of Deg is significantly positive, and only a slight change in the magnitude of the value occurs, while the direction does not change. This study’s findings are clearly robust given the consistency of these results with previous findings. Second, since the overall network density in Fig. 1 shows a significant decrease only in 2013, the study sample is divided into two subsamples, sample 1 for the 2007–2012 period and sample 2 for the 2013–2019 period, using 2013 as the dividing line, as shown in columns 3 and 4 of Table 3, respectively. The coefficients of Deg are all significantly positive at the 1% level, which is consistent with the findings above. Furthermore, this paper uses carbon emission intensity as a substitute test for CEE. Carbon emission intensity refers to the carbon emission per unit of economic output. Typically, improving CEE means reducing the carbon emission intensity. Therefore, in the regression results of column (4), as the degree centrality increases, the carbon emission intensity decreases accordingly. Moreover, the benchmark test results are robust. Finally, column (5) presents the regression results with both the explanatory and control variables lagged by one period. The degree centrality and lagged degree centrality both maintain a positive correlation with CEE and are significant at the 1% level.

Table 3 Robustness tests.
Full size table

Heterogeneity test

Heterogeneity of geographical location

On the basis of the division criteria issued by the State Council in 2014, the sample cities are divided into four regions, and the influence of degree centrality on CEE under the influence of geographical location is examined separately. The results are shown in Table 4. The coefficient of Deg in the eastern region is significant at the 1% level, and the coefficient of Deg in the western region is significant at the 5% level, which means that an increase in the degree centrality of the ERN significantly increases CEE in these two regions. The coefficients of Deg in the central and northeastern regions are not significant. The values of the coefficients for cities in the eastern and western regions are 0.090 and 0.093, respectively, which are closer to the coefficient of 0.097 for the national sample.

Table 4 Regression results under the heterogeneity of geographical location.
Full size table

Heterogeneity of resource endowments

According to the State Council’s National Sustainable Development Plan for Resource-based Cities (2013–2020), we divide the 254 sample cities into resource-based cities and non-resource-based cities. The effect of degree centrality on CEE under the influence of the resource endowment is examined separately, as shown in Table 5. In non-resource-based cities, the coefficient of Deg is significantly positive at the 1% level, with a coefficient size of 0.099. In resource-based cities, the coefficient of Deg is significantly positive at the 1% level, with a coefficient size of 0.09. These results indicate that the contribution of degree centrality to CEE is slightly stronger in non-resource cities.

Table 5 Heterogeneity of resource endowments.
Full size table

Heterogeneity of urban size

To evaluate the heterogeneity of urban size, cities are categorized by population into large, medium-sized, and small cities, and Table 6 presents the results. The coefficient of Deg is significantly positive at the 1% level in both large and medium–sized cities. In small cities, the coefficient of Deg is significantly positive at the 10% level. From these values, it can be seen that degree centrality makes the greatest contribution to CEE in large cities and exceeds the coefficient level in the baseline regression, and the ability of small and medium-sized cities to contribute to CEE is closer.

Table 6 Heterogeneity of urban size.
Full size table

Quantile regression

Furthermore, we explore the effect of the degree centrality of the ERN on CEE under different quantile conditions using quantitative regression. Quantile levels of 0.1, 0.25, 0.5, 0.75 and 0.9 are selected for parameter estimation, as shown in Table 7. The direction of the effect coefficients of Deg on CEE is exactly the same at different quantile levels, and all are significant at the 1% level, which is in agreement with the previous findings. Degree centrality’s contribution to CEE increases continuously with CEE, as shown by the coefficients ranging from 0.013 to 0.114.

Table 7 Quantile regression results.
Full size table

Heterogeneity of economic scale

To evaluate the heterogeneity of urban economic development levels, the cities are divided into four states on the basis of the quantile of per capita GDP: very high, high, medium, and low. Table 8 shows the results. In the two types of cities with high levels of economic development, the coefficient of Deg is significantly positive. This shows that the higher the economic level of a city is, the greater its status in the ERN, and the greater its ability to promote CEE improvement. The possible reason is that the higher the economic level of such cities is, the more public financial allocations are used to govern the environment, overcome green innovative technologies, and improve energy efficiency. Given their special financial funds, these cities are more likely to seek technical and knowledge assistance and establish environmental governance relationships to reduce their carbon emissions.

Table 8 Heterogeneity of economic scale.
Full size table

Mediating effect

With energy consumption as a mediating variable, the regression results are presented in Table 9. In column 2, Deg’s coefficient is significantly negative, suggesting that with the strengthening of environmental regulation, taking a more important position in the ERN decreases the energy consumption of a region. Moreover, in column 3, energy consumption has a negative effect on CEE, and degree centrality makes a positive contribution to CEE; i.e., energy consumption plays a partial mediating role in the relationship between degree centrality and CEE. One possible reason for this result is that China currently relies mainly on thermal power generation, and coal, which is the main fossil fuel for thermal power generation, produces a large amount of carbon dioxide during combustion and is the main source of China’s high CO2 emissions (Ma et al. 2022). Reducing energy consumption is the most effective way to improve CEE (Chen et al. 2022). Therefore, increasing environmental regulation and issuing more linkages in the ERN can reduce energy consumption and thus improve CEE. Therefore, the stronger the environmental supervision is, the more important it is in the ERN, which can urge the transformation of the energy structure and gradually shift from a fossil energy consumption structure to a clean energy consumption structure. As a result, the carbon emissions will also decrease, and CEE can be correspondingly improved.

Table 9 Mediating effect test.
Full size table

To verify the existence of the mediating effect, this paper used the Sobel test. Table 10 shows the test results. Among them, the Z statistic exceeds 0.97, meaning that the null hypothesis cannot be accepted. Therefore, energy consumption acts as a mediating agent in the relationship between degree centrality and CEE. The indirect effect is 0.009, the direct effect is 0.054, and the percentage of the mediating effect is 14.10%.

Table 10 Sobel test.
Full size table

Moderating effect

Green innovation and FDI are chosen as the moderating variables, and the regression results are shown in Table 11. Column 1 shows that the coefficient of Deg×GI is significantly positive at the 10% level. This result indicates that under the influence of green innovation, the more associative relationships cities issue and the more important the positions they occupy in the ERN, the more they can promote CEE. This result is similar to the finding of Huang and Yi (2023) that environmental regulation may indirectly affect CEE by influencing green innovation. Green innovation can reduce carbon emissions in the process of production and consumption and directly improve CEE by promoting innovation in energy conservation, pollution prevention, waste recycling and other technologies. Green innovation promotes the industrial structure upgrading and promotes the transformation of high-pollution and high-energy consumption industries to low-carbon and environmentally friendly industries, thus indirectly reducing carbon emissions. In addition, green innovation enhances the sense of social responsibility of enterprises, guides them to pay more attention to environmental protection and sustainable development, and provides power for improving CEE.

Table 11 Regression results of the moderating effects.
Full size table

Column 2 shows that the coefficient of Deg × FDI is positive with a significance level of 1%, which indicates that the more linkages and more important positions cities have in the ERN, the more CEE is promoted by FDI. This result is also consistent with the “pollution halo hypothesis”, which states that a large inflow of FDI also contributes to the development of low-carbon, environmentally friendly technology and experience (Hao and Liu 2015) and that incorporating these technologies and experiences into local enterprises’ low-carbon technologies can reduce emissions (Mert and Caglar 2020). In addition, in the process of complying with the environmental regulations of the host country, FDI enterprises carry out technological innovation and process improvement to adapt to stricter environmental protection standards, thus indirectly promoting CEE improvement.

Spatial econometric analysis

Since carbon emissions have a certain diffusion effect on the spatial scale, this paper constructed spatial econometric models to test the spatial spillover effect of the degree centrality of the ERN on CEE. Prior to executing a spatial regression analysis, a spatial correlation test should be conducted. Therefore, Moran’s I test is conducted in this paper, as presented in Table 12. Under the geographical distance matrix, the Moran’s I values of both the degree centrality and CEE from 2007 to 2019 are greater than 0 and significant at the 1% level. These results indicate that degree centrality and CEE have a positive spatial correlation between cities, indicating high-high or low-low spatial clustering characteristics.

Table 12 Global Moran’s I of degree centrality and CEE.
Full size table

For comparison, the regression results of the spatial lag model and the spatial error model are also presented in Table 13. The coefficient of the spatial lag term of CEE in the SDM is 0.887 and is significant at the 1% level, indicating that the CEE of a region is positively influenced by the CEE of neighboring regions. The coefficient of Deg is 0.094 and is significant at the 1% level, which is closer to the value in Table 2. To better distinguish the spatial spillover effect of degree centrality on CEE, this paper divided the total effect into direct effects and indirect effects. As presented in Table 14, the direct effect of degree centrality is 0.078 and is significant at the 1% level; that is, degree centrality makes a significant contribution to the CEE of a region. The indirect effect of degree centrality is −4.020 and is significant at the 1% level, showing that degree centrality has a significant negative spatial spillover effect, i.e., degree centrality increases the CEE of a region but decreases the CEE of surrounding regions through the spillover effect. The possible reason is that core cities often implement stricter environmental regulatory policies, which not only limit local pollution emissions but also may lead to the transfer of some highly polluting industries to surrounding cities, thereby exacerbating the environmental pressure on surrounding cities. There may be a competitive relationship between core cities and surrounding cities in the allocation and utilization of environmental resources. If the core city excessively occupies resources, it may lead to a shortage of resources in surrounding cities, thereby affecting their environmental governance capabilities. The mobility of natural factors such as air and water flow makes it possible for pollution problems in core cities to spread to surrounding areas, causing adverse effects on the environmental quality of surrounding cities. Finally, the total effect is negative because the negative effect of the indirect effect is greater than the positive effect of the direct effect. This result indicates that while the core cities in the ERN enjoy positive effects, they should strengthen their cooperation with neighboring cities and take the initiative to establish relationships with neighboring cities to avoid the creation of a “pollution paradise”.

Table 13 Spatial econometric regression results.
Full size table
Table 14 Decomposition of the spatial effects.
Full size table

Conclusions and policy implications

On the basis of SNA, this paper selected 2007–2019 panel data covering 254 cities in China, established an ERN through a modified gravity model, described the characteristics of the ERN, and explored the effect of degree centrality on CEE. The conclusions are as follows:

First, from 2007 to 2019, the cities of the ERN were not connected well to each other, resulting in a loose network structure. Nevertheless, the overall network density values showed an increasing trend over time. The cities of the Yangtze River Delta, such as Wuxi, Suzhou, and Shanghai, occupied the center of the ERN. Only 55 cities had degree centrality values above the average in 2019, and only Dalian had degree centrality values above the average in the northeast region. The eastern region had both core cities in the network and cities at the edge of the ERN, with more serious bifurcation.

Second, the empirical results showed that the effect of degree centrality on CEE is significantly positive, meaning that an increase in a city’s central position in the ERN increases CEE. This finding remains significant after the dependent variable is replaced and the study sample is reclassified.

Third, the degree centrality of eastern and western cities positively contributes to CEE, whereas the degree centrality of central and northeastern cities does not significantly affect CEE. The positive impact of degree centrality on CEE in non-resource-based cities is greater than that in resource-based cities. The positive impact of degree centrality on CEE in large cities is greater than that in medium-sized cities and small cities. The contribution of degree centrality to CEE increases with increasing CEE, according to quantile regression. In cities with the highest level of economic development, degree centrality contributes the most to CEE.

Fourth, the degree centrality of the ERN can promote CEE through energy consumption, and green innovation and FDI positively moderate the relationship between the degree centrality of the ERN and CEE. The degree centrality enhances the CEE of a city but reduces the CEE of surrounding cities through the spatial spillover effect, and the inhibition of the CEE of nearby cities is greater than the promotion of the CEE of local cities.

On the basis of the findings above, the following policy implications are proposed:

First, we should promote low-carbon and green lifestyles to residents, popularize knowledge of energy conservation and sustainable consumption, and carry out low-carbon projects such as community gardens and second-hand markets in the community to stimulate residents’ environmental awareness. In addition, by organizing low-carbon lifestyle competitions to recognize exemplary families, collaborating with transportation departments to promote public transportation and green travel, and implementing government and corporate green procurement policies, we can encourage broader environmental actions. Providing energy-saving renovation subsidies can motivate households and businesses to adopt renewable energy, while strengthening environmental education and media promotion can further increase public awareness of environmental protection so that the ERN can be expanded to include more regions and industries.

Second, when formulating environmental regulation policies, governments at all levels should fully consider the characteristics of their regions and formulate different carbon emission reduction regulations to achieve minimum environmental costs and maximum CEE. For example, cities in the eastern and western regions should continue to increase their environmental regulation efforts and play a role in promoting CEE. Small and medium–sized cities should strengthen their interaction and cooperation with large cities to enhance their central position in the ERN. The central cities, represented by Suzhou and Shanghai, should exploit their own strengths and influence to explore new paths of environmental regulation and lead other cities in China to reduce their carbon emissions while ensuring economic development. Cities located at the periphery of the network ought to consider the unique characteristics of the region, increase exchanges with the core cities, take the initiative to learn about environmental governance experience and technology, and continuously explore environmental governance models that meet their own characteristics. The key to strengthening the interaction and cooperation between small and medium-sized cities and large cities in environmental supervision is to establish an information sharing mechanism between cities to ensure real-time circulation of environmental data. We should jointly develop cross-regional environmental protection plans and standards and collaborate on pollution control.

Third, local governments should encourage enterprises to promote and apply green technologies to improve their energy use efficiency, reduce their reliance on traditional fossil energy sources and lower their energy consumption. The government should also ensure that green technologies are actually applied to production activities and that environmental regulation can play a better role. At the same time, local governments should establish a black list to regulate the behavior of foreign investment, raise the threshold of entry for foreign investment, and avoid becoming a “pollution paradise” for foreign investment.

Fourth, to alleviate the potential negative impact of environmental policies in core cities on surrounding areas, the key is to establish regional coordination mechanisms and unify environmental standards to prevent unreasonable flows of industries and capital. We should share environmental governance technologies, provide financial and tax incentives, and encourage enterprises to adopt environmental protection measures. Moreover, environmental impact assessments should be strengthened, policy transparency should be improved, and public participation should be promoted. Cross-regional funds should be established to support environmental improvement projects in surrounding cities. Through these measures, the coordination of regional environmental supervision can be improved, ensuring the effective implementation of environmental regulations and reducing the adverse effects of core city policies on surrounding areas.

This paper still has certain limitations and needs to be continuously adjusted and improved in future research. Owing to limitations in data availability and processing methods, only the ERN of 254 cities in China are analyzed. Subsequent research should consider expanding the sample to all cities nationwide or at a more micro level at the county level. Second, further analysis is needed on more features of the ERN, such as rights features, subordination features, and spatial clustering features. In addition, the mechanism by which the centrality of ERN affects CEE needs further refinement and exploration.