Introduction

Extensive research has been conducted on effective teaching strategies in mathematics, as evidenced by numerous studies documented in scientific literature. In particular, meta-analytic studies have been pivotal in identifying the teaching methods that yield the highest effectiveness in meeting the diverse needs of students (Pellegrini et al., 2021; Johnson et al., 2000; Dignath and Büttner, 2008; Donker et al., 2014; Cheng et al., 2019). These comprehensive analyses offer valuable insights into instructional approaches that enhance learning outcomes in mathematics. However, despite the information available, it is important to acknowledge that the existing literature still presents some gaps in understanding, leaving certain aspects of the problem relatively unexplored. One such area deserving further investigation revolves around the influence of cultural factors on effective mathematics instruction. As education systems worldwide become more diverse, recognizing the impact of cultural contexts on teaching practices becomes imperative. By delving into the interplay between cultural backgrounds and instructional strategies, researchers can gain deeper insights into how to tailor math education to various student populations.

Our study investigates the teaching strategies associated with higher mathematics achievements for 4th-grade students in the Arab region. The current body of research on effective teaching strategies in mathematics has predominantly concentrated on a select few developed countries, thereby creating a notable gap in reliable evidence for regions with distinct cultural and social characteristics, such as Arab countries (Almutairi et al., 2020). Consequently, these regions may face challenges in developing their educational curricula based on robust empirical findings. Recognizing the need to address this disparity, it becomes crucial to expand the scope of investigation to encompass a broader range of cultural contexts, particularly within Arabic-speaking countries. We investigate data for the seven countries participating in the Trends in International Mathematics and Science Study (TIMSS) 4th grade mathematics assessment. These countries share similar cultures and characteristics of their education systems. For example, in all these countries, education is segregated by gender, and achievement differences between boys and girls are among the largest in TIMSS-participating countries. The organization, teaching approaches, and learning culture also tend to share similar characteristics across Arab countries (Matar et al., 2014).

The Arab region lacks evidence in terms of educational research, despite some recent attention. In fact, only after investments implemented in the last years (Hallinger and Hammad, 2019), the area has started to be the focus of research in education (Boujaoude and Dagher, 2009). Nonetheless, scientific and technical disciplines retain a delay in terms of evidence coming from research in education (Kayan-Fadlelmula et al., 2022). Educational research in this landscape requires the use of specific methodologies which can account for the distinct cultural features of the Arab world (Oplatka and Arar, 2017), given that the approach to scientific learning is still heavily influenced by religion and tradition (Boujaoude and Noureddine, 2020). Therefore, the topic of the most effective teaching strategies can be of particular interest given the lack of evidence from this particular area, and how the effectiveness of the strategies themselves may be different from other areas given the specific cultural landscape of the Arab world.

Moreover, it is crucial to recognize that students’ individual characteristics play a significant role in shaping the effectiveness of various teaching strategies (Giambona and Porcu, 2015). As learners possess unique needs, abilities, and learning styles, a one-size-fits-all approach to instruction may not yield optimal results. Instead, tailoring teaching strategies to align with the specific requirements and characteristics of students becomes essential for promoting meaningful learning experiences. By understanding how individual factors influence the effectiveness of different instructional methods, educators can make informed decisions regarding pedagogical approaches that cater to the diverse needs of their students. Therefore, this study aims to bridge the research gap in the field of effective teaching strategies in mathematics, focusing specifically on Arabic-speaking countries. By examining the cultural nuances, technological landscape, and individual characteristics of students in this context, the study seeks to provide valuable insights that can inform the development of targeted and contextually relevant instructional practices. The ultimate goal is to contribute to the enhancement of mathematics education in the region, enabling educators to design curricula and implement teaching strategies that align with the unique needs and cultural dynamics of the Arab countries.

In this research, data from the 2019 TIMSS serve as the foundation for examining the relationship between student characteristics and the effectiveness of different teaching strategies in improving educational achievements. By utilizing this comprehensive dataset, the study aims to shed light on how various instructional approaches impact student outcomes. Furthermore, the investigation delves into the role of additional control variables, such as students’ socioeconomic background, which can be proxied by the availability of home resources. The theoretical framework developed by Spagnolo et al. (2020) provides a guiding structure for exploring the influence of these control variables. By employing the TIMSS data, the research allows for a multi-level analysis that considers the variation in the association between teaching strategies and student outcomes at the student, school, and country levels. This approach acknowledges that educational outcomes are influenced by factors operating at different levels of the educational system. By investigating these variations, the study can provide a comprehensive understanding of how teaching strategies interact with student characteristics within different contexts. The paper proceeds as follows: the first section reviews the relevant literature on the topic of the most effective teaching strategies in mathematics, the second section presents the data and the econometric methodology in detail, the third section presents the results of our analyses. The last section concludes and provides policy recommendations.

Literature review

Teacher-guided instruction, assessments, and feedback

Cognitive science provides a list of steps to promote knowledge transfer and retention, which include introducing small chunks of new material at once, systematic revision of the taught material, teacher support, and feedback while learning, presentation of problem-solving models, scaffolding, and constant supervision of whether students understand the material (Rosenshine, 2012). The effects of the teachers’ support on students’ learning are never one-dimensional. Thus, each strategy will have a different impact on student learning and perception of a subject (Suldo et al., 2009). Yet, teachers must be aware that there is no universal method to teach and learn effectively (Serin et al., 2009). Teachers can optimize the effects of teaching by understanding the strengths and weaknesses of students and learning how to address them effectively, which can accelerate the learning process (Sulaiman et al., 2010). The optimal teaching strategies require teachers to give feedback, be responsive, support students, and be flexible with the workload distribution (Reeve, 2002; Juuti et al., 2010). Such an environment can help teachers stimulate students’ interest in a subject and reduce their anxiety (Lapointe et al., 2005; Hidi and Renninger, 2006), as well as improve students’ cognitive engagement (Fredricks et al., 2005; Lazarides and Ittel, 2013). Using data from TIMSS, Eriksson et al. (2019) show how relating mathematics to daily life has a negative impact on achievements, while instead memorizing formulas and listening to the teacher have a positive one.

Many studies connect teacher support to student achievement (e.g., Malecki and Demaray, 2003; Lapointe et al., 2005; Lazarider and Ittel, 2013), as the former may exist in various forms and are crucial in creating an environment that promotes learning (Malecki and Demaray, 2003). Support in the form of feedback and promotion of learning has been shown to positively impact students’ academic outcomes (Wong et al., 2018). These practices are important to implement in each learning strategy to optimize student achievement, as teacher support correlates positively with students’ mathematics achievement and enhances the perception of the value of a subject outside of the school context (Rudasill et al., 2010; Han et al., 2023).

Research by Ünal (2017) has shown that mathematics teachers prefer teaching methods that do not require a lot of preparation, such as asking questions and lectures with demonstrations. The author highlights that teachers considered strategies that required more preparation, although significantly improving students’ cognitive engagement, to be a waste of their time (Ünal, 2017). Instructional goals, experience, and personal preferences can affect the teaching methods teachers prefer (Uibu and Kikas, 2014). In mathematics, the most preferred teaching strategies are found to be a question/answer methodology, and demonstrations (Ünal, 2017). Direct instruction and group work are also among the preferred strategies (Birgili et al., 2016).

The use of techniques of direct instruction, such as demonstration, in-depth explanations, and guided practice, provides an improvement in the academic achievement of students (Cadette et al., 2016; Stockard et al., 2018; Mason and Otero, 2021; Powell, 1980; Smith and Land, 1981; Wragg, 1989; Rosenshine and Stevens, 1984; Harris, 1998;) and improves independent problem-solving. This claim is supported by a longitudinal study conducted on American students from low-income families. Results have shown that disadvantaged students participating in classes conducted with direct instruction scored similarly to or higher than the national median in mathematics (Gestern et al., 1986). Moreover, Wong et al. (2018) analyzed Canadian students’ mathematics achievement in teacher instruction. They showed that a one-point increase in teacher instructional support leads to an increase of more than six points in students’ scores. Strati et al. (2017) also suggest that direct instruction helps students engage with assigned tasks. Overall, using instructional strategies that actively engage students in learning, focus on learning as a process, and use assessment can greatly improve students’ critical thinking in the mathematical context (Ebiendele, 2012).

Independent study and problem-solving

Another teaching approach that has gained recognition in the field of mathematics education is putting emphasis on independent study and problem-solving. These student-centered approaches place a strong emphasis on active exploration and discovery, encouraging students to ask questions, analyze data, and construct their understanding of mathematical concepts. By adopting this approach, students become active participants in their learning journey, engaging in meaningful investigations and problem-solving activities. This method significantly enhances students’ conceptual understanding, problem-solving abilities, engagement, and overall achievement in mathematics classes (Boaler, 2022; Chen, 2013; Krajcik and Czerniak, 2018; Tishman, Jay, and Perkins, 1993; Kuhn, 1999). This approach allows students to explore mathematical ideas hands-on and experientially. Students develop a deeper and more robust understanding of mathematical concepts by posing questions, conducting investigations, and collaborating with their peers. Through active participation in the learning process, they acquire knowledge and develop critical thinking skills, problem-solving strategies, and the ability to apply mathematical principles to real-world situations. Research has shown that inquiry-based instruction cultivates a positive learning environment where students are encouraged to think creatively, take risks, and develop a growth mindset toward mathematics (Boaler, 2022). By fostering a sense of ownership and autonomy in their learning, students are more likely to feel motivated and engaged, leading to improved outcomes in conceptual understanding and overall achievement.

Strategies engaging students with hands-on activities, allowing them to discover concepts through experimentation and problem-solving, are effective in motivating students to learn and in helping them to understand the relevance of this subject to their future lives (Bybee, 2010). Furthermore, hands-on activities like experiments and lab work allow students to apply their knowledge and skills in real-world contexts (Duit and Treagust, 2003). Using manipulatives is an effective strategy for exploiting a hands-on approach to mathematics (Sztajn, et al. 2012; Adams and Wiemelt, 2016). Minds-on activities, such as discussions and debates, help students develop critical thinking skills and engage with scientific concepts meaningfully (Windschitl et al., 2008).

A study by Waterman et al. (2020) found that students who received instruction highly focused on real-world application of mathematics scored significantly higher on a standardized mathematics test than students who received traditional instruction. A paper by Roschelle et al. (2000) further highlights this connection. Results of the Jasper Project show that students who participated in classes that developed their real-world mathematics experience reported a significant improvement in understanding and engagement in solving mathematics problems. Moreover, these students developed a more positive attitude towards mathematics. Ünal (2017) underlines the importance of the relationship between mathematical thinking and problem-solving and physical, social, and academically-designed learning contexts. Empowering students and giving them the confidence to solve problems independently is important. This can be done by engaging them in hands-on activities, where the teacher fulfills a more passive role. It is also valid to show students the value of their work and embrace their creativity. Therefore, according to the author, problem-solving should be the primary strategy in mathematics classrooms. A hands-on approach can also be merged with cooperative learning. It is one of the teaching strategies that encourages students to work in small groups to complete a task or solve a problem and increase social interaction and knowledge sharing among students (Johnson and Johnson, 1991). This can be a very effective method for students to learn critical thinking, problem-solving, and teamwork.

Research aims and questions

Based on the reviewed literature and recognizing the limitations of the TIMSS data, we propose to test how different teaching strategies are associated with 4th-grade student mathematics achievement. Our main research question is related to the relationship between mathematics achievement and teachers’ reliance on guided instruction or independent study. Our first hypothesis is that independent study is associated with higher student achievement. We test it by including the index of independent study in the multilevel regression, controlling for a set of indicators as explained below. Our second hypothesis is that teacher-guided instruction leads to improved student achievement. We test both hypotheses in the same model and separately, allowing the possibility that teacher use both strategies effectively in their classroom.

Additional research questions are related to the equity effects of relying on one of the teaching strategies. We test it using a random slope multilevel model by checking whether the slope of the index of home resources for learning is affected by the use of a particular strategy. First, we hypothesize that the use of teacher-guided instruction is beneficial for the students with disadvantaged background. This would be indicated by a negative interaction term between the index of teacher-guided instruction and the index of home resources for learning. In other words, we hypothesize that the frequent use of teacher-guided instruction alleviates the gaps between students with different socioeconomic backgrounds. Second, we hypothesize that the independent practice is more beneficial for students with privileged background, which would be indicated by a positive interaction term between the index of independent practice and the index of home resources for learning.

When testing these hypotheses, we control for non-malleable characteristics or other factors that could possibly affect achievement. Thus, we control for gender (student and teacher), school absences, and home resources for learning (a proxy for family socioeconomic background). TIMSS results show that these characteristics are associated with student achievement, especially in Arab countries where gender gaps and the share of students often missing school are above the average (Mullis et al., 2020). In addition, we consider student attitudes (liking math, self-confidence, and perception of instruction clarity) and school safety (bullying), which are also strongly associated with achievement in most countries and often used in the modeling of TIMSS and other data (for example, Wiberg et al., 2024; Xin, 2022; Özyıldırım and Karadağ, 2024). Finally, we control for the teacher’s formal education level and whether she or he has a mathematics degree, two characteristics that could be related to both the choice of teaching methods and student achievement. In the multilevel regression model, we also control for several indicators of teacher feedback and the use of assessments and homework, which are important characteristics of teaching discussed above. We expect these indicators to correlate positively with mathematics results. We also control for the emphasis on academic success, which reflects the school environment and shows a significant correlation with achievement in Arab countries (Mullis et al., 2020). Finally, we control for the overall use of various techniques used by teachers in their classrooms by including an index of active instruction. Higher values on this index indicate a higher frequency but also a variety of techniques applied by teachers.

The following two sections provide a detailed discussion of the data, variables, and multilevel regression models.

Data and variable selection

TIMSS is one of the leading international student assessments measuring students’ mathematics and science achievement in grades 4 and 8. The TIMSS 2019 edition is the seventh iteration of the assessment, administered every four years since 1995. It is organized by the IEA (International Association for the Evaluation of Educational Achievement) with an international consortium of experts and participating countries. The fourth-grade assessment had participation from 58 nations in 2019. Students who take part in TIMSS are typically in their fourth year of formal education, as long as their average age during the testing period is at least 9.5 years.

Within the TIMSS framework, the analysis of teaching strategies and their impact on mathematics achievement encompasses mathematics teachers in 4th grade. To investigate the relationship between teaching strategies and mathematics achievement, the study comprehensively examines both general teaching strategies and those specific to mathematics instruction. The study focuses on data gathered from Arabic-speaking countries participating in the 2019 TIMSS assessment. These countries include Bahrain, Kuwait, Morocco, Oman, Qatar, Saudi Arabia, and the United Arab Emirates. By including data from these specific countries, the research aims to provide insights into the teaching strategies employed in the Arabic-speaking context and their implications for mathematics achievement. By examining a diverse range of countries within the Arabic-speaking region, the study considers the cultural, educational, and contextual factors that may influence teaching practices and student outcomes in mathematics. Table 1 presents information on the size of the TIMSS datasets for the countries we included in our analysis, which we conducted using the Stata statistical software, including survey weights, and separately using student probability weights and classroom probability weights; for our analyses, we used the first plausible value in mathematics as the dependent variable. Our initial sample consisted of 60 956 students and 2653 mathematics teachers from the seven Arab countries.

Table 1 Samples for the Arab countries included in our analyses.
Full size table

This approach recognizes the importance of considering each country’s unique characteristics and educational systems when analyzing the impact of teaching strategies on mathematics achievement. By incorporating both general teaching strategies and mathematics-specific strategies, the study offers a comprehensive analysis of the various instructional approaches employed by teachers in the participating Arabic-speaking countries. This approach enables us to identify the teaching strategies most closely associated with improved mathematics achievement and provides valuable insights for educators and policymakers in the region. For our analysis, we included the teaching strategies made available by the TIMSS framework that relate to general or mathematics-specific teaching. Given the many available indicators, this allows us to understand which strategies are the most effective and how they may affect each other when considered together.

We grouped the different items referring to teaching strategies using item response theory. In particular, a partial credit model was applied to the ordinal items included in the teacher questionnaire. As a result, our methodology allows us to group teaching strategies depending on the content of several TIMSS items. This simplifies the analysis since the indicators obtained with item response theory will represent more general teaching practices. Nevertheless, at the same time, our choices allow us to maintain a substantial and reasonable distinction between the teaching strategies themselves, thus grasping several different teaching methods implemented by teachers in the class.

We included several indicators related to mathematics teachers and their instructional practices. At the teacher level, we consider the teacher’s education and degree in mathematics, the years of experience, the teacher’s gender, and formal education (as computed on the ISCED scale). We consider explaining new mathematics, explaining how to solve problems, memorizing rules, and working in the whole class as guided instruction; conversely, we consider making students practice procedures and apply what was learned as independent study. We further define the frequency of observing students’ work and asking students questions as in-class assessments, while the frequency of short assessments, longer tests, and long-term projects as formal assessments. Three more strategies were included: first, we considered the frequency of assigning homework; second, we added the frequency of feedback (which comprises correcting, discussing, and monitoring the completeness of homework); third, we envisage the frequency of tests on computers or tables (defined as computer-based-assessment, or CBA). To include further teaching methods in our investigation, we consider relating to student lives, explaining the answers provided by the teacher, bringing interesting material, challenging students to go beyond simple instruction, encouraging class discussion, linking knowledge, encouraging the development of the student’s problem solving, and encourage to express ideas as indicators of active instruction (these are the strategies which TIMSS surveys both for mathematics and science instruction). For these teaching strategies, teachers are asked the extent to which they use these strategies, with the possible answers being “Every or almost every lesson”, “About half the lessons”, “Some lessons”, or “Never”. In addition to these teaching strategies variables, we further use the emphasis on academic success, safe and orderly school, and teaching limited by student needs as control indexes, in the same way in which they are defined by the TIMSS framework but computed for Arabic-speaking countries only—this allows to have indicators that correctly indicate the situation of teachers and schools in this region.

In the same way, we considered student-level control variables, including gender, frequency of absences, bullying, availability of home resources (which corresponds to the index of socioeconomic status), liking mathematics, confidence in mathematics, and clarity in mathematics instruction (these last three indicators were averaged), in addition to mathematics achievements. The choice of these variables has been made for two separate reasons. On the one hand, they can be important control variables, thus we include them since they may affect the robustness of our estimations. On the other hand, they may also affect the effectiveness of teaching strategies themselves, given that—for instance—a more difficult class environment may prevent the teacher from implementing more advanced teaching strategies. Furthermore, the choice of teaching strategies may also, in return, affect the class environment or student attitudes. Thus, it is essential to include indicators of bullying and student attitudes in our models.

All the variables have been scaled so that higher values correspond to better outcomes (so, for instance, a higher value of bullying corresponds to a lower frequency thereof). The indicators were standardized so as to have an average equal to 0 and a standard deviation equal to 1 in the teacher- and student-level samples. The indexed computed at the student level were additionally decomposed in order to have a between- and a within-class effect in the multilevel model, obtaining variables centered on the class average. Table 2 presents the description and summary statistics of the variables used in the analyses.

Table 2 Description of the variables and summary statistics.
Full size table

Methodology

We employ two mixed models with different specifications to assess how teaching strategies impact mathematics achievement. We consider four specifications for the multilevel models with random intercept, with an additional six specifications for the multilevel models with random intercept and coefficients. Given the complexity of the TIMSS database, we use survey weights for the population estimates due to the random sampling of schools, classrooms, and students. To this aim, we use student probability weights and classroom probability weights separately. We further scale the student-level weights so that they sum to the sample size of the classroom clusters. The equation for the mixed model, where i indicates students and j indicates classrooms:

$${{\rm{Y}}}_{{\rm{ij}}}={{\rm{\beta }}}_{0{\rm{j}}}+{{\rm{\beta }}}_{1{\rm{j}}}{{\rm{X}}}_{{\rm{ij}}}+{{\rm{e}}}_{{\rm{ij}}}$$
(1)

where \({Y}_{{ij}}\) is a vector of responses – in our analyses, the plausible values of mathematics achievements, \({X}_{{ij}}\) is a matrix of fixed effects, and \({e}_{{ij}}\) is the error at the student level. In our analyses, the dependent variable \({Y}_{{ij}}\) is educational achievements in mathematics, while the fixed effect independent variables—which compose the matrix \({X}_{{ij}}\) – include teaching strategies and teacher and student characteristics. A second level equation can be added, describing the intercepts at the classroom level:

$${{\rm{\beta }}}_{0{\rm{j}}}={{\rm{\gamma }}}_{00}+{{\rm{\gamma }}}_{01}{{\rm{W}}}_{{\rm{j}}}+{{\rm{u}}}_{0{\rm{j}}}$$
(2)

In the equation, \({W}_{j}\) indicates the classroom-level predictors (which in our analyses include teacher characteristics, strategies, and the classroom-level averages of the indicators of bullying, student attitudes, and home resources), while \({u}_{0j}\) is a random error component. In the model, our assumptions are that the random components are normally distributed and not correlated.

We further expand the model in order to capture the effect that teaching strategies may have on the relationship between socioeconomic background (proxied by the availability of home educational resources) and achievements in mathematics. Here, we consider the slope of the socioeconomic background index to vary randomly within classrooms, explaining this random variability using different teaching strategies. These additional assumptions are considered in the following equation:

$${{\rm{\beta }}}_{1{\rm{j}}}={{\rm{\gamma }}}_{10}+{{\rm{\gamma }}}_{11}{{\rm{W}}}_{{\rm{j}}}+{{\rm{u}}}_{1{\rm{j}}}$$
(3)

Our methodology allows us to assess if the variance of random components that explain the coefficient of socioeconomic background is significantly different from zero. Furthermore, if this is not verified, teaching strategies can be used to explain the relationship. In our model, we assume that the random errors at the second level present unstructured covariance. Our random coefficient models are used to estimate the interaction between the different teaching strategies in mathematics and socioeconomic background. In this case, a positive coefficient would imply that a more frequent use of a given strategy would increase the impact of socioeconomic background.

Results

This section presents the results of our data analyses for 4th-grade students. For the first multilevel model (Eq. 2), we have four different specifications. In the first (1), we consider the empty model with no fixed effects, thus only accounting for the variance in achievements determined by classes and students. In the second (2), we include student variables only in the fixed effects matrix. In the third (3), we add teacher variables to the second specification. Lastly, in the fourth specification (4), we add teaching strategies to the third specification.

We have five different specifications for the second multilevel model (Eq. 3). Specifications (1) to (4) consider student- and teacher-level independent variables, then include an emphasis on academic success, the index of active instruction, the index of guided instruction, and the index of independent study separately in each specification. Lastly, specification (5) considers all these teaching strategies indexes together. Table 3 presents the results of the multilevel regression in the different specifications, while Table 4 shows the random coefficient model specifications results.

Table 3 Multilevel regressions with random intercept at the classroom level.
Full size table
Table 4 Multilevel regressions, random coefficient models.
Full size table

Our choice of models allows us to assess the consistency of our estimations and account for different factors. In particular, in the models with random intercept at the classroom level (Table 3), we included teaching strategies in the last specification to account for their impact after checking the effect of all the other student-, teacher-, and classroom-level variables. Furthermore, we computed the Intra-Class Correlation coefficient (ICC), which allows us to see how much of the overall variance in achievements can be attributed to classroom-level indicators (with the residual being due to student-level ones). It can be noted how this value is consistently above 30%, indicating a significant presence of inequalities between classrooms, which shows how significant gaps still exist in the quality of education provided to students.

In the random coefficient models (Table 4), we included the main teaching strategies identified previously, further including the interactions explaining the within-classroom slope of socioeconomic background (which is proxied by the index of availability of home resources). This allows us to evaluate to what extent the effectiveness of these teaching strategies is dependent on the level of socioeconomic background of the school and the student. In other words, we assess whether these strategies are more or less impact depending on whether there is a higher or lower availability of educational resources, providing evidence on the extent to which a lack of such resources may impair the effectiveness of teaching strategies themselves.

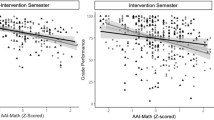
In the first specifications of the multilevel regressions, in terms of teaching strategies, the results indicate that guided instruction is negatively associated with achievements. It also shows that independent study is positively correlated with scores in mathematics. For the control variables, higher mathematics results are associated with lower bullying, more positive student attitudes, higher home resources, and a lower frequency of absences, both when considered at the student and at the class levels. Both homework and computer-based assessments are negatively associated with achievements. For emphasis on academic success, an increase by one standard deviation corresponds to an improvement of around 7% in the standard deviation of student achievement. In all the specifications of the multilevel model, more variance is found at the student level than at the class level, which is something that can indicate that the residual student characteristics account for a more substantial share of the overall variance in mathematics achievements—yet the share of variance explained by the class remains substantial.

In the random coefficient models, as before, guided instruction is negatively associated with achievements, while independent study shows a positive association. The interaction between these two teaching strategies and socioeconomic background is not significant. Only the emphasis on academic success is significantly associated with the slope of home resources on mathematics achievements. As in the previous models, the variance decomposition results show more variability at the residual student level than at the class level. Overall, the random slope model shows that both our expectations cannot be confirmed as guided instruction does not alleviate the relationship between achievement and socioeconomic background and that reliance on independent study does not increase social gaps in mathematics achievement.

Conclusions and policy recommendations

This paper studied the effectiveness of teaching practices on educational achievements in mathematics of 4th-grade students attending schools in Arab countries participating in the 2019 TIMSS assessment. The cognitive survey and the questionnaires administered to students and teachers allowed us to study how scores in mathematics are associated with individual characteristics and instructional strategies. We employed multilevel random intercept and random coefficient models for this aim. We used student-level variables (such as gender, the frequency of bullying, and the availability of home resources) and teacher-level variables (such as the teacher’s gender, formal education, and degree) and constructed indexes of mathematics instruction and student and classroom characteristics using item response theory.

The main research question of the paper is related to the association of mathematics achievement with teacher-guided instruction and with teachers’ reliance on independent practice. Our results suggest that strategies that involve guided instruction (such as explaining how to solve problems or having students memorize rules) are negatively associated with achievements, controlling for all other strategies and background characteristics. Conversely, independent study strategies (such as making students practice procedures and apply what was learned) are positively associated with achievements, conditional on other variables. Moreover, the results of random slope models suggest that neither of these strategies is associated with a change in the effect of socioeconomic background on student achievement. These findings should be interpreted cautiously. Our regression models control for a rich set of background characteristics and assessment strategies, but the results are based on associations, not causal effects. Moreover, the definitions of guided and independent practice used in TIMSS data are pretty specific. They both assume a relatively large teacher involvement, so none can be called “unguided” practice in the spirit of Kirschner et al. (2006). However, the results should be interpreted in the context of Arab countries, where traditionally, the expectation towards students is to memorize and repeat information rather than to practice independently and provide critical interpretations of their findings. In this context, our results show that less guided practice is positively associated with student mathematics achievement.

Our results confirm that school safety (less frequent bullying), less frequent absenteeism, positive attitudes (liking mathematics, self-confidence, perception of clarity in mathematics teaching), and better availability of educational resources at home are all positively associated with mathematics achievement. These outcomes are robust, being verified at both the student and class levels and consistently across the four model specifications of fixed-effects models and the six model specifications of random-effects models. They also align with previous research we reviewed in the paper. Our results also show that various assessment strategies are not significantly related to mathematics achievement. On the other hand, the random intercept and the random coefficient models show that school emphasis on academic achievement is positively associated with math scores and strengthens the relationship with home resources. |In other words, while teaching strategies do not alter the relationship between family background and achievement, a higher emphasis on academic success increases inequalities in mathematics achievement in Arab countries by leveraging the results of students with higher resources at home.

Based on the study’s findings, we suggest a greater emphasis on using independent study as a teaching strategy in mathematics classrooms in Arab countries. Independent study encourages students to take ownership of their learning, explore mathematical concepts at their own pace, and develop self-directed learning skills. By promoting independent study, teachers can foster students’ autonomy and enhance their critical thinking and problem-solving abilities. Secondly, the mathematics education system should stress the importance of academic success. Emphasizing the significance of academic achievement can motivate students to set higher goals and strive for excellence in their mathematical learning. However, this approach may increase existing inequalities in academic achievement. Therefore, efforts should ensure that all students, regardless of their socioeconomic background, have equitable access to resources and support to aid their academic success.

Additionally, at the school level, addressing safety concerns and creating a conducive learning environment is crucial. Bullying, as identified in the study, negatively impacts mathematics achievement. Therefore, schools should implement appropriate measures to prevent and address bullying incidents, ensuring students feel safe and supported in their learning environment. Furthermore, schools should foster positive student attitudes towards mathematics, promoting a culture where students value and enjoy learning the subject. This can be achieved through engaging instructional practices, creating opportunities for student collaboration and exploration, and highlighting the relevance of mathematics to real-world applications.