Introduction

Number sense (NS) encompasses the capacity of individuals to comprehend the meanings of numbers, to determine the relationships between them, to compare their magnitudes, to understand the effects of operations, and to recognize appropriate reference points (McIntosh et al., 2005; Reys et al., 1999; Yang, 2019a, 2019b). Proficiency in NS and arithmetic operations is very important for mental reasoning and problem-solving skills (National Council of Teachers of Mathematics [NCTM], 2000). Therefore, NS plays a fundamental role in mathematics education and is included in the curriculum in many countries. However, studies conducted around the world and in Turkey reveal that a large proportion of primary and secondary school students show deficiencies in NS skills (Facun & Nool, 2012; İymen & Duatepe-Paksu, 2015; Li & Yang, 2010; Yang & Sianturi, 2021). Students’ NS performances are based on the strategies they use (Yang & Li, 2008; Yang & Lin, 2015), their grade level (Akkaya, 2016; Jordan et al., 2007) and cultural context (Aunio et al., 2006). The positive relationship between NS and mathematical achievement emphasizes the importance of the development of these skills in terms of academic achievement (Akkaya, 2016; Çekirdekci et al., 2016; Jordan et al., 2010; Kayhan Altay, 2010; Mohamed & Johnny, 2010; Tunalı, 2018; Yang et al., 2008). In addition, counting skills and NS have been identified as determinants of primary school mathematics achievement (Birgin et al., 2021; Sari & Olkun, 2021).

Many studies have been conducted on number sense around the world, and there are important studies in this field in Türkiye (Almeida et al., 2016; Can & Yetkin Özdemir, 2020; Dehaene, 1997; McIntosh et al., 1997; Reynvoet et al., 2021; Şengül & Zora, 2023). However, research on the SD performance of gifted students (GS) is limited (Diezmann & English, 2001; Rotigel & Fello, 2004; Wang et al., 2017). Original studies examining the differences between the NS skills of gifted and typically developing students (DS) are extremely rare (Yang & Chang, 2023; Tertemiz et al., 2023). Studies show that gifted children are able to use flexible strategies in their problem-solving processes (Diezmann & English, 2001; Reynvoet et al., 2021). In the literature, it has been stated that individuals with strong NS have the ability to develop and implement flexible and effective problem-solving strategies (Şengül & Gülbağcı, 2012; Yang & Li, 2013).

Gifted students have the potential to use number sense not only as a foundation of knowledge but also as a tool for strategy development and creative problem-solving. This makes NS a critical element in the understanding and development of problem-solving skills. A detailed examination of the NS performance and strategies of gifted students is necessary to understand how these skills differ from those of typically developing students. This type of research can contribute to educational policies and guide the development of effective teaching strategies suitable for different learning needs. Understanding the use of NS by gifted students can support the design of more flexible and creative problem-solving methods in education. Thus, both academic success increases and evidence-based solutions are produced for the needs of different student groups. In conclusion, the comparative examination of NS performances and strategies has a critical role in improving not only mathematical competence but also effective teaching approaches for different groups of students. This research will contribute to global educational goals that support mathematical thinking skills.

Number sense: definition, components, and importance in mathematics education

Number sense is defined as an important cognitive capacity that guides individuals’ conceptual understanding of numbers, their interaction with operations, and problem-solving processes. In the literature, number sense has been addressed by various disciplines, leading to the development of several definitions. Cognitive psychology and neuroscience research emphasize the biological foundations and evolutionary development of number sense, while educational sciences argue that this capacity can be developed through teaching and is directly related to academic achievement. These different approaches suggest that number sense is an innate ability shaped by environmental factors.

Cognitive research shows that number sense is one of the fundamental building blocks of the human mind, related to cognitive mechanisms that allow individuals to make sense of quantities. According to Geary, number sense includes individuals’ abilities to understand numbers, establish relationships between numbers, and compare numerical magnitudes. This concept is not limited to numerical operations but also includes cognitive processes such as perceiving numbers and understanding broader concepts associated with numbers (Geary, 2004; Geary et al., 2009). Number sense is a fundamental factor influencing mathematical success and may be a determinant of mathematical learning difficulties, especially for children aged 6-9 (Geary et al., 2009; Jordan et al., 2010). Geary also states that number sense is a factor that enhances mathematical problem-solving skills and is also associated with more complex cognitive processes (Geary, 2012). This indicates that number sense plays an important role in individuals’ overall cognitive development, and the meaning of numbers and their representations are part of a broader range of cognitive skills (Geary, 2012). McIntosh and colleagues (2005) define number sense as the ability to develop skills in using numbers, acquiring knowledge about operations, and applying this knowledge flexibly. Dehaene (1997) argues that number sense is an evolved capacity supported by the approximate number system (ANS). ANS is defined as a mechanism that allows individuals to intuitively estimate the magnitudes of numbers, an innate ability. Neuroscientific research also sheds light on the biological foundations of number sense. Leibovich and colleagues (2016) highlight that number sense is not unique to humans and that many animal species have similar quantitative evaluation processes. Vandervert (2017) states that number sense is supported by the cerebellum, while Reys and colleagues (1999) describe it as the ability to understand the meaning of numbers, their magnitudes, and the effects of operations. These studies show that number sense is not only a skill that can be developed through education but also a biological capacity supported by specific neurocognitive mechanisms.

From the perspective of mathematics education, the critical role of number sense in the learning process is clear. McIntosh and colleagues (2005) view number sense as the foundation for advanced problem-solving skills, while Van de Walle and colleagues (2010) state that number sense includes individuals’ abilities to comprehend the meanings of numbers, compare their magnitudes, and demonstrate flexibility when performing operations. The National Council of Teachers of Mathematics (NCTM, 2000) argues that the development of number sense increases individuals’ capacity to perform calculations, make estimations, and understand mathematical relationships. Fuchs and colleagues (2006) show that number sense supports flexible thinking skills and contributes to developing more efficient strategies by reducing cognitive load. Developmental studies reveal that number sense develops early and is a critical factor in predicting mathematical success. Jordan and colleagues (2007, 2009) emphasize the importance of supporting number sense in early childhood, while Mazzocco and colleagues (2011) state that this skill plays a central role in acquiring basic mathematical skills. Gökçe and colleagues (2022) highlight that number sense improves students’ ability to make estimations and perform operations, stressing that it should be integrated into teaching processes.

The development of number sense emerges as an important factor affecting students’ mathematical success and advanced mathematical skills. Whitacre and colleagues (2020) emphasize that number sense is often used to refer to different cognitive constructs in the literature, which can lead to conceptual confusion. The researchers argue that number sense can be examined at three fundamental structural levels: (1) the innate and evolutionary mechanism of the Approximate Number System (ANS), (2) the informal number sense that develops in early childhood, and (3) the educationally shaped number sense, which includes skills such as strategic use of operations, estimation, and understanding numerical relationships. These constructs are not stages of the same process but are qualitatively distinct concepts. Therefore, it is crucial to clearly specify which construct is being focused on in number sense research. In this study, the thinking processes and strategies used related to number sense among both gifted and typically developing middle school students were examined, with particular emphasis on educational number sense, which can be developed through instruction. Consequently, rather than focusing on innate biological mechanisms or intuitive systems, the study concentrates on the cognitive and educational aspects of students’ ability to form relationships with numbers, make sense of operations, and develop problem-solving strategies. In this study, the focus has been on aspects of number sense such as individuals’ ability to make sense of numbers, identify relationships between numbers, compare magnitudes, and understand the effects of operations (McIntosh et al., 2005; Reys et al., 1999; Yang, 2019a, 2019b).

These studies demonstrate that number sense plays a critical role in individuals’ interactions with numbers and in their mathematical thinking processes. To better understand the number sense, this concept has been divided into various sub-components (Greeno, 1991; İymen & Duatepe-Paksu, 2015; Kayhan Altay, 2010; Markovits & Sowder, 1994; McIntosh et al., 2005; Reys et al., 1999; Yang & Li, 2008; Yang & Lin, 2015; Yang, 2019a, 2019b). For example, Reys et al. (1999) classified the five basic components of number sense based on the work of McIntosh, Reys, and Reys (2005). Comparisons between different classifications have revealed that the most common components of number sense are the use of multiple representations of numbers and the understanding of the magnitudes of numbers (Şengül & Gülbağcı, 2013).

In addition, Şengül and Gülbağcı (2013), in their research on the categorization of the components of the number sense, stated that there is no universally accepted classification in the literature. It has been stated that the most comprehensive classification was proposed by McIntosh et al. (2005). This indicates that there is no vague and precise definition of the limits of the number sense. Previous studies reveal that the components of the number sense vary according to the mathematics curriculum, grade level, and subject content, and different definitions are made for the components that express the same skill (Birgin & Peker, 2024). Singh (2009) proposed five main components based on the classification prepared by McIntosh, Reys, Reys, Bana and Farrell (1997). These components are also used in this study and are described in Table 1 (McIntosh et al., 2005; McIntosh et al., 1997; Singh, 2009).

Table 1 Components of number sense with descriptions and examples.
Full size table

Students with sufficient knowledge of number sense (NS) are able to develop effective strategies for making mathematical assessments and solving complex problems (NCTM, 2000). Students with strong number sense can produce appropriate solutions to the problems they encounter in their daily lives and education, they can use their mathematical knowledge comfortably, and they know when to apply their strategies. They can also perform calculations from the mind by manipulating numbers, can easily spot patterns and connections, and love to play with numbers (Jordan et al., 2006; Maghfirah & Mahmudi, 2018; Mohamed & Johnny, 2010; Yang & Chang, 2023).

Studies emphasizing the importance of number sense have revealed that these skills need to be developed, especially in primary school students (Dehaene, 1997; Greeno, 1991; Halberda & Feigenson, 2008). According to NCTM (2000) standards, students are expected to understand number systems, relationships, and numerical values, and to be able to make accurate predictions by comprehending the connections between operations. Although the number sense is not directly addressed in the post-2005 mathematics curriculum in Türkiye, skills such as mental calculation and estimation are included in the curriculum (MoNE, 2009; 2018). While the post-2009 curriculum places more emphasis on number sense skills, the 2018 curriculum emphasizes topics such as addition, subtraction, rounding, estimation strategies, and understanding of the relationships between operations. In the study by Karabey et al. (2019), it was stated that the number sense skills of Turkish secondary school students were not emphasized enough in the curriculum, but there were activities associated with some goals. Similarly, it is seen that mathematics programs prepared for gifted students do not include enough number sense acquisitions. National-level studies (Akkaya, 2016; Birgin & Peker, 2024; Iymen, 2012; Kayhan Altay, 2010) have shown that there are inadequacies in the development of number sense skills. In particular, it is emphasized that more research needs to be done on the differences between the number sense performance of gifted students and typically developing students.

Giftedness, gifted students in Turkey

The concept of giftedness has become an important research topic, especially in Turkey’s education and psychology literature, and it has garnered increasing attention. This concept refers to individuals who possess significantly higher abilities in certain areas compared to their peers. Over time, definitions of giftedness have evolved in line with different theoretical approaches, transforming into a multidimensional understanding that aims to consider not only cognitive abilities but also creative, social, and emotional developments. In the early period, Terman’s intelligence tests defined giftedness mainly based on IQ levels, where individuals in the top 2% of standard tests were considered gifted (Terman, 1926). In this definition, the focus was on high intelligence as the basis of giftedness, but in the following years, this understanding expanded to include social, emotional, and creative potentials (Schroth & Helfer, 2009). Similarly, Hollingworth’s (1927) approach linked giftedness with IQ scores of 130 and above.

Different theoretical models defining giftedness have expanded the scope of the concept and contributed to the development of a multidimensional perspective. Renzulli’s Three-Ring Conception of Giftedness (2016) introduced a new educational direction by emphasizing that giftedness involves not only high cognitive abilities but also creativity and task commitment as motivational components. Gagné’s Differentiated Model of Giftedness and Talent (2008) offers a developmental perspective by defining talent as an achievement that results from the interaction between innate potential and environmental as well as intrapersonal catalysts. Sternberg’s Triarchic Theory of Intelligence (1997) highlights cognitive diversity by focusing on analytical, creative, and practical dimensions of intelligence. Although Gardner’s Theory of Multiple Intelligences (2000) has raised awareness regarding different learning styles in the educational field, it has been subject to criticism for its limited empirical validity and is therefore considered controversial within the literature. This diversity has led to a more holistic approach in identifying gifted individuals and addressing their educational needs, by incorporating factors beyond intelligence tests—such as creativity, motivation, and environmental interaction. In Turkey, the Anadolu-Sak Intelligence Scale (ASIS), implemented by the Ministry of National Education, effectively evaluates the cognitive abilities of children aged 4-12 while providing an approach aligned with international standards (Sak et al., 2016).

From the past to the present, the definition of giftedness has moved beyond a narrow view based solely on cognitive intelligence. Now, a multidimensional perspective is accepted, which embraces the understanding of learnable and developable abilities and includes social and emotional characteristics in the definitions (Baker, 2001). The concept of potential, not limited to academic success, such as creativity, defines giftedness not only by intelligence but also by the individual’s unique strengths (Besançon et al., 2013). Moreover, the inclusion of gifted students in educational processes necessitates an equal opportunity approach, reinforcing the importance of policies aimed at bridging the differences between specific ethnic groups and socioeconomic levels.

Studies have revealed that gifted students exhibit advanced mathematical abilities based on advanced number sense (NS) and cognitive strategies from an early age. It has been noted that these students often develop abstract reasoning skills, innovative problem-solving approaches, and a deep understanding of mathematical concepts (Clark, 2002; Maker, 2003; Rotigel& Fello, 2004). The correlation between number sense and mathematical achievement is well documented, emphasizing that gifted students not only excel in mathematics, but also develop unique methods of understanding and benefiting from numerical relationships (Wang et al., 2017; Altıntaş et al., 2023). However, research on the number sense performances of gifted individuals has been limited (Özdemir, 2019). This situation reveals the need for more studies to examine how the cognitive abilities of gifted students affect mathematics learning and success. The available literature suggests that these students’ focus, adaptability, and metacognitive skills contribute significantly to their achievement in mathematics (Diezmann et al., 2004; Juter& Sriraman, 2011).

Previous studies on number sense

Number sense (NS) is a critical concept that deepens students’ mathematical thinking processes and enriches their problem-solving skills with flexible strategies. In the literature, there are many studies that deal with the relationship between NS and academic achievement, learning strategies and individual differences (Aktaş & Özdemir, 2017; Gürefe et al., 2017; Harç, 2010; Kayhan Altay, 2010; Mohamed & Johnny, 2010; Tunalı, 2018). These studies highlight the impact of NS on math achievement and reveal that it has an important role in understanding the observed differences among students. The study conducted by Birgin and Peker (2024) in Türkiye revealed that NS performance was significantly affected by contextual factors such as gender, school location, parental education level, perceptions of mathematics teachers, and parental support. The study highlighted the importance of contextual variables, emphasizing the indirect effects of NS on academic achievement. Singh et al. (2019) stated that strong NS skills are a key determinant of improving overall math performance. On the other hand, Akkaya (2016) revealed that students tend to prefer rule-based approaches as they progress in grade level, which may negatively affect NS skills. NS has a strong relationship with mathematical learning areas. Samasunda’s (2024) study showed that there is a direct link between algebraic thinking and NS, and that deficiencies in students’ algebraic skills may be due to poor NS skills. In this context, it has been stated that the development of NS, especially at the middle and high school level, can play a key role in improving students’ algebra performance. Can and Yetkin Özdemir (2020) examined the impact of context-based tasks on NS strategies, but revealed conflicting findings regarding the impact of such tasks on students. This suggests that contextual complexities should be taken into account in NS teaching.

It has been revealed in many studies that students generally resort to rule-based methods in NS problems and are inadequate in developing flexible strategies (Alsawaie, 2012; Can & Yetkin Özdemir, 2020; Yang, 2019b). Şengül and Zora (2023) analyzed the strategies used by students at different levels of academic achievement in NS problems related to fractions, showing that there are significant differences in the use of strategies. International literature, on the other hand, highlights the NS deficiencies of primary and secondary school students and their inability to develop flexible strategies (Aunio et al., 2006; Yang &Sianturi, 2021). Studies on the differences in NS performance and strategies between gifted and typically developing students are limited. Tertemiz et al. (2023) revealed the significant differences between these two groups, but stated that these differences should be examined in detail. Similarly, Wang et al. (2017) highlighted the relationship between NS and symbolic math performance of gifted students, drawing attention to the importance of NS in the cognitive processes of these individuals. Yang and Chang (2023), on the other hand, stated that the performance differences between the two groups of students are not clear and that more research needs to be done in this area.

The available literature suggests that NS performance and strategies have not been examined in detail on a component basis among gifted and typically developing students. In this direction, this study aims to analyze the NS skills of gifted and typically developing students at the 6th grade level and the strategies they use in NS problems on the basis of NS components. This comprehensive analysis aims to gain an in-depth understanding of students’ numerical intuition, as well as to contribute to the development of effective strategies for teachers and other students. The research, which aims to fill this gap in the literature, will be a guide for the improvement of NS teaching strategies.

Research questions

This study focused on the detailed examination and comparative presentation of the NS performances and the strategies students use to solve NS problems in terms of NS components of students with typical development and gifted students in 6th grades in Turkey. Thus, it is considered that focusing on the strategies of students at different intelligence levels while solving NS problems by taking into account the NS components will contribute to the literature and offer a different perspective for the discussions about the relationship between Number sense (NS), Number sense components (NSC), problem solving strategies and intelligence levels in the field literature. In this context, the following research questions were formulated and tried to be answered.

  1. 1.

    How are the NS performances of gifted and typically developing students?

  2. 2.

    Is there a significant difference in NS performance of students based on student characteristics (gifted-typically developing students)?

  3. 3.

    What are the strategies employed by gifted and typically developing students when solving problems in the NS test?

  4. 4.

    How do the strategies used by gifted and typically developing students when solving problems in the NS test differ according to NSC?

Methods

Research model

In this research, within the framework of a mixed-method approach where both quantitative and qualitative research methods are used together, an explanatory sequential design is employed. Explanatory design is a mixed-methods design where the researcher begins with a quantitative phase and then proceeds to search for specific outcomes in a second phase (Creswell & Clark, 2017). In this design, quantitative and qualitative processes are sequentially conducted within one or more research components or between components (Leech & Onwuegbuzie, 2009).

The use of a mixed-methods approach in this study was aimed at providing a more comprehensive analysis by integrating both quantitative and qualitative data. The quantitative phase allowed for an overall understanding of the performance levels of gifted and typically developing students, while the qualitative phase helped to explore and explain the strategies employed by students when solving number sense (NS) problems, thereby facilitating a deeper understanding of the findings (Tashakkori & Teddlie, 2010). The selection of students for both the quantitative and qualitative dimensions of the research is elaborated in detail under the sampling section.

Participants

The quantitative participants group comprises 6th-grade students (11-12 years old) from a province in the Southern region of Turkey. This group includes 63 gifted students (34 Females, 29 Males) who have an IQ of 130 or higher, determined through an examination administered by the Ministry of National Education. Additionally, there are 53 students (30 Females, 23 Males) exhibiting typical development. A convenient sampling method was employed for selection, with gifted students attending a Science and Art Center within the same province, while typically developing students attend public schools in the same province. In Turkey, students identified as gifted receive supplementary education in Science and Art Centers alongside their regular schooling. Gifted students in this study scored 130 or above on the ASIS intelligence test administered by the Ministry of National Education. Typically developing students are those who have not exceeded the specified IQ range in this test.

The qualitative sample group consists of 28 students in total, with 14 gifted students and 14 typically developing students. These students were selected using the criterion sampling method based on the quantitative research group. Selection criterion was being among the upper group 27% performers in the NS performance test and volunteering to participate in the study. The process for determining the sample is presented in Fig. 1.

Fig. 1
figure 1

Sample determination in the mixed methods process.

Full size image

The reason for selecting 6th-grade students in the research is that the necessary background knowledge to solve problems in the Number sense test (NST) (Fractions, Decimal representation, Percentages), has been imparted to students through the mathematics curriculum until the end of the 6th grade.

Data collection tool

The data collection tool comprised 25 questions derived from the NST, as adapted by Singh (2009) from McIntosh et al. (1997). Original version of the NS test, certain questions were excluded due to their lack of suitability for the students’ level, following consultation with field experts in mathematics education and experts working with gifted individuals. In addition, after the NST, was prepared, the opinions of a language expert were taken for translation control and in this direction, arrangements were made in the questions where the measurement units (gallons, miles, etc.) that are not used in Turkey in the original form were used, and the test was finalized. In Table 2, the components of the NST, the distribution of questions related to these components and sample items are given.

Table 2 Sample items according to NSC.
Full size table

Qualitative data was obtained using document analysis and interview techniques. As documents, the responses of 28 students to the NST problems were utilized. The interviews were conducted with the same students to determine the strategies they used while solving the problems in the NST.

The interviews began one week after the completion of the NST problem-solving tasks, and the process of interviewing all students took approximately one month. Prior to the interviews, the students were shown their responses to each question again to help them recall their answers. The interview questions were designed to deeply analyze the students’ problem-solving processes and strategies. To this end, four open-ended questions were asked to encourage students to explain their solution processes and preferred methods. The questions focused on eliciting detailed information about the students’ approaches to reaching the solution, the steps they followed, the strategies they used, and the reasons behind their preferred methods.

Collection and analysis of the data

The research data underwent analysis employing both quantitative and qualitative methodologies. As quantitative data analysis methods, descriptive statistics were employed to calculate arithmetic mean and standard deviation values. Additionally, a t-test was conducted to determine whether there was a significant difference between the NS performance averages of gifted and typically developing students. In the quantitative data collection process, each student was given 75 seconds for each question and instructed to complete the solution within the specified time. In the NST consisting of 25 items, correct answers were scored as 1 and incorrect answers as 0. The reliability analysis of the NS test was performed by calculating the Cronbach's Alpha coefficient. As a result of the reliability analysis, the Cronbach's Alpha value was calculated as 0.926. For the Cronbach Alpha (α) coefficient to be acceptable, it must be 0.70 and above (Creswell, 2009). Cohen, Manion, and Morrison (2007) accept the Cronbach Alpha coefficient as very reliable if it is above 0.90, highly reliable if it is between 0.80 and 0.90, and reliable if it is between 0.70 and 0.80.

After the students finished answering the questions in the test, students in the qualitative sample of the study were interviewed to find out the strategy they used while solving the questions. During the interviews, the focus was on determining the strategies used while solving the problems, rather than whether the answers were correct or incorrect. The qualitative data collection process lasted approximately one month. During this process, each student was interviewed individually in a quiet room. Each interview lasted between 40 to 45 minutes. The interviews were recorded by a recorder after the necessary consent had been obtained from the students. The audio recordings obtained from the interviews were transcribed, and they were analyzed descriptively. Descriptive analysis is the summarization and interpretation of research data according to predetermined themes (Yıldırım & Şimşek, 2013). To keep the identities of the interviewed students confidential, the students were given S1, S2, … codes.

The strategies used in solving NS problems are coded in four categories: Rule-based strategy (RBS), NS-based strategy (NSBS), partly number-sense-based strategy (PNSBS). The meanings and Other Responses, content of these strategies are given in Fig. 2.

Fig. 2
figure 2

Strategies.

Full size image

To ensure the validity of the qualitative data, member checking was employed. In this process, the transcripts obtained from the interview recordings were returned to the students, and their feedback on the accuracy of the transcripts was confirmed. Additionally, during the coding process, two researchers independently conducted coding, and the inter-rater reliability was calculated, resulting in a 94% agreement rate (Miles & Huberman, 1994). These procedures significantly enhanced the validity of the obtained data.

Findings

Findings and interpretations of students’ number sense

In Table 3, the average scores and standard deviations obtained by students from the NST are provided separately for each student type. Additionally, the results of t-tests conducted to determine whether there are significant differences in the mean scores obtained from the NST among different student types are presented.

Table 3 Average Scores of Students on the Test According to NSC and t-test results.
Full size table

From the table, it is seen that gifted students achieved higher scores in all components and in total (p < 0.01). However, it is noteworthy that the standard deviation value of the scores of gifted students is higher (4.97 > 2.44) compared to the typically developing students. This finding shows that the scores of gifted students exhibit a more heterogeneous distribution. In summary, gifted students perform significantly higher on the number sense (NS) test than students with typical development.

Findings and interpretations regarding the strategies employed

The average NS score of the students in these two groups from the total answers obtained from the 25 items in the NST is 20.57 (Gifted upper group), 7.92 (Typically developing upper group), respectively. A total of 350 data points (14 × 25) were obtained from interviews conducted to determine the strategies employed by students in the gifted upper group. The distribution of the strategies used by these students according to the NSC is given (Table 4).

Table 4 Strategies used by gifted students in the upper group according to NSC.
Full size table

According to the table, the most common strategy is NSBS (Number Sense-Based Strategies) with 44.28%, followed by PNSBS (Pre-number Sense-Based Strategies) with 34.28% and RBS (Rote-based Strategies) with 14%. The components for which the NSBS strategy is most frequently used are to understand the process impact (3rd Component-70%), using equivalence representation (4th Component-66.07%) and understanding of the concept of numbers (1st Component-50%). The most common components of the PNSBS strategy are the use of multiple representations (2nd Component-61.42%) and calculation and counting strategies (5th Component-50%). In the 5th component, where calculation and counting strategies are implemented, RBS is the most frequently used strategy, with a utilization rate of 32.85%.

A total of 350 data points (14 × 25) were obtained from interviews conducted to determine the strategies employed by the students in the upper group exhibiting typical development. The distribution of the strategies used by these students according to the NSC is given below (Table 5).

Table 5 Strategies used by typically developing students in the upper group according to NSC.
Full size table

As a result of the analysis, 21.71% of the strategies used by typical students were determined as NSBS (Number Sense-Based Strategies), 24% of them were determined as PNSBS (Pre-number Sense-Based Strategies), and 28.85% of them were determined as RBS (Rote-based Strategies). The most common component of the NSBS strategy was understanding the process impact (Component 3-28.57%). The most frequently used component of the PNSBS strategy is the use of multiple representations (2nd Component-31.42%). In the 5th component, where calculation and counting strategies are applied, RBS is the most widely used strategy, with a usage rate of 39.28%.

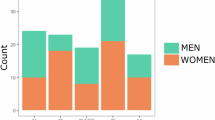
The findings regarding Table 3 and Table 4 have been visualized for easier interpretation. The graph is presented below (Fig. 3).

Fig. 3
figure 3

Graph illustrating the strategies used by gifted students (GS) and typically developing students (TDS) in the upper groups according to the NSC.

Full size image

Figure 3 shows that gifted students, who exhibit high number sense (NS) performance, predominantly prefer number sense-based strategies (NSBS) and partially number sense-based strategies (PNSBS), while typically developing students tend to lean more toward rule-based strategies (RBS). The data reveal that although both groups include students with high-level performance, gifted students’ NS performance (20.57) is significantly higher compared to typically developing students’ NS performance (7.92). This suggests that the preference for number sense-based strategies among gifted students is not only a strategic choice but also may be related to their cognitive capacity, intelligence and number sense levels. These findings highlight the need to move beyond rule-based approaches in teaching processes, emphasizing strategies that support mathematical reasoning and number sense.

Both gifted and typically developing students are observed to utilize NSBS most frequently in problems involving the third component in NST. Below is the solution provided by a gifted student who used a NSBS in a problem involving the 3.component, along with explanations (Fig. 4).

Fig. 4
figure 4

The solution of S12 (GS).

Full size image

The explanation of the student who gave the answer in Fig. 4 for item 3 is as follows: “When we divide the number 29 by the number 1, we reach the result of 29. The number 0.8 is less than 1. So we divide 29 by a number smaller than 1. In this case, our answer would be greater than 29 (S12). The solution and students’ views on this issue are examined together, and it can be said that S12 uses an NSBS.

Typically developing students are observed to use RBS most frequently in problems involving the 4. component in NST. Below is the solution provided by a typically developing student who used an RBS in a problem involving the fourth component, along with explanations (Fig. 5).

Fig. 5
figure 5

The solution of the S10 (TDS).

Full size image

The student’s explanation for the answer in Fig. 5 for Item 24 is as follows: “As I showed on the answer sheet. I multiplied the number 6 by 347. I divided my result by 43 and reached the result of about 28. I said it would be the most appropriate A option (S10)”. The solution and students’ views on this subject are examined together, and it can be said that S10uses RBS. Here, the student used the algorithm, made a processing mistake and selected the wrong option.

Below are the responses of a gifted student and a typically developing student to a problem involving the 4th component in an NST (Fig. 6).

Fig. 6
figure 6

The solutions of the S5 (GS) and S11 (TDS).

Full size image

The explanation of S5, who gave the answer in Fig. 6 for item 9, is as follows: “I have added one from 146 to 144. There were two 145. The other two numbers are already greater than 145. As a result, there are 4,145 s in option A. There are 4 results greater than 145 in option B (S5).“The solution and students’ views on this issue are examined together, and it can be said that S5 used an NSBS.

The explanation of S11, who gave the answer in Fig. 6 for item 9 is as follows: “I have collected four 145 s one by one. I gathered all the numbers on the other side one by one. When I compared the results, I found that option B was higher than the result (S11).”The solution and students’ views on this issue are examined together, and it can be said that S11 used an RBS.

Discussion and conclusions

The findings of this study reveal that the number sense (NS) performance of gifted students is higher than that of typically developing students, and this difference is statistically significant. This result is consistent with previous research showing that gifted students have a stronger sense of number with improved cognitive capacities and problem-solving strategies (Authors, 2022; Arabacı, 2023; Yang & Chang, 2023). Gifted students’ elevated number sense can be attributed not only to advanced cognitive abilities but also to enriched educational experiences. While much of the literature highlights cognitive capacity, it is equally important to consider how teaching strategies, learning environments, and access to advanced opportunities shape the development of number sense. Studies have shown that gifted students tend to approach problem-solving flexibly, employing methods such as estimation and comparison to efficiently tackle numerical tasks (Alelyani, 2021; McCoach & Flake, 2018; Subani et al., 2024; Yang & Chang, 2023; Wang et al., 2017). In the literature, it is emphasized that gifted students’ number sense performance is related to their ability to use more flexible and effective problem-solving strategies (Authors, 2022). Gallagher (2019) indicates that the metacognitive skills of gifted students are different from those of typically developing students and that these students have a deeper understanding and strategic thinking ability in the process of solving mathematical problems.

Flexible problem-solving strategies are not distinct from number sense; instead, they represent its active application. Through the use of techniques like estimation and comparison, gifted students outperform their peers by solving problems more efficiently. Number sense fosters a flexible mindset in mathematical processes, enabling students to employ a broader set of strategies and attain higher achievement. Wang et al. (2017) also found a positive correlation between gifted students’ number sense performance and their overall mathematical success, reinforcing the broader impact of number sense beyond problem solving. Although cognitive abilities are frequently highlighted in discussions of gifted students’ numerical skills, the influence of differentiated instruction and enriched curricula must not be overlooked. Such tailored educational approaches may significantly contribute to performance outcomes, suggesting that the observed advantages stem from the interplay of cognitive and environmental factors.

Research conducted by Callahan et al. (2017) emphasizes that the enriched programs in which gifted students are trained support their cognitive development and reinforce their mathematical abilities. Strategies used in education have had an impact on students’ numerical flexibility (Clements & Sarama, 2011; Siegler, 2016). Enriched educational environments are designed to advance the cognitive capacities of gifted students and directly contribute to the development of the sense of number. Creating enriched learning environments tailored to the specific needs of gifted students is a critical strategy for these students to develop their sense of number and increase their overall mathematical achievement. The Enriched Education Model developed by Renzulli and Reis (2014) clearly reveals the contribution of customized teaching practices for gifted students to the development of cognitive skills. In this regard, curriculum designers should focus on learning environments that promote a deeper understanding of number relationships and quantities. Activities should not only enhance number sense but also encourage the adoption of diverse problem-solving approaches throughout the learning process.

Another important finding of this study is that gifted students exhibited higher averages in each component of their number sense performance compared to typically developing students. This indicates a greater propensity among gifted students to use flexible and effective problem-solving strategies, which likely contributes to their higher achievement. Nonetheless, these advantages may be significantly shaped by the instructional methods and resources tailored to their specific learning needs. The literature confirms that gifted students have a stronger sense of number and that these students have a significant advantage compared to their peers with typical development in the field of number sense (Tertemiz et al., 2023; Wang et al., 2017; Yang & Chang, 2023). The effect of number sense on mathematical achievement is especially pronounced for gifted students, and their success in mathematical processes is based on their more flexible thinking skills. These findings reveal that gifted students’ sense of number is stronger than their typically developing peers, and this difference is reinforced by the effect of educational opportunities as well as cognitive abilities. The development of a sense of number not only increases mathematical achievement but also provides students with important skills such as problem-solving and creative thinking. These findings emphasize that more specific and enriched strategies should be applied in the education of gifted students and that the sense of number directly contributes to the mathematical achievement of these students. It is also important to consider that the identification and assessment of giftedness vary significantly across educational contexts. Future research should explore how cognitive traits and educational experiences interact in shaping number sense development and how differing definitions of giftedness influence these interpretations.

Qualitative analysis findings reveal that gifted students mostly use number sense-based strategies (NSBS) while solving number sense problems, while typically developing students prefer rule-based strategies (RBS). These findings are in line with previous research. Studies by Jordan et al. (2010), Major and Perger (2014), and Mohamed and Johnny (2010) show that individuals with a low sense of number adopt more rule-based strategies.

These differences are related to students’ cognitive abilities, learning styles, and educational processes. Research shows that gifted students develop mathematical problem-solving strategies in a more flexible and creative way. For example, gifted students exhibit higher levels of performance in number sense, including flexibility in numerical calculations, numerical estimation, and quantitative reasoning (Şengül & Dede, 2014; Altıntaş et al., 2023). The use of number sense-based strategies (NSBS) by these students during problem solving is directly related to their high cognitive abilities and solid mathematical knowledge (Öztürk et al., 2019). A study by Çekirdekçi and Yorulmaz (2021) indicates that gifted students develop creative problem-solving strategies (Çekirdekçi & Yorulmaz, 2021). In this context, it is emphasized that curricula should have more supportive features for developing the number sense skills of gifted students (Abacı & Tüzün, 2023). The reasons behind typically developing students’ tendency to use rule-based strategies (RBS) are often rooted in more traditional teaching methods and rules. These students tend to focus more on procedural knowledge when understanding mathematical concepts, preferring rule-based solutions over flexibility (Takır, 2016; Yenilmez & Yıldız, 2018). A study by Öztürk et al. (2019) highlights that students who struggle with understanding mathematical concepts tend to resort to RBS, which inhibits the development of their number sense skills (Öztürk et al., 2019). Additionally, studies show that these students typically have lower performance in number sense and often rely on rule-based approaches (Çekirdekçi & Yorulmaz, 2021). In this context, customizing educational strategies according to students’ cognitive abilities and learning styles plays a crucial role in supporting the development of number sense skills.

The predominance of rule-based strategies in the mathematical thinking processes of typically developing students indicates that they adopt a structured and algorithmic approach. This finding is similar to most studies in the literature (Alsawaie, 2012; Can & Yetkin Özdemir, 2020; Yang, 2019b). This tendency is especially evident in the first, fourth, and fifth components of the number sense. In the first component, students generally use structured rules such as substitution and the decimal number system in recognizing numbers and understanding their values (Dedeoğlu & Eğerci, 2021). While this supports students’ ability to solve mathematical operations through standardized algorithms, it can limit the development of flexible strategies. In the fourth component, students prefer to use the algorithms they have learned while constructing arithmetic relationships, which allows them to take a safe approach to problem solving. Researchers such as Major and Perger (2014) and Ader (2021) state that such rule-based approaches may limit students’ flexible thinking skills. In the fifth component, students prefer to reach solutions to problems that require mental processing by repeating the rules they have learned. This finding shows that the development of the sense of number is a process and that rule-based strategies are more dominant, especially in the early periods (Ulusoy, 2020; Yıldırım & Köse, 2018). In this context, it is recommended that educators apply more flexible and enriched teaching methods. Callahan et al. (2017) state that enriched educational environments that support mathematical thinking strengthen students’ problem-solving skills. Oğuz and Kalender (2018), on the other hand, state that diversification of teaching strategies is effective in increasing students’ mathematical thinking and flexible strategy use skills.

In summary, the findings of this study reveal that gifted students perform significantly better in number sense compared to typically developing students, and this difference is linked to cognitive abilities and educational opportunities. Gifted students demonstrate more flexible and creative problem-solving skills by using number sense-based strategies (NSBS), while typically developing students tend to rely on rule-based strategies (RBS). For education policymakers and curriculum developers, these findings highlight the need for differentiated curricula and teaching methods tailored to the needs of both student groups. In particular, adopting enriched and flexible teaching strategies for gifted students can further enhance their cognitive abilities and problem-solving skills. On the other hand, more structured and guided approaches for lower-performing students can support the development of their number sense skills. These findings emphasize the necessity of applying effective learning strategies for both groups.

Theoretical implications

This study provides significant findings regarding the development of number sense in gifted and typically developing students. The higher performance of gifted students reinforces the role of cognitive capacities in mathematical thinking and problem-solving (Gallagher, 2019; McCoach & Flake, 2018). Additionally, the relationship between flexible problem-solving strategies and the development of number sense supports cognitive learning theory and highlights how these students apply their metacognitive skills. The role of educational experiences in the development of number sense is also crucial; enriched educational programs support cognitive development and contribute to strengthening mathematical skills (Callahan et al., 2017).

Practical implications

The practical implications of this study emphasize the need for differentiated teaching strategies based on students’ cognitive abilities and developmental needs. For gifted students, the curriculum should be enriched with opportunities for flexible and creative problem-solving, allowing students to use various problem-solving methods (e.g., making predictions). This promotes creative thinking. For typically developing students, more structured teaching methods should be used to gradually develop flexible thinking skills. Learning environments that foster the development of number sense and enhance mathematical achievement should be provided for both groups. In conclusion, differentiating teaching strategies based on students’ cognitive and developmental needs will effectively enhance all students’ mathematical achievement and problem-solving skills.

Limitations of the study and suggestions for future research

This study has several limitations. Firstly, the sample group was selected from a specific geographical area, which may limit the generalizability of the findings. Since the research was conducted with students from only one region, the performance of students from different cultural and socio-economic backgrounds was not considered. This limits the applicability of the results to a broader student population. Additionally, during the data collection process, interviews were conducted only with volunteer students from the top 27% of number sense performance. This resulted in the omission of data regarding the problem-solving strategies of students with lower and average performance levels.

Future research should aim to expand the sample size and include students from different geographical regions with diverse socio-economic backgrounds to enhance the generalizability of the findings. Moreover, more data should be collected on both gifted and typically developing students. Studies focused on students with lower performance levels can help identify more effective teaching methods for supporting the development of their number sense. Designing structured teaching methods for these students can positively impact the development of their number sense. In addition, the impact of teaching methods used by teachers on students’ problem-solving strategies should be examined in more depth. Investigating how enriched educational programs and flexible teaching strategies contribute to the development of number sense will provide valuable insights for practical applications. Furthermore, teaching strategies should not only be differentiated based on cognitive abilities but also aligned with students’ learning styles. Finally, there should be an increased focus on studies related to the teaching of metacognitive skills and flexible problem-solving strategies. Integrating metacognitive strategies into educational programs can help strengthen students’ strategic thinking skills.