Introduction

Floods, as extreme hydrological events, are influenced by multiple factors such as rainfall, snowmelt, and glacier meltwater, along with the combined effects of these elements1,2,3,4,5. There are significant differences in flood formation mechanisms at both global and regional scales. Studies on floods in the contiguous United States6, Europe7,8, and globally9 indicate that floods are influenced by multiple factors simultaneously, with compounding effects being prevalent. Studies conducted in central Europe10, Norway11, the western United States12,13, the Himalayas and Karakoram14, and globally15 show that the contribution of rainfall to floods is increasing, while the contribution of snowmelt to floods is decreasing. In addition, Zhang et al. 15 found that the increase in floods triggered by heavy rainfall was offset by the decrease in snow-related floods, resulting in no significant overall change in global floods. Studies in Norway11, northeastern Europe16, eastern Canada17, and the western United States13 indicate that snowmelt-driven floods are occurring earlier in the year. The studies above demonstrate that climate change is significantly impacting the factors driving floods and their combined effects, both regionally and globally. This results in more complex and dynamic flood mechanisms in different areas.

The Tianshan Mountains, often referred to as the “Water Tower of Central Asia,” provide crucial water sources for the majority of the rivers in the region18. Climate warming has led to reduced snow cover and glacier retreat in the Tianshan Mountains18,19,20. This has altered the seasonal distribution of runoff and diminished the stability of water resource systems that depend on snowmelt and glacier meltwater21,22. These changes have increased the uncertainty regarding flood formation and variation, posing severe challenges for flood forecasting and water resource management. The majority of the studies on floods in the alpine glacierized catchments of the Tianshan region have focused on the statistical analysis of flood frequency, duration, and intensity23,24, with relatively few investigations into the mechanisms driving these floods. Further, flood mechanisms in a catchment can change over time, especially under the influence of climate change25. For example, rising temperatures affect snow dynamics in cold regions, leading to more extreme rainfall events. This makes catchments that primarily rely on snowmelt more susceptible to extreme rainfall, thereby altering the seasonality and magnitude of regional floods11,12,26. Therefore, systematic research on the changes in flood mechanisms is essential.

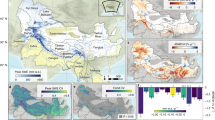
Building on the importance of the Tianshan Mountains as a critical water source for Central Asia, the Kumalak River catchment serves as a representative alpine glacierized catchment for studying flood mechanisms in this region (Fig. 1a). It is also referred to in other studies as Kumalak27,28,29, Kunma Like30,31, Kumaric32, Sari-Djaz33, or Sary-Djaz-Kumaric34. The Kumalak River, the principal tributary of the Aksu River, spans a total length of 306 km and descends by 2209 m. The drainage area, primarily controlled by the Xiehela outlet, spans 12,816 km², with approximately 82% of its area located within the borders of Kyrgyzstan. The elevation within the Kumalak River catchment ranges from 1450 m to 7100 m, averaging 3700 m. The catchment has glacier coverage amounting to 18.49% of its total area35. Located deep within the Eurasian continent, the Kumalak River catchment is characterized by an arid climate. The multi-year daily average maximum temperature at the Tien-Shan station (elevation 3639 m) ranges from −15 °C to 15 °C (Fig. 1b). Regional precipitation varies significantly due to complex terrain, with uneven distribution throughout the year, mainly concentrated from April to September (Fig. 1c, d), accounting for about 86.5% of the annual precipitation36. The streamflow in the Kumalak River catchment is primarily replenished by snowmelt, glacier meltwater, and rainfall. These sources significantly contribute to the total annual streamflow, with snowmelt accounting for 11.2% to 27.1%29,30, glacier meltwater for 28.2% to 56%29,30,32,33, and rainfall for 28.5% to 60.6%29,30. These unique hydrological characteristics make the Kumalak River catchment an ideal case for investigating the effects of snowmelt, glacier meltwater, and rainfall dynamics on flood mechanisms in alpine regions.

Fig. 1: Overview of the study area.
figure 1

a The geographic location of the study area. b The multi-year daily average maximum temperature over 1960–2018 at the Tien-Shan station (elevation 3639 m). c The multi-year daily average precipitation over 1960–2018 at the Koilu station (elevation 2800 m). d The multi-year daily average precipitation over 1960–2018 at the Uc-Koskon station (elevation 2884 m).

Full size image

An effective way to identify flood mechanisms is to quantify the contribution of driving factors to every event, revealing the links between flood events and runoff components. Long Short-Term Memory (LSTM) networks37 have successfully applied DL architectures to model dynamic hydrological variables38,39,40,41. The recurrent structure and unique gating mechanisms of LSTM networks enable the accurate capture of nonlinearities and temporal dependencies among variables37. In addition, applying interpretive techniques to LSTM models to extract captured patterns from “black-box” models helps in identifying flood mechanisms6,8. For example, flooding mechanisms in the contiguous United States6 and river flooding mechanisms and their changes in Europe8 have been revealed by interpretive LSTM models.

This study investigated the factors influencing floods in the Kumalak River catchment, a typical alpine glacierized catchment on the southern slope of the Tianshan Mountains, from 1960 to 2018 using an improved interpretable DL approach that was developed by Jiang et al. 6. First, the SWAT-Glacier model and the degree–day factor model were employed independently to calculate daily amounts of snowmelt, glacier meltwater, and rainfall. Then, these factors were independently used as inputs for the LSTM models. Next, the additive decomposition method42 was applied to decompose the information and quantify the effective previous time steps contributing to the simulation of floods. Finally, the integrated gradients technique43 was employed to quantify the feature importance scores of the hydrological component factors in the simulation of floods.

This study aims to address the following questions: (a) How does the additive decomposition method applied to the LSTM model help identify the key time window that captures the drivers of flood events? (b) Can the LSTM model, using integrated gradients to assess feature importance, effectively identify the dominant drivers of flood events in the alpine glacierized Kumalak River catchment? (c) what are the specific, quantified contributions of hydrological components (i.e., snowmelt, glacier meltwater, and rainfall) to flood events in this catchment?

Results

Dominant driving factors of floods revealed by feature importance

The Kumalak River catchment exhibits two distinct streamflow peaks annually (Supplementary Fig. 4). The first peak, occurring in spring and typically observed in May, is defined as the Annual Maximum Flood in Spring (AMFSp), driven primarily by early snowmelt. The second peak, occurring in summer (late July to early August), is sustained by meltwater (a combination of snowmelt and glacier meltwater) and is defined as the Annual Maximum Flood (AMF). In this study, the term “flood” refers specifically to peak streamflow events and does not imply inundation or damage44. With these definitions in place, the study examined the dominant drivers of AMF and AMFSp events using feature importance derived from the LSTM-SG and LSTM-DDF models.

For AMF events from 1960 to 2018, the LSTM-SG model results indicate that the multi-year average total feature importance over a seven-day window was 0.14 for snowmelt, 1.32 for glacier meltwater, and 0.11 for rainfall (Fig. 2a–c). The LSTM-DDF model shows multi-year averages of 0.12 for snowmelt, 1.75 for glacier meltwater, and 0.13 for rainfall (Fig. 2d–f). Both models identify glacier meltwater as the dominant driving factor for AMF events. From 1960 to 2018, both models show increasing trends for the total feature importance over a seven-day window for snowmelt and rainfall, and a decreasing trend for glacier meltwater (Fig. 2a–f).

Fig. 2: Multi-year averages and trends of total feature importance over a seven-day window for snowmelt, glacier meltwater, and rainfall in AMF (1960–2018) and AMFSp (1961–2018) events using LSTM-SG and LSTM-DDF models.
figure 2

a–c Total feature importance for snowmelt, glacier meltwater, and rainfall for AMF events in LSTM-SG model. d–f Total feature importance for snowmelt, glacier meltwater, and rainfall for AMF events in LSTM-DDF model. g–i Total feature importance for snowmelt, glacier meltwater, and rainfall for AMFSp events in LSTM-SG model. j–l Total feature importance for snowmelt, glacier meltwater, and rainfall for AMFSp events in LSTM-DDF model. The Zc value indicates the significance of the Mann-Kendall trend test, with * at the 0.10 level, ** at the 0.05 level, and *** at the 0.01 level.

Full size image

For AMFSp events from 1961 to 2018, the LSTM-SG model shows that the multi-year average total feature importance over a seven-day window was 0.29 for snowmelt, 0.04 for glacier meltwater, and 0.11 for rainfall (Fig. 2g–i). The LSTM-DDF model indicates multi-year averages of 0.39 for snowmelt, 0.07 for glacier meltwater, and 0.10 for rainfall (Fig. 2j–l). Both models consistently identify snowmelt as the dominant driving factor for AMFSp events. From 1961 to 2018, both models show a decreasing trend in the contribution of snowmelt to AMFSp events (Fig. 2g, j).

Relative contributions of flood drivers in a seven-day window

To compare with dominant driving factors of floods revealed by feature importance, the proportions of seven-day antecedent snowmelt, glacier meltwater, and rainfall for AMF and AMFSp events were calculated using the SWAT-Glacier model (i.e., the sum of every factor over a seven-day window divided by the total of snowmelt, glacier meltwater, and rainfall during the same period). Similarly, the relative contributions of these drivers were estimated using the degree–day factor model for both AMF and AMFSp events.

For AMF events, the SWAT-Glacier model shows that the multi-year average relative contributions of snowmelt, glacier meltwater, and rainfall from 1960 to 2018 were 10.01%, 60.49%, and 29.50%, respectively, indicating a combined relative contribution of 70.50% from meltwater (Fig. 3a). In the degree–day factor model, these relative contributions were 12.21%, 60.92%, and 26.86%, respectively (Fig. 3b), with the relative contribution of meltwater being 73.13%. These findings indicate that glacier meltwater was the dominant driver for AMF events, supporting the results from the LSTM-SG and LSTM-DDF models.

Fig. 3: Relative contributions of snowmelt, glacier meltwater, and rainfall in AMF and AMFSp events over a seven-day window.
figure 3

a, c The relative contributions of snowmelt, glacier meltwater, and rainfall in the SWAT-Glacier model for AMF and AMFSp events, respectively. The lines represent averages from 18 outputs in the SWAT-Glacier model, with shaded areas indicating one standard deviation. b, d These contributions in the degree–day factor model for AMF and AMFSp events, respectively. The lines represent averages from 464 outputs in the degree–day factor model, with shaded areas indicating one standard deviation. The interpretation of Zc is consistent with that in Fig. 2.

Full size image

For AMFSp events, the SWAT-Glacier model indicates that the multi-year average relative contributions of snowmelt, glacier meltwater, and rainfall from 1961 to 2018 were 48.49%, 22.08%, and 29.42%, respectively (Fig. 3c). In the degree–day factor model, these relative contributions were 56.08%, 16.12%, and 27.79%, respectively (Fig. 3d). These findings indicate that snowmelt was the dominant driver for AMFSp events, consistent with the results from the LSTM-SG and LSTM-DDF models.

Contribution of rainfall to flood magnitude

Results from the SWAT-Glacier and degree–day factor models indicate an increased relative contribution of rainfall to AMF and AMFSp magnitudes (Fig. 3). From 1960 to 2018, significant upward trends were observed in both the annual average maximum temperature (p = 0.00) and streamflow (p = 0.01), while the annual total precipitation did not exhibit a significant trend (p > 0.05) (Fig. 4a, c–e). A Pearson correlation coefficient of 0.49 between temperature and streamflow suggests that rising temperatures may be a key contributor to increased streamflow (Fig. 4a, e). Over this period, annual snowmelt (p > 0.05) and glacier meltwater (p = 0.00) decreased in both models, while the annual total rainfall significantly increased (p = 0.00) (Fig. 4f–h, j–l). Both AMF and AMFSp events occurred earlier in the year, with AMF events showing a significant advance (p = 0.03) (Fig. 4i, m).

Fig. 4: Trends of meteorological and hydrological variables over 1960–2018 in the Kumalak River catchment.
figure 4

a Annual average maximum temperature at the Tien-Shan station. b Pearson correlation between annual average maximum temperature and annual average streamflow. c, d Annual total precipitation at Koilu and Uc-Koskon stations, respectively. e Annual average streamflow at the Xiehela outlet. f–h Annual snowmelt, glacier meltwater, and rainfall derived from the SWAT-Glacier model. j–l Annual snowmelt, glacier meltwater, and rainfall from the degree–day factor model. i, m Day of the year for AMF and AMFSp events, respectively. Dashed lines represent trend slopes, with associated p-values indicating statistical significance: typically, p < 0.01 indicates strong significance, p < 0.05 suggests statistical significance, and p > 0.05 denotes non-significance.

Full size image

These findings were consistent with prior research in the Kumalak River catchment. Li et al. 29 reported that the contribution of rainfall to streamflow increased significantly by 0.93 mm/year over 1970–2010, while snowmelt streamflow slightly decreased by 0.12 mm/year, indicating that more precipitation was falling as rainfall rather than snowfall due to rising temperatures in the Kumalak River catchment. Duethmann et al. 33 observed that rising temperatures were the primary driver of the increase of streamflow in the Kumalak River catchment, with rainfall showing an increasing trend. Similar trends have been noted in various regions globally, including central Europe10, Norway11, the western United States12,13, the Himalayas and Karakoram14, and globally15, where the contribution of rainfall to floods increased, while the contribution of snowmelt to floods decreased. This shift towards more rainfall-driven flood regimes underscores the growing importance of rainfall in altering flood dynamics.

Results from the SWAT-Glacier and degree–day factor models indicate a decreasing trend in the relative contribution of glacier meltwater to AMF and AMFSp events (Fig. 3), primarily due to reductions in glacier melt and snowmelt. With global warming, more precipitation has fallen as rainfall rather than snowfall (Fig. 4h, l). This shift has amplified the influence of rainfall on flood events in this catchment, directly increasing the relative contribution of rainfall to flood formation and leading to a proportional decrease in the contribution of glacier meltwater.

Although glacier meltwater is the primary driver of AMF events and snowmelt is the primary driver of AMFSp events, the relative contribution of rainfall to both AMF and AMFSp events is increasing. Additionally, climate warming has led to a gradual reduction in glacier area, which may have decreased the overall volume of glacier meltwater (Fig. 4g, k), thereby partially reducing its relative contribution to floods. These changes indicate that, under the influence of climate warming, the role of rainfall in flood mechanisms in the Kumalak River catchment has gradually strengthened, while the relative contribution of glacier meltwater to flood formation has weakened.

Discussion

Given the location of the Kumalak River catchment in a high-altitude region with limited observational data and complex hydrological processes, both the SWAT-Glacier and degree–day factor models were used to comprehensively calculate daily snowmelt, glacier meltwater, and rainfall. These models complement each other in terms of data requirements, computational efficiency, and physical process simulation, providing a diversified solution for hydrological calculations in data-scarce alpine catchments.

The SWAT-Glacier model is a physics-based hydrological model that incorporates a glacier dynamics module, enabling comprehensive simulation of how meteorological factors, including air temperature, precipitation, radiation, and wind speed, influence runoff through various hydrological processes such as snowmelt, evapotranspiration, glacier melt, and groundwater. This model is particularly effective in snow- and glacier-dominated catchments, where it captures the dynamic changes in glacier meltwater and snow accumulation, providing a deeper understanding of these processes. By calculating glacier melt runoff within each hydrological response unit and routing it through the river network, the SWAT-Glacier model provides a detailed simulation of hydrological processes across the catchment.

However, the complexity of the SWAT-Glacier model leads to high data requirements and computational costs. The model requires detailed observational data, including digital elevation model data, soil property data, and land-use data, along with specific meteorological measurements. In regions with limited meteorological and hydrological data, the accuracy of the model may be constrained, indicating that the performance of the model is highly dependent on the quality of observational data. Additionally, the calibration procedure generally involves a large number of distributed hydrological parameters, increasing both complexity and time costs.

Due to the scarcity and uncertainty of precipitation observations in the high-altitude regions of central Asia, actual precipitation is likely significantly underestimated45. To improve the calculation accuracy of snowmelt, glacier meltwater, and rainfall, this study also employed ERA5 reanalysis data with a spatial resolution of 0.1° × 0.1° for temperature and precipitation, covering the Kumalak River catchment with 141 grids. The degree–day factor model was applied within each grid to estimate snowmelt, glacier meltwater, and rainfall using temperature thresholds. This grid-based model offers advantages in simplicity and computational efficiency, allowing for rapid processing of large datasets and providing quantitative insights into the impact of climate change on runoff components. Requiring only temperature, precipitation, and glacier area data, with minimal parameter settings and a straightforward structure, the model minimizes uncertainties often associated with more complex approaches. Consequently, the degree–day factor model could be an effective supplementary tool for estimating runoff components in high-altitude regions with limited observational data.

However, the model has limitations in providing a detailed analysis of how climate factors influence runoff through specific hydrological processes. Although it accounts for updates in glacier area, it lacks the capability to account for other hydrological processes, including evapotranspiration, which is closely related to meteorological variables such as wind speed and radiation. Therefore, while the degree–day factor model is well-suited for simplified hydrological simulations, it may fall short in capturing the complexity of intricate hydrological processes.

The use of both the SWAT-Glacier and degree–day factor models in this study is justified by their complementary strengths, providing a robust framework for understanding hydrological components in the Kumalak River catchment. The SWAT-Glacier model, as a semi-distributed, physics-based hydrological model, captures complex hydrological dynamics through detailed simulations of snowmelt, glacier meltwater, and rainfall, offering valuable insights into the interactions between meteorological factors and runoff in snow- and glacier-dominated catchments. The degree–day factor model offers simplicity and computational efficiency, requiring only basic inputs such as air temperature, precipitation, and glacier area data, making it ideal for data-scarce regions. By combining the detailed process simulations of the SWAT-Glacier model with the efficiency of the degree–day factor model, this study leverages their strengths to achieve a comprehensive assessment of hydrological processes in a high-altitude catchment with limited observational data.

The model parameters were calibrated/constrained by results derived from previous research, which included the contributions of snowmelt, glacier meltwater, and rainfall, as well as glacier mass balance. These parameters were used to constrain the models for key outputs, such as outlet streamflow, glacier melt rates, and the relative contributions of snowmelt, glacier meltwater, and rainfall to the annual total streamflow. The use of both models together produced reliable simulation results. The SWAT-Glacier model estimated that the multi-year average contributions to the annual total streamflow in the Kumalak River catchment from 1960 to 2018 were 20.21–23.08% from snowmelt, 39.75–44.34% from glacier meltwater, and 25.74–33.90% from rainfall, using 18 sets of optimal outputs. The degree–day factor model, using 464 sets of optimal outputs, estimated multi-year average contributions of 11.21–38.32% for snowmelt, 32.51–47.95% for glacier meltwater, and 28.51–44.49% for rainfall. These findings closely align with previous studies, which reported multi-year average contributions of 11.2–27.1% for snowmelt29,30, 28.2–56% for glacier meltwater29,30,32,33, and 28.5–60.6% for rainfall29,30 in the Kumalak River catchment.

Applying the additive decomposition method to the LSTM model addresses the transparency limitations in decision-making associated with the black-box nature of DL. This method enables quantification and visualization of information within each gating unit of the LSTM model, making it possible to observe that only information from recent time steps, closest to the target feature being simulated, has a dominant contribution to the simulation target (Fig. 5). Information from earlier time steps is almost entirely forgotten, providing insights into how the LSTM makes decisions using retained information. Additionally, it helps identify which specific recent time-step window retains major information used to simulate the target feature. This is significant as it avoids preconceived assumptions about time windows impacting flood mechanisms, preventing the interpretative process from being constrained by biases or pre-existing views on local hydrological system functions.

Fig. 5: Information decomposition of internal signals during the simulation of representative flood events.
figure 5

a Information decomposition from the 10th fold of the LSTM-SG model during the simulation of the AMF on July 1, 2016. b Information decomposition from the 10th fold of the LSTM-DDF model during the simulation of the AMF on July 1, 2016. c Information decomposition from the 10th fold of the LSTM-SG model during the simulation of the AMFSp on May 14, 2018. d Information decomposition from the 10th fold of the LSTM-DDF model during the simulation of the AMFSp on May 14, 2018. Subplots (i) to (iii) show the snowmelt, glacier meltwater, and rainfall amounts in the previous 180 days used to simulate floods. The multiple lines in subplots (iv) to (ix) denote signals in the respective hidden units. Subplots (x) to (xii) correspond to the information at every time step extracted from the second column.

Full size image

The integrated gradients technique applied to the LSTM model enables the calculation of feature importance scores, quantifying the contribution of each input feature to the simulation of flood events and providing insights into the decision-making process of the model in generating these simulations. The LSTM model accurately identifies the input features with the most significant contribution to the simulation of floods. Glacier meltwater is determined to be the primary driver for AMF events, while snowmelt is recognized as the dominant driver of AMFSp events. Interpretable DL methods effectively capture key flood characteristics by using snowmelt, glacier meltwater, and rainfall data to clarify how these variables drive model simulations. This capability strengthens confidence in the capacity of DL models to identify flood mechanisms and supports optimism about their applicability in addressing complex hydrological questions. By quantifying the influence of distinct hydrological components, these methods enable a transparent assessment of model behavior, making them particularly valuable for investigating flood dynamics in response to changes in the contribution of hydrological components due to climate variation.

To explore flood mechanisms, two LSTM models with distinct input datasets were constructed: the LSTM-SG model, which used snowmelt, glacier meltwater, and rainfall data from the SWAT-Glacier model, and the LSTM-DDF model, which used the same variables calculated by the degree–day factor model. The output of each LSTM model reflected the characteristics and quality of the input data. A comparison of the feature importance scores for snowmelt, glacier meltwater, and rainfall over a seven-day window in simulating flood events revealed slight differences between the two LSTM models, driven by variations in input data. These results show that LSTM model reliability depends strongly on input data quality, emphasizing the need for high-quality inputs to ensure reliable results. Although DL methods like LSTM models can offer new insights by revealing complex patterns between hydrological components and streamflow, they cannot replace fundamental hydrological calculations, such as those for snowmelt, glacier meltwater, and rainfall, which provide the physical basis for understanding flood dynamics. DL can serve as a complementary tool, adding valuable perspectives to the analysis of flood mechanisms. The application of DL in hydrological research should be guided by the specific scientific questions being addressed.

The Kumalak River catchment is located in the mountainous regions of Central Asia. The catchment area above the Xiehela outlet is 12,887 km², with elevations ranging from 1435 m to 7126 m and an average elevation of 3750 m. The terrain is complex, with steep slopes, causing significant variation in the water cycle and hydrological processes over small areas. This has led to substantial differences in the spatiotemporal distribution of flood formation processes. In addition, the catchment has very few meteorological observation stations: Tien-Shan (elevation 3639 m), Koilu (elevation 2800 m), and Uc-Koskon (elevation 2884 m). The scarcity of observational data in mountainous areas, especially above 4000 m, makes it difficult to use fully physical-based hydrological and land surface models to analyze flood processes.

In the future, it will be beneficial to consider the effects of energy balance and wind-blown snow processes, among other factors, when calculating the amounts of snowmelt, glacier meltwater, and rainfall. Energy balance models can enhance the accuracy of these simulations by considering factors such as solar radiation, temperature, and wind speed46. Wind-blown snow can affect snow accumulation and meltwater generation, influencing hydrological models47. Incorporating remote sensing data, such as satellite observations of snow cover and glacier extents, can provide better calibration and validation for models48,49. Exploring the use of deep learning to identify complex patterns in large datasets can improve our understanding of flood mechanisms, thereby providing valuable insights for physical models50. Future studies should consider the impacts of climate change on hydrological processes by exploring changes in precipitation patterns, temperature regimes, and glacier dynamics under different climate scenarios51. These approaches could help improve our understanding of flood mechanisms and support the development of adaptive water resource management strategies for the Kumalak River catchment.

Methods

Calculation of snowmelt, glacier meltwater, and rainfall amounts

SWAT-Glacier model

The SWAT-Glacier model, an extension of the Soil and Water Assessment Tool35,52, was utilized in this study to calculate snowmelt, glacier meltwater, and rainfall. By incorporating a glacier dynamic module, the SWAT-Glacier model could simulate glacial hydrological processes. This model calculates glacier melt and accumulation in each hydrological response unit. The parameters in the SWAT-Glacier model are detailed in the study by Fang et al. 35. After multiple objective calibration using the ε-NSGAII algorithm, the 18 best parameter sets were obtained. The model was then run with these parameter sets, resulting in 18 groups of daily snowmelt, glacier meltwater, and rainfall data for the Kumalak River from 1960 to 2018.

Within specific hydrological response units, glacier surface temperature is determined by a functional relationship involving the glacier surface temperature of the previous day and the average air temperature of the current day. The formula for calculating glacier surface temperature is as follows:

$${T}_{gla({I}_{day})}={T}_{gla({I}_{day}-1)}\cdot (1-{L}_{gla})+{T}_{av}\cdot {L}_{gla},$$
(1)

where \({T}_{av}\) represents the average air temperature (°C) on day \({I}_{day}\) and \({L}_{gla}\) denotes the temperature lag factor. The closer the value of \({L}_{gla}\) is to 1, the less the influence of the previous day’s glacier surface temperature and the greater the influence of the current day’s average air temperature.

The glacier meltwater at a specific elevation band is calculated on a daily basis using Eq. (2):

$$GL{A}_{melt}=\left\{\begin{array}{ccc}G{F}_{mlt}\cdot GL{A}_{\mathrm{cov}}\cdot \left(\frac{{T}_{gla}+{T}_{\max }}{2}-G{T}_{mlt}\right) & , & {T}_{\max } \,>\, G{T}_{mlt}\\ 0 & , & {T}_{\max }\,\le\, G{T}_{mlt}\end{array}\right.$$
(2)

where \(GL{A}_{melt}\) represents the amount of glacier meltwater (mm) on the current day, \(G{F}_{mlt}\) denotes the glacier melt factor (mm/[°C·d]) \(GL{A}_{\mathrm{cov}}\) is the fraction of the glacier coverage in each HRU, \({T}_{\max }\) indicates the maximum air temperature (°C), and \(G{T}_{mlt}\) refers to the glacier melt base temperature (°C).

The intra-annual variation in the glacier melt factor (\(G{F}_{mlt}\)) follows a sine function, as shown in Eq. (3):

$$G{F}_{mlt}=\frac{gmfmx-gmfmn}{2}\cdot \,\sin \left(\frac{{2}\pi}{365}\cdot ({I}_{day}-121)\right)+\frac{gmfmx+gmfmn}{2}$$
(3)

where \(gmfmx\) represents the maximum glacier melt factor (mm/[°C·d]) within the year, which is set on August 1st; \(gmfmn\) indicates the minimum glacier melt factor (mm/[°C·d]) within the year, set on February 1st; and \({I}_{day}\) refers to the day of the year.

Glacier volume is estimated from glacier area, using the following formula:

$$V=0.04\times {\left(\frac{A}{1000000}\right)}^{1.35}$$
(4)

where \(V({m}^{3})\) is the volume of the individual glacier, and \(A({m}^{2})\) is the glacier area.

Based on the relationship between glacier area and glacier volume, the relative changes in glacier volume \((\delta V)\) and glacier area \((\delta A)\) are updated, with the calculation formula as follows:

$$\delta V=\frac{GL{A}_{mlt}\times A}{V}$$
(5)
$$\delta A={\left(\frac{(1+\delta {V})* {V}}{0.04* {10}^{9}}\right)}^{(\frac{1}{1.35})}$$
(6)

The streamflow data for the Kumalak River at the Xiehela outlet were obtained from the Chinese Hydrological Yearbook and the Xinjiang Tarim River Basin Authority. The daily data covered 1960–2011 and 2016–2018, and monthly data spanned 1960–2018. The MissForest method53 was employed to reconstruct the missing daily streamflow data from 2012 to 2015 (see Supplementary Figs. 1, 2). The standardized daily streamflow from 1960 to 2018 at the Xiehela outlet of the Kumalak River is shown in Supplementary Fig. 3. Daily meteorological data, including maximum/minimum temperature, precipitation, sunshine hour, relative humidity, and wind speed from 1955 to 2018, were collected from the China Meteorological Administration (http://data.cma.cn/) and the SC-Earth dataset54. Four precipitation stations, that is, Chon-Ashu, UC-Koskon, Koilu, and Aksu, and two temperature stations, namely, Tian Shan and Aksu were used. Two stations with wind, solar radiation, and relative humidity data from Aksu and Aheqi were used for the model setup. Digital elevation model data, soil data, and land-use data were also used for the subbasin and hydrological response unit delineation35. The glacier map was derived from the second Chinese Glacier Inventory55 (CGI) for the Chinese region and the updated Randolph Glacier Inventory56 (RGI 6.0) for the Kyrgyzstan region. These datasets were combined to create a comprehensive glacier dataset for the Kumalak River catchment, which was used as input in both the SWAT-glacier model and the degree–day factor model.

In this study, a 5-year period (1955–1959) was used for the model warm-up. Daily data from 2001 to 2005 were used for model calibration, and daily data from 2006 to 2011 were used to test the model performance. Model calibration was performed using the ε-NSGAII algorithm, a second-generation multi-objective evolutionary algorithm known for its effectiveness and reliability in determining optimal parameter sets for hydrological models57,58. Two objective functions were used: the match between observed and simulated daily streamflow (Nash-Sutcliffe Efficiency, NSE) and the bias in simulated glacier melt contribution. For daily streamflow simulation, the median NSE value was 0.67; for the bias in simulated glacier melt contribution to runoff, BIAS was less than 0.05.

Degree–day factor model

This study used the ERA5-Land dataset with a resolution of 0.1° × 0.1° to extract hourly temperature and total precipitation data for the Kumalak River catchment, covering 141 grids (Supplementary Fig. 6). The hourly data were converted into daily maximum temperature and total precipitation. The reanalysis maximum temperature for every grid was corrected using the daily maximum temperature at the Tien-Shan station and the linear scaling method59. The reanalysis daily total precipitation for every grid was bias-corrected using the daily precipitation data from the Koilu and Uc-Koskon stations and the quantile mapping method60.

The degree–day factor model61,62 was used to calculate snowmelt, glacier meltwater, and rainfall amounts for every grid within the catchment. The snowfall base temperature was used to differentiate between snowfall and rainfall. The daily snowmelt and rainfall amounts were aggregated across all of the grids within the catchment. The catchment-scale glacier meltwater was calculated through a weighted average of the meltwater from glaciers across all of the grids, with weights determined by the ratio of glacier area in every grid (Supplementary Fig. 6). This study referenced the parameter range settings used by Fang et al. 35 for calculating snowmelt, glacier meltwater, and rainfall amounts (Supplementary Table 1).

The formula for calculating snowfall is as follows:

$${S}_{f}(t)=\left\{\begin{array}{ccc}P(t) & , & {T}_{\max }(t) \,<\, {T}_{snow}\\ 0 & , & {T}_{\max }(t)\,\ge\, {T}_{snow}\end{array}\right.$$
(7)

where \({S}_{f}(t)\) denotes the snowfall (mm) on day t, \(P(t)\) reflects the total precipitation (mm) on day \(t\), \({T}_{\max }(t)\) indicates the maximum temperature (°C) on day \(t\), and \({T}_{snow}\) is the temperature for snowfall (°C).

The formula for calculating snowmelt is as follows:

$${S}_{m}(t)=\left\{\begin{array}{ccc}\min (FDD\cdot ({T}_{\max }(t)-{T}_{melt}),{S}_{d}(t-1)) & , & {T}_{\max }(t)\,\ge\, {T}_{melt}\\ 0 & , & {T}_{\max }(t) \,<\, {T}_{melt}\end{array}\right.$$
(8)

where \({S}_{m}(t)\) denotes the snowmelt (mm) on day \(t\), \({S}_{d}(t-1)\) indicates the snow depth (mm) from the previous day, \({T}_{\max }(t)\) represents the maximum temperature (°C) on day \(t\), \({T}_{melt}\) is defined as the base temperature (°C) for snow melting, and \(FDD\) refers to the snowmelt factor (mm/[°C·d]).

The formula for calculating rainfall is as follows:

$$R(t)=\left\{\begin{array}{ccc}P(t) & , & {T}_{\max }(t)\,\ge\, {T}_{snow}\\ 0 & , & {T}_{\max }(t) \,<\, {T}_{snow}\end{array}\right.$$
(9)

where \(R(t)\) represents the rainfall (mm) on day \(t\), \(P(t)\) indicates the total precipitation (mm) on day \(t\), \({T}_{\max }(t)\) denotes the maximum temperature (°C) on day \(t\), and \({T}_{snow}\) is the temperature (°C) for snowfall.

The formula for estimating the glacier meltwater for the current day at every grid is as follows:

$$GL{A}_{melt}=\left\{\begin{array}{ccc}G{F}_{mlt}\cdot GL{A}_{\mathrm{cov}}\cdot ({T}_{\max }-G{T}_{mlt}) & , & {T}_{\max } \,>\, G{T}_{mlt}\\ 0 & , & {T}_{\max }\,\le\, G{T}_{mlt}\end{array}\right.$$
(10)

where \(GL{A}_{melt}\) represents the glacier melt amount (mm) for the current day, \(G{F}_{mlt}\) denotes the glacier melt factor (mm/[°C·d]) for the day, \(GL{A}_{\mathrm{cov}}\) indicates the fraction of glacier coverage in the current grid, \({T}_{\max }\) is the maximum air temperature (°C) for the day, and \(G{T}_{mlt}\) represents the glacier melt base temperature (°C). The change in glacier coverage was calculated using a glacier retreat rate of 0.65% annually in the Kumalak River catchment63. The annual variation of the glacier melt factor follows a sine function, with the calculation formula as follows:

$$G{F}_{mlt}=\frac{gmfmx-gmfmn}{2}\cdot \,\sin \left({\frac{2\pi }{365}\cdot ({I}_{day}-121)}\right)+\frac{gmfmx+gmfmn}{2}$$
(11)

where \(gmfmx\) represents the maximum glacier melt factor (mm/[°C·d]) within the year, set on August 1st; \(gmfmn\) indicates the minimum glacier melt factor (mm/[°C·d]) within the year, set on February 1st; and \({I}_{day}\) refers to the day of year.

There were 75,625 parameter combinations that were formed within the parameter ranges. These combinations were used to generate 75,625 data series for snowmelt, glacier meltwater, and rainfall. For every parameter combination, the contributions of snowmelt, glacier meltwater, and rainfall to the annual total runoff from 1960 to 2018 were calculated, and their multi-year average contribution ratios were derived. Existing research on the Kumalak River was used to set the multi-year average contribution ratios as follows: snowmelt exceeds 11.2%29, glacier meltwater is between 28.2–48%29,33, and rainfall exceeds 28.5%30. There were 464 parameter combinations that met the standards under these conditions. These eligible combinations indicated that the multi-year average contributions of snowmelt, glacier meltwater, and rainfall to the annual total runoff were 11.21–38.32%, 32.51–47.95%, and 28.51–44.49%, respectively.

LSTM models and interpretation methods

LSTM models

The DL model in this study consists of a single LSTM37 layer and a dense layer (Supplementary Fig. 7a). It uses three inputs, daily snowmelt, glacier meltwater, and rainfall, over the previous 180 time steps to simulate streamflow. The choice of 180 time steps is based on the study by Kratzert et al. 64. The LSTM network transfers information from one time step to the next using a cell state \(({c}_{t})\) and a hidden state \(({h}_{t})\) (Supplementary Fig. 7c). At every time step \(t\), it updates these states using the prior cell states \(({c}_{t-1},\,{h}_{t-1})\) and the current input \(({x}_{t})\). The final hidden state \(({h}_{T})\) is then used to simulate streamflow through a dense layer.

Supplementary Fig. 7b illustrates the information flow within an LSTM cell. This overview is relevant to the additive decomposition method. Sherstinsky65 provides a detailed explanation of LSTM architecture. An LSTM cell updates through six steps. It calculates the forget gate (\({f}_{t}\), block 1), candidate cell state (\({\tilde{c}}_{t}\), block 2), input gate (\({i}_{t}\), block 3), and output gate (\({o}_{t}\), block 4) using the previous hidden state and current input. The prior cell state (\({c}_{t-1}\)) is updated using these gates (block 5). The new cell state (\({c}_{t}\)) and output gate produce the hidden state (\({h}_{t}\)) through a nonlinear transformation (block 6). In our case, \({c}_{t}\) and \({h}_{t}\) are vectors of length 32, and the dense layer in Supplementary Fig. 7c reduces these 32 features into a single streamflow value.

To enhance the robustness of model evaluation and analysis, 10 independent LSTM models were fitted (Supplementary Fig. 7d). The data were divided into 10 folds, maintaining the temporal sequence. Every fold was tested once with a model trained on the remaining nine folds. The performance of every model was evaluated using the testing data (1/10 of the total data). During the training process, 70% of the training data was used to update the model parameters of every epoch until no further loss reduction was observed in the remaining 30% (validation data). The hyperparameter settings are shown in Supplementary Table 2.

Two LSTM models, referred to as LSTM-SG and LSTM-DDF, were constructed. The LSTM-SG model used daily averages of snowmelt, glacier meltwater, and rainfall from 18 sets of the best SWAT-Glacier simulation results as inputs. The LSTM-DDF model used daily averages of snowmelt, glacier meltwater, and rainfall from the 464 sets calculated by the degree–day factor method. The performance of the LSTM-SG and LSTM-DDF models in simulating the daily streamflow in the Kumalak River catchment at the Xiehela outlet from 1960 to 2018 is shown in Supplementary Fig. 8. The study period for AMF was from 1960 to 2018, and for AMFSp, it was from 1961 to 2018, due to the time step setting of 180 days for the LSTM models.

Additive decomposition to assess LSTM decisions

The additive decomposition method42 can be used to explore the internal behavior of LSTM models and has been successfully applied to study flooding mechanisms across the contiguous United States6. This method can peek into the “black box” structure of LSTM models to ascertain how the hidden information is processed and to quantify the information actually contributed at every time step \(t\) during the simulations of streamflow in the LSTM models. As shown in Supplementary Fig. 7c, the model output \(y\) is composed of information accumulated over \(T\) time steps and can be viewed as the sum of information contributed at every time step \(t\) (represented by circle 3), which is further a product of the first two items (represented by circle 1 and circle 2). The information contributed at every time step is the portion of information obtained at that time step to be retained after “forgetting” by the cells that follow.

Given that 10 independent models were trained using the 10-fold validation method, 10 sequences of time-wise information actually contributed were generated for every streamflow peak (i.e., \({h}_{1},\,{h}_{2},\,\cdot \cdot \cdot ,\,{h}_{180}\), which is simplified as \({h}_{i}^{\bullet }\), indicating information actually contributed at each of the 180 time steps). Then, the 10 sequences were averaged into one sequence (i.e., \({\bar{h}}_{1},\,{\bar{h}}_{2},\,\cdot \cdot \cdot ,\,{\bar{h}}_{180}\), which is simplified as \({\bar{h}}_{i}^{\bullet }\)). The values of \({\bar{h}}_{i}^{\bullet }\) at every time step were then summed across all of the AMF events and divided by the number of events to produce one sequence (i.e., \({\bar{h}}_{1}^{{\prime} },\,{\bar{h}}_{2}^{{\prime} },\,\cdot \cdot \cdot ,\,{\bar{h}}_{180}^{{\prime} }\), which was simplified as \({\bar{h}}_{i}^{{\prime} \bullet }\)). The same process was applied to the AMFSp events.

The average information contributed at every time step for all AMF and AMFSp events in the LSTM-SG and LSTM-DDF models was calculated using the additive decomposition method (Supplementary Fig. 9). The information from the most recent seven-day period had a decisive impact on the simulations of AMF and AMFSp events, which led to the selection of this time window for investigating the factors driving floods in this catchment.

Integrated gradients for feature importance

The integrated gradients technique, which was developed by Sundararajan et al. 43, was used to interpret trained models by calculating the time-wise feature importance of three input variables for every output sample (i.e., daily streamflow). This gradient-based method traces the specific contributions of input features to the output of the model. It assigns importance scores to every feature, such as rainfall, at every time step before flooding. A large positive score indicates a significant increase in network output, a large negative score indicates a decrease, and a score close to zero indicates minimal influence. This method has been successfully applied to study river flooding mechanisms and their changes in Europe8.

This study focused specifically on the integrated gradients scores for the AMF and AMFSp events to gain insights into the drivers of flooding. The input layer of the model included snowmelt \((S)\), glacier meltwater \((G)\), and rainfall \((R)\) over the past 180 days (i.e., \({X}_{1}^{S},\,{X}_{2}^{S},\,\cdot \cdot \cdot ,\,{X}_{180}^{S};\,{X}_{1}^{G},\,{X}_{2}^{G},\,\cdot \cdot \cdot ,\,{X}_{180}^{G};\,{X}_{1}^{R},\,{X}_{2}^{R},\,\cdot \cdot \cdot ,\,{X}_{180}^{R}\)), and the output layer produced the streamflow of the same day. Ten independent models were trained, and they generated 10 sequences of time-wise feature importance for every streamflow peak. All of the sequences had the same dimensions as the inputs (i.e., \({\varphi }_{1}^{S},\,{\varphi }_{2}^{S},\,\cdots ,\,{\varphi }_{180}^{S};\,{\varphi }_{1}^{G},\,{\varphi }_{2}^{G},\,\cdots ,\,{\varphi }_{180}^{G};\,{\varphi }_{1}^{R},\,{\varphi }_{2}^{R},\,\cdots ,\,{\varphi }_{180}^{R}\), indicating the feature importance scores obtained at each of the 180 time steps for every input variable). Then, the 10 sequences were averaged at every time step into one sequence (\({\bar{\varphi }}_{1}^{S},\,{\bar{\varphi }}_{2}^{S},\,\cdots ,\,{\bar{\varphi }}_{180}^{S};\,{\bar{\varphi }}_{1}^{G},\,{\bar{\varphi }}_{2}^{G},\,\cdots ,\,{\bar{\varphi }}_{180}^{G};\,{\bar{\varphi }}_{1}^{R},\,{\bar{\varphi }}_{2}^{R},\,\cdots ,\,{\bar{\varphi }}_{180}^{R}\)), simplified as \({\bar{\varphi }}_{i}^{\bullet }\), to reduce the impact of the stochasticity from training different LSTMs. The sums of the feature importance scores for the three inputs (snowmelt, glacier meltwater, and rainfall) over a seven-day window period were calculated independently for every streamflow peak and were represented as \({\sum }_{1}^{7}{\bar{\varphi }}_{i}^{S}\), \({\sum }_{1}^{7}{\bar{\varphi }}_{i}^{G}\), and \({\sum }_{1}^{7}{\bar{\varphi }}_{i}^{R}\), respectively. The seven-day window refers to the day of the streamflow peak occurrence and the six days preceding it. The framework of interpretive DL methods for identifying flood drivers is presented in Supplementary Fig. 5. The AMF event from July 1, 2016, and the AMFSp event from May 14, 2018, were chosen as case studies to illustrate flood mechanisms, using feature importance determined through the integrated gradients method (Supplementary Fig. 10).