Introduction

The El Niño-Southern Oscillation (ENSO) is the most prominent mode of the year-to-year climate variability on Earth, featuring strong sea surface temperature (SST) anomalies in the tropical central-eastern Pacific1,2,3. ENSO remarkably impacts global weather and climate, ecosystems, agriculture, and the water cycle through teleconnection mechanisms4,5,6. ENSO is also one of the most important sources of subseasonal-to-seasonal climate predictability overworld7. Thus, improving the understanding of the factors driving the ENSO variability is of paramount importance.

It is widely acknowledged that oceanic dynamics and air–sea interaction in the tropical Pacific play a pivotal role in the formation and development of ENSO1,8,9. However, the diversity and complexity of ENSO events, particularly the recent increased occurrence of central Pacific-type El Niño events and the reduced ENSO prediction skill after the late 1990s, cannot be fully explained by processes solely within the tropical Pacific7,10,11. Recent studies suggested that atmospheric variability over the extra-tropics could influence ENSO evolution12,13,14,15,16,17. In particular, extratropical forcing may enhance the ENSO predictability13,18.

The Arctic Oscillation (AO) is the predominant pattern of atmospheric interannual variability over the extratropical Northern Hemisphere. It is featured by opposite anomalies of atmospheric pressure between the Arctic and northern mid-latitudes, exhibiting a vertical barotropic structure in the troposphere19,20. The AO influences climate across the mid- and high-latitudes, such as the record-breaking cold winter in 2009–10 over Eurasia21,22. Research indicates that the impacts of the AO are not limited to mid- and high-latitudes but can extend into the tropics23,24,25,26. Specifically, the boreal spring AO exerts notable influences on the subsequent ENSO by inducing westerly anomalies over the equatorial western Pacific27,28,29. Observations reveal that many winter ENSO events are preceded by strong spring AO anomalies, including the four strong El Niño events of 1972–73, 1982–83, 1997–98, and 2015–16 (positive AO anomalies), as well as the strong La Niña events of 1988–89, 1999–2000, and 2010–11 (negative AO anomalies) (Fig. S1). Further, a study has documented the crucial role of the spring AO in triggering the onset of the exceptionally strong 2015–16 El Niño29.

Understanding the stability of the AO-ENSO relationship is crucial for ENSO prediction. Interdecadal changes in the impact of spring AO on ENSO have been noted30, but this finding is based on relatively short data. In addition, the underlying causes of the fluctuating influence of AO on ENSO remain unexplored. Here, we show that the effect of AO on ENSO displays multidecadal fluctuations using multiple observational and reanalysis datasets dating back to 1900. We identify the Atlantic Multidecadal Variability (AMV) as a pivotal factor influencing the AO-ENSO connection by modulating the Pacific center of the AO. AMV is the dominant mode of multidecadal variations of SST in the North Atlantic31,32,33,34. We further examine the mechanisms behind the impact of AMV on the AO-ENSO relationship through observational analyses, Pacemaker experiments, and AMIP model simulations.

Results

Influence of AO on ENSO and its multidecadal variation

The physical mechanism by which the spring AO influences the subsequent winter ENSO throughout the analysis period is outlined below (Fig. S2). Positive spring AO-associated anticyclonic anomaly over the mid- and high-latitude North Pacific (i.e., the Pacific center of the AO) induces an anomalous cyclone over the subtropics through the interaction between the low-frequency mean flow and synoptic-scale eddy activity28,35,36. This cyclonic anomaly counters the mean northeasterly winds, resulting in Pacific Meridional Mode-like (PMM) positive sea surface temperature (SST) anomalies in the subtropical North Pacific, which then persist and extend southward to the tropical central Pacific during the following summer through wind-evaporation-SST feedback (Fig. S2a, b)13,14,37. Then, the tropical central Pacific SST warming triggers deep convection, initiating a positive air–sea feedback loop that strengthens the western Pacific equatorial westerlies and induces eastward-propagating Kelvin waves, ultimately leading to El Niño in the subsequent winter (Fig. S2).

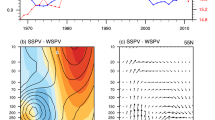
We further explore the interdecadal changes in the relationship between the spring AO and the subsequent winter ENSO. The 21-year running correlation of the MA(0) AO index with the D(0)JF(1) Niño3.4 index effectively illustrates this variation (Fig. 1a). Five SLP datasets, including NCEP1, HadSLP, ERA20C, ERA5, JRA55, are utilized to compute the spring AO index. Two SST datasets, including HadISST and ERSSTv5, are employed to calculate the Niño3.4 index. The connection between the spring AO and ENSO shows consistent multidecadal changes based on the above different datasets, with statistically significant correlations from the late 1960s to the late 1990s and before the mid-1920s, corresponding to periods with the negative AMV phase (Fig. 1a and Fig. S3). In contrast, the relationship between the spring AO and ENSO is weak from the mid-1920s to the late 1960s and after the late 1990s, consistent with the positive AMV phase (Fig. 1a and Fig. S3). The multidecadal variation in the AO-ENSO relationship is notably out of phase with that of the AMO index, with correlation coefficients of −0.90, −0.93, and 0.89 derived from the three reanalysis datasets (Fig. 1c–e). Furthermore, the correlation coefficients between the MA(0) AO index and the D(0)JF(1) Niño3.4 index reach 0.57, 0.47, and 0.48 during negative AMV phases for various datasets considered, all significant at the 99% confidence level (Fig. 1f). In contrast, the correlations between the spring AO and ENSO are weak during positive AMV phases (Fig. 1f). Negative (positive) AMV phases are defined as those years when the normalized AMV index (see “Materials and Methods” section) exceeds (falls below) zero. The differences in the spring AO-ENSO correlation between negative and positive AMV phases are statistically significant at the 95% confidence level, as determined by Fisher’s r-to-z transformation (Methods).

Fig. 1: Impact of the AMV on the AO-ENSO connection.
figure 1

a 21-year running correlation of the spring (March–April-mean, MA(0)) AO index with the following winter (December–January–February-mean, D(0)JF(1)) Niño3.4 index. The smoothed spring AMV index (bars) is also shown in (a). SLP data used to calculate the AO index are obtained from the HadSLP2, ERA20C, NCEP1, ERA5, and JRA55. SST data used to calculate the Niño3.4 SST index are obtained from the HadISST dataset. Horizontal line in (a) indicates the correlation significant at the 90% confidence level. Scatter diagram of the AMO index against the spring AO-ENSO correlation with a 21-yr moving window obtained from the b HadSLP2, c ERA20C, d NCEP1, e ERA5, and f JRA55. Red lines in (b–f) indicate the best linear fit and gray lines indicate the 95% confidence range of the linear regression. g Correlation coefficient between the spring AO index and the following winter Niño3.4 index during positive and negative phases of the AMV.

Full size image

Evolution of SST, precipitation, and wind anomalies in association with the spring AO is further investigated during both negative and positive AMV phases (Fig. 2). In negative AMV phases, the positive phase of the spring AO corresponds to a dipolar atmospheric pattern over the North Pacific, featuring an anomalous anticyclone over the mid- and high-latitude North Pacific and an anomalous cyclone over the subtropical North Pacific (Fig. 2a). The subtropical North Pacific anomalous cyclone induces positive SST anomalies, which propagate southward to the tropical Pacific, generating westerly anomalies in the equatorial western-central Pacific in the subsequent summer through a WES feedback mechanism (Fig. 2a, b). These low-level westerly wind anomalies contribute to the development of El Niño in the ensuing winter by triggering eastward-propagating Kelvin waves and positive air–sea interaction (Fig. 2b–d, i–l)1,27,28. The spring AO-generated maximum SST warming reaches 1.6 °C in the tropical central-eastern Pacific in D(0)JF(1) (Fig. 2d). During positive AMV phases, atmospheric anomalies are weak in boreal spring over the North Pacific (Fig. 2e). Consequently, the connection between the spring AO and subsequent ENSO cannot be established (Fig. 2e–h and m–p).

Fig. 2: Evolution of spring AO-related anomalies during two phases of AMV.
figure 2

Anomalies of SST (shadings, °C) and 850-hPa winds (vectors, m s−1) in MAM(0), JJA(0), SON(0), and D(0)JF(1) regressed upon the spring AO index during the negative (a–d, first column) and the positive (e–h, second column) AMV phases. i–l and m–p are similar to (a–d) and (e–h), but for precipitation anomalies. We only show the SST and precipitation anomalies exceed the 95% confidence level. Wind anomalies in both directions less than 0.3 m s−1 are not shown.

Full size image

Mechanism for the modulation of AMV on AO-ENSO connection

The above analyses indicate that the AMV plays a crucial role in regulating the AO-ENSO relationship. Next, we examine the mechanism by which the AMV modulates the influence of AO on ENSO. We demonstrate that the AMV regulates the connection between spring AO and ENSO by influencing the North Pacific center of the AO.

During negative AMV phases, the Pacific center of the AO is strong, featured by notable positive geopotential height and SLP anomalies over the mid- and high-latitude North Pacific (Fig. 3a, c), which induce pronounced atmospheric anomalies over the subtropical North Pacific through the interaction between the mean flow and the synoptic-scale eddy activity28,38. Specifically, anomalous anticyclone over the mid-latitude North Pacific (i.e., the Pacific center of the positive AO) leads to a weakening of westerly winds and synoptic-scale eddy activity over the North Pacific around 40°–50 °N (Fig. S4a, b)28,35,36. Reduction in synoptic-scale eddy activity over the mid-latitude is accompanied by anticyclonic vorticity forcing to its north and cyclonic vorticity forcing to its south (as depicted by geopotential height tendency anomalies, Fig. S4c). The cyclonic vorticity forcing over the subtropical Pacific (Fig. S4c) accounts for the formation of the spring AO-related cyclonic anomaly. The resulting subtropical North Pacific cyclonic anomalies and SST warming impact ENSO development by inducing westerly wind anomalies over the equatorial western Pacific (28). In sharp contrast, the North Pacific component of the AO weakens remarkably during positive AMV phases (Fig. 3b, d). Accordingly, the spring AO fails to produce significant atmospheric anomalies over the subtropical North Pacific and thus has a weak influence on ENSO. We have further created scatter plots of the North Pacific component of the spring AO against the summertime westerly wind anomalies over the tropical western Pacific and against the AO-ENSO connection. Results reveal that in decades when the North Pacific portion of the AO is more prominent, surface westerly wind anomalies generated by the spring AO over the equatorial western Pacific in JJA(0) are more pronounced (Fig. 3f). Stronger westerly winds over the western Pacific exert a greater influence on the subsequent ENSO (Fig. 3g). Therefore, the connection between spring AO and ENSO is more robust during periods of negative AMV when the Pacific center of the AO is stronger (Fig. 3e).

Fig. 3: North Pacific component of the AO.
figure 3

Spring SLP (a, b, unit: hPa) and 500-hPa geopotential height anomalies (c, d, unit: m) regressed on the spring AO index during different AMV phases. Anomalies significant at the 95% confidence level are stippled in (a–d). Scatter diagram of the spring AO-ENSO correlation against e the North Pacific component of the spring AO (unit: m), and against g the spring AO-related 850-hPa westerly wind anomalies in JJA(0) over the tropical western Pacific (TWP, 5 °S–10 °N, 145°–160 °W) (unit: m s−1) for the 21-year running period. f Scatter diagram of the North Pacific component of the spring AO (unit: m) against the spring AO-related 850-hPa westerly wind anomalies in JJA(0) over the TWP (unit: m s−1). The North Pacific component of the AO is defined as spring AO-related geopotential height anomalies averaged over 40°–60 °N, 155 °E–160 °W (box region in a–d). Red lines in (e–g) indicate the best linear fit, and gray lines indicate the 95% confidence range of the linear regression.

Full size image

We now investigate the mechanism by which the AMV modulates the Pacific center of the AO. The AO consists of two primary components over the mid-latitudes: one over the North Pacific and the other over the North Atlantic19,20. The North Pacific component of the AO is closely associated with the atmospheric anomalies associated with the Aleutian Low and the Pacific North American (PNA) teleconnection, and the North Atlantic component is linked to the North Atlantic Oscillation (NAO)39,40,41,42,43,44,45,46. It has demonstrated that the AO could be considered as a combination of the AL/PNA and NAO41,44,46,47,48. The North Atlantic component of the AO is stable. This is consistent with the fact that the relationship between the AO and the NAO stays significant during the analysis period (Fig. S5). However, the Pacific center of the AO exhibits notable variability44,45,46. When the coupling between the North Pacific and the North Atlantic is weak (strong), the North Pacific component of the AO is weak (strong)42,44,46. The coupling between the North Pacific and the North Atlantic is associated with an eastward propagation of atmospheric Rossby wave from the North Pacific to the North Atlantic, triggered by North Pacific atmospheric anomalies40,41,42,44,49. The coupling between the North Pacific and the North Atlantic, to a large extent, can be indicated by the AL-NAO connection. The spring AL-NAO connection exhibits notable multidecadal variations, showing a strong out-of-phase relation with the AMO index (Fig. 4a, R = –0.81). During the negative AMV phases, there is a significant connection between the spring AL index and the NAO index (R = 0.51), depicted by a robust eastward propagation of atmospheric Rossby wave from the North Pacific to the Atlantic (Fig. 4g). This significant AL-NAO connection is associated with a strong Pacific center of the AO (Fig. 4c), thus contributing to a pronounced influence of the AO on ENSO (Fig. 4d). In contrast, during positive AMV phases, the connection between the AL and the NAO is weak (R = 0.13), indicated by the weak eastward-propagating atmospheric Rossby wave flux from the North Pacific to the North Atlantic (Fig. 4h). Consequently, the Pacific center of the AO and the influence of the AO on ENSO are insignificant.

Fig. 4: Mechanism for multidecadal variation of the North Pacific component of the AO.
figure 4

a 21-year running correlation between the spring Aleutian Low index and the NAO index (blue curve). AMV index is also shown in (a). b Scatter diagram of the AMV index against the spring ALI-NAO correlation with a 21-yr moving window. c Scatter diagram of the North Pacific component of the spring AO against the ALI-NAO correlation with a 21-yr moving window. d Scatter diagram of the spring ALI-NAO correlation against the spring AO-ENSO correlation with a 21-yr moving window. Red lines in (e–g) indicate the best linear fit, and gray lines indicate the 95% confidence range of the linear regression. Anomalies of spring SLP (e, f, unit: hPa), 500-hPa geopotential height and wave activity flux (g, h, unit: m) regressed on the spring NAO index during positive and negative AMV phases. Anomalies significant at the 95% confidence level are stippled in (e–h).

Full size image

Then, how does AMV modulate the coupling between the North Pacific and the North Atlantic? Negative AMV phases induce an atmospheric teleconnection propagating from the North Atlantic across Eurasia to the North Pacific, leading to negative SLP and geopotential height anomalies over the North Pacific, and contributing to a deeper AL (Fig. 5a, b). A deeper AL results in stronger atmospheric planetary wave activity flux propagating from the North Pacific to the North Atlantic, inducing enhancement of the North Pacific-North Atlantic coupling and thus a strengthening of the North Pacific center of the AO.

Fig. 5: Pacemaker Experiments and AMIP model simulations.
figure 5

Differences of a SLP (unit: hPa), b 500-hPa geopotential height (unit: m), and wave activity flux (unit: m2 s−2) between the negative and positive AMV phases in observations. Stippling regions indicate differences that are significantly different from zero at the 95% confidence level. c The spring AMV index for the ensemble mean of the North Atlantic Pacemaker experiments. The differences of d SLP, e 500-hPa geopotential height, and wave activity flux between negative and positive AMV phases for the ensemble mean of the North Atlantic Pacemaker experiments. f The differences of the spring SLP between 1993 and 2004 and 1979 and 88 for the ensemble mean of 30 CMIP6 AMIP experiments. Stippling regions in (d–f) indicate the differences are significant at the 95% confidence level. g Climatology of spring SLP average over 40°–60°N, 150°E–120°W during 1993–2004 and 1979–88 obtained from the 30 CMIP6 AMIP experiments. Multi-model mean (MME) of the 30 models is also shown in (g). Error bars denote 1.0 standard deviation of the 10,000 inter-realizations of the bootstrap test (see “Materials and Methods” section).

Full size image

In summary, a negative AMV phase deepens the AL by triggering an atmospheric Rossby wave train over the mid- and high-latitudes. The deepening of the AL may induce a stronger eastward-propagating Rossby wave from the North Pacific to the North Atlantic41,42,44, leading to a stronger coupling between the North Pacific and the North Atlantic, and thus a stronger North Pacific component of the spring AO. This further explains a stronger influence of the spring AO on the subsequent winter ENSO via the air–sea interaction process28. It is noted that deeper AL may correspond to strong atmospheric disturbance and stronger divergence anomalies in the upper troposphere, which indicates a stronger atmospheric Rossby wave source. In addition, deeper AL corresponds to a stronger westerly jet over the North Pacific, which is also favorable for the eastward propagation of the Rossby wave.

It should be noted that the atmospheric anomalies of the wave train over Eurasia related to the AMV are weaker compared to the atmospheric anomalies over the North Pacific and North Atlantic. This may be due to the fact that the interaction between the synoptic-scale eddy and the low-frequency mean flow is important in the formation and maintenance of the atmospheric Rossby wave train. The North Pacific and the North Atlantic are the regions with strong synoptic-scale eddy activity and strong wave-mean flow interaction35,50. Strong wave-mean flow interactions over the North Pacific and the North Atlantic may maintain and enhance the atmospheric anomalies induced by the AMV.

The North Atlantic pacemaker experiments (see “Materials and Methods” section) conducted using the CESM version 6 that participated in the CMIP6 Decadal Climate Prediction Project confirm the impact of AMV on AL. The ensemble mean of the AMV index is similar to the observed, showing positive AMV phases from the early 1920s to the early 1960s, and after the late 1990s and negative AMV phases before the early 1920s and from the early 1960s to the late 1990s (Fig. 5c). Similar to the observed, an atmospheric wave train is found from the North Atlantic across Eurasia to the North Pacific, leading to prominent negative SLP and geopotential height anomalies over the mid- and high-latitude North Pacific, indicative of a stronger AL during negative AMV phases (Fig. 5d, e).

The 30 AMIP model simulations from CMIP6, in which the AGCM models were forced by the observational SST data from 1979 to 2014, further illustrate the influence of the AMV. SLP is notably lower during 1979–98 (negative AMV phase) than during 1999–2014 (positive AMV phase) based on the ensemble mean of 30 CMIP6 AMIP experiments (Fig. 5f). All the 30 CMIP6 models produce a stronger AL during the negative than positive AMV phases (Fig. 5g). This is consistent with the results of the North Atlantic pacemaker experiments. Therefore, the results derived from both the North Atlantic pacemaker experiments and AMIP experiments confirm a deeper AL during negative AMV phases. In addition, we note that the North Atlantic pacemaker experiments and the 30 CMIP6 AMIP simulations exhibit slight discrepancies, including larger SLP differences over the North Pacific and smaller SLP differences over the North Atlantic. In addition, the mid-latitude wave train induced by the AMV in the observations and the North Atlantic pacemaker experiments cannot be seen in the AMIP simulations. These discrepancies are probably due to the fact that the differences between the two periods (i.e., 1993–2004 and 1979–1988) in the AMIP model simulations represent not only the impacts of AMV but also the impacts of global warming tendency and other components of internal climate variability.

Studies indicated that the stratospheric polar vortex has an influence on the AL-NAO connection and the North Pacific component of the AO44,48,51,52. The connections between the AL and the NAO and the North Pacific center of the AO are stronger (weaker) when the stratospheric polar vortex is stronger (weaker)44,51,52. We show that negative AMV phases are favorable to a stronger polar vortex compared to the positive AMV phases (Fig. S6a, b). When the polar vortex is stronger, more vertically propagating planetary waves that originate from northern Eurasia and the North Pacific are reflected downward to North America and the North Atlantic (Fig. S6c, d). This may also contribute to a stronger connection between the North Pacific and North Atlantic pressure patterns, and create a stronger North Pacific center of the AO.

The above analysis suggests that both horizontal Rossby wave propagation and vertical wave propagation may play an important role in modulating the connection between the North Pacific and the North Atlantic. However, it is still unclear which pathway is more important. The relative roles of horizontal Rossby wave propagation and vertical wave propagation in connecting the North Pacific and the North Atlantic and in explaining the multidecadal modulation effect of the AMV on the AO-ENSO connection should be further investigated in the future.

Discussion

This study reveals that the AO-ENSO relationship displays remarkable multidecadal variations, which is primarily controlled by the AMV. The influence of the spring AO on the following winter ENSO is prominent (weak) during the negative (positive) AMV phases. During the negative AMV phase, the Pacific center of the AO is stronger, inducing stronger subtropical Pacific atmospheric anomalies via wave-mean flow interaction28, which then leads to stronger surface westerlies over the tropical western Pacific via WES feedback. These westerly wind bursts exert a more pronounced influence on the following ENSO evolution via triggering eastward-propagating Kelvin waves and positive air–sea interaction. We show that negative AMV induces an atmospheric wave train over mid- and high-latitude and leads to a deeper AL based on the observational analysis and the North Atlantic Pacemaker Experiments. Deeper AL triggers stronger planetary Rossby atmospheric activity flux from the North Pacific to the North Atlantic, leads to a stronger AL-NAO connection, and contributes to a stronger North Pacific center of the AO and thus a stronger influence of the AO on ENSO. In addition, a stronger stratospheric polar vortex during negative AMV phases might also favor a stronger AL-NAO connection, and thus a stronger North Pacific center of the AO. These results have far-reaching implications for the prediction of ENSO and provide a deeper understanding of the impact of extratropical atmospheric variability on the tropical air–sea coupled system.

Further, wintertime SST warming (cooling) in the North Atlantic related to the positive (negative) AMV may induce a zonal overturning circulation over the mid- and high-latitudes with upward (downward) motion over the North Atlantic and downward (upward) motion over the North Pacific53. The downward (upward) motion anomalies over the North Pacific might also contribute to a (weaker) stronger AL53. However, we cannot detect clear zonal overturning circulation anomalies over the mid- and high-latitudes of the North Pacific and North Atlantic in springtime. This mechanism remains to be explored.

It should be noted that the AMV is an Atlantic phenomenon, but the differences in the spring AO-related atmospheric circulation and SST anomalies are more pronounced in the North Pacific than in the North Atlantic. In particular, the difference in the North Atlantic component of the AO (i.e., the NAO-like atmospheric anomalies) is quite marginal between the negative and positive AMV phases. Studies have shown that the NAO is strongly associated with SST anomalies in the mid-latitude North Atlantic54,55. This suggests that AMV-associated SST anomalies in the subtropical North Atlantic may play a more important role in driving AO-related North Pacific atmospheric changes in spring than AMV-related SST anomalies in the mid-latitude North Atlantic. The relative roles of the subtropical and mid-latitude North Atlantic SST anomalies related to the AMV in modifying the spring AO-related atmospheric anomalies over the North Pacific and in modulating the spring AO-ENSO connection need to be further investigated.

This study shows that the connection between the AL and the NAO shows significant interdecadal variations. One question is whether the NAO is significantly stronger when it occurs in conjunction with the AL. We have examined the SLP anomalies regressed on the spring NAO index in years when the spring NAO and AL indices have the opposite and same phases (Fig. S7). It turns out that the magnitude of the spring NAO-related SLP meridional dipole anomalies over the North Atlantic is comparable when the spring NAO and AL have the opposite and same phases (Fig. S7). This implies that the AL may not have a significant modulating effect on the NAO amplitude. Studies have shown that the air–sea interaction and the wave-mean-flow interaction over the North Atlantic are crucial for the NAO variability55,56,57.

We have examined the NAO-related and AMV-related SST anomalies in the North Atlantic (Fig. S8). The NAO-related SST anomalies show a meridional tripolar pattern in the North Atlantic, with significant SST warming in the tropical North Atlantic and mid-latitudes around 40°–60°N, and SST cooling in the subtropical northwestern Atlantic near 30°N (Fig. S8a). The AMV-related SST anomalies also feature a tripolar anomaly pattern with same-sign anomalies (Fig. S8b). In addition, the centers of action in Fig. S8a are quite similar to those in Fig. S8b. Given that the AMV primarily represents decadal-scale variability and the NAO exhibits broad peaks in the spectrum covering seasonal to decadal timescales, this implies that the decadal variability of the NAO can partly overlap with that of the AMV. Therefore, the AMV-like SST anomaly and the NAO might be considered as two physical variables of a specific atmosphere-ocean phenomenon when focusing on the decadal timescale.

In addition to the mechanism described above, the AMO may also influence the North Pacific component of the AO by modulating the storm track activity and the westerly jet over the mid-latitude North Pacific. Changes in storm track activity are closely related to changes in the westerly jet over the North Pacific35,36. An increase in the storm track is accompanied by an increase in the westerly jet and vice versa35,36. Previous studies attributed the interdecadal change in North Pacific atmospheric anomalies associated with the spring AO around the early 1970s to the change in the North Pacific storm track activity58. It is shown that the increased storm track activity after the early 1970s led to an increase in the strength of the synoptic-scale eddy feedback to the low-frequency mean flow, resulting in more pronounced atmospheric anomalies over the North Pacific58. This suggests that the AMO may also modulate the springtime atmospheric anomalies by altering the North Pacific storm track. Figure S9a, c shows differences in the North Pacific 200-hPa zonal wind and storm track activity between negative and positive AMO phases. The westerly jet and storm track over the North Pacific are stronger during negative than positive AMO phases (Fig. S9a, b), in agreement with Zhang and Delworth33. The enhanced storm track and westerly winds over the North Pacific may lead to stronger AO-related atmospheric anomalies in the North Pacific, contributing to a stronger influence of the AO on the subsequent winter ENSO during the negative AMO phase.

The spatial pattern of SLP anomalies over the North Pacific associated with the interannual variation of the spring AO bears some resemblances to the spatial pattern of SLP anomalies associated with the interannual variation of the spring AL. Here, the AL index is defined as the regionally averaged SLP anomalies over 40°–60°N and 155°E–160°W. Thus, studies have shown that the North Pacific center of the AO (i.e., the atmospheric anomalies over the North Pacific associated with interannual variation of the AO) has a close relationship with the atmospheric anomalies associated with interannual variation of the AL39,40,41,42,43,44,45,46. However, the correlation coefficient between the spring AO index and the spring AL index during 1948–2022 is 0.21, which is only significant at the 90% confidence level. This suggests that the North Pacific center of the AO is not totally the same as the atmospheric anomalies associated with interannual variation of the AL.

The correlation coefficient between the interannual variation of the AO and the interannual variation of the AL is not high because the North Pacific center of the AO is not stable (Fig. 3a, b). That is to say, significant SLP anomalies cannot always be observed over the North Pacific related to the interannual variation of the spring AO. However, significant SLP anomalies can always be observed over the North Pacific in association with the interannual variation of the AL. In particular, for the decades during the negative AMV phase, significant SLP anomalies can be observed over the North Pacific in association with the spring AO (Fig. 3a). During these decades, the North Pacific center of the AO is closely related to the interannual variation of the AL. In contrast, the North Pacific center of the AO is weak for the decades during the positive AMV phase (Fig. 3b). During these decades, the North Pacific center of the AO has a weak relationship with the interannual variation of the AL. Therefore, the North Pacific center of the AO has a relationship with the atmospheric anomalies associated with interannual variation of the AL. However, it cannot indicate that the North Pacific center of the AO is identical to the atmospheric anomalies associated with interannual variation of the AL.

Since the interannual variation of the spring AO index is related to the interannual variation of the spring AL index, one may wonder whether the AMV also has a pronounced modulating effect on the connection between the spring AL and the following ENSO. To address this issue, we have calculated the 21-year running correlation of the spring AL index with the subsequent winter Niño3.4 index. It shows that the spring AL has a significant relationship with the following winter ENSO after the late 1990s (Fig. S10). However, the interdecadal change in the relationship between the interannual variation of the spring AL and the subsequent ENSO is not similar to the phase shift of the AMV (Fig. S10). Therefore, the AMV has a weak modulation of the relationship between the interannual variation of the spring AL and the subsequent ENSO.

In addition to ENSO, AO could also exert notable impacts on other tropical climate variability, for example, the Indian Ocean dipole (IOD) that can exert a notable impact on global climate26,59, and the tropical cyclone activity over the tropical North Pacific24,60. Evolutions of wind and SST anomalies regressed upon the spring AO index over the tropical Indian Ocean during different phases of the AMV show that the impact of the AO on the IOD is weak (strong) during positive (negative) AMV phases (Fig. S11). Furthermore, during negative AMV phases, large-scale positive GPI anomalies (indicating an increase in TC genesis) in JJAS(0) associated with preceding spring AO are seen over the tropical North Pacific around 150°E–90°W and 0°–15°N (Fig. S12a). In addition, a pronounced decrease in GPI is observed over the western part of the tropical western North Pacific and around 20°–30°N, 120°E–150°W (Fig. S12a). In sharp contrast, GPI anomalies are weak over the tropical Pacific during the positive AMV phase. These results suggest that AMV is an important controller for the impact of the AO on the tropical climate system.

The AMV may shift from a positive to a negative phase due to internal climate variability in the next twenty years61. This suggests that the spring AO may provide an additional source of predictability for the tropical climate modes through the stronger impact on the ENSO and the tropical climate variability in the near future.

Materials and methods

Data and methods

Monthly and daily mean SLP, geopotential height, winds, and precipitation rate from the National Centers for Environmental Prediction–National Center for Atmospheric Research (NCEP-NCAR) reanalysis62. We also use Monthly SLP data from the ECMWF twentieth-century reanalysis (ERA20C63), the Hadley Centre Sea Level Pressure Dataset (HadISLP64), European Centre for Medium-Range Weather Forecasts fifth generation atmospheric reanalysis (ERA565, Hersbach et al.65), and Japanese 55-Year Reanalysis data (JRA5566, Ebita et al.66) to confirm the robustness of results. Studies have indicated that SLP data are less reliable prior to 190067,68,69. Therefore, we only use the data after 1900.

Two SST datasets are used, including the Extended Reconstructed Sea Surface Temperature dataset version 5 provided by the National Oceanic and Atmospheric Administration (ERSSTv570) and the Hadley Centre Sea Ice and Sea Surface Temperature dataset (HadISST71). ERSSTv5 SST data are available from 1854 to the present and have a resolution of 2° × 2°. HadISST SST data spans from 1870 to the present have a resolution of 1° × 1°. ENSO variability is represented by the Niño3.4 SST index, which is defined as the regional mean SST anomalies over 5°S–5°N and 120°–170°W. The AMV index is defined as area-mean SST anomalies in the region of 0°–70°N and 0°–60°W32. The long-term trend of SST anomalies was deleted before defining the AMV index.

Synoptic-scale eddy activity (also called storm track) is defined as the root mean square of the 2–7-day band-pass filtered geopotential height anomalies at a specific pressure level38. Spring AO refers to the March–April-mean AO index28. This is because the March–April-mean AO index has the largest correlation with the following Niño3.4 index28. Spring AO index is calculated as the principal component time series of the EOF1 of SLP anomalies in MA(0) over 20°–90°N and 0°–360°E.

Geopotential height tendency

The geopotential height tendency is used to quantitatively examine the feedback of synoptic-scale eddy activity on low-frequency mean flows. The geopotential height tendency resulting from the eddy vorticity flux forcing can be written as follows35,36:

$$F=\frac{f}{g}{\nabla }^{-2}[-\nabla \cdot \overline{(\overrightarrow{{{\bf{V}}}^{\text{'}}}{\zeta }^{\text{'}})}]$$
(1)

where \(g\) and \(f\) represent the acceleration of gravity and the Coriolis parameter, respectively. \(\overrightarrow{{{\bf{V}}}^{\text{'}}}\) and \({\zeta }^{\text{'}}\) denote the synoptic-scale winds and vorticity, respectively. The overbar indicates the mean in boreal spring in this study. Note that the synoptic-scale vorticity is calculated using synoptic-scale winds.

Fisher’s r-z transformation

Fisher’s r-z transformation is employed to examine the significance of the difference between two correlations. Firstly, the two correlations (i.e., r1 and r2) are subjected to the Fisher transform as follows72:

$${{\rm{Z}}}_{1}=0.5\times \,\mathrm{ln}\left[\frac{1+{r}_{1}}{1-{r}_{1}}\right]$$
(2)
$${\rm{Z}}_{2}=0.5\times \,\mathrm{ln}\left[\frac{1+{r}_{2}}{1-{r}_{2}}\right]$$
(3)

Secondly, the standard parametric test is employed to estimate the null hypothesis of the equality of the Z1 and Z2, which is expressed as:

$${\rm{u}}=\frac{{Z}_{1}-{Z}_{2}}{\sqrt{\left[\frac{1}{{N}_{1}-3}+\frac{1}{N2-3}\right]}}$$
(4)

Here, N1 and N2 denote the sample sizes of two-time series, respectively. The test statistic u satisfies the normal distribution. The significance level is then estimated based on a two-tailed Student’s t-test.

Genesis potential index

The genesis potential index (GPI) is employed to investigate the influence of large-scale conditions related to the AO on TC formation, which is expressed as follows73:

$${\rm{GPI}}={|{10}^{5}\eta |}^{3/2}\times {(1+0.1{V}_{{\rm{shear}}})}^{-2}\times {\left(\frac{H}{50}\right)}^{3}\times {\left(\frac{{V}_{pot}}{70}\right)}^{3}\times \left(1-\frac{\omega }{0.1}\right)$$
(5)

where η, H, Vpot, and Vshear represent absolute vorticity at 850-hPa, the 700-hPa relative humidity, the TC maximum potential intensity, and the vertical wind difference between 200-hPa and 850-hPa, respectively.

Three-dimensional wave activity flux

We employ the three-dimensional wave activity flux to examine the propagation of planetary waves, which is written as follows74:

$${{\rm{F}}}_{s}=p\,\cos \varphi \left(\begin{array}{c}\frac{1}{2{a}^{2}{\cos }^{2}\varphi }\left[{\left(\frac{\partial {\psi }^{\text{'}}}{\partial \lambda }\right)}^{2}-{\psi }^{\text{'}}\frac{{\partial }^{2}{\psi }^{\text{'}}}{\partial {\lambda }^{2}}\right]\\ \frac{1}{2{a}^{2}\,\cos \varphi }\left[\frac{\partial {\psi }^{\text{'}}}{\partial \lambda }\frac{\partial {\psi }^{\text{'}}}{\partial \varphi }\right]-{\psi }^{\text{'}}\frac{{\partial }^{2}{\psi }^{\text{'}}}{\partial \lambda \partial \varphi }\\ \frac{2{\Omega }^{2}{\sin }^{2}\varphi }{{{\rm{N}}}^{2}a\,\cos \varphi }\left[\frac{\partial {\psi }^{\text{'}}}{\partial \lambda }\frac{\partial {\psi }^{\text{'}}}{\partial z}-{\psi }^{\text{'}}\frac{{\partial }^{2}{\psi }^{\text{'}}}{\partial \lambda \partial z}\right]\end{array}\right)$$
(6)

where Ω, a, φ, λ, H, N, ψ’ indicate the Earth’s rotation rate, the Earth’s radius, latitude, longitude, constant scale height, buoyancy frequency, and stream function, respectively. z = −H lnp and p = pressure/1000 hPa.

North Atlantic Pacemaker experiments

We use the North Atlantic Pacemaker experiments conducted with the community earth system model version 1 (CESM1) in this study to investigate the influence of AMV on the mean state of atmospheric circulation over the North Pacific. In these experiments, the model is run by time-varying radiative forcing according to the CMIP6 historical simulation protocol, but with time-evolving SST anomalies in the North Atlantic (5°N–55°N, with a linearly tapering buffer zone extending to the equator and 60°N) that nudged to the Extended Reconstruction of Sea Surface Temperature version 3b (ERSSTv3b) observations during 1920–2013. That is to say, the evolution of the ERSSTv3b observed SST anomalies in the North Atlantic are maintained in each simulation. In other regions, the model is freely coupled. It should be mentioned that only the SST anomalies, not the total SST, are nudged to ERSSTv3b observations. This can maintain the model’s mean state, avoiding any model biases. Detailed descriptions of the Pacemaker experiments are referred to Kosaka and Xie75. The North Atlantic Pacemaker experiments of the CESM include ten realizations available from 1920 to 2013. Each realization was forced by slightly different initial conditions, and we employed the ensemble mean of the ten integrations to investigate the influence of AMV.

CMIP6 AMIP model simulations

We also use simulations from 30 AMIP models (Table S1) participating in CMIP6 to confirm the impact of AMV on the mean state of atmospheric circulation over the North Pacific76. In the CMIP6 AMIP simulations, observational SST over 1979–2014 was prescribed to force the Atmospheric General Circulation Model. The ensemble mean of AMIP simulations from the 30 models is employed to evaluate the impact of AMV. Detailed information of the 30 AMIP models is provided in Supporting Table 1.

Bootstrap test

We use a bootstrap test77 to assess the statistical significance of the difference in mean SLP over the North Pacific between the negative and positive phases of the AMV derived from the 30 AMIP models. Firstly, we calculate the mean SLP values for the negative and positive AMV phases, respectively, across the 30 AMIP models. Subsequently, we perform random resampling of the mean SLP values for both the negative and positive AMV phases to generate 10,000 samples. During this resampling process, it is possible for the mean SLP value to be selected multiple times within any given model. The standard deviation is then computed for each AMV phase based on the 10,000 generated samples. If the difference in the mean SLP value between the negative and positive AMV phases exceeds the sum of the standard deviations of the two sets of 10,000 samples, the difference is considered significant at the 95% confidence level.