Introduction

Heatwaves have had a significant impact on human life and caused disasters. During 1980–2014, 783 excess deaths related to extreme heat were reported across 164 cities in 36 countries1. Economically, heatwaves resulted in significant losses, with their impacts in Europe estimated to account for 0.3–0.5% of the region’s gross domestic product in the selected years2. Heatwaves struck many cities in the Northern Hemisphere in the boreal summer of 20233, with widespread reports of heatwaves in the southwest of the United States and Mexico, southern Europe, and northern China. Overall, a long-term increase in heatwaves since the 1950s has been observed4. Heatwaves are expected to continue to increase in the future5. It has been suggested that human-induced global warming is the primary cause of the long-term increase in heatwaves6.

In light of the fact that heatwaves are caused by abnormally high temperatures, the factors that affect temperature are also responsible for heatwaves7. Internal climate variability, in addition to the external forcing of greenhouse gases, regulates regional or global temperatures on short-term timescales, such as interannual to decadal8,9,10. Internal climate variability comprises modes of oceanic and atmospheric circulation variations, wherein oceanic variability modes exert a remote influence on land temperature by perturbing atmospheric circulation10,11,12. Atmospheric circulations, such as Rossby waves13,14, blocking15,16, North Atlantic Oscillation17, and jet streams18, have frequently been associated with heatwaves in the mid-latitude regions of the Northern Hemisphere.

Therefore, the fundamental causes of heatwaves can be classified as external forcing and internal climate variability. Internal climate variability can modulate decadal to multi-decadal climate changes, primarily due to decadal oceanic variability19,20,21. For example, it has been extensively demonstrated that oceanic variability plays a crucial role in regulating the decadal trends of global average temperature, including its dominant influence on slowing global warming in the early 2000s8,10,22,23. In terms of weather extremes, the oceanic variability of the Atlantic and Pacific Oceans, such as Atlantic Multidecadal Oscillation (AMO) and Interdecadal Pacific Oscillation (IPO)24,25, has been suggested to influence the decadal trends of heatwaves in many regions across the Northern Hemisphere through Rossby wave train propagation and ocean-atmosphere coupling mechanisms26,27,28,29,30. The phase shift of the AMO from cold to warm had significantly contributed to the increasing trend of European heatwaves during 1980–2021 by intensifying the mid-latitude North Atlantic jet, accounting for ~43% of the observed trend31. The IPO has been associated with variations in surface air temperature and precipitation over Australia and the southwestern United States32. Moreover, the transition of the IPO from a negative to a positive phase contributed to the decline and subsequent recovery of the Indian summer monsoon around 199933. The combination of the negative phase of the IPO and the positive phase of the AMO has been shown to enhance the East Asian polar front jet and suppress the East Asian subtropical jet during summer, primarily through changes in the meridional temperature gradient and the Eady growth rate34.

However, it is unclear to what extent oceanic variability has caused changes in heatwaves over 2013–2023. This study sought to provide an answer to this query. We examined the variations in Northern Hemisphere land heatwaves across decadal timescale and corresponding spatial pattern. The contributions of heatwaves over Northern Hemisphere land areas were then analyzed across temporal and spatial scales. Using statistical methods, we quantified the impact of AMO and IPO on decadal heatwave fluctuations and explored their underlying physical mechanisms. To further isolate their individual contributions and verify the physical mechanisms involved, we employed pacemaker experiments from the Coupled Model Intercomparison Project Phase 6 (CMIP6)35 to investigate the decadal heatwave fluctuations forced by AMO and IPO.

Results

Heatwave trends, fluctuations, and patterns

Here we identify that heatwave cumulative intensity (HWCI) was mainly examined in this study. HWCI was defined as the cumulative temperature exceedance over the threshold for heatwave events from May to September of each year (see Methods). Therefore, HWCI covers not only heatwave frequency but also heatwave intensity and duration4,18.

The average HWCI in the Northern Hemisphere significantly increased from 1940 to 2023 (Fig. 1a, red line). In particular, HWCI has been rapidly growing since 1985 (black curve), coinciding with rapid global warming, as illustrated by Fig. SPM.1b in ref. 36. HWCI showed considerable interannual and decadal fluctuations, as indicated by the gray and purple curves in Fig. 1a, based on Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) decomposition37. HWCI increased drastically over the recent decade from 2013 to 2023, with 2023 experiencing the most severe heatwaves since 1940. The decadal components contributed 71% to the 20.7 °C decade-1 HWCI trend over 2013–2023. Therefore, decadal fluctuations have played a crucial role in the escalating heatwaves over 2013–2023 in the Northern Hemisphere. In contrast to the quick HWCI increase for 2013–2023, the decadal component of HWCI (purple curve) showed a decreasing trend for 1940–1985 (Fig. 1a). The multidecadal down-trending and up-trending in HWCI during 1940–1985 and 1985–2023, respectively (purple curve), combined with the long-term increasing trend (red line), contributed to the decelerated and accelerated HWCI increase before and after 1985 (black curve).

Fig. 1: Heatwave cumulative intensity (HWCI) for May to September at various timescales.
figure 1

a Time series of HWCI averaged over the Northern Hemisphere land, and its interannual variability, long-term trend, and decadal variability components based on CEEMDAN decomposition37, derived from European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis version 5 (ERA5) reanalysis data provided by the ECMWF in 1° × 1° grids. The slopes of the linear fitting are in units of °C decade-1. The light and deep shadings indicate the two periods of 1940–1985 and 1985–2023. b Time series of decadal component of HWCI averaged over the Northern Hemisphere land, and its smoothed and anomaly components based on Five-point Smoothing (see Methods). Since this method may lead to overestimation at the boundaries, the subsequent analysis excluded the four boundary years (1940, 1941, 2022, 2023). The slopes of the linear fitting are in units of °C decade-1. The light and deep shadings indicate the two periods of 1942–1985 and 1985–2021.

Full size image

Extreme events, such as heatwaves, are primarily driven by both background temperature state and temperature variability38,39. Therefore, we decomposed HWCI into a smoothed component (HWCIS) and an anomaly component (HWCIA) (see Methods). As the decomposition method applied at the boundaries may result in overestimated values near the edges, the subsequent analysis excluded the four boundary years (1940, 1941, 2022, 2023) to ensure the robustness of the results. We found that, from 2013 to 2021, the decadal components of HWCIS and HWCIA accounted for 44% and 13% of the increase in HWCI, respectively (Fig. 1b). While the decadal component of HWCI was primarily influenced by HWCIS, HWCIA still played a substantial role, particularly over 2013–2021.

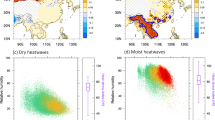
In addition to this temporal increase, spatial heterogeneity in HWCI trends became apparent, with non-uniform changes across the Northern Hemisphere (Fig. 2a). For example, southern and eastern Russia exhibited strong diminishing trends, contrasting with significant increases in six regions: Southern North America (SNA), Europe, North Africa, Northern Central Asia (NCA), northern Russia and eastern China (Fig. 2a). HWCIS dominated the HWCI increase across most of the Northern Hemisphere, with contributions exceeding 85% in North Africa and northern Russia and reaching 83% and 78% in SNA and NCA, respectively. Notably, over eastern China, the HWCI increase was almost entirely driven by HWCIS, with HWCIA contributing negligibly. However, HWCIA remained a significant driver in Europe, where HWCIS and HWCIA contribute equally, each explaining about 50% of the HWCI increase (Fig. 2a). These patterns were consistent with the results based on heatwave frequency (Figs. S1 and S2).

Fig. 2: Spatial variability of the decadal component of HWCI over 2013–2021.
figure 2

a The 2013–2021 linear trend in the decadal component of HWCI. Significant trends at the 95% confidence level (two-sided P < 0.05), assessed with a random-phase resampling test55, are marked with dots. The outlined polygons denote some designated analysis domains. b, c Same as a but for the decadal component of HWCIS and HWCIA. Proportions of HWCIS and HWCIA in each region, as shown in the pie chart presented in (a).

Full size image

Modulation of decadal heatwave fluctuations by decadal oceanic variability

Decadal oceanic variability played a significant role in influencing decadal variability in heatwaves. Here, we calculated the decadal variability of AMO and IPO based on ERA5 data, applying the method of Enfield et al.40 to AMO and the approach of Henley et al.41 to IPO. The resulting AMO and IPO are shown in Fig. S5.

Decadal oceanic variability primarily influenced HWCI trends through its impact on HWCIS, accounting for 43% of the variance in decadal component of HWCIS averaged over Northern Hemisphere land (Fig. 3a). From 1985 to 2021, decadal HWCIS fluctuations induced by oceanic variability (bars in Fig. 3a) showed an increasing trend of 1.6 °C decade-1, contributing 26% of the observed 6.1 °C decade-1 trend in HWCI (Fig. 1b). Of the two dominant modes, AMO and IPO contributed 51% and 49%, respectively, to decadal HWCIS fluctuations over the period 1942–2021 (Fig. 3b). AMO (red curve) and IPO (green curve) exhibited both multidecadal and decadal fluctuations (Fig. 3b and Fig. S5a). Therefore, AMO and IPO jointly dominated multidecadal and decadal oceanic variability generated 26% of the increasing trend in HWCI during 1985–2021 (Fig. 1).

Fig. 3: Contribution of decadal oceanic variability to decadal HWCIS fluctuations.
figure 3

a Regression of the decadal component of HWCIS (pale red curve in Fig. 1b) using the decadal oceanic variability, as represented by the decadal components of AMO and IPO for May–September (Fig. S5). The regression is significant at 95% confidence (P < 0.05), assessed with a random-phase resampling test55. b Relative contribution by the individual modes for 1942–2021 and the linear fitting for 2013–2021.

Full size image

From 2013 to 2021, AMO and IPO drove the trends in decadal HWCIS by 2.9 °C decade-1 and 7.0 °C decade-1, respectively, corresponding to relative contributions of 29% and 71% (Fig. 3b). Collectively, these two oceanic modes accounted for 63% of the observed HWCI trend (9.9 °C decade-1 out of 15.6 °C decade-1, Fig. 1b) during this period. Compared to the 1985–2021 trend, where decadal oceanic variability contributed 26% of the observed HWCI increase, the influence of decadal oceanic variability was substantially amplified over 2013–2021. Notably, the individual contributions of both AMO and IPO to the HWCIS trend during 2013–2021 were markedly higher than their respective impacts over 1985–2021 (Fig. 3b). This indicates that decadal oceanic variability played a more dominant role in driving hemispheric HWCIS growth over 2013–2021 than that since 1985.

While HWCIS predominantly determined the long-term (1942–2021) fluctuations of the decadal component of HWCI, HWCIA played an indispensable role over 2013–2021 (Fig. 1b). Both during 1942–2021 and 2013–2021, decadal oceanic variability explained a larger share of decadal HWCIS changes than decadal HWCIA (Fig. S6 and Fig. 4). However, from 2013 to 2021, decadal oceanic variability made a significant contribution to increases in the decadal component of HWCIA across some regions, such as Europe (Fig. 4d). Notably, in northern Russia during 2013–2021, the spatial patterns of the contributions of decadal oceanic variability to HWCIS and HWCIA exhibited opposite signs (Fig. 4c, d). This spatial discrepancy arises because HWCIS is primarily determined by the background temperature state, whereas HWCIA is co-determined by the horizontal gradient of the background temperature state and high-frequency circulation variability39,42. Consequently, these distinct drivers lead to spatially divergent patterns in the contributions of decadal oceanic variability to HWCIS and HWCIA.

Fig. 4: Spatial contributions of decadal oceanic variability to HWCIS and HWCIA.
figure 4

a Explained variance (R2) of decadal HWCIS in the Northern Hemisphere based on regression with decadal oceanic variability. c 2013–2021 linear trend in the time series of the decadal oceanic variability-induced HWCIS. b, d Same as a and c but for HWCIA. The time series of the decadal oceanic variability-induced HWCIS and HWCIA were calculated as the regression of the decadal components of HWCIS and HWCIA at each grid on the time series in Fig. 3a and Fig. S6 for 1942–2021. Significant regression coefficients at the 95% confidence level (two-sided P < 0.05), assessed with a random-phase resampling test55, are marked with dots.

Full size image

Building on this, we further assessed the role of decadal oceanic variability in driving HWCI over 2013–2021. In Europe, it was the dominant driver, explaining up to 58% of the observed rise in HWCI (Fig. 5). Furthermore, it contributed over 20% to HWCI in regions such as North Africa, SNA, eastern China and NCA. By contrast, the influence of decadal oceanic variability on HWCI was minimal in northern Russia (Fig. 5). Comparing the results of retaining the two boundary years of 2022 and 2023, it was found that the contribution rate of decadal oceanic variability across all regions was 20–30% higher than when these years were excluded (Fig. 5 and Fig. S7). This difference was primarily attributed to two factors: first, this contribution rate focuses on data with a relatively short time span (2013–2023); second, the most severe heatwaves since 1940 occurred in 2023 (Fig. 1a). Thus, after excluding the two boundary years of 2022 and 2023, the study period was further shortened, and the intensity of heatwaves was significantly reduced.

Fig. 5: Contribution of decadal oceanic variability to HWCI changes over the six regions.
figure 5

Regional mean trends in HWCI for 2013–2021 over the six regions shown in Fig. 2a, as well as the contribution of decadal oceanic variability, as represented by regional mean linear trends in the decadal oceanic variability-regressed time series (Fig. 4c, d). The percentage numbers indicate the contribution ratios of the decadal oceanic variability.

Full size image

In terms of spatial patterns, both the positive AMO and the negative IPO exerted significant influences on HWCIS across the Northern Hemisphere, with the positive AMO playing a dominant role (Figs. 3a and 6a, c). This dominance arose from the strong alignment of the positive AMO with HWCIS on multidecadal timescales (Figs. 1b and 3b). In particular, the positive AMO influenced HWCIS over SNA and North Africa more substantially than the negative IPO. Over Europe, both the positive AMO and negative IPO contributed substantially and similarly to HWCIS, with regionally averaged correlation coefficients of 0.25 and −0.28, respectively (Fig. 6a, c). In contrast, HWCIS over eastern China was predominantly governed by the negative IPO, with a regionally averaged correlation coefficient of -0.27, whose strength (in terms of absolute value) was greater than that of the positive AMO (r = 0.17, Fig. 6a, c). For HWCIA, the AMO exhibited a significant positive correlation (r = 0.23) in the eastern SNA region, while showing a significant negative correlation (r = −0.19) in the central SNA region (Fig. 6b). However, its influence was less pronounced in other regions, where correlations were generally weak ( | r | < 0.15) and statistically insignificant (Fig. 6b). Conversely, the IPO still demonstrated a significant negative correlation with HWCIA over Europe (r = −0.16, Fig. 6d).

Fig. 6: Patterns of decadal HWCI fluctuations tied to decadal oceanic variability.
figure 6

a, c Correlation coefficients between AMO and IPO for May–September and the decadal components of HWCIS for 1942–2021, respectively. b, d Same as (a, c) but for the decadal components of HWCIA. Significant correlations at the 95% confidence level (two-sided P < 0.05), assessed with a random-phase resampling test55, are marked with dots.

Full size image

To further investigate the underlying mechanisms through which the positive AMO and the negative IPO influence Northern Hemisphere heatwaves, the 200hPa geopotential height anomalies and associated wave activity fluxes induced by the positive AMO and the negative IPO were calculated using composite analysis (Fig. 7 and Fig. S8). Driven by the positive AMO, the Rossby wave activity fluxes propagated eastward along a mid- to high-latitude circumglobal waveguide that originated in the North Atlantic. The main branch traversed Europe, NCA, and East Asia, then entered the northern North Pacific, extended across northern North America, and finally returned to the North Atlantic, thereby closing a circumglobal teleconnection (CGT) loop (Fig. 7a). Meanwhile, two low-latitude branches emerged: one plunged directly from the North Atlantic source region into North Africa, whereas the other dived from East Asia into the tropical North Pacific via eastern China and then continued toward SNA (Fig. 7a). The Rossby wave train excited by the negative IPO originated over the North Pacific, extended eastward to SNA, and subsequently entered the tropical North Atlantic (Fig. 7b). There, it bifurcated: the main branch propagated into the mid-latitude North Atlantic, swept across Europe, NCA, and eastern China, and ultimately closed over the North Pacific, forming a CGT wave train (Fig. 7b). The secondary branch continued downstream toward North Africa (Fig. 7b).

Fig. 7: Mechanisms linking decadal HWCI fluctuations to decadal oceanic variability.
figure 7

a Composite 200 hPa geopotential height (Z200) anomalies and wave activity fluxes for the positive AMO minus the negative AMO phases for 1942–2021. The white dots indicate significant correlations at the 95% confidence level (two-sided P < 0.05), assessed with a random-phase resampling test55. The arrows represent the pathways of Rossby wave trains linking the positive AMO to Northern Hemisphere heatwaves, based on T-N wave activity flux54 (see Methods) and as shown in Fig. S8. b Same as a but for the negative IPO minus the positive IPO phases. c Schematic of wave activity flux pathways induced by the positive AMO and the negative IPO.

Full size image

Overall, Europe, NCA, and eastern China were persistently influenced by the primary CGT wave train during both the positive AMO and the negative IPO (Fig. 7). Europe exhibited the most pronounced impacts, as both the positive AMO and negative IPO significantly increased HWCIS there (Figs. 6 and 7), a result consistent with the largest contribution of decadal oceanic modes to European HWCI shown in Fig. 5. For the NCA region, the influence of the wave activity fluxes from both modes was relatively weak. This region was primarily characterized by low-pressure geopotential height anomalies (Fig. 7a, b), where HWCIS was lower than under high-pressure conditions. In contrast, increased HWCIS over eastern China was more strongly associated with the negative IPO, whose primary wave train extended directly towards eastern China before returning to the North Pacific (Fig. 7b). SNA and North Africa were primarily influenced by the positive AMO through the East Asia–tropical North Pacific branch and a direct southward branch from the North Atlantic, respectively (Fig. 7a). However, the negative IPO also contributed to these regions: for SNA, through the initial downstream extension of its main CGT wave train; and for North Africa, through a secondary Atlantic branch forming downstream (Fig. 7b). Unlike the five regions analyzed above, northern Russia remained entirely unaffected by teleconnections from either the positive AMO or the negative IPO (Fig. 7), with decadal oceanic variability exhibiting the lowest contribution to HWCI here (Fig. 5).

Implications of AMO and IPO on heatwaves

The effects of AMO and IPO on heatwaves were investigated further using the CMIP6 historical experiment (HIST) and pacemaker experiments, which set “pacemaker” in the Atlantic and Pacific Oceans by restoring the observed historical SSTs in the AMO (resAMO) and IPO (resIPO) domains43, respectively. Hence, the resAMO and resIPO experiments have the same historical external forcing as the HIST experiment, but with stronger signals forced by the historical AMO and IPO evolutions.

The historical phase evolution of AMO and IPO was better simulated in the pacemaker experiments compared to the HIST experiments (Fig. S9, Figs. S10, S11 and S12). Specifically, in the resAMO and resIPO experiments, the AMO and IPO phases simulated by the MRI-ESM2-0 model showed high agreement with observations, with correlation coefficients of at least 0.63 for AMO and 0.49 for IPO across all ensemble members (Fig. S9c, d). In contrast, the HIST experiment exhibited significantly lower correlation coefficients, ranging from 0.12 to 0.45 (Fig. S9a, b). Conversely, the BCC-CSM2-MR model produced opposite results, with AMO and IPO phases in the pacemaker experiments showing even lower correlations than those in the HIST experiments (Figs. S9 and S12).

Building on this, we analyzed the observed oceanic modes AMO and IPO in relation to HWCIS and HWCIA from three experiments. Among the four ensemble members of the resAMO experiment, the first ensemble member of MRI-ESM2-0 performed best (Fig. 8a–d). It successfully simulated the impact of the positive AMO phase on HWCIS in Europe and its partial contribution over SNA, as evidenced by close alignment with observations (1942–2012) (Fig. 8a and Fig. S13a). This further supported Europe as the region where heatwaves were most strongly modulated by decadal oceanic variability (Fig. 5). The first MRI-ESM2-0 ensemble member also captured the enhanced HWCIS over NCA and North Africa under the positive AMO phase (Fig. 8a and Fig. S13a). For the HIST experiment, while the first two ensemble members of MRI-ESM2-0 also simulated the signal of the positive AMO enhancing HWCIS across multiple Northern Hemisphere regions, their simulation of the magnitude of HWCIS on specific local areas was less accurate than that in the resAMO experiment (Fig. S14a–d and Fig. 8a–d). This result was consistent with the fact that this member had the highest AMO-phase correlation coefficient (0.76, significant at the 95% level) across both the resAMO and HIST simulations (Fig. S9).

Fig. 8: Simulated decadal HWCIS fluctuations tied to observed decadal oceanic variability.
figure 8

a–d Correlation coefficients between observed May–September AMO and the decadal components of HWCIS for 1942–2012 across two models and the four ensemble members in the resAMO experiment, respectively. Significant correlations at the 95% confidence level (two-sided P < 0.05), assessed with a random-phase resampling test55. e–h Same as (a–d) but for observed May–September IPO in the resIPO experiment.

Full size image

Regarding the resIPO experiment, comparisons with observations (1942–2012) showed that the simulated relationship between the negative IPO and HWCIS largely failed to reach statistical significance across most Northern Hemisphere regions (Fig. 8e–h). However, the second and third ensemble members of MRI-ESM2-0, which best simulated the IPO phase, produced the spatially most consistent patterns with observations (1942–2012) (Fig. S13c and Fig. 8f, g). Other members showed some resemblance in certain areas but exhibited opposite modes elsewhere (Fig. 8e, h). Furthermore, the four ensemble members of the HIST experiment largely failed to match the observed patterns (1942–2012) (Figures S14e–h). Overall, these phenomena indicated that the ensemble members in the resAMO and resIPO experiments with better-simulated AMO and IPO phases produced more accurate HWCIS simulations. Since HWCIA was simulated poorly compared to HWCIS in the CMIP6 models (Figs. S15 and S16), HWCI due to HWCIS should be focused on in future research to improve the simulation. Consequently, incorporating AMO and IPO forcings improved the agreement between model-simulated and observed HWCI.

To determine whether this improved agreement arose from physical mechanisms, we evaluated the capability of both the resAMO and resIPO experiments to simulate the observed mechanisms linking the positive AMO and negative IPO phases to Northern Hemisphere heatwaves (Fig. 9). For the positive AMO phase in the resAMO experiment, the first and second MRI-ESM2-0 ensemble members demonstrated the highest skill in replicating the 200 hPa geopotential height anomalies and the associated Rossby wave propagation pathways identified in observations (1942–2012) (Fig. 9a, b and Fig. S17a). They accurately captured the wave flux influence pathways over North Africa (direct southward branch), Europe, NCA, eastern China (main CGT branch), and SNA (East Asia–tropical North Pacific branch), including local 200hPa geopotential height anomalies, the primary circumglobal waveguide, and its two downstream low-latitude branches (Fig. 9a, b). The third MRI member captured the spatial coherence of the broad wave flux path but exhibited deviations in the magnitude and positioning of local geopotential height anomalies (Fig. 9c). And the BCC-CSM2-MR ensemble member performed poorly in replicating these features (Fig. 9d).

Fig. 9: Mechanisms linking simulated decadal HWCI fluctuations to decadal oceanic variability.
figure 9

a–d Composite 200 hPa geopotential height (Z200) anomalies and wave activity fluxes for the positive AMO minus the negative AMO phases during 1942–2012 across two models and the four ensemble members in the resAMO experiment, respectively. Significant correlations at the 95% confidence level (two-sided P < 0.05), assessed with a random-phase resampling test55. e–h Same as (a–d) but for the negative IPO minus the positive IPO phases in the resIPO experiment.

Full size image

For the negative IPO phase in the resIPO experiment, only the second MRI member reproduced regional geopotential height anomalies linked to the observed wave train (1942–2012) (Fig. 9f and Fig. S17b). At the large scale, this member also best simulated the full CGT wave train–originating in the North Pacific, extending to SNA, bifurcating into the mid-latitude Atlantic branch (affecting Europe, NCA, and eastern China) and the secondary North Africa branch–closely matching observations (1942–2012) (Fig. 9f and Fig. S17b). The third MRI member partially captured the main propagation route but failed to resolve the pathway over Eurasia clearly (Fig. 9g). The first MRI-ESM2-0 member and the BCC-CSM2-MR member exhibited deficiencies in simulating both local impacts and the large-scale teleconnection pathways (Fig. 9e, h). Additionally, in the resAMO experiment, all MRI-ESM2-0 ensemble members reproduced enhanced signals in regions where the positive AMO exerted greater influence on HWCIS than the negative IPO (e.g., SNA, North Africa). Similarly, for the resIPO experiment, the same ensemble members better captured signals in regions dominated by the negative IPO, exemplified by eastern China. These results corroborate the distinct dynamical pathways associated with the two modes. Furthermore, the resAMO experiment better reproduces signals in regions where the AMO dominates HWCIS, whereas the resIPO experiment more accurately captures signals in areas primarily influenced by the IPO.

Based on the relationships between decadal HWCIS fluctuations and oceanic variability, the observed periodic characteristics of decadal oceanic variability can be utilized to statistically predict near-term decadal fluctuations in HWCIS. Fourier analysis was used to determine the periodic decadal oceanic variability. Without taking into account the interannual fluctuations, the near-term changes in HWCIS can be inferred by combining the oceanic variability-induced decadal HWCIS fluctuations and the observed long-term trend (Fig. 10). Using the periodic fluctuations of AMO and IPO modes, along with their regression relationship with the HWCI shown in Fig. 3a, the HWCIS was projected to experience down-trending (purple curve with circles) decadal fluctuations in the coming decade (Fig. 10). Together with the long-term increasing trend (red line with circles), the HWCIS increase is expected to slow down (black curve with circles) during the next decade. Although the prediction was not sophisticated, the results imply that the current accelerated HWCIS increase is expected to turn slow once the current up-trending decadal oceanic variability swings to its down-trending phase.

Fig. 10: Prediction of HWCIS5 over 2022–2040.
figure 10

Near-term prediction of HWCIS from 2022 to 2040 by combining the Fourier analysis of the oceanic variability-induced decadal HWCIS fluctuations (bars in Fig. 3a) and the long-term trend in observations (red line in Fig. 1a).

Full size image

Discussion

This study aided in our understanding of the factors driving heatwave escalations in recent decades. We found that although HWCIS governed heatwave fluctuations across the Northern Hemisphere land regions, HWCIA played a significant role during 2013–2021, both temporally and spatially. In addition to the long-term increasing trends in heatwaves caused by anthropogenic greenhouse gas emissions44,45, we demonstrated that the decadal oceanic variability regulated the heatwave fluctuations over land in the Northern Hemisphere. The positive AMO and negative IPO influence the increase in heatwaves across different regions of the Northern Hemisphere through distinct Rossby wave trains, and this teleconnection pattern explains the spatial heterogeneity of heatwaves induced by oceanic forcing. Furthermore, pacemaker experiments verify that incorporating both AMO and IPO forcing improves model simulations of Northern Hemisphere heatwaves. Specifically, the resAMO experiment better reproduces signals in regions strongly influenced by the AMO, while the resIPO experiment performs better in regions dominated by the IPO.

Meanwhile, the study has some shortcomings. For example, the AMO and IPO exhibit a degree of multicollinearity46,47, which may affect the interpretability of multiple linear regression results and the reliability of the regression model48. Although we further isolated the AMO and IPO for individual analysis using pacemaker experiments, these experiments only included four model members, three of which belong to the MRI-ESM2-0 model. This constrains the robustness of the overall model results and introduces substantial uncertainty. Future research should employ improved statistical methods and incorporate more model members to conduct a more in-depth analysis of these issues.

Previous research highlighted the role of oceanic variability-induced global mean temperature fluctuations in accelerating or decelerating global warming on decadal timescales8,9,10,11. Expanding on this, this study further revealed that the magnitudes of oceanic variability-induced decadal heatwave fluctuations could be comparable to those of the human-induced background heatwave increase during the decadal period. For example, an empirical prediction can be made using the periodic oceanic variability-induced heatwave fluctuations and the long-term trend in observations. The results indicate that the current heatwave escalations are projected to slow down in the coming decades once the decadal oceanic variability changes its phase (Fig. 10).

Ocean modulation-induced heatwave fluctuations will thus substantially exaggerate (e.g., 2013–2021) or mask the human-induced increase in heatwaves at decadal timescales, depending on the phase of the decadal oceanic variability. Ocean modulation-induced heatwave fluctuations are crucial for understanding the observed variations and predicting the near-term changes in heatwaves. Moreover, the heatwave patterns modulated by the ocean are critical. While the AMO and IPO regulate the hemispheric mean decadal oscillations in heatwaves, heatwaves fluctuate in some regions at odds with the hemispheric mean or even in opposing trends. Therefore, whether the ocean also modulates the declining trends of regional heatwaves requires further investigation.

Methods

Observational data

The observational hourly 2 m air temperature data were based on the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis version 5 (ERA5) reanalysis data provided by the ECMWF in 1° × 1° grids from 1940 to the present49 (finally updated in 2023-10-13). The observational SST dataset was the National Oceanic and Atmospheric Administration (NOAA) Extended Reconstruction SSTs version 5 (ERSSTv5) provided by the NOAA PSL, Boulder, Colorado, USA, in 2° × 2° grids from 1854 to the present50 (downloaded in 2023-10-09).

Numerical experiments

The three experiments and two models used in this study are introduced in Table S1. The three experiments include historical (HIST) simulation from 1850 to 2014, Atlantic (resAMO) and Pacific (resIPO) pacemaker simulations from 1870 to 2014. The two pacemaker experiments from the Global Monsoons Model Inter-comparison Project (GMMIP)43 of the CMIP635 were used to assess the impact of AMO and IPO forcing on the heatwaves. In the experiments, “pacemaker” was set in the AMO domain (0°N–70°N, 70°W–0°W) and the tropical lobe of the IPO domain (20°S–20°N, 175°E–75°W) by restoring the observed historical SST within the domain, respectively, whereas SST in other ocean regions was freely coupled. The pacemaker experiments used the same external forcing as the HIST experiment. Only the BCC-CSM2-MR and MRI-ESM2-0 models have all of the variables needed for our investigation. Therefore, we only examined the outputs from the two models. In all experiments, there were one ensemble member for BCC-CSM2-MR and three ensemble members for MRI-ESM2-0.

Heatwave definition, metrics, and trends

We identify heatwaves from May to September in the Northern Hemisphere (10°N–80°N) that meet three criteria: (i) temperature extreme—the daily maximum 2 m air temperature (Tmax) above the 90th percentile4,18,26,51; (ii) uncomfortable temperature for humans—above 0 °C; and (iii) persistence of the extreme event—at least three consecutive days exceed the two thresholds4,18. Previous studies have revealed an artificial discontinuity in and out of the base period52. Therefore, we chose all the years of the target period as the base period to determine the percentile. To enlarge the sample size for a more robust percentile estimation, the centered 15-day moving window for each day was used18,51. Thus, the sample size for calculating the percentile for each day is 84 (years) × 15 (days/year) = 1260 for 1940–2023. In order to mitigate biases arising from the use of a seasonal running window, the mean seasonal cycle was removed before calculating the extreme thresholds53. In addition to heatwave frequency, heatwave cumulative intensity (HWCI) was mainly examined in this study. HWCI was defined as the cumulative temperature exceedance over the 90th percentile threshold for heatwave events from May to September of each year. Therefore, HWCI covers not only heatwave frequency but also heatwave intensity and duration4,18.

Decomposition of HWCI

To analyze the driving factors behind extreme events, such as heatwaves, which are typically influenced by both background temperature state and temperature variability38,39, we employed a decomposition-based approach to quantify their respective contributions.

First, the climatology of the two years before and after each year was removed from the original temperature data T(year). The decomposition is defined as follows:

$${T}_{ano}(year)=T(year)-\frac{1}{5}\mathop{\sum }\limits_{i=-2}^{2}T(year+i)$$
(1)

where year (1941 < year < 2022) represents the time step. To avoid the boundary overestimation effect of this decomposition method, data from the boundary years (1940, 1941, 2022, and 2023) were excluded to ensure robustness.

Then, the climatology of the original temperature data T(year) from the preceding five years was added back to the Tano(year), resulting in the temperature variability component, Tvar(year).

$${T}_{var}(year)=\frac{1}{5}\mathop{\sum }\limits_{i=1940}^{1944}T(i)+{T}_{ano}(year)$$
(2)

After decomposing the temperature data, the HWCIA driven by temperature variability was calculated, and the HWCIS driven by background temperature state was calculated using the following formula:

$$HWC{I}_{A}=f({T}_{\mathrm{var}}(t))$$
(3)
$$HWC{I}_{S}=HWCI-HWC{I}_{A}$$
(4)

CEEMDAN

The complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN)37 was used to decompose the variability of time series into various components at distinct frequencies called intrinsic mode functions (IMFs). The first IMF, IMF1, has the highest frequency, whereas the last IMF has the lowest. In this study, the time series of HWCI and heatwave frequency over the Northern Hemisphere land from 1940 to 2023 were first detrended, followed by CEEMDAN decomposition, which resulted in six IMFs. The interannual and decadal components in Fig. 1a were the IMF1, and the sum of IMF2, IMF3, IMF4, IMF5, and IMF6, respectively. The decadal components of oceanic modes were also the sum of IMFs 2 through 6.

T-N wave activity flux

The propagation of stationary Rossby wave packets is assessed using the T-N Wave Activity Flux (WAF) formula54. This method diagnoses Rossby wave propagation independent of wave phase and parallel to the local group velocity under the geostrophic approximation. The formulas are as follows:

$$\psi ^{\prime} =\frac{g}{f.Z^{\prime} }$$
(5)
$$W=\frac{p\,\cos \phi }{2|U|}\left\{\begin{array}{c}\frac{U}{{a}^{2}{\cos }^{2}\phi }\left[{\left(\frac{\partial \psi ^{\prime} }{\partial \lambda }\right)}^{2}-\psi ^{\prime} \frac{{\partial }^{2}\psi ^{\prime} }{\partial {\lambda }^{2}}\right]+\frac{V}{{a}^{2}\,\cos \phi }\left[\frac{\partial \psi ^{\prime} }{\partial \lambda }\frac{\partial \psi ^{\prime} }{\partial \phi }-\psi ^{\prime} \frac{{\partial }^{2}\psi ^{\prime} }{\partial \lambda \partial \phi }\right]\\ \frac{U}{{a}^{2}\,\cos \phi }\left[\frac{\partial \psi ^{\prime} }{\partial \lambda }\frac{\partial \psi ^{\prime} }{\partial \phi }-\psi ^{\prime} \frac{{\partial }^{2}\psi ^{\prime} }{\partial \lambda \partial \phi }\right]+\frac{V}{{a}^{2}}\left[{\left(\frac{\partial \psi ^{\prime} }{\partial \phi }\right)}^{2}-\psi ^{\prime} \frac{{\partial }^{2}\psi ^{\prime} }{\partial {\phi }^{2}}\right]\end{array}\right\}$$
(6)

where p is the normalized pressure after dividing by 1000 hPa. U and V represent the basic flow in the zonal and meridional directions, respectively. |U | = (u, v) and \(\psi {\prime}\) are the horizontal wind and the anomalous geostrophic streamfunction. ϕ and λ represent latitude and longitude, respectively. a stands for the Earth’s radius. The prime symbol indicates the anomaly after removing the zonal mean value.

Linear trend

The linear trend was determined using linear regression based on the least squares method. The statistically significant linear trend threshold at the 95% confidence level (P < 0.05) is determined from the probability distribution functions of 1000 instances of the linear trend between two red noise samples with the same autoregressive characteristics as the original signals55.

Multiple linear regression

Multiple linear regression was used to detect the relationships between the decadal components of the HWCI and oceanic variability. As shown in Fig. 3a, the independent variable was the decadal component of the HWCI averaged over the Northern Hemisphere land, and the dependent variables were the AMO and IPO. The statistically significant multiple linear regression threshold at the 95% confidence level (P < 0.05) is determined from the probability distribution functions of 1000 instances of the multiple linear regression among multiple red noise samples with the same autoregressive characteristics as the original signals55. The relative contribution of each term to the regressed independent variable (yreg) was calculated using Equation (14) in ref. 56. The formula is as follows:

$${R}_{i}=\frac{1}{m}\mathop{\sum }\limits_{i=1}^{m}\left[{T}_{i}^{2}/\left(\mathop{\sum }\limits_{i=1}^{n}{T}_{i}^{2}\right)\right]$$
(7)

where m is the length of data series,\({T}_{i}={a}_{1}{X}_{1},{a}_{2}{X}_{2},\mathrm{..}.,{a}_{n}{X}_{n}\), the terms in the equations.

Correlation coefficient

The Pearson sample linear cross-correlation method was used to calculate the correlation coefficients. The statistically significant correlation threshold at the 95% confidence level (P < 0.05) is determined from the probability distribution functions of 1000 instances of the correlation coefficient between two red noise samples with the same autoregressive characteristics as the original signals55.