Introduction

Deep neural networks (DNN) have made significant progress in the field of brain-inspired learning for various applications, including voice and image recognition1,2. For practical purposes, such computation-intensive tasks can be performed in graphic processing units3. This suggests the notion that within the frames of the von Neumann paradigm, the on-chip application of DNN is significantly constrained due to the segregation of memory and processing units.

For this reason, the next-generation computer technology is shifting towards memory-centric architectures, such as in-memory, near-memory, and neuromorphic computing4,5,6. Compared to conventional silicon devices, emerging memory technologies can make a massive contribution to achieving optimal memory applicable in neuromorphic computing7,8,9,10. These memory devices include two-terminal resistive random-access memory (RRAM)7, phase-change memory11, magnetoresistive memory (STT-MRAM)12, and three-terminal ferroelectric transistors (FeFET)4,13. As a nonvolatile memory, RRAM is noted to be a strong candidate with high density14, fast switching (~10–100 ns)15, low power16, CMOS compatibility, and excellent endurance/retention properties17.

In an attempt to further simplify the neural network, recent studies have obtained a beneficial compromise between reducing the immense model size (~16–32X) and deterioration of learning accuracy18,19. This compromise was achieved by quantizing 32-bit floating weights to 1-bit binary (−1, +1) precision. Consequently, the inference computation is also simplified, where the vector-matrix multiplication operation with floating weights can be replaced by addition/subtraction in a Binary Neural Network18. In turn, this simplification can be further optimized into an XNOR and bit-counting operation in XNOR-Net19. It is noted that the model can provide improvements in energy efficiency, computation rate, and cost by using a weight-pruning technique, thus achieving ternary precision (−1, 0, +1)20. Therefore, such algorithms can be practically implemented using binary RRAM devices as synaptic networks21,22,23,24.

In conventional cross-point architectures, frequently used for two-terminal memories, the critical mask steps increase rapidly as the stack number increases25. This limits both bit-cost efficiency and the integration density of the whole array. To overcome such limitations, 3D vertical stacking technologies, such as VNAND for flash memories26 and VRRAM for resistive memories, are currently implemented to achieve high-density arrays with optimal bit-costs25,27,28,29. VRRAMs have demonstrated good write/read margins, energy consumption, and parallel programming properties23,27,30. However, using conventional metal materials as a word-plane (WP) electrode may, owing to its intrinsic parasitic properties, limit both planar and vertical sizes of 3D VRRAM28. In addition, recently proposed techniques for weighted-sum (WS) operations with binary RRAM devices limit the full application of multiple layers31. The specified factors impede 3D VRRAM application in neuromorphic computing for large image dataset recognition.

Therefore, a holistic approach integrating emerging devices, circuits, and system-level analysis is required to overcome these issues. With its remarkable electronic and thermal conductivity, graphene is a potential candidate to replace metal-based interconnects for various devices, including 3D VRRAM32,33. In the case of the VRRAM, integrating graphene sheets as a WP electrode will drastically change the response of the individual devices within an array34,35,36, thus requiring a distinctive programming scheme to have a positive impact on the system. Consequently, inspired by the studies on 1-bit ternary precision quantization18,19,20, applications with RRAM devices21,22,23,24, and 3D VRRAM technology25,27,28,29,30, this work investigated the potential of the graphene-based VRRAM array as a memory-centric, neuromorphic computing platform. The graphene edges were used as electrodes in individual devices to extract device characteristics for statistical analysis. Based on the intrinsic behavior of the devices, a large-scale multilayer 3D vertical RRAM array was simulated for read, write, and weighted-sum operations. With XNOR algorithm-inspired architecture, the graphene-based VRRAMs resulted in considerably higher recognition accuracy compared to VRRAMs using conventional metals such as Pt. The difference was found to be the result of both the improvement of the device and the enhanced performance of the interconnect.

Results

3D VRRAM single device structure and response

In this work, fabricated TiN/HfOx/Pt and TiN/HfOx/graphene structures are referred to as Pt-RRAM and Gr-RRAM, respectively, denoting 3D VRRAM with platinum (Pt) and graphene plane electrodes. Figure 1a,b depicts the cross-sectional schematic of Pt-RRAM and Gr-RRAM single devices with two stacked layers. In 3D VRRAM, the active memory cells are sandwiched between pillar and multilayer plane electrodes27,35,37. The thicknesses of Pt and graphene electrodes are 5 nm and ~3 Å, respectively. Figure 1c–e shows the high-resolution transmission electron microscopy (TEM) image of cross-sections of both Pt-RRAM and Gr-RRAM devices. The Al2O3 layer was used as an adhesion promoter since it has higher surface energy compared to thermally oxidized SiO2. Nevertheless, fabricating an extra adhesion layer is not a crucial stage, as high-quality graphene can be transferred directly on the SiO2 substrate37.

Fig. 1: 3D VRRAM single device structure.
figure 1

a, b Single device cross-sectional schematic for a Pt and b graphene plane electrode-based VRRAM with two layers. In this work, TiN/HfOx/graphene and TiN/HfOx/Pt 3D VRRAM structure can be further referred to as Gr-RRAM and Pt-RRAM, respectively. c High-resolution TEM image of Pt-RRAM device from previous work34 (Scale bar: 5 nm). d High-resolution TEM image of Gr-RRAM device (Scale bar: 30 nm). e Layer 1 example image, where graphene was transferred on top of the Al2O3 layer serving as an adhesion promoter. (Scale bar: 5 nm). f Typical semilogarithmic I–V curve of the top and bottom layers for both Pt- and Gr-RRAM devices.

Full size image

The DC I–V characteristics of Pt-RRAM and Gr-RRAM devices with two layers are shown in Fig. 1f. In contrast to the Pt-based devices, we can achieve unconventional switching in VRRAM with graphene plane electrodes, where one of the noticeable distinctions includes the inverted polarity of the programming voltage. In conventional 3D memory, the SET operation is achieved by applying the positive bias on the pillar electrode (TiN) and negative on the WP electrode (Pt)27,28, whereas for Gr-RRAM, the SET is carried out by applying a negative bias on the pillar electrode (TiN) and positive on the plane electrode (graphene). This difference can be explained by the fact that in RRAMs, TiN is commonly used as an oxygen reservoir, and a TiOxN1−x interfacial layer is formed at the TiN/HfOx interface, facilitating the accumulation and the discharge of the oxygen ions27. Although such a principle is also applicable to Gr-RRAM35,37, distinctive device features were implemented by utilizing graphene as an active electrode, as it can also be operated as a stand-alone oxygen reservoir34. Conducting the soft dielectric breakdown and initiating the primary defects in the bulk metal oxide layer determines the further behavior of the Gr-RRAM device by activating one of the electrodes. This means that the polarity of the forming voltage of graphene-based VRRAM with TiN/HfOx/graphene structure dictates toward which electrode (TiN or graphene) oxygen ions will initially migrate, assigning the consequent programming operation characteristics. More detailed illustrations are shown in Supplementary Fig. 1.

The stochasticity in device response, and programming schemes

Before estimating VRRAM array performance, it is important to ascertain the repeatability of the single devices in temporal means. The device DC responses for 30 cycles are shown in Fig. 2a,b for Pt-RRAM and Gr-RRAM devices, where median curves are shown in blue and red, respectively. Furthermore, Supplementary Fig. 2 shows the SET voltage variations in distinctive quasi-static sweeps for 100 cycles in both VRRAMs, whereas cycle-to-cycle variations (σ/μ) were found to be 13 and 6.4% for Pt-RRAM and Gr-RRAM devices, respectively. The switching voltages and the currents are considerably lower for Gr-RRAM than for Pt-RRAM due to its much thinner graphene electrode and its highly focused electrical field at the edge34. The lack of a TiOxN1−x barrier layer, which impedes current conductance at the pillar electrode and the active memory interface, is another reason for low voltage operation34,36.

Fig. 2: The programming scheme based on the switching characteristics.
figure 2

a, b Illustration of cycle-to-cycle variation in DC I-V characteristics of a Pt-RRAM, where the median curve is shown in blue, and b Gr-RRAM, where the median curve is shown in the red lines. c, d Programming and reading protocols based on experimental results for c Pt-RRAM and d Gr-RRAM devices for further implementation in 3D VRRAM array simulation.

Full size image

Due to the stochastic nature and the unconventional switching behavior of the Gr-RRAM devices, a protocol must be set up for safe write and read operations based on experimental results. As these devices have asymmetric bipolar characteristics, the write operation can be categorized as SET and RESET, shown in Fig. 2c, d. As a result, one can establish criteria for array programming conditions depending on the biasing scheme. For the considered ½ bias scheme in a 3D Pt-RRAM array, the safe programming conditions should include the applied voltage pulse in the range of 1.5 to 2 V for SET and −1.5 to −2.4 V for RESET to ensure the switching without ½ bias disturbance of half-selected cells (i.e., VW = {2 V, −2.4 V}). In Gr-RRAMs, a voltage range of −1.0 to −1.5 V for SET and 0.4 to 0.5 V for RESET are expected to perform the current switching in the selected RRAM cell; therefore, the applied pulse should have an amplitude of VW = {−1.5, 0.5 V}. Otherwise, the resistive switching in the metal oxide may result in probabilistic behavior, in which the switching probability roughly follows the Gaussian distribution. For a safe reading operation, the read pulse should be in the range of 0.1 V to ½ bias of the minimum safe write amplitude; in this work, it is 0.1 V (i.e., VR = 0.1 V).

Figure 3a, b displays the DC characteristics from five randomly chosen Pt-RRAM and Gr-RRAM devices. Supplementary Fig. 3 shows the cumulative distribution function for HRS and LRS in several measured devices. Overall, both VRRAMs show comparable uniformity while Gr-RRAM has a larger memory window. The magnitudes of HRS and LRS are relatively high with graphene WP, which is beneficial for array applications. Under pulse measurements, Gr-RRAM has a tolerable fluctuation at a 1.5 V/500 ns programming condition while maintaining a minimum detected ON/OFF ratio greater than 10 (Fig. 3c). From the retention test, the read noise can be retrieved before the unintended resistance shift under various thermal stresses ranging from ~145 to 200 °C (shown in Fig. 3d). As expected, the read noise is more substantial at the elevated temperature. To further estimate the array performance, it is essential to build a single device model that can accurately reflect the VRRAM resistive switching behaviors. Therefore, the Verilog-A compact model was configured based on the concepts of tunneling gap evolution, accurately demonstrated in the Stanford RRAM design38,39,40,41, and conductive filament (CF) radial evolutions42,43. One of the pillars of this work is based on the statistical study achieved by the extensive experimental measurements. Consequently, the RRAM model was defined considering the intrinsic programming variations and read noise. Figure 3e,f shows the experimental and simulated models of the DC characteristics with a tolerable fitting. The programming energy of the Gr-RRAM device is drastically smaller, due to reduced switching voltage and current (IW = 5 μA), than the Pt-RRAM (IW = 80 μA), as shown in Supplementary Fig. 4.

Fig. 3: The study and modeling of the devices’ responses.
figure 3

a, b Spatial DC curves from randomly selected a Pt-RRAM and b Gr-RRAM devices. All the measured devices exhibit similar behavior for multiple cycles. c Endurance pulse test of the Gr-RRAM device, where the minimum detected ON/OFF ratio is greater than 10×. d Retention time results of Gr-RRAM before unintended resistance shift occurs under reading voltage (0.1 V bias) and various thermal stresses ranging from ~145 to 200 °C. The read noise at different temperatures is retrieved, where the measurement of the RRAM resistance state showed strong fluctuations in elevated temperature environments. Inset: Resistance distribution example under 155 °C thermal stress prior to the unintended shift. e, f Experimental mean and simulated Verilog-A model switching characteristics for e Pt-RRAM with 80 μA switching current (IW), and f Gr-RRAM with IW = 5 μA.

Full size image

The modeling of the 3D VRRAM array with graphene word planes

Figure 4a illustrates a virtual 3D VRRAM array schematic with a 2D graphene film as the WP electrode. The thickness tdi of the isolation layer (SiO2 dielectric) is selected according to the type and dimensions of the plane electrode. The vertical density of the 3D array highly depends on the isolation layer and word plane thicknesses; thus, Gr-RRAM brings favorable impact. More detailed information can be found in Supplementary Note 1. Array biasing is performed using the WPs and bit-lines (BLs) connected to the pillar electrodes (y-axis), whereas specific memory cells are selected via vertical transistors44 controlled by selector-lines (SLs) (connected in the x-axis). Figure 4b, c shows the selected cell programming and reading scheme. For the ½ bias write operation, the selected WP and BL are fully biased (VW) and grounded, respectively, while all other unselected cells are either half-biased VW/2 on both sides or not selected by vertical transistors. For the single device read operation, all WPs and BLs are grounded except for the selected WP, which is biased to VR. Following such a pattern of array biasing, we believe, will avert unintentional write and considerably alleviate the sneak current effect27,30.

Fig. 4: 3D VRRAM array structure.
figure 4

a A schematic of a virtual 3D VRRAM array with atomically thin graphene WP. b, c Array biasing scheme for write and read operations, respectively. d Planar array-based WS operation scheme, where BLs are utilized as the neuron output.

Full size image

Vector-matrix multiplication (VMM) is one of the critical operations in neuromorphic computing, and a simple cross-point array is advantageous because it can perform a WS operation easily, due to Kirchhoff’s law, at the junctions. However, the stacked 3D VRRAM design requiring only a single pivotal lithography step is more bit-cost efficient27. To exploit both the bit-cost efficiency and the WS operation scheme in a vertical memory structure, several scenarios to conduct the WS operation in the VRRAM array have been proposed. In one study31, pillar electrodes were exploited as input neurons, whereas WPs were utilized as WS output neurons, allowing a 1TkR configuration (k is the number of layers). However, in this structure, the number of output neurons will heavily rely on the number of the stacked WPs, which in turn are dependent on the technology etching aspect ratio. Alternatively, the WPs and SLs can be combined to perform the VMM operation23, in which the selected and unselected WPs are biased to VR and 0 V, respectively, and selected BLs should be grounded (Fig. 4d). Thus, the output current read in each BL represents the WS of the input voltages and conductance of memory cells located along the y-axis of the planar array.

For a large-scale simulation of the VRRAM array in HSPICE with RRAM models, the 2 × 2 × 2-size 3D sub-circuit with one virtual node was used as a building block30,45, as shown in Supplementary Fig. 5. For both computationally accurate and efficient array simulation, the voltage-dependent VRRAM model was specifically designed to incorporate the intrinsic behavior of the Pt-RRAM and Gr-RRAM devices. The main simulation parameters for the VRRAM array are listed in Table 1.

Table 1 VRRAM array simulation parameters.
Full size table

It is worth noting that the electronic properties of graphene can be further enhanced by doping with nitrogen, boron, or FeCl333,46,47. In contrast to the pristine graphene sheet, the resistivity is expected to be reduced by increasing the carrier concentration during the doping process. Supplementary Fig. 6 summarizes recent studies in obtaining highly conductive graphene interconnects through doping with various materials. On the single memory cell level, since the overall proportion of the change in the switching resistance states in HfOx based VRRAM is significantly larger than the graphene’s actual sheet resistance, it was presumed that doping the graphene will not have a fundamental effect on the individual device response. Nevertheless, in the large 3D array architecture, where interconnect parasitics have a major impact on signal degradation, doping the monolithic graphene word plane can be the area for continued development. Therefore, the reasonable assumption that VRRAM with doped graphene plane electrode (referred to as DGr-RRAM) has similar switching characteristics as the pristine one (Gr-RRAM) but with lower sheet resistance was made. As doped graphene, owing to its relatively high conductivity, can be operated in favor of planar size increase, its potentials in the 3D vertical memory array for neuromorphic computing were also evaluated. Applied interconnect resistivities of metal and graphene materials for WP and pillar electrodes were estimated from the International Technology Roadmap for Semiconductors table48 and reports33,49. In addition, more detailed information regarding the parameterization of WP and pillar electrodes can be found in Supplementary Note 2 and Supplementary Fig. 7. For the selector transistors with a sub-45 nm node, a Predictive Technology Model was used50,51. It should be noted that graphene formation in the practical application may be challenging; the difficulties are mostly associated with graphene (1) synthesis and (2) transfer processes. For synthesis, although the chemical vapor deposition method provides large-area high-quality uniform graphene sheet growth, there are certain thermal limitations (<400–500 °C) imposed by the back-end-of-line (BEOL) process. Nevertheless, some studies have made significant advancements in graphene synthesis compatible with current and next-generation semiconductor technologies52. Since transfer-free approaches predominantly require deposition at elevated temperatures opposing BEOL limitations, therefore, in some synthesis techniques, graphene transfer may appear to be an inescapable stage. Due to the quality issues of the wet transfer related to the polymer residues left on the graphene, which degrade its electronic properties, the dry transfer process offers a more promising solution. In this regard, there have been several progressive works that demonstrate the dry transfer potential of graphene53,54. Such high-quality formation and process integration challenges are among the fundamental issues for all 2D materials. Nevertheless, the research interest is increasing significantly in these areas, mainly because it is believed that with enough advancement, there is a high possibility that 2D materials will synchronize with the current electronics paradigm.

The array performance in programming, read, and WS operations

Figure 5a,b illustrates the simulation results for accessed voltage drop over the selected furthest cell for various planar array sizes during the SET/RESET processes of the worst-case scenario. The Pt-RRAM array can no longer meet the minimum access voltage requirement beyond the 128 × 128 planar array size since the voltage range is going down to the probabilistic region (Fig. 2c) with no guarantee of the resistive switching of the selected cell. Nevertheless, this does not apply to graphene-based VRRAM arrays, as selected Gr-RRAM or DGr-RRAM cells can be safely programmed at all considered array sizes. Various components in the circuit, specifically the WP electrode and vertical transistors, contribute to the IR drop and sneak-path issues of the input voltage pulse. The evolutions of voltage drop over the WP and transistor as a function of the array size for all devices are shown in Supplementary Fig. 8. Due to WP interconnect resistance, limited saturation current in the vertical transistors, and 1TkR configuration of VRRAM, high switching currents are undesirable during programming. Fortunately, the low switching currents in Gr-RRAMs can forcefully reduce the effective resistance of the array. In this study, the 416 × 224 array size is particularly significant for further estimation of image recognition performance. Three investigated types of VRRAM can satisfy the read margin requirements for sense amplifiers to differentiate HRS and LRS states (Fig. 5c). Figure 5d,e indicates that energy consumption can be reduced by an average of ~262X for RESET (sub-pJ levels) and ~8X for SET operations in Gr-RRAM arrays, compared to Pt-RRAM arrays. Notably, the energy consumption ratio in the array simulation is reduced by two, in contrast to the experimentally measured results of the single devices, which can be explained by the presence of the half-selected cell in the ½ biasing condition.

Fig. 5: Comparison of the Pt-, Gr-, and DGr-RRAM performances in 3D structure with 8-layers at the various planar array sizes.
figure 5

a, b Write access voltage for a SET and b RESET processes. c Read margin at VR = 0.1 V where the minimum current difference is required to exceed 100 nA to distinguish HRS and LRS states. d, e Array programming energy consumption in d SET and e RESET operations. f Read inaccuracy during the WS operation at the worst-case weight pattern. g Read inaccuracy as a function of multiple BLs reading, which is important for parallel inference computing for the 416 × 224 × 8 VRRAM array size, necessary for MNIST data recognition. h Shmoo plot with different switching currents (IW) and metal WP electrode thicknesses, including the special case of Gr-RRAM. i Comparison of write voltage drop change as a function of WP thickness on various circuit components at IW = 5 μA (top) and 100 μA (bottom).

Full size image

Along with programming and reading of the selected cells, the WS is a crucial operation for further implementing VRRAMs in neuromorphic computing. Similar to the 2D cross-point array42, the VMM efficiency of specific VRRAM arrays can also be evaluated as a deviation of WS from the expected ideal value, known as read inaccuracy (Fig. 5f). Both Gr-RRAM and DGr-RRAM arrays show superior effectiveness in WS operations, not exceeding a 10% deviation of accuracy, which does not apply to Pt-RRAM. We have noticed that a large number of parallel BL readings during the inference process causes the read inaccuracy to grow (Fig. 5g), related to the increase in sneak-path current. Therefore, eight BLs for parallel inference were found to be optimal. Nevertheless, the VRRAM array with a doped graphene plane electrode can promote more BL numbers for parallel computing, owing to its low specific resistivity.

Figure 5h demonstrates the Shmoo plot, which indicates the performance of a 416 × 224 × 8-size 3D array system, according to various conditions of switching current (IW) and metal WP thickness. Metal films experience a sharp increase in resistivity, becoming comparable to insulators, as thickness goes below 5 nm28,49. With the studied Pt-RRAM switching characteristics, the WP thickness should exceed 30 nm to succeed in all operations, including WS for in-memory computation. Therefore, fabricating at this thickness may oppose the known trend of stacking more layers and obtaining a high-dense memory structure. At sub-3 nm thickness, a VRRAM array with a conventional metal plane electrode is expected to fail regardless of the switching current. On the other hand, Gr-RRAM with only 0.3 nm WP thickness can pass in all necessary operations, owing to its intrinsic properties and switching characteristics. A comparison of write voltage drop on different components as a function of WP thickness is shown in Fig. 5i. Below 5 nm WP thickness, the voltage drop on a selected cell declines considerably due to a drastic increase in circuit parasitic resistance. Shmoo plot results suggest that the design of metal-based VRRAMs, including Pt-RRAM, needs to be further optimized by device engineering to accomplish all procedures by meeting the requirements for switching current, WP resistivity, and 3D array density.

The XNOR operation-based architecture of 3D VRRAM arrays

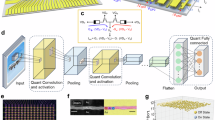
The recognition performance of the VRRAM array can be assessed using handwritten digits from the Modified National Institute of Standards and Technology (MNIST) database55. In this work, a 2-layer perceptron (MLP) topology, shown in Fig. 6a, with 400 input, 200 hidden, and 10 output neurons is used to estimate the productivity of Pt and graphene-based 3D VRRAMs. To reduce the WP planar size and implement the ternary XNOR operation, the original image is cropped and binarized (Fig. 6b). For the training process1, the required weight update can be determined using the gradient descent method shown in Eq. (1).

$${\Delta}W_{ij} = \alpha \cdot \delta _j^b\left( l \right)V_i^b\left( l \right)\,{\mathrm{for}}\,b = 1,...,B$$
(1)

where α is the learning rate, B is the batch size within which the samples are computed for the sequential weight update, and Vi, δj are the specific neuron input value and output error, respectively, for the lth layer with mxn synapse size. The detailed information about the training flow is shown in Supplementary Fig. 9. Due to the inexpensive stacking properties of the 3D VRRAM arrays, the in situ training itself can be performed in 6-bit or higher weight precisions, and further, can be optimized to 1-bit ternary precision by following the instructions shown in Fig. 6c and Supplementary Table 3, Note 3. For optimal online learning, it is expected to have 6-bit precision for binary RRAM devices56 or 64 distinct conductance levels for analog ones. Alternatively, for the ex-situ training, VRRAM can be directly quantized to ternary levels for further image classifications.

Fig. 6: The neural network structure for VRRAM arrays.
figure 6

a A 2-layer MLP neural network used in this work with binary (black/white) input signals. b Schematic and table of the XNOR operation with 1-bit ternary (−1/0/1) synapses. c Weight quantizing to a 1-bit ternary precision scheme, where the sign and three MSB (i.e., condition bits) determine the ternary level (Supplementary Table 3). d The proposed XNOR operation-focused architecture for 3D VRRAM arrays.

Full size image

Furthermore, with the use of the XNOR operation for ternary weights (Fig. 6b), the computational and energy resources can be reduced, provided the reduction is made by bit-count operations and natural weight pruning. Figure 6d shows the XNOR architecture implemented in 3D VRRAM, where the synaptic weight matrix is achieved with two vertical layers. The output current flowing in the specific BL depends primarily on input and weight logic values. For instance, input logic value “1” can be represented by applying positive and negative read pulses to the top and bottom layers, respectively. Thus, given that the top VRRAM is in LRS and the bottom one is in HRS, the expected current flowing in the pillar electrode is ILRS–IHRS, which can be represented as “1”, following the XNOR logic. In addition, natural synaptic pruning can be obtained by programming both VRRAMs to HRS states, leading to the extremely small current output considered as a logic “0”. Although a monolithic WP pattern limits the input vector range used for different RRAMs along the BL (Fig. 6d), the input “0” can be achieved by turning off the corresponding vertical transistor23. However, due to the 1TkR configuration, the whole pillar will be in an idle state. This may restrain multiple-layer parallel computing for large datasets with diverse input values. Alternatively, provided with adequate compensation, XNOR architecture can be a possible solution for layer-based partial WS of the large datasets that can be integrated with the high-stackable characteristics of the 2D graphene. It is worth noting that this work focuses on evaluating the impact of graphene in the XNOR operation-focused 3D VRRAM architecture for neuromorphic computing applications despite the graphene process integration challenges. Therefore, as an alternative, the device-circuit-architecture/algorithm levels holistic approach was applied, which also included the simulation of the programming and in-memory computing potential of the large-scale array using the graphene-based RRAM model, which was verified by extensive experimental measurements (Supplementary Note 4).

The learning performance of 1-bit ternary VRRAM arrays

Figure 7a demonstrates the evolution of neural network training accuracy based on the ideal neuromorphic devices with floating, 6-bit, and 1-bit ternary synaptic precisions. The MLP accuracy with floating weights is ~98%, reaching the baseline software benchmark. Given that the error-free VRRAM array with seven stacked layers acts as an artificial synapse network, the 2% accuracy degradation is expected. Furthermore, in comparison with floating-weight precision there is only a 3% decline at the 1-bit ternary neural network. Such a network requires only two stacked layers in the VRRAM array, as shown in Fig. 6d. Nevertheless, fluctuations in learning evolution increase considerably as weight precision is being compressed. It is worth noting that the learning outcomes are highly likely to be downgraded in a real VRRAM array, depending on the device properties, circuit parasitics, array dimensions, etc. Particularly, due to the deviations (read inaccuracy) in the WS, which is a crucial operation in neuro-inspired computing, the recognition performance may deteriorate noticeably. Figure 7b presents the learning outcomes, considering the worst-case scenario of the read inaccuracy values corresponding to the Pt-, Gr-, and DGr-RRAM 3D arrays in the inference process. The learning accuracy for Pt-RRAM is significantly decreased, followed by substantial stochasticity; this outcome can be explained by the high read inaccuracy values shown in Fig. 5f. However, the accuracy of graphene-based VRRAMs is comparable to that of an artificial neural network based on an error-free VRRAM array, owing to the intrinsic properties of graphene, its interface with the active memory layer, and 1-bit ternary synaptic architecture with XNOR operation. Such architecture shows little susceptibility to minor deviations in the read accuracy. In addition, for precise analysis of the WS effect on classification accuracy, a Monte Carlo simulation was conducted, as shown in Fig. 7c. Read inaccuracy values were selected in a uniformly random manner, ranging from minimum to maximum values according to the VRRAM type. Under the competent performance of graphene-based VRRAMs in the WS operation, the accuracy range is higher and more concise than the Pt-RRAM array, approximately following the Gaussian probability.

Fig. 7: The training accuracy of VRRAM array-based neural network estimated through simulation.
figure 7

a Evolution of the training accuracy according to the epoch for neural network (NN) models, including weights with original 32-bit floating-point precision, 6-bit precision (for 64 distinctive conductance states in a multilevel cell), and 1-bit ternary precision. b Evolution of the accuracy in the NN model with ternary synaptic precision with an injected worst-case scenario of the read inaccuracy values corresponding to the Pt-, Gr- and DGr-RRAM arrays in the inference process. c Accuracy distribution from 100,000 MC simulation runs. Inset: magnified plot for Gr- and DGr-RRAM arrays. Due to high read inaccuracy in Pt-RRAM, the overall accuracy levels degrade significantly. Comparing Gr- and DGr-RRAM, some random inaccuracies can, to a certain extent, be favorable during the inference operation. The effect of read and write noise (including cycle-to-cycle and device-to-device variations) on the recognition accuracy for d Gr-RRAM, e Pt-RRAM, and f DGr-RRAM arrays.

Full size image

Figure 7d–f shows the MLP simulation results projected on Pt and graphene-based 3D VRRAM arrays, considering the intrinsic read and write noises. As a result of the intrinsic properties of the device and its characteristics on the circuit level described previously, the accuracy downgrade rate of the Pt-RRAM is relatively higher than that of graphene-based RRAM devices. Consequently, integrating graphene does not only affect the interconnect characteristics and dimensions of the 3D VRRAM array, but also the unconventional switching mechanisms have a favorable impact on both circuit and architecture levels. In addition, by quantizing the neural network to 1-bit ternary precision and implementing the XNOR operation in the 3D VRRAM array for inference computation, the effect of read and write noises is less forceful than it is in analog synapses with floating precision (Supplementary Fig. 10). Here, the write noise combines both cycle-to-cycle and device-to-device variations. Consequently, based on the experimentally obtained read and write noises of the device (Fig. 3d and Supplementary Fig. 2), one can expect a recognition accuracy of ~83.5% in the Pt-RRAM and ~94.1% in the Gr-RRAM arrays. Since the holistic approach was applied in this study to evaluate the graphene impact in the 3D array architecture for neuromorphic computing applications, it is important to compare with other studies. Therefore, the benchmark comparison with related studies in the field of 2D materials integration into memory technology, circuit analysis of the large-scale memristor arrays, and neuromorphic computing using resistive switching devices is provided in Supplementary Note 4, Figure 11, and Table 4 in the Supplementary Information.

Discussion

In summary, this study investigated the potential performance of the Pt and graphene-based 3D VRRAM arrays as on-chip computing platforms. Replacing the conventional metal word-plane with sub-nm thin graphene increases the possible number of vertical stacks and reduces the effective parasitic resistance allowing safe read and write procedures in larger planar array sizes. Due to the low switching currents and voltages of individual devices, programming of the furthest cell consumed much lower energy on the circuit level than a conventional system. The Gr-RRAM array can successfully conduct a VMM operation resulting in a tolerable read accuracy deviation at >90k planar array size. Furthermore, the design of the XNOR algorithm-inspired architecture for the 3D VRRAM array allows the implementation of 1-bit ternary synaptic weights for the image recognition tasks. In particular, XNOR architecture has the potential to supplement the highly stackable nature of the graphene-based VRRAM arrays for parallel processing of multiple layers. This study highlights the importance of a holistic approach to correlating the material and device engineering, circuit structuring, and algorithm building to design a memory-centric, next-generation computing system.

Methods

Fabrication summary

Two-layer VRRAM devices with graphene WPs were prepared sequentially following the highlighted stages, including graphene transfer, trench forming, and deposition of metal oxide and pillar electrodes. Initially, 5 nm thin Al2O3 dielectric was deposited by atomic layer deposition (ALD) on a SiO2 (100 nm)/Si substrate for adhesion promotion, followed by graphene sheet transfer (monolayer sandwiched by copper foil, Graphene supermarket). Ti(3 nm)/Pt(30 nm) metal pads for probing were deposited by evaporation. A SiO2 (60 nm) passivation layer was deposited using LPCVD. To form the second and higher layers of the WP, the described process must be repeated34,37. Next, one pivotal lithography process was conducted to form the trench by dry etching; subsequently, HfO2 (5 nm) and TiN were deposited by ALD and sputtering, respectively.

Device characterization

High-resolution TEM images were obtained using a Tecnai TF-20 Field Emission Gun/TEM@200 kV (FEI company, UK). Electrical characterization was obtained using an Agilent Parameter Analyzer 4155C (Agilent, CA, USA) with an 81150A arbitrary signal function generator (Keysight, CA, USA) and Switch Matrix 707B (Keithley, OH, USA) for pulse measurement (retention, endurance tests).

Circuit analysis

3D VRRAM arrays with conventional Pt and graphene WPs were modeled as a matrix of 2 × 2 × 2-size subcircuits with one virtual node. Gr-RRAM and Pt-RRAM were designed as voltage-dependent models based on the experimentally verified individual device response. As a result, XNOR operation-inspired VRRAM arrays with 8 vertical layers and various planar sizes for individual cell programming, read, and network WS procedures for the worst-case scenario were simulated in HSPICE software (Synopsys, CA, USA). The detailed information regarding the characteristics of WP and pillar electrodes is shown in Supplementary Figs. 5,7 and Supplementary Note 2.

Neural Network simulation

The ANN, with 400 input, 200 hidden, and 10 output neurons, was simulated in MATLAB software (MathWorks, MA, USA); 60,000 and 10,000 cropped and binarized MNIST data were used for training and testing operations. The considered cycle-to-cycle, device-to-device variations, and read noise at elevated environment temperatures were derived from experimental results (Supplementary Fig. 9).