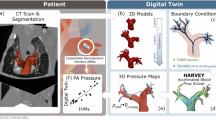
Abstract
Monitoring fluid intake and output for congestive heart failure (CHF) patients is an essential tool to prevent fluid overload, a principal cause of hospital admissions. Addressing this, bladder volume measurement systems utilizing bioimpedance and electrical impedance tomography have been proposed, with limited exploration of continuous monitoring within a wearable design. Advancing this format, we developed a conductivity digital twin from radiological data, where we performed exhaustive simulations to optimize electrode sensitivity on an individual basis. Our optimized placement demonstrated an efficient proof-of-concept volume estimation that required as few as seven measurement frames while maintaining low errors (CI 95% −1.11% to 1.00%) for volumes ≥100 mL. Additionally, we quantify the impact of ascites, a common confounding condition in CHF, on the bioimpedance signal. By improving monitoring technology, we aim to reduce CHF mortality by empowering patients and clinicians with a more thorough understanding of fluid status.
Similar content being viewed by others
Introduction
CHF affects approximately 6.5 million adults in the United States and is commonly accompanied by fluid overload conditions, which account for most CHF hospitalizations1,2. In critical care and inpatient settings, clinicians monitor urine output to assess a patient’s fluid balance, renal function, and overall metabolic state to optimize the titration of diuretics and other treatments. In outpatient settings, patients are expected to weigh themselves at the same time daily to monitor for any sudden weight changes indicative of fluid overload3. However, in both environments there are concerns about proper volume monitoring, whether it is infection risk from the monitoring method used or patient adherence to a routine4,5.
The current gold standard of urine output monitoring in hospitals are indwelling urinary catheters. The catheter allows for urine to flow freely from the bladder into a drainage bag, the volume of which medical staff can then measure. The drawback of an invasive approach is the catheter introduces an infection vector to the patient, resulting in 1 million urinary tract infections annually in the United States. The additional healthcare costs to treat the infections is estimated to range from $115 million to $1.82 billion annually4. Moreover, use of a catheter may be a contraindication for the patient6. To prevent infections, reduce costs, and address contraindications, noninvasive bladder monitoring methods are greatly needed.
Non-invasive methods do not require the patient to matriculate to obtain a reading, therefore can monitor bladder volume directly. One method used to influence clinical decisions today is ultrasound. The technique requires a trained clinician to manually perform periodic scans to assess bladder volume. General purpose ultrasound devices have large errors of 21.8% and remain largely dependent on the technician operating them7. The large error of conventional ultrasound methods arises from the positioning of the scanner and volume estimation algorithm, which itself is dependent on the current bladder volume7. Dedicated handheld ultrasound scanners, such as BVI 9400™ and Prime™ from BladderScan® can have smaller errors6. Nonetheless, both require a trained technician present to take measurements, resulting in noncontinuous monitoring. Recent advancements in miniaturization of ultrasound transducers have enabled the development of wearable systems that could increase scan frequency. However, these systems have largely focused on detecting voiding8,9 or bladder state detection (full vs empty) to help patients manage incontinence rather than bladder volume estimation10.
Continuous bladder volume estimation in a wearable form factor would allow additional populations, such as those who take diuretics, to better manage their illness. Other sensing modalities compatible with the constraints of a wearable size and power are near-infrared spectroscopy (NIRS) and bioimpedance analysis (BIA). NIRS uses an LED and a detector flushed with the skin to measure light absorbed at specific wavelengths, typically at a high absorption coefficient for water in the urine6. Literature to date has shown this technology can successfully detect the bladder state, full vs empty, in laboratory controlled environments using single subject11,12 and small group of subjects (N = 5)13. It is known that adipose tissues attenuate NIRS signals14 but the implications within the context of bladder volume estimation have yet to be published. Thus, while NIRS can accomplish bladder fill state sensing in laboratory settings, volume estimation has yet to be realized. In contrast, BIA have shown promise for volume estimation.
Several studies have found a well correlated change in voltage as bladder volume is perturbed in simulation and in vivo15,16,17,18. While BIA has demonstrated promise, it cannot effectively localize the fluid to the bladder. Electrical impedance tomography (EIT) can overcome this challenge by utilizing multiple electrodes to take impedance measurements from several positions and operating on a priori knowledge of the skin boundary allows for reconstruction of conductivity maps18,19. The general flow of data acquisition and computation is presented in Fig. 1a. These methods have comparable estimation errors seen in ultrasound, which already used clinically6,10. The development of these systems has focused on remaining compatible with existing hardware, such as the Goe MF II. These hardware systems use the neighboring method of electrode addressing20, visualized in Fig. 1b, which is not specifically optimized for monitoring the bladder. Prediction of volume using EIT requires reconstruction of a small image, typically 32 × 32 pixels21, rather than reconstruction in the 3D domain or larger image to avoid exponential growth of operations and memory usage as illustrated in Fig. 1c.

a Typical EIT system functional overview for data collection used to produce a conductivity reconstruction and volume estimation. b Cross-section of our digital twin, showing sensitivity patterns (50 kHz) when using nearest neighbor addressing on the first row of electrodes. The active electrodes use the same coloring scheme as visualized in (d), where the darker colorings indicate the source. In the PDF version of this article, please click anywhere on the figure or caption to play the video in a separate window. The first few measurement frames are iterated through. c Illustration of volume estimation number of operations and memory usage as refinement steps increase dependent on dimensionality. d Our pipeline for selecting electrode geometry and addressing scheme to optimize sensitivity to the bladder. Electrodes selected for the optimized configuration are shown in light purple.
Creating wearable systems that can non-invasively and continuously monitor bladder volume in clinical settings, the ideal electrode stimulation pattern and reduction in computational resources during estimation are required. To achieve these goals, we performed a comprehensive analysis of the optimal electrode geometry that used a conductivity digital twin derived from radiological data (Fig. 1d). Once an optimized placement was selected, we simulated 16 bladder volumes to understand trends in measurement frames with the largest voltage change and voltage change ratio (VCR) as the bladder fills. We demonstrated the number of frames required for volume estimation can be reduced, and computational complexity can be constrained to be computed on a mobile or wearable device. Finally, we evaluated the impact of ascites, a common confounding condition in CHF patients22, on the observed signals.
Results
Optimization of electrode geometry sensitivity to the bladder
We designed digital twin frequency-dependent studies using anatomically accurate geometry, shown in Fig. 2a, to assess and optimize bioimpedance electrode placement, which is fundamental to measuring tissue conductivity changes related to bladder volume. When the bladder fills with urine and expands, the transfer impedance changes, which can be correlated with the bladder volume. A pseudo three by nine matrix electrode configuration was placed on the lower anterior abdomen to allow for evaluation of the optimal placement for detecting the transfer impedance change. In a tetrapolar bioimpedance system, two pairs of contact electrodes are used; one pair injects a safe, imperceptible AC signal into the tissue, while the other pair measures the resultant voltage across the tissue19,23. We performed exhaustive simulations, iterating over all electrode pairings. The simulations utilized the conductivity of five tissues and one material via a four-pole Cole-Cole relaxation model. The digital twin was simulations were computed in COMSOL Multiphysics®v6.0 with the AC/DC physics module24.
a Diagram of the digital twin model with domains labeled whose Cole-Cole parameters were specified. b Sensitivity electrode matrix overlaid with cumulative sensitivity to the bladder for simulated volumes. Electrode IDs are included on edge columns, where column one is positioned on the right side of the twin. c Measurement frame absolute sensitivity distribution for all unique combinations of electrode pairings. d Frequency dependent proportion of shared frames across bladder volumes at various percentiles. The Pearson correlation coefficient between the values at varying frequencies is r ≥ 0.999. e Similarity matrix of shared measurement frames in the third quartile across injection current frequencies.
The electrode placement simulations utilized two bladder volumes; a lower volume segmented from radiological data measured at 144 mL, and a larger volume 598 mL bladder derived from the original segmented bladder. We computed sensitivity, S, a unitless measure of a given volume’s weight in the transfer impedance measurement19. The electrodes with the highest cumulative sensitivity to the volume of the bladder across all measurement frames were medial. When the lower bladder volume was simulated, the inferior row of electrodes were the most sensitive, with the medial electrode having the highest cumulative S (Fig. 2b). As the bladder volume expands laterally into the abdomen, the electrodes with the largest S track this movement, with the second row of electrodes providing the most sensitive measurements. Interestingly, for both volumes, there was clustering of high S in the electrode matrix: one central group around the medial electrode and two groups on the lateral sides of the patient. These patterns on the electrode geometry remained the same across stimulation frequencies injected by the current carrying (CC) electrodes.
We observed an initial steep decline in sensitivity when ranking measurement frames, as illustrated in (Fig. 2c). For a bladder volume of 144 mL, the maximum sensitivity value (∣S∣) was 2.00, which dropped to half its maximum value within the top 4.1% of the frames. The 598 mL bladder experienced a slower decay of sensitivity of halving its maximum of 2.93 within the top 9.6% of frames. The difference in decay rates suggests that a given frame’s sensitivity rank is dependent on the accompanying bladder volume. Additionally, we observed that the frames of the highest sensitivity are not likely to be shared across volumes (Fig. 2d). Frames in the 95th percentile & above were shared ≤53.4% of the time. The injection frequency in the range simulated had a minimal effect (r = 0.999). This observation is supported by the similarity matrix in Fig. 2e showed a difference of ≤1% across all frequency permutations. From our observations, we conclude that an optimized electrode geometry must account for volume dependent sensitivity, as measurement frames may not consistently maintain their percentile ranking. Additionally, a single frequency within the range 5 kHz to 200 kHz simulated is sufficient to characterize the geometry’s sensitivity.
To select the optimized geometry from the sensitivity electrode matrix, we considered the similarity of electrodes’ sensitivity between volumes. We selected 16 positions of largest S for each volume, chosen to remain compatible with a typical EIT system with 16 electrodes, resulting in 11 overlapping positions: 1, 2, 4, 5, 6, 7, 8, 9, 14, 15, 18 (see Fig. 2b). Historically, the lower volume estimations have been prone to the greatest reconstruction errors6,10,25. To address this issue, we designed an optimal electrode geometry with a bias toward lower bladder volumes to mitigate the higher error rates associated with these estimations. The optimized configuration, consisting of 15 electrodes shown in light purple in Fig. 1d, was selected to improve the robustness of bladder volume assessments across a range of physiological conditions. A visualization of improved sensitivity cross-section and current paths through the digital twin are shown in Fig. 3.

a 3D view of the digital twin, highlighting the sensitivity distribution through the internal tissues. The current injection electrodes are in blue, using a 50 kHz AC, and the voltage sensing electrodes are in green. b A view of the digital twin visualizing current density, where faster arrow movement and warmer tones indicate higher densities. In the PDF version of this article, please click anywhere on the figure or caption to play the video in a separate window.
Voltage magnitude and VCR behavior
The optimized electrode geometry was simulated across a wide range of bladder volumes. The simulations were configured to drive a constant current, which allows impedance variations to be easily calculated from the measured voltage at the electrodes. We selected VCR and the voltage magnitude’s real component to assess measurement frame performance. These metrics allow for characterization of impedance signal changes and their ability to be sensed by an ADC. Due to the highly skewed nature of VCR and the presence of infinitesimal initial condition for some frames leading to explosive growth, we applied the interquartile range (IQR) outlier detection method with an IQR multiplier of 4.5. The filtering removed ≤3.1% of measurement frames across all bladder volumes.
We found that the measurement frames with the largest changes in voltage did not necessarily correspond to a larger VCR as seen in (Fig. 4a–c). As the bladder volume increases from 151 mL to 598 mL, the effect is more pronounced as the Pearson’s correlation coefficient, r decreased from −0.170 to −0.237. In detail, for the 598 mL bladder (Fig. 4c), ∣ΔVBV∣ in the third quartile had a range of 1.04 mV to 2.46 mV and a mean ∣VCRBV∣ of (5.85 ± 4.95)%. The ∣VCRBV∣ had a third quartile range of 14.1% to 73.9%, with a mean ∣ΔVBV∣ of (351 ± 336) μV.
For all subsections, the VCR is with respect to a residual bladder volume of 10 mL and with outliers removed. a–c Observations of absolute real voltage and VCR across a range of bladder volumes (injection current 50 kHz). Additional single excitation frequency graphs can be found in Supplementary Figs. 1 to 5. d Frequency response of absolute real voltage and VCR.
The maximal change in VCR and voltage remained non-overlapping across the frequency spectrum simulated (Fig. 4d). However, as the injection frequency increases, the spread of values tends towards the origin slightly. The same IQR filtered frames appearing in both the 5 kHz and 200 kHz were compared. We observed the maximum ∣ΔVBV∣ decreased from 2.59 mV to 2.11 mV, a 18.5% drop. The ∣VCRBV∣ was less affected with a decrease of 75.1% to 74.8%, a 0.3% drop.
Bladder volume estimation using selected measurement frames
To determine the minimal number of measurement frames required for volume estimation, we designed a proof of concept BIA estimation algorithm. Least Absolute Shrinkage and Selection Operator (LASSO) was selected for linear regression and feature selection26, where the features were the individual measurement frames from the optimized electrode geometry. Hyperparameter tuning for a 50 kHz stimulation yielded the best relative errors with λ = 1.62 × 10−4 and used seven measurement frames for prediction. The relative error of predicted bladder volumes, shown in Fig. 5b had limits of agreement of −0.06 ± 3.80%, (CI 95% −1.11% to 1.00%) for volumes ≥100 mL and MAE 6.09 mL for <100 mL. The frames selected by LASSO primarily chose those with large voltage changes (Fig. 5c).
a An assortment of the bladder meshes used in simulation. The 144 mL bladder was segmented from radiological data and served as the base geometry other volumes were designed from. b Modified Bland Altman plot showing the relative volume errors for volumes ≥100 mL. c Measurement frames selected by LASSO voltage change from a 10 mL bladder volume baseline.
Grade I ascites measurement frame impact
We characterized the potential confounding effects of ascites, a build-up of fluid in the abdomen frequently occurring in clinical populations that require bladder volume monitoring, by simulating two low-grade ascites (Fig. 6a, b). The ∣ΔVBV∣ across all conditions is presented in Fig. 6c, where the voltages had an average change of 3.13% and 4.09% due to the 95 mL and 200 mL ascites, respectively. This change was most pronounced for measurement frames that had lower ∣ΔVBV∣ initially. The first quartile of measurements had a mean change of 9.52% whereas the third quartile had a mean change of 1.93%. Similarly, the VCR had more pronounced changes within the first quartile of measurements, with a mean difference of 5.05% from the no ascites baseline. We observed values in the third quartile to change by a 1.73% on average. A breakdown of these effects by ascites volume can be found in Fig. 6d, e.
For all graphs, the bladder volume increased from 10 mL 598 mL. All quartiles were calculated from the baseline condition of no ascites. a Overview of ascites simulations. b Digital twin model in a sliced view showing the placement of the ascitic fluid domain. The fluid was present along the anterior, below the subcutaneous fat. c Absolute voltage change from a bladder volume of 10 mL to 598 mL with varying levels of ascitic fluid. The measurement frame rank from the simulation without ascites is maintained across conditions to visualize drift from this state. d Comparisons of voltage changes due to the presence of ascites across the quartiles of ∣ΔVBV∣. e The change in VCR due to the presence of ascites broken-down by the quartiles of VCR.
Discussion
In our study, we investigated the bioimpedance signal using a digital twin to aid the design of non-invasive systems for continuous bladder monitoring within a wearable form factor, with the goal of achieving clinically relevant volume estimations. Our key findings include: (1) selecting measurement frames that maximize information in the region of interest can significantly reduce the number of frames needed for accurate volume estimation; (2) our proof-of-concept volume estimation methodology demonstrated low relative error across a wide range of bladder volumes; (3) this performance was achieved through optimizing electrode geometry to enhance bladder volume sensing at the individual electrode level; (4) our results suggest that maximizing the VCR often involves a tradeoff with changes in voltage magnitude; and (5) we established bounds on the impact of ascites on the bioimpedance signal. These insights collectively advance the potential of bladder volume monitoring technologies, particularly as they evolve towards practical, wearable formats.
EIT commonly addresses the electrodes by the neighboring method using 16 electrodes, which requires N × (N − 3) measurement frames resulting in 208 measurements required for reconstruction6,20,21,27,28. Using the standard estimation technique shown in Fig. 1a, the number of measurements required could theoretically be reduced as only half the measurements are linearly independent27 but may impact error performance. In this work, we demonstrated that direct estimation of bladder volume using optimized frames could significantly reduce the number of measurements by up to 96.6 % without negatively impacting estimation errors.
When comparing our results to other simulation-based studies, our proof-of-concept algorithm achieves similar or outperforms existing methods. For instance, in a study by Schlebusch, et al. we demonstrated improved accuracy over the equivalent circular diameter method, which had a relative error of 16.0%, and the singular value difference method (4.7%). However, global impedance (0.1%) and neural networks (0.8%) achieved lower errors27. Another study by Sun, et al. tested configurations with varying number of electrode rows, with the lowest error observed being 7.3% (CI 95% −5.6% to 20.1%) for vol ≥100 mL29. Our method errors showed no consistent trend in error across volumes, contrasting with other reported algorithms where errors are typically higher for lower bladder volumes across sensing modalities6,25,27,28,29,30.
The effectiveness of a non-invasive bladder volume monitoring system as a replacement for catheterization in clinical applications depends heavily on its accuracy across the expected range of volumes. While our estimation errors are compared against other computational models, it is important to consider the performance of devices currently used in clinical practice. For instance, evaluations of the BVI 9400™ overestimation by +17.5% (CI 95% 8.8% to 26.3%), whereas the Prime™ underestimated volumes by −4.1% (CI 95% −8.8% to 0.5%) without a pre-scan, and −6.3% (CI 95% −11.6% to −1.1%) across all observed volumes. Although these errors may suffice for certain clinical applications, they do not meet the stringent ±5% error margin required for postoperative care31. This emphasizes the need for continued advancements of methodologies in simulation and the translation of these improvements into real-world systems to bridge this gap in performance.
Bioimpedance measurement technology is well-suited to tackle challenges posed by clinical and at-home environments. Advancements in this field have enabled the development of smaller, more power-efficient sensors, capable of operating within a wearable form factor and providing runtime in the tens of hours before needing to charge32,33. While previous research has primarily focused on desktop bioimpedance acquisition systems6, wearable EIT have recently emerged34. Historically, reconstruction and volume estimation algorithms were designed for desktop systems, where computational power and memory resources are abundant and less constrained compared to wearable systems6,27,35,36.
In this work, we demonstrate the feasibility of reducing computational complexity and memory requirements to allow for continuous monitoring from a mobile or wearable device, all while maintaining acceptable estimation errors. The approach not only reduces the dependency on desktop systems, but also supports ambulatory use in settings beyond the clinic.
The restricted power and memory resources of wearable devices require careful trade-offs between computational efficiency and battery life. Microcontrollers, commonly used in wearable systems with battery life measured in days, are significantly more limited in memory compared to their desktop counterparts32,33. For instance, performing reconstruction with GREIT for a 32 by 32 pixel image using 16 electrodes and neighboring addressing utilizes a reconstruction matrix of 828 kB. In contrast, direct estimation from selected frames is far more memory-efficient, using only 0.027 kB for the column vector weights when for the seven frames selected from LASSO. A similar order of magnitude decrease in computation time of 142 ms for reconstruction versus 4.6 μs per estimation on microprocessors with limited resources. These optimizations make it feasible to process measurements directly on microprocessors, such as those from Microchip or Nordic, eliminating the need for desktop systems and further enabling ambulatory use. Detailed calculations and assumptions can be found in the supplementary materials.
The placement of electrodes plays a critical role in the performance of volume estimation methodologies. Bioimpedance and EIT techniques are particularly sensitive to electrode positioning, as the spatial arrangement directly affects the accuracy of impedance measurements and subsequent image reconstructions19. To address this sensitivity, our method introduces an optimization approach to electrode placement by evaluating a subset of configurations from a matrix. By doing so, we were able to evaluate \({{\mathrm{C}}^{25}_{15}}=3.27\) million placement configurations, significantly more than existing studies, which typically test only a handful (one to seven) electrode placements per study16,20,27,28,37,38. Furthermore, prior research has explored only a limited number of electrode geometries (≈10) and remained limited in the exploration of novel electrode stimulation patterns within two-dimensional geometries.
These prior works investigated electrode geometries using semicircular30,38 and two-dimensional geometries20,28,37. For one-dimensional geometries, semicircular arrangements have been shown to be more sensitive to the bladder volume compared to ring arrangements29,30,38. In two-dimensional electrode geometries, the inclusion of the superior dimension enhances sensitivity and improves global impedance measurements20,28. Based on these observations, we concentrated on electrode placements on the lower anterior abdomen, as configurations in this region outperformed other tested arrangements.
Consistent with previous findings20,28 that multiple rows of electrodes improve sensitivity to the bladder, our results visualize the shift in electrodes contributions to measurement frame sensitivity. By analyzing this dynamic, we strategically optimized electrode placement to enhance sensitivity to bladder volume, particularly for smaller bladder volumes, which are more challenging to estimate accurately6,25,27,28,29,30. The optimized configuration resulted in three electrode groupings, one medial and two lateral. To improve reproducibility when placed, the medial electrode located in row three was aligned with the navel as a landmark. Our optimized 15-electrode geometry allows for current systems to take advantage of the increased sensitivity.
The neighboring electrode pairs protocol is widely used in EIT literature due to its excellent proportional selectivity, making it useful for various applications. However, it struggles with sensitives to tissues deeper in the body compared to other addressing methods39. In the context of monitoring bladder volume, the signal of interest is from a given region of tissue, not the tissue as a whole. Therefore, we seek to maximize the signal from the bladder. We observed that patterns that maximize a change in voltage magnitude had CC electrodes that spanned rows and voltage sensing electrodes that were not neighboring each other, as shown in Fig. 3.
We also found that the maximum of the VCR and the real voltage component changes are not from the same measurement frames. Often, the frames with large VCR occur due to having a small initial voltage. When bladder volume is perturbed, even a small voltage change can produce large VCRs. For example, all VCRs larger than 50% had a change of ≤500 μV (Fig. 4c). In wearables, the analog front ends that take bioimpedance measurements have stringent power requirements compared to their desktop counterparts, resulting in ADCs that may have reduced resolution or sample rate40,41. The step size resolution of the ADC may correspond to a substantial change in bladder volume, resulting in poor accuracy. Therefore, the VCR should not be optimized without consideration of the change in the resultant voltage magnitude. Optimization of the voltage magnitude itself would lead to frames where the ADC step size corresponds to considerably smaller steps in bladder volume.
The non-invasive bladder monitoring system design has been driven by the pursuit of providing clinicians and patients with a better understanding of bladder volume without the risks of infection from catheterization. Prior studies have aimed to assist individuals with nerve damage or other forms of bladder dysfunction by alerting them when it is time to relieve themselves. Additionally, accurate urine output measurements can benefit the management of primary conditions unrelated to urologic function6. One such condition of special interest to us is CHF. A common symptom of CHF, and a primary cause of emergency room admissions, is fluid overload2. Fluid overload can manifest as ascites, which occur in the peritoneal space located just above the bladder22. Our study simulated low-volume grade I ascites in the digital twin to quantify the bounds of expected impact on the bioimpedance signal. This approach offers a framework for other studies to interpolate their signals to approximate the impact ascites may have on their volume estimation algorithms.
A key strength of utilizing digital twins for studies, is the ability to explore an unparalleled number of electrode configurations and variable effects without confounding factors in a resource-efficient manner. Several studies have found success using computational studies, using fewer conductivity domains than this work or in two-dimensions, to successfully predict configurations that perform effectively in vivo16,20,28. While we make our best effort to replicate in vivo, some simplifications and complexities may not be captured. Limitations of this work include the reliance on the dielectric properties of blood to represent ascitic fluid domain, use of muscle as a simplification of the tissues in the abdominopelvic cavity that were not individually segmented, and simplification of the dynamic range of urine conductivity due to hydration status27. Our digital twin utilized an EKG gel electrode skin interface for current injection and voltage sensing, which has different interface characteristics compared to other electrode types such as dry electrodes42. The proof-of-concept direct volume estimation using LASSO does not account for the impact of intersubject variability due to factors like waist circumference, subcutaneous fat thickness, nor urine conductivity variation16,43. In the ascites simulations, the fluid domain was modeled in the worst-case placement closest to the electrodes, rather than distributed throughout the peritoneal membrane.
In conclusion, our study developed a fundamental understanding of key components of bioimpedance-based bladder volume monitoring through simulations with an anatomically accurate digital twin. By analyzing electrode geometry at an individual level, we were able to consider millions of configurations to optimize sensitivity to the bladder, particularly at lower volumes. Using the novel geometry, we demonstrated that frame selection can enable computationally efficient volume estimation algorithms suitable for wearable devices and significantly reduce the number of measurements required for estimation. The optimization of the signal from the bladder is often a trade-off between a large VCR or voltage magnitude response. Furthermore, we evaluated the robustness of bioimpedance approaches when confronted with complications such as ascites, showing promising results. Future work should aim to investigate the influence of patient-specific characteristics on the bioimpedance signal to develop effective normalization methods. Furthermore, conducting in vivo measurements will help validate our findings and provide insights into potential artifacts due to motion or postural position changes.
Methods
Digital twin design
To engineer a conductivity digital twin that remains as closely related to in vivo conditions as possible and minimizes artifacts from abstracted anatomy geometry, the model geometry was directly segmented from radiological data using ITK-Snap44. The approach ensures highly accurate replication of anatomical structures. The DICOM data was sourced from patient CMB-PCA-MSB-07483 in the Cancer Moonshot Biobank - Prostate Cancer Collection45. We selected the patient due to their age and weight, aligning with the typical range expected within CHF patient populations. Although the data is in a cancer collection, the position of their nodules did not interfere with the anatomy of interest, making for an ideal foundation of the digital twin.
The segmentations are labeled on a per-voxel basis, resulting in the tissue having a topographical appearance with a high number of facets. Additionally, semi-automated segmentation can erroneously include parts of tissues or create boundaries that will pose problems when meshing for finite element analysis (FEA). While some of these issues can be addressed in ITK-SNAP, others cannot; therefore, the tissue geometries were imported into Fusion36046 for post-processing to remove elements that would cause issues in FEA & dramatically reduce the facet count. The resulting height of the digital twin is a 40 cm section of the torso. The skin itself is not directly segmented, but rather the air-body interface in the radiological scan was utilized to create the outer boundary of the skin. The surface is then thickened inward to 1.5 mm within the range of recorded dermis values47.
The final digital twin mesh consisted of the electrodes, skin, fat, pelvic girdle, bladder (144 mL volume), and background tissue domains resulted in 2,507,927 mesh elements. The average element quality as measured by skewness was 0.666 with a minimum element quality of 0.087. The few elements of quality ≤0.1 are not in regions of tissue of interest nor where high currents are expected to pass, thus are not likely to effect convergence of the solution48.
Additional bladder volumes were sequentially designed by sculpting the previous bladder surface in Fusion360. The radiologically derived bladder served as the initial surface. The behavior of shape changes due to filling and voiding followed biomechanic principles, where regions with expected large deformation fields experienced more manipulation of the mesh compared to regions of weaker deformation fields49. Twelve bladder volumes in approximate 50 mL steps were created and an additional five random volumes. One of the bladders did not successfully form a union in COMSOL, due to the use of partitions via work planes to assist in meshing, was excluded from analysis. The remaining 16 volumes ranged from 10 mL to 598 mL ensure coverage of filling volumes and typical capacities in adults50. Table 1 provides a summary of the domains’ geometry sources and dimensions.
Electric currents parameterization
Six simulation frequencies-5, 10, 20, 50, 100, 200 kHz-were used, with a drive current of 1 mA for all simulations. The frequency-dependent conductivities of tissues were based on the widely accepted dielectric dispersion models described by Gabrie (1996) and Peyman & Gabriel (2012). While these studies report the dielectric properties for several tissues across broad frequency range, there is an increased margin of error for low-frequency (≤1 MHz). Few studies report accurate sub-megahertz tissue properties, and those that do cover a limited number of tissues with high intra-specimen variability, and differing methodologies for reporting dielectric values51. As a result, we utilized the values from the gold-standard studies for the tissue domains. The complex permittivity \({\hat{\varepsilon }}_{r}\), modeled using a 4-pole Cole-Cole dispersion, presented in equation 152. The specific parameters for the Cole-Cole model were sourced from the tissue database compiled by51. Readers can find a summary of dielectric properties used for each domain in Table 1.
Here, \({\hat{\varepsilon }}_{r}\) represents the complex relative permittivity, ε∞ is the relative permittivity as ω → ∞, ε0 and σ0 denotes the permittivity and conductivity at DC, respectively. The term χm accounts for the susceptibility of the mth pole, which is characterized by the change in relative permittivity Δεm, relaxation time τm, and fractional coefficient αm.
The muscle domain serves as the background tissue to provide a simplification of the numerous tissues in the abdominopelvic cavity, excluding the bladder, bone, and fat domains. The reported conductivity of tissues in this cavity typically ranges from 0.1 Sm−1 to 0.5 Sm−1 in the 10 kHz to 100 kHz frequency range51. Since much of the abdominopelvic cavity consists of muscular tissue, which itself has conductivity values near the mean for these tissues, it is often modeled as muscle in other studies16,25,30. Thus, the dielectric properties of muscle tissue were utilized to represent the background tissue in our model.
The gel electrodes are modeled using a dielectric dispersion approach, with values derived from a study on the dielectric properties of physiotherapy, ECG, and EMG gel electrodes within 10 kHz to 10 MHz range53. The study does not report the Cole-Cole parameters; therefore, we manually extracted relative permittivity (εr) and conductivity (σ) values from the published graphs. These values were then interpolated in COMSOL using a piecewise cubic method that closely approximated the original data.
Electrode geometry placement and optimization
Three rows of EKG gel electrodes (2.5 cm × 2.5 cm) were arranged in a semicircular pattern, with nine columns below the navel. The anterior abdominal placement was chosen based on previous studies, which demonstrated electrode configurations in this region outperform those with posterior placements16,20,38. Electrode sizing was chosen based on the commonly available dimensions of EKG electrodes, ensuring ease of access and availability to researchers. The bottom row is vertically centered 2.8 cm proximal to the inferior bladder wall and 5.8 cm below the anterior superior iliac spine (ASIS). The electrodes were spaced by grid projection of the electrode’s center point (6.0 cm horizontal, 3.5 cm vertical) from the coronal and sagittal planes onto the skin’s surface. Electrodes were extruded 0.5 cm normal to the skin at the center point. The extruded electrodes were imported into COMSOL to allow for its computeraided design (CAD) kernel to handle the electrode skin interfacing through boolean operations.
By allowing COMSOL to form the interface, we are ensured a tight interface between the electrodes and skin. However, the CAD engine in COMSOL created invalid geometry during this process for a few electrodes on highly curved surfaced due to the thin shell nature of the skin domain. To resolve the domain issues, problematic electrodes may be shifted by up to 2 mm or corners trimmed by no more than 12% of the original surface area. The naming convention of the electrodes starts on the patient’s lower-right side with electrode one located in row one, column one. The process resulted in 25 of the 27 targeted electrodes successfully forming a union in simulation software.
Electrodes were evaluated based on their sensitivity to the bladder. The sensitivity S was calculated by using the reciprocal lead field method19,48, selecting two electrode pairs from the stored simulation results. One pair served as the CC and the other pair will be the voltage sensing, commonly referred to as pick-up (PU) electrodes. Although voltage sensing electrodes do not normally drive a significant current, their reciprocal field is needed for this operation, as shown in equation (3). \({J}_{cc}^{{\prime} }\) and \({J}_{pu}^{{\prime} }\) represents the CC and PU current density fields, respectively. The current I is the current driven between electrodes allows for the normalization to a unity current. By selecting electrodes with maximal sensitivity across all \({{\mathrm{C}}^{25}_{2}}\cdot{{\mathrm{C}}^{23}_{2}}=75,900\) combinations, the signal of urine in the bladder is subsequently globally maximized.
Measurement frame trends and volume estimation
All sixteen bladder volumes were simulated to understand the behavior of the bioimpedance signal across a broad range of fill volumes, providing insights into how the bioimpedance measurements change with bladder expansion. The comprehensive simulation approach aimed to capture the sensitivity of the bioimpedance technique to varying bladder states, from empty to full. The analysis of the measurement data was conducted using two metrics: the VCR, defined in (4) and absolute change in voltage magnitude15.
Here, V represents the measured voltage at an arbitrary bladder volume, and V0 is the baseline voltage, corresponding to an empty bladder with 10 mL of residual urine. The VCR expresses the change in voltage relative to the baseline, providing a normalized measure of how the bioimpedance signal fluctuates as filling occurs. By using the two metrics, we can assess the benefits of each metric.
We used the measurement frames as features in a proof of concept BIA volume estimation algorithm based on an optimized electrode geometry. We chose LASSO for linear regression and feature selection. Feature selection aimed to reduce the \({{\mathrm{C}}^{15}_{2}}\cdot{{\mathrm{C}}^{13}_{2}}=8,190\) measurement frames from all possible electrode addressing combinations to a manageable number that could be collected within seconds, assuming a 100 Hz output data rate. We performed a hyperparameter λ search with 25 logarithmically spaced values from 10−5 to 10−2, refining the search within the decade of minimal error.
Ascites simulation configuration
The simulations conducted thus far have assumed that the patient is free from ascites; however, it is crucial to recognize that ascites can occur in patients who have CHF. Ascites is a condition where fluid builds up in the peritoneal cavity surrounding the liver, spleen, stomach, and parts of the gastrointestinal tract22,54. In healthy individuals, the peritoneal cavity contains 25 mL to 50 mL of fluid. Grade I ascites is diagnosed via ultrasound when at least 100 mL of fluid is present. Grade II follows a similar diagnosis pathway where at least 1 L of fluid is present, typically distending the abdomen. Grade III is characterized by a severely distended abdomen due to the presence of several liters of fluid22.
We evaluated the impact of grade I ascites on the measurement frames by using two ascites volumes to establish the range of expected effects. These simulations were conducted using the optimized electrode geometry for three bladder volumes 10 mL, 300 mL, and 598 mL. The ascitic fluid was modeled by abstracting the fluid throughout the peritoneal space to a layer of fluid closest to the electrodes, under the subcutaneous fat. The abstraction was performed as the contribution of the electrical impedance of tissues drops rapidly by a r−4 factor as distance from the electrode increases19. Therefore, the ascitic fluid with the largest impact on the measured bioimpedance signal will be closest to the electrodes. The ascitic fluid layer abstraction was designed in CAD using a swept rectangular extrusion extending between the left and right ASIS, following a smooth contour of the subcutaneous fat boundary. The lowest point of the extrusion was 38 mm below the ASIS and the dimensions of the swept face are provided in Table 2. Well-characterized dielectric properties of ascitic fluids within the frequency range of interest were not found. As a result, we used the dielectric properties of blood to approximate its value, as ascitic fluid is a byproduct of unabsorbed blood filtrate22,52.
Data availability
The radiological data used can be found in the Cancer Moonshot Biobank – Prostate Cancer Collection, available at https://doi.org/10.7937/25T7-6Y12. Generated simulation data from this study is not available for sharing due to industry sponsorship, which has resulted in proprietary work.
Code availability
Code used publicly available data analysis techniques and regression algorithms detailed in the methods section.
References
Jackson, S. L. et al. National burden of heart failure events in the United States, 2006 to 2014. Circ. Heart Fail. 11, e004873 (2018).
Doelken, P., Huggins, J. T., Goldblatt, M., Nietert, P. & Sahn, S. A. Effects of coexisting pneumonia and end-stage renal disease on pleural fluid analysis in patients with hydrostatic pleural effusion. Chest 143, 1709–1716 (2013).
Yancy, C. W. et al. 2013 ACCF/AHA Guideline for the Management of Heart Failure: A Report of the American College of Cardiology Foundation/American Heart Association Task Force on Practice Guidelines. Circulation 128, https://doi.org/10.1161/CIR.0b013e31829e8776 (2013).
Werneburg, G. T. Catheter-associated urinary tract infections: current challenges and future prospects. Res. Rep. Urol. ume 14, 109–133 (2022).
Michalsen, A., Konig, G. & Thimme, W. Preventable causative factors leading to hospital admission with decompensated heart failure. Heart 80, 437–441 (1998).
Nasrabadi, M. Z., Tabibi, H., Salmani, M., Torkashvand, M. & Zarepour, E. A comprehensive survey on non-invasive wearable bladder volume monitoring systems. Med. Biol. Eng. Comput. 59, 1373–1402 (2021).
Byun, S.-S. et al. Accuracy of bladder volume determinations by ultrasonography: are they accurate over entire bladder volume range? Urology 62, 656–660 (2003).
Van Leuteren, P., Klijn, A., De Jong, T. & Dik, P. SENS-U: validation of a wearable ultrasonic bladder monitor in children during urodynamic studies. J. Pediatr. Urol. 14, 569.e1–569.e6 (2018).
Kwinten, W., Van Leuteren, P., Van Duren - Van Iersel, M., Dik, P. & Jira, P. SENS-U: continuous home monitoring of natural nocturnal bladder filling in children with nocturnal enuresis - a feasibility study. J. Pediatr. Urol. 16, 196.e1–196.e6 (2020).
Hafid, A. et al. State of the art of non-invasive technologies for bladder monitoring: a scoping review. Sensors 23, 2758 (2023).
Fong, D. D. et al. Restoring the sense of bladder fullness for spinal cord injury patients. Smart Health 9-10, 12–22 (2018).
Molavi, B., Shadgan, B., Macnab, A. J. & Dumont, G. A. Noninvasive optical monitoring of bladder filling to capacity using a wireless near infrared spectroscopy device. IEEE Trans. Biomed. Circuits Syst. 8, 325–333 (2014).
Macnab, A. J., Pourabbassi, P., Hakimi, N., Colier, W. N. J. M. & Stothers, L. A wearable optical sensor monitoring bladder urine volume to aid rehabilitation following spinal cord injury. in (eds Shadgan, B. & Gandjbakhche, A. H.) Biophotonics in Exercise Science, Sports Medicine, Health Monitoring Technologies, and Wearables IV, 1 https://www.spiedigitallibrary.org/conference-proceedings-of-spie/12375/2650381/A-wearable-optical-sensor-monitoring-bladder-urine-volume-to-aid/10.1117/12.2650381.full. (SPIE, San Francisco, United States, 2023).
Craig, J. C., Broxterman, R. M., Wilcox, S. L., Chen, C. & Barstow, T. J. Effect of adipose tissue thickness, muscle site, and sex on near-infrared spectroscopy derived total-[hemoglobin + myoglobin]. J. Appl. Physiol. 123, 1571–1578 (2017).
Shida, K. & Yagami, S. A non-invasive urination-desire sensing system based on four-electrodes impedance measurement method http://ieeexplore.ieee.org/document/4152957/. ISSN: 1553-572X (2006).
Li, Y. et al. Analysis of measurement electrode location in bladder urine monitoring using electrical impedance. Biomed. Eng. OnLine 18, 34 (2019).
Reichmuth, M., Schurle, S. & Magno, M. A non-invasive wearable bioimpedance system to wirelessly monitor bladder filling https://ieeexplore.ieee.org/document/9116378/ (2020).
Noyori, S. S., Nakagami, G. & Sanada, H. Non-invasive urine volume estimation in the bladder by electrical impedance-based methods: a review. Med. Eng. Phys. 101, 103748 (2022).
Grimnes, S. & Martinsen, O. G. Bioimpedance and bioelectricity basics (Elsevier Academic Press, 2008).
Schlebusch, T. & Leonhardt, S. Effect of electrode arrangements on bladder volume estimation by electrical impedance tomography. J. Phys. Conf. Ser. 434, 012080 (2013).
Adler, A. et al. GREIT: a unified approach to 2D linear EIT reconstruction of lung images. Physiol. Meas. 30, S35–S55 (2009).
Moore, C. M. Cirrhotic ascites review: pathophysiology, diagnosis and management. World J. Hepatol. 5, 251 (2013).
Kassanos, P. Bioimpedance sensors: a tutorial. IEEE Sens. J. 21, 22190–22219 (2021).
COMSOL Multiphysics® v. 6.0. https://www.comsol.com/support/knowledgebase/1223. COMSOL AB, Stockholm, Sweden.
Rosa, B. M. G. & Yang, G. Z. Bladder volume monitoring using electrical impedance tomography with simultaneous multi-tone tissue stimulation and DFT-Based impedance calculation inside an FPGA. IEEE Trans. Biomed. Circuits Syst. 14, 775–786 (2020).
Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 58, 267–288 (1996).
Schlebusch, T., Nienke, S., Leonhardt, S. & Walter, M. Bladder volume estimation from electrical impedance tomography. Physiol. Meas. 35, 1813–1823 (2014).
Leonhäuser, D. et al. Evaluation of electrical impedance tomography for determination of urinary bladder volume: comparison with standard ultrasound methods in healthy volunteers. Biomed. Eng. OnLine 17, 95 (2018).
Sun, J. et al. Bladder volume estimation using 3-D electrical impedance tomography based on fringe field sensing. IEEE Trans. Instrum. Meas. 72, 1–10 (2023).
Liang, X., Xu, L., Tian, W., Xie, Y. & Sun, J. Effect of stimulation patterns on bladder volume measurement based on fringe effect of EIT sensors https://ieeexplore.ieee.org/document/9010111/ (2019).
Brouwer, T. A., Van Den Boogaard, C., Van Roon, E. N., Kalkman, C. J. & Veeger, N. Non-invasive bladder volume measurement for the prevention of postoperative urinary retention: validation of two ultrasound devices in a clinical setting. J. Clin. Monit. Comput. 32, 1117–1126 (2018).
Sanchez-Perez, J. A. et al. A wearable multimodal sensing system for tracking changes in pulmonary fluid status, lung sounds, and respiratory markers. Sensors 22, 1130 (2022).
Mabrouk, S. et al. Robust longitudinal ankle edema assessment using wearable bioimpedance spectroscopy. IEEE Trans. Biomed. Eng. 67, 1019–1029 (2020).
Pennati, F. et al. Electrical impedance tomography: from the traditional design to the novel frontier of wearables. Sensors 23, 1182 (2023).
Baran, B. et al. Application of machine learning algorithms to the discretization problem in wearable electrical tomography imaging for bladder tracking. Sensors 23, 1553 (2023).
Dunne, E. Machine learning applied to electrical impedance tomography for the improved management of nocturnal enuresis. Ph.D. thesis, National University of Ireland Galway (2021).
Duongthipthewa, O., Uliss, P., Pattarasritanawong, P., Sukaimod, P. & Ouypornkochagorn, T. Analysis of current patterns to determine the bladder volume by electrical impedance tomography (eit) https://doi.org/10.1145/3397391.3397433 (2020).
Liu, K. et al. Investigation of bladder volume measurement based on fringe effect of electrical impedance tomography sensors. IEEE Open J. Instrum. Meas. 1, 1–10 (2022).
Kauppinen, P., Hyttinen, J. & Malmivuo, J. Sensitivity distribution visualizations of impedance tomography measurement strategies. Int. J. Bioelectromagnet. 8, 63–71 (2006).
Gil, L. Power Optimization Techniques for Low Power Signal Chain Applications https://www.analog.com/en/resources/analog-dialogue/articles/power-optimization-techniques-for-low-power-signal-chain-applications.html (2022).
Berarducci, M. Balancing ADC Size, Power, Resolution and Bandwidth in Precision Data-acquisition Systems https://www.ti.com/lit/ta/sszt111/sszt111.pdf?ts=1729799517826&ref_url=https%253A%252F%252Fwww.bing.com%252F (2021).
Nichols, C. J., Mabrouk, S. A., Ozmen, G. C., Gazi, A. H. & Inan, O. T. Validating adhesive-free bioimpedance of the leg in mid-activity and uncontrolled settings. IEEE Trans. Biomed. Eng. 70, 2679–2689 (2023).
Schlebusch, T. et al. Impedance ratio method for urine conductivity-invariant estimation of bladder volume. J. Electr. Bioimpedance 5, 48–54 (2014).
Yushkevich, P. A. et al. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. NeuroImage 31, 1116–1128 (2006).
Cancer Moonshot Biobank. Cancer Moonshot Biobank - Prostate Cancer Collection (CMB-PCA) https://wiki.cancerimagingarchive.net/x/EgGtBQ (2022).
Autodesk Fusion 360 v. 15.3.0.1657. https://www.autodesk.com/products/fusion-360. Autodesk, California, U.S.A.
Yadav, N., Parveen, S., Chakravarty, S. & Banerjee, M. Skin anatomy and morphology. in (eds Dwivedi, A., Agarwal, N., Ray, L. & Tripathi, A. K.) Skin Aging & Cancer, 1–10 http://link.springer.com/10.1007/978-981-13-2541-0_1. (Springer Singapore, 2019).
Pettersen, F.-J. & Høgetveit, J. O. From 3D tissue data to impedance using Simpleware ScanFE+IP and COMSOL Multiphysics - a tutorial. J. Electr. Bioimpedance 2, 13–32 (2011).
Miftahof, R. N. & Nam, H. G. Biomechanics of the Human Urinary Bladder https://doi.org/10.1007/978-3-642-36146-3. (Springer Berlin Heidelberg, Heidelberg, 2013).
Graham, S. D., Keane, T. E. & Glenn, J. F. (eds.) Glenn’s urologic surgery (Wolters Kluwer Health/Lippincott Williams & Wilkins, 2010).
IT’IS Foundation. Tissue Properties Database V4.1 https://itis.swiss/virtual-population/tissue-properties/downloads/database-v4-1/ (2022).
Gabriel, C. Compilation of the dielectric properties of body tissues at RF and microwave frequencies. Tech. Rep. Al/OE-TR-1996-0004, Occupational and Environmental Health Directorate, Radiofrequency Radiation Division, Brooks Air Force Base, Texas (USA) https://apps.dtic.mil/sti/citations/ADA303903 (1996).
Lin, F. et al. A comparative study of the electrodes gels’ electrical properties in the measurement issues of intrabody communication. Beijing Inst. Technol. 31, 71–80 (2022).
Khan, S. & Linganna, M. Diagnosis and management of ascites, spontaneous bacterial peritonitis, and hepatorenal syndrome. Clevel. Clin. J. Med. 90, 209–213 (2023).
Acknowledgements
The work was supported by Becton, Dickinson and Company. The funder played no role in study design, data collection, analysis and interpretation of data, or the writing of this manuscript.
Author information
Authors and Affiliations
Contributions
H.T.C.—conceptualization, methodology, simulation design, analysis, & writing (draft, review). J.A.B.—conceptualization, methodology, & writing (draft, review). S.M.—supervision, conceptualization, methodology, & writing (review). N.R.—conceptualization. O.T.I.—supervision, conceptualization, methodology, & writing (review). All authors have read and approved the revised manuscript.
Corresponding author
Ethics declarations
Competing interests
Two of the authors, Inan and Mabrouk, are co-founders of Arthroba Inc., a start-up commercializing wearable joint health monitoring technologies, such as bioimpedance, for knee health monitoring. While these technologies relevant to Arthroba are not related to the work presented here, we disclose this financial interest to be completely transparent. The other authors have no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Crane, H.T., Berkebile, J.A., Mabrouk, S. et al. Digital twin driven electrode optimization for wearable bladder monitoring via bioimpedance. npj Digit. Med. 8, 73 (2025). https://doi.org/10.1038/s41746-025-01441-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41746-025-01441-4