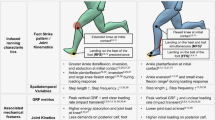
Abstract
Running biomechanics studies the mechanical forces experienced during running to improve performance and prevent injuries. This study presents the development of a digital twin for predicting bone stress in runners. The digital twin leverages a domain adaptation-based Long Short-Term Memory (LSTM) algorithm, informed by wearable sensor data, to dynamically simulate the structural behavior of foot bones under running conditions. Data from fifty participants, categorized as rearfoot and non-rearfoot strikers, were used to create personalized 3D foot models and finite element simulations. Two nine-axis inertial sensors captured three-axis acceleration data during running. The LSTM neural network with domain adaptation proved optimal for predicting bone stress in key foot bones—specifically the metatarsals, calcaneus, and talus—during the mid-stance and push-off phases (RMSE < 8.35 MPa). This non-invasive, cost-effective approach represents a significant advancement for precision health, contributing to the understanding and prevention of running-related fracture injuries.
Similar content being viewed by others
Introduction
Running frequently results in lower limb bone stress injuries due to its repetitive, weight-bearing nature. Epidemiological evidence suggests that annually, runners face injury incidence rates ranging between 24 and 77%1. Notably, stress fractures in the metatarsal bones, while accounting for up to 4% of all sports-related injuries2, are among the most common types of fractures observed in runners due to the repetitive impact on the forefoot during running1.
During running, the mid- to forefoot experiences high stress, particularly from mid-stance to push-off phases. Morphologically, metatarsal bones are characterized by their cylindrical shape and relatively thinner structure compared to other bones. This anatomical design is effective in facilitating the windlass mechanism, enhancing stability, and attenuating shock impact during loading3. However, this structural configuration also predisposes them to increased fracture risk. Mechanical loading on bones results in the accumulation of microdamage. A stress fracture occurs when a bone, subjected to high-stress magnitudes, cannot promptly repair this microstructural damage under intense cyclic loads4,5.
While bone staple strain gauges can quantify the stress experienced by bones, including the metatarsals6,7 and tibia8,9,10, their invasive nature makes them impractical for assessing and monitoring internal bone loading during running. Instead, mathematical and biomechanical modeling provides a feasible alternative for in silico load estimation. Beam theory-based reconstructions of bone models have been employed to evaluate stress in the second metatarsal11 and tibia12. However, these geometric models may oversimplify the mechanical complexities present in real-world scenarios. They often overlook shape deformations under stress and the interactions between soft tissue and bone13,14.
Conversely, surrogate finite element (FE) simulation provides a potentially more accurate biomechanical model for foot stress analysis in running, albeit being computationally intensive and time-consuming, particularly when developing models based on personalized geometries. This highlights a critical challenge in achieving both accuracy and efficiency in biomechanical modeling. Consequently, relevant research often faces a dilemma: either simplifying geometries or conducting case studies. This leads to a trade-off between developing a comprehensive FE model13,14 and undertaking pilot studies with limited statistical significance15. To overcome this limitation, the use of advanced techniques for high-fidelity and personalized reconstruction of lower limb musculoskeletal anatomy is promising16. This can be achieved by leveraging low-fidelity real-world measurements, such as those from inertial sensors or smartphone cameras, and integrating them with insights derived from neuromusculoskeletal simulations17.
In recent decades, data-driven approaches have gained significant popularity, largely due to advancements in computational capabilities and the refinement of machine learning algorithms. Deep learning algorithms, in particular, are increasingly favored in the field of running biomechanics, reflecting a shift from traditional laboratory-based investigations to real-world estimations17,18. The integration of various wearable sensors facilitates real-time evaluation, circumventing the need for conventional and cumbersome feature engineering processes. This approach has been applied in running to classify gait characteristics such as performance level19, foot posture20, and strike pattern21,22, and to predict sequential data, including metabolic energy expenditure23, ground reaction force24,25, joint kinematics26,27,28, and joint kinetics29,30,31.
In this context, one-dimensional convolutional neural network (CNN1D) and long short-term memory (LSTM) architectures have demonstrated strong capabilities in predicting time-series data for human activity recognition32,33, gait analysis30,34, and running biomechanics24,35. Temporal convolutional networks (TCN) are designed to extract temporal features for sequential data prediction and have proven highly effective in predict lower limb movements34. Recently, transformers, known for their use in natural language processing tasks such as machine translation and text generation, have been adapted for biomechanical applications36. Central to these transformers is the attention mechanism (AM), which has been integrated into bidirectional-LSTM architectures to estimate lower extremity kinematics during running, yielding promising results28.
Despite the considerable potential of data-driven methods in this field, most existing models focus on predicting external forces (e.g., ground reaction forces) or joint kinetics, which, while useful, do not fully capture internal mechanical stresses within bones. Overuse injuries, such as stress fractures, are primarily driven by repetitive internal bone stresses, which may not be directly inferred from joint kinetics or external forces alone. Previous studies have shown that external load metrics often exhibit weak correlations with internal tibial bone stress37,38, highlighting the need for direct stress estimations at the bone level. Understanding bone stresses in vivo is crucial for injury prevention, particularly in high-impact activities such as running, where excessive localized stress accumulation can lead to microdamage and stress fractures.
This study aims to bridge this gap by developing and validating a novel digital twin framework for predicting metatarsal bone stresses. In this study, a digital twin refers to a computational model that dynamically mirrors the biomechanical behavior of an individual’s foot during running, integrating real-time sensor data with subject-specific anatomical and mechanical properties to predict internal bone stresses39,40. The framework integrates personalized FE models, informed by statistical shape modeling (SSM) and free-form deformation (FFD) techniques, with deep learning predictions. The model is trained using wearable sensor accelerations as inputs and FE-predicted bone stresses as outputs. To comprehensively validate the framework, we evaluate its predictive performance across different foot strike patterns, specifically comparing rearfoot and non-rearfoot strikers. This approach enables precise estimation of stresses on key foot bones—specifically the metatarsals, talus, and calcaneus—thereby advancing the field of running biomechanics and contributing to more effective injury prevention strategies through the use of digital twin technology.
Results
The statistical analysis showed no significant differences in von Mises stress levels between rearfoot and non-rearfoot strikers during the mid-stance (Fig. 1a) and push-off (Fig. 1b) phases. Comparisons of the performance across the six selected models are presented in Supplementary Table 1, with LSTM + MLP exhibiting the highest accuracy. The model’s interpretability with different IMU sensor inputs is presented in Supplementary Fig. 1. The FE simulation results for the vertical compression-deformation relationship fell within the standard deviation of the experimental measurements, confirming the model’s validity. Table 1 details the accuracies of the predicted mean and peak von Mises stresses. During the mid-stance phase, the calcaneus (0.47 ± 0.29 MPa) and talus (1.14 ± 0.66 MPa) demonstrated lower prediction accuracy for mean bone stress, as measured by root mean squared error (RMSE), compared to M1-M5 (1.24 ± 0.77 MPa, 1.88 ± 1.13 MPa, 1.79 ± 1.07 MPa, 1.85 ± 1.11 MPa, and 2.16 ± 1.30 MPa, respectively). However, the mean MAPE was higher for the calcaneus and talus at 22.12%, compared to 16.17% for M1-M5. Predicted peak stresses for the calcaneus and talus showed slightly better accuracy in terms of MAE, RMSE, and MAPE (1.24 MPa, 1.30 MPa, and 8.77% respectively) compared to M1-M5 (3.79 MPa, 4.14 MPa, and 11.45% respectively).
The analysis showed that the peak bone stress accuracy, in terms of percentage error, generally surpassed that of mean bone pressure, with a significance level of p < 0.05 (see Table 1 and Fig. 2). The mean MAE and MAPE for peak stresses in M1-M5 during the push-off phase were 6.56 MPa and 11.45%, respectively. Figure 3 illustrates the Pearson correlation coefficient (r) and Bland-Altman plots comparing predicted stresses with reference von Mises stresses obtained from FE modeling.
Figure 4 depicts the comparison of prediction accuracy for rearfoot and non-rearfoot strikers during the mid-stance and push-off phases, using RMSE, r, and Bland-Altman plots. The results indicated consistency between the two groups, except for the von Mises stress in M1 and M4 (p = 0.005 and 0.03, respectively) during the mid-stance phase and for stresses in M2 and M3 (p = 0.026 and 0.049, respectively) during the push-off phase, where the non-rearfoot group presented smaller errors.
Discussion
The study presents a novel approach for predicting foot bone stress during running, utilizing wearable sensors combined with a domain adaptation-based LSTM algorithm. The stress data were derived from FE simulations, with models generated from foot scans coupled with FFD-based SSM. The findings showed promising results in predicting stresses in M1-M5, calcaneus, and talus during the mid-stance phase, as well as in M1-M5 during the push-off phase. Notably, the study achieved foot stress evaluation using low-cost and convenient sensors and scanners, underscoring its potential for future implementation.
Previous studies often simplified computational models11,12,13,14 or limited participant numbers15,41,42, potentially compromising statistical significance due to computational cost considerations. This study overcomes these limitations by reconstructing surrogate FE models for bone stress evaluation, utilizing comprehensive volumetric models based on detailed, person-specific geometries on foot and ankle joints without reducing the sample size. This was achieved through SSM coupled with FFD, as proposed and validated in a previous study43. Specifically, a 3D personalized foot-ankle model was built via SSM generation of the foot surface, which informs bone reconstruction based on FFD. The in-silico simulation results presented in this study are consistent with previous findings regarding second metatarsal stress14.
Research in biomechanics and sports medicine has sought to identify thresholds of bone stress that, when exceeded, increase the risk of injury, particularly stress fractures. These thresholds are often linked to repetitive loading cycles that exceed the bone’s capacity for repair, leading to microdamage accumulation4,44. In running biomechanics, metatarsal stress fractures are more likely when peak bone stress during repetitive impact loading consistently surpasses critical values, which can vary based on factors such as bone density, strain rate, and physical condition5. However, the precise identification of harmful bone stress thresholds remains an ongoing challenge4,5. Our model contributes to this effort by enabling real-time monitoring and prediction of bone stress levels, potentially establishing more personalized and accurate thresholds for runners. By accurately estimating bone stresses, these models can inform personalized training programs, reduce the risk of stress fractures, and enhance rehabilitation protocols through precise stress level control.
CNN, LSTM, and TCN have demonstrated strong capabilities in predicting biomechanical variables from time-series data, such as acceleration or joint kinematics18,31,45. For instance, kinematic and kinetic parameters have been investigated to predict tibial stress fracture in running46,47. LSTM, in particular, excels at capturing long-term dependencies in time-series data, outperforming self-attention-based transformers. This study demonstrated that integrating an LSTM-MLP model with domain adaptation-based transfer learning can enhance prediction performance. The proposed model accurately predicted peak stresses during the mid-stance phase of running, with an RMSE of 3.33 ± 1.5 and an r of 0.83 ± 0.04, and during the push-off phase, with an RMSE of 7.19 ± 1.17 and an r of 0.84 ± 0.02. Prior studies have focused on predicting joint contact forces to better understand bone stress variations during running31,48,49. Building on this foundation, the present study provides a significant and timely contribution to the existing body of evidence16,17,50,51 by demonstrating the potential of internal bone stress monitoring for predicting overuse running injuries.
This study demonstrated that the deep learning model was more accurate at predicting peak stresses than mean stresses, as evidenced by lower RMSE and MAPE values. This indicates that the proposed pipeline is particularly adept at detecting peak loading conditions on bones, rather than average loads. Zandbergen et al.37 reported no strong correlation between acceleration and internal tibial bone loads, while ground reaction force features also showed weak associations with tibial loads during running38. Together, these prior findings and our model’s superior accuracy in predicting peak stresses underscore the importance of peak characteristics in training data-driven algorithms to estimate internal bone loads. This aligns with fatigue failure theory, which identifies repeated peak stresses—rather than average loads—as primary contributors to microdamage accumulation and injury (e.g., stress fractures) under cyclic loading52. The proposed model’s ability to capture the relationship between acceleration and bone stress, a task where traditional methods often struggle, further highlights the utility of peak-focused approaches for injury risk prediction.
Physics-based methods often require significant simplifications, therefore reducing its reliability53. Our use of an ML model is justified by its ability to process large datasets and provide real-time predictions, crucial for practical, scalable applications in running biomechanics. This study underscores the strong generalizability of the proposed data-driven model for both rearfoot and non-rearfoot strikers. Different strike patterns exhibit varying biomechanical characteristics54, suggesting unique biodynamic adaptations for each. This study found that no statistical difference in peak stresses between rearfoot and non-rearfoot strike runners, which is consistent with previous findings11,14. However, ground reaction forces may differ between these cohorts, underlining the crucial role of personalized foot geometries in stress simulation. Internal loading, possibly adapted through mechanobiology, may not be accurately represented by external forces alone during running55. This gap is what machine learning technology or data-driven learning aims to bridge, as shown in this study and other recent studies31,56. Previous studies have utilized various data-driven approaches to project knee57 and ankle31 joint moments and contact forces, tibial bone loading56, and Achilles tendon stress58. To our knowledge, this is the first study to employ transfer learning-based deep learning with wearable technology for predicting internal foot loading. Our approach can be seamlessly integrated into current wearable sensor-based biomechanical assessments, offering a scalable solution that enhances personalized injury prevention and management, while paving the way for future research to explore its applicability across diverse populations and sports activities.
In our correlation analysis, we observed a systematic trend in the residuals, suggesting that the linear relationship may not fully capture the underlying data structure. This pattern indicates that the variance of the residuals might increase or decrease with the predicted values, meaning that the errors are not consistent across all levels of the independent variable. The presence of these trends underscores the importance of considering both correlation and agreement between predicted and actual values when evaluating model performance. This systematic bias could potentially lower the overall mean difference, which suggests that while the Pearson correlation indicates a strong linear relationship, there may be underlying issues with the model’s accuracy across the full range of data59. The observed bias highlights areas where the model could be refined, particularly in its ability to predict extreme values. Future work should focus on improving the model’s calibration across the entire data range, possibly by incorporating non-linear modeling techniques or adjusting the model to better account for the variability observed in the residuals.
Although this study presents promising findings, it also has limitations. As this study derived loading conditions from plantar pressure during barefoot running, future studies should incorporate footwear as a covariate to enhance the model’s applicability. Furthermore, training foot shape models under various weight-bearing conditions, such as different gait patterns and load distributions, could be beneficial, as it would introduce more variations into the dataset, potentially leading to more accurate and generalized models60. Future studies should also evaluate the performance and generalizability of the proposed approach in female runners to account for gender-specific biomechanical differences and broaden the applicability of the findings. Additionally, the running stance phases were simulated using three quasi-static models, which might oversimplify the FE models. Explicit modeling may more accurately represent foot-ankle biodynamics in future studies.
In summary, this study presents a cutting-edge predictive model for foot bone stress that leverages wearable sensors and LSTM with domain adaptation. The model offers a cost-effective and innovative alternative to traditional biomechanical analyses. Utilizing personalized 3D foot models, our approach achieves high accuracy in predicting foot bone stress during the stance phase, crucial for preventing injuries among runners. The model’s effectiveness across various running styles highlights its potential for personalized assessments. Despite its strengths, the study’s limitations underscore the need for further validation across a more diverse demographic. Overall, our findings represent a significant advancement in integrating machine learning with running biomechanics and clinical practice. This work contributes to digital health by providing accessible, data-driven insights for injury prevention in running, enhancing the potential for personalized healthcare solutions.
Methods
Participants
Following recommendations from a prior evidence-based study18, we recruited fifty male participants, comprising 38 rearfoot and 12 non-rearfoot strikers (age: 22.7 ± 3.9 years; height: 1.76 ± 0.06 m; mass: 67.7 ± 9.6 kg; BMI: 21.8 ± 2.7 kg/m2). Recruitment was facilitated via social media and by distributing posters in universities and running clubs. All participants in the study engaged in recreational running and maintained a minimum weekly mileage of 20 km. None had experienced musculoskeletal injuries in the lower limbs in the preceding six months. Participants were free to withdraw from the study at any time without providing a reason. In accordance with the Declaration of Helsinki, this study was approved by the ethics committee of Ningbo University (RAGH20201137), and written informed consent was obtained from all participants prior to the commencement of the experiments.
Data acquisition
Figure 5 provides an overview of the study’s flow diagram. Participants were given 10–15 min to warm up, which included running on a treadmill at a self-selected pace for a few minutes, followed by stretching exercises, familiarizing themselves with the experimental setting, and calibrating their running pace. Plantar pressure was captured using a Footscan® plate system (RSscan International, Belgium, frequency: 350 Hz), securely positioned at the center of a pathway. The design of the plate, with consistent surrounding dimensions, ensured optimal running comfort. Plantar pressure data were gathered using the mid-gait protocol61, in which participants ran at a self-selected speed. The starting position was adjusted to ensure accurate placement of the right foot on the sensor platform during the fourth step. The strike index, indicating a rearfoot striking pattern, was determined when the center of pressure was within 0–0.33 of the foot length at initial contact62. Additionally, two nine-axial inertial sensors (IMeasureU V1, New Zealand, frequency: 100 Hz, weight: 12 g) were affixed to the foot dorsum and distal anteromedial tibia. These sensors recorded three-axis acceleration data, which were synchronized with the plantar pressure measurements using a gait event detection algorithm63. Barefoot running was chosen to eliminate the influence of footwear on plantar pressure measurements and allow for a direct assessment of internal foot loading. Three appropriate trials were selected from the right foot (dominant side) based on consistent self-selected pace, confirmed foot strike pattern, and high data integrity, with complete and accurate plantar pressure and acceleration data.
a Acquisition of sensor data from the foot and ankle joint; b Generation of foot-ankle models from foot scans, informed by statistical shape modeling (SSM) coupled with free-form deformation (FFD); c Application of a data-driven approach, using inertial sensor data as inputs and bone stress as outputs; d Finite element simulation projects bone stress during the mid-stance and push-off phases of running. Note: IMU inertial measurement unit, SSM statistical shape modeling, PC principal component, FFD free-form deformation.
An Easy-Foot-Scan machine (OrthoBaltic, Lithuania) was utilized to capture the 3D surface contours of participants’ feet. During the scanning process, participants were instructed to stand still with their feet positioned shoulder-width apart, distributing their weight evenly between both legs, while placing the right foot on the scanner’s surface. This procedure adhered to a pre-established methodology64. The scanned foot surface data served as input for a pipeline combining SSM and FFD, as detailed in Xiang et al.43. A pre-trained statistical shape model, based on principal component analysis (PCA) with skin measurements as inputs, was employed to generate subject-specific foot surfaces. These surfaces were then used to reconstruct internal bone meshes via FFD. A summary diagram has been included in Supplementary Fig. 2 to further elucidate the process.
Foot and ankle joint computational modeling
Figure 6 illustrates the FE modeling and validation process. The following steps were taken to generate 3D meshes from 2D geometries in HyperMesh 2020 (Altair Engineering, Inc., Troy, USA): the soft tissue and inner bone surface were initially meshed using triangular elements (size: 3 mm). A volume Boolean operation was then performed to capture the encapsulated soft tissue geometry, which was meshed using tetrahedral elements (C3D4). Subsequently, bones were meshed as tetrahedral elements. A mesh convergence test was conducted to minimize discretization error and determine the appropriate mesh size. Mesh sizes tested ranged from 5 mm to 1 mm in 10% intervals65. The nodes and elements in these models varied between 53,000 to 56,000 and 273,000 to 278,000, respectively. The meshes were assembled in Abaqus 2022 (Simulia, Dassault Systèmes, USA). Models representing quasi-static gait phases were then simulated and solved.
a Geometry acquisition from foot scanning and reconstruction, informed by statistical shape modeling (SSM) coupled with free-form deformation (FFD); b Finite element simulation for the initial contact, mid-stance, and push-off phases during running, employing plantar pressure as the loading condition; c Model validation was performed by comparing vertical compression to displacement and by comparing plantar pressure during standing across five reconstructed models with experimental measurements.
The materials used to reconstruct the FE models were assumed to be homogeneous, isotropic, and linearly elastic (see Table 2). The Young’s modulus I and Poisson’s ratio (v) values were set at 7300 MPa and 0.3 for bones66, and 1.15 MPa and 0.45 for soft tissue41, respectively. Slip ring connectors were employed to represent plantar fascias, connecting and gliding between the medial and lateral processes of the calcaneal tuberosity and the base of the metatarsals42. The Achilles tendon force was calculated in OpenSim67 to represent the cumulative force from the soleus, medial, and lateral gastrocnemius muscles. Axial forces were applied to the posterior tuberosity of the calcaneus to simulate this Achilles tendon force. During simulations, the encapsulated soft tissue and bones were bound together using a tie constraint.
Plantar pressure was applied directly to the FE models as the loading condition. Plantar pressure during the initial contact, mid-stance, and push-off phases of the stance was measured separately from the toes, forefoot, midfoot, and rearfoot regions, as defined in the Footscan® software (Gait v7.0, RSScan International, Belgium). The boundary condition was set by fixing the 3D displacement of the proximal top of the models. The incremental effect was set to imitate the cumulative impact of gait following the initial contact and mid-stance phases. The FE simulation models were validated by comparing the vertical compression-deformation relationship and peak plantar pressure during standing (0.136 ± 0.01 MPa vs. 0.143 ± 0.01 MPa) between the simulation results from five participants and experimental measurements reported in a previous study68, as depicted in Fig. 6c.
Data-driven approaches
Three-axial acceleration data were normalized and padded to 300 data points, allocating 100 points for each phase: initial contact, mid-stance, and push-off. Consequently, the input features were defined as:
where \(x(t)\) is the concatenated vector at time step \(t\), \(T\) indicates the transpose operation applied to the vector \(x(t)\), and \({R}^{3* n}\) denotes a 3n-dimensional real space.
In this study, the number of sensors (n) was 2, and the output features \({y}_{t}\in \,{R}^{7+5}\). The response features comprised mean and maximum values of von Mises stresses for the calcaneus and talus at initial contact, the first to fifth metatarsals, calcaneus, and talus during the mid-stance phase, and the first to fifth metatarsals during the push-off phase, summing up to 28 features in total. Each feature from the input and output data was standardized by removing the mean and scaling to unit variance independently69. The mean and standard deviation, computed from the training/validation set, were utilized for centering and scaling the corresponding testing set to prevent data leakage.
The models were trained participant-wise and validated using a leave-one-out cross-validation approach. This practice ensures that data from the test set is not exposed during training, thereby guaranteeing robust generalization of the model.
For this investigation, six scenarios were designed for model training: TCN, CNN, LSTM, CNN + LSTM, LSTM + MLP (multilayer perceptron networks), and LSTM + AM. The selected architectures were chosen for their established effectiveness in biomechanical time-series prediction, computational efficiency, and suitability for short, high-frequency wearable sensor data. The formula for the forget gate in the LSTM model is expressed as:
where \(\sigma\) represents the sigmoid function, \({x}_{t}\) is the input, \({h}_{t-1}\) is the previous hidden state, \({W}_{f}\) is the weight matrix between the forget gate and input gate, and \({b}_{f}\) is the connection bias at time step \(t\). The equations for the cell state \({C}_{t}\) and hidden state \({h}_{t}\) are given by:
where \({i}_{t}\) is the input gate, \({\widetilde{C}}_{t}\) denotes the candidate for the cell state at time step \(t\), and \({o}_{t}\) represents the output gate.
A supervised domain adaptation algorithm was implemented to extract domain-invariant biomechanical features, enhancing model generalization and performance by designating the trained model as the source domain and the test dataset as the target domain70. In this framework, label prediction corresponds to estimating bone stress values, while domain classification helps distinguish data distributions between the source and target domains. The optimization follows an adversarial training strategy, where the model minimizes the task-specific loss (bone stress prediction) while maximizing the domain classification loss, thereby improving generalization across different subjects and running conditions. To achieve this, a Gradient Reversal Layer was integrated allowing the model to learn domain-invariant features that cannot be easily distinguished by the domain classifier. The objective function was optimized by identifying the saddle point:
where \({L}_{y}^{i}\) and \({L}_{d}^{i}\) represent the loss functions for label prediction and domain classification, respectively, estimated for the i-th training example. The architecture of the domain adaptation-based LSTM is depicted in Fig. 7. The deep learning models were developed using the Tensorflow framework (2.5.0) and trained on an Nvidia Tesla A100 GPU with 80 gigabytes of memory.
Hyperparameter tuning was conducted using Optuna 3.3.0, leveraging Bayesian hyperparameter optimization with the Tree-Structured Parzen Estimator algorithm. To enhance computing efficiency, each scenario underwent 100 trials, with early pruning of unpromising ones. The sampler initially operates as a random sampler, recording hyperparameter settings and objective values from previous trials. It then suggests hyperparameter values for subsequent trials based on the past promising past results. Hyperparameters, including the optimizer, learning rate, activation function, drop rate, epochs, batch size, convolutional layers, MLP layers, LSTM units, numbers of TCN filters, TCN dilations, convolutional kernel size, and dense units, were fine-tuned to achieve optimal solutions across different scenarios. The results for hyperparameter tuning are shown in Supplementary Table 2. Attention mechanisms were employed to enhance interpretability by identifying the most critical features in the sensor data for stress prediction. Specifically, weights from the bidirectional LSTM were fed into a self-attention layer, and the resulting scores were normalized and visualized. Evaluation metrics, including the Pearson’s product-moment correlation coefficient (r), mean squared error, RMSE, mean error (ME), mean absolute error (MAE) and mean absolute percentage error (MAPE), were calculated to estimate the prediction performance by comparing the FE-derived reference values with the predictive values on the test sets.
Statistical analysis
An independent t-test was conducted to assess the statistical differences in peak von Mises stress between rearfoot and non-rearfoot strikers. This comparison was included to validate the framework’s ability to detect biomechanically meaningful differences between distinct gait patterns. Additionally, we compared the predictive accuracy of peak stresses between rearfoot and non-rearfoot strikers using RMSE. When the Shapiro-Wilk test indicated a violation of the normality assumption, the Wilcoxon rank-sum test was employed for statistical analysis. The significance level was set at p < 0.05.
The performance of the predictive model was evaluated by calculating Pearson’s correlation coefficient (r) to assess the strength of the linear relationship between predicted and actual bone stresses, and by generating Bland-Altman plots to examine the agreement between these values. The Bland-Altman analysis involved calculating the mean difference and the limits of agreement (mean difference ± 1.96 SD) to identify any systematic errors or trends across the range of observed data.
Data availability
The statistical shape models used in this study are freely available at https://doi.org/10.5281/zenodo.13297928. The finite element models are freely available at https://simtk.org/projects/foot3d-model. All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Code availability
The statistical modeling algorithms and codes are available at: https://github.com/musculoskeletal/gias3. The code for model training is available at: https://github.com/Biomechicshub/Bone_stressPred.
References
van Mechelen, W. Running injuries: a review of the epidemiological literature. Sports Med. 14, 320–335 (1992).
Chuckpaiwong, B., Cook, C., Pietrobon, R. & Nunley, J. A. Second metatarsal stress fracture in sport: comparative risk factors between proximal and non-proximal locations. Br. J. Sports Med. 41, 510–514 (2007).
Welte, L. et al. The extensibility of the plantar fascia influences the windlass mechanism during human running. Proc. R. Soc. B 288, 20202095 (2021).
Hoenig, T. et al. Bone stress injuries. Nat. Rev. Dis. Primers 8, 1–20 (2022).
Warden, S. J., Davis, I. S. & Fredericson, M. Management and prevention of bone stress injuries in long-distance runners. J. Orthop. Sports Phys. Ther. 44, 749–765 (2014).
Arndt, A., Ekenman, I., Westblad, P. & Lundberg, A. Effects of fatigue and load variation on metatarsal deformation measured in vivo during barefoot walking. J. Biomech. 35, 621–628 (2002).
Milgrom, C. et al. Metatarsal strains are sufficient to cause fatigue fracture during cyclic overloading. Foot Ankle Int. 23, 230–235 (2002).
Burr, D. B. et al. In vivo measurement of human tibial strains during vigorous activity. Bone 18, 405–410 (1996).
Milgrom, C. et al. In vivo strains at the middle and distal thirds of the tibia during exertional activities. Bone Rep. 16, 101170 (2022).
Milgrom, C. et al. The effect of muscle fatigue on in vivo tibial strains. J. Biomech. 40, 845–850 (2007).
Ellison, M. A., Kenny, M., Fulford, J., Javadi, A. & Rice, H. M. Incorporating subject-specific geometry to compare metatarsal stress during running with different foot strike patterns. J. Biomech. 105, 109792 (2020).
Rice, H. M. et al. Tibial stress during running following a repeated calf-raise protocol. Scand. J. Med. Sci. Sports 30, 2382–2389 (2020).
Ellison, M. A., Akrami, M., Fulford, J., Javadi, A. A. & Rice, H. M. Three dimensional finite element modelling of metatarsal stresses during running. J. Med. Eng. Technol. 44, 368–377 (2020).
Ellison, M. A., Fulford, J., Javadi, A. & Rice, H. M. Do non-rearfoot runners experience greater second metatarsal stresses than rearfoot runners? J. Biomech. 126, 110647 (2021).
Xiang, L. et al. Evaluating function in the hallux valgus foot following a 12-week minimalist footwear inteasparagusrvention: a pilot computational analysis. J. Biomech. 132, 110941 (2022).
Fernandez, J. et al. A narrative review of personalized musculoskeletal modeling using the Physiome and Musculoskeletal Atlas Projects. J. Appl. Biomech 39, 304–317 (2023).
Lloyd, D. G., Jonkers, I., Delp, S. L. & Modenese, L. The history and future of neuromusculoskeletal biomechanics. J. Appl. Biomech. 39, 273–283 (2023).
Xiang, L. et al. Recent machine learning progress in lower limb running biomechanics with wearable technology: a systematic review. Front. Neurorob. 16, 913052 (2022).
Liu, Q. et al. Classification of runners’ performance levels with concurrent prediction of biomechanical parameters using data from inertial measurement units. J. Biomech. 112, 110072 (2020).
Xiang, L. et al. Foot pronation prediction with inertial sensors during running: a preliminary application of data-driven approaches. J. Hum. Kinet. 88, 29–40 (2023).
Xiang, L. et al. Automatic classification of barefoot and shod populations based on the foot metrics and plantar pressure patterns. Front. Bioeng. Biotechnol. 10, 843204 (2022).
Tan, T., Strout, Z. A., Cheung, R. T. H. & Shull, P. B. Strike index estimation using a convolutional neural network with a single, shoe-mounted inertial sensor. J. Biomech. 139, 111145 (2022).
Slade, P., Kochenderfer, M. J., Delp, S. L. & Collins, S. H. Sensing leg movement enhances wearable monitoring of energy expenditure. Nat. Commun. 12, 4312 (2021).
Tan, T., Strout, Z. A. & Shull, P. B. Accurate impact loading rate estimation during running via a subject-independent convolutional neural network model and optimal IMU placement. IEEE J. Biomed. Health Inf. 25, 1215–1222 (2020).
Alcantara, R. S., Edwards, W. B., Millet, G. Y. & Grabowski, A. M. Predicting continuous ground reaction forces from accelerometers during uphill and downhill running: A recurrent neural network solution. PeerJ 10, e12752 (2022).
Hernandez, V., Dadkhah, D., Babakeshizadeh, V. & Kulić, D. Lower body kinematics estimation from wearable sensors for walking and running: a deep learning approach. Gait Posture 83, 185–193 (2021).
Gholami, M., Napier, C. & Menon, C. Estimating lower extremity running gait kinematics with a single accelerometer: a deep learning approach. Sensors 20, 2939 (2020).
Rezaie Zangene, A. et al. An efficient attention-driven deep neural network approach for continuous estimation of knee joint kinematics via sEMG signals during running. Biomed. Signal. Process. Control 86, 105103 (2023).
Mundt, M. et al. Prediction of ground reaction force and joint moments based on optical motion capture data during gait. Med. Eng. Phys. 86, 29–34 (2020).
Siu, H. C., Sloboda, J., McKindles, R. J. & Stirling, L. A. A neural network estimation of ankle torques from electromyography and accelerometry. IEEE Trans. Neural Syst. Rehabil. Eng. 29, 1624–1633 (2021).
Xiang, L. et al. Integrating an LSTM framework for predicting ankle joint biomechanics during gait using inertial sensors. Comput. Biol. Med. 170, 108016 (2024).
Ronao, C. A. & Cho, S. B. Human activity recognition with smartphone sensors using deep learning neural networks. Expert Syst. Appl. 59, 235–244 (2016).
Ordóñez, F. J. & Roggen, D. Deep convolutional and LSTM recurrent neural networks for multimodal wearable activity recognition. Sensors 16, 115 (2016).
Bin Hossain, M. S., Guo, Z. & Choi, H. Estimation of lower extremity joint moments and 3D ground reaction forces using IMU sensors in multiple walking conditions: a deep learning approach. IEEE J. Biomed. Health. Inf. 27, 2829–2849 (2023).
Johnson, W. R. et al. Multidimensional ground reaction forces and moments from wearable sensor accelerations via deep learning. IEEE Trans. Biomed. Eng. 68, 289–297 (2021).
Vaswani, A. et al. Attention is all you need, 31st Conference on Neural Information Processing Systems (NeurIPS 2017). (Long. Beach. CA, USA, 2017).
Zandbergen, M. A. et al. Peak tibial acceleration should not be used as indicator of tibial bone loading during running. Sports Biomech. 1, 1–18 (2023).
Matijevich, E. S., Branscombe, L. M., Scott, L. R. & Zelik, K. E. Ground reaction force metrics are not strongly correlated with tibial bone load when running across speeds and slopes: Implications for science, sport and wearable tech. PLoS ONE 14, e0210000 (2019).
Grieves, M. Digital twin: manufacturing excellence through virtual factory replication. White Paper 1, 1–7 (2014).
Lloyd, D. G. et al. Maintaining soldier musculoskeletal health using personalised digital humans, wearables and/or computer vision. J. Sci. Med. Sport 26, S30–S39 (2023).
Cheung, J. T.-M., Zhang, M. & An, K. N. Effects of plantar fascia stiffness on the biomechanical responses of the ankle-foot complex. Clin. Biomech. 19, 839–846 (2004).
Wong, D. Wai-Chi, Wang, Y., Zhang, M. & Leung, A. Kam-Lun Functional restoration and risk of non-union of the first metatarsocuneiform arthrodesis for hallux valgus: a finite element approach. J. Biomech. 48, 3142–3148 (2015).
Xiang, L. et al. A hybrid statistical morphometry free-form deformation approach to 3D personalized foot-ankle models. J. Biomech. 168, 112120 (2024).
Burr, D. B. Why bones bend but don’t break. J. Musculoskelet. Neuronal Interact. 11, 270–285 (2011).
Halilaj, E. et al. Machine learning in human movement biomechanics: best practices, common pitfalls, and new opportunities. J. Biomech. 81, 1–11 (2018).
Milner, C. E., Ferber, R., Pollard, C. D., Hamill, J. & Davis, I. S. Biomechanical factors associated with tibial stress fracture in female runners. Med. Sci. Sports Exerc. 38, 323–328 (2006).
Pohl, M. B., Mullineaux, D. R., Milner, C. E., Hamill, J. & Davis, I. S. Biomechanical predictors of retrospective tibial stress fractures in runners. J. Biomech. 41, 1160–1165 (2008).
Sasimontonkul, S., Bay, B. K. & Pavol, M. J. Bone contact forces on the distal tibia during the stance phase of running. J. Biomech. 40, 3503–3509 (2007).
Ferber, R., Osis, S. T., Hicks, J. L. & Delp, S. L. Gait biomechanics in the era of data science. J. Biomech. 49, 3759–3761 (2016).
Rahlf, A. L. et al. A machine learning approach to identify risk factors for running-related injuries: study protocol for a prospective longitudinal cohort trial. BMC Sports Sci. Med. Rehabil. 14, 75 (2022).
Saxby, D. J. et al. Machine learning methods to support personalized neuromusculoskeletal modelling. Biomech. Model. Mechanobiol. 19, 1169–1185 (2020).
Romani, W. A., Gieck, J. H., Perrin, D. H., Saliba, E. N. & Kahler, D. M. Mechanisms and management of stress fractures in physically active persons. J. Athl. Train. 37, 306–314 (2002).
Matijevich, E. S., Scott, L. R., Volgyesi, P., Derry, K. H. & Zelik, K. E. Combining wearable sensor signals, machine learning and biomechanics to estimate tibial bone force and damage during running. Hum. Mov. Sci. 74, 102690 (2020).
Lieberman, D. E. et al. Foot strike patterns and collision forces in habitually barefoot versus shod runners. Nature 463, 531–535 (2010).
Xiang, L. et al. Rethinking running biomechanics: a critical review of ground reaction forces, tibial bone loading, and the role of wearable sensors. Front. Bioeng. Biotechnol. 12, 1377383 (2024).
Elstub, L. J. et al. Tibial bone forces can be monitored using shoe-worn wearable sensors during running. J. Sports Sci. 40, 1741–1749 (2022).
Boswell, M. A. et al. A neural network to predict the knee adduction moment in patients with osteoarthritis using anatomical landmarks obtainable from 2D video analysis. Osteoarthritis Cartilage 29, 346–356 (2021).
Martin, J. A. & Thelen, D. G. A trained neural network model accurately predicts Achilles tendon stress during walking and running based on shear wave propagation. J. Biomech. 157, 111699 (2023).
Giavarina, D. Understanding Bland Altman analysis. Biochem. Med. 25, 141–151 (2015).
Schuster, R. W., Cresswell, A. & Kelly, L. Reliability and quality of statistical shape and deformation models constructed from optical foot scans. J. Biomech. 115, 110137 (2021).
Wearing, S. C., Urry, S., Smeathers, J. E. & Battistutta, D. A comparison of gait initiation and termination methods for obtaining plantar foot pressures. Gait Posture 10, 255–263 (1999).
Altman, A. R. & Davis, I. S. A kinematic method for footstrike pattern detection in barefoot and shod runners. Gait Posture 35, 298–300 (2012).
Aubol, K. G. & Milner, C. E. Foot contact identification using a single triaxial accelerometer during running. J. Biomech. 105, 109768 (2020).
Xiang, L., Mei, Q., Fernandez, J. & Gu, Y. Minimalist shoes running intervention can alter the plantar loading distribution and deformation of hallux valgus: a pilot study. Gait Posture 65, 65–71 (2018).
Henninger, H. B., Reese, S. P., Anderson, A. E. & Weiss, J. A. Validation of computational models in biomechanics. Proc. Inst. Mech. Eng., Part H: J. Eng. Med. 224, 801–812 (2010).
Nakamura, S., Crowninshield, R. D. & Cooper, R. R. An analysis of soft tissue loading in the foot-A preliminary report. Bull. Prosthet. Res. 10, 27–34 (1981).
Delp, S. L. et al. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 54, 1940–1950 (2007).
Cheung, J. T.-M., Zhang, M. & An, K.-N. Effect of Achilles tendon loading on plantar fascia tension in the standing foot. Clin. Biomech. 21, 194–203 (2006).
Kettaneh, N., Berglund, A. & Wold, S. PCA and PLS with very large data sets. Comput. Stat. Data Anal. 48, 69–85 (2005).
Ganin, Y. et al. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 17, 2030–2096 (2016).
Acknowledgements
We acknowledge the support from the Zhejiang Province Science Fund for Distinguished Young Scholars (LR22A020002), the Key R&D Program of Zhejiang Province (2021C03130), the National Key Research and Development Program of China (2024YFC3607300), the Ningbo key R&D Program (2022Z196), and the China Scholarship Council (L.X. and Z.G.).
Author information
Authors and Affiliations
Contributions
Conceptualization: L.X., Y.G., and J.F.; Methodology: L.X., V.S., A.W., and J.F.; Investigation: L.X., Z.G., and K.D.; Visualization: L.X. and K.D.; Validation: L.X., Z.G., A.W., and J.F.; Supervision: V.S., A.W., and J.F.; Writing—original draft: L.X.; Writing—review & editing: V.S., A.W., Y.G., and J.F.; Funding acquisition: Y.G. All authors have read and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Xiang, L., Gu, Y., Deng, K. et al. Integrating personalized shape prediction, biomechanical modeling, and wearables for bone stress prediction in runners. npj Digit. Med. 8, 276 (2025). https://doi.org/10.1038/s41746-025-01677-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41746-025-01677-0