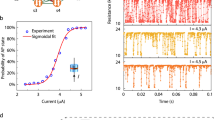
Abstract
Probabilistic Ising machines could be used to solve computationally hard problems more efficiently than deterministic algorithms on von Neumann computers. Stochastic magnetic tunnel junctions are potential entropy sources for such Ising machines. However, scaling up stochastic magnetic tunnel junction probabilistic Ising machines requires the fine control of a small magnetic energy barrier and duplication of area-intensive digital-to-analogue converter elements across large numbers of devices. The non-spintronic components of these machines are also typically created using general-purpose processors or field-programmable gate arrays. Here we report a probabilistic computer that is based on an application-specific integrated circuit fabricated using 130-nm foundry complementary metal–oxide–semiconductor technology and uses voltage-controlled magnetic tunnel junctions as its entropy source. With the system, we implement integer factorization as a representative hard optimization problem using probabilistic Ising-machine-based invertible logic gates created with 1,143 probabilistic bits. The application-specific integrated circuit uses stochastic bit sequences read from an adjacent voltage-controlled magnetic tunnel junction chip. The magnetic tunnel junctions are thermally stable in the absence of a voltage and synchronously generate random bits without the use of digital-to-analogue converter elements using the voltage-controlled magnetic anisotropy effect.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
Source data are provided with this paper. Other data that support the plots in this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Finocchio, G. et al. The promise of spintronics for unconventional computing. J. Magn. Magn. Mater. 521, 167506 (2021).
Finocchio, G. et al. Roadmap for unconventional computing with nanotechnology. Nano Futur. 8, 012001 (2023).
Kalinin, K. P. & Berloff, N. G. Large-scale sustainable search on unconventional computing hardware. Preprint at https://arxiv.org/abs/2104.02553 (2021).
Borders, W. A. et al. Integer factorization using stochastic magnetic tunnel junctions. Nature 573, 390–393 (2019).
Mohseni, N., McMahon, P. L. & Byrnes, T. Ising machines as hardware solvers of combinatorial optimization problems. Nat. Rev. Phys. 4, 363–379 (2022).
Aadit, N. A. et al. Massively parallel probabilistic computing with sparse Ising machines. Nat. Electron. 5, 460–468 (2022).
Newell, G. F. & Montroll, E. W. On the theory of the Ising model of ferromagnetism. Rev. Mod. Phys. 25, 353 (1953).
Griffiths, R. B. Correlations in Ising ferromagnets. I. J. Math. Phys. 8, 478–483 (1967).
Okuyama, T., Hayashi, M. & Yamaoka, M. An Ising computer based on simulated quantum annealing by path integral Monte Carlo method. In 2017 IEEE International Conference on Rebooting Computing (ICRC) 1–6 (IEEE, 2017).
Zhang, T. et al. A review of Ising machines implemented in conventional and emerging technologies. IEEE Trans. Nanotechnol. 23, 1–4 (2024).
Yoshimura, C. et al. Implementation and evaluation of FPGA-based annealing processor for Ising model by use of resource sharing. Int. J. Netw. Comput. 7, 154–172 (2017).
Okuyama, T. et al. Binary optimization by momentum annealing. Phys. Rev. E 100, 012111 (2019).
Goto, H., Lin, Z. & Nakamura, Y. Boltzmann sampling from the Ising model using quantum heating of coupled nonlinear oscillators. Sci. Rep. 8, 7154 (2018).
Kanao, T. & Goto, H. High-accuracy Ising machine using Kerr-nonlinear parametric oscillators with local four-body interactions. npj Quantum Inf. 7, 18 (2021).
Marandi, A., Wang, Z., Takata, K., Byer, R. L. & Yamamoto, Y. Network of time-multiplexed optical parametric oscillators as a coherent Ising machine. Nat. Photon. 8, 937–942 (2014).
Okawachi, Y. et al. Demonstration of chip-based coupled degenerate optical parametric oscillators for realizing a nanophotonic spin-glass. Nat. Commun. 11, 4119 (2020).
Tezak, N. et al. Integrated coherent Ising machines based on self-phase modulation in microring resonators. IEEE J. Sel. Topics Quantum Electron. 26, 5900115 (2019).
Lo, H., Moy, W., Yu, H., Sapatnekar, S. & Kim, C. H. An Ising solver chip based on coupled ring oscillators with a 48-node all-to-all connected array architecture. Nat. Electron. 6, 771–778 (2023).
Cilasun, H. et al. A coupled-oscillator-based Ising chip for combinatorial optimization. Nat. Electron. 8, 537–546 (2025).
Mallick, A. et al. Using synchronized oscillators to compute the maximum independent set. Nat. Commun. 11, 4689 (2020).
Bashar, M. K., Lin, Z. & Shukla, N. Stability of oscillator Ising machines: not all solutions are created equal. J. Appl. Phys. 134, 144901 (2023).
Bashar, M. K., Li, Z., Narayanan, V. & Shukla, N. An FPGA-based max-k-cut accelerator exploiting oscillator synchronization model. In 2024 25th International Symposium on Quality Electronic Design (ISQED) 1–8 (IEEE, 2024).
Tatsumura, K., Dixon, A. R. & Goto, H. FPGA‑based simulated bifurcation machine. In 2019 International Conference on Field Programmable Logic and Applications (FPL) 59–66 (IEEE, 2019).
Tatsumura, K. et al. Scaling out Ising machines using a multi-chip architecture for simulated bifurcation. Nat. Electron. 4, 208–217 (2021).
Kashimata, T., Yamasaki, M., Hidaka, R. & Tatsumura, K. Efficient and scalable architecture for multiple‑chip implementation of simulated bifurcation machines. IEEE Access 12, 36606–36621 (2024).
Litvinenko, A. et al. A spinwave Ising machine. Commun. Phys. 6, 227 (2023).
Litvinenko, A., Khymyn, R., Ovcharov, R. & Åkerman, J. A 50-spin surface acoustic wave Ising machine. Commun. Phys. 8, 58 (2023).
Camsari, K. Y., Sutton, B. M. & Datta, S. P-bits for probabilistic spin logic. Appl. Phys. Rev. 6, 011305 (2019).
Kaiser, J. & Datta, S. Probabilistic computing with p-bits. Appl. Phys. Lett. 119, 150503 (2021).
Grimaldi, A. Evaluating spintronics-compatible implementations of Ising machines. Phys. Rev. Appl. 20, 024005 (2023).
Si, J. et al. Energy-efficient superparamagnetic Ising machine and its application to traveling salesman problems. Nat. Commun. 15, 3457 (2024).
Singh, N. S. et al. CMOS plus stochastic nanomagnets enabling heterogeneous computers for probabilistic inference and learning. Nat. Commun. 15, 2685 (2024).
Hamerly, R. et al. Experimental investigation of performance differences between coherent Ising machines and a quantum annealer. Sci. Adv. 5, eaau0823 (2019).
Weinberg, P. et al. Scaling and diabatic effects in quantum annealing with a D-wave device. Phys. Rev. Lett. 124, 090502 (2020).
Shao, Y. et al. Probabilistic computing with voltage-controlled dynamics in magnetic tunnel junctions. Nanotechnology 34, 495203 (2023).
Aadit, N. A. et al. Computing with invertible logic: combinatorial optimization with probabilistic bits. In 2021 IEEE International Electron Devices Meeting (IEDM) 40–43 (IEEE, 2021).
Grimaldi, A. et al. Spintronics-compatible approach to solving maximum-satisfiability problems with probabilistic computing, invertible logic, and parallel tempering. Phys. Rev. Appl. 17, 024052 (2022).
Chowdhury, S., Camsari, K. Y. & Datta, S. Accelerated quantum monte carlo with probabilistic computers. Commun. Phys. 6, 85 (2023).
Fukushima, A. et al. Recent progress in random number generator using voltage pulse-induced switching of nano-magnet: a perspective. APL Mater. 9, 030905 (2021).
Shao, Y. & Khalili Amiri, P. Progress and application perspectives of voltage-controlled magnetic tunnel junctions. Adv. Mater. Technol. 8, 2300676 (2023).
Sutton, B., Camsari, K. Y., Behin-Aein, B. & Datta, S. Intrinsic optimization using stochastic nanomagnets. Sci. Rep. 7, 44370 (2017).
Camsari, K. Y. et al. From charge to spin and spin to charge: stochastic magnets for probabilistic switching. Proc. IEEE 108, 1322–1337 (2020).
Lv, Y., Bloom, R. P. & Wang, J.-P. Experimental demonstration of probabilistic spin logic by magnetic tunnel junctions. IEEE Magn. Lett. 10, 4510905 (2019).
Camsari, K. Y., Faria, R., Sutton, B. M. & Datta, S. Stochastic p-bits for invertible logic. Phys. Rev. X 7, 031014 (2017).
Camsari, K. Y., Salahuddin, S. & Datta, S. Implementing p-bits with embedded MTJ. IEEE Electron Device Lett. 38, 1767–1770 (2017).
Ikeda, S. et al. A perpendicular-anisotropy CoFeB–MgO magnetic tunnel junction. Nat. Mater. 9, 721–724 (2010).
Worledge, D. et al. Spin torque switching of perpendicular Ta|CoFeB|MgO-based magnetic tunnel junctions. Appl. Phys. Lett. 98, 022501 (2011).
Khalili Amiri, P. et al. Switching current reduction using perpendicular anisotropy in CoFeB–MgO magnetic tunnel junctions. Appl. Phys. Lett. 98, 112507 (2011).
Maruyama, T. et al. Large voltage-induced magnetic anisotropy change in a few atomic layers of iron. Nat. Nanotechnol. 4, 158–161 (2009).
Amiri, P. K. & Wang, K. L. Voltage-controlled magnetic anisotropy in spintronic devices. Spin 2, 1240002 (2012).
Shao, Y. et al. Sub-volt switching of nanoscale voltage-controlled perpendicular magnetic tunnel junctions. Commun. Mater. 3, 87 (2022).
Aggarwal, S. et al. Demonstration of a reliable 1 Gb standalone spin-transfer torque MRAM for industrial applications. In 2019 IEEE International Electron Devices Meeting (IEDM) 2.1.1–2.1.4 (IEEE, 2019).
Parkin, S., More, N. & Roche, K. Oscillations in exchange coupling and magnetoresistance in metallic superlattice structures: Co/Ru, Co/Cr, and Fe/Cr.Phys. Rev. Lett. 64, 2304 (1990).
Rukhin, A. et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications Vol. 22 (US Department of Commerce, Technology Administration, National Institute of Standards and Technology, 2001).
Clark, L. T. et al. Asap7: a 7-nm FinFET predictive process design kit. Microelectron. J. 53, 105–115 (2016).
Efabless. Caravel Revision 43d0ce33. GitHub https://github.com/efabless/caravel (2022).
Skywater. Skywater foundry standard cell libraries. https://skywater-pdk.readthedocs.io/en/main/contents/libraries/ (2020).
Bohr, M. Moore’s law leadership. In Intel Technology and Manufacturing Day (Intel, 2017).
Lee, H. et al. Array-level analysis of magneto-electric random-access memory for high-performance embedded applications. IEEE Magn. Lett. 8, 4305905 (2017).
Krizakova, V. et al. Field-free switching of magnetic tunnel junctions driven by spin–orbit torques at sub-ns timescales. Appl. Phys. Lett. 116, 232406 (2020).
Acknowledgements
This work was supported by the US National Science Foundation (NSF) under award nos. 2322572 (P.K.A.), 2425538 (P.K.A.), 2311296 (P.K.A.), 2311295 (K.Y.C.) and 2400463 (P.K.A.), and by a gift from Nokia Corporation (P.K.A.). We thank Canon ANELVA Corporation for part of the work on magnetic thin-film deposition and characterization. E.R. and G.F. acknowledge financial support from the project PRIN 2020LWPKH7 funded by the Italian Ministry of Universities and Research (MUR) and the PETASPIN Association (www.petaspin.com). E.R. also acknowledges the project PON Capitale Umano (CIR_00030) funded by the MUR.
Author information
Authors and Affiliations
Contributions
P.K.A. initiated the project and conceived the idea with contributions from Y.S., E.R., C.D., J.A., G.F. and K.Y.C. C.D. and J.A. designed the ASIC chip, implemented the RNG board, and performed the related testing and simulations. P.K.A. designed the V-MTJ devices with contributions from Y.S. N.D.M. and J.A.K. fabricated the V-MTJ devices. C.D., J.A. and P.K.A. wrote the manuscript with contributions from other authors. All authors discussed the results, contributed to the data analysis and commented on the manuscript. C.D. and J.A. contributed equally to this work. The study was performed under the leadership of P.K.A.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Electronics thanks Brandon Zink, Daisuke Suzuki and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Revised ASIC PIM experimental results.
Frequency plot for the end state of experimental factorization attempts of the 24-bit semiprime 12,441,691 on the second ASIC which utilized the modified p-bit mapping. For readability, both orderings of each factor pair are treated as a single data point, of which the correct solution pair of 3119 and 3989 appears in a plurality of trials. A CMOS-based random number generator integrated within the PIM design area was used to generate the necessary pseudo-random numbers. The temperature was kept constant at a value of 4, over the approximately 0.8 s of convergence during each trial.
Extended Data Fig. 2 Parallel design data flow block diagram.
Data flow block diagram of a probabilistic Ising machine (PIM) with parallel updates of 5 p-bit groups, corresponding to the best possible colouring of the graph. As with the serially updating version, the input equation for each probabilistic bit (p-bit) is calculated as its h value added to a J-vector scaled sum of other p-bit values. In contrast to the serially updating version, a probabilistic logic unit (PLU) exists for every collection of at most 5 p-bits, with a p-bit of each group assigned to every PLU. If a completely even distribution is impossible, then a small number of PLUs will have less than 5 p-bits assigned and consequently be inactive for the missing p-bit group’s clock cycle.
Extended Data Fig. 3 Parallel-updating p-bit results.
a Plot of the proportions of simulated factorization trials of the 20-bit semiprime 894,479 for which the correct factor pair of 883 and 1013 was found for different parallelization sizes. The bottom axis describes the count of groups of p-bits which update simultaneously. The leftmost point has a group for each updating p-bit and thus no parallelization, while the rightmost point has 5 p-bit groups, equivalent to the best colouring of the connectivity graph. The top axis describes the number of non-input p-bits within each group if they were evenly distributed, however the connectivity structure prevents a perfectly even distribution. Temperature was linearly swept between 20 and 4 with a timeout of 223 iterations. Each datapoint represents 100 trials. b The number of iterations needed to achieve a 10% probability of finding the solution in each trial of the same problem. Each datapoint represents the minimum trial timeout length when at least 20 of 200 trials found the solution pair when iterations were increased from 0 with a 5,000-iteration step size. Temperature was linearly swept between 20 and 4.
Extended Data Fig. 4 Scaling projections.
a Approximate scaling of the count of probabilistic bits (p-bits) that can be integrated per 1 mm2 area at various node sizes. As the number of p-bits increases, their proportion of the total area approaches unity, so the area of other components can be neglected in the large number of p-bits limit. This is done for the Intel and SkyWater (SKY130) p-bit projection, in which self-reported transistor and routed gate densities are compared to synthesized designs for a random 5-connected p-bit from the factorization ASIC. The SKY130 6-20-bit factorizer plot represents the density of the manufactured design, which is low due to lack of tight density constraints applied during synthesis. The Cadence 45 nm Generic PDK (GPDK) and Arizona State Predictive PDK (ASAP) points are routed designs created using Cadence Genus and Innovus. b Projected problem size (number of bits) that can be implemented at various node sizes, considering the SkyWater and Intel reported densities for a 10 mm2 and 25 mm2 design area, respectively.
Extended Data Fig. 5 Parallelization projection.
Projected relative increase in the area, update rate, and update rate to area ratio of parallelized versions of the 80-bit factorizer design compared to a synthesized serial version on an ASAP 7 nm node. Integrated V-MTJ for random number generation and an approximately equal distribution of probabilistic bits (p-bits) to each group is assumed.
Supplementary information
Supplementary Information
Supplementary Notes 1 and 2, Figs. 1–4 and Table 1.
Source data
Source Data Fig. 1
Statistical source data.
Source Data Fig. 5
Statistical source data.
Source Data Extended Data Fig./Table 1
Statistical source data.
Source Data Extended Data Fig./Table 3
Statistical source data.
Source Data Extended Data Fig./Table 4
Statistical source data.
Source Data Extended Data Fig./Table 5
Statistical source data.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Duffee, C., Athas, J., Shao, Y. et al. An integrated-circuit-based probabilistic computer that uses voltage-controlled magnetic tunnel junctions as its entropy source. Nat Electron 8, 784–793 (2025). https://doi.org/10.1038/s41928-025-01439-6
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41928-025-01439-6
This article is cited by
-
Probabilistic computers based on digital logic and magnetic nanodevices
Nature Electronics (2025)